Voltage Regulation of an Isolated DC Microgrid with a Constant Power Load: A Passivity-based Control Design
Abstract
:1. Introduction
- Design of a global controller (primary and secondary controller included) using a unique nonlinear approach to satisfy the desired performance of MG under CPL effects.
- Estimation of the unknown load from an energy-based observer, reducing the total number of sensors.
- Simulations and experimental validation of the designed controller using a realistic MG prototype and comparison with a classical technique.
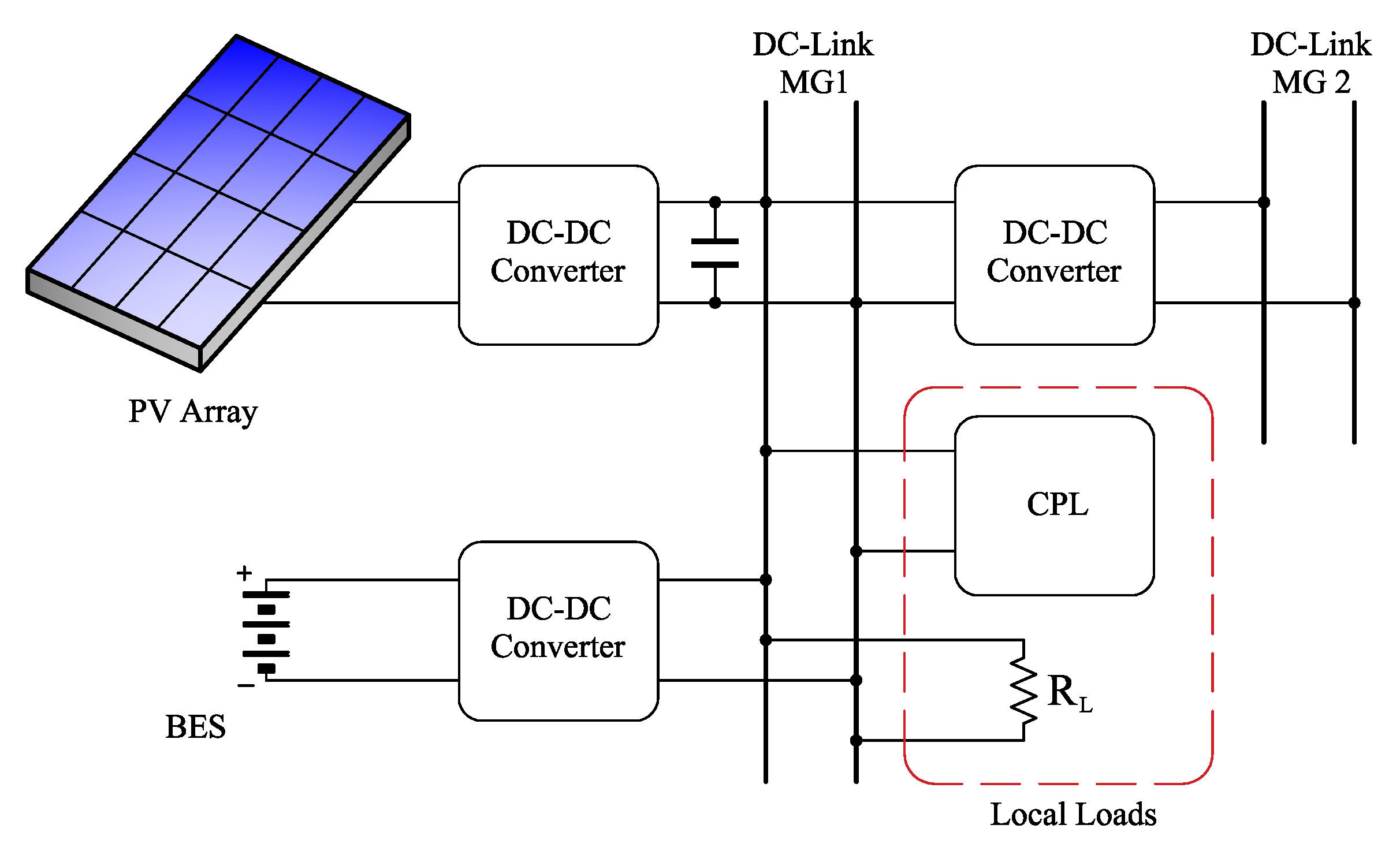
2. Modeling of the Microgrid
3. IDA-PBC Control
Load Power Estimation
4. Results
4.1. Simulation Results
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Goel, S.; Sharma, R. Performance evaluation of stand alone, grid connected and hybrid renewable energy systems for rural application: A comparative review. Renew. Sustain. Energy Rev. 2017, 78, 1378–1389. [Google Scholar] [CrossRef]
- Montoya, O.D.; Serra, F.M.; De Angelo, C.H. On the Efficiency in Electrical Networks with AC and DC Operation Technologies: A Comparative Study at the Distribution Stage. Electronics 2020, 9, 1352. [Google Scholar] [CrossRef]
- Singh, S.; Gautam, A.R.; Fulwani, D. Constant power loads and their effects in DC distributed power systems: A review. Renew. Sustain. Energy Rev. 2017, 72, 407–421. [Google Scholar] [CrossRef]
- Kumar, D.; Zare, F.; Ghosh, A. DC Microgrid Technology: System Architectures, AC Grid Interfaces, Grounding Schemes, Power Quality, Communication Networks, Applications, and Standardizations Aspects. IEEE Access 2017, 5, 12230–12256. [Google Scholar] [CrossRef]
- Vásquez, L.O.P.; Ramírez, V.M.; Thanapalan, K. A Comparison of Energy Management System for a DC Microgrid. Appl. Sci. 2020, 10, 1071. [Google Scholar] [CrossRef] [Green Version]
- Xu, Q.; Zhang, C.; Wen, C.; Wang, P. A Novel Composite Nonlinear Controller for Stabilization of Constant Power Load in DC Microgrid. IEEE Trans. Smart Grid 2019, 10, 752–761. [Google Scholar] [CrossRef]
- Pang, S.; Nahid-Mobarakeh, B.; Pierfederici, S.; Phattanasak, M.; Huangfu, Y.; Luo, G.; Gao, F. Interconnection and Damping Assignment Passivity-Based Control Applied to On-Board DC–DC Power Converter System Supplying Constant Power Load. IEEE Trans. Ind. Appl. 2019, 55, 6476–6485. [Google Scholar] [CrossRef]
- Esteban, F.D.; Serra, F.M.; De Angelo, C.H. Control of a DC-DC Dual Active Bridge Converter in DC Microgrids Applications. IEEE Lat. Am. Trans. 2021, 19, 1261–1269. [Google Scholar] [CrossRef]
- Magaldi, G.L.; Serra, F.M.; De Angelo, C. IDA-PBC control of an isolated microgrid used as electric vehicle charging station. In Proceedings of the 2017 XVII Workshop on Information Processing and Control (RPIC), Mar del Plata, Argentina, 20–22 September 2017. [Google Scholar] [CrossRef]
- Zeng, J.; Zhang, Z.; Qiao, W. An Interconnection and Damping Assignment Passivity-Based Controller for a DC–DC Boost Converter With a Constant Power Load. IEEE Trans. Ind. Appl. 2014, 50, 2314–2322. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Garces, A.; Serra, F.; Hernández, J.C. Stabilization of MT-HVDC grids via passivity-based control and convex optimization. Electr. Power Syst. Res. 2021, 196, 107273. [Google Scholar] [CrossRef]
- Wei, J.; Zhang, Y.; Wang, J.; Wu, L. Distribution LMP-Based Demand Management in Industrial Park via a Bi-Level Programming Approach. IEEE Trans. Sustain. Energy 2021, 12, 1695–1706. [Google Scholar] [CrossRef]
- Merabet, A.; Tawfique Ahmed, K.; Ibrahim, H.; Beguenane, R.; Ghias, A.M.Y.M. Energy Management and Control System for Laboratory Scale Microgrid Based Wind-PV-Battery. IEEE Trans. Sustain. Energy 2017, 8, 145–154. [Google Scholar] [CrossRef]
- Elmouatamid, A.; Ouladsine, R.; Bakhouya, M.; El Kamoun, N.; Khaidar, M.; Zine-Dine, K. Review of Control and Energy Management Approaches in Micro-Grid Systems. Energies 2021, 14, 168. [Google Scholar] [CrossRef]
- Yan, H.W.; Narang, A.; Tafti, H.D.; Farivar, G.G.; Pou, J. Reduced Battery Usage in a Hybrid Battery and Photovoltaic Stand-Alone DC Microgrid with Flexible Power Point Tracking. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 11–15 October 2020. [Google Scholar] [CrossRef]
- Yan, H.W.; Farivar, G.G.; Tafti, H.D.; Ceballos, S.; Pou, J. Simplified Hybrid Control Strategy for Stand-Alone DC Microgrid with Photovoltaic System to Extend Battery Lifespan. In Proceedings of the 2021 IEEE 12th Energy Conversion Congress Exposition-Asia (ECCE-Asia), Singapore, 24–27 May 2021. [Google Scholar] [CrossRef]
- Montoya, O.D. Numerical Approximation of the Maximum Power Consumption in DC-MGs With CPLs via an SDP Model. IEEE Trans. Circuits Syst. II Express Briefs 2019, 66, 642–646. [Google Scholar] [CrossRef]
- De Bessa, I.V.; de Medeiros, R.L.P.; Bessa, I.; Ayres Junior, F.A.C.; de Menezes, A.R.; Torres, G.M.; Chaves Filho, J.E. Comparative Study of Control Strategies for Stabilization and Performance Improvement of DC Microgrids with a CPL Connected. Energies 2020, 13, 2663. [Google Scholar] [CrossRef]
- Hassan, M.A.; Li, E.P.; Li, X.; Li, T.; Duan, C.; Chi, S. Adaptive Passivity-Based Control of dc–dc Buck Power Converter With Constant Power Load in DC Microgrid Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 2029–2040. [Google Scholar] [CrossRef]
- Herrera, L.; Zhang, W.; Wang, J. Stability Analysis and Controller Design of DC Microgrids With Constant Power Loads. IEEE Trans. Smart Grid 2017, 8, 881–888. [Google Scholar] [CrossRef]
- AL-Nussairi, M.K.; Bayindir, R.; Padmanaban, S.; Mihet-Popa, L.; Siano, P. Constant Power Loads (CPL) with Microgrids: Problem Definition, Stability Analysis and Compensation Techniques. Energies 2017, 10, 1656. [Google Scholar] [CrossRef]
- Dragičević, T. Dynamic Stabilization of DC Microgrids With Predictive Control of Point-of-Load Converters. IEEE Trans. Power Electron. 2018, 33, 10872–10884. [Google Scholar] [CrossRef] [Green Version]
- Chang, X.; Li, Y.; Li, X.; Chen, X. An Active Damping Method Based on a Supercapacitor Energy Storage System to Overcome the Destabilizing Effect of Instantaneous Constant Power Loads in DC Microgrids. IEEE Trans. Energy Convers. 2017, 32, 36–47. [Google Scholar] [CrossRef]
- Solsona, J.A.; Gómez Jorge, S.; Busada, C.A. Nonlinear Control of a Buck Converter Which Feeds a Constant Power Load. IEEE Trans. Power Electron. 2015, 30, 7193–7201. [Google Scholar] [CrossRef]
- Hassan, M.A.; Su, C.L.; Chen, F.Z.; Lo, K.Y. Adaptive Passivity-Based Control of DC–DC Boost Power Converter Supplying Constant Power and Constant Voltage Loads. IEEE Trans. Ind. Electron. 2021. [Google Scholar] [CrossRef]
- Ortega, R.; Loría, A.; Nicklasson, P.J.; Sira-Ramírez, H. Passivity-Based Control of Euler-Lagrange Systems; Springer: London, UK, 1998. [Google Scholar] [CrossRef]
- Ortega, R.; van der Schaft, A.; Maschke, B.; Escobar, G. Interconnection and damping assignment passivity-based control of port-controlled Hamiltonian systems. Automatica 2002, 38, 585–596. [Google Scholar] [CrossRef] [Green Version]
- Serra, F.M.; De Angelo, C.H. IDA-PBC controller design for grid connected Front End Converters under non-ideal grid conditions. Electr. Power Syst. Res. 2017, 142, 12–19. [Google Scholar] [CrossRef]
- Soriano-Rangel, C.A.; He, W.; Mancilla-David, F.; Ortega, R. Voltage Regulation in Buck–Boost Converters Feeding an Unknown Constant Power Load: An Adaptive Passivity-Based Control. IEEE Trans. Control Syst. Technol. 2020, 8, 5053–5064. [Google Scholar] [CrossRef]
- He, W.; Ortega, R. Design and Implementation of Adaptive Energy Shaping Control for DC–DC Converters with Constant Power Loads. IEEE Trans. Ind. Informat. 2020, 16, 5053–5064. [Google Scholar] [CrossRef]
- Ravada, B.R.; Tummuru, N.R. Control of a Supercapacitor-Battery-PV Based Stand-Alone DC-Microgrid. IEEE Trans. Energy Convers. 2020, 35, 1268–1277. [Google Scholar] [CrossRef]
- Mojallizadeh, M.R.; Badamchizadeh, M.A. Adaptive Passivity-Based Control of a Photovoltaic/Battery Hybrid Power Source via Algebraic Parameter Identification. IEEE J. Photovolt. 2016, 6, 532–539. [Google Scholar] [CrossRef]
- Dòria-Cerezo, A.; Espinosa-Pérez, G.; Batlle, C. Passivity-based control of a wound-rotor synchronous motor. IET Control Theory Appl. 2010, 4, 2049–2057. [Google Scholar] [CrossRef]
- Binkowski, T. A Conductance-Based MPPT Method with Reduced Impact of the Voltage Ripple for One-Phase Solar Powered Vehicle or Aircraft Systems. Energies 2020, 13, 1496. [Google Scholar] [CrossRef] [Green Version]
- Serra, F.M.; De Angelo, C.H.; Forchetti, D.G. Interconnection and damping assignment control of a three-phase front end converter. Int. J. Electr. Power Energy Syst. 2014, 60, 317–324. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
| and | 2.5 mH |
| 540 F | |
| and | 0.3 |
| (UC and BC) | 20 kHz |
| PV array | 2 × 260 Wp |
| BES type, | Lead-acid, 6×12 V |
| CPL | 300–600 W |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magaldi, G.L.; Serra, F.M.; de Angelo, C.H.; Montoya, O.D.; Giral-Ramírez, D.A. Voltage Regulation of an Isolated DC Microgrid with a Constant Power Load: A Passivity-based Control Design. Electronics 2021, 10, 2085. https://doi.org/10.3390/electronics10172085
Magaldi GL, Serra FM, de Angelo CH, Montoya OD, Giral-Ramírez DA. Voltage Regulation of an Isolated DC Microgrid with a Constant Power Load: A Passivity-based Control Design. Electronics. 2021; 10(17):2085. https://doi.org/10.3390/electronics10172085
Chicago/Turabian StyleMagaldi, Guillermo Luciano, Federico Martin Serra, Cristian Hernán de Angelo, Oscar Danilo Montoya, and Diego Armando Giral-Ramírez. 2021. "Voltage Regulation of an Isolated DC Microgrid with a Constant Power Load: A Passivity-based Control Design" Electronics 10, no. 17: 2085. https://doi.org/10.3390/electronics10172085
APA StyleMagaldi, G. L., Serra, F. M., de Angelo, C. H., Montoya, O. D., & Giral-Ramírez, D. A. (2021). Voltage Regulation of an Isolated DC Microgrid with a Constant Power Load: A Passivity-based Control Design. Electronics, 10(17), 2085. https://doi.org/10.3390/electronics10172085









