FPGA Implementation of the Range-Doppler Algorithm for Real-Time Synthetic Aperture Radar Imaging
Abstract
:1. Introduction
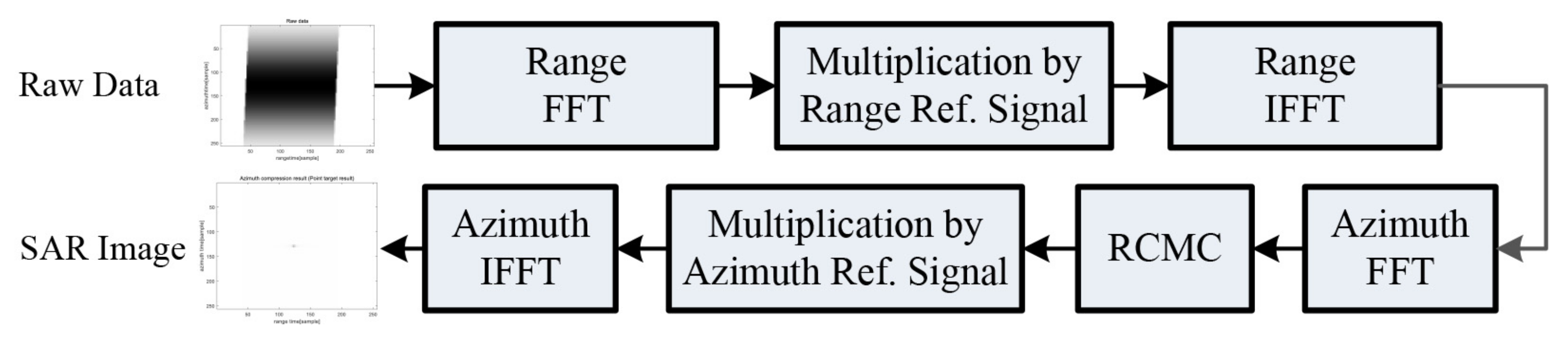
2. Range-Doppler Algorithm
3. Proposed Hardware Architecture
3.1. Matched Filtering Unit (MFU)
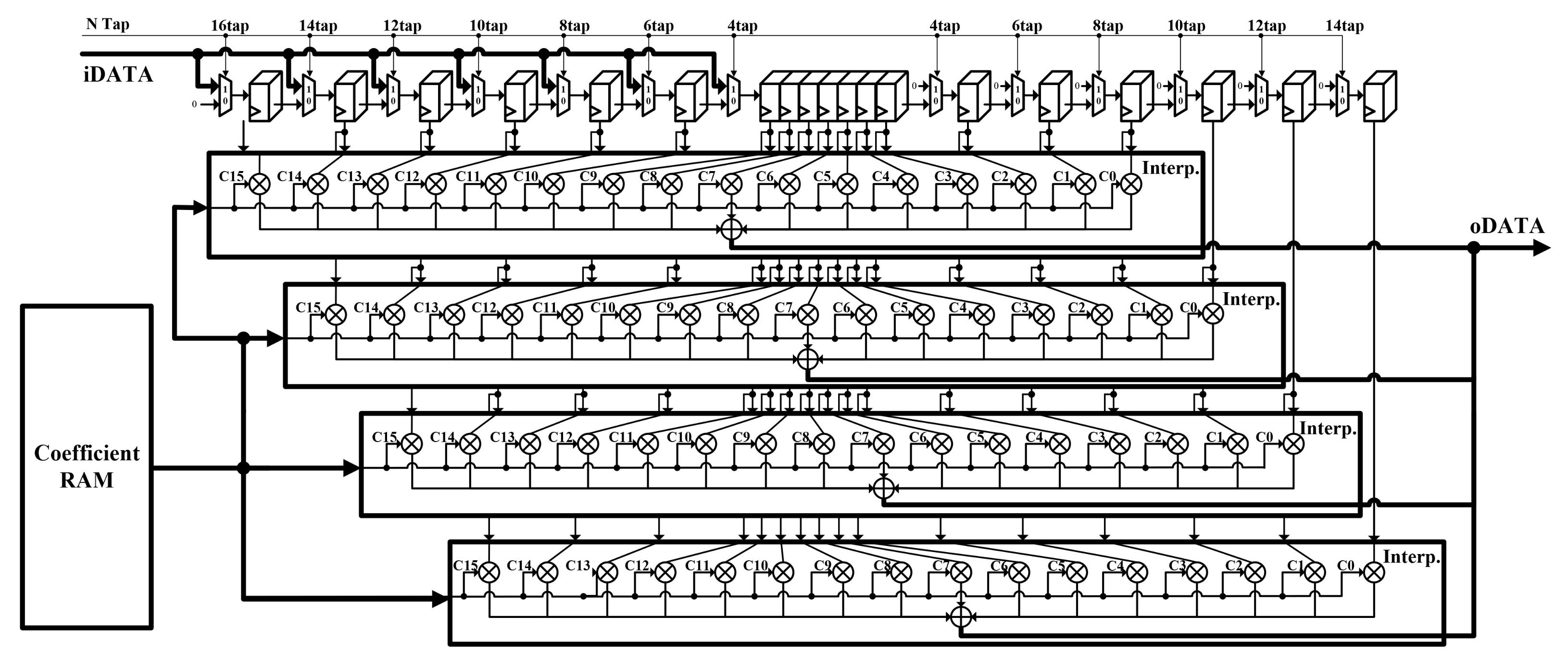
3.2. Range Cell Migration Correction Processing Unit (RPU)
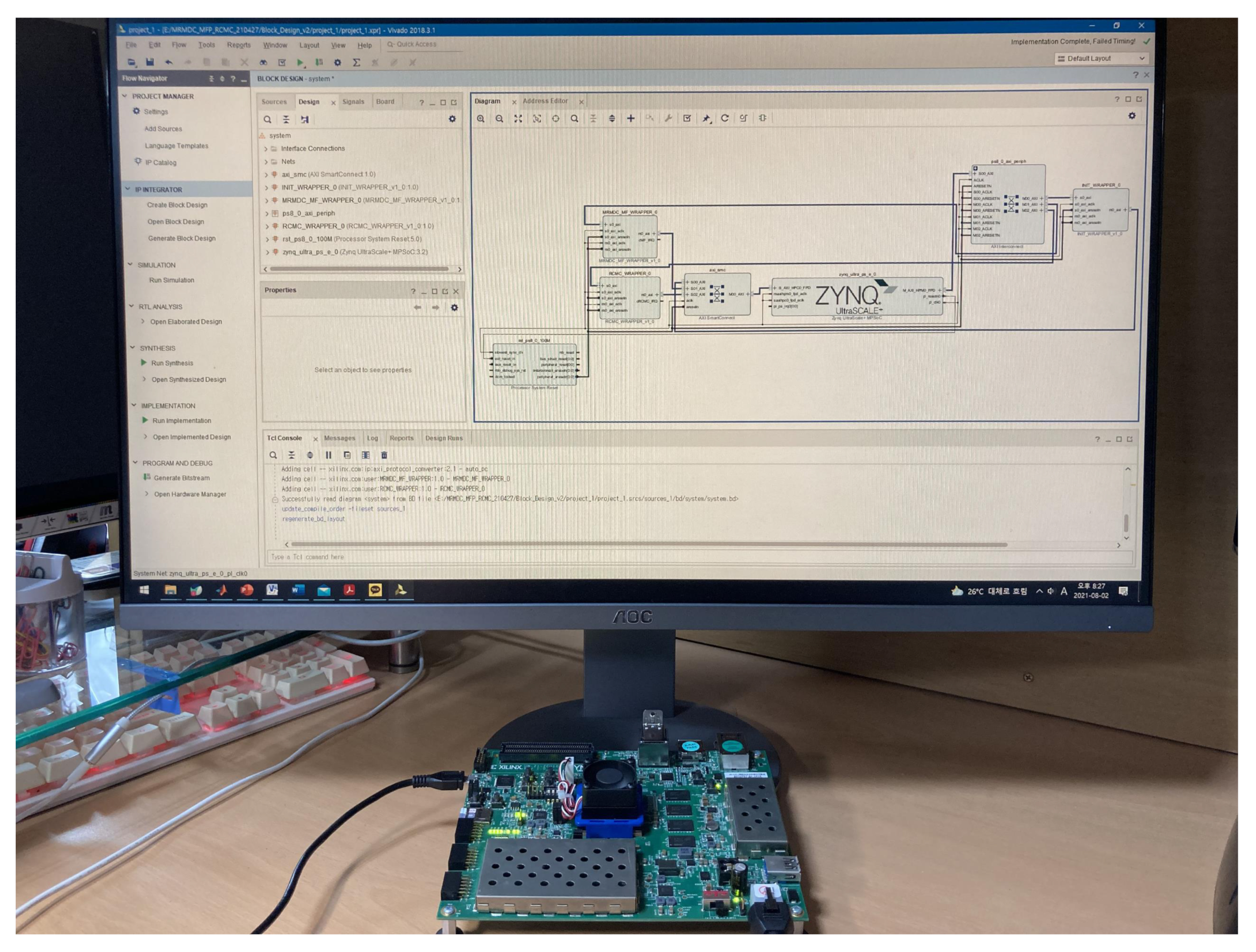
4. Implementation and Acceleration Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chan, Y.K.; Koo, V.C. An introduction to synthetic aperture radar (SAR). Prog. Electromagn. Res. B 2008, 3, 27–60. [Google Scholar] [CrossRef] [Green Version]
- Soumekh, M. Synthetic Aperture Radar Signal Processing with MATLAB Algorithms; Wiley Interscience: New York, NY, USA, 1999. [Google Scholar]
- Quegan, S. Spotlight synthetic aperture radar: Signal processing algorithms. J. Atmos. Sol.-Terr. Phys 1997, 59, 597–598. [Google Scholar] [CrossRef]
- Curlander, J.C.; McDonough, R.N. Synthetic Aperture Radar: Systems and Signal Processing; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Kim, S.M.; Jeon, S.Y.; Kim, J.B.; Lee, U.M.; Shin, S.H.; Choi, Y.W.; Ka, M.H. Multichannel W-Band SAR System on a Multirotor UAV Platform With Real-Time Data Transmission Capabilities. IEEE Access 2020, 8, 144413–144431. [Google Scholar] [CrossRef]
- Deguchi, T.; Sugiyama, T.; Kishimoto, M. R&D of drone-borne SAR system. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2/W13, 263–267. [Google Scholar]
- Zhu, C.; Guan, Y. Study of ground moving target parameters estimation and imaging for Mini-SAR. In Proceedings of the International Conference on Image, Vision and Computing (ICIVC), Chengdu, China, 2–4 June 2017; pp. 587–591. [Google Scholar]
- Edwards, M.; Madsen, D.; Stringham, C.; Margulis, A.; Wicks, B.; Long, D.G. MicroASAR: A small, robust LFM-CW SAR for operation on UAVS and small aircraft. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Boston, MA, USA, 7–11 July 2008; Volume 5, pp. 514–517. [Google Scholar]
- Essen, H.; Stanko, S.; Sommer, R.; Johannes, W.; Wahlen, A.; Wilcke, J.; Hantscher, S. Millimetre Wave SAR for UAV Operation. In Proceedings of the 2011 Asia-Pacific Microwave Conference, Melbourne, Australia, 5–8 December 2011. [Google Scholar]
- Zaugg, E.C.; Hudson, D.L.; Long, D.G. The BYU μSAR: A Small, Student–Built SAR for UAV Operation. In Proceedings of the 2006 IEEE International Symposium on Geoscience and Remote Sensing, Denver, CO, USA, 31 July–4 August 2006. [Google Scholar]
- Hang, L.; Sheng, J.; Xing, M.; Qiao, Z.; Xiong, T.; Bao, Z. Wavenumber-Domain Autofocusing for Highly Squint UAV SAR imagery. IEEE Sens. J. 2012, 12, 1574–1588. [Google Scholar]
- Britton, A.; Joynson, D. An all weather millimetre wave imaging radar for UAVs. Aeronaut. J. 2001, 105, 609–612. [Google Scholar] [CrossRef]
- Gebrehiwot, A.A.; Hashemi-Beni, L. Three-Dimensional Inundation Mapping Using UAV Image Segmentation and Digital Surface Model. ISPRS Int. J. Geo-Inform. 2021, 10, 144. [Google Scholar] [CrossRef]
- Bimber, O.; Kurmi, I.; Schedl, D.C. Synthetic Aperture Imaging With Drones. IEEE Comput. Graph. Appl. 2019, 39, 8–15. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.W.; Keon, S.K.; Ok, J.W.; You, E.N.; Kim, D.J.; Sim, Y.W.; Lee, D.H. Real-Time Image Reconstruction for Compact Drone-Borne SAR using GPU Signal Processing. J. Korean Inst. Electromagn. Eng. Sci. 2019, 30, 780–783. [Google Scholar] [CrossRef]
- Shao, Y.F.; Wang, R.; Deng, Y.K.; Liu, Y.; Chen, R.; Liu, G.; Loffeld, O. Fast Backprojection Algorithm for Bistatic SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1080–1084. [Google Scholar] [CrossRef]
- Araujo, G.F.; d’Amore, R.; Fernandes, D. Cost-sensitive FPGA implementation of SAR range-doppler algorithm. IEEE Aerosp. Electron. Syst. Mag. 2018, 33, 54–68. [Google Scholar] [CrossRef]
- Hou, N.; Zhang, D.; Du, G.; Song, Y. An FPGA-based multi-core system for synthetic aperture radar data processing. In Proceedings of the International Conference on Anti-Counterfeiting, Security and Identification (ASID), Macao, China, 12–14 December 2014. [Google Scholar]
- Hossain, M.A.; Elshafiey, I.; Alkanhal, M.A.; Mabrouk, A. Real-time implementation of UWB-OFDM synthetic aperture radar imaging. In Proceedings of the IEEE International Conference on Signal and Image Processing Applications (ICSIPA), Kuala Lumpur, Malaysia, 16–18 November 2011. [Google Scholar]
- Duarte, R.P.; Cruz, H. Reconfigurable Accelerator for On-Board SAR Imaging Using the Backprojection Algorithm. In International Symposium on Applied Reconfigurable Computing; Springer: Berlin/Heidelberg, Germany, 2020; pp. 392–401. [Google Scholar]
- Crasto, N.; Kumar, T.K.; Anuradha, D.; Barua, P.; Nemani, S. FPGA implementation of back projection algorithm for radar imaging. In Proceedings of the International Conference on Radar, Ottawa, ON, Canada, 29 April–3 May 2013; pp. 97–100. [Google Scholar]
- Hettiarachchi, D.L.N.; Balster, E. Fixed Point Processing of the SAR Back Projection Algorithm on FPGA. TechRxiv 2021. Preprint. [Google Scholar]
- Wang, D.; Zhu, D.; Liu, R. Video SAR High-speed Processing Technology Based on FPGA. In Proceedings of the IEEE MTT-S International Microwave Biomedical Conference (IMBioC), Nanjing, China, 6–8 May 2019; Volume 1, pp. 1–4. [Google Scholar]
- Li, W.; Xu, Z.; Zhu, D. The FPGA implementation of real-time spotlight SAR imaging. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 6703–6706. [Google Scholar]
- Zhu, D.; Zhang, J.; Mao, X.; Zhang, Y.; Wang, X.; Li, Y.; Ding, Y.; Guo, J.; Shi, J. A miniaturized high resolution SAR processor using FPGA. In Proceedings of the EUSAR 2016: 11th European Conference on Synthetic Aperture Radar, Hamburg, Germany, 6–9 June 2016; pp. 1–4. [Google Scholar]
- Linchen, Z.; Jindong, Z.; Daiyin, Z. FPGA implementation of polar format algorithm for airborne spotlight SAR processing. In Proceedings of the IEEE International Conference on Dependable Autonomic and Secure Computing, Chengdu, China, 21–22 December 2013; Volume 33, pp. 143–147. [Google Scholar]
- Yang, C.; Li, B.; Chen, L.; Wei, C.; Xie, Y.; Chen, H.; Yu, W. A Spaceborne Synthetic Aperture Radar Partial Fixed–Point Imaging System Using a Field–Programmable Gate Array–Application-Specific Integrated Circuit Hybrid Heterogeneous Parallel Acceleration Technique. Sensors 2017, 17, 1493. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Chen, H.; Xie, Y. An FPGA-Based Four-Channel 128k-Point FFT Processor Suitable for Spaceborne SAR. Electronics 2021, 10, 816. [Google Scholar]
- Woo, J.C.; Lim, B.G.; Kim, Y.S. Modification of the Recursive Sidelobe Minimization Technique for the Range-Doppler Algorithm of SAR Imaging. J. Electromagn. Waves Appl. 2011, 25, 1783–1794. [Google Scholar] [CrossRef]
- Clemente, C.; Soraghan, J.J. Range Doppler SAR processing using the fractional Fourier transform. In Proceedings of the 11th International Radar Symposium, Vilnius, Lithuania, 16–18 June 2010. [Google Scholar]
- Le, C.; Chan, S.; Cheng, F.; Fang, W.; Fischman, M.; Hensley, S.; Johnson, R.; Jourdan, M.; Marina, M.; Parham, B.; et al. Onboard FPGA-based SAR processing for future spaceborne systems. In Proceedings of the IEEE 2004 Radar Conference, Philadelphia, PA, USA, 29–29 April 2004; pp. 15–20. [Google Scholar]
- Wang, D.; Ali, M.; Blinka, E. Synthetic Aperture Radar (SAR) Implementation on a TMS320C6678 Multicore DSP; Texas Instruments: Dallas, TX, USA, 2015. [Google Scholar]
- Raei, E.; Modarres-Hashemi, M.; Shankar, M.B. Range Cell Migration Correction by Fractional Fourier Transform in Synthetic Aperture Radars. In Proceedings of the 20th International Radar Symposium (IRS), Ulm, Germany, 26–28 June 2019; pp. 1–10. [Google Scholar]
- Hao, R.; Guo, T. Signal Processing Based Remote Sensing Data Simulation in Radar System. J. Electr. Comput. Eng. 2017, 2017, 6780305. [Google Scholar] [CrossRef] [Green Version]
- Cumming, I.; Wong, F. Digital Processing of Synthetic Aperture Radar Data; Artech House: Boston, MA, USA, 2005. [Google Scholar]
- Langemeyer, S.; Pirsch, P.; Blume, H. A FPGA architecture for real-time processing of variable-length FFTs. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011. [Google Scholar]
- Qureshi, F.; Takala, J.; Volkova, A.; Hilaire, T. Multiplierless unified architecture for mixed radix-2/3/4 FFTs. In Proceedings of the 2017 25th European Signal Processing Conference (EUSIPCO), Kos Island, Greece, August 28–2 September 2017; Volume 25, pp. 1334–1338. [Google Scholar]
- Jung, Y.C.; Cho, J.C.; Jung, Y.H. Design and Implementation of Multi-channel FFT Processor for MIMO Systems. J. Adv. Navig. Technol. 2017, 21, 659–665. [Google Scholar]
- Jang, S.H.; Yang, G.J.; Lee, S.J.; Jung, Y.H. Area-efficient FFT processor for MIMO-OFDM based SDR systems. IEICE Electron. Express 2013, 10, 20130490. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.; Park, S. Modified SDF Architecture for Mixed DIF/DIT FFT. In Proceedings of the 2007 IEEE International Symposium on Circuits and Systems (ISCAS), New Orleans, LA, USA, 27–30 May 2007; pp. 2590–2593. [Google Scholar]
- Jeon, H.H.; Jung, Y.C.; Lee, S.J.; Jung, Y.H. Area-Efficient Short-Time Fourier Transform Processor for Time–Frequency Analysis of Non-Stationary Signals. Appl. Sci. 2020, 10, 7208. [Google Scholar] [CrossRef]
- Jang, J.K.; Sunwoo, M.H. Efficient Scheduling Schemes for Low-Area Mixed-radix MDC FFT Processor. J. Inst. Electron. Inf. Eng. 2017, 54, 29–35. [Google Scholar]
- Di, W.; Chen, C.; Liu, Y. FPGA-based parallel system for synthetic aperture radar imaging. In Proceedings of the 2018 International Conference on Electronics Technology (ICET), Chengdu China, 23–27 May 2018; pp. 430–433. [Google Scholar]
- Sugimoto, Y.; Ozawa, S.; Inaba, N. Near Real-Time Sar Image Focusing Onboard Spacecraft. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8038–8041. [Google Scholar]




| Unit | CLB | CLB LUT | Block RAMs | DSP | Max. Operating Clock Freq. |
|---|---|---|---|---|---|
| MFU | 8836 | 48,077 | 8 | 112 | 314 MHz |
| RPU | 914 | 3465 | 4 | 256 | 312 MHz |
| Image Size | Execution Time (s) | |||
|---|---|---|---|---|
| Full SW | RCMC Accel. | MF/FFT Accel. | Full Accel. | |
| 256 × 256 | 0.805 | 0.691 | 0.122 | 0.007 |
| 512 × 512 | 3.648 | 3.114 | 0.574 | 0.030 |
| 1024 × 1024 | 16.114 | 13.850 | 2.420 | 0.188 |
| 2048 × 2048 | 70.330 | 61.276 | 9.951 | 0.823 |
| Work | Platform | Image Size | Hardware Resources | RCMC | Operating Freq. (MHz) | Exec. Time (s) | Tech. (nm) | (s) |
|---|---|---|---|---|---|---|---|---|
| Proposed | Zynq UlatraScale+ | 2048 × 2048 | CLB: 9750 CLB LUT: 51,542 Block RAMs: 12 DSP: 368 | O | 300 | 0.823 | 16 | 0.2 |
| [17] | Intel Altera Cyclone E IV | 2048 × 2048 | Logic Elements: 65,209 Logic Registers: 35,069 Memory (kbit): 814 Embedded Multipliers: 297 | O | 500 | 20.31 | 60 | 1.3 |
| [18] | Xilinx Virtex-6 | 2048 × 4096 | N/A | X | 130 | 12.03 | 40 | 0.57 |
| [19] | Xilinx Virtex-6 | 900 × 2048 | N/A | O | 200 | 2.08 | 40 | 0.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, Y.; Jeong, D.; Lee, M.; Lee, W.; Jung, Y. FPGA Implementation of the Range-Doppler Algorithm for Real-Time Synthetic Aperture Radar Imaging. Electronics 2021, 10, 2133. https://doi.org/10.3390/electronics10172133
Choi Y, Jeong D, Lee M, Lee W, Jung Y. FPGA Implementation of the Range-Doppler Algorithm for Real-Time Synthetic Aperture Radar Imaging. Electronics. 2021; 10(17):2133. https://doi.org/10.3390/electronics10172133
Chicago/Turabian StyleChoi, Yeongung, Dongmin Jeong, Myeongjin Lee, Wookyung Lee, and Yunho Jung. 2021. "FPGA Implementation of the Range-Doppler Algorithm for Real-Time Synthetic Aperture Radar Imaging" Electronics 10, no. 17: 2133. https://doi.org/10.3390/electronics10172133
APA StyleChoi, Y., Jeong, D., Lee, M., Lee, W., & Jung, Y. (2021). FPGA Implementation of the Range-Doppler Algorithm for Real-Time Synthetic Aperture Radar Imaging. Electronics, 10(17), 2133. https://doi.org/10.3390/electronics10172133







