Physics-Informed Neural Network for High Frequency Noise Performance in Quasi-Ballistic MOSFETs
Abstract
:1. Introduction
2. Theoretical Models
2.1. Thermal Noise Model
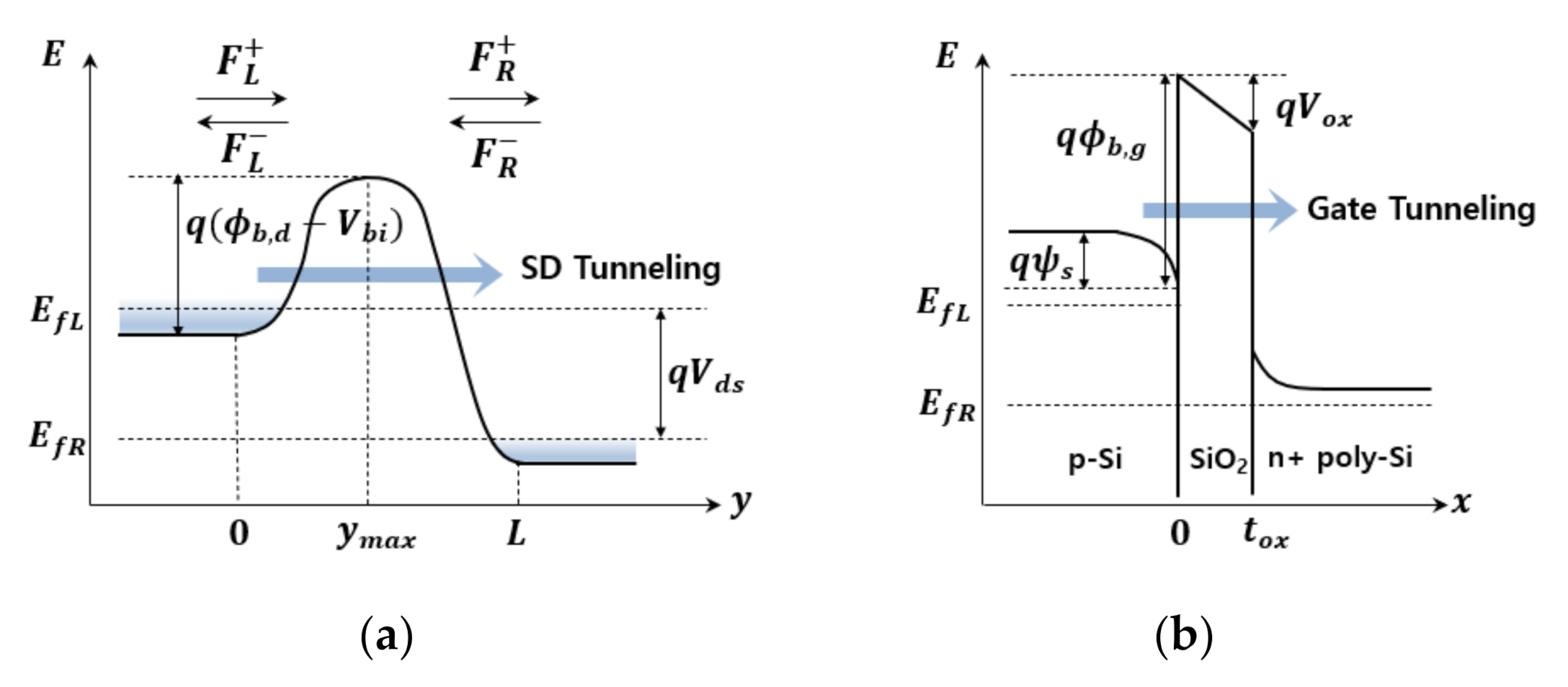
2.2. Shot Noise Model
3. Artificial Neural Network Model
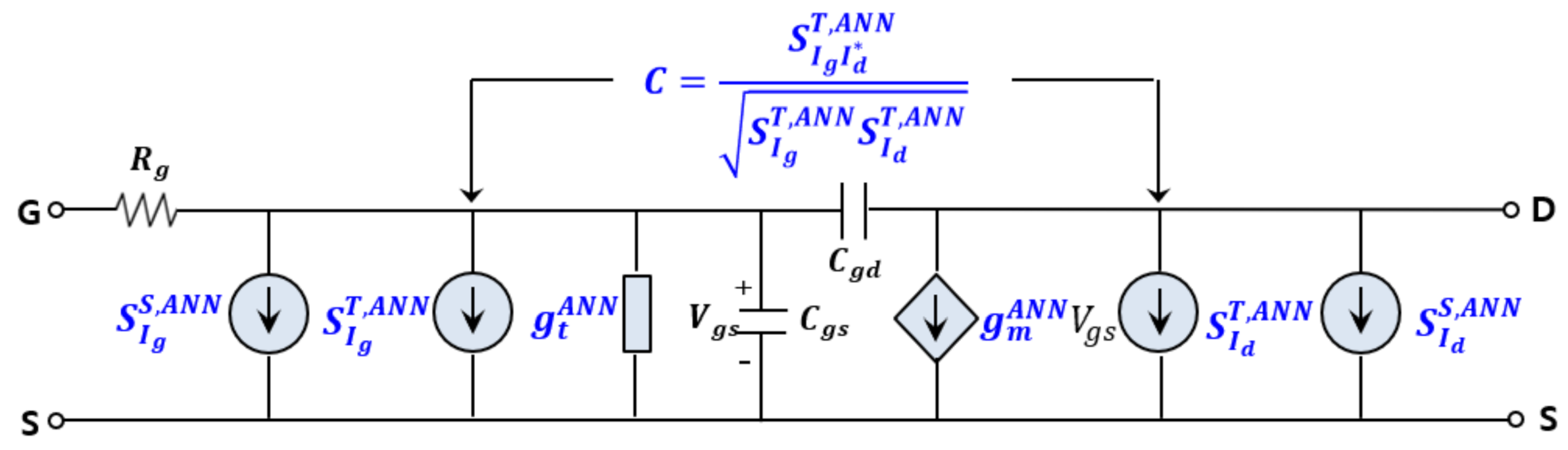
3.1. RBF-ANN and RBF-DANN
3.2. RBF-IANN
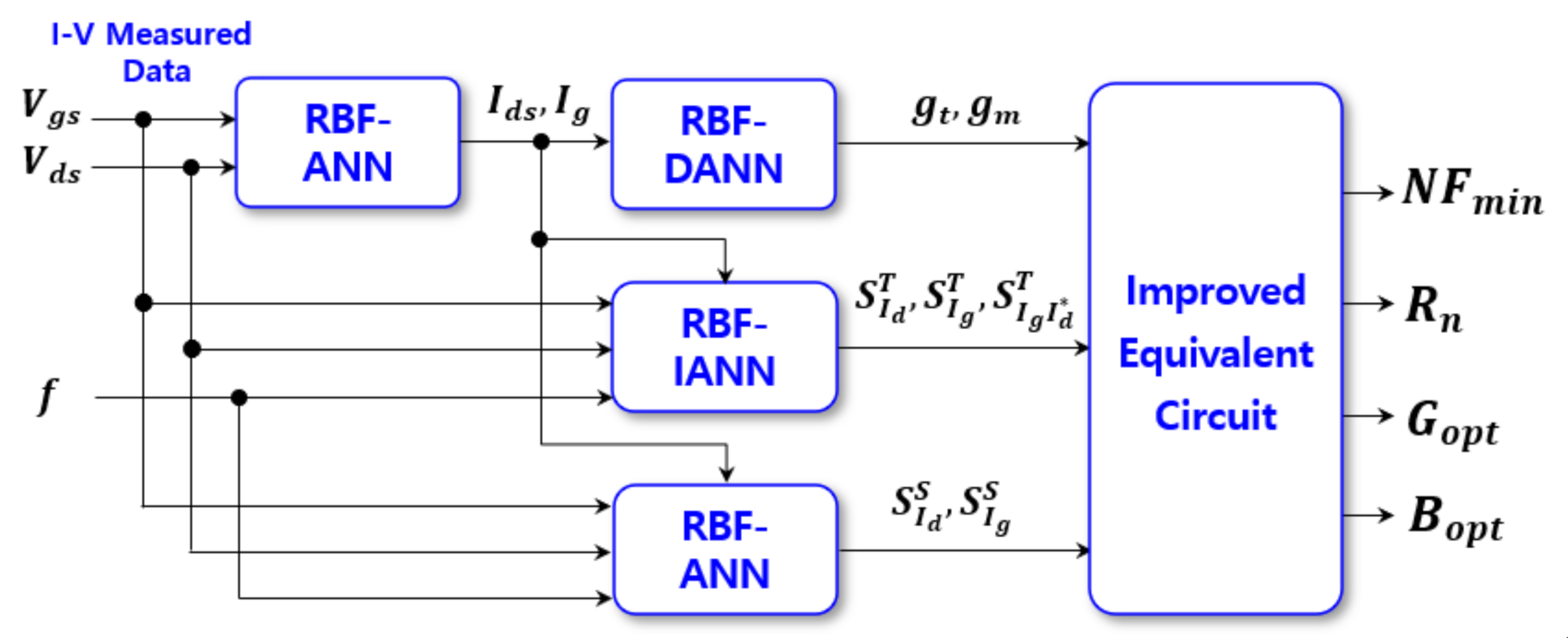
3.3. ANN Structure for Noise Performance
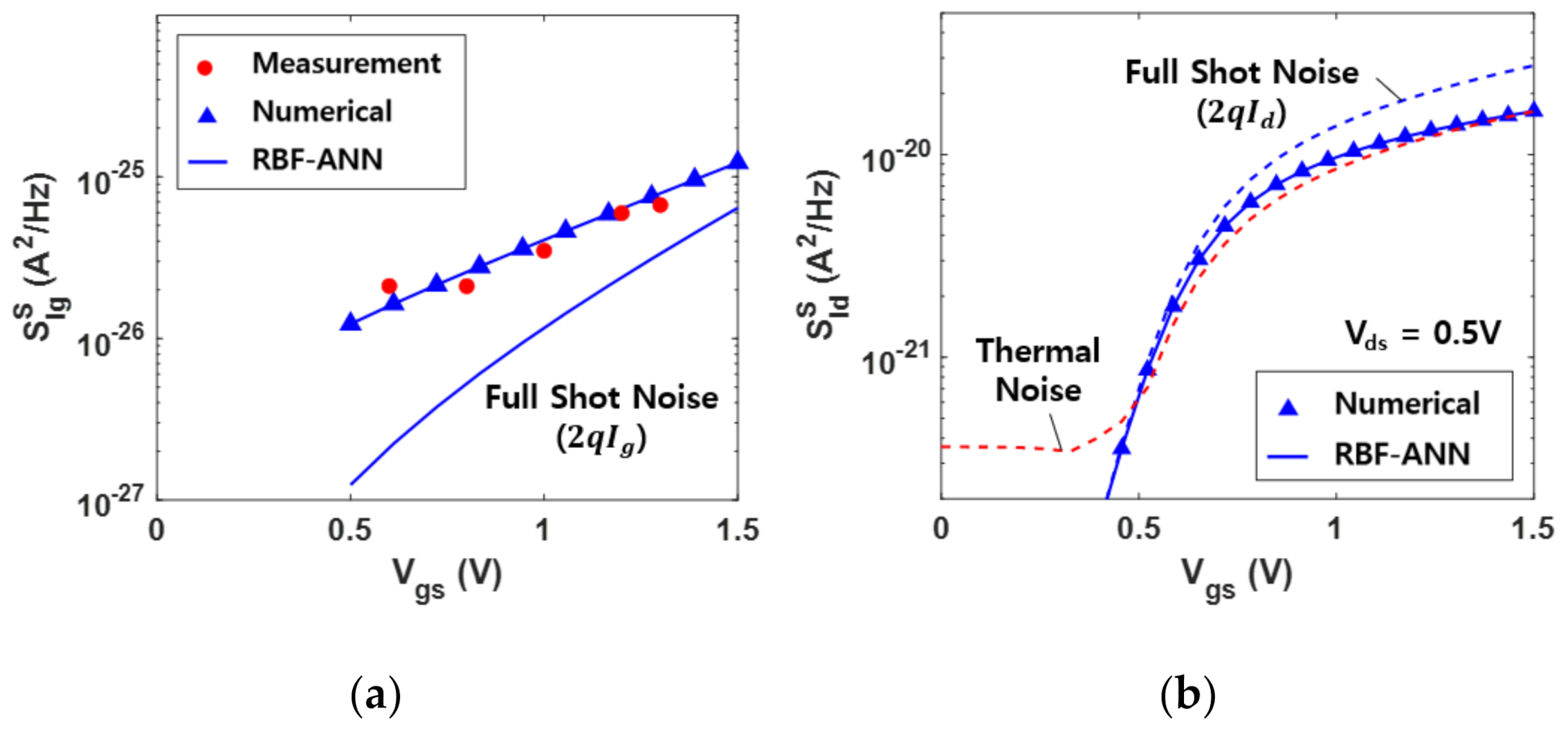
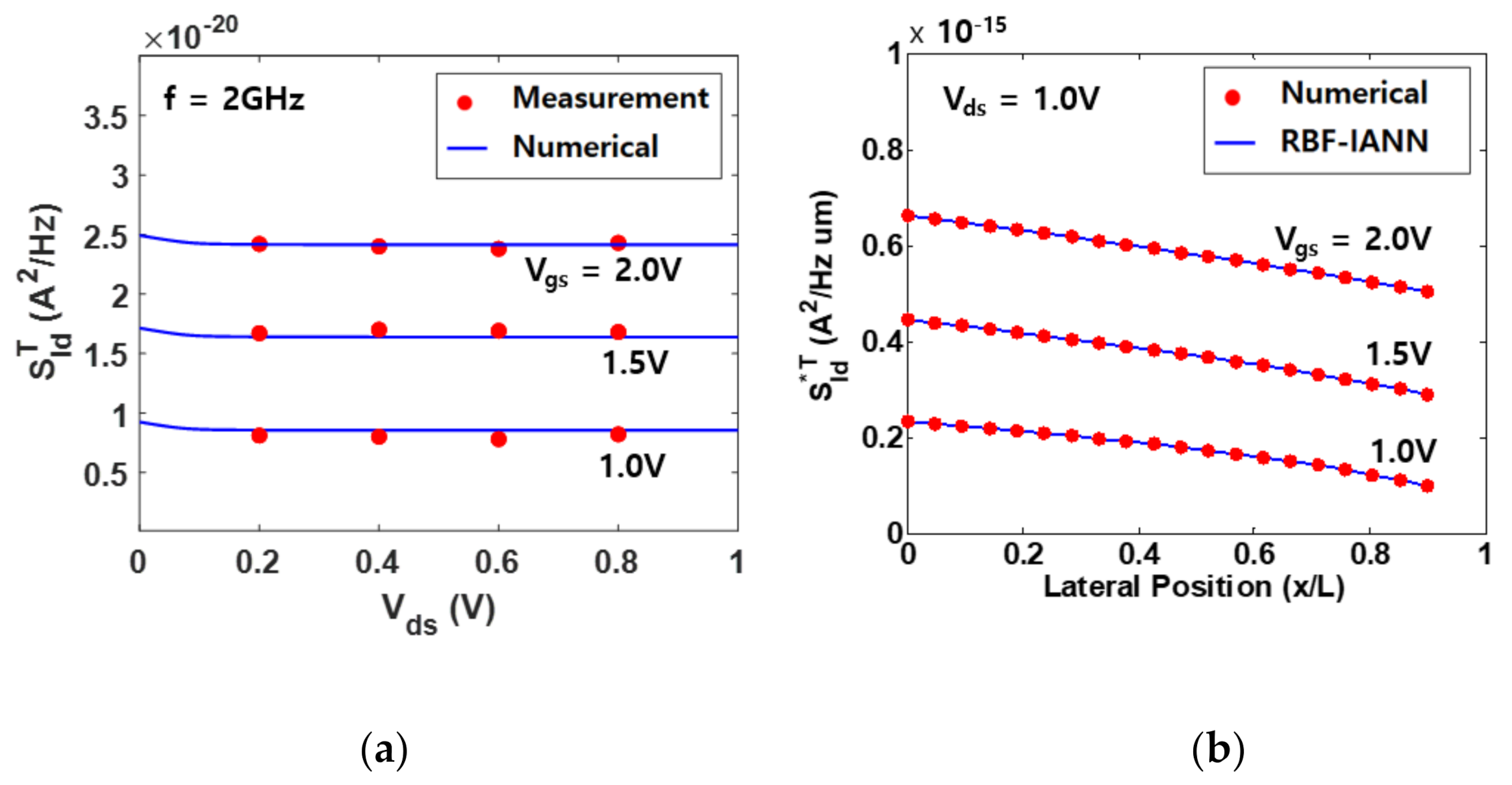
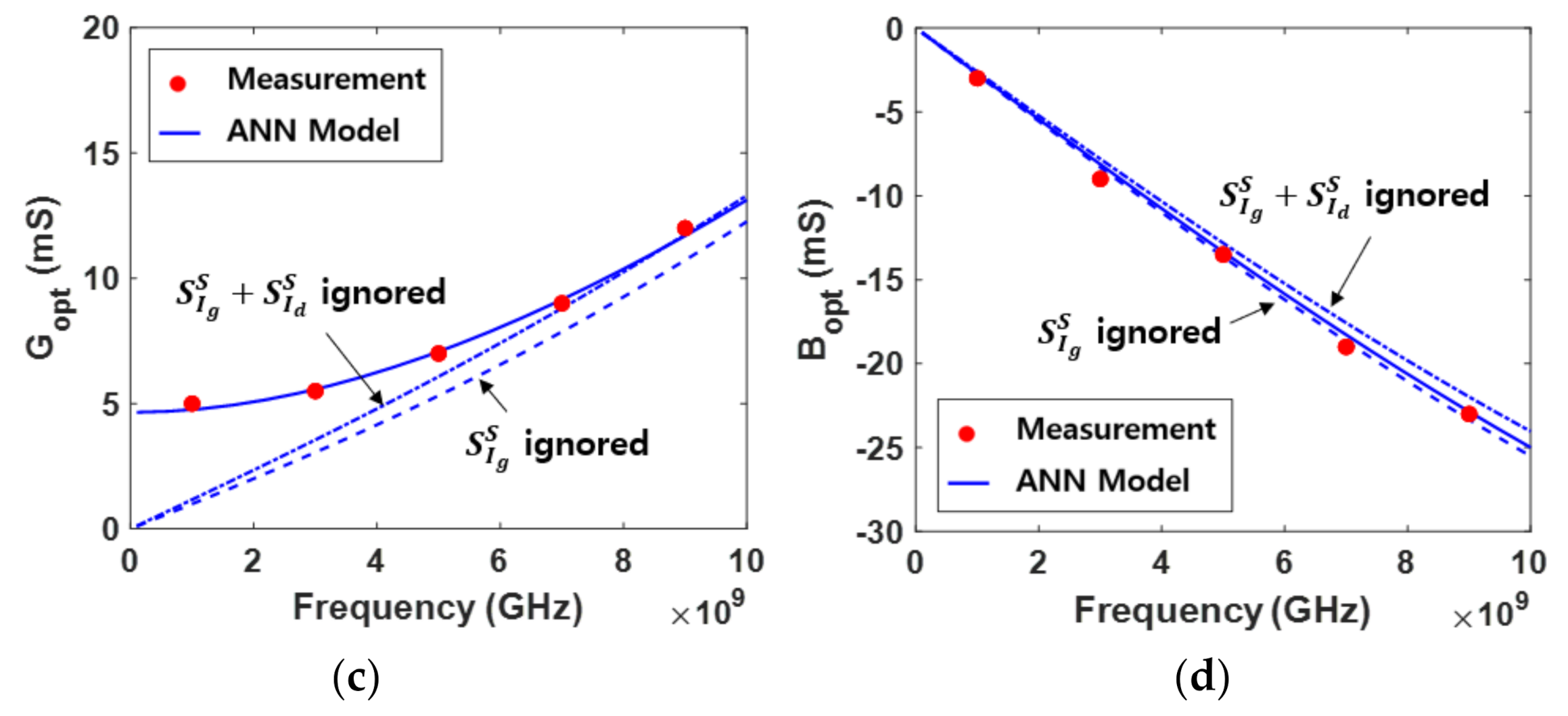
4. Model Verification
5. Conclusions
Funding
Conflicts of Interest
References
- Chen, X.; Chen, C.H.; Lee, R. Fast evaluation of the high-frequency channel noise in nanoscale MOSFETs. IEEE Trans. Electron. Devices 2018, 65, 1502–1508. [Google Scholar] [CrossRef]
- Deen, M.J.; Chen, C.H.; Asgaran, S.; Rezvani, G.A.; Tao, J.; Kiyota, Y. High frequency noise of modern MOSFETs: Compact modeling and measurement issues. IEEE Trans. Electron. Devices 2006, 53, 2062–2081. [Google Scholar] [CrossRef]
- Han, K.; Gil, J.; Song, S.S.; Han, J.; Shin, H.; Kim, C.K.; Lee, K. Complete high-frequency thermal noise modeling of short-channel MOSFETs and design of 5.2GHz low noise amplifier. IEEE J. Solid-State Circuits 2005, 40, 726–734. [Google Scholar]
- Han, K.; Shin, H.; Lee, K. Analytical drain thermal noise current model valid for deep submicron MOSFETs. IEEE Trans. Electron. Devices 2004, 51, 261–269. [Google Scholar] [CrossRef]
- Asgaran, S.; Deen, M.J.; Chen, C.H. Analytical modeling of MOSFETs channel noise and noise parameters. IEEE Trans. Electron. Devices. 2004, 51, 2109–2114. [Google Scholar] [CrossRef]
- Jeon, J.; Kim, Y.; Kang, M. Investigation of the induced gate noise of nanoscale MOSFETs in the very high frequency region. Semicond. Sci. Technol. 2016, 31, 065004. [Google Scholar] [CrossRef]
- Jeon, J.; Yun, Y.; Kim, J.; Park, B.G.; Lee, J.D.; Shin, H. On the characteristics and spatial dependence of channel thermal noise in nanoscale metal oxide semiconductor field effect transistors. Jpn. J. Appl. Phys. 2008, 47, 2636–2640. [Google Scholar] [CrossRef]
- Ohmori, K.; Amakawa, S. Direct white noise characterization of short-channel MOSFETs. IEEE Trans. Electron. Devices 2021, 68, 1478–1482. [Google Scholar] [CrossRef]
- Jeon, J.; Kang, M. Shot noise effect on noise source and noise parameter of 10-nm-scale quasi-ballistic n-/p-type MOS devices. Jpn. J. Appl. Phys. 2016, 55, 054102. [Google Scholar] [CrossRef]
- Naveh, Y.; Likharev, K.K. Modeling of 10nm-scale ballistic MOSFET’s. IEEE Electron Device Lett. 2000, 21, 242–244. [Google Scholar] [CrossRef]
- Lin, Y.K.; Duarte, J.P.; Kushwaha, P.; Agarwal, H.; Chang, H.L.; Sachid, A.; Salahuddin, S.; Hu, C. Compact modeling source-to-drain tunneling in sub-10nm GAA FinFET with industry standard model. IEEE Trans. Electron. Devices 2017, 64, 3576–3581. [Google Scholar] [CrossRef]
- Hiblot, G.; Rafhay, Q.; Boeuf, F.; Ghibaudo, G. Analytical relationship between subthreshold swing of thermionic and tunneling currents. Electron. Lett. 2014, 50, 1745–1747. [Google Scholar] [CrossRef]
- Cheng, H.; Liu, T.; Zhang, C.; Yang, Z.; Liu, Z.; Nakazato, K.; Zhang, Z. Nanowire gate-all-around MOSFETs modeling: Ballistic transport incorporating the source-to-drain tunneling. Jpn. J. Appl. Phys. 2020, 59, 1–9. [Google Scholar] [CrossRef]
- Mugnaini, G.; Iannaccone, G. Channel noise modeling of nanoMOSFETs in a partially ballistic transport regime. J. Comput. Electron. 2006, 5, 91–95. [Google Scholar] [CrossRef]
- Iannaccone, G.; Betti, A.; Fiori, G. Suppressed and enhanced shot noise in one dimensional field-effect transistors. J. Comput. Electron. 2015, 14, 94–106. [Google Scholar] [CrossRef]
- Iannaccone, G. Analytical and numerical investigation of noise in nanoscale ballistic field effect transistors. J. Comput. Electron. 2004, 3, 199–202. [Google Scholar] [CrossRef] [Green Version]
- Jia, X.; He, L. Research of shot noise based on realistic nano-MOSFETs. AIP Adv. 2017, 7, 055202. [Google Scholar] [CrossRef] [Green Version]
- Spathis, C.; Birbas, A.; Georgakopoulou, K. Semi-classical noise investigation for sub-40nm metal-oxide-semiconductor field-effect transistors. AIP Adv. 2015, 5, 087114. [Google Scholar] [CrossRef]
- Ranuarez, J.C.; Deen, M.J.; Chen, C.H. A review of gate tunneling current in MOS devices. Microelectron. Rel. 2006, 46, 1939–1956. [Google Scholar] [CrossRef]
- Clerc, R.; O’Sullivan, P.; McCarthy, K.G.; Ghibaudo, G.; Pananakakis, G.; Mathewson, A. A physical compact model for direct tunneling from NMOS inversion layers. Solid-State Electron. 2001, 45, 1705–1716. [Google Scholar] [CrossRef]
- Gehring, A.; Selberherr, S. Modeling of tunneling current and gate dielectric reliability for nonvolatile memory devices. IEEE Trans. Device Mater. Reliab. 2004, 4, 306–319. [Google Scholar] [CrossRef]
- Mao, L.F.; Li, X.J.; Wang, Z.O.; Wang, J.Y. The gate leakage current in graphene field-effect transistor. IEEE Electron Device Lett. 2008, 29, 1047–1049. [Google Scholar] [CrossRef]
- Lee, J.; Bosman, G.; Green, K.R.; Ladwig, D. Noise model of gate-leakage current in ultrathin oxide MOSFETs. IEEE Trans. Electron. Devices 2003, 50, 2499–2506. [Google Scholar]
- Manghisoni, M. Gate current noise in ultrathin oxide MOSFETs and its impact on the performance of analog front-end circuits. IEEE Trans. Nucl. Sci. 2008, 55, 2399–2407. [Google Scholar] [CrossRef]
- Huang, A.D.; Zhong, Z.; Wu, W.; Guo, Y.X. An artificial neural network-based electrothermal model for GaN HEMTs with dynamic trapping effects consideration. IEEE Trans. Microw. Theory Technol. 2016, 64, 2519–2528. [Google Scholar] [CrossRef]
- Li, X.; Gao, J.; Boeek, G. Microwave nonlinear device modeling by using an artificial neural network. Semicond. Sci. Technol. 2006, 21, 833–840. [Google Scholar] [CrossRef]
- Lee, J. Physics-guided neural modeling for low-dimensional thermoelectric module. IEEE Electron Device Lett. 2019, 40, 1812–1815. [Google Scholar] [CrossRef]
- Li, M.; Irsoy, O.; Cardie, C.; Xing, H.G. Physics-inspired neural networks for efficient device compact modeling. IEEE J. Explor. Solid-State Compu. Devices Circuits 2016, 2, 44–49. [Google Scholar] [CrossRef]
- Zhang, L.; Chan, M. Artificial neural network design for compact modeling of generic transistors. J. Comput. Electron. 2017, 16, 825–832. [Google Scholar] [CrossRef]
- Jarndal, A. On neural network based electro- thermal modeling of GaN devices. IEEE Access. 2019, 7, 94205–94214. [Google Scholar] [CrossRef]
- Wu, T.; Guo, J. Speed up quantum transport device simulation on ferroelectric tunnel junction with machine learning methods. IEEE Trans. Electron. Devices 2020, 67, 5229–5235. [Google Scholar] [CrossRef]
- Wang, J.; Kim, Y.H.; Ryu, J.; Jeong, C.; Choi, W.; Kim, D. Artificial neural network-based compact modeling methodology for advanced transistors. IEEE Trans. Electron. Devices 2021, 68, 1318–1325. [Google Scholar] [CrossRef]
- Mehta, K.; Wong, H.Y. Prediction of FinFET current-voltage and capacitance-voltage curves using machine learning with autoencoder. IEEE Electron Device Lett. 2021, 42, 136–139. [Google Scholar] [CrossRef]
- Carrillo-Nunez, H.; Dimitrova, N.; Asenov, A.; Georgiev, V. Machine learning approach for predicting the effect of statistical variability in Si junction-less nanowire transistors. IEEE Electron Device Lett. 2019, 40, 1366–1369. [Google Scholar] [CrossRef] [Green Version]
- Pregaldiny, F.; Lallement, C.; van Langevelde, R.; Mathiot, D. An advanced explicit surface potential model physically accounting for the quantization effects in deep-submicron MOSFETs. Solid-State Electron. 2004, 48, 427–435. [Google Scholar] [CrossRef]
- Aleshkin, V.Y.; Reggiani, L. Electron transport and shot noise in double-barrier resonant diodes: The role of Pauli and Coulomb correlations. Phys. Rev. B. 2001, 64, 245333. [Google Scholar] [CrossRef]
- Aleshkin, V.Y.; Reggiani, L. Comparative analysis of sequential and coherent tunneling in resonant diodes. Phys. Rev. B. 2006, 73, 165320. [Google Scholar] [CrossRef]
- Marin, E.G.; Bader, S.J.; Jena, D. A new holistic model of 2-D semiconductor FETs. IEEE Trans. Electron. Devices 2018, 65, 1239–1245. [Google Scholar] [CrossRef]
- Cheng, Y.; Denn, J.M.; Chen, C.H. MOSFET modeling for RF IC design. IEEE Trans. Electron. Devices 2005, 52, 1286–1303. [Google Scholar] [CrossRef]
- Cheng, Y.; Matloubian, M. High frequency characterization of gate resistance in RF MOSFETs. IEEE Electron Device Lett. 2001, 22, 98–100. [Google Scholar] [CrossRef]
- Weatherspoon, M.H.; Martinez, H.A.; Langoni, D.; Foo, S.Y. Small-signal modeling of microwave MESFETs using RBF-ANNs. IEEE Trans. Instrum. Meas. 2007, 56, 2067–2072. [Google Scholar] [CrossRef]
- Djeffal, F.; Dibi, Z.; Hafiane, M.L.; Arar, D. Design and simulation of a nanoelectronic DG MOSFET current source using artificial neural networks. Mater. Sci. Eng. C 2007, 27, 1111–1116. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, H.; Zhang, B.; Du, K.L. Using radial basis function networks for function approximation and classification. ISRN Appl. Math. 2012, 2012, 1–34. [Google Scholar] [CrossRef] [Green Version]
- Navid, R.; Jungemann, C.; Lee, T.H.; Dutton, R.W. High-frequency noise in nanoscale metal oxide semiconductor field effect transistors. J. Appl. Phys. 2007, 101, 124501. [Google Scholar] [CrossRef] [Green Version]
- Wang, J. Bias non-conservation characteristics of drain current noise of 40nm n-MOSFETs in high-frequency band. Electron. Lett. 2017, 53, 1671–1672. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J. Physics-Informed Neural Network for High Frequency Noise Performance in Quasi-Ballistic MOSFETs. Electronics 2021, 10, 2219. https://doi.org/10.3390/electronics10182219
Lee J. Physics-Informed Neural Network for High Frequency Noise Performance in Quasi-Ballistic MOSFETs. Electronics. 2021; 10(18):2219. https://doi.org/10.3390/electronics10182219
Chicago/Turabian StyleLee, Jonghwan. 2021. "Physics-Informed Neural Network for High Frequency Noise Performance in Quasi-Ballistic MOSFETs" Electronics 10, no. 18: 2219. https://doi.org/10.3390/electronics10182219
APA StyleLee, J. (2021). Physics-Informed Neural Network for High Frequency Noise Performance in Quasi-Ballistic MOSFETs. Electronics, 10(18), 2219. https://doi.org/10.3390/electronics10182219




