Space-Time Loop Tiling for Dynamic Programming Codes
Abstract
:1. Introduction
2. Background
| for (i=1; i <=N; i++) for (j=1; j <=M; j++) { for (k=1; k <=i; k++) m1[i][j] = max(m1[i][j], H[i-k][j] - W[k]); //s0 for (k=1; k <=j; k++) m2[i][j] = max(m2[i][j], H[i][j-k] - W[k]); //s1 H[i][j] = max(0,H[i-1,j-1]+ s(a[i],b[i]), m1[i][j], m2[i][j]); //s2 } |
| for (i = N-1; i>=0; i--){ for ( j=i+1; j<= N; j++){ for ( k = i; k<=j-l; k++){ c[i][j] += c[i][j-1] + paired(k,j) ? c[i][k-1] + c[k+1][j-1] : 0; } } } |
| for (i=n-1; i >=1; i--) for (j = i+1; j <= n ; j += 1) for (k = i+1; k <j; k += 1) { c[i][j]= min(c[i][j], w[i][j]+c[i][k]+c[k][j]); } |
3. Overview of Space-Time Tiling
4. Space-Time Tiling
4.1. Tiling a Simple Loop Nest
4.2. Imperfectly Nested Loops
- Form relation , representing dependences in the global iteration space, by means of replacing each named tuple, , of relation R with the tuple resulting due to relation on tuple ;
- Apply the operator of the iscc calculator to relation to calculate distance vectors in the common iteration space.
- Initialize a common direction vector of length d, , as follows;, , .
- If the j-th element of the distance vectors is a global schedule constant, say c, then if , proceed to ; or else = “-”, , proceed to .If the j-th element of at least one distance vector is negative (positive) and the corresponding iterator is incremented (decremented), then= “-”, ;If , proceed to ; otherwise return vector , the end.
- ;
- If == “+”, then form the following sets;; ;
- ; if then proceed to step 2;
- Form set as follows;.
4.3. Parallel Code Generation
4.4. Formal Algorithm
| Algorithm 1: Space-time loop tiling. |
| Input: Arbitrarily nested affine loops of depth d; variables , defining the width of subspaces regarding to iterator ; variable defining the number of time partitions within a time slice. |
| Output: Parallel tiled code. |
Method:
|
5. Applying Space-Time Tiling to the Examined Loop Nests
| for( c0 = 0; c0 <= floord(N - 1, 8); c0 += 1) #pragma omp parallel for for( c1 = max(0, c0-(N+15)/16+1); c1 <= min(c0, (N - 1) / 16); c1 += 1) for( c3 = 16 * c0 + 2; c3 <= min(min(min(2 * N, 16 * c0 + 32), N + 16 * c1 + 16), N + 16 * c0 - 16 * c1 + 16); c3 += 1) { for( c4 = max(max(-c0 + c1 - 1, -((N + 14) / 16)), c1 - (c3 + 13) / 16); c4 < c0 - c1 - (c3 + 13) / 16; c4 += 1) for( c6 = max(max(16*c1 + 1, -16*c0 + 16*c1 + c3 - 16), -N + c3); c6 <= min(min(16*c1 + 16, -16*c0 + 16*c1 + c3 - 1), c3 + 16*c4 + 14); c6 += 1) for(c10 = max(1, c3+16*c4 - c6); c10 <= c3 + 16*c4 - c6 + 15; c10 += 1) m2[c6][(c3-c6)] = MAX(m2[c6][(c3-c6)] ,H[c6][(c3-c6)-c10] + W[c10]); if (c0 >= 2 * c1 + 1 && c3 >= 16 * c0 + 19) for( c6 = max(-16*c0 + 16*c1 + c3 - 16, -N + c3); c6 <= 16*c1 + 16; c6++) for( c10 = max(1, -16*c1 + c3 - c6 - 32); c10 < -16*c1 + c3-c6-16; c10++) m2[c6][(c3-c6)] = MAX(m2[c6][(c3-c6)] ,H[c6][(c3-c6)-c10] + W[c10]); for( c4 = max(max(-c1 - 1, -((N + 14) / 16)), c0 - c1 - (c3 + 13) / 16); c4 <= 0; c4 += 1) { if (N + 16 * c1 + 1 >= c3 && 16 * c0 + 17 >= c3 && c1 + c4 == -1) for( c10 = max(1, -32 * c1 + c3 - 17); c10 < -32 * c1 + c3 - 1; c10 += 1) m2[(16*c1+1)][(-16*c1+c3-1)] = MAX(m2[(16*c1+1)][(-16*c1+c3-1)] ,H[(16*c1+1)][(-16*c1+c3-1)-c10] + W[c10]); for( c6 = max(max(max(16*c1 + 1, -16*c0 + 16*c1 + c3 - 16), -N + c3), -16*c4 - 14); c6 <= min(min(N, 16*c1+16), -16*c0 + 16*c1 + c3-1); c6++){ for( c10 = max(1, 16*c4 + c6); c10 <= min(c6, 16*c4 + c6 + 15); c10++) m1[c6][(c3-c6)] = MAX(m1[c6][(c3-c6)] ,H[c6-c10][(c3-c6)] + W[c10]); for( c10 = max(1, c3 + 16 * c4 - c6); c10 <= min(c3 - c6, c3 + 16 * c4 - c6 + 15); c10 += 1) m2[c6][(c3-c6)] = MAX(m2[c6][(c3-c6)] ,H[c6][(c3-c6)-c10] + W[c10]); if (c0 == 0 && c1 == 0 && c3 <= 15 && c4 == 0) H[c6][(c3-c6)] = MAX(0, MAX( H[c6-1][(c3-c6)-1] + s(a[c6], b[c6]), MAX(m1[c6][(c3-c6)], m2[c6][(c3-c6)]))); } } if (c3 >= 16) for( c6 = max(max(16 * c1 + 1, -16 * c0 + 16 * c1 + c3 - 16), -N + c3); c6 <= min(min(N, 16 * c1 + 16), -16 * c0 + 16 * c1 + c3 - 1); c6 += 1) H[c6][(c3-c6)] = MAX(0, MAX( H[c6-1][(c3-c6)-1] + s(a[c6], b[c6]), MAX(m1[c6][(c3-c6)], m2[c6][(c3-c6)]))); } |
| for( c0 = max(0, floord(l - 2, 8) - 1); c0 <= floord(N - 3, 8); c0 += 1) #pragma omp parallel for for( c1 = (c0 + 1) / 2; c1 <= min(min(c0, c0 + floord(-l + 1, 16) + 1), (N - 3) / 16); c1 += 1) for( c3 = max(l, 16*c0 - 16*c1 + 2); c3 <= min(N-1, 16*c0-16*c1+17); c3++) for( c4 = max(0, -c1 + (N - 1) / 16 - 1); c4 <= min((-l + N) / 16, -c1 + (-l + N + c3 - 2) / 16); c4 += 1) for( c6 = max(max(-N + 16 * c1 + 2, -N + c3), -16 * c4 - 15); c6 <= min(min(-1, -N + 16 * c1 + 17), -l + c3 - 16 * c4); c6 += 1) for( c10 = max(16*c4, -c6); c10 <= min(16*c4 + 15, -l+c3-c6); c10++) c[(-c6)][(c3-c6)] += c[(-c6)][(c3-c6)-1] + paired(c10,(c3-c6)) ? c[(-c6)][c10-1] + c[c10+1][(c3-c6)-1] : 0; |
| for( c0 = 0; c0 <= floord(n - 2, 8); c0 += 1) #pragma omp parallel for for( c1 = (c0 + 1) / 2; c1 <= min(c0, (n - 2) / 16); c1 += 1) for( c3 = max(2, 16*c0-16*c1+1); c3 <= min(n - 1, 16*c0 - 16*c1 + 16); c3++) for( c4 = max(0, -c1 + (n + 1) / 16 - 1); c4 <= min((n - 1) / 16, -c1 + (n + c3 - 2) / 16); c4 += 1) for( c6 = max(max(-n + 16 * c1 + 1, -n + c3), -16 * c4 - 14); c6 <= min(min(-1, -n + 16 * c1 + 16), c3 - 16 * c4 - 1); c6 += 1) for( c10 = max(16*c4, -c6+1); c10 <= min(16*c4 + 15, c3-c6-1); c10++) c[(-c6)][(c3-c6)] = MIN(c[(-c6)][(c3-c6)], w[(-c6)][(c3-c6)]+c[(-c6)][c10]+c[c10][(c3-c6)]); |
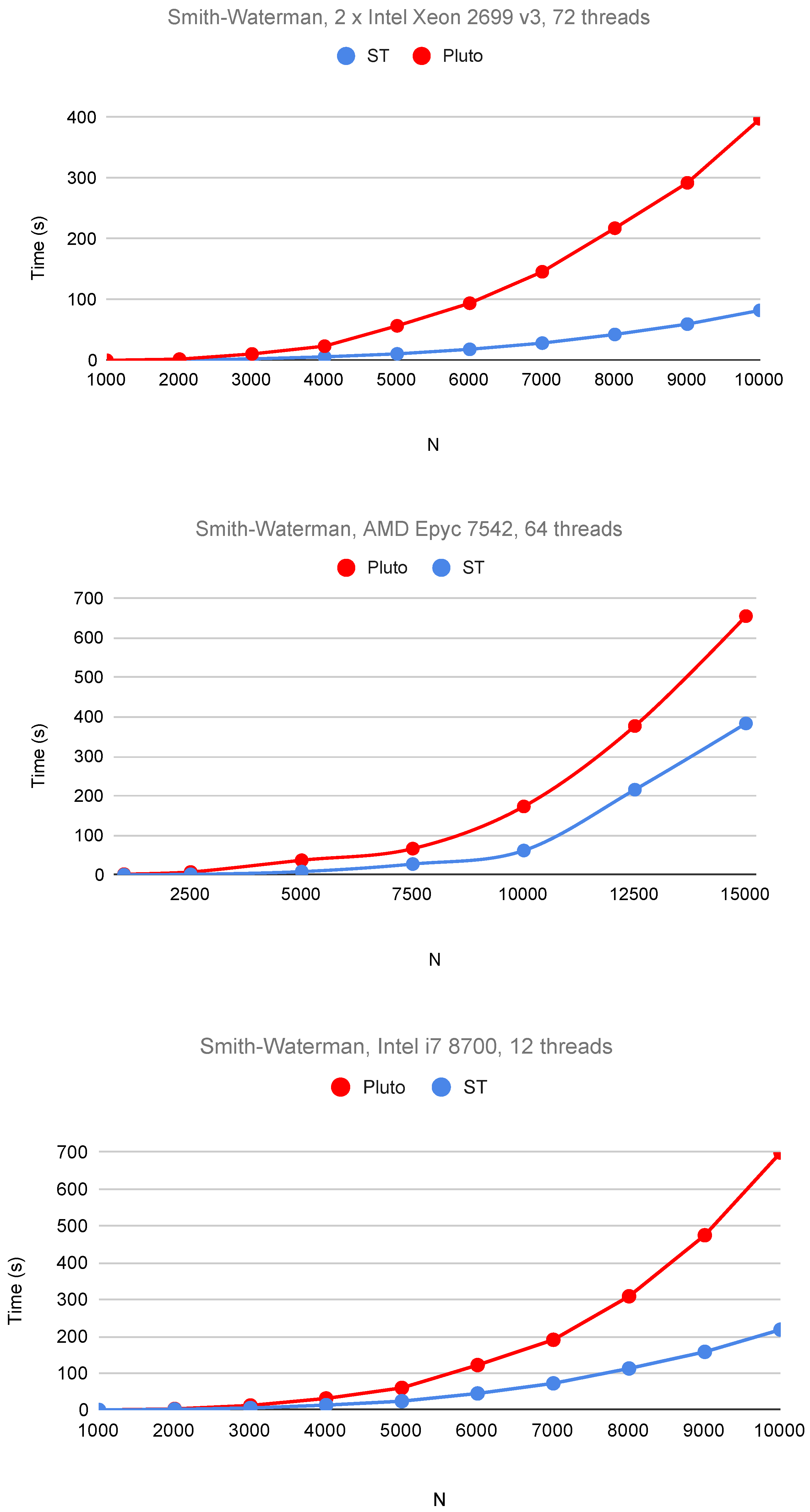
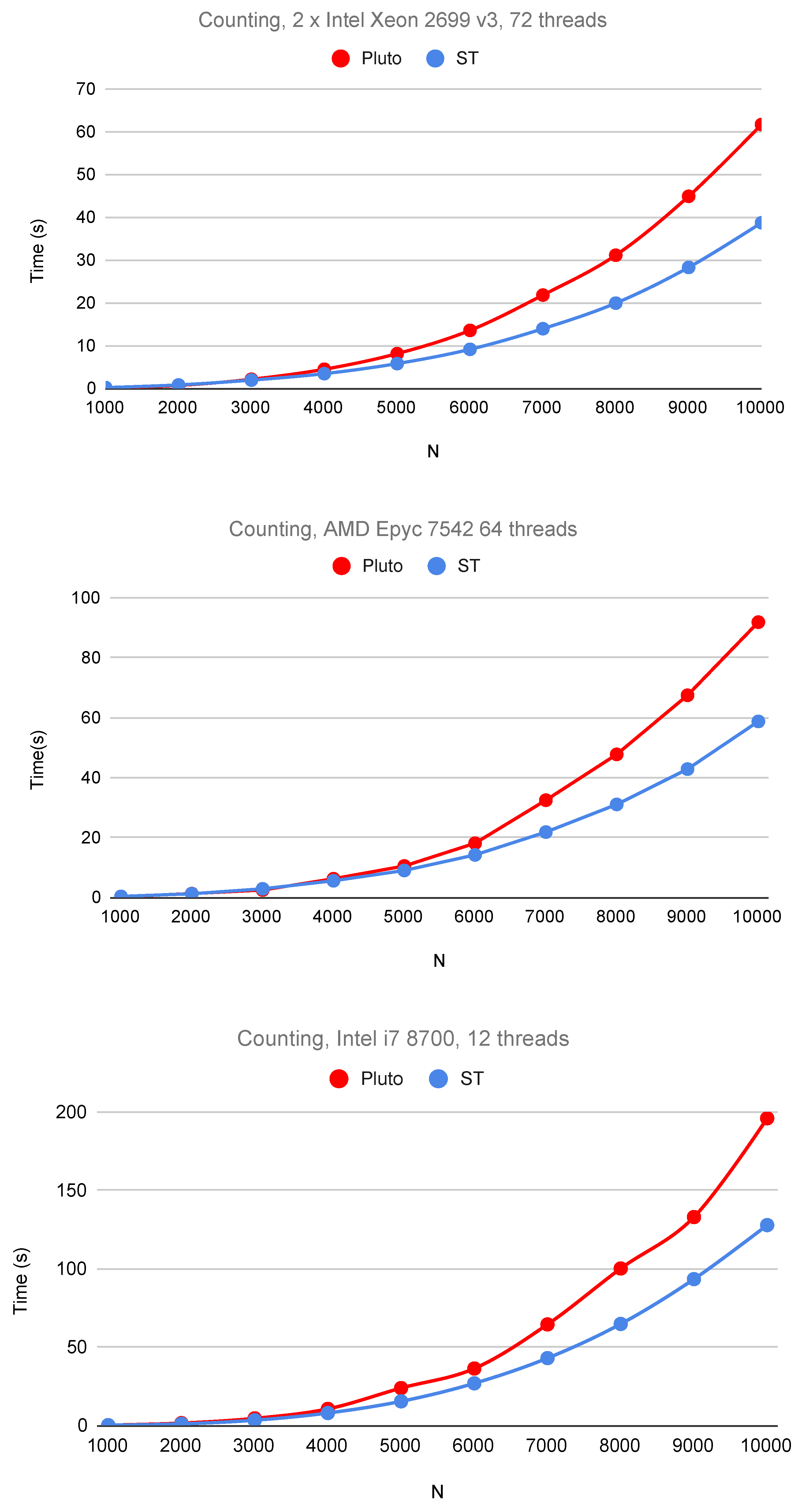
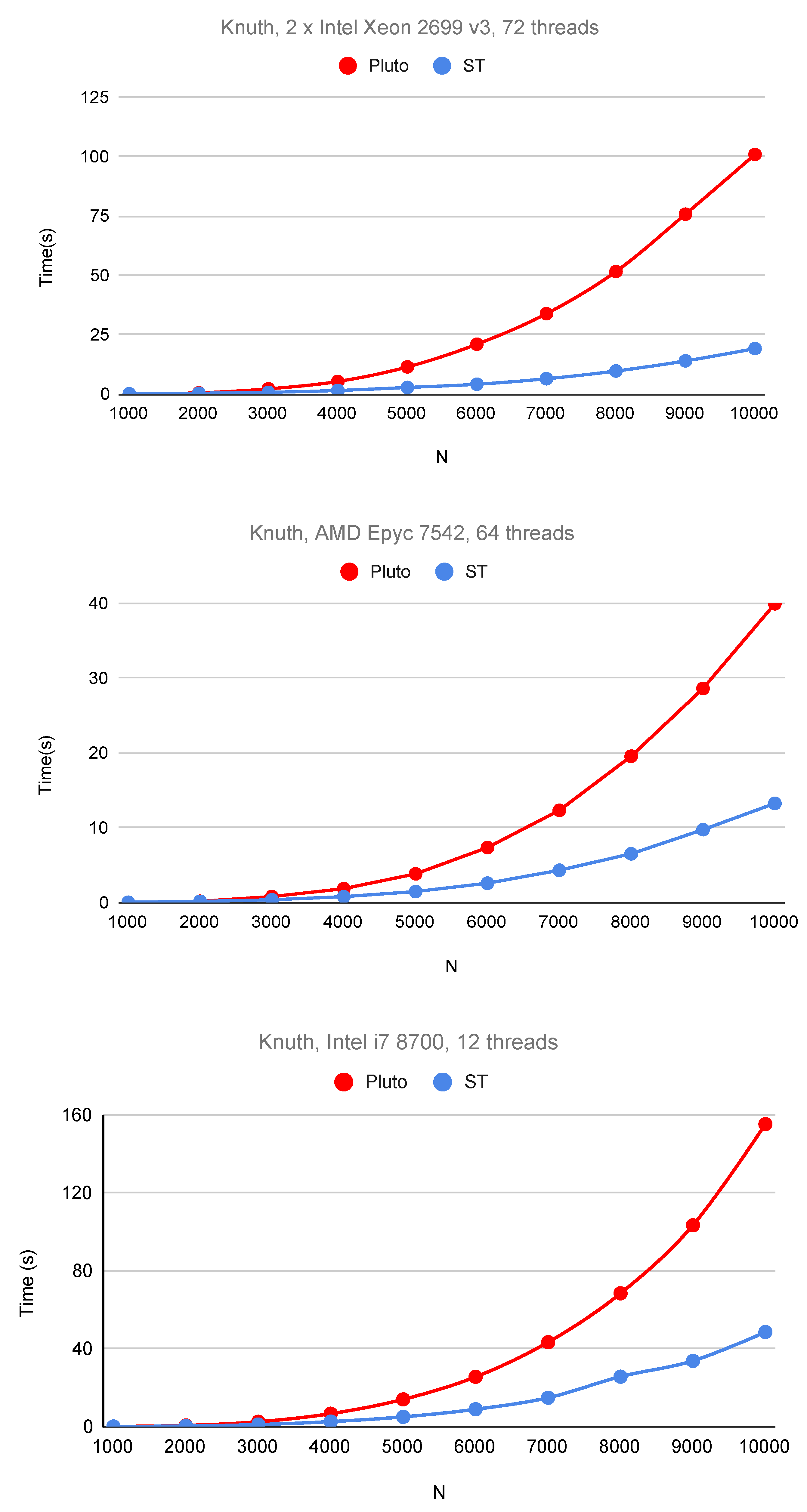
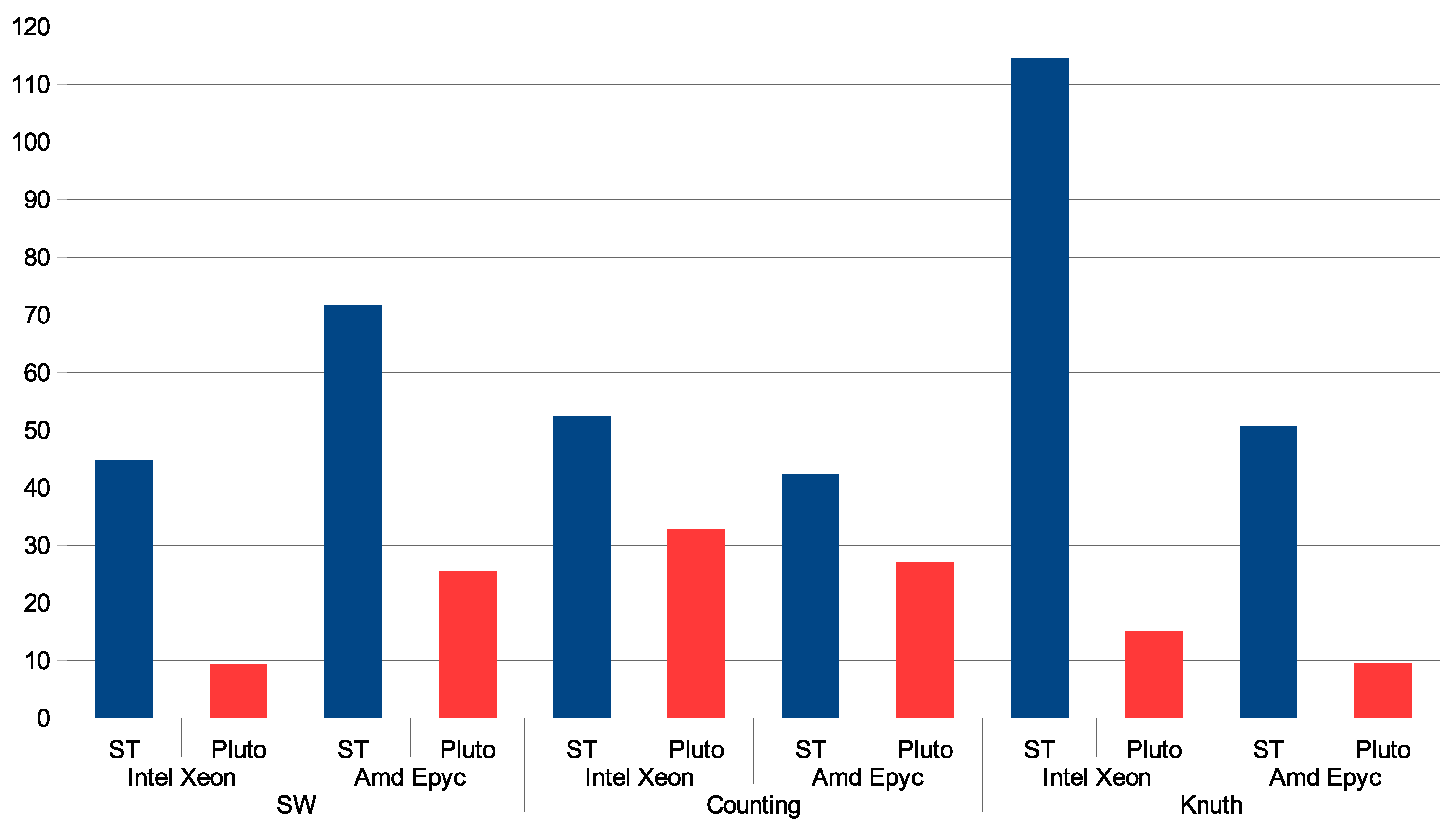
6. Experimental Study
7. Related Work
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| NPDP | Non-serial polyadic dynamic programming; |
| SW | Smith–Waterman; |
| ATF | Affine Transformation Framework. |
References
- Liu, L.; Wang, M.; Jiang, J.; Li, R.; Yang, G. Efficient Nonserial Polyadic Dynamic Programming on the Cell Processor. In Proceedings of the 2011 IEEE International Symposium on Parallel and Distributed Processing Workshops and Phd Forum, Anchorage, AK, USA, 16–20 May 2011; pp. 460–471. [Google Scholar]
- Li, J.; Ranka, S.; Sahni, S. Multicore and GPU algorithms for Nussinov RNA folding. BMC Bioinform. 2014, 15, S1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, C.; Sahni, S. Cache and energy efficient algorithms for Nussinov’s RNA Folding. BMC Bioinform. 2017, 18, 518. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Frid, Y.; Gusfield, D. An improved Four-Russians method and sparsified Four-Russians algorithm for RNA folding. Algorithms Mol. Biol. 2016, 11, 22. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jacob, A.; Buhler, J.; Chamberlain, R.D. Accelerating Nussinov RNA Secondary Structure Prediction with Systolic Arrays on FPGAs. In Proceedings of the 2008 International Conference on Application-Specific Systems, Architectures and Processors, Leuven, Belgium, 2–4 July 2008; pp. 191–196. [Google Scholar] [CrossRef] [Green Version]
- Mathuriya, A.; Bader, D.A.; Heitsch, C.E.; Harvey, S.C. GTfold: A Scalable Multicore Code for RNA Secondary Structure Prediction. In Proceedings of the 2009 ACM Symposium on Applied Computing, New York, NY, USA, 8–12 March 2009; pp. 981–988. [Google Scholar]
- Markham, N.R.; Zuker, M. UNAFold. In Bioinformatics: Structure, Function and Applications; Keith, J.M., Ed.; Humana Press: Totowa, NJ, USA, 2008; pp. 3–31. [Google Scholar]
- Lorenz, R.; Bernhart, S.H.; Höner zu Siederdissen, C.; Tafer, H.; Flamm, C.; Stadler, P.F.; Hofacker, I.L. ViennaRNA Package 2.0. Algorithms Mol. Biol. 2011, 6, 26. [Google Scholar] [CrossRef]
- Trifunovic, K.; Nuzman, D.; Cohen, A.; Zaks, A.; Rosen, I. Polyhedral-model guided loop-nest auto-vectorization. In Proceedings of the 2009 18th International Conference on Parallel Architectures and Compilation Techniques, Raleigh, NC, USA, 12–16 September 2009; pp. 327–337. [Google Scholar]
- Palkowski, M.; Bielecki, W. Parallel tiled Nussinov RNA folding loop nest generated using both dependence graph transitive closure and loop skewing. BMC Bioinform. 2017, 18, 290. [Google Scholar] [CrossRef] [Green Version]
- Wonnacott, D.; Jin, T.; Lake, A. Automatic tiling of “mostly-tileable” loop nests. In Proceedings of the IMPACT 2015: 5th International Workshop on Polyhedral Compilation Techniques, Amsterdam, The Netherlands, 19–21 January 2015. [Google Scholar]
- Mullapudi, R.T.; Bondhugula, U. Tiling for Dynamic Scheduling. In Proceedings of the 4th International Workshop on Polyhedral Compilation Techniques, Vienna, Austria, 20 January 2014; Rajopadhye, S., Verdoolaege, S., Eds.; 2014. Available online: https://acohen.gitlabpages.inria.fr/impact/impact2014/ (accessed on 1 September 2021).
- Bondhugula, U.; Hartono, A.; Ramanujam, J.; Sadayappan, P. A practical automatic polyhedral parallelizer and locality optimizer. In Proceedings of the 29th ACM SIGPLAN Conference on Programming Language Design and Implementation, London, UK, 15–20 June 2008; Volume 43, pp. 101–113. [Google Scholar]
- Griebl, M. Automatic Parallelization of Loop Programs for Distributed Memory Architectures; Univ. Passau: Passau, Germany, 2004. [Google Scholar]
- Irigoin, F.; Triolet, R. Supernode partitioning. In Proceedings of the 15th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL88, San Diego, CA, USA, 10–13 January 1988; ACM: New York, NY, USA, 1988; pp. 319–329. [Google Scholar]
- Lim, A.; Cheong, G.I.; Lam, M.S. An Affine Partitioning Algorithm to Maximize Parallelism and Minimize Communication. In Proceedings of the 13th international conference on Supercomputing, Rhodes, Greece, 20–25 June 1999; ACM Press: Portland, OR, USA, 1999; pp. 228–237. [Google Scholar]
- Ramanujam, J.; Sadayappan, P. Tiling multidimensional itertion spaces for multicomputers. J. Parallel Distrib. Comput. 1992, 16, 108–120. [Google Scholar] [CrossRef]
- Wolf, M.E.; Lam, M.S. A data locality optimizing algorithm. In Proceedings of the Proceedings of the ACM SIGPLAN 1991 Conference on Programming Language Design and Implementation, Toronto, Canada, 24–28, June 1991; Volume 26, pp. 30–44. [Google Scholar]
- Xue, J. Loop Tiling for Parallelism; Kluwer Academic Publishers: Norwell, MA, USA, 2000. [Google Scholar]
- Bielecki, W.; Skotnicki, P. Insight into tiles generated by means of a correction technique. J. Supercomput. 2019, 75, 2665–2690. [Google Scholar] [CrossRef] [Green Version]
- Palkowski, M.; Bielecki, W. Tuning iteration space slicing based tiled multi-core code implementing Nussinov’s RNA folding. BMC Bioinform. 2018, 19, 12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Smith, T.; Waterman, M. Identification of common molecular subsequences. J. Mol. Biol. 1981, 147, 195–197. [Google Scholar] [CrossRef]
- Waterman, M.S.; Smith, T.F. RNA secondary structure: A complete mathematical analysis. Math. Biosci. 1978, 42, 257–266. [Google Scholar] [CrossRef]
- Knuth, D.E. Optimum binary search trees. Acta Inform. 1971, 1, 14–25. [Google Scholar] [CrossRef]
- Bondhugula, U. Effective Automatic Parallelization and Locality Optimization Using the Polyhedral Model. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2008. [Google Scholar]
- Verdoolaege, S.; Grosser, T. Polyhedral Extraction Tool. In Proceedings of the 2nd International Workshop on Polyhedral Compilation Techniques, Paris, France, 23 January 2012. [Google Scholar]
- Verdoolaege, S. Counting affine calculator and applications. In Proceedings of the First International Workshop on Polyhedral Compilation Techniques (IMPACT’11), Charmonix, France, 3 April 2011. [Google Scholar]
- Verdoolaege, S.; Janssens, G. Scheduling for PPCG. Report CW 2017, 706. [Google Scholar] [CrossRef]
- Wolfe, M. Loops skewing: The wavefront method revisited. Int. J. Parallel Program. 1986, 15, 279–293. [Google Scholar] [CrossRef]
- Bondhugula, U.; Bandishti, V.; Pananilath, I. Diamond tiling: Tiling techniques to maximize parallelism for stencil computations. IEEE Trans. Parallel Distrib. Syst. 2016, 28, 1285–1298. [Google Scholar] [CrossRef]
- Grosser, T.; Cohen, A.; Holewinski, J.; Sadayappan, P.; Verdoolaege, S. Hybrid hexagonal/classical tiling for GPUs. In Proceedings of the Annual IEEE/ACM International Symposium on Code Generation and Optimization, Orlando, FL, USA, 14–15 February 2014; pp. 66–75. [Google Scholar]
- Bielecki, W.; Palkowski, M. Tiling arbitrarily nested loops by means of the transitive closure of dependence graphs. Int. J. Appl. Math. Comput. Sci. (AMCS) 2016, 26, 919–939. [Google Scholar] [CrossRef] [Green Version]
- Javanmard, M.M.; Ahmad, Z.; Kong, M.; Pouchet, L.N.; Chowdhury, R.; Harrison, R. Deriving parametric multi-way recursive divide-and-conquer dynamic programming algorithms using polyhedral compilers. In Proceedings of the 18th ACM/IEEE International Symposium on Code Generation and Optimization, San Diego, CA, USA, 22–26 February 2020; pp. 317–329. [Google Scholar]

| Tile and Code Features | Sets Used | Sets Not Used |
|---|---|---|
| Shape | Arbitrary; tile surfaces are perpendicular to axes , in general, and the tile surfaces along the reminding axes can be arbitrary. | Tiles are rectangular. |
| Size | Limited to the number of instances inside a time slice within the space tile calculated as . | Not limited when m is less than the loop nest depth. |
| Dimension | m | |
| Parallelism degree | m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bielecki, W.; Palkowski, M. Space-Time Loop Tiling for Dynamic Programming Codes. Electronics 2021, 10, 2233. https://doi.org/10.3390/electronics10182233
Bielecki W, Palkowski M. Space-Time Loop Tiling for Dynamic Programming Codes. Electronics. 2021; 10(18):2233. https://doi.org/10.3390/electronics10182233
Chicago/Turabian StyleBielecki, Wlodzimierz, and Marek Palkowski. 2021. "Space-Time Loop Tiling for Dynamic Programming Codes" Electronics 10, no. 18: 2233. https://doi.org/10.3390/electronics10182233
APA StyleBielecki, W., & Palkowski, M. (2021). Space-Time Loop Tiling for Dynamic Programming Codes. Electronics, 10(18), 2233. https://doi.org/10.3390/electronics10182233







