An Eleven-Level Switched-Capacitor Inverter with Boosting Capability
Abstract
:1. Introduction
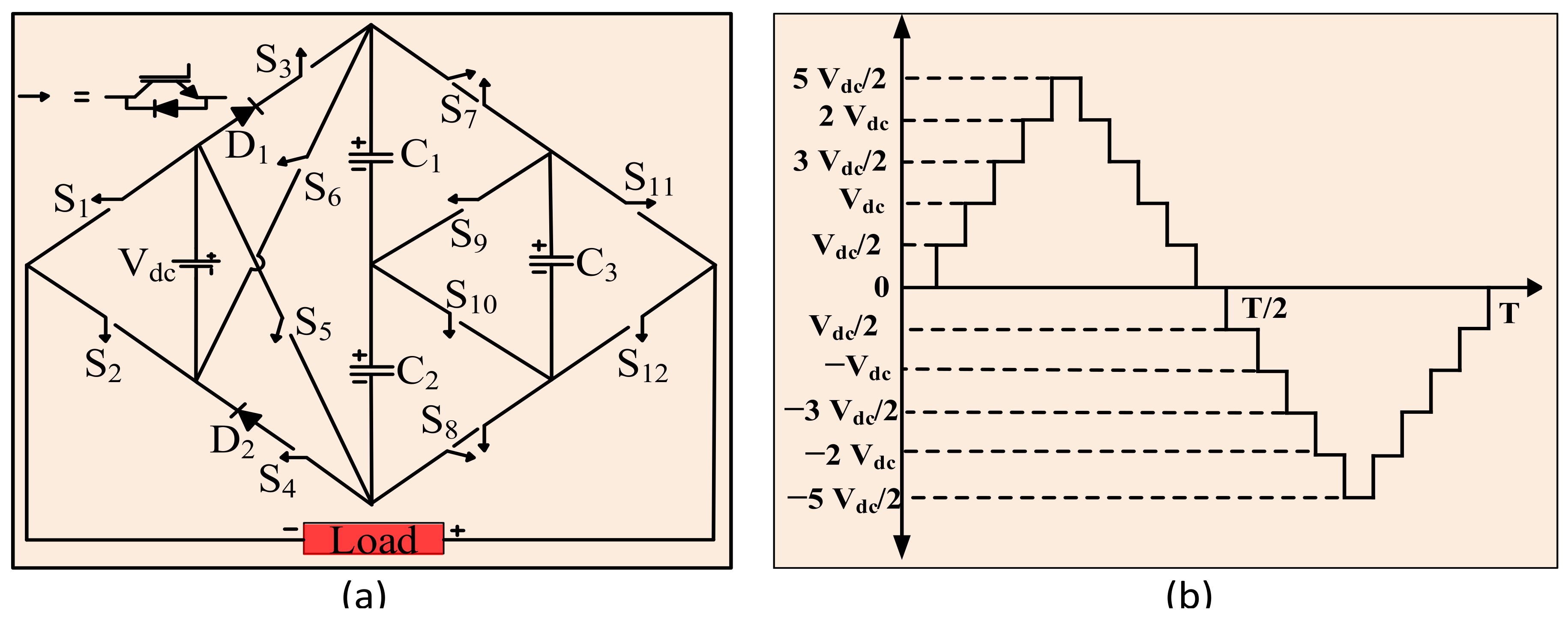
2. Proposed Switched-Capacitor Topology
2.1. Circuit Analysis
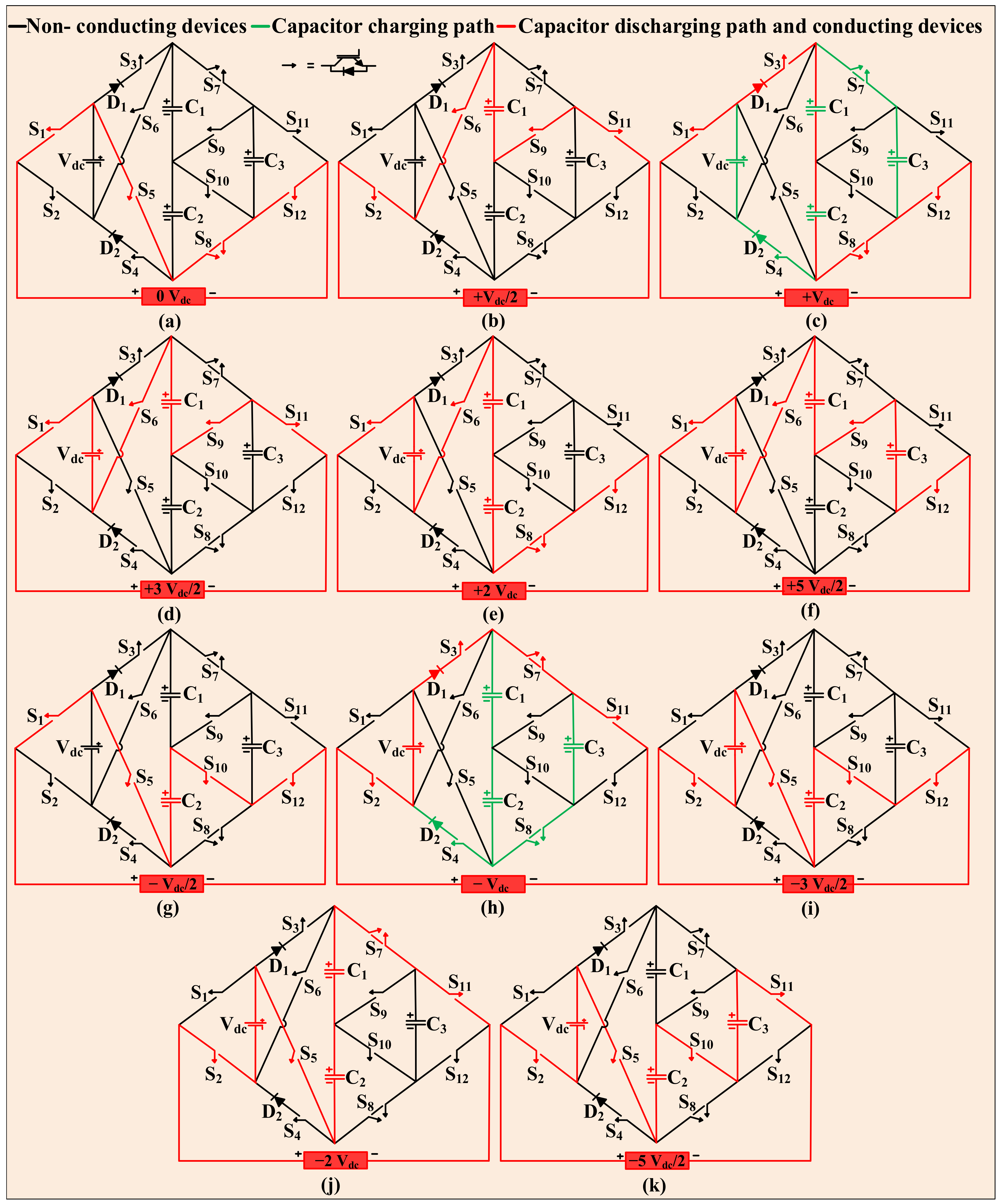
2.2. Working of the Topology for Different Voltage Levels
- Zero level: Zero voltage at the load is obtained by turning the switches S1, S5, S8, and S12 on, as depicted in Figure 2a.
- 0.5 Vdc level: The required energy is supplied to the load terminals by the energy stored in C1 by turning S2, S6, S9, and S11 on, as shown in Figure 2b.
- 1 Vdc level: The energy stored in capacitors C1 and C2 is used to generate this level by turning S1, S3, S8, and S12 on. At the same time, all the capacitors are charged in this mode by turning S4 and S7 on, as shown in Figure 2c.
- 1.5 Vdc level: The required energy to generate this level at the output is obtained by the supply voltage of 1 Vdc and the energy stored in C1 by turning S1, S6, S9, and S11 on, as shown in Figure 2d.
- 2 Vdc level: The energy stored in capacitors C1 and C2 and the input supply of 1 Vdc are used to generate this level by turning S1, S6, S8, and S12 on, as shown in Figure 2e.
- 2.5 Vdc level: The energy stored in capacitors C1 and C3 and the input supply of 1 Vdc are used to generate this level by turning S1, S6, S9, and S12 on, as depicted in Figure 2f.
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | S11 | S12 | C1 | C2 | C3 | Output Voltage |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Y | N | N | N | Y | N | N | Y | N | N | N | Y | NC | NC | NC | 0 |
| N | Y | N | N | N | Y | N | N | Y | N | Y | N | D | NC | NC | Vdc/2 |
| Y | N | Y | Y | N | N | Y | Y | N | N | N | Y | C | C | C | Vdc |
| Y | N | N | N | N | Y | N | N | Y | N | Y | N | D | NC | NC | 3 Vdc/2 |
| Y | N | N | N | N | Y | N | Y | N | N | N | Y | D | D | NC | 2 Vdc |
| Y | N | N | N | N | Y | N | N | Y | N | N | Y | D | NC | D | 5 Vdc/2 |
| Y | N | N | N | Y | N | N | Y | N | N | N | Y | NC | NC | NC | 0 |
| Y | N | N | N | Y | N | N | N | N | Y | N | Y | NC | D | NC | −Vdc/2 |
| N | Y | Y | Y | N | N | Y | Y | N | N | Y | N | C | C | C | −Vdc |
| N | Y | N | N | Y | N | N | N | N | Y | N | Y | NC | D | NC | −3 Vdc/2 |
| N | Y | N | N | Y | N | Y | N | N | N | Y | N | D | D | NC | −2 Vdc |
| N | Y | N | N | Y | N | N | N | N | Y | Y | N | NC | D | D | −5 Vdc/2 |
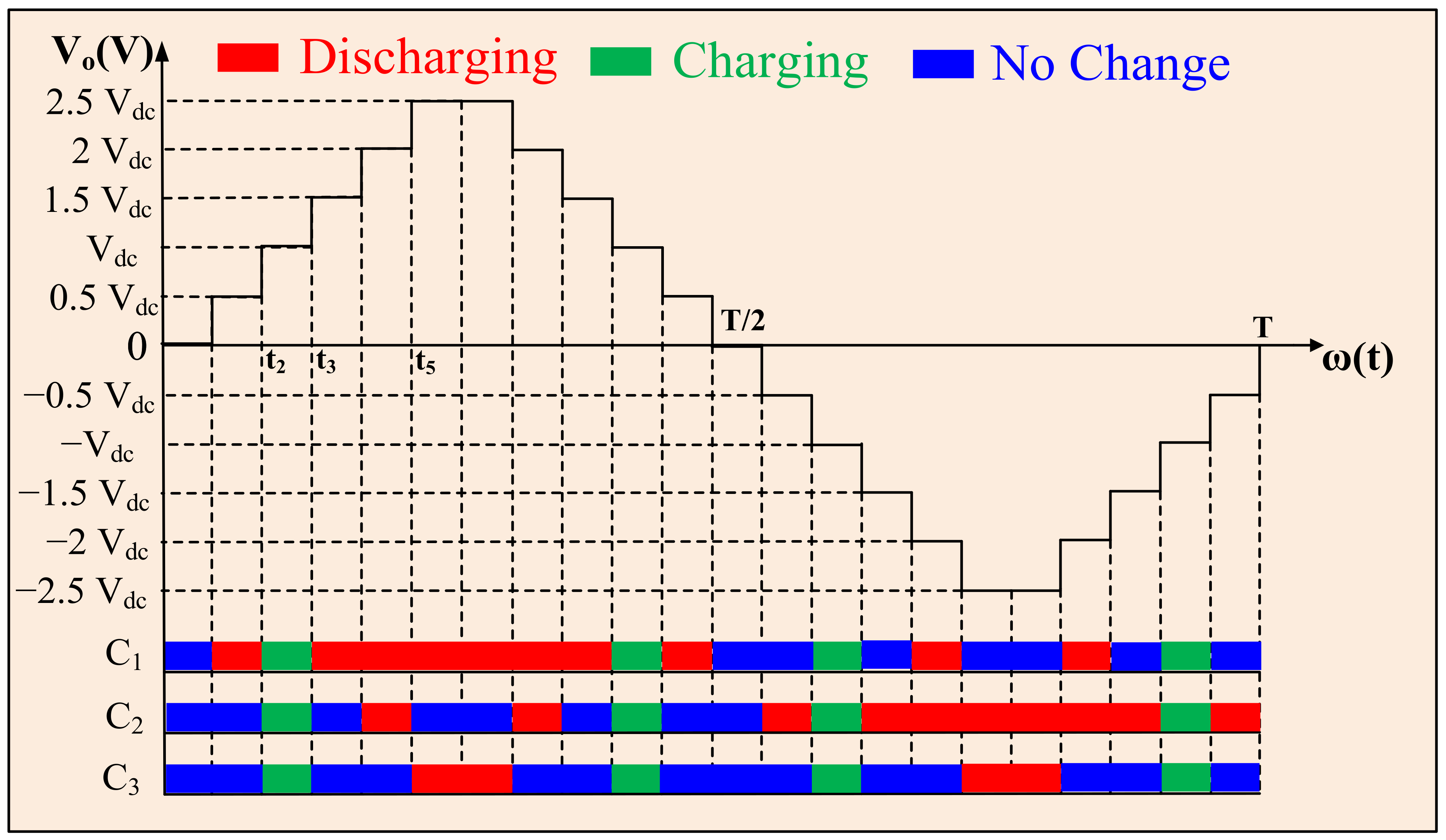
2.3. Capacitor Voltage Balance and Capacitance Calculation
2.4. Power Loss Analysis
2.4.1. Ripple or Charging Loss (PR)
2.4.2. Ohmic Loss (PO)
2.4.3. Switching Loss (PS)
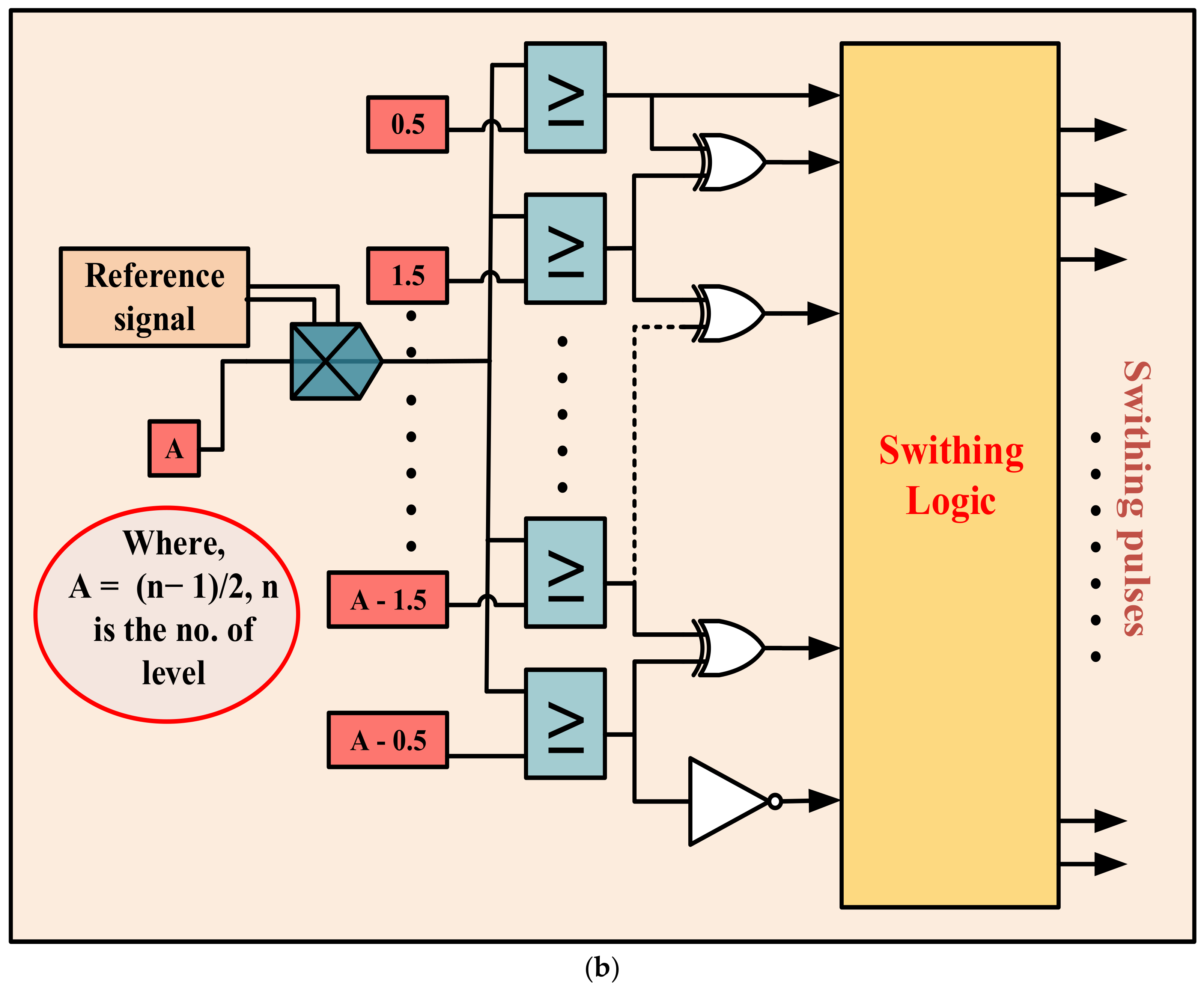
2.5. Nearest Level Control (NLC)
3. Comparative Analysis
4. Results and Discussion
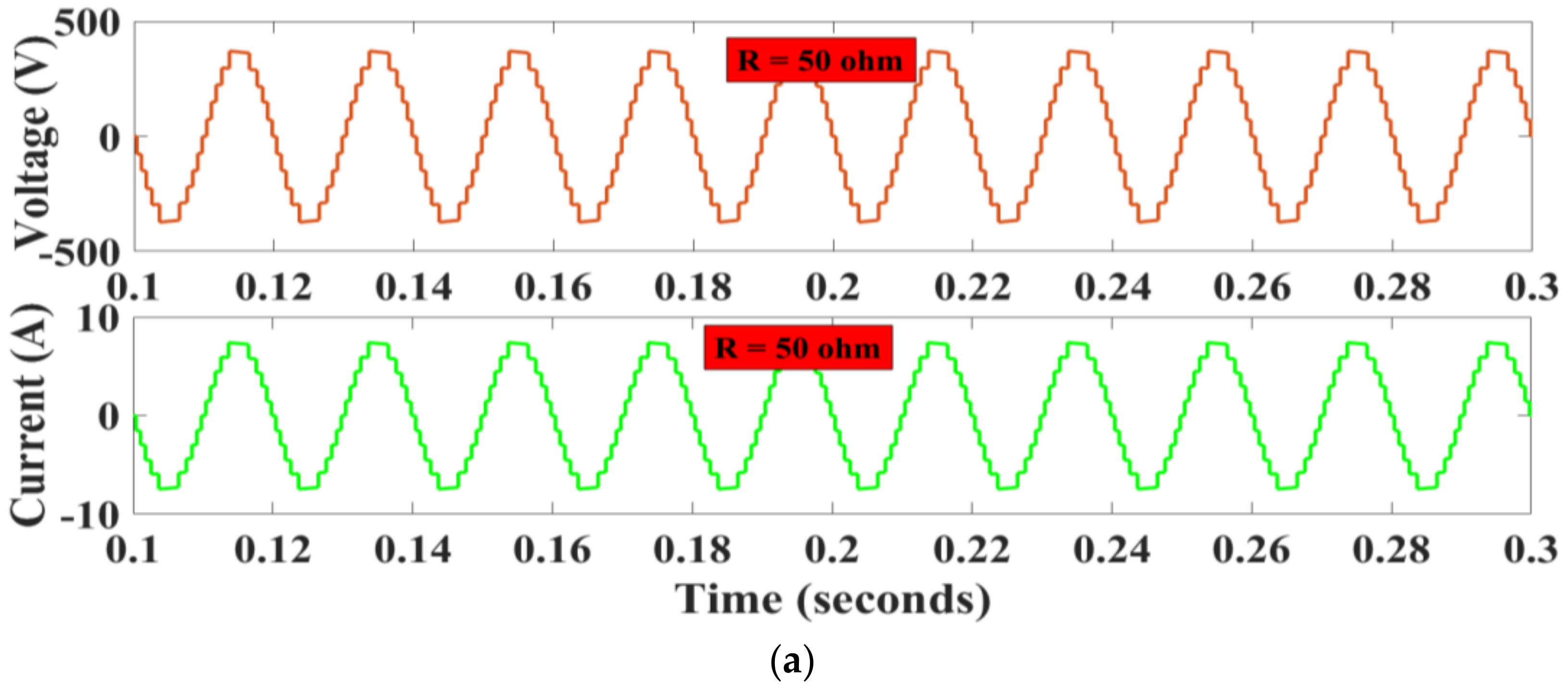
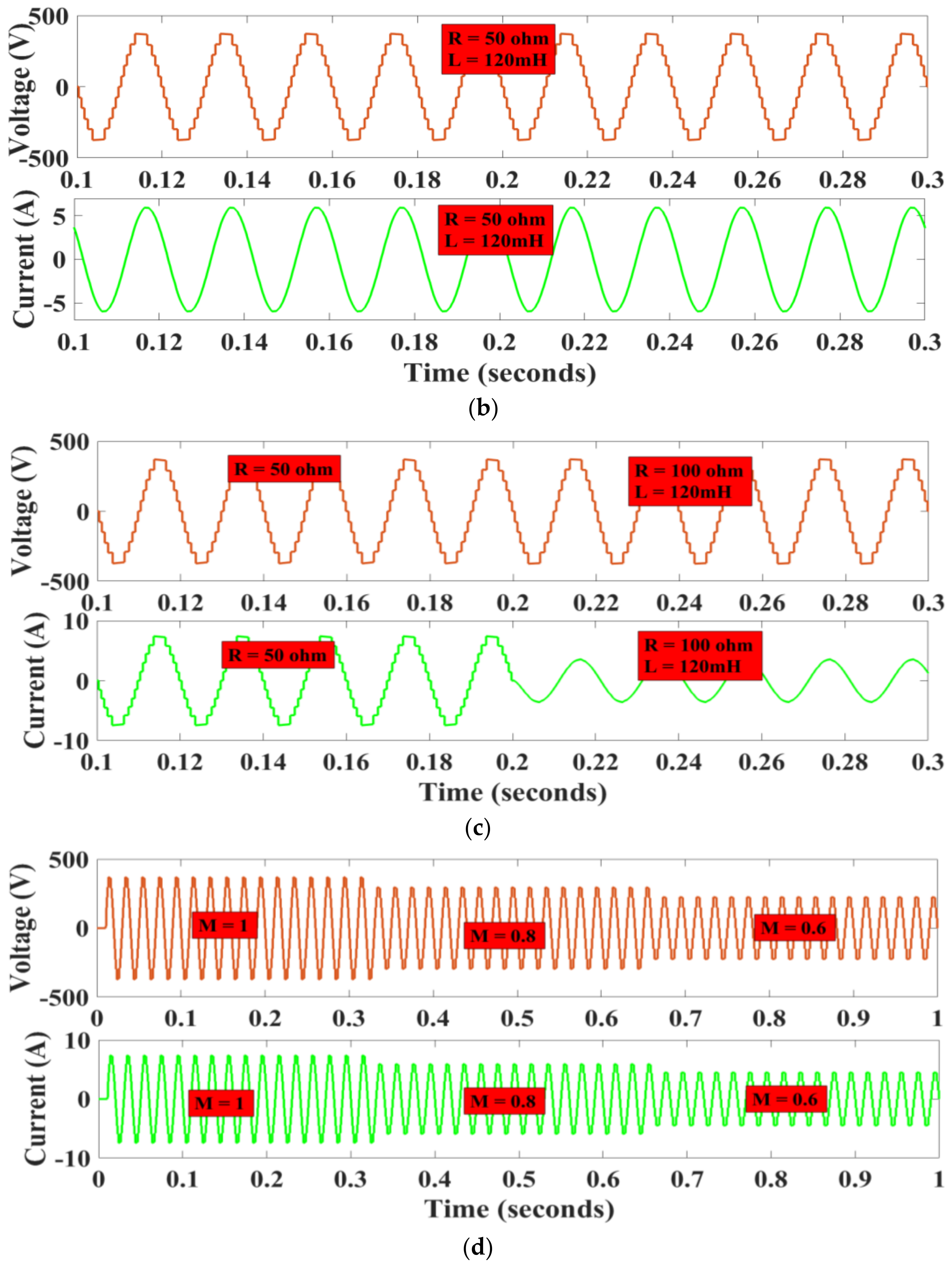
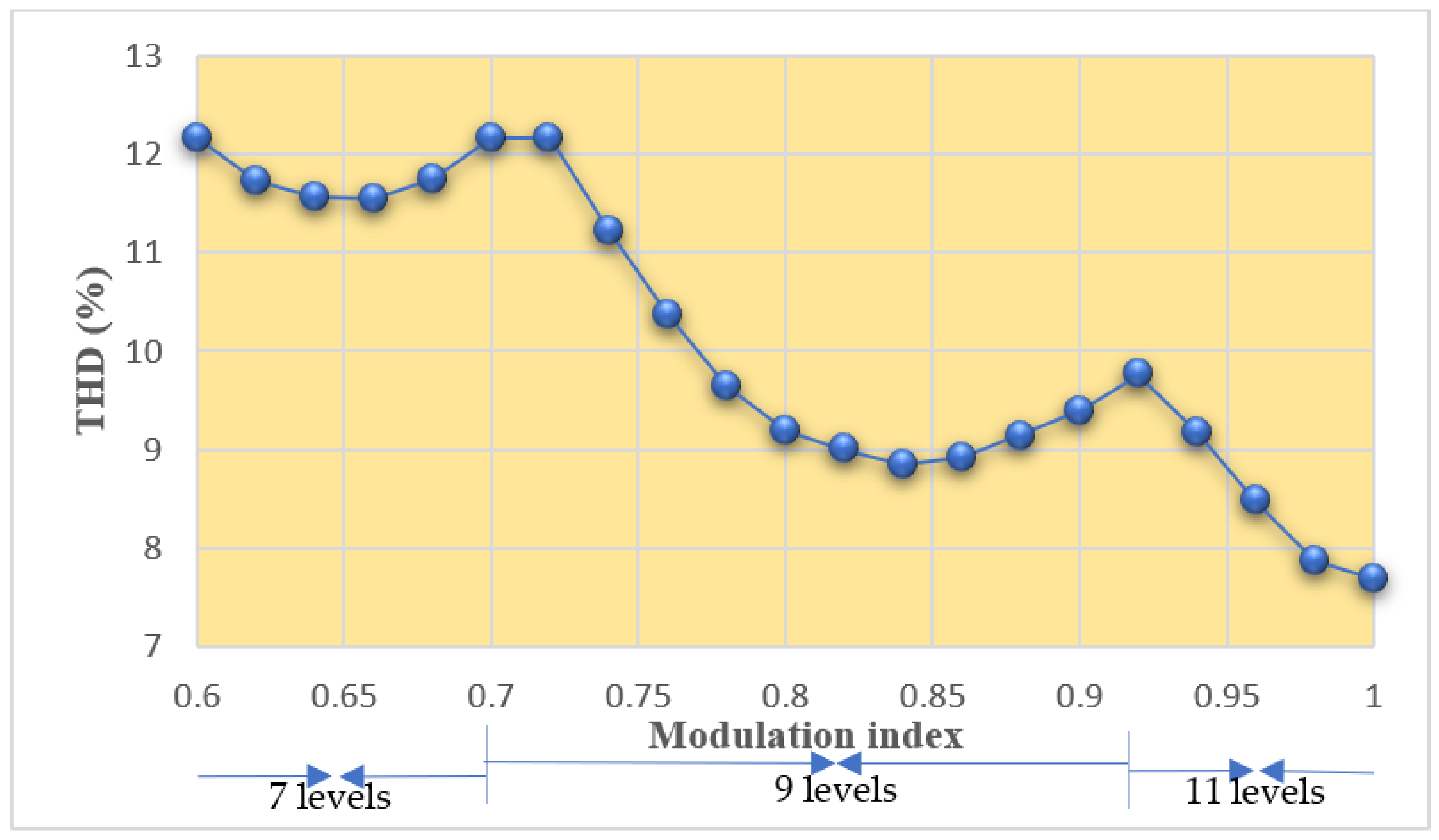
4.1. Simulation Results
4.2. Hardware Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sandeep, N.; Yaragatti, U.R. Design and implementation of a sensorless multilevel inverter with reduced part count. IEEE Trans. Power Electron. 2017, 32, 6677–6683. [Google Scholar] [CrossRef]
- Tayyab, M.; Sarwar, A.; Tariq, M.; Chakraborty, R.K.; Ryan, M.J. Hardware-in-the-loop implementation of projectile target search algorithm for selective harmonic elimination in a 3-phase multilevel converter. IEEE Access 2020, 9, 30626–30635. [Google Scholar] [CrossRef]
- Sathik, M.J.; Vijayakumar, K.; Member, S. Compact Switched Capacitor Multilevel Inverter (CSCMLI) with self voltage balancing and boosting ability. IEEE Trans. Power Electron. 2018, 34, 4009–4013. [Google Scholar] [CrossRef]
- Naik, B.S.; Suresh, Y.; Venkataramanaiah, J.; Panda, A.K. A hybrid nine-level inverter topology with boosting capability and reduced component count. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 316–320. [Google Scholar] [CrossRef]
- Hussan, M.R.; Ansari, M.K.; Lodi, K.A.; Sarwar, A.; Tariq, M.; Husain, H. Genetic algorithm based optimal operation of a modified H-bridge single phase multilevel inverter. In Proceedings of the 2019 International Conference on Power Electronics, Control and Automation (ICPECA 2019), New Delhi, India, 16–17 November 2019. [Google Scholar] [CrossRef]
- Prabaharan, N.; Palanisamy, K. A comprehensive review on reduced switch multilevel inverter topologies, modulation techniques and applications. Renew. Sustain. Energy Rev. 2017, 76, 1248–1282. [Google Scholar] [CrossRef]
- Shiva Naik, B.; Suresh, Y.; Venkataramanaiah, J. Experimental verification of a hybrid multilevel inverter with voltage-boosting ability. Int. J. Circuit Theory Appl. 2020, 48, 420–434. [Google Scholar] [CrossRef]
- Kim, K.M.; Han, J.K.; Moon, G.W. A High step-up switched-capacitor 13-level inverter with reduced number of switches. IEEE Trans. Power Electron. 2021, 36, 2505–2509. [Google Scholar] [CrossRef]
- Sandeep, N. A 13-level switched-capacitor-based boosting inverter. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 998–1002. [Google Scholar] [CrossRef]
- Sedaghati, F.; Majareh, S.H.L. A multilevel inverter based on cascade connection of submultilevel units with reduced switch count. Int. J. Circuit Theory Appl. 2019, 47, 1152–1172. [Google Scholar] [CrossRef]
- Rana, R.A.; Patel, S.A.; Muthusamy, A.; Lee, C.W.; Kim, H.J. Review of multilevel voltage source inverter topologies and analysis of harmonics distortions in FC-MLI. Electronics 2019, 8, 1329. [Google Scholar] [CrossRef] [Green Version]
- Hussan, M.R.; Sarwar, A.; Siddique, M.D.; Mekhilef, S.; Ahmad, S.; Sharaf, M.; Zaindin, M.; Firdausi, M. A novel switched-capacitor multilevel inverter topology for energy storage and smart grid applications. Electronics 2020, 9, 1703. [Google Scholar] [CrossRef]
- Xun, Z.; Ding, H.; He, Z. A novel switched-capacitor inverter with reduced capacitance and balanced neutral-point voltage. Electronics 2021, 10, 947. [Google Scholar] [CrossRef]
- Hussan, M.R.; Sarwar, A.; Siddique, M.D.; Iqbal, A.; Alamri, B. A cross connected asymmetrical switched-capacitor multilevel inverter. IEEE Access 2021, 9, 96416–96429. [Google Scholar] [CrossRef]
- Lin, W.; Zeng, J.; Hu, J.; Junfeng, L. Hybrid nine-level boost inverter with simplified control and reduced active devices. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 2038–2050. [Google Scholar] [CrossRef]
- Panda, N.; Das, B.; Chakrabarti, A.; Kasari, P.R.; Bhattacharaya, A.; Chatterjee, D. A new grid interactive eleven-level hybrid inverter topology for medium-voltage application. IEEE Trans. Ind. Appl. 2020, 57, 869–881. [Google Scholar] [CrossRef]
- Priyadarshi, A.; Kar, P.K.; Karanki, S.B. A single source transformer-less boost multilevel inverter topology with self-voltage balancing. IEEE Trans. Ind. Appl. 2020, 56, 3954–3965. [Google Scholar] [CrossRef]
- Siddique, M.D.; Mekilef, S.; Shah, N.M.; Memon, M.A. Optimal design of a new cascaded multilevel inverter topology with reduced switch count. IEEE Access 2019, 7, 24498–24510. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.A.; Sarebanzadeh, M.; Rivera, M.; Babaei, E.; Wheeler, P. A reduced single-phase switched-diode cascaded multilevel inverter. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 3556–3569. [Google Scholar] [CrossRef]
- Sun, X.; Wang, B.; Zhou, Y.; Wang, W.; Du, H.; Lu, Z. A single DC source cascaded seven-level inverter integrating switched-capacitor techniques. IEEE Trans. Ind. Electron. 2016, 63, 7184–7194. [Google Scholar] [CrossRef]
- Bana, P.R.; Panda, K.P.; Panda, G. Power quality performance evaluation of multilevel inverter with reduced switching devices and minimum standing voltage. IEEE Trans. Ind. Inform. 2020, 16, 5009–5022. [Google Scholar] [CrossRef]
- Alishah, R.S.; Hosseini, S.H.; Babaei, E.; Sabahi, M. A new general multilevel converter topology based on cascaded connection of submultilevel units with reduced switching components, DC sources, and blocked voltage by switches. IEEE Trans. Ind. Electron. 2016, 63, 7157–7164. [Google Scholar] [CrossRef]
- Khan, M.N.H.; Forouzesh, M.; Siwakoti, Y.P.; Li, L.; Blaabjerg, F. Switched capacitor integrated (2n + 1)-level step-up single-phase inverter. IEEE Trans. Power Electron. 2020, 35, 8248–8260. [Google Scholar] [CrossRef]
- Siddique, M.D.; Reddy, B.P.; Iqbal, A.; Mekhilef, S. Reduced switch count-based N-level boost inverter topology for higher voltage gain. IET Power Electron. 2020, 13, 3505–3509. [Google Scholar] [CrossRef]
- Reddy, B.P.; Siddique, M.D.; Iqbal, A.; Mekhilef, S.; Rahman, S.; Maroti, P.K. 7L-SCBI topology with minimal semiconductor device count. IET Power Electron. 2020, 13, 3199–3203. [Google Scholar] [CrossRef]



| 11-Level MLI | Nsw | Ndr | Nd | Ndc | Nc | Gain | TSVp.u | Efficiency (%) |
|---|---|---|---|---|---|---|---|---|
| [16] | 12 | 6 | 0 | 1 | 5 | 1 | 3.0 | 97.32 |
| [18] | 8 | 7 | 0 | 3 | 1 | 1 | 4.4 | - |
| [21] | 9 | 9 | 1 | 3 | 1 | 1 | 4.2 | 96 |
| [22] | 10 | 10 | 4 | 2 | 2 | 1 | 5.2 | 93.85 |
| [23] | 17 | 17 | 1 | 1 | 5 | 1 | 3.33 | 96.5 |
| Proposed | 14 | 9 | 2 | 1 | 3 | 2.5 | 3.0 | 96.75 |
| DC voltage sources | 150 V |
| Capacitors | 4700 μF, 200 V, 2200 μF, 200 V |
| Load resistance | 50 Ω, 100 Ω |
| Load inductance | 120 mH |
| Output frequency | 50 Hz |
| Switching frequency | 50 Hz |
| DC Voltage Sources | 25 V (Vdc) |
| Capacitors | 4700 μF, 100 V, 2200 μF, 100 V |
| Load Resistance | 30 Ω, 50 Ω, 60 Ω |
| Load Inductance | 50 mH |
| Output frequency | 50 Hz |
| Switching frequency | 50 Hz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussan, M.R.; Sarwar, A.; Khan, I.; Tariq, M.; Tayyab, M.; Alhosaini, W. An Eleven-Level Switched-Capacitor Inverter with Boosting Capability. Electronics 2021, 10, 2262. https://doi.org/10.3390/electronics10182262
Hussan MR, Sarwar A, Khan I, Tariq M, Tayyab M, Alhosaini W. An Eleven-Level Switched-Capacitor Inverter with Boosting Capability. Electronics. 2021; 10(18):2262. https://doi.org/10.3390/electronics10182262
Chicago/Turabian StyleHussan, Md Reyaz, Adil Sarwar, Irfan Khan, Mohd Tariq, Mohammad Tayyab, and Waleed Alhosaini. 2021. "An Eleven-Level Switched-Capacitor Inverter with Boosting Capability" Electronics 10, no. 18: 2262. https://doi.org/10.3390/electronics10182262
APA StyleHussan, M. R., Sarwar, A., Khan, I., Tariq, M., Tayyab, M., & Alhosaini, W. (2021). An Eleven-Level Switched-Capacitor Inverter with Boosting Capability. Electronics, 10(18), 2262. https://doi.org/10.3390/electronics10182262









