Restoration of Dimensions for Ancient Drawing Recognition

Abstract

This study aims to investigate and determine the actual size of the “cheok” scale—The traditional weights and measures of Korea—To aid in data construction on the recognition of ancient drawings in the field of artificial intelligence. The cheok scale can be divided into Yeongjocheok, Jucheok, Pobaekcheok, and Joryegicheok. This study calculated the actual dimensions used in the drawings of Tonga and Eonjo contained in Jaseungcha Dohae by Gyunam Ha BaeckWon, which helped us analyze the scale used in the southern region of Korea in the 1800s. The scales of 1/15 cheok and 1/10 cheok were used in the Tonga and Eonjo sections in Jaseungcha Dohae, and the actual dimensions in the drawing were converted to the scale used at the time. Owing to the conversion, the dimensions in the drawings of Tonga were converted to 30.658 cm per cheok, and ~31.84 cm per cheok for Eonjo. In this manner, the actual dimensions used in the southern region of Korea around the year 1800 were restored. Through this study, the reference values for drawing recognition of machinery drawings in Korea around 1800 were derived.

1. Introduction

Long before deep learning technology was commonly utilized for image recognition, there was continuous research on the recognition of engineering drawings. However, using the conventional geometry-based object recognition technique, it was difficult to recognize various classes and objects containing deformation and noise. In contrast, this problem can be solved by using deep learning technology primarily based on convolutional neural networks (CNNs), which are a representative technique that have drawn considerable research attention recently for their ability to recognize the type and location of objects in images as long as sufficient and high-quality training data are available. In recent years, deep learning development tools such as TensorFlow, Keras, PyTorch, and Theano have been released. These tools support efficient construction, training, and use of deep learning models and parallel processing using GPUs without extra coding, which makes it convenient for non-experts to utilize deep learning technology in their research [1,2,3,4,5]. For this reason, classical drawing recognition is difficult due to the presence of many different dimensions. This paper aims to restore different metrology lengths using proportional expressions.

To train a deep learning model to recognize drawings, the structure of the training data and data generation need to be defined. Ancient drawing data pose problems in this regard, such as the accuracy of the number values in the drawings, and their restoration to the weights and measures of contemporary times [6,7,8,9,10].

The problem of assuring uniformity and consistency in the measurements of length and volume has been addressed by all human civilizations in history. In most civilizations, lengths taken from the human body—such as the length of a hand, an arm, a foot, or overall height—were used as direct measurement scales. This phenomenon was commonly found in various cultural activities in ancient human societies [11,12,13,14,15].

In the history of the Joseon Dynasty, the scales used in the private sector were categorized into Yeongjocheok, Jucheok, and Pobaekcheok, depending on their purpose. Yeongjocheok, which was also called Mokcheok, was mainly used in the woodworking and construction sectors. Pobaekcheok was primarily employed in the fabric trade, and tended to be shorter than the set standard, in order to prevent losses during the process of selling fabrics. There was a dual system of weights and measures: a governmental system, which was used for tax collection, and a private sector system, which was used for commercial and economic activities. Indeed, there was an organic relationship between the two systems, and the overall trend was that the regulatory governmental weights and measures unified many different weights and measures in the private sector. However, in reality, the two different scales of government and the private sector existed in parallel [16].

This study first analyzes the difference between the weights and measures officially recognized by the central government of the Chosun Dynasty in the 1800s, and the weights and measures that were used in the regional provinces. In Section 2, from the content of Jaseungcha Dohae by Gyunam Ha BaeckWon, Tonga and Eonjo—whose weight and measure scales can be calculated—are described. In Section 3, measurements on the drawings are performed for Tonga and Eonjo, and the calculated values are converted to Yeongjocheok and average scale values are obtained.

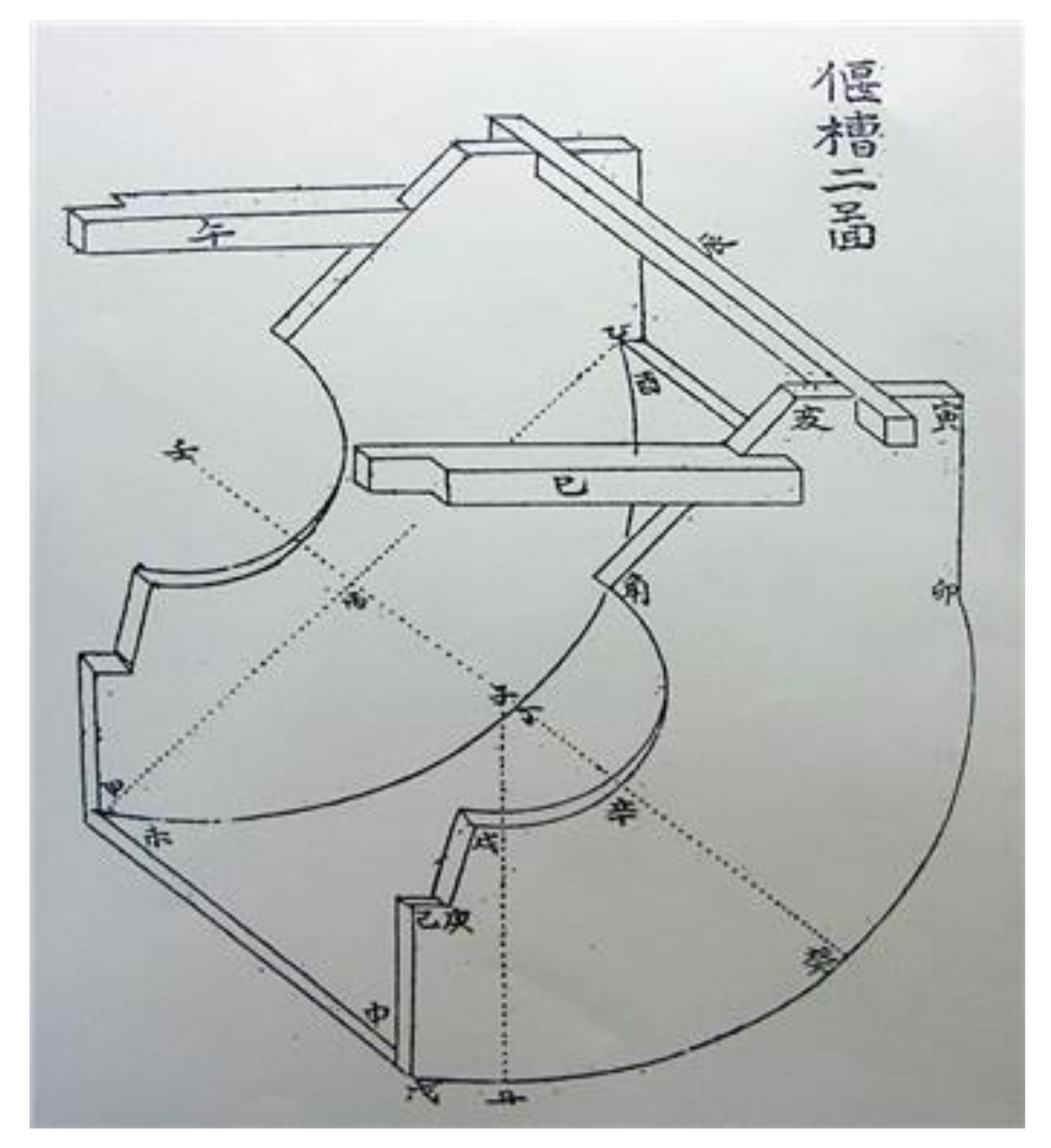
2. Jaseungcha Dohae

Ha BaeckWon was around 30 years old when he wrote Jaseungcha Dohae and Jaseungcha Dohaesul, a guide and manual with drawings for a device called the Jaseungcha. He wrote in the preface, “While I was reading through numerous books in my spare time and thinking through various ideas, an idea dawned on me that enabled me to develop and complete a device called Jaseungcha. The aim of developing this device is to benefit people by saving people’s physical efforts and labor through the use of this device.”

The structure of the Jaseungcha comprises three parts: the cylinder, the gear, and the frame. The essence of the operating mechanism is that a turbine is rotated by the flow velocity of the stream, and the rotating turbine lifts the piston and pumps up the water. The modern analysis of the Jaseungcha sample demonstrates that the device requires advanced technologies, and can only be designed and fabricated with in-depth knowledge of hydromechanics and mathematics. The significance of Jaseungcha Dohae lies in that it reveals the principles and calculation formulas required for drafting a blueprint of the device, which was used during the latter periods of the Joseon Dynasty in the 1800s.

Ha BaeckWon made a comment in the Tonga and Eonjo sections of Jaseungcha Dohae that “1 of 15 cheok unit was used in the Tonga drawing, while 1 of 10 cheok unit was used in the Eonjo drawing.”

This indicates that the actual size of each part in the Jaseungcha was reduced by the scale of $\frac{1}{15}$ and $\frac{1}{10}$ in the drawings. The currently known standard lengths of Yeongjocheok are 1 cheok = 30.6 cm, 1 chon = 3.06 cm, and 1 pun = 0.3 cm. In this regard, this study aims to calculate the actual size of the parts presented in the Tonga section of Jaseungcha Dohae and to analyze the proportional relationship of the actual size of the parts using the industrial–academic method used at the time.

Figure 1 shows the dimensions presented in the Tonga blueprint of Jaseungcha Dohaesul. The figure shows that the length of one column on the base plate of Tonga is marked as 42 cheok by Ha BaeckWon.

This value in terms of the current known Yeongjocheok is $42\times 3.06=128.52$ cm, which gives 8.568 cm when reduced by $\frac{1}{15}$. That is, the length of the column on the base plate of the Tonga drawing in the original copy of Jaseungcha Dohae is measured at 8.568 cm, which indicates that Ha BaeckWon prepared the drawing at a scale of 1/15 according to the standards of Yeongjocheok. In addition, considering that the drawing is based on a three-dimensional plan, the reduction in the dimensions of the frontal view and those of the sides and the top surface needs to be considered.

Figure 2 is a blueprint of Eonjo in Jaseungcha Dohae. Ha BaeckWon made detailed records of the length of the curved surface and the radius. He also explained that he did not go through the fabrication process of Eonjo, and only recorded the figures by calculation, with the drawing being based on a scale of $\frac{1}{10}$.

3. Measurement and Analysis of Jaseungcha Dohae

The analysis of the measurement data of the drawings in Jasungcha Dohae is presented as follows. The data were measured using an electronic Vernier caliper and a transparent measuring instrument that allows the measurement of the thickness of the lines and size of the letter types after copying the original Jasungcha Dohae in the same size. Figure 3 is flowchart of the algorithm.

Due to the lack of measurement data on the classical drawings, the proportional formula was measured based on the data described. Measurement methods and analysis followed the following sequence:

-

Collection of drawings describing proportional formulae;

-

Copying of classical drawings to the same size;

-

Measurement of the length of each line in the drawing;

-

Storage of neural network learning data for each line segment;

-

Implementation of machine learning through the average value of each line.

3.1. Scale Analysis of Tonga in Jaseungcha Dohae

The measurements of scale for the Tonga section of Jaseungcha Dohae and Yeongjocheok conversion were performed for each part of the Tonga. The base and column parts, along with the upper plate and parts applied with scale perspective, were measured, and the connecting part with Eonjo was classified as the Eonjo section for the measurement.

Table 1. Comparison of base dimensions.

Location of the Parts					Cheok	Drawing	15X	Converted Cheok
Base	East	Length	Upper	Left	4.2	85.78	1286.7	306.36
				Right	4.2	86.61	1299.15	309.32
			Lower		4.2	86.88	1303.2	310.29
		Circumference	Upper	Width	0.4	7.68	115.2	288
				Length	0.4	6.33	94.95	237.38
			Lower	Width	0.4	7.93	118.95	297.38
				Length	0.4	8.58	128.7	321.75
	West	Length	Upper	Left	4.2	86.10	1291.5	307.5
				Right	4.2	86.61	1299.15	309.32
			Lower		4.2	86.28	1294.2	308.14
		Circumference	Upper	Width	0.4	8.41	126.15	315.37
				Length	0.4	5.76	86.4	216
			Lower	Width	0.4	8.14	122.1	305.25
				Length	0.4	7.96	119.4	298.5
	North	Length	Upper	Upper	4.2	103.99	1559.85	371.39
				Lower	4.2	104.53	1567.95	373.32

outlines the measurements of 19 samples—the base part of Tonga. The Tonga base, which is a hexahedral wooden structure that forms the main part of the structure, was designed with 4 cheoks of 2 chons in length, and the thickness of the wood is 4 chons. When the units are converted to modern centimeters, the length is about 1.5 m, and the thickness of the wood is over 12 cm, indicating a considerably robust and thick design. If Yeongjocheok is calculated based on the actual dimensions, the value is 310.41 mm, which after scale conversion is equivalent to approximately 31 cm.

As can be seen in

Table 2. Comparison of column dimensions.

Location of the Parts				Cheok	Drawing	15X	Converted Cheok
Column	Length	Front		5.7	101.97	1529.55	305.91
		Back		5.7	101.97	1529.55	305.91
	Circumference	Front		0.4	8.53	127.95	319.88
		Back		0.4	8.53	127.95	319.88
	Depth	Front	Left	0.3	7.25	108.75	362.5
			Right	0.3	7.25	108.75	362.5
		Back	Left	0.3	5.90	88.5	295
			Right	0.3	5.90	88.5	295

and

Table 3. Comparison of Seungtongga (drainage line) dimensions.

Location of the Parts				Cheok	Drawing	15X	Converted Cheok
Seungtongga	Connecting Part	Distance		4.25	8.69	130.35	306.71
		Width		0.1	2.08	31.2	312
		Length		0.65	13.21	198.15	304.85
	Latch	Inner side	Left	0.4	8.05	120.75	301.88
			Right	0.4	8.05	120.75	301.88
		Surface	Left	0.3	4.76	71.4	238
			Right	0.3	4.83	71.4	238
		Depth	Left	0.15	2.89	43.35	289
			Right	0.15	2.89	43.35	289

, in the part where the dimension becomes smaller than 4 cheoks or 3 cheoks, the error due to the thickness of the brush used at the time tends to be larger, and in general, drawing with the dimension exceeding 3 cheoks is less affected by the thickness of the brush. Table 2 lists the measured and compared lengths of the columns. According to the data recorded in Jaseungcha Dohae, the length was 5 cheoks and 7 chons, but considering that the connection was made using a butterfly latch by digging the groove of the column, this part was excluded and, thus, the column length was measured to be 5 cheoks, which was used as the reference value. The frontal figure showed a ratio close to that of the Yeongjocheok, but the part where perspective was applied showed a certain degree of error. Measurements ranged between 29.5 cm and 31.98 cm. For longer columns, in the blueprint, the actual measurement value of 5 cheoks and 7 chons was 101.97 cm, and when this value was multiplied by 15, the result was 1529.55 cm, while when this value was again divided by 5 cheoks and 7 chons, the value of Yeongjocheok for actual measurement was 30.59 cm—approximately 30.6 cm.

Table 3 outlines the dimensions of the Seungtongga part, which connects the path of water that is pumped and raised. The direction of flow in Seungtongga is described in detail, and it can be seen that the larger lengths in the drawing are more or less similar to those in Yeongjocheok, while other smaller dimensions show differences depending on the size of the brush.

Table 4. Comparison of pendulum support dimensions.

Location of the Parts			Cheok	Drawing	15X	Converted Cheok
Pendulum support	Height	Left	2.67	54.11	811.65	303.99
		Right	2.67	54.11	811.65	303.99
	Lower side	Left	0.25	4.88	73.2	292.8
		Right	0.25	4.88	73.2	292.8
	Left and Right side	Left	0.3	6.30	94.5	315
		Right	0.3	6.30	94.5	315

outlines the dimensions of the pendulum support—a part that connects the rotating shaft of the turbine stemming from Eonjo. From the bottom, data values of large dimensions showed similar results to Yeongjocheok, and errors occurred as the dimensions decreased due to the thickness of the brush.

The scale of each part described in Jaseungcha Dohae was compared with the dimensions of the actual drawing. Measurements in the drawings were made with an electronic Vernier caliper, multiplied by 15, and then divided by the recorded “cheok/pun/ri.” The measurement shows that the thickness of the line segment is approximately 1 mm, which when multiplied by 15 and divided by the scale results in an error of 15 mm. That is, if the error for the thickness of the brush is converted into cheok/pun/ri, the measurement error may occur within the range of 15 mm for each part. Accordingly, the mean value through matching was calculated for the measurement dimensions of each part.

If the data for each part are a_i, the following can be represented for 51 measurements:

∑ a_i ÷ 51 = 15635.79 ÷ 51 = 306.58

(1)

This value indicates that the measurement scale of the devices manufactured in the Hwasun Dongbok area is approximately 306.58 mm. At the time, there were active exchanges between Hwasun Dongbok area and Najumok; thus, the length scale was not significantly different between the two regions.

3.2. Scale Analysis of Tonga in Jaseungcha Dohae

The scale of each part of the Eonjo section described in Jaseungcha Dohae was compared with the dimensions of the actual drawing. Measurements in the drawings were made with an electronic Vernier caliper, which were multiplied by 10 and then divided by the recorded “cheok/pun/ri”.

Table 5. Comparison of Eonjo support dimensions.

Location of the Parts			Cheok	Drawing	15X	Converted Cheok
Eonjo support	Height		0.53	10.95	164.25	309.9
	Depth	Inside		19.56	293.4	302.47
		Outside	0.97	19.56	293.4	302.47
	Outer groove	Upper	0.1	2.29	34.35	343.5
		Lower	0.1	2.29	34.35	343.5
	Inner groove	Upper	0.2	3.76	56.4	282
		Lower	0.2	3.65	54.75	273.75

outlines the dimensions of the part connected to Eonjo, which is designed in the form of a support that is connected from Tonga to Eonjo.

Table 6. Comparison of Eonjo dimensions.

Location of the Parts			Cheok	Drawing	10X	Converted Cheok
Eonjo	Chord		3.77	114.91	1149.1	304.8
	Si part		1.06	32.75	327.5	308.96
	Base	Thickness	0.1	2.33	23.3	233
		Width	2	64.54	645.4	322.7
	Large side width		2.2	67.73	67.73	307.86

outlines the dimensions of the pendulum support—a part that connects the rotating shaft of the turbine stemming from Eonjo. From the bottom, data values of large dimensions showed similar results to Yeongjocheok, and errors occurred as the dimensions decreased due to the thickness of the brush. In particular, in the part that represents the rotating body, the error due to the thickness of the brush was significantly large.

Table 7. Comparison of dimensions of the side and corner parts of Eonjo.

Location of the Parts			Cheok	Drawing	10X	Converted Cheok
Eonjo	Side	Length	4.8	145.74	1457.4	303.625
		Thickness	0.1	2.86	28.6	286
	Corner	Radius	2.3	70.98	709.8	308.61
		Height	1.5	72.94	729.4	486.26
		Radius	0.8	24.62	246.2	307.8

compares the dimensions of various other parts. Similar to other parts of Eonjo, in

Table 8. Comparison of dimensions of other parts of Eonjo.

Location of the Parts	Cheok	Drawing	10X	Converted Cheok
Dimensions of other parts of Eonjo	0.47	13.4	134	285.11
	1	29.52	295.2	295.2
	0.2	5.08	50.8	254
	1.1	33.41	334.1	303.73
	0.8	24.5	245	306.25
	0.16	4.74	47.4	296.25
	2.06	79.11	791.1	304.27
	2	60.13	601.3	300.65
	0.2	5.99	59.9	299.5

, the smaller the dimension, the larger the error, and the closer the value is to 1 cheok, the closer it was measured to 30 cm.

The thickness of the line segment is approximately 1 mm, which is multiplied by 10 and divided by the scale, resulting in an error of 10 mm. That is, if the error for the thickness of the brush is converted into cheok/pun/ri, the measurement error may occur within the range of 10 mm for each part. Accordingly, the mean value through matching was calculated for the measurement dimensions of each part.

If the data for each part are a_i, the following can be represented for 26 measurements:

∑ a_i ÷ 26 = 306.62

(2)

In this case, if the average value is calculated by excluding the upper and lower outliers, a scale conversion value of approximately 302.20 can be obtained.

4. Conclusions

From the middle of the 1700s to the early 1800s, the Hwasun Dongbok area was a region that played a central role in Silhak—a Korean Confucian social reform movement promoting the use of science and technology, by Seokdang Na GyeongJeok and Gyunam Ha BaeckWon. Driven by advances made in communications, Seokdang Na GyeongJeok produced Honcheoneui—an armillary sphere for Hong Daeyong—while Gyunam Ha BaeckWon, who was a generation younger than him, wrote Jaseungcha Dohae—a guide with drawings for an automatic water pump called the Jaseungcha. Both instruments were fabricated and designed based on a profound level of mathematics and physics at the time. In this context, it is important and natural to examine and determine the weights and measures of the times, which we believe will form the basis for producing innovative products and tools today.

In this study, to restore the actual scales used and applied in Korea in the 1800s, measurements were taken with drawings presented in Jaseungcha Dohae. The average of the converted values for each dimension was 306.58 mm in Tonga, which used 1/15 scale in drawings, and the average of the converted values in Eonjo, which used the scale of 1/10 cheok, was 306.62 mm. The measurements were taken using an electronic Vernier caliper that can measure up to 1/100 mm, and a transparent measuring instrument that can measure the thickness of the line. In the measurement process, for small dimensions of less than 4 chon, there was a significant error between the thickness of the line and the thickness of the actual scale due to the thickness of the brush, but for dimensions larger than 1 cheok, more accurate values were obtained.

The average conversion values of Tonga and Eonjo, which are 306.58 mm and 306.62 mm, respectively, are within the range of 303–330 mm—the conversion standard of Yeongjocheok used as a standard after the mid-Joseon period.

Based on this study, new data for the analysis of ancient drawings were obtained in the field of drawing recognition and analysis. The restoration of actual values using the proportional relationship of ancient drawings will be of great use to the restoration of various traditional scientific instruments and the composition of the actual scale. It is expected that the follow-up studies will support research on more accurate scales, and various other devices using the scales.