Analysis of an Inhomogeneous Circularly Polarized Hollow Dielectric Resonator Antenna Using Perturbation Theory
Abstract
:1. Introduction
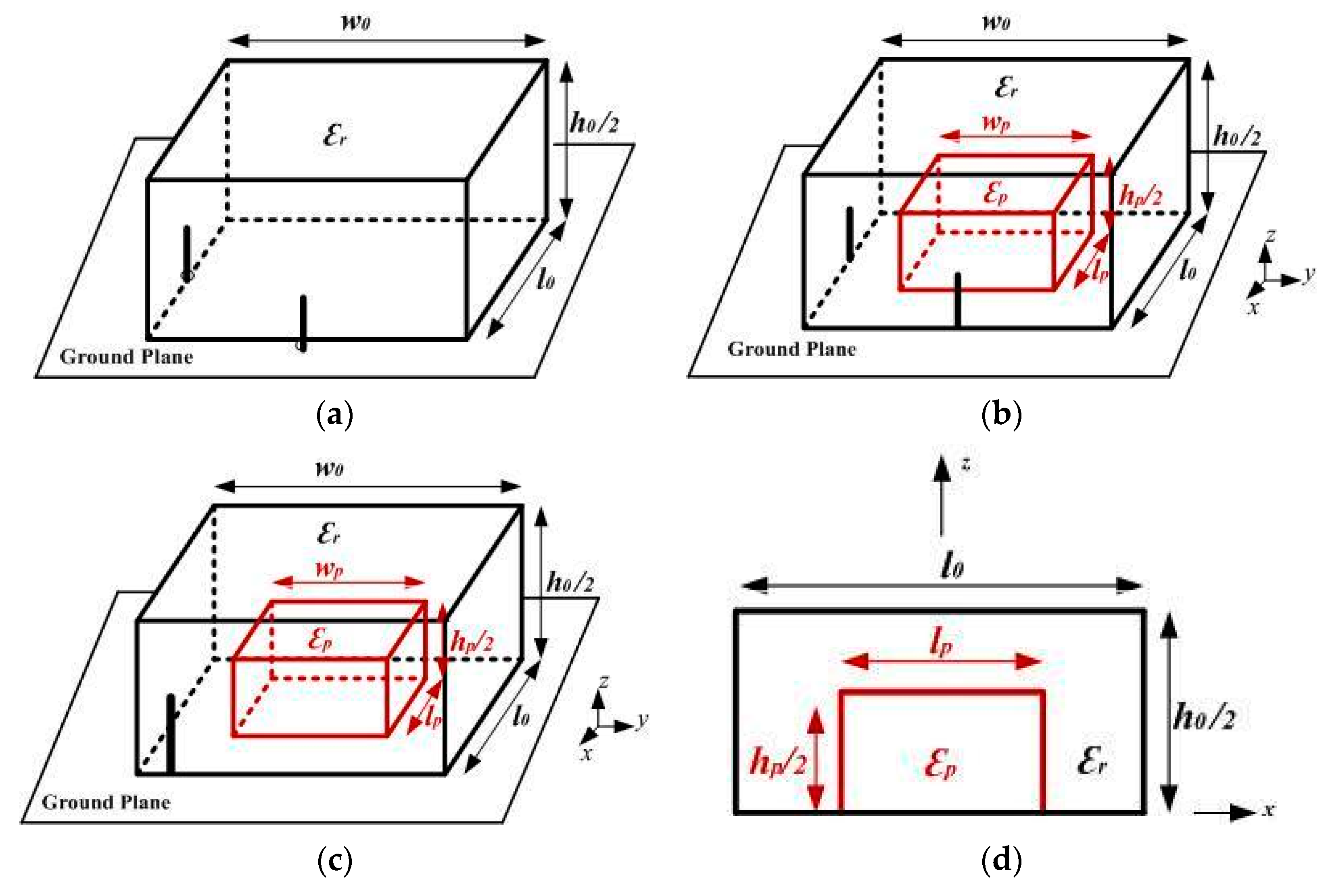
2. Theoretical Implementation
2.1. Resonant Frequency of the Mode of an Inhomogeneous RDRA Using Perturbation Theory
2.2. Resonant Frequency of the Mode of the Inhomogeneous RDRA Using Perturbation Theory
2.3. Resonant Frequency of a Circularly Polarized Inhomogeneous RDRA Using Perturbation Theory
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Field Equations forandMode of Homogeneous Rectangular DRA | |
| Mode | Mode |
| A is the arbitrary constant and are the wave numbers along the x, y, and z directions, respectively. | |
References
- Varshney, G. Gain and Bandwidth Enhancement of a Singly Fed Circularly Polarized Dielectric Resonator Antenna. IET Microw. Antennas Propag. 2020, 14, 1323–1330. [Google Scholar] [CrossRef]
- Ali, I.; Jamaluddin, M.H.; Gaya, A.; Rahim, H.A. A Dielectric Resonator Antenna with Enhanced Gain and Bandwidth for 5G Applications. Sensors 2020, 20, 675. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, M.D.; Pan, Y.M.; Sun, Y.X.; Leung, K.W. Wideband Circularly Polarized Substrate-Integrated Embedded Dielectric Resonator Antenna for Millimeter-Wave Applications. IEEE Trans. Antennas Propag. 2020, 68, 1145–1150. [Google Scholar] [CrossRef]
- Pan, Y.M.; Leung, K.W.; Luk, K.M. Design of the millimeter-wave rectangular dielectric resonator antenna using a higher-order mode. IEEE Trans. Antennas Propag. 2011, 59, 2780–2788. [Google Scholar] [CrossRef]
- Varshney, G.; Singh, R.; Pandey, V.S.; Yaduvanshi, R.S. Circularly Polarized Two-Port MIMO Dielectric Resonator Antenna. Prog. Electromagn. Res. M 2020, 91, 19–28. [Google Scholar] [CrossRef]
- Gotra, S.; Varshney, G.; Yaduvanshi, R.S.; Pandey, V.S. Dual-band circular polarisation generation technique with the miniaturisation of a rectangular dielectric resonator antenna. IET Microw. Antennas Propag. 2019, 13, 1742–1748. [Google Scholar] [CrossRef]
- Majeed, A.H.; Abdullah, A.S.; Elmegri, F.; Sayidmarie, K.H.; Abd-Alhameed, R.A.; Noras, J.M. Dual-segment S-shaped aperture-coupled cylindrical dielectric resonator antenna for X-band applications. IET Microw. Antennas Propag. 2015, 9, 1673–1682. [Google Scholar] [CrossRef] [Green Version]
- Varshney, G.; Gotra, S.; Pandey, V.S.; Yaduvanshi, R.S. Inverted-Sigmoid Shaped Multi-Band Dielectric Resonator Antenna with Dual Band Circular Polarization. IEEE Trans. Antennas Propag. 2018. [Google Scholar] [CrossRef]
- Kishk, A.A. An elliptic dielectric resonator antenna designed for circular polarization with single feed. Microw. Opt. Technol. Lett. 2003, 37, 454–456. [Google Scholar] [CrossRef]
- Turitsyna, E.G.; Webb, S. Simple design of FBG-based VSB filters for ultra-dense WDM transmission ELECTRONICS LETTERS 20th January 2005. Electron. Lett. 2005, 41, 40–41. [Google Scholar] [CrossRef]
- Shaik, L.A.; Saha, C.; Arora, S.; Das, S.; Siddiqui, J.Y.; Iyer, A.K. Bandwidth control of cylindrical ring dielectric resonator antennas using metallic cap and sleeve loading. IET Microw. Antennas Propag. 2017, 11, 1742–1747. [Google Scholar] [CrossRef]
- Ghosh, B.; Bhattacharya, D.; Sinha, P.D.; Werner, D.H. Design of Circular Waveguide Annular Slot-Coupled Two-Layer DRA for Linear and Circular Polarizations. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 1012–1016. [Google Scholar] [CrossRef]
- Petosa, A.; Ittipiboon, A. Dielectric Resonator Antennas: A Historical Review and the Current State of the Art. IEEE Antennas Propag. Mag. 2010, 52, 91–116. [Google Scholar] [CrossRef]
- Gürel, Ç.S.; Co, H.; Akal, Ö. Accurate Resonant Frequency Computation of Multisegment Rectangular Dielectric Resonator Antennas. J. Electromagn. Waves 2010, 37–41. [Google Scholar] [CrossRef] [Green Version]
- Rashidian, A.; Forooraghi, K.; Tayefeh, M.R. Design algorithm of multisegment dielectric resonator antennas (MSDRAs). In Proceedings of the Asia-Pacific Radio Science Conference, Qingdao, China, 24–27 August 2004; pp. 134–137. [Google Scholar]
- Petosa, A.; Simons, N.; Siushansian, R.; Ittipiboon, A.; Cuhaci, M. Design and Analysis of Multisegment Dielectric Resonator Antennas. IEEE Trans. Antennas Propag. 2000, 48, 738–742. [Google Scholar] [CrossRef]
- Rashidian, A.; Forooraghi, K.; Allgodarz, M.T. Investigations on two-segment dielectric resonator antennas. Microw. Opt. Technol. Lett. 2005, 45, 533–537. [Google Scholar] [CrossRef]
- Fakhte, S.; Oraizi, H. Derivation of the resonant frequency of rectangular dielectric resonator antenna by the perturbation theory. Appl. Comput. Electromagn. Soc. J. 2016, 31, 894–900. [Google Scholar]
- Sehrawat, N.; Kanaujia, B.K.; Agarwal, A. Calculation of the resonant frequency of a rectangular dielectric resonator antenna using perturbation theory. J. Comput. Electron. 2019, 18, 211–221. [Google Scholar] [CrossRef]
- Darimireddy, N.K.; Reddy, R.R.; Prasad, A.M. Wideband Circularly Polarized Cylindrical Dielectric Resonator Antennas with Rectangular Curved Slots [Antenna Applications Corner]. IEEE Antennas Propag. Mag. 2020, 62, 65–73. [Google Scholar] [CrossRef]
- Trinh-Van, S.; Yang, Y.; Lee, K.Y.; Hwang, K.C. A wideband circularly polarized pixelated dielectric resonator antenna. Sensors 2016, 16, 1349. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reddy, R.V.; Ameen, M.; Chaudhary, R.K.; Kumar Gangwar, R. Compact wideband circularly polarized rectangular DRA with right angled conformal strip feed. In Proceedings of the 2019 IEEE Indian Conference on Antennas and Propogation (InCAP), Ahmedabad, India, 19–22 December 2019; pp. 4–7. [Google Scholar] [CrossRef]
- Trinh-Van, S.; Yang, Y.; Lee, K.Y.; Hwang, K.C. Single-Fed Circularly Polarized Dielectric Resonator Antenna with an Enhanced Axial Ratio Bandwidth and Enhanced Gain. IEEE Access 2020, 8, 41045–41052. [Google Scholar] [CrossRef]
- Lu, K.; Leung, K.W.; Pan, Y.M. Theory and experiment of the hollow rectangular dielectric resonator antenna. IEEE Antennas Wirel. Propag. Lett. 2011, 10, 631–634. [Google Scholar] [CrossRef]
- Maity, S.; Gupta, B. Theory and experiments on horizontally inhomogeneous Rectangular Dielectric Resonator Antenna. AEU-Int. J. Electron. Commun. 2017, 76, 158–165. [Google Scholar] [CrossRef]
- Schaap, M.G.; Robinson, D.A.; Friedman, S.P.; Lazar, A. Measurement and Modeling of the TDR Signal Propagation through Layered Dielectric Media. Soil Sci. Soc. Am. J. 2003, 67, 1113–1121. [Google Scholar] [CrossRef]
- Chan, Y.; Knight, J. Determining water content and saturation from dielectric measurements in layered materials commonly made to determine water and in turn to determine accuracy with which water content or saturation information can be obtained from dielectric homogeneous mi. Water Resour. 1999, 35, 85–93. [Google Scholar] [CrossRef]
- Chan, C.Y.; Knight, R.J. Laboratory measurements of electromagnetic wave velocity in layered sands. Water Resour. Res. 2001, 37, 1099–1105. [Google Scholar] [CrossRef]
- Robinson, D.A.; Jones, S.B.; Wraith, J.M.; Or, D.; Friedman, S.P. A Review of Advances in Dielectric and Electrical Conductivity Measurement in Soils Using Time Domain Reflectometry. Vadose Zo. J. 2003, 2, 444. [Google Scholar] [CrossRef]
- Park, C.H.; Behrendt, A.; LeDrew, E.; Wulfmeyer, V. New approach for calculating the effective dielectric constant of the moist soil for microwaves. Remote Sens. 2017, 9, 732. [Google Scholar] [CrossRef] [Green Version]
- Harrington, R.F. Times Harmonic Electromagnetic Fields; McGraw-Hill: New York, NY, USA, 1961. [Google Scholar]
- Petosa, A.; Thirakoune, S. Rectangular dielectric resonator antennas with enhanced gain. IEEE Trans. Antennas Propag. 2011, 59, 1385–1389. [Google Scholar] [CrossRef]
- Abdulmajid, A.A.; Khalil, Y.; Khamas, S. Higher Order Mode Circularly Polarized Two-Layer Rectangular Dielectric Resonator Antenna. Antennas Wirel. Propag. Lett. 2018, 1225, 1–4. [Google Scholar] [CrossRef]
- Varshney, G. Wideband THz absorber: By merging the resonance of dielectric cavity and graphite disk resonator. IEEE Sens. J. 2020, 21, 1635–1643. [Google Scholar] [CrossRef]
- Kumar, R.; Varshney, G.; Yaduvanshi, R.S.; Kumar, D.; Pandey, V.S. Dual-Band Dielectric Resonator Antenna with Multi- Frequency Circular Polarization. IET Microw. Antennas Propag. 2020, 14, 435–439. [Google Scholar] [CrossRef]
- Patel, P.; Mukherjee, B.; Mukherjee, J. Wideband Circularly Polarized Rectangular Dielectric Resonator Antennas using Square Shaped Slots. IEEE Antennas Wirel. Propag. Lett. 2015, 15, 1309–1312. [Google Scholar] [CrossRef]
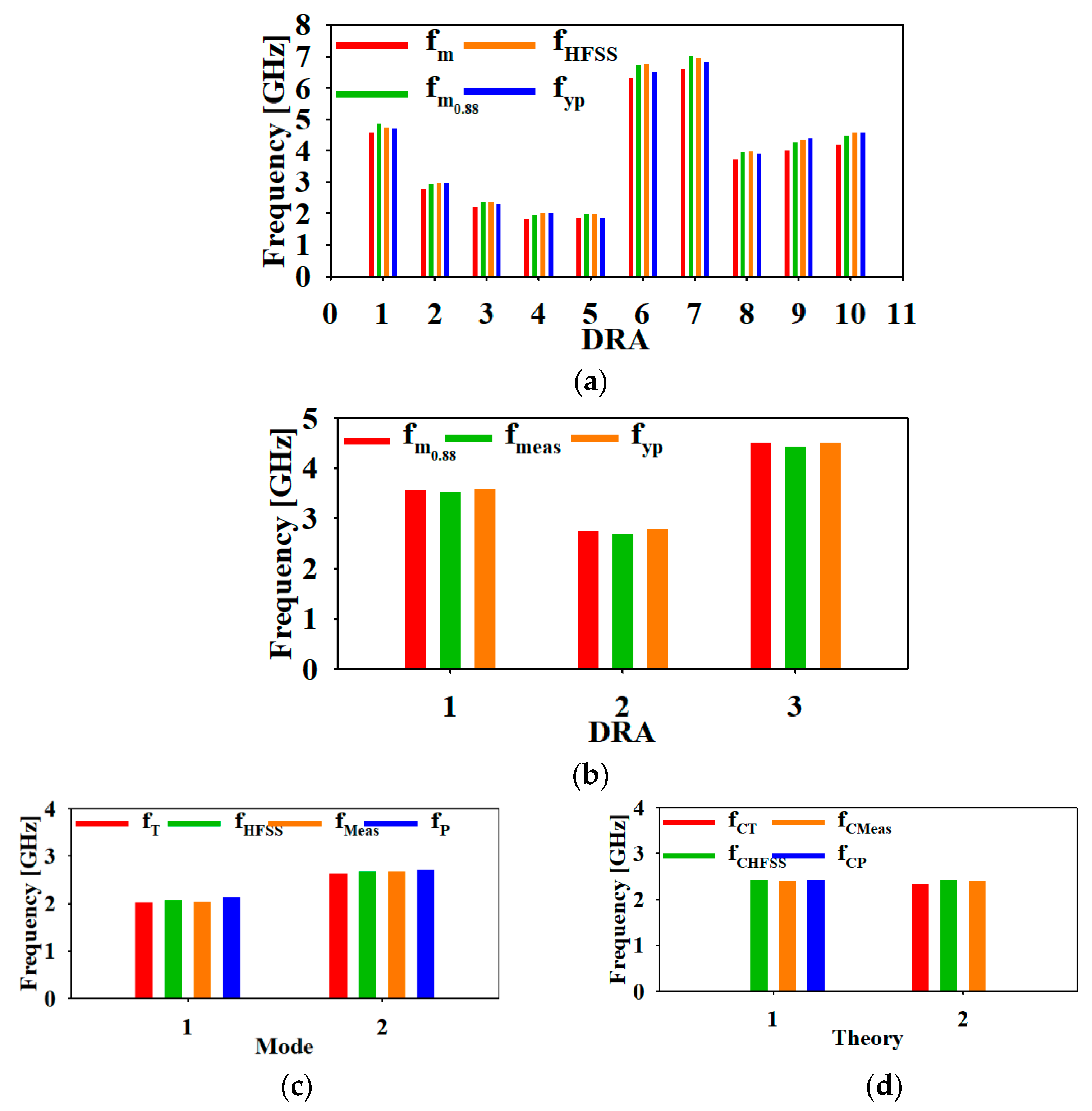
| DRA | Dimensions (mm) | [25] | [25] | [25] | % Error | % Error | % Error | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 25 | 10 | 10 × 10 × 16 | 5 | 4.565 | 4.865 | 4.737 | 4.6992 | −2.9 | 3.5 | 0.8 |
| 2 | 80 | 25 | 10 × 9 × 24 | 6 | 2.761 | 2.942 | 2.954 | 2.9632 | −6.8 | −0.7 | −0.3 |
| 3 | 80 | 40 | 15 × 4 × 30 | 1 | 2.215 | 2.359 | 2.365 | 2.2818 | −2.9 | 3.4 | 3.6 |
| 4 | 100 | 50 | 10 × 20 × 20 | 10 | 1.836 | 1.957 | 2.011 | 2.0228 | −9.2 | 3.3 | −0.6 |
| 5 | 100 | 10 | 15 × 8 × 20 | 3 | 1.850 | 1.972 | 1.982 | 1.8456 | 0.2 | 6.8 | 7.4 |
| 6 | 40 | 10 | 6 × 5 × 8 | 2 | 6.324 | 6.742 | 6.754 | 6.4953 | −2.6 | 3.8 | 4.0 |
| 7 | 40 | 10 | 6 × 4 × 12 | 2 | 6.592 | 7.023 | 6.966 | 6.8365 | −3.6 | 2.7 | 1.9 |
| 8 | 100 | 30 | 6 × 6 × 12 | 3 | 3.707 | 3.952 | 3.977 | 3.9166 | −5.4 | 0.9 | 1.5 |
| 9 | 80 | 40 | 5 × 9 × 12 | 4 | 4.000 | 4.264 | 4.353 | 4.3974 | −9.0 | −3.0 | −1.0 |
| 10 | 80 | 40 | 5 × 5 × 12 | 1 | 4.193 | 4.469 | 4.590 | 4.5719 | −8.3 | −2.3 | 0.4 |
| DRA | Dimensions (mm) | [25] | [25] | % Error | % Error | ||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 25 | 10 | 25 × 42 × 10 | 25 | 3.569 | 3.52 | 3.5845 | −0.4 | −1.8 |
| 2 | 25 | 10 | 25 × 8 × 50 | 5 | 2.757 | 2.68 | 2.794 | −1.3 | −4.1 |
| 3 | 10 | 25 | 25 × 30 × 10 | 5 | 4.511 | 4.43 | 4.5044 | 0.1 | −1.7 |
| Mode | [24] | [24] | [24] | % Error | % Error | % Error | |
|---|---|---|---|---|---|---|---|
| 2.03 | 2.08 | 2.04 | 2.14 | −5.6 | −5.1 | −3.3 | |
| 2.63 | 2.67 | 2.2.67 | 2.71 | −3.2 | −3.5 | −1.7 |
| Theory | Optimal Axial Ratio Point | % Error | % Error | |||
|---|---|---|---|---|---|---|
| [24] | [24] | [24] | ||||
| Proposed | - | 2.24 | 2.4 | 2.425 | 0.2 | 1 |
| Proposed [24] | 2.33 * | 2.24 | 2.4 | - | 3.9 | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sehrawat, N.; Kanaujia, B.K.; Agarwal, A.; Varshney, G. Analysis of an Inhomogeneous Circularly Polarized Hollow Dielectric Resonator Antenna Using Perturbation Theory. Electronics 2021, 10, 2273. https://doi.org/10.3390/electronics10182273
Sehrawat N, Kanaujia BK, Agarwal A, Varshney G. Analysis of an Inhomogeneous Circularly Polarized Hollow Dielectric Resonator Antenna Using Perturbation Theory. Electronics. 2021; 10(18):2273. https://doi.org/10.3390/electronics10182273
Chicago/Turabian StyleSehrawat, Neetu, Binod Kumar Kanaujia, Anshul Agarwal, and Gaurav Varshney. 2021. "Analysis of an Inhomogeneous Circularly Polarized Hollow Dielectric Resonator Antenna Using Perturbation Theory" Electronics 10, no. 18: 2273. https://doi.org/10.3390/electronics10182273






