Energy-Efficient Virtual Network Function Reconfiguration Strategy Based on Short-Term Resources Requirement Prediction

Abstract

In Network Function Virtualization, the resource demand of the network service evolves with the change of network traffic. VNF dynamic migration has become an effective method to improve network performance. However, for the time-varying resource demand, how to minimize the long-term energy consumption of the network while guaranteeing the Service Level Agreement (SLA) is the key issue that lacks previous research. To tackle this dilemma, this paper proposes an energy-efficient reconfiguration algorithm for VNF based on short-term resource requirement prediction (RP-EDM). Our algorithm uses LSTM to predict VNF resource requirements in advance to eliminate the lag of dynamic migration and determines the timing of migration. RP-EDM eliminates SLA violations by performing VNF separation on potentially overloaded servers and consolidates low-load servers timely to save energy. Meanwhile, we consider the power consumption of servers when booting up, which is existing objectively, to avoid switching on/off the server frequently. The simulation results suggest that RP-EDM has a good performance and stability under machine learning models with different accuracy. Moreover, our algorithm increases the total service traffic by about 15% while ensuring a low SLA interruption rate. The total energy cost is reduced by more than 20% compared with the existing algorithms.

1. Introduction

In recent years, with the emergence of new network technologies and the growing customer demands, the business model of operators is undergoing a revolutionary change. Network Function Virtualization (NFV), which is a promising network technology in this revolution [1], decouples network functions from hardware so that they can run as software on Virtual Machines (VMs) of commodity servers. Virtual Network Function (VNF) is instantiated on a VNF Instance (VNFI) implemented with a VM [2], which is allocated resources such as CPU, RAM, and discs.

Operators use Service Function Chain (SFC) to provide customized network services for users in NFV [3]. The network efficiency closely depends on the mapping of VNF and the routing of SFC. Meanwhile, as the network slices run, traffic arrivals of each specific service fluctuate over time, which may result in the mismatch between SFC resource requirements and resource availability of servers, which has an adverse effect on Quality of Service (QoS) and resource utilization [4]. When one certain VNF placement and resource allocation policy failed to meet the current network requirements, NFV Orchestrator (NFVO) provides reconfiguration for SFCs including vertical scaling, horizontal scaling, and dynamic migration. Horizontal scaling makes full use of resource fragmentation but is only feasible when the available resources in the server are sufficient, while dynamic migration can be a flexible solution in an overloaded state but incurs overhead in the meantime.

However, servers are constantly turned on as the dynamic arrival and departure of SFC, which leads to many servers in low-utilization. Additionally, research shows that a server which is idle, even with no workload, continues to consume 70% of its peak energy consumption and causes a severe waste of energy [5]. In addition, since the traffic of the network is time-varying, the resource demand of VNF changes all the time. Servers may overload which leads to overall performance decline and SLA violations or maybe in a low-load state which further aggravates energy waste. Hence, one of the most important goals for operators is to minimize energy consumption without violating SLA. The major issue to be solved is to find a VNF reconfiguration strategy for time-varying traffic rate which minimizes energy consumption with less migration cost and ensuring SLA simultaneously.

Given the aforementioned problems, the main contributions of this paper are as follows.

• We consider the boot-up energy cost of infrastructures to establish a more accurate energy consumption model;
• In consideration of the real SFC request scenarios, we use a time-varying traffic dataset. We adopt LSTM models to predict the resource demand of VNFs in short term and make use of the prediction result, making it possible to migrate VNF in advance proactively in certain timing;
• We propose the RP-EDM algorithm to minimize the energy consumption of the network while considering SLA. The migration is executed non-periodically, considering servers in overload and low load conditions simultaneously. Additionally, we simulate our algorithm using different prediction models to verify the superiority of our proposed strategy.

2. Related Work

Most previous studies involving VNF energy saving have reported kinds of reactive-driven mechanisms. The authors of [6,7,8] consider the low-load state, where VNFs are consolidated into fewer servers so that some servers are able to shut down to save energy. The work in [6] consolidated the same type of Network Functions (NFs) to minimize the number of VNFI, considering the characteristics of NF types and SFC delay constraint. The author constructed an ILP model and proposed a heuristic algorithm called GNFC which is executed periodically and reduces the reconfiguration rate. The work in [7] proposed an algorithm called VCMM, which used a greedy mechanism to migrate VNFs into fewer servers. Multiple conflicting goals including energy consumption, bandwidth usage, and migration cost are considered in VCMM executed regularly as SFCs dynamically arrive and depart. The author used a neural network trained from historical data to determine the probability of a server being shut down. However, the authors of [6,7] migrate VNFs periodically without considering the timing of consolidation and lack a solution for server overload caused by SFC dynamic resource requirements. The work in [8] proposed a cold migration strategy, which determines the placement of VNFI for each traffic segment in a stable cycle scenario. Aiming at minimizing the migration cost and operation consumption, the author proposed an energy-aware algorithm based on the Viterbi algorithm called MEAVR. However, in the real scenario, the traffic flow is of high variability in short-term and irregular periodicity in long-term that is not obvious rather than cyclically stable. Therefore, the findings of [8] cannot cope with short-term time-varying traffic that is nonstationary in real scenario.

There is a lack of research on the timing of migration in terms of reactive migration, which is, however, one of the key issues to reduce the long-term energy consumption of the network, that is, when to consolidate or separate VNFs. An appropriate migration timing should be chosen to avoid unnecessary and expensive VNF migrations, as well as SLA violation or massive energy waste caused by failure to migrate in time. VNF migration does optimize performance, but also involves migration overhead like increasing bandwidth consumption. The long-term energy consumption of the network varies in migrating at different times. In addition, it is necessary to ensure that the switched-on server works as long as possible and should not be turned on/off frequently. Studies have shown that the energy consumption of the server during startup should not be ignored [9]. Since the server runs at full load when starting up, the power consumption is 33% higher than that in standby. Meanwhile, the instantaneous current increases sharply to several times of that in standby, which is gradually devastating hardware such as CPU, motherboard, etc., and is detrimental to the lifetime of devices as is reported in [10]. Therefore, servers in a low load state should be shut down timely to save energy but avoid being restarted soon.

One feasible method to cure the time lag problem [2] is the proactive resource prediction approach. In ref. [11], a DBN prediction algorithm based on online learning was proposed to predict the amount of resources required by VNF and virtual link, and to solve overload problems by using the prediction results. The work in [12] proposed a CAT-LSTM model to predict the resource requirements of a VNF by using SFC data and improved the accuracy by adding aspect embedding and attention. CAT-LSTM is proved to be efficient in predicting the CPU idle percentage of a certain VNF in a given SFC. However, the authors of [12] do not consider how to use these prediction results to optimize resource allocation.

For the challenges above, this paper proposes the Energy-Efficient Dynamic Migration Algorithm Based on Short-Term Resource Requirement Prediction (RP-EDM). We consider the reconfiguration problem driven by evolving resource demand, focusing on a real time-varying traffic scenario. RP-EDM takes advantage of VNF resources demand predicted by LSTM models and is aware of the short-term change of resources in advance, which makes it possible to determine the timing of migration and migrate ahead of schedule. When servers are under low load, RP-EDM consolidates VNFs into fewer servers and shuts down some of the servers for the sake of saving energy. Additionally, when servers are overloaded, RP-EMD separates the VNFs on the overloaded node timely so as not to violate SLA. We evaluate the effectiveness of our algorithm in energy saving by simulations on real network topology.

Table 1. Comparison of the research content of previous works.

Ref.	Time-Varying Traffic	Aperiodic Execution	Consolidation	Separation	Boot-Up Energy	Proactive Migration	Use Prediction Results
[6]	✓	✕	✓	✕	✕	✕	✕
[7]	✓	✕	✓	✕	✕	✕	✕
[8]	✕	✕	✓	✕	✕	✕	✕
[10]	✓	✕	✓	✓	✓	✕	✕
[11]	✓	✕	✕	✓	✕	✓	✓
[12]	✓	✕	✕	✕	✕	✕	✕
Our approach	✓	✓	✓	✓	✓	✓	✓

shows the critical technical contributions of previous works. In addition, we display the difference between our work and others.

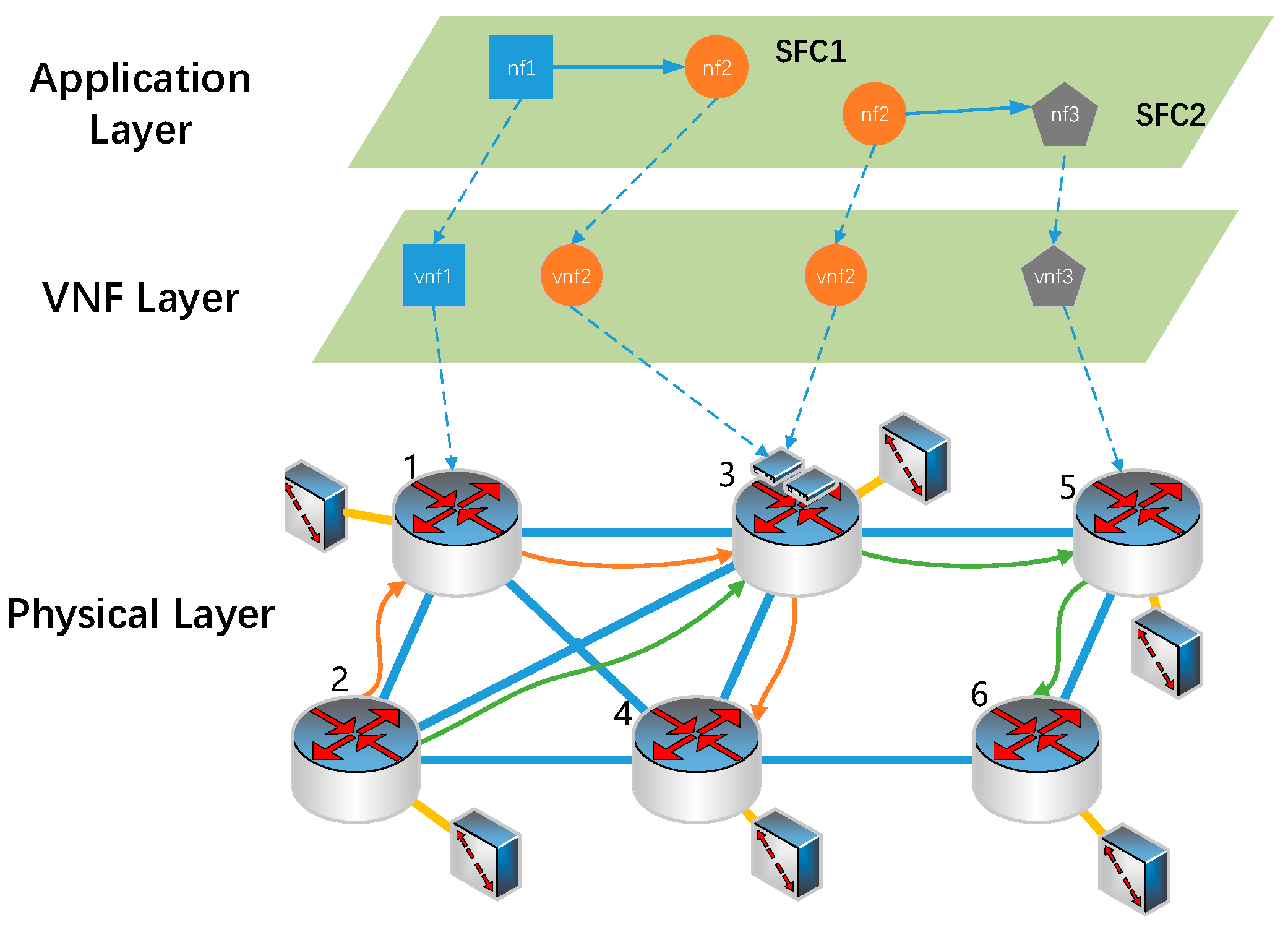
3. System Model and Problem Description

In this section, we define the network model and describe SFC and VNF, then formulate the problem of VNF migration.

3.1. Network Model

We consider a three-layer NFV network architecture as [6]. As shown in Figure 1, physical nodes connect with each other via links in the physical layer. In the VNF layer, VNF is instantiated on the physical node that provides the required resources. In the application layer, different types of NFs making up the SFCs are deployed on the corresponding types of VNFs.

We represent the physical network as an undirected graph $G=(V^S,E^S)$, where $V^S$ represents the set of physical nodes and $E^S$ represents the set of physical links. The CPU capacity of node $v_i^s\in V^S$ are $C_i^S$, and each unit of CPU resource represents the resources required to process one data packet. The memory capacity $M_i^S$ means the available megabytes of $v_i^s$. We use $P_i^{\max }$ to indicate the maximum power consumption of $v_i^s$. Additionally, $e_{ij}^s\in E^S$ represents the edge connecting $v_i^s$ and $v_j^s$, and the physical link bandwidth and delay are $B{W}_{ij}^S$ and $L_{ij}^S$, respectively.

3.2. SFC and VNF

Let $F$ be the set of VNF types. The CPU resource and memory resource consumed by a server when instantiating a VNF of type $f\in F$ is $c^f$ and $m^f$, respectively.

We denote the set of SFCs as $S$. Each $sf{c}^j\in S$ can be represented as $sf{c}^j=\langle v_{j,in}^s,v_{j,out}^s,V_j^{NF},E_j^{NF},l_j\rangle$, where $v_{j,in}^s$ and $v_{j,out}^s$ are the ingress and egress. $V_j^{NF}$ is a set of ordered NFs that traffic passes through. $E_j^{NF}$ represents the set of logical links connecting VNFs between the ingress and egress. Additionally, $l_j$ represents the end-to-end latency allowed by the request. The CPU and memory resource requirements for the u-th NF $v_{j,u}^{nf}\in V_j^{NF}$ are $c_{j,u}^{nf}$ and $m_{j,u}^{nf}$. The traffic segment between $(v_{j,u}^{nf},v_{j,v}^{nf})$ is represented as a logical link $e_{j,uv}^{nf}\in E_j^{NF}$, where the bandwidth requirement is $b{w}_{j,uv}^{nf}$.

We define a decision variable $t_{j,u}^f\in \{0,1\}$ to indicate the types of NFs in the SFC. $t_{j,u}^f\in \{0,1\}$ is 1 when $v_{j,u}^{nf}\in V_j^{NF}$ is of type $f$.

$$t_{j,u}^f=\{\begin{array}{c}1\\ 0\end{array}\begin{array}{c} \mathrm{if} v_{j,u}^{nf} \mathrm{is} \mathrm{of} \mathrm{type} f\in F\\ \mathrm{otherwise}\end{array}$$

(1)

We suppose the ingress and egress have no type, so $t_{j,u}^f\in \{0,1\}$ is 0 all the time. Decision variable ${\eta }_{j,u}^i\in \{0,1\}$ is 1 when logical node $v_{j,u}^{nf}$ maps to physical node $v_i^s$.

$${\eta }_{j,u}^{i,t}=\{\begin{array}{c}1\\ 0\end{array}\begin{array}{c}\mathrm{if} v_{j,u}^{nf} \mathrm{is} \mathrm{mapped} \mathrm{to} v_i^s \mathrm{during} t\\ \mathrm{otherwise}\end{array}$$

(2)

Decision variable ${\tau }_{j,uv}^{pq}\in \{0,1\}$ is 1 when the traffic segment $e_{j,uv}^{nf}$ flows through the physical link $e_{pq}^s\in E^S$.

$${\tau }_{j,uv}^{pq,t}=\{\begin{array}{c}1\\ 0\end{array}\begin{array}{c}\mathrm{if} e_{j,uv}^{nf} \mathrm{is} \mathrm{mapped} \mathrm{to} e_{pq}^s \mathrm{during} t\\ \mathrm{otherwise}\end{array}$$

(3)

A NF of type $f$ is able to map to $v_i^s$ only when the physical node has instantiated the VNF of type $f$. State variable ${\beta }_f^i\in \{0,1\}$ is 1 when there is a VNF of type $f$ on physical node $v_i^s$.

$${\beta }_f^i=\{\begin{array}{c}1\\ 0\end{array}\begin{array}{c}\mathrm{if} \mathrm{a} \mathrm{VNF} \mathrm{of} \mathrm{type} f \mathrm{is} \mathrm{assigned} \mathrm{on} v_i^s\\ \mathrm{otherwise}\end{array}$$

(4)

$${\beta }_f^{i,t}=1, \mathrm{if} {\displaystyle \sum _{sf{c}^j\in S}{\displaystyle \sum _{v_{j,u}^{nf}\in V_j^{NF}}{\eta }_{j,u}^{i,t}{t}_{j,u}^f\ge 1, \forall v_i^s\in V^S, f\in F, t\in T}}$$

(5)

Due to the dynamic change of traffic, we describe the relationship between the incoming traffic bandwidth and the resource requirement of $v_{\mathrm{j},v}^{nf}\in V_j^{NF}$ at $t$ by

$$c_{j,v}^{nf}(t)=b{w}_{j,uv}^{nf}(t){\displaystyle \sum _{f\in F}{t}_{j,v}^{f}coef{f}_c^f}\forall t\in T$$

(6)

$$m_{j,v}^{nf}(t)=b{w}_{j,uv}^{nf}(t){\displaystyle \sum _{f\in F}{t}_{j,v}^{f}coef{f}_m^f}\forall t\in T$$

(7)

where $coef{f}_c^f$ and $coef{f}_m^f$ represent CPU coefficient and resource coefficient, respectively. Since the traffic flow may be scaled as it passes through each NF, we denote the relationship between the incoming bandwidth of the NF $v_{\mathrm{j},v}^{nf}$ and the bandwidth requirement of the logical link connected to it with

$$b{w}_{j,uv}^{nf}(t)=b{w}_{j,ku}^{nf}(t){\displaystyle \sum _{f\in F}{t}_{j,v}^{f}rati{o}^f}\forall t\in T$$

(8)

where $v_k^{nf},v_u^{nf},v_v^{nf}\in V_i^{NF}$ is a set of ordered NFs, and $rati{o}^f$ is the bandwidth scaling ratio of VNF in type $f$.

To describe the migration process, we define a set of variables related to the state of servers and VNF migration. ${\delta }_i^t\in \{0,1\}$ equals to 1 when $v_i^s$ is turned on during $t$, and vice versa. ${\xi }_{j,u}^t\in \{0,1\}$ equals 1 when the virtual node $v_{j,u}^{nf}$ will be migrated during $t$. ${\rho }_i^t\in \{0,1\}$ equals 1 when $v_i^s$ which is powered on will be switched off in next period. Additionally, ${\lambda }_i^t\in \{0,1\}$ equals 1 when $v_i^s$ which is powered off will be switched on in the next period.

We define a set of variables associated with resource requirement prediction, which includes CPU, disk, memory and other system resource usages, such as the number of processes, OS load and so on. To simplify, in this paper, we consider CPU requirement prediction. We use $c_{j,u}^{nf}(t+n) (n=1,2,\cdots )$ to represent the CPU requirement of $v_{j,u}^{nf}$ in the future time $t+n$ by predicting. $c_i^s(t+n) (n=1,2,\cdots )$ is used to indicate the CPU usage of the node $v_i^s$ in the future time $t+n$, which is calculated by

$$c_i^s(t+n)={\displaystyle \sum _{f\in F}{\beta }_f^{i,t+n}{c}^f+}{\displaystyle \sum _{sf{c}^j\in S}{\displaystyle \sum _{v_{j,u}^{nf}\in V_j^{NF}}{\eta }_{j,u}^{i,t+n}{r}_{j,u}^{nf}}}(t+n)\forall v_i^s\in V^S,\forall t\in T$$

(9)

Meanwhile, we represent the overload threshold and low load threshold of the physical node by $th{r}_{over}$ and $th{r}_{low}$, respectively.

The above variables meet the following constraints:

Each NF of the SFCs should be deployed on one unique physical node, which can be formulated by

$${\displaystyle \sum _{v_i^s\in V^S}{\eta }_{j,u}^{i,t}=1}\forall sf{c}^j\in S, \forall v_{j,u}^{nf}\in V_j^{NF},\forall t\in T$$

(10)

Each virtual link should be mapped to one physical link. Since the virtual link may be extended across nodes, we have

$${\displaystyle \sum _{e_{pq}^s\in E^S}{\tau }_{j,uv}^{pq,t}\ge 1}\forall sf{c}^j\in S, \forall e_{j,uv}^{nf}\in E_j^{NF},\forall t\in T$$

(11)

The CPU and memory capacity of physical nodes need to satisfy the constraint of computational capability, which can be expressed by

$${\displaystyle \sum _{f\in F}{\beta }_f^{i,t}{c}^f+}{\displaystyle \sum _{sf{c}^j\in S}{\displaystyle \sum _{v_{j,u}^{nf}\in V_j^{NF}}{\eta }_{j,u}^{i,t}{c}_{j,u}^{nf}}}(t)\le C_i^S\forall v_i^s\in V^S,\forall t\in T$$

(12)

$${\displaystyle \sum _{f\in F}{\beta }_f^{i,t}{m}^f+}{\displaystyle \sum _{sf{c}^j\in S}{\displaystyle \sum _{v_{j,u}^{nf}\in V_j^{NF}}{\eta }_{j,u}^{i,t}{m}_{j,u}^{nf}}}(t)\le M_i^S\forall v_i^s\in V^S,\forall t\in T$$

(13)

The bandwidth constraint of physical links meets

$${\displaystyle \sum _{sf{c}^j\in S}{\displaystyle \sum _{e_{j,uv}^{nf}\in E_j^{NF}}{\tau }_{j,uv}^{pq,t}b{w}_{j,uv}^{nf}(t)\le B{W}_{pq}^S}}\forall e_{pq}^s\in E^S,\forall t\in T$$

(14)

The latency constraint of SFCs also needs to be satisfied, which can be given by

$${\displaystyle \sum _{e_{j,uv}^{nf}\in E_j^{NF}}{\displaystyle \sum _{e_{pq}^s\in E^S}{\tau }_{j,uv}^{pq,t}{L}_{pq}^S\le l_j}}\forall sf{c}^j\in S,\forall t\in T$$

(15)

Each pair of connected VNF $(v_{j,u}^{nf},v_{j,v}^{nf})$ satisfies traffic conservation. Given a logical link $e_{j,uv}^{nf}$ and a physical node $v_i^s$, we have

$$\begin{array}{l}{\displaystyle \sum _{v_q^s\in {\Omega }^{+}(v_p^s)}{\tau }_{j,uv}^{qp,t}-}{\displaystyle \sum _{v_q^s\in {\Omega }^{-}(v_p^s)}{\tau }_{j,uv}^{pq,t}}\\ =\{\begin{array}{c}{\eta }_{j,v}^{p,t}-{\eta }_{j,u}^{p,t},\\ 1,\\ -1,\\ 0,\end{array}\begin{array}{c}\forall v_{j,u}^{nf},v_{j,v}^{nf}\in V_j^{NF}\\ \forall v_{j,v}^{nf}\in \{v_{j,out}^s\}, v_{j,out}^s=v_p^s, v_{j,u}^{nf}\in V_j^{NF}\\ \forall v_{j,u}^{nf}\in \{v_{j,in}^s\}, v_{j,in}^s=v_p^s, v_{j,v}^{nf}\in V_j^{NF}\\ \mathrm{otherwise}\end{array},\forall sf{c}^j\in S,\forall t\in T\end{array}$$

(16)

where ${\Omega }^{+}(v_p^s)$ and ${\Omega }^{-}(v_p^s)$ represent the set of upstream and downstream nodes, respectively. The node which NFs deployed on should be turned on, thus we have

$${\delta }_i^t\ge {\eta }_{j,u}^{i,t}\hspace{1em}\forall v_{j,u}^{nf}\in V_j^{NF}, \forall sf{c}^j\in S, \forall v_i^s\in V^S, \forall t\in T$$

(17)

The following constraints are used to represent the migration of virtual node $v_{j,u}^{nf}$. If the physical nodes that $v_{j,u}^{nf}$ mapped before and after the traffic change are different, then $v_{j,u}^{nf}$ should be migrated.

$${\xi }_{j,u}^t\ge {\eta }_{j,u}^{i,t}-{\eta }_{j,u}^{i,t+1}\forall v_{j,u}^{nf}\in V_j^{NF}, \forall sf{c}^j\in S, \forall v_i^s\in V^S, \forall t\in T$$

(18)

The physical node may switch on/off before and after the traffic change, which satisfies

$${\lambda }_i^t\le {\delta }_i^t-{\delta }_i^{t+1}\forall v_i^s\in V^S,\forall t\in T$$

(19)

$${\rho }_i^t\ge {\delta }_i^t-{\delta }_i^{t+1}\forall v_i^s\in V^S,\forall t\in T$$

(20)

3.3. NF Energy-Efficient Migration Problem

In this paper, we established the system energy consumption model for SFC migration and designed the migration algorithm to minimize the long-term total energy consumption. The energy consumption of the physical node is defined as

$$E_{sn}={\displaystyle \sum _{t\in T}(E_s^t+E_d^t)}$$

(21)

where $E_s^t$ is the static energy consumption, which is a basic part of consumption existing since the server turned on and stably consumed even if the server is idle [13]. $E_d^t$ is the dynamic energy consumption, which includes the energy consumption of physical resources such as CPU, RAM, network and disk caused by the time-varying traffic load. Studies have shown that the dynamic energy consumption of servers mainly depends on CPU utilization and has little correlation with other physical resources [14]. Therefore, we assume that there is a linear relationship between the base power and the maximum power of the physical node $v_i^s\in V^S$, and the ratio is $a$. Therefore, the energy consumption of a unit time $\Delta t$ can be expressed as

$$E_{sn}^t=E_s^t+E_d^t={\displaystyle \sum _{v_i^s\in V^S}{\delta }_i^{t}a{P}_i^{\max }\Delta t}+{\displaystyle \sum _{v_i^s\in V^S}(1-a)u_i^{CPU,t}{P}_i^{\max }\Delta t}$$

(22)

$$u_i^{CPU,t}=\frac{{\displaystyle \sum _{f\in F}{\beta }_f^{i,t}{c}^f+}{\displaystyle \sum _{sf{c}^j\in S}{\displaystyle \sum _{v_{j,u}^{nf}\in V_j^{NF}}{\eta }_{j,u}^{i,t}{c}_{j,u}^{nf}(t)}}}{C_i^S}$$

(23)

where $u_i^{CPU,t}$ is the CPU utilization of $v_i^s$ during $t$.

The cost of migration is mainly from memory migration and power consumption caused by server startup. In this paper, the energy consumption of migration is defined as

$$E_{mig}={\displaystyle \sum _{t\in T}(E_{mig,m}^t+E_{mig,c}^t})$$

(24)

where $E_{mig,m}^t$ is the cost of migrating the memory of VNF and $E_{mig,c}^t$ is the energy cost of server switching on from shutdown. The energy consumption of VNF memory migration is mainly caused by the extra energy consumed by the source host and the target host [13], so we have

$$E_{mig,m}^t={\displaystyle \sum _{sf{c}^j\in S}{\displaystyle \sum _{\forall v_{j,u}^{nf}\in V_j^{NF}}{\xi }_{j,u}^t\frac{m_{j,u}^{nf}(t)}{L_{pac}}{t}_{pac}{\displaystyle \sum _{v_i^s\in V^S}(1-a)({\eta }_{j,u}^{i,t}{P}_i^{\max }}+{\eta }_{j,u}^{i,t+1}{P}_i^{\max })}}$$

(25)

where $L_{pac}$ is the length of the packet carrying the memory stream, and $t_{pac}$ is the processing time of the memory packet. Since the server has power consumption which should not be ignored at the startup moment, we denote the ratio between startup power consumption and maximum power consumption as $b$. Thus, we have

$$E_{mig,c}^t={\displaystyle \sum _{v_i^s\in V^S}{\lambda }_i^{t}b{P}_i^{\max }}$$

(26)

Therefore, the optimal object is to minimize the total energy consumption of the system, as

$$\min E_{total}=E_{sn}+E_{mig}$$

(27)

The energy saving migration problem of VNFs proposed in this paper is an NP-hard problem. To prove this conclusion, we construct a simple energy saving migration problem and merge it into the NP-Hard problem which has been verified. Considering the whole network has several SFCs made up of one VNF, each of the physical nodes is instantiated with all types of VNFs. The delay of physical link is far less than the maximum latency of SFCs and is allocated with enough bandwidth. In this case, the problem is transformed into a VNF embedding problem considering node resource constraints. This problem is simplified to load $N$ boxes of volume $c_{j,u}^{nf},v_{j,u}^{nf}\in V_j^{NF}$ on $V^S$, aiming to maximize the loading flow, which is known as the KLP (Knapsack Loading Problems), that is a proven NP-hard problem [15].

4. Algorithm Design

In the previous section, we proved that the NF energy-saving migration problem is an NP-hard problem. Therefore, in this section, we propose an energy-efficient NF dynamic migration algorithm based on short-term resources requirement prediction (RP-EDM) to solve the problem above. As is presented in Figure 2, we first input the historical network resource information to the prediction model and obtain the resource prediction results of every NF. Then these results are input to RP-EDM. A sub-algorithm termed Resource Prediction Based Network Function Separation (PNFS) is executed on each overloaded physical node according to prediction and output the migrate strategy to minimize energy consumption while the services are uninterrupted; another sub-algorithm called Resource Prediction Based Network Function Consolidation (PNFC) is executed for the possible low-load nodes and output the reconfiguration strategy including the migration timing, destination nodes, routes, aiming at migrating all NFs on target nodes and close them, so as to reduce the network energy consumption. Finally, RP-EDM joins the migration strategy obtained by the above two sub-algorithms to output the final reconfiguration strategy.

RP-EDM follows the following principle:

Overloaded servers should be executed PNFS immediately to ensure that services are not interrupted. Since the server switch on may cause extra energy consumption, in order to avoid unnecessary overhead, we first choose the target node for NF from the servers that have been turned on, if no candidates are available, then switching on other servers is considered.

It is necessary to clarify which node is under low-load condition and when to consolidate it because NFs consolidation brings migration costs. This problem can be interpreted from another perspective, that is, determining servers that should be consolidated and shut down in each time period. The consolidated servers are expected to shut down as long as possible to avoid servers switching on/off frequently.

Different SFCs have different flow fluctuation characteristics. For SFCs with a fast fluctuation and large fluctuation ranges, the migration is supposed to execute frequently, so that the change in resource demand caused by traffic fluctuations can be monitored sensitively to prevent service interruption; for SFCs with a slow fluctuation, the migration should not be executed frequently in order to avoid unnecessary servers switching on and migration cost. RP-EDM uses the maximum normal-load time according to prediction to measure whether the current migration is worthwhile. For NFs which do not need migration, we use flexible horizontal scaling to scale resources.

4.1. RP-EDM Algorithm

The RP-EDM, as presented in Algorithm 1, takes the resources requirement prediction results of nodes as the input. RP-EDM first executes the sub-algorithm NFS on nodes that are predicted to be overloaded in the next period and then obtains the migrating strategy (lines 1–3). Here, we propose an adaptive overload threshold. ${\theta }_i^t$ is used, as is defined in Equation (28), to represent the overload threshold bias of $v_i^s$ in $t$.

$${\theta }_i^t=count(L_i^t)\cdot RMSE$$

(28)

where $count(L_i^t)$ is the number of NFs deployed on $v_i^s$, and $RMSE$ is the root mean square error of the prediction model. Then, the sub-algorithm NFC is executed to output the nodes that needed to be consolidated during the current period and the consolidation strategies of all NFs on them (Line 4). It is worth noting that the reconfiguration strategies output by the above sub-algorithms are not the final strategy of the current period. For instance, the following scenario may occur: $v_{k,w}^{nf}$ are supposed to migrate twice in the current period, that is, from $v_1^s$ to $v_2^s$, then from $v_2^s$ to $v_3^s$. To prevent NF from multi-step migration which increases migration energy consumption, line 6 ensures that at most one migration occurs for each NF in the current period, and updates the policy output by sub-algorithms to one migration pattern, that is, $v_{k,w}^{nf}$ migrating from $v_1^s$ to $v_3^s$. Finally, the actual migrations occur (line 7) to get the updated VNF mapping. In this way, the separation policy is no longer migrating from the minimum resource requirement NF until normal load but follows a strategy that minimizes the migration cost of making overloaded nodes normally loaded.

The sub-algorithms NFS and NFC will be discussed in the next section.

Algorithm 1 RP-EDM

Input:$G=(V^S,E^S)$, the switch on/off policy of the network ${\delta }^t$ in the current period $t$, CPU requirement of all nodes by predicting $C^{predict}=\{c_i^s(t+n) (n=1,2,\cdots )|\forall v_i^s\in V^S\}$;

Output: New mapping strategy of $G$ after reconfiguration;

1  for each $v_i^s\in V^S$ do

2   if $c_i^s(t+1) \ge th{r}_{over}{C}_i^S-{\theta }_i^t$ then

3    ${\pi }_s\leftarrow NFS(G,{\delta }^t,v_i^s,L_i^t,C^{predict})$;

4  ${\pi }_c\leftarrow NFC(G,{\delta }^t,L_i^t,C^{predict})$;

5  for each $(v_{k,w}^{nf},v_{tar}^s)\in {\pi }_s\cup {\pi }_c$ do

6   update $v_{tar}^s$, ensure $v_{k,w}^{nf}$ only migrate once;

7   migrate $v_{k,w}^{nf}$ to $v_{tar}^s$;

8  return $G$;

4.2. Resource Prediction Based Network Function Separation Algorithm

For the source node $v_{sou}^s$ that is about to be overloaded, PNFS needs to be executed immediately to ensure that the service is not interrupted. NFS outputs the migration strategy, including which NFs to be migrated, and the respective target nodes and route mappings. We proposed the NFS Algorithm as presented in Algorithm 2. We construct NFs set $L_{sou}^t$ deployed on $v_{sou}^s$ ordered from small to large according to the memory requirements of NFs (line 1). The main loop (lines 2–21) goes on as long as $v_{sou}^s$ is still overloaded and has NFs that can be separated existing. $v_{k,w}^{nf}\in L_{sou}^t$ is found with the least memory requirement (line 3). Next, the candidate set of target nodes $A$ is determined for $v_{k,w}^{nf}$, which consists of on/off nodes $A_{on}$ and $A_{off}$ that satisfy the following requirements except $\{v_{sou}^s\}$ itself (line 4). When migrating $v_{k,w}^{nf}$ to $v_i^s\in A$, at least one new path can be found that meets the bandwidth constraint and the delay constraint of $sf{c}^k$. Next, lines 5–12 determine the target node. First, according to the resource prediction results, the maximum duration $n^i$ is calculated for which $v_i^s$ will remain unloaded in the future when migrating $v_{k,w}^{nf}$ to $\forall v_i^s\in A$. Moreover, the migration energy cost $E_{mig,kw}^{i,t}$ (lines 5–7) is calculated. We choose the node with the largest duration cost ratio as the target node $v_{tar}^s$, considering that the target node should not migrate frequently and the migration energy consumption should be minimized.

We consider powered-on nodes in the candidate set firstly, and then power-off nodes (lines 9–12). In line 13, we look for all possible paths after the migration of NF $v_{k,w}^{nf}$ from $v_{sou}^s$ to $v_{tar}^s$, sorted by the path delay. Next, we traverse from the shortest path until we find a path $P$ that meets the link bandwidth constraint and the latency constraint of $sf{c}^k$, and $v_{tar}^s$ has enough resources for deploying $v_{k,w}^{nf}$. Then the migration is considered feasible and is added to ${\pi }_s$. Then $v_{k,w}^{nf}$ is deleted from $L_{sou}^t$ (lines 14 to 15). Since the mapping of NFs on $v_{sou}^s$ and $v_{tar}^s$ changes, we update the predicted CPU usage of both (line 16). If $v_{tar}^s$ is newly switched on, we update its on/off state (line 17). If there is no suitable migration path that can be found, $v_{tar}^s$ is removed from $A$ and the possibility of migration to a sub-optimal target node is considered (lines 18–20). If no suitable path can be found for all nodes in $A$, then $v_{k,w}^{nf}$ is removed from $L_{sou}^t$ (line 22). Then, the above operations are performed on other NFs in $L_{sou}^t$ until $v_{sou}^s$ is no longer overloaded.

Algorithm 2 Resource Prediction Based Network Function Separation (PNFS)

Input:$G=(V^S,E^S)$, the switch on/off policy of the network ${\delta }^t$ in the current period $t$, the over-loader node $v_{sou}^s$, CPU requirement of all nodes by predicting $C^{predict}=\{c_i^s(t+n) (n=1,2,\cdots )|\forall v_i^s\in V^S\}$;

Output: The separation strategy ${\pi }_s$;

1 $L_{sou}^t\leftarrow \{v_{j,u}^{nf}|{\eta }_{j,u}^{sou,t}=1,v_{j,u}^{nf}\in V_j^{NF},sf{c}^j\in S\}$;

2 while$c_{sou}^s(t+1) \ge th{r}_{over}{C}_{sou}^S-{\theta }_{sou}^t$ and$L_{sou}^t\ne \varnothing$ do

3  select NF $v_{k,w}^{nf}|v_{k,w}^{nf}=\arg (\underset{v_{j,u}^{nf}\in L_{sou}^t}{\min } m_{j,u}^{nf}(t))$;

4  Find the target node candidate set $A\leftarrow A_{off}\cup A_{on}-\{v_{sou}^s\}$ for $v_{k,w}^{nf}$. A set of all nodes on and off whose paths meet delay constraints and bandwidth constraints of $sf{c}^k$;

5  for each $v_i^s\in A$ do

6   $n^i\leftarrow \underset{n=1,2,\cdots }{\max } \{n|c_i^s(t+n)+c_{k,w}^{nf}(t+n)<th{r}_{over}{C}_i^S-{\theta }_i^{t+n},\forall v_i^s\in A\}$;

7   Calculate energy cost $E_{mig,kw}^{i,t}$;

8  if $A\ne \varnothing$ then

9   if $A_{on}\ne \varnothing$ then

10    select target node $v_{tar}^s|v_{tar}^s=\arg (\underset{v_i^s\in A_{on}-\{v_i^s\}}{\max } n^i/E_{mig,kw}^{i,t})$;

11   else

12    select $v_{tar}^s|v_{tar}^s=\arg (\underset{v_i^s\in A_{off}}{\max } n^i/E_{mig,kw}^{i,t})$;

13   if find satisfied path $P$ for ${\eta }_{k,w}^{tar,t}=1$ then

14    ${\pi }_s\leftarrow {\pi }_s.add(\{{\eta }_{k,w}^{tar,t}=1\};\{{\tau }_{j,uv}^{pq,t}=1|v_{j,u}^{nf},v_{j,v}^{nf}\in V_j^{NF} p,q\in P\})$;

15    $L_{sou}^t\leftarrow L_{sou}^t.remove(v_{k,w}^{nf})$;

16    update $c_{sou}^s(t+n)$ and $c_{tar}^s(t+n)$;

17    update ${\delta }_{tar}^t\leftarrow 1 | \mathrm{if} {\lambda }_{tar}^t=1$;

18   else

19    $A\leftarrow A.remove(v_{tar}^s)$;

20    go to line 5;

21  else

22   $L_{sou}^t\leftarrow L_{sou}^t.remove(v_{k,w}^{nf})$;

23 return${\pi }_s$;

4.3. Resource Prediction Based Network Function Consolidation Algorithm

In order to save energy, we consolidate servers with low load and reduce the number of powered-on servers. Therefore, we propose the PNFC as shown in Algorithm 3. According to the resource prediction results, we construct a set $N_{low}^t$ that is in descending order by node low load duration. Next, lines 2–23 are the main loop of PNFC. Unlike the PNFS, consolidation is not required. Each time NFC starts at the node $v_{sou}^s$ with the longest duration of low load and terminates if the consolidation fails. The set of ongoing NFs on $v_{sou}^s$ is $L_{sou}^t$ (line 4). The consolidation succeeds when all NFs in $L_{sou}^t$ are successfully migrated to the target node and the source node can be turned off successfully (lines 5–18). One NF $v_{j,u}^{nf}\in L_{sou}^t$ is chosen randomly and the target node candidate set $A_{on}$ is found, which consists of powered-on nodes with adequate available resources and can find paths that meet bandwidth constraint and latency constraint of $sf{c}^j$. Lines 8–10 calculate every node’s normal load duration after migrating $v_{j,u}^{nf}$ to it and migration cost. The node with the highest ratio of normal load duration to migration cost is chosen as the target node $v_{tar}^s$ (line 11). As dynamic energy cost before and after the migration can be interpreted as a kind of transfer, we assume that it has little change and would not affect the total energy consumption for the sake of simplicity. It is considered worthy that the total migration cost of all nodes in $L_{sou}^t$ migrating twice is less than the static energy saved by turning off $v_{sou}^s$ (line 12). Next, we find the set of all possible paths and start from the shortest path, until we find a path $P$ that satisfied all constraints. That means the migration of $v_{j,u}^{nf}$ from $v_{sou}^s$ to $v_{tar}^s$ is feasible. The migration strategy (NF mapping strategy and path mapping strategy) is added to ${\pi }_c$ and $v_{j,u}^{nf}$ deleted from $L_{sou}^t$. Then, the remaining NFs continue to migrate in $L_{sou}^t$ and the network parameters are updated. If no satisfied path is found, the consolidation of $v_{j,u}^{nf}$ fails and NFC is terminated (lines 13–18). If all NFs in $L_{sou}^t$ can be migrated successfully, the $v_{sou}^s$ can be shut down. $v_{sou}^s$ is deleted from $N_{low}^t$ and the next low-load node continues to be consolidated (lines 19–21).

Algorithm 3 Resource Prediction Based Network Function Consolidation (PNFC)

Input:$G=(V^S,E^S)$, the switch on/off policy of the network ${\delta }^t$ in the current period $t$, the over-loader node $v_{sou}^s$, CPU requirement of all nodes by predicting $C^{predict}=\{c_i^s(t+n) (n=1,2,\cdots )|\forall v_i^s\in V^S\}$;

Output: The consolidation strategy ${\pi }_c$;

1 create set $N_{low}^t=\{n_{low}^i|\forall v_i^s\in V^S\}$, where $n_{low}^i=\underset{n=1,2,\cdots }{\max } \{n|c_i^s(t+n)\le th{r}_{low}{C}_i^S\}$;

2 while$N_{low}^t\ne \varnothing$ and $\underset{n_{low}^i\in N_{low}^t}{\max } n_{low}^i>1$ do

3  select node $v_{sou}^s|v_{sou}^s=\arg (\underset{n^i\in N^t}{\max } n_{low}^i)$;

4  $L_{sou}^t\leftarrow \{v_{j,u}^{nf}|{\eta }_{j,u}^{sou,t}=1,v_{j,u}^{nf}\in V_j^{NF},sf{c}^j\in S\}$;

5  while $L_{sou}^t\ne \varnothing$ do

6   select NF $v_{j,u}^{nf}|v_{j,u}^{nf}\in L_{sou}^t$;

7   Find the target node candidate set $A_{on}\leftarrow \{v_i^s|{\delta }_i^t=1,v_i^s\in V^S-\{v_{sou}^s\}\}$ for $v_{j,u}^{nf}$. A set of all nodes on and off whose paths meet delay constraints and bandwidth constraints of $sf{c}^j$;

8   for each $v_i^s\in A_{on}$ do

9    $n^i\leftarrow \underset{n=1,2,\cdots }{\max } \{n|th{r}_{low}{C}_i^S<c_i^s(t+n)+c_{j,u}^{nf}(t+n)<th{r}_{over}{C}_i^S,\forall v_i^s\in A\}$;

10    Calculate energy cost $E_{mig,ju}^{i,t}$;

11   select target node $v_{tar}^s|v_{tar}^s=\arg (\underset{v_i^s\in A_{on}}{\max } n^i/E_{mig,ju}^{i,t})$;

12   if $2E_{mig,ju}^{tar,t}count(L_i^t)<a{P}_{sou}^{\max }{n}_{low}^{sou}$ then

13    if find satisfied path $P$ for ${\eta }_{j,u}^{tar,t}=1$ then

14     ${\pi }_c\leftarrow {\pi }_c.add(\{{\eta }_{j,u}^{tar,t}=1\};\{{\tau }_{j,mn}^{pq,t}=1|v_{j,m}^{nf},v_{j,n}^{nf}\in V_j^{NF} p,q\in P\})$;

15     $L_{sou}^t\leftarrow L_{sou}^t.remove(v_{j,u}^{nf})$;

16     update $c_{sou}^s(t+n)$ and $c_{tar}^s(t+n)$;

17    else

18     break;

19  if $L_{sou}^t=\varnothing$ then

20   $N_{low}^t.remove(n_{low}^i)$;

21   ${\delta }_{sou}^t\leftarrow 0$;

22  else

23   break;

24 return${\pi }_c$;

5. Performance Evaluation

5.1. Simulation Setup

In order to evaluate the effectiveness of the above algorithm, this paper evaluates the above algorithm on NSFNET network topology, and the simulation is implemented and run on SFCSim [16], an SFC simulation platform based on Python environment.

The physical network is shown in Figure 3, with 14 physical nodes and 21 links. The CPU resources and memory resources capacity of the server are set to be evenly distributed in $\left(250,300\right) \mathrm{MIPS}$ and $\left(600,1000\right) \mathrm{GB}$ [17]. The maximum power of the server is evenly distributed in $\left(170,230\right) \mathrm{W}$. We set the link bandwidth capacity to $500 \mathrm{Mbps}$ and the link delay evenly distributed in $\left(1,4\right) \mathrm{ms}$. We assume that the ratio of server basic power to maximum power is 0.7 and the ratio of server power-on power to maximum power consumption is 0.15. The traffic packet length is set to be 1500 bytes. Furthermore, the packet processing time is $160 \mathsf{\mu }\mathrm{s}$ [8]. The low load threshold and the overload threshold are 0.3 and 0.9, respectively [18].

We consider three types of VNFs. Each SFC randomly selects some VNFs. In addition, the length of each SFC is randomly chosen from 1 to 3. Meanwhile, ingress and egress are chosen randomly from $V^S$. The bandwidth factor $rati{o}^f$ of different types of VNFs is selected from $\left(0.5,1,1.5\right)$. To simplify the problem, we assume that no resources are needed to instantiate the VNF, and resources are only needed when deploying the NF. The CPU coefficient $coef{f}_c^f$ and memory coefficient $coef{f}_m^f$ of different types of VNFs are evenly distributed in $\left(0.2,0.5\right)$. The maximum latency of SFC is $30 \mathrm{ms}$ [17]. We use the traffic data set from Clearwater VNF Dataset [19]. We consider the network has 25 SFCs in 24 h, and the arrival time of the requests is dynamically controlled according to the Poisson distribution. Each request has an exponentially distributed life cycle, with an average of 1000 min.

5.2. Simulation Result and Analysis

We use the following metrics to evaluate the performance of the algorithm. Total energy consumption: the sum of energy consumption and migration energy consumption of all server nodes in the network. Total service traffic: the total traffic processed by the SFCs accepted by the network. Energy bandwidth ratio: the ratio of total network energy consumption to total bandwidth, which measures the energy consumption for processing a unit bandwidth. Service outage time rate: for SFCs that have not reached the life cycle but are interrupted early due to insufficient resources, we define the service interruption time as the time from the interruption to the end of the life cycle. The outage time rate is the ratio of the interruption time to the life cycle.

We compared the basic LSTM and the CAT-LSTM [12] to predict the CPU resource requirements of each NFs in the network. The results of model training are presented in

Table 2. Comparison of the results of CAT-LSTM and basic LSTM averaged across all VNFs from SFCs, for the number of RNN units = 80, learning rate = 0.001, the max number of iterations = 800 with early stop, prediction time = 5 s, amount of historical data = 15 s.

Metric	Basic-LSTM	CAT-LSTM
loss	0.3316	0.0345
mse	30.4405	13.9401
rmse	5.5172	3.7336

. These prediction results are used as the input of RP-EDM to evaluate the performance of RP-EDM. For the impact of different prediction accuracy on the performance of RP-EDM, we also set RP-EDM-Precise as a reference to indicate the limit situation when the prediction accuracy is 100%. Meanwhile, we compare RP-EDM with the GNFC in [6] which is executed periodically, and the Never Migrate Strategy. GNFC algorithm is executed hourly. In order to ensure that the deployment algorithm cannot affect our comparative analysis, the SFC deployment in the above comparison algorithms all adopt the shortest path priority deployment algorithm.

The total traffic of network services is shown in Figure 4a. RP-EDM-Precise, RP-EDM-Basic-LSTM, and RP-EDM-CAT-LSTM are 14.40–46.52% higher than Never Migrate in total traffic. Since GNFC only makes consolidation and does not consider server overload, it further exacerbates the service interruption. Due to the low accuracy of RP-EDM-Basic-LSTM, it cannot be aware of server overload accurately, resulting in service interruption. Besides, the total service traffic is 2.59% lower than RP-EDM-CAT-LSTM. The energy consumption bandwidth is shown in Figure 4b. As time goes by, the migrations continue, and the energy consumption bandwidth ratio is on the decline and converges gradually. The energy consumption bandwidth ratio of the RP-EDM series algorithm is lower than that of GNFC and Never Migrate, which suggests that our algorithm requires lower energy consumption processing a unit of traffic, which is effective in reducing long-term network energy consumption. At the same time, RP-EDM-CAT-LSTM which has a higher prediction accuracy is closer to the optimal RP-EDM-Precise. Its energy consumption bandwidth ratio is 9.40% lower than RP-EDM-Basic-LSTM.

The SLA violation rate and service outage time rate are shown in Figure 4c. The request acceptance rate of the RP-EDM series algorithm is higher than the comparison algorithm while the SLA violation rate and service outage time rate are lower. This is because RP-EDM combines separation and consolidation simultaneously. For nodes that are predicted to be overloaded, PNFC executes immediately to restore the normal load of the overloaded node, so as not to violate the SLA. According to the accuracy of different prediction models, adaptive overload thresholds are used to ease the service interruption problem caused by prediction errors to a certain extent. However, the interruption time is still 6.08–9.15% higher than the optimal RP-EDM-Precise.

In order to analyze the impact of our algorithm on energy consumption more intuitively, we compare different algorithms on the total energy of the network when serving equal traffic with adequate resources. The total energy for 24 h is shown in Figure 5. The energy increase of the RP-EDM series algorithms is relatively small, and the total energy is lower than that of GNFC 20.84–40.65%. This is because our algorithm uses the prediction results of CPU resources and considers the boot-up energy, according to the future network situation, considers the node energy and migration energy comprehensively. Monitoring the network every minute, RP-EDM selects those servers to be consolidated and ensures they will not be turned on soon after being shut down, which can not only turn off low-load servers to save energy, but also avoid frequent startup and migration. Additionally, we can see that models with different accuracy do have different impacts on the RP-ED. RP-EDM-CAT uses a higher-precision prediction model, whose performance is close to the optimal RP-EDM-Precise. While, RP-EDM-Basic -LSTM is unable to accurately detect the low load of the node in advance due to its low prediction accuracy, and the unsuitability of consolidating leads to high energy consumption.

Figure 6a,b shows the migration times in each period. Compared with GNFC executed every hour, we can see that RP-EDM migrates in some periods, while the migration times in some periods are 0, presenting aperiodic overall. The total migration times of our algorithm are lower than that of the comparison algorithm under both high and low loads. This is because RP-EDM monitors in real time, but it does not migrate every cycle. Instead, it determines whether to migrate certain NF or not based on the predicted resource requirements. The advantage of RP-EDM in determining migration timing lies in the reduction of frequent migration and switching on/off and consolidation of low-load servers timely, which is further reflected in the saving of network energy.

The above results show that the migration strategy considering the prediction results of short-term NF resource demand is effective in improving network performance, especially in reducing the long-term energy consumption and keeping the SLA violation rate low. This fact illustrates the prediction is nontrivial for improving user experience. At the same time, the accuracy of the prediction model has a great influence on the optimization of network energy. A higher prediction accuracy tends to be conducive to determining the migration timing and reducing the service outage time.

6. Conclusions

6.1. Summary of the Performance

In order to solve the problem of network energy consumption caused by the dynamic changes of resource demand during SFCs processing, this paper used the prediction results of short-term network resource demand and proposed the RP-EDM algorithm to determine the migration time. The simulation results show that our algorithm can reduce long-term network energy consumption. In addition, the combination of the prediction and migration algorithms improves network service capabilities and effectively reduces the number of SLA violations. Additionally, we find that the accuracy of prediction model largely affects the performance of the algorithm. In future research, we will focus on modeling the VNF resource prediction more accurately and propose a model with high accuracy and strong generalization.

6.2. Limitation of This Study

Although this study takes many factors into account, it still has some limitations that will affect its performance. First, we adopted the shortest path priority algorithm when deploying VNFs. There are situations where the deployment fails when available resources are available on the network, which directly affects the request acceptance rate. Second, the most important limitation lies in the fact that the prediction models we use are not accurate enough in predicting time-varying flow, which directly reflects in the performance. On the one hand, it is not sensitive enough to overload nodes, which will cause service interruption. On the other hand, potential low-load nodes cannot be sensed, which reduces energy saving performance. Third, in this work, one model can only predict one VNF, multiple models should be trained to predict different VNFs for one SFC, which increases the complexity and training time of model training. In future work, we will examine these points and attempt to conduct some research on learning models for this problem.

6.3. Potential Future Research Directions

It is recommended that further research be undertaken in the following directions.

A regression model with high accuracy on predicting resource demand needs to be established. Learning the features between the target VNF and resource demand, other VNFs on the same SFC, the characteristics of SFC would help us to establish a greater degree of accuracy on this matter. Such information can be added to the training set by embedding. Meanwhile, since the resource demand changes over time, after a period of time, the initial training model will fail to predict new samples. Therefore, it is necessary to update the sample data online to realize real-time optimization of the model.

Traditional heuristic VNF migration algorithms cannot adapt well to dynamic network traffic and structure. Although, in our study, we introduced the prediction of resource demand by Supervised Learning to eliminate this lag as much as possible. Another direction lies in Reinforcement Learning (RL) for assisting VNF reconfiguration, which dynamically updating decision-making strategies are significant to achieve long-term network energy optimization. It would be interesting to assess and compare the effects of heuristic algorithms and RL algorithms. Further research regarding the role of RL would be of great help in curing the VNF reconfiguration problem.