Challenges in Application of Petri Nets in Manufacturing Systems
Abstract
:1. Introduction
- (1)
- showing the recent works using Petri nets in the domain of manufacturing systems;
- (2)
- identifying the current challenges;
- (3)
- indicating the future trends in research.
2. A Brief Theory Background
3. Recent Research in Petri Nets
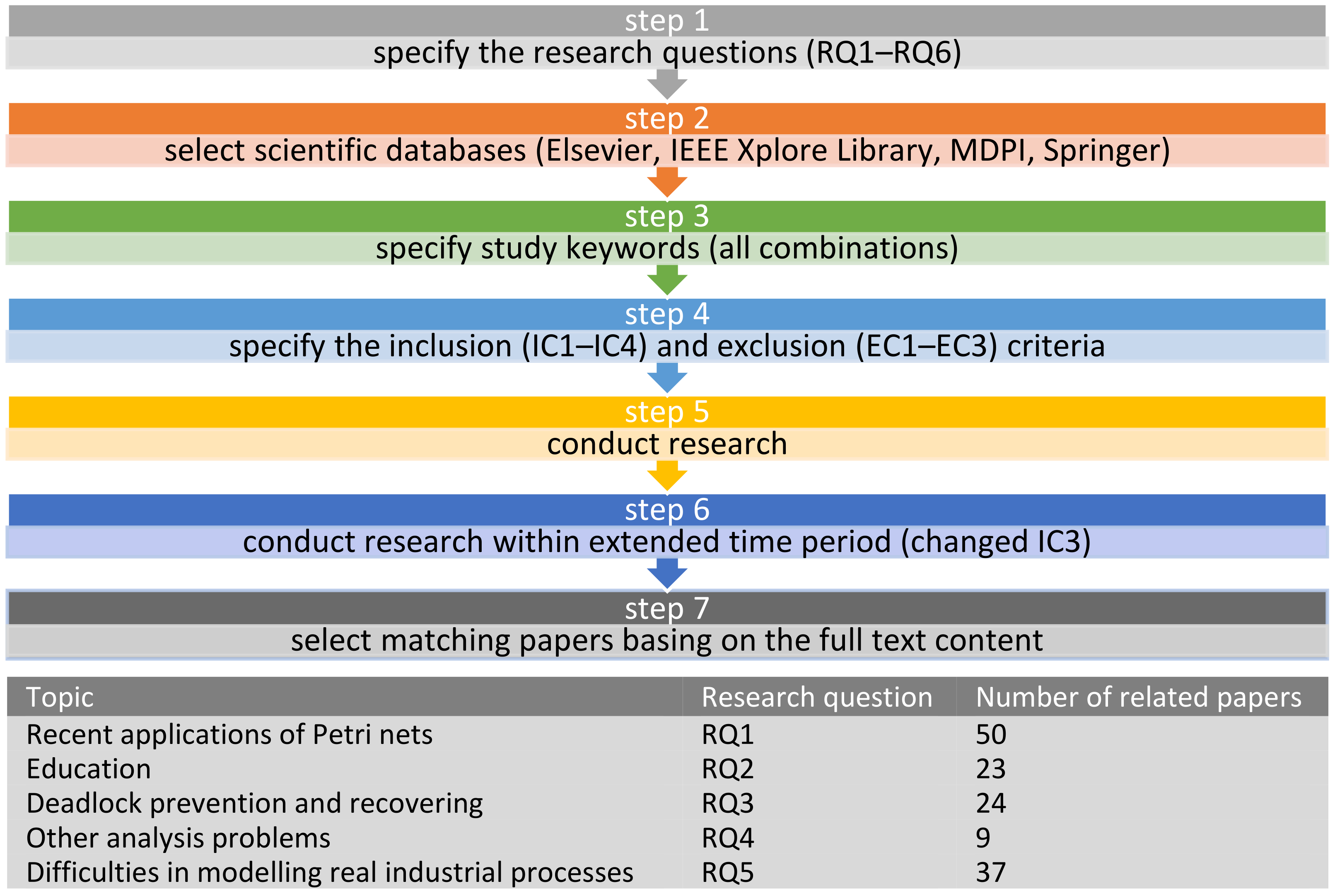
3.1. Review Methodology
3.2. Recent Applications of Petri Nets
4. Challenges Regarding Education in Respect of Application of Petri Net Models
5. Challenges Regarding Deadlock Prevention and Recovering
6. Challenges Regarding Other Analysis Problems
7. Difficulties in Modelling of Real Industrial Processes
8. Conclusions and Trends for the Future
- (1)
- Development and application of extended and high-level models and of methods for their analysis;
- (2)
- Developing models able to represent reconfigurability, unreliable resources and fault occurrences, and methods of analysis for such models;
- (3)
- Reducing the reachability graph or even eliminating it in the process of design analysis and verification;
- (4)
- Incorporating time into general models;
- (5)
- Simulations based on PN models;
- (6)
- Putting PNs into practice to enable everyday use of the thus-far developed approaches.
Author Contributions
Funding
Conflicts of Interest
References
- Petri, C.A. Kommunikation mit Automaten. Ph.D. Thesis, Universität Bonn, Bonn, Germany, 1962. [Google Scholar]
- Silva, M. Half a century after Carl Adam Petri’s Ph.D. thesis: A perspective on the field. Annu. Rev. Control 2013, 37, 191–219. [Google Scholar] [CrossRef]
- David, R.; Alla, H. Discrete, Continuous, and Hybrid Petri Nets; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Reisig, W.; Rozenberg, G. Carl Adam Petri: Ideas, Personality, Impact; Springer Nature Switzerland AG: Cham, Switzerland, 2019. [Google Scholar]
- Giua, A.; Silva, M. Petri nets and Automatic Control: A historical perspective. Annu. Rev. Control 2018, 45, 223–239. [Google Scholar] [CrossRef]
- Seatzu, C. Modeling, analysis, and control of automated manufacturing systems using Petri nets. In Proceedings of the IEEE 2019 24th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), Zaragoza, Spain, 10–13 September 2019; pp. 27–30. [Google Scholar]
- Karatkevich, A. Dynamic Analysis of Petri Net-Based Discrete Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Giua, A.; Silva, M. Modeling, analysis and control of Discrete Event Systems: A Petri net perspective. IFAC-PapersOnLine 2017, 50, 1772–1783. [Google Scholar] [CrossRef]
- Zhong, C.; He, W.; Li, Z.; Wu, M.; Qu, T. Deadlock analysis and control using Petri net decomposition techniques. Inf. Sci. 2019, 482, 440–456. [Google Scholar] [CrossRef]
- Wolf, K. Petri net model checking with LoLA 2. In Proceedings of the International Conference on Application and Theory of Petri Nets and Concurrency 2018, Bratislava, Slovakia, 24–29 June 2018; Springer: Cham, Switzerland, 2018; pp. 351–362. [Google Scholar]
- Wolf, K. How Petri Net Theory Serves Petri Net Model Checking: A Survey. In Transactions on Petri Nets and Other Models of Concurrency XIV; LNCS 2019; Koutny, M., Pomello, L., Kristensen, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; Volume 11790. [Google Scholar]
- Grobelna, I.; Wiśniewski, R.; Grobelny, M.; Wiśniewska, M. Design and Verification of Real-Life Processes With Application of Petri Nets. IEEE Trans. SMC Syst. 2017, 47, 2856–2869. [Google Scholar] [CrossRef]
- Grobelna, I. Model checking of reconfigurable FPGA modules specified by Petri nets. J. Syst. Archit. 2018, 89, 1–9. [Google Scholar] [CrossRef]
- Thong, W.J.; Ameedeen, M.A. A survey of Petri net tools. In Advanced Computer and Communication Engineering Technology; Springer: Cham, Switzerland, 2015; pp. 537–551. [Google Scholar]
- van Hee, K.; Oanea, O.; Post, R.; Somers, L.; van der Werf, J.M. Yasper: A tool for workflow modeling and analysis. In Proceedings of the 6th International Conference on Application of Concurrency to System Design, Turku, Finland, 28–30 June 2006; pp. 279–282. [Google Scholar]
- Yu, Q.; Cai, L.; Tan, X. Airport Emergency Rescue Model Establishment and Performance Analysis Using Colored Petri Nets and CPN Tools. Int. J. Aerosp. 2018, 2018, 2858375. [Google Scholar] [CrossRef] [Green Version]
- Dingle, N.J.; Knottenbelt, W.J.; Suto, T. PIPE2: A tool for the performance evaluation of generalised stochastic Petri Nets. ACM Sigmetr. Per 2009, 36, 34–39. [Google Scholar] [CrossRef]
- Davidrajuh, R.; Skolud, B.; Krenczyk, D. Performance Evaluation of Discrete Event Systems with GPenSIM. Computers 2018, 7, 8. [Google Scholar] [CrossRef] [Green Version]
- Gomes, L.; Moutinho, F.; Pereira, F. IOPT-tools—A Web based tool framework for embedded systems controller development using Petri nets. In Proceedings of the 23rd International Conference on Field programmable Logic and Applications, Porto, Portugal, 2–4 September 2013; p. 1. [Google Scholar]
- Qamsane, Y.; Tajer, A.; Philippot, A. A synthesis approach to distributed supervisory control design for manufacturing systems with Grafcet implementation. Int. J. Prod. Res. 2017, 55, 4283–4303. [Google Scholar] [CrossRef]
- Erasmus, J.; Vanderfeesten, I.; Traganos, K.; Grefen, P. Using business process models for the specification of manufacturing operations. Comput. Ind. 2020, 123, 103297. [Google Scholar] [CrossRef]
- Azangoo, M.; Taherkordi, A.; Blech, J.O. Digital Twins for Manufacturing Using UML and Behavioral Specifications. In Proceedings of the 25th IEEE International Conference on Emerging Technologies and Factory Automation, Vienna, Austria, 8–11 September 2020; pp. 1035–1038. [Google Scholar]
- Steimer, C.; Fischer, J.; Aurich, J.C. Model-based design process for the early phases of manufacturing system planning using SysML. Procedia CIRP 2017, 60, 163–168. [Google Scholar] [CrossRef]
- Komenda, J.; Lahaye, S.; Boimond, J.L.; van den Boom, T. Max-plus algebra in the history of discrete event systems. Annu. Rev. Control 2018, 45, 240–249. [Google Scholar] [CrossRef]
- Papadopoulos, C.T.; Li, J.; O’Kelly, M.E. A classification and review of timed Markov models of manufacturing systems. Comput. Ind. Eng. 2019, 128, 219–244. [Google Scholar] [CrossRef]
- Recalde, L.; Silva, M.; Ezpeleta, J.; Teruel, E. Petri Nets and Manufacturing Systems: An Examples-Driven Tour. In Lectures on Concurrency and Petri Nets: Advances in Petri Nets 2004; Desel, J., Reisig, W., Rozenberg, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 742–788. [Google Scholar]
- Margherita, E.G.; Braccini, A.M. Managing industry 4.0 automation for fair ethical business development: A single case study. Technol. Forecast. Soc. Chang. 2021, 172, 121048. [Google Scholar] [CrossRef]
- Zeinalnezhad, M.; Chofreh, A.G.; Goni, F.A.; Klemeš, J.J.; Sari, E. Simulation and Improvement of Patients’ Workflow in Heart Clinics during COVID-19 Pandemic Using Timed Coloured Petri Nets. Int. J. Environ. Res. Public Health 2020, 17, 8577. [Google Scholar] [CrossRef] [PubMed]
- Zheng, P.; Wang, H.; Sang, Z.; Zhong, R.Y.; Liu, Y.; Liu, C.; Mubarok, K.; Yu, S.; Xu, X. Smart manufacturing systems for Industry 4.0: Conceptual framework, scenarios, and future perspectives. Front. Mech. Eng. 2018, 13, 137–150. [Google Scholar] [CrossRef]
- Qu, Y.J.; Ming, X.G.; Liu, Z.W.; Zhang, X.Y.; Hou, Z.T. Smart manufacturing systems: State of the art and future trends. J. Adv. Manuf. Technol. 2019, 103, 3751–3768. [Google Scholar] [CrossRef]
- Lee, E.A. Cyber Physical Systems: Design Challenges. In Proceedings of the 11th IEEE International Symposium on Object and Component-Oriented Real-Time Distributed Computing, Orlando, FL, USA, 5–7 May 2008; pp. 363–369. [Google Scholar]
- Jazdi, N. Cyber physical systems in the context of Industry 4.0. In Proceedings of the IEEE International Conference on Automation, Quality and Testing, Robotics, Cluj-Napoca, Romania, 22–24 May 2014; pp. 1–4. [Google Scholar]
- Kučera, E.; Haffner, O.; Drahoš, P.; Leskovský, R.; Cigánek, J. PetriNet Editor + PetriNet Engine: New Software Tool For Modelling and Control of Discrete Event Systems Using Petri Nets and Code Generation. Appl. Sci. 2020, 10, 7662. [Google Scholar] [CrossRef]
- Chen, C.-N.; Liu, T.-K.; Chen, Y.J. Human-Machine Interaction: Adapted Safety Assistance in Mentality Using Hidden Markov Chain and Petri Net. Appl. Sci. 2019, 9, 5066. [Google Scholar] [CrossRef] [Green Version]
- Contador, J.C.; Satyro, W.C.; Contador, J.L.; Spinola, M.D. Flexibility in the Brazilian Industry 4.0: Challenges and Opportunities. Glob. J. Flex. Syst. Manag. 2020, 21, 15–31. [Google Scholar] [CrossRef]
- Bashir, M.; Hong, L. Global Supervisory Structure for Decentralized Systems of Flexible Manufacturing Systems Using Petri Nets. Processes 2019, 7, 595. [Google Scholar] [CrossRef] [Green Version]
- Rezig, S.; Ghorbel, C.; Achour, Z.; Rezg, N. PLC-based implementation of supervisory control for flexible manufacturing systems using theory of regions. Int. J. Autom. Control 2019, 13, 619–640. [Google Scholar] [CrossRef]
- Long, F.; Zeiler, P.; Bertsche, B. Modelling the flexibility of production systems in Industry 4.0 for analysing their productivity and availability with high-level Petri nets. IFAC-PapersOnLine 2017, 50, 5680–5687. [Google Scholar] [CrossRef]
- Holovatyy, A.; Teslyuk, V.; Kryvinska, N.; Kazarian, A. Development of Microcontroller-Based System for Background Radiation Monitoring. Sensors 2020, 20, 7322. [Google Scholar] [CrossRef] [PubMed]
- Davidrajuh, R. A New Modular Petri Net for Modeling Large Discrete-Event Systems: A Proposal Based on the Literature Study. Computers 2019, 8, 83. [Google Scholar] [CrossRef] [Green Version]
- Wenzelburger, P.; Allgöwer, F. A Petri Net Modeling Framework for the Control of Flexible Manufacturing Systems. IFAC-PapersOnLine 2019, 52, 492–498. [Google Scholar] [CrossRef]
- Hu, L.; Liu, Z.; Hu, W.; Wang, Y.; Tan, J.; Wu, F. Petri-net-based dynamic scheduling of flexible manufacturing system via deep reinforcement learning with graph convolutional network. J. Manuf. Syst. 2020, 55, 1–14. [Google Scholar] [CrossRef]
- Kaid, H.; Al-Ahmari, A.; Li, Z.; Davidrajuh, R. Intelligent Colored Token Petri Nets for Modeling, Control, and Validation of Dynamic Changes in Reconfigurable Manufacturing Systems. Processes 2020, 8, 358. [Google Scholar] [CrossRef] [Green Version]
- Wisniewski, R.; Bazydło, G.; Szcześniak, P.; Grobelna, I.; Wojnakowski, M. Design and Verification of Cyber-Physical Systems Specified by Petri Nets—A Case Study of a Direct Matrix Converter. Mathematics 2019, 7, 812. [Google Scholar] [CrossRef] [Green Version]
- Wiśniewski, R.; Wiśniewska, M.; Jarnut, M. C-Exact Hypergraphs in Concurrency and Sequentiality Analyses of Cyber-Physical Systems Specified by Safe Petri Nets. IEEE Access 2019, 7, 13510–13522. [Google Scholar] [CrossRef]
- Wisniewski, R.; Bazydło, G.; Szcześniak, P.; Wojnakowski, M. Petri Net-Based Specification of Cyber-Physical Systems Oriented to Control Direct Matrix Converters With Space Vector Modulation. IEEE Access 2019, 7, 23407–23420. [Google Scholar] [CrossRef]
- Rocha, J.-I.; Páscoa Dias, O.; Gomes, L. Improving Synchronous Dataflow Analysis Supported by Petri Net Mappings. Electronics 2018, 7, 448. [Google Scholar] [CrossRef] [Green Version]
- Hayashi, V.; Ruggiero, W. Non-Invasive Challenge Response Authentication for Voice Transactions with Smart Home Behavior. Sensors 2020, 20, 6563. [Google Scholar] [CrossRef]
- Lu, Z.; Liu, J.; Dong, L.; Liang, X. Maintenance Process Simulation Based Maintainability Evaluation by Using Stochastic Colored Petri Net. Appl. Sci. 2019, 9, 3262. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Zhu, Y.; Cheng, B.; Lin, C.; Chen, J. A Petri Net-Based Approach for Supporting Traceability in Cyber-Physical Manufacturing Systems. Sensors 2016, 16, 382. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.-C.; You, J.-X.; Li, Z.; Tian, G. Fuzzy Petri nets for knowledge representation and reasoning: A literature review. Eng. Appl. Artif. Intell. 2017, 60, 45–56. [Google Scholar] [CrossRef]
- Markiewicz, M.; Gniewek, L. A Program Model of Fuzzy Interpreted Petri Net to Control Discrete Event Systems. Appl. Sci. 2017, 7, 422. [Google Scholar] [CrossRef] [Green Version]
- Hong, Z.; Feng, Y.; Li, Z.; Tian, G.; Tan, J. Reliability-Based and Cost-Oriented Product Optimization Integrating Fuzzy Reasoning Petri Nets, Interval Expert Evaluation and Cultural-Based DMOPSO Using Crowding Distance Sorting. Appl. Sci. 2017, 7, 791. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Fei, Z.; Chang, Q.; Li, S. Energy Saving Operation of Manufacturing System Based on Dynamic Adaptive Fuzzy Reasoning Petri Net. Energies 2019, 12, 2216. [Google Scholar] [CrossRef] [Green Version]
- Seung-Yun, K.; Yilin, Y. A self-navigating robot using Fuzzy Petri nets. Robot. Auton. Syst. 2018, 101, 153–165. [Google Scholar]
- Rani, S.; Jain, A.; Castillo, O. Research trends on fuzzy logic controller for mobile robot navigation: A scientometric study. J. Autom. Mob. Robot. Intell. Syst. 2020, 14, 87–108. [Google Scholar] [CrossRef]
- Wang, L.; Dai, W.; Ai, J.; Duan, W.; Zhao, Y. Reliability Evaluation for Manufacturing System Based on Dynamic Adaptive Fuzzy Reasoning Petri Net. IEEE Access 2020, 8, 167276–167287. [Google Scholar] [CrossRef]
- Wang, J. Timed Petri Nets: Theory and Application; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 9. [Google Scholar]
- Guo, Z.; Zhang, Y.; Zhao, X.; Song, X. A Timed Colored Petri Net Simulation-Based Self-Adaptive Collaboration Method for Production-Logistics Systems. Appl. Sci. 2017, 7, 235. [Google Scholar] [CrossRef] [Green Version]
- Kammoun, M.A.; Ezzeddine, W.; Rezg, N.; Achour, Z. FMS Scheduling under Availability Constraint with Supervisor Based on Timed Petri Nets. Appl. Sci. 2017, 7, 399. [Google Scholar] [CrossRef] [Green Version]
- Shailesh, T.; Nayak, A.; Prasad, D. An UML Based Performance Evaluation of Real-Time Systems Using Timed Petri Net. Computers 2020, 9, 94. [Google Scholar] [CrossRef]
- Lefebvre, D. Dynamical Scheduling and Robust Control in Uncertain Environments with Petri Nets for DESs. Processes 2017, 5, 54. [Google Scholar] [CrossRef]
- Sun, X.; Li, R.; Yuan, Z. Anomaly Detection in Discrete Manufacturing Systems by Pattern Relation Table Approaches. Sensors 2020, 20, 5766. [Google Scholar] [CrossRef] [PubMed]
- Mejía, G.; Pereira, J. Multiobjective scheduling algorithm for flexible manufacturing systems with Petri nets. J. Manuf. Syst. 2020, 54, 272–284. [Google Scholar] [CrossRef]
- Cavone, G.; Dotoli, M.; Seatzu, C. A Survey on Petri Net Models for Freight Logistics and Transportation Systems. IEEE Trans. Intell. Transp. Syst. 2018, 19, 1795–1813. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Wang, L.; Cai, G. An Extended Object-Oriented Petri Net Model for Vulnerability Evaluation of Communication-Based Train Control System. Symmetry 2020, 12, 1474. [Google Scholar] [CrossRef]
- Moutinho, F.; Campos-Rebelo, R.; Lagartinho-Oliveira, C.; Moreira, E.; Almeida, B.; Gomes, L. NOVA Mobility Assistive System: Developed and Remotely Controlled with IOPT-Tools. Electronics 2020, 9, 1328. [Google Scholar] [CrossRef]
- Riouali, Y.; Benhlima, L.; Bah, S. Extended Batches Petri Nets Based System for Road Traffic Management in WSNs. J. Sens. Actuator Netw. 2017, 6, 30. [Google Scholar] [CrossRef] [Green Version]
- Riouali, Y.; Benhlima, L.; Bah, S. An Integrated Turning Movements Estimation to Petri Net Based Road Traffic Modeling. J. Sens. Actuator Netw. 2019, 8, 49. [Google Scholar] [CrossRef] [Green Version]
- López, J.; Sánchez-Vilariño, P.; Sanz, R.; Paz, E. Implementing Autonomous Driving Behaviors Using a Message Driven Petri Net Framework. Sensors 2020, 20, 449. [Google Scholar] [CrossRef] [Green Version]
- Prilandita, N.; McLellan, B.; Tezuka, T. Modeling Autonomous Decision-Making on Energy and Environmental Management Using Petri-Net: The Case Study of a Community in Bandung, Indonesia. Challenges 2016, 7, 9. [Google Scholar] [CrossRef] [Green Version]
- López, J.; Santana-Alonso, A.; Díaz-Cacho Medina, M. Formal Verification for Task Description Languages. A Petri Net Approach. Sensors 2019, 19, 4965. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Z.; Zhao, T.; Wang, S.; Ju, H. New Model-Based Analysis Method with Multiple Constraints for Integrated Modular Avionics Dynamic Reconfiguration Process. Processes 2020, 8, 574. [Google Scholar] [CrossRef]
- Fonseca i Casas, P.; Lijia Hu, D.; Guasch i Petit, A.; Figueras i Jové, J. Simplifying the Verification of Simulation Models through Petri Net to FlexSim Mapping. Appl. Sci. 2020, 10, 1395. [Google Scholar] [CrossRef] [Green Version]
- Zurawski, R.; Zhou, M. Petri nets and industrial applications: A tutorial. IEEE Trans. Ind. Electron. 1994, 41, 567–583. [Google Scholar] [CrossRef]
- Rodriguez-Andina, J.J.; Gomes, L.; Bogosyan, S. Current Trends in Industrial Electronics Education. IEEE Trans. Ind. Electron. 2010, 57, 3245–3252. [Google Scholar] [CrossRef]
- Cerone, A.; Roggenbach, M.; Schlingloff, H.; Schneider, G.; Shaikh, S. Teaching Formal Methods for Software Engineering-Ten Principles; Informatica Didactica; University of Potsdam: Potsdam, Germany, 2015. [Google Scholar]
- Gašević, D.; Devedžić, V. Software support for teaching Petri nets: P3. In Proceedings of the 3rd IEEE International Conference Advanced Technologies, Athens, Greece, 9–11 July 2003; pp. 300–301. [Google Scholar]
- Gašević, D.; Devedžić, V. Teaching Petri nets using P3. J. Educ. Technol. Soc. 2004, 7, 153–166. [Google Scholar]
- Mei, C.; Zhang, X.; Zhao, W.; Periyasamy, K.; Headington, M. A tool for teaching Petri nets. J. Comput. Sci. Coll. 2011, 26, 181–188. [Google Scholar]
- Vörös, A.; Darvas, D.; Molnár, V.; Klenik, A.; Hajdu, Á.; Jámbor, A.; Bartha, T.; Majzik, I. PetriDotNet 1.5: Extensible Petri net editor and analyser for education and research. In Proceedings of the International Conference on Applications and Theory of Petri Nets and Concurrency, Toruń, Poland, 19–24 June 2016; Springer: Cham, Switzerland, 2016; pp. 123–132. [Google Scholar]
- Vörös, A.; Darvas, D.; Hajdu, Á.; Klenik, A.; Marussy, K.; Molnár, V.; Bartha, T.; Majzik, I. Industrial applications of the PetriDotNet modelling and analysis tool. Sci. Comput. Program. 2018, 157, 17–40. [Google Scholar] [CrossRef] [Green Version]
- Amparore, E.G.; Donatelli, S. GreatTeach: A tool for teaching (stochastic) Petri nets. In Proceedings of the International Conference on Applications and Theory of Petri Nets and Concurrency, Bratislava, Slovakia, 24–29 June 2018; Springer: Cham, Switzerland, 2018; pp. 416–425. [Google Scholar]
- Kučera, E.; Haffner, O.; Drahoš, P.; Cigánek, J.; Leskovský, R.; Štefanovič, J. New Software Tool for Modeling and Control of Discrete-Event and Hybrid Systems Using Timed Interpreted Petri Nets. App. Sci. 2020, 10, 5027. [Google Scholar] [CrossRef]
- Kučera, E.; Haffner, O.; Leskovský, R. PN2ARDUINO-A New Petri Net Software Tool for Control of Discrete-event and Hybrid Systems Using Arduino Microcontrollers. In Proceedings of the Federated Conference on Computer Science and Information Systems, Leipzig, Germany, 1–4 September 2019; pp. 915–919. [Google Scholar]
- Gomes, L.; Bogosyan, S. Current Trends in Remote Laboratories. IEEE Trans. Ind. Electron. 2009, 56, 4744–4756. [Google Scholar] [CrossRef]
- Márquez, M.; Mejías, A.; Herrera, R.; Andújar, J.M. Programming and testing a PLC to control a scalable industrial plant in remote way. In Proceedings of the 4th Experiment@ International Conference, Algarve, Portugal, 6–8 June 2017; pp. 105–106. [Google Scholar]
- Hernandez-Jayo, U.; Garcia-Zubia, J. Remote measurement and instrumentation laboratory for training in real analog electronic experiments. Measurement 2016, 82, 123–134. [Google Scholar] [CrossRef]
- Yayla, A.; Korkmaz, H.; Buldu, A.; Sarikas, A. Development of a remote laboratory for an electronic circuit design and analysis course with increased accessibility by using speech recognition technology. In Computer Applications in Engineering Education; Wiley: Hoboken, NJ, USA, 2020; pp. 1–14. [Google Scholar]
- Rubio, E.; Santana, I.; Esparza, V.; Rohten, J. Remote laboratories for control education: Experience at the universidad del Bío-Bío. In Proceedings of the IEEE International Conference on Automatica (ICA-ACCA), Curicó, Chile, 19–21 October 2016; pp. 1–6. [Google Scholar]
- Ali, W. Online and remote learning in higher education institutes: A necessity in light of COVID-19 pandemic. Higher Educ. Stud. 2020, 10, 16–25. [Google Scholar] [CrossRef]
- Korečko, Š. Interactive Approach to Coloured Petri Nets Teaching; Tech. Rep. IK-TR3; Eötvös Loránd University, Faculty of Informatics: Budapest, Hungary, 2018. [Google Scholar]
- Korečko, Š. Project-Based Approach to Teaching Event-Driven Simulation. In Proceedings of the 42nd International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 20–24 May 2019; pp. 1604–1608. [Google Scholar]
- Reis, A.C.B.; Barbalho, S.C.M.; Zanette, A.C.D. A bibliometric and classification study of Project-based Learning in Engineering Education. Production 2017, 27, e20162258. [Google Scholar] [CrossRef] [Green Version]
- Schmitz, D.; Moldt, D.; Cabac, L.; Mosteller, D.; Haustermann, M. Utilizing Petri Nets for Teaching in Practical Courses on Collaborative Software Engineering. In Proceedings of the 16th International Conference on Application of Concurrency to System Design, Torun, Poland, 19–24 June 2016; pp. 74–83. [Google Scholar]
- Ezpeleta, J.; Colom, J.M.; Martinez, J. A Petri net based deadlock prevention policy for flexible manufacturing systems. IEEE Trans. Robot. Autom. 1995, 11, 173–184. [Google Scholar] [CrossRef] [Green Version]
- Uzam, M. An optimal deadlock prevention policy for flexible manufacturing systems using Petri net models with resources and the theory of regions. Int. J. Adv. Manuf. Technol. 2002, 19, 192–208. [Google Scholar] [CrossRef]
- Kaid, H.; Al-Ahmari, A.; El-Tamimi, A.M.; Nasr, E.A.; Li, Z. Design and implementation of deadlock control for automated manufacturing systems. S. Afr. J. Ind. Eng. 2019, 30, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Messinis, S.; Vosniakos, G.C. An agent-based flexible manufacturing system controller with Petri-net enabled algebraic deadlock avoidance. Rep. Mech. Eng. 2020, 1, 77–92. [Google Scholar] [CrossRef]
- Li, S.; Wei, X.; Cai, Y.; Ma, B.; Hou, C. An elementary siphon-based deadlock control algorithm with maximally reachable number to cope with deadlock problems in ordinary Petri nets. Adv. Mech. Eng. 2017, 9, 1–14. [Google Scholar] [CrossRef]
- Rezig, S.; Turki, S.; Rezg, N. Compute Optimization of Petri Net Controllers Using the Algebraic Method. Appl. Sci. 2019, 9, 2633. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.F.; Wu, N.Q.; Li, Z.W.; Qu, T. On a maximally permissive deadlock prevention policy for automated manufacturing systems by using resource-oriented Petri nets. ISA Trans. 2019, 89, 67–76. [Google Scholar] [CrossRef]
- Uzam, M.; Zhou, M.C. An improved iterative synthesis method for liveness enforcing supervisors of flexible manufacturing systems. Int. J. Prod. Res. 2006, 44, 1987–2030. [Google Scholar] [CrossRef]
- Gu, C.; Li, Z.; Wu, N.; Khalgui, M.; Qu, T.; Al-Ahmari, A. Improved Multi-Step Look-Ahead Control Policies for Automated Manufacturing Systems. IEEE Access 2018, 6, 68824–68838. [Google Scholar] [CrossRef]
- Li, X.; Liu, G.; Li, Z.; Wu, N.; Barkaoui, K. Elementary Siphon-Based Robust Control for Automated Manufacturing Systems With Multiple Unreliable Resources. IEEE Access 2019, 7, 21006–21019. [Google Scholar] [CrossRef]
- Xiang, Z. Deadlock Avoidance of Flexible Manufacturing Systems by Colored Resource-Oriented Petri Nets with Novel Colored Capacity. In Verification and Evaluation of Computer and Communication Systems; VECoS 2020, LCNS 2020; Ben Hedia, B., Chen, Y.F., Liu, G., Yu, Z., Eds.; Springer: Cham, Switzerland, 2020; Volume 12519. [Google Scholar]
- Kaid, H.; Al-Ahmari, A.; Li, Z.; Davidrajuh, R. Single Controller-Based Colored Petri Nets for Deadlock Control in Automated Manufacturing Systems. Processes 2020, 8, 21. [Google Scholar] [CrossRef] [Green Version]
- Luo, J.; Liu, Z.; Zhou, M.; Xing, K.; Wang, X.; Li, X.; Liu, H. Robust deadlock control of automated manufacturing systems with multiple unreliable resources. Inf. Sci. 2019, 479, 401–415. [Google Scholar] [CrossRef]
- Salaheldin Elsayed, M.; El Kafrawy, P.; Wu, N. Modeling and Deadlock Control of Reconfigurable Multi-Unit Resource Systems. IEEE Access 2020, 8, 133605–133621. [Google Scholar] [CrossRef]
- Kaid, H.; Al-Ahmari, A.; Li, Z.; Davidrajuh, R. Automatic Supervisory Controller for Deadlock Control in Reconfigurable Manufacturing Systems with Dynamic Changes. Appl. Sci. 2020, 10, 5270. [Google Scholar] [CrossRef]
- Gu, C.; Ma, Z.; Li, Z.; Giua, A. Verification of Nonblockingness in Bounded Petri Nets With a Semi-Structural Approach. In Proceedings of the IEEE 58th Conference on Decision and Control (CDC), Nice, France, 11–13 December 2019; pp. 6718–6723. [Google Scholar]
- Pomares-Angelino, R.; López-Mellado, E. Automated Modelling of Deadlock-free Petri Nets Using Duplicated Transition Labels. In Proceedings of the 17th International Conference on Electrical Engineering, Computing Science and Automatic Control, Mexico City, Mexico, 11–13 November 2020; pp. 1–7. [Google Scholar]
- Li, L.; Basile, F.; Li, Z. Closed-Loop Deadlock-Free Supervision for GMECs in Time Petri Net Systems. IEEE Trans. Autom. Control 2020. [Google Scholar] [CrossRef]
- Pan, Y.-L. One Computational Innovation Transition-Based Recovery Policy for Flexible Manufacturing Systems Using Petri nets. Appl. Sci. 2020, 10, 2332. [Google Scholar] [CrossRef] [Green Version]
- Dong, Y.; Chen, Y.; Li, S.; El-Meligy, M.A.; Sharaf, M. An Efficient Deadlock Recovery Policy for Flexible Manufacturing Systems Modeled With Petri Nets. IEEE Access 2019, 7, 11785–11795. [Google Scholar] [CrossRef]
- Row, T.C.; Syu, W.M.; Pan, Y.-L.; Wang, C.-C. One Novel and Optimal Deadlock Recovery Policy for Flexible Manufacturing Systems Using Iterative Control Transitions Strategy. Math. Probl. Eng. 2019, 2019, 4847072. [Google Scholar] [CrossRef]
- Hu, M.; Yang, S.; Chen, Y. Partial Reachability Graph Analysis of Petri Nets for Flexible Manufacturing Systems. IEEE Access 2020, 8, 227925–227935. [Google Scholar] [CrossRef]
- Valmari, A. The State Explosion Problem. In Lectures on Petri Nets I: Basic Models: Advances in Petri Nets; ACPN 1996, LNCS 1998; Reisig, W., Rozenberg, G., Eds.; Springer: Berlin/Heidelberg, Germany, 1998; Volume 1491, pp. 429–528. [Google Scholar]
- Ren, H.; Xu, J.; Liang, Y.; Rehman, A.U.; Umer, U. On state-space compression and state reachability retrieval of Petri nets. Adv. Mech. Eng. 2019, 11. [Google Scholar] [CrossRef] [Green Version]
- Finkbeiner, B.; Gieseking, M.; Hecking-Harbusch, J.; Olderog, E.-R. AdamMC: A Model Checker for Petri Nets with Transits against Flow-LTL. In Computer Aided Verification 2020; Lahiri, S.K., Wang, C., Eds.; Springer: Cham, Switzerland, 2020; pp. 64–76. [Google Scholar]
- Esparza, J.; Nielsen, M. Decidability Issues for Petri Nets—A survey. J. Inf. Process. Cybern. 1994, 30, 143–160. [Google Scholar]
- Wang, J. Deterministic Timed Petri Nets. In Timed Petri Nets; The Kluwer International Series on Discrete Event Dynamic Systems; Springer: New York, NY, USA, 1998; Volume 9, pp. 37–61. [Google Scholar]
- Costelha, H.; Lima, P. Modelling, analysis and execution of robotic tasks using Petri nets. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 1449–1454. [Google Scholar]
- Wisniewski, R.; Grobelna, I.; Karatkevich, A. Determinism in Cyber-Physical Systems Specified by Interpreted Petri Nets. Sensors 2020, 20, 5565. [Google Scholar] [CrossRef]
- Lohstroh, M.; Incer Romeo, I.; Goens, A.; Derler, P.; Castrillon, J.; Lee, E.A.; Sangiovanni-Vincentelli, A. Reactors: A Deterministic Model for Composable Reactive Systems. In Cyber Physical Systems; Model-Based Design, LNCS 2020; Chamberlain, R., Edin Grimheden, M., Taha, W., Eds.; Springer: Cham, Switzerland, 2020; Volume 11971. [Google Scholar]
- Lohstroh, M.; Schoeberl, M.; Goens, A.; Wasicek, A.; Gill, C.; Sirjani, M.; Lee, E.A. Invited: Actors Revisited for Time-Critical Systems. In Proceedings of the 56th ACM/IEEE Design Automation Conference, Las Vegas, NV, USA, 2–6 June 2019; pp. 1–4. [Google Scholar]
- Sirjani, M.; Lee, E.A.; Khamespanah, E. Model Checking Software in Cyberphysical Systems. In Proceedings of the IEEE 44th Annual Computers, Software, and Applications Conference (COMPSAC), Madrid, Spain, 13–17 July 2020; pp. 1017–1026. [Google Scholar]
- Lynch, N.A. Distributed Algorithms; Elsevier: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Falcone, A.; Garro, A. Pitfalls and Remedies in Modeling and Simulation of Cyber Physical Systems. In Proceedings of the IEEE/ACM 24th International Symposium on Distributed Simulation and Real Time Applications, Prague, Czech Republic, 14–16 September 2020; pp. 1–5. [Google Scholar]
- Alcaraz-Mejia, M.; Lopez-Mellado, E.; Ramirez-Trevino, A. Fault recovery of manufacturing systems based on controller reconfiguration. In Proceedings of the IEEE/SMC International Conference on System of Systems Engineering, Los Angeles, CA, USA, 26–28 April 2006; Volume 6. [Google Scholar]
- Ramirez-Trevino, A.; Ruiz-Beltran, E.; Aramburo-Lizarraga, J.; Lopez-Mellado, E. Structural Diagnosability of DES and Design of Reduced Petri Net Diagnosers. IEEE Trans. SMC Part A Syst. Hum. 2012, 42, 416–429. [Google Scholar] [CrossRef]
- Kaid, H.; Al-Ahmari, A.; Nasr, E.A.; Al-Shayea, A.; Kamrani, A.K.; Noman, M.A.; Mahmoud, H.A. Petri net model based on neural network for deadlock control and fault detection and treatment in automated manufacturing systems. IEEE Access 2020, 8, 103219–103235. [Google Scholar] [CrossRef]
- Alzalab, E.A.; Yu, Z.; Wu, N.; Kaid, H. Fault-Recovery and Repair Modeling of Discrete Event Systems Using Petri Nets. IEEE Access 2020, 8, 170237–170247. [Google Scholar] [CrossRef]
- Ran, N.; Wang, S.; Su, H.; Wang, C. Fault diagnosis for discrete event systems modeled by bounded Petri nets. Asian J. Control 2017, 19, 1532–1541. [Google Scholar] [CrossRef]
- Blanke, M.; Frei, W.C.; Kraus, F.; Patton, J.R.; Staroswiecki, M. What is Fault-Tolerant Control? IFAC Proc. 2000, 33, 41–52. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Jiang, J. Bibliographical review on reconfigurable fault-tolerant control systems. Annu. Rev. Control 2008, 32, 229–252. [Google Scholar] [CrossRef]
- Clarke, E.M., Jr.; Grumberg, O.; Kroening, D.; Peled, D.; Veith, H. Model Checking; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Clarke, E.M.; Klieber, W.; Nováček, M.; Zuliani, P. Model checking and the state explosion problem. In LASER Summer School on Software Engineering 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1–30. [Google Scholar]
- Clarke, E.M.; Zuliani, P. Statistical model checking for cyber-physical systems. In Proceedings of the International Symposium on Automated Technology for Verification and Analysis, Taipei, Taiwan, 11–14 October 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 1–12. [Google Scholar]
- Agha, G.; Palmskog, K. A survey of statistical model checking. ACM Trans. Model. Comput. Simul. 2018, 28, 1–39. [Google Scholar] [CrossRef]
- Himmiche, S.; Aubry, A.; Marangé, P.; Duflot-Kremer, M.; Pétin, J.F. Using Statistical-Model-Checking-Based Simulation for Evaluating the Robustness of a Production Schedule. In Service Orientation in Holonic and Multi-Agent Manufacturing; Studies in Computational Intelligence; Borangiu, T., Trentesaux, D., Thomas, A., Cardin, O., Eds.; Springer: Cham, Switzerland, 2018; Volume 762. [Google Scholar]
- Grobelna, I. Formal Verification of Control Modules in Cyber-Physical Systems. Sensors 2020, 20, 5154. [Google Scholar] [CrossRef] [PubMed]
- Torres, P.J.R.; Mercado, E.I.S.; Rifón, L.A. Probabilistic Boolean network modeling and model checking as an approach for DFMEA for manufacturing systems. J. Intell. Manuf. 2018, 29, 1393–1413. [Google Scholar]
- Huang, X.; Ding, Z.; Bi, Z.; Wang, Y.; Zheng, K.; Huang, X. Model Checking of Systems with Unreliable Machines Using PRISM. In Proceedings of the 9th International Conference on Information Technology in Medicine and Education, Hangzhou, China, 19–21 October 2018; pp. 872–876. [Google Scholar]
- Pakonen, A.; Tahvonen, T.; Hartikainen, M.; Pihlanko, M. Practical applications of model checking in the Finnish nuclear industry. In Proceedings of the 10th International Topical Meeting on Nuclear Plant Instrumentation, Control and Human Machine Interface Technologies, San Francisco, CA, USA, 11–15 June 2017; pp. 1342–1352. [Google Scholar]
- Gómez-Martínez, E.; de Lara, J.; Guerra, E. Extensible Structural Analysis of Petri Net Product Lines. In Transactions on Petri Nets and Other Models of Concurrency XV; Koutny, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2021; pp. 27–49. [Google Scholar]
- Reisig, W. Associative composition of components with double-sided interfaces. Acta Inform. 2019, 56, 229–253. [Google Scholar] [CrossRef]
- Margherita, E.G.; Bua, I. The Role of Human Resource Practices for the Development of Operator 4.0 in Industry 4.0 Organisations: A Literature Review and a Research Agenda. Businesses 2021, 1, 18–33. [Google Scholar] [CrossRef]
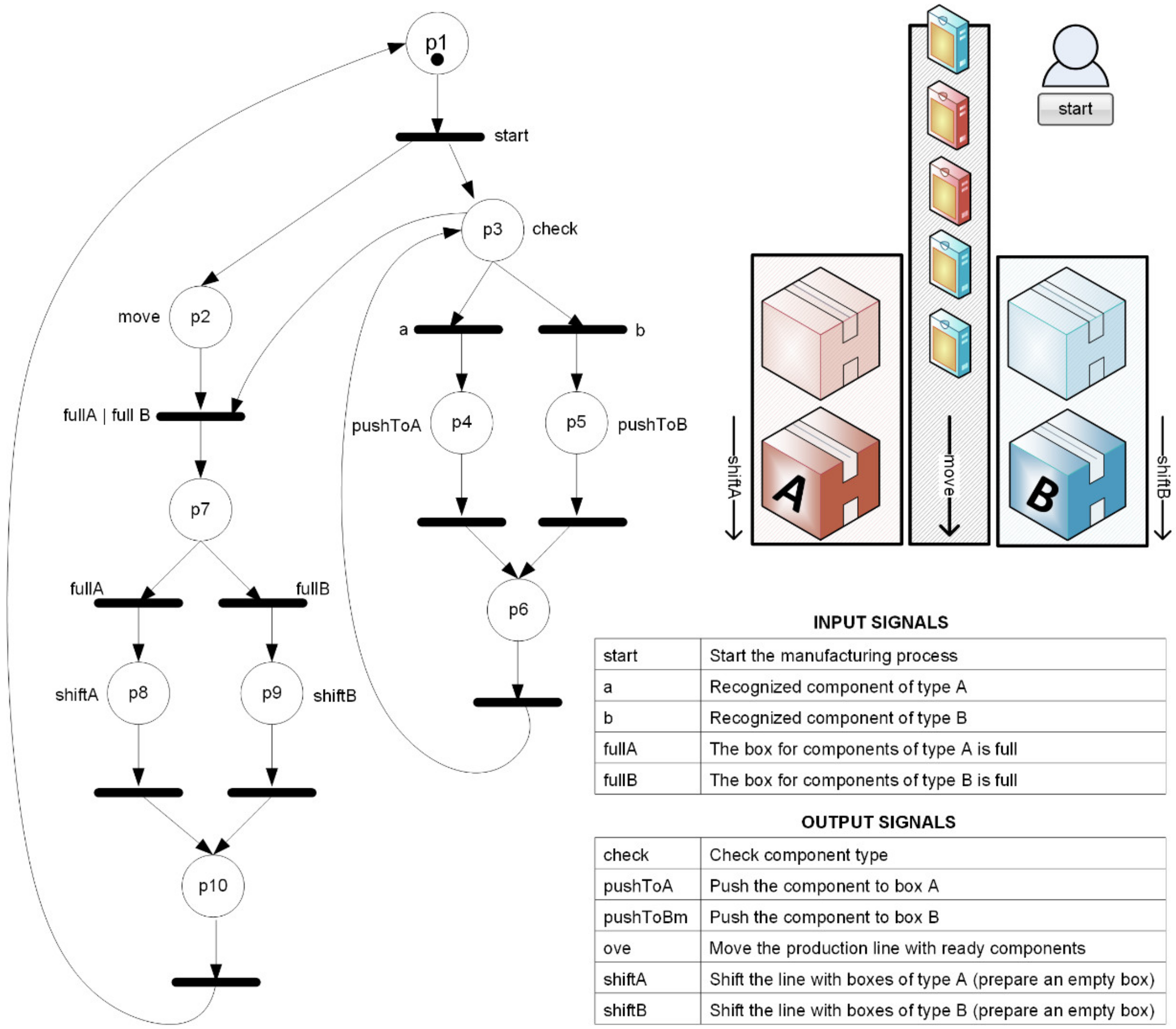
| Thematic Group | Publication | Year | Contributions |
|---|---|---|---|
| Trends in industrial electronic education | [76] | 2010 | Identification of trends. Discussion for the needs and challenges of industrial electronic education both at university level and in lifelong learning. Overview of state-of-the-art learning methodologies and tools. |
| Remote laboratories and education | [76] | 2010 | Analysis of trends. Prediction about the increasing popularity of remote laboratories. |
| [86] | 2009 | Remote laboratories dedicated for autonomous learning activities. Overview of state-of-the-art technologies in the development of remote laboratories. | |
| [87] | 2017 | Remote programming and testing of physical devices. Proposition of practical classes in several subjects at the University of Huelva (Spain). | |
| [88] | 2016 | Remote building and testing of real analogue electronic circuits. | |
| [89] | 2020 | A remote laboratory application that aims to increase the accessibility of electronic circuit design and analysis courses by using speech recognition technology. | |
| [90] | 2016 | Remote laboratories for controlled education with flexible time access. Introducing remote laboratories at the Universidad del Bío-Bío (Chile). | |
| [91] | 2020 | Emphasising self-motivation of students. Highlighting that staff members should use technology to enhance learning. Online and remote learning as a necessity in times of lockdowns and social distancing due to COVID-19 pandemic. | |
| Petri net software tools for education | [78,79] | 2003, 2004 | P3—PN software tool. Learning PNs in a more obvious and quicker way in order to use them for hardware modelling. |
| [80] | 2011 | Simple tool intended to teach the beginners | |
| [81,82] | 2016, 2018 | PetriDotNet—an extensible PN editor and analyser for education and research. Suitable also for design, development, and analysis of industrial systems. | |
| [83] | 2018 | GreatTeach—a tool for teaching stochastic PNs | |
| [84,85] | 2020, 2019 | PN2ARDUINO—a tool for modelling and control of discrete-event and hybrid systems using timed interpreted PNs. The proposed tool can improve education and practice in cyber-physical systems (Industry 4.0). | |
| Teaching Petri nets | [77] | 2015 | Recommended principles for teaching formal methods for software engineering. |
| [92] | 2018 | An interactive approach to teaching coloured PNs. Suitable for short and intensive courses. | |
| [93] | 2019 | Project-based learning to a graduate course focusing on the event-driven simulation with coloured PNs. | |
| [94] | 2017 | Project-based learning in engineering education. | |
| [95] | 2016 | The teaching of PNs for software development. Best practices for teaching in practice. |
| Authors and Reference | Year | Contributions |
|---|---|---|
| Kaid, H. at al. [98] | 2019 | Classical method from [96] combined with transformation of a PN model into a ladder diagram, an effective method for PLC implementation from a controlled system model represented by PNs. |
| Messinis, S. and Vosniakos, G.C. [99] | 2020 | Efficient design of a controller using agents. Computation of minimal siphons using the linear algebra. |
| Li, S. et al. [100] | 2017 | Control place and transition added to a siphon of an ordinary PN. The proposed deadlock control algorithm can obtain a live controlled system, whose reachable number (MRN) is the same as that of an original uncontrolled net. |
| Rezig, S. et al. [101] | 2019 | Optimal PN supervisor able to respect the control specifications is calculated. Design a set of controllers based on the properties of PNs and not on reachability graph generation for bounded PNs. |
| Chen, H.F. et al. [102] | 2019 | Resource-oriented PNs used to model systems for deadlock prevention. Various types of illegal markings that can be structurally identified. Illegal markings prevented by using polynomial algorithms or by solving the linear programming problems. |
| Gu, C. et al. [104] | 2018 | Improved multi-step look-ahead control policies. Deadlock avoidance polices applicable to complex situations, including a model with one-unit resource shared by two or more perfect resource-transition circuits not containing each other. |
| Li, X. et al. [105] | 2019 | Two-step robust deadlock control policy for systems of the simple sequential process with resources based on elementary siphons: the first step (elementary siphons control) derives a live controlled system without considering resource failures, the second one deals with failure-induced deadlock control issues. |
| Xiang Z. [106] | 2020 | Coloured capacity concept in coloured resource-oriented PNs. All control places used to forbid illegal markings are displaced by the coloured capacity and the deadlock is avoided by the new execution rule. |
| Kaid, H. et al. [107] | 2020 | Two-step robust deadlock control approach. Deadlock prevention based on strict minimal siphons to create a controlled PN model. All obtained control places merged into a single control place based on the coloured PN. |
| Luo, J. et al. [108] | 2019 | Siphon-based deadlock avoiding in systems with multiple resource failures. A PN model developed to characterise the failure and repair of unreliable resources. A robust deadlock prevention controller is proposed. |
| Salaheldin Elsayed, M. et al. [109] | 2020 | New PN model for modelling a limited reconfigurability. Efficient integrated policy for designing supervisors for multi-unit resource systems based on a class of PNs. Siphon-based deadlock prevention policy. |
| Kaid, H. et al. [110] | 2020 | Automatic supervisory control in reconfigurable manufacturing systems with dynamic changes. Two-step solution for quick and accurate reconfiguration of supervisory controllers for deadlock control. |
| Gu, C. et al. [111] | 2019 | Semi-structural verification of the nonblockingness. An algorithm to construct a novel structure (minimax basis reachability graph). No exhaustive exploration of the state space, therefore significant practical efficiency. |
| Pomares-Angelino, R. and López-Mellado, E. [112] | 2020 | Automated synthesis of deadlock free PN from event sequences. Novel method for determining substructures that yield deadlocks. Algorithms with polynomial-time complexity. |
| Li, L. et al. [113] | 2020 | Deadlock-freeness in timed PN systems with uncontrollable transitions with the enforcement of generalised mutual exclusion constraints. Online computation of a graph (Reduced Modified State Class Graph) for online control synthesis procedure. |
| Authors and Reference | Year | Contributions |
|---|---|---|
| Pan, Y.-L. [114] | 2020 | Transition-based control policy to solve the deadlock problem. Detection of all legal markings and all deadlock markings via state space exploration. The system can recover from all initial deadlock and quasi-deadlock markings. |
| Dong, Y. et al. [115] | 2019 | Solving deadlock problems by adding a set of recovery transitions. A vector intersection approach to compute a recovery transition to recover multiple deadlock markings, with lower computational complexity. |
| Row, T.C. et al. [116] | 2019 | Iterative method to obtain maximally permissive states on the basis of control transitions. Adding special transitions to recover from the deadlock markings, with full state space exploration. Focus on crucial dead markings. All markings are live and reachable once these crucial markings are controlled. |
| Hu, M. et al. [117] | 2020 | Computationally efficient method to find dead markings. Bad markings detected by solving an integer linear programming problem to detect possible markings with empty syphons and the set of markings in the dead-zone is calculated to find all first-met bad markings. |
| Education | Deadlock Prevention and Recovering | Other Analysis Problems | Modelling of Real Industrial Processes |
|---|---|---|---|
| Conditions of remote education | permissive policy for systems with unreliable resources and failures | dealing with the state explosion problem | how to properly construct large fault-tolerant models |
| How to fit interdisciplinary aspects into a limited course | deadlock avoidance and/or recovery of reconfigurable systems | efficient composition/decomposition of big systems | how to deal with large state spaces |
| decreasing computational complexity of the methods | developing efficient software tools | how to correctly incorporate time into models |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grobelna, I.; Karatkevich, A. Challenges in Application of Petri Nets in Manufacturing Systems. Electronics 2021, 10, 2305. https://doi.org/10.3390/electronics10182305
Grobelna I, Karatkevich A. Challenges in Application of Petri Nets in Manufacturing Systems. Electronics. 2021; 10(18):2305. https://doi.org/10.3390/electronics10182305
Chicago/Turabian StyleGrobelna, Iwona, and Andrei Karatkevich. 2021. "Challenges in Application of Petri Nets in Manufacturing Systems" Electronics 10, no. 18: 2305. https://doi.org/10.3390/electronics10182305
APA StyleGrobelna, I., & Karatkevich, A. (2021). Challenges in Application of Petri Nets in Manufacturing Systems. Electronics, 10(18), 2305. https://doi.org/10.3390/electronics10182305







