Performance Assessment of W-Band Radiometers: Direct versus Heterodyne Detections
Abstract
:1. Introduction
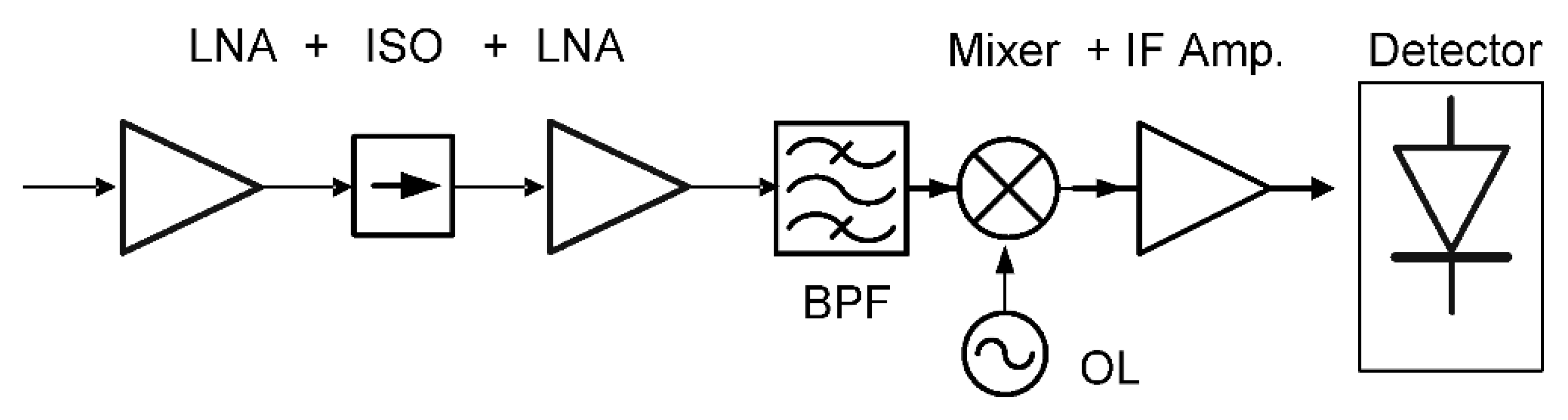
2. W-Band Radiometer Topologies
2.1. Low Noise Amplifiers in W Band
2.2. Bandpass Filter
2.3. Sub-Harmonic Mixer
2.4. IF Amplifier
2.5. IF Detector and Video Amplifier
2.6. W-Band Detector and Video Amplifier
3. Radiometer Simulations: Total Power and Dicke Modes
3.1. Super-Heterodyne Radiometer in Total Power Operation
3.2. Direct Detection Radiometer in Total Power Operation
3.3. Comparison of Super-Heterodyne and Direct Detection Radiometers in Total Power Operation
3.4. Super-Heterodyne Radiometer in Dicke Operation
3.5. Direct Detection Radiometer in Dicke Operation
3.6. Comparison of Super-Heterodyne and Direct Detection Radiometers in Dicke Operation
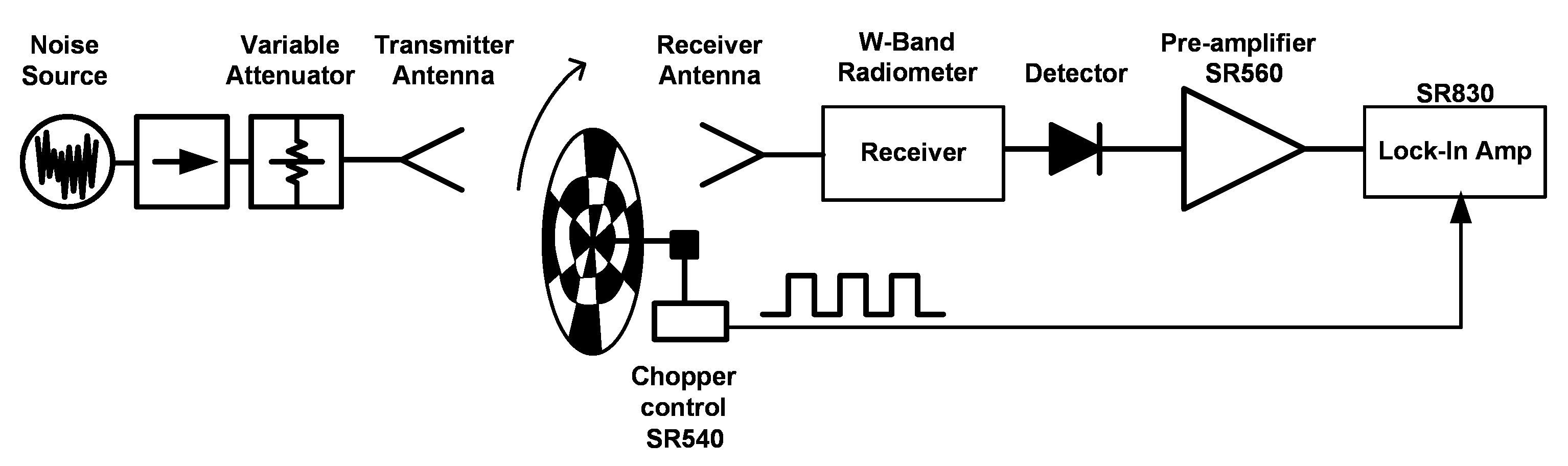
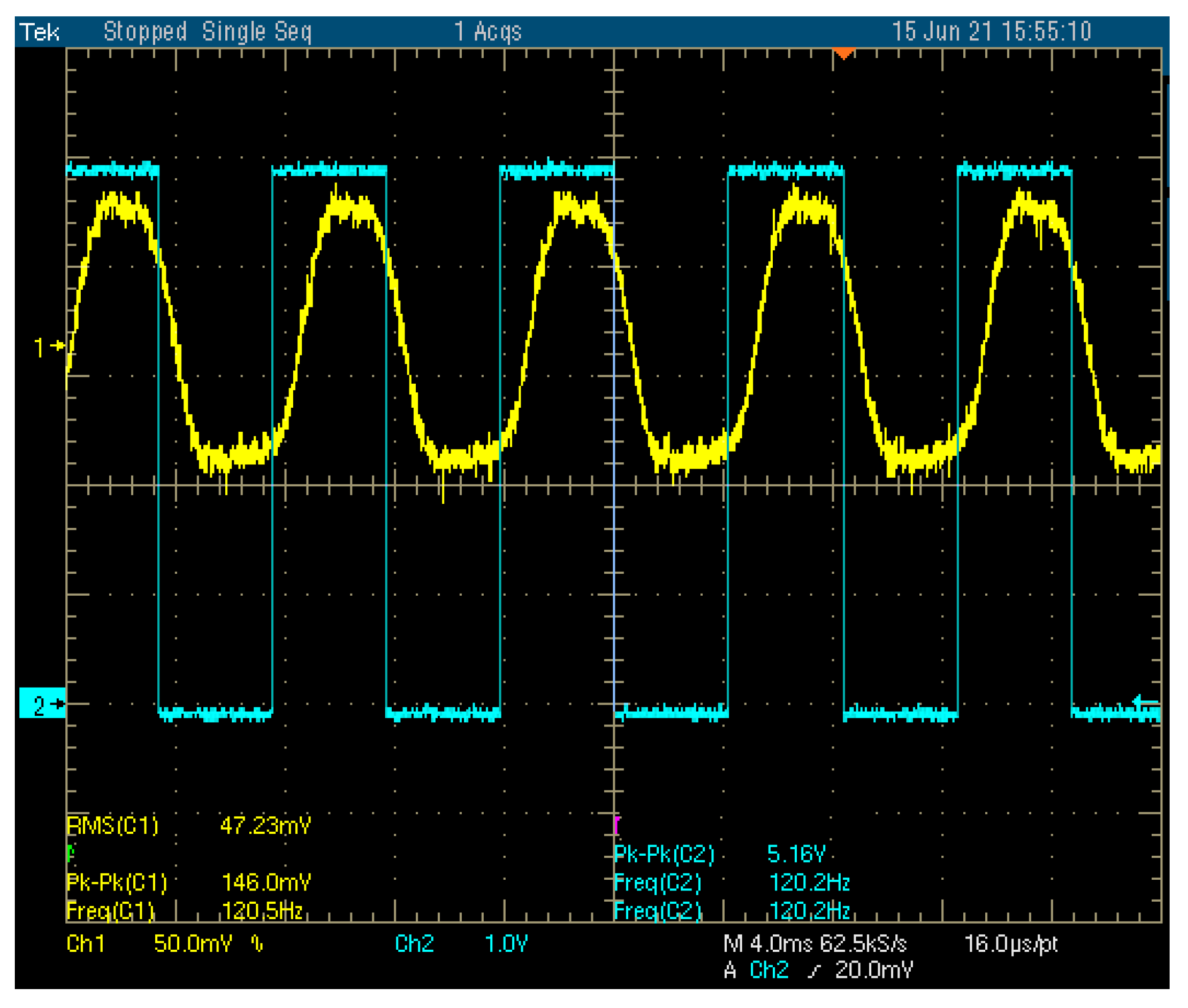
4. Characterization of Radiometers
4.1. Super-Heterodyne Radiometer
4.1.1. Total Power Radiometer
4.1.2. Dicke Radiometer
4.2. Direct Detection Radiometer
4.2.1. Total Power Radiometer
4.2.2. Dicke Radiometer
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pospieszalski, M.W.; Wollack, E.J.; Bailey, N.; Thacker, D.; Webber, J.; Nguyen, L.D.; Le, N.; Lui, M. Design and Performance of Wideband, Low-Noise, Millimeter-Wave Amplifiers for Microwave Anisotropy Probe Radiometers. In Proceedings of the 2000 IEEE MTT-S International Microwave Symposium Digest (Cat. No.00CH37017), Boston, MA, USA, 11–16 June 2000; pp. 217–220. [Google Scholar]
- Lamarre, J.M.; Puget, J.L.; Bouchet, F.; Ade, P.A.; Benoit, A.; Bernard, J.P.; Bock, J.; De Bernardis, P.; Charra, J.; Couchot, F.; et al. The Planck High Frequency Instrument, a third generation CMB experiment, and a full sky submillime-ter survey. New Astron. Rev. 2003, 47, 1017–1024. [Google Scholar] [CrossRef] [Green Version]
- Prisner, T.F.; van der Est, A.; Bittl, R.; Lubitz, W.; Stehlik, D.; Möbius, K. Time-resolved W-band (95 GHz) EPR spectroscopy of Zn-substituted reaction centers of Rhodobacter sphaeroides R-26. Chem. Phys. 1995, 194, 361–370. [Google Scholar] [CrossRef]
- Yujiri, L.; Shoucri, M.; Moffa, P. Passive millimeter wave imaging. IEEE Microw. Mag. 2003, 4, 39–50. [Google Scholar] [CrossRef] [Green Version]
- Shoucri, M.; Davidheiser, R.; Hauss, B.; Lee, P.; Mussetto, M.; Young, S.; Yujiri, L. A passive millimeter wave camera for landing in low visibility conditions. In Proceedings of the AIAA/IEEE Digital Avionics Systems Conference, 13th DASC, Phoenix, AZ, USA, 30 October–3 November 1994. [Google Scholar]
- Del Torto, F.; Bersanelli, M.; Cavaliere, F.; De Rosa, A.; D’Arcangelo, O.; Franceschet, C.; Gervasi, M.; Mennella, A.; Pagana, E.; Simonetto, A.; et al. W-band prototype of platelet feed-horn array for CMB polarisation measurements. J. Instrum. 2011, 6, P06009. [Google Scholar] [CrossRef] [Green Version]
- Kraus, J.D. Radio Astronomy, 2nd ed.; Cygnus-Quasar Books: Powell, OH, USA, 1986. [Google Scholar]
- Tiuri, M. Radio astronomy receivers. IRE Trans. Antennas Propag. 1964, 12, 930–938. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing—Active and Passive; Artech House Inc.: Norwood, MA, USA, 1981; Volume I. [Google Scholar]
- Dicke, R.H. The measurements of thermal radiation at microwave frequencies. Rev. Sci. Instrum. 1946, 17, 268–275. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, S. A Comparison of Two Radiometer Circuits. Proc. IRE 1955, 43, 1663–1666. [Google Scholar] [CrossRef]
- Aja, B.; Artal, E.; De La Fuente, L.; Pascual, J.; Mediavilla, A.; Roddis, N.; Kettle, D.; Winder, W.; Cara, L.; De Paco, P. Very low-noise differential radiometer at 30 GHz for the PLANCK LFI. IEEE Trans. Microw. Theory Tech. 2005, 53, 2050–2062. [Google Scholar] [CrossRef] [Green Version]
- Cano, J.L.; Villa, E.; Teran, V.; Gonzalez, E.; De La Fuente, L.; Artal, E.; Mediavilla, A. A W-band polarimeter for radio astronomy applications: Design and simulation. In Proceedings of the 2015 International Conference on Electromagnetics in Advanced Applications (ICEAA), Turin, Italy, 7–11 September 2015; pp. 452–455. [Google Scholar]
- Bischoff, C.; Brizius, A.; Buder, I.; Chinone, Y.; Cleary, K.; Dumoulin, R.N.; Kusaka, A.; Monsalve, R.; Næss, S.; Newburgh, L.B.; et al. THE Q/U IMAGING EXPERIMENT INSTRUMENT. Astrophys. J. 2013, 768, 9. [Google Scholar] [CrossRef] [Green Version]
- Gutiérrez, J.; Pascual, J.P.; Tazón, A. Merged simulation procedure for W-band imaging systems. Int. J. RF Microw. Comput. Eng. 2018, 28, e21284. [Google Scholar] [CrossRef]
- Doo, J.; Park, W.; Choe, W.; Jeong, J. Design of Broadband W-Band Waveguide Package and Application to Low Noise Amplifier Module. Electronics 2019, 8, 523. [Google Scholar] [CrossRef] [Green Version]
- Ustundag, B.; Turkmen, E.; Cetindogan, B.; Guner, A.; Kaynak, M.; Gurbuz, Y. Low-Noise Amplifiers for W-Band and D-Band Passive Imaging Systems in SiGe BiCMOS Technology. In Proceedings of the 2018 Asia-Pacific Microwave Conference (APMC), Kyoto, Japan, 6–9 November 2018; pp. 651–653. [Google Scholar]
- Lardizabal, S.; Hwang, K.C.; Kotce, J.; Brown, A.; Fung, A. Wideband W-Band GAN LNA MMIC with State-of-the-Art Noise Figure. In Proceedings of the 2016 IEEE Compound Semiconductor Integrated Circuit Symposium (CSICS), Austin, TX, USA, 23–26 October 2016; pp. 1–4. [Google Scholar]
- Terán Collantes, J.V. Low Noise Receivers for Millimetre-Wave Bands Radio Astronomy. Ph.D. Thesis, University of Cantabria, 2017. Available online: https://repositorio.unican.es/xmlui/handle/10902/11503 (accessed on 19 September 2021).
- Advanced Design System (ADS). Available online: https://www.keysight.com/es/en/products/software/pathwave-design-software/pathwave-advanced-design-system.html (accessed on 8 July 2021).
- Aja, B.; Pascual, J.P.; De La Fuente, L.; Gallegos, J.; Artal, E. A New Method to Obtain Total Power Receiver Equivalent Noise Temperature. In Proceedings of the 33rd European Microwave Conference, Munich, Germany, 2–10 October 2003; pp. 355–358. [Google Scholar]
- Pascual, J.P.; Aja, B.; De La Fuente, M.L.; Pomposo, T.; Artal, E. System Simulation of a Differential Radiometer Using Standard RF-Microwave Simulators. Simulation 2005, 81, 735–755. [Google Scholar] [CrossRef]
- May, J.W.; Rebeiz, G.M. Design and Characterization of W-Band SiGe RFICs for Passive Millimeter-Wave Imaging. IEEE Trans. Microw. Theory Tech. 2010, 58, 1420–1430. [Google Scholar] [CrossRef]
- Weissbrodt, E.; Kallfass, I.; Hulsmann, A.; Tessmann, A.; Leuther, A.; Massler, H.; Ambacher, O. W-band radiometer system with switching front-end for multi-load calibration. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 3843–3846. [Google Scholar]
- Quan, L.; Yong-Hong, Z.; Qi-Ke, C.; Yong, F.; Jian-Yu, Y.; Liang-Chao, L. The W Band Radiometer for Imaging. In Proceedings of the 2007 International Conference on Communications, Circuits and Systems, Kokura, Japan, 11–13 July 2007; pp. 1306–1308. [Google Scholar]
- Xie, L.; Zhang, H.; Fan, Y. W-Band Radiometer Front End Module for Real-Time Imaging. Microw. J. 2014, 57, 80–90. [Google Scholar]
- Li, L.C.; Yang, J.Y.; Xiong, J.T.; Wu, J.J.; Jiang, Z.M.; Zheng, X. W Band Dicke-Radiometer for Imaging. Int. J. Infrared Millim. Waves 2008, 29, 879–888. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, C.-C.; Chen, Z.; Heydari, P. A W-band CMOS Receiver Chipset for Millimeter-Wave Radiometer Systems. IEEE J. Solid-State Circuits 2011, 46, 378–391. [Google Scholar] [CrossRef]
- Dacquay, E.; Tomkins, A.; Yau, K.H.K.; Laskin, E.; Chevalier, P.; Chantre, A.; Sautreuil, B.; Voinigescu, S.P. D-Band Total Power Radiometer Performance Optimization in an SiGe HBT Technology. IEEE Trans. Microw. Theory Tech. 2012, 60, 813–826. [Google Scholar] [CrossRef]
- Kanar, T.; Rebeiz, G.M. A low-power SiGe D-band total power radiometer with NEPmin of 1.4 fW/Hz½ and NETD of 0.25K. In Proceedings of the 2016 IEEE MTT-S International Microwave Symposium (IMS), San Francisco, CA, USA, 22–27 May 2016; pp. 1–4. [Google Scholar]
- Frounchi, M.; Alizadeh, A.; Ying, H.; Coen, C.T.; Gasiewski, A.J.; Cressler, J.D. Millimeter-Wave SiGe Radiometer Front End With Transformer-Based Dicke Switch and On-Chip Calibration Noise Source. IEEE J. Solid-State Circuits 2021, 56, 1464–1474. [Google Scholar] [CrossRef]
- Feng, G.; Yi, X.; Meng, F.; Boon, C.C. A W-Band Switch-Less Dicke Receiver for Millimeter-Wave Imaging in 65 nm CMOS. IEEE Access 2018, 6, 39233–39240. [Google Scholar] [CrossRef]
- Bi, X.; Arasu, M.A.; Zhu, Y.; Je, M. A Low Switching-Loss W-Band Radiometer Utilizing a Single-Pole-Double-Throw Distributed Amplifier in 0.13-um SiGe BiCMOS. IEEE Trans. Microw. Theory Tech. 2016, 64, 226–238. [Google Scholar] [CrossRef]
- Malotaux, S.; Babaie, M.; Spirito, M. A Total-Power Radiometer Front End in a 0.25-um BiCMOS Technology with Low 1/f -Corner. IEEE J. Solid-State Circuits 2017, 52, 2256–2266. [Google Scholar] [CrossRef]
- Peng, P.; Chen, P.; Kao, C.; Chen, Y.; Lee, J. A 94 GHz 3D Image Radar Engine With 4TX/4RX Beamforming Scan Tech-nique in 65 nm CMOS Technology. IEEE J. Solid-State Circuits 2015, 50, 656–668. [Google Scholar] [CrossRef]
- Zhang, Y.; Martin, R.D.; Shi, S.; Wright, A.A.; Yao, P.; Shreve, K.; Mackrides, D.; Harrity, C.; Prather, D.W. 95-GHz Front-End Receiving Multichip Module on Multilayer LCP Substrate for Passive Millimeter-Wave Imaging. IEEE Trans. Compon. Packag. Manuf. Technol. 2018, 8, 2180–2189. [Google Scholar] [CrossRef]
- Gutiérrez, J.; Zeljami, K.; Pascual, J.P.; Fernández, T.; Tazón, A. Comparison of Microstrip W-Band Detectors Based on Zero Bias Schottky-Diodes. Electronics 2019, 8, 1450. [Google Scholar] [CrossRef] [Green Version]

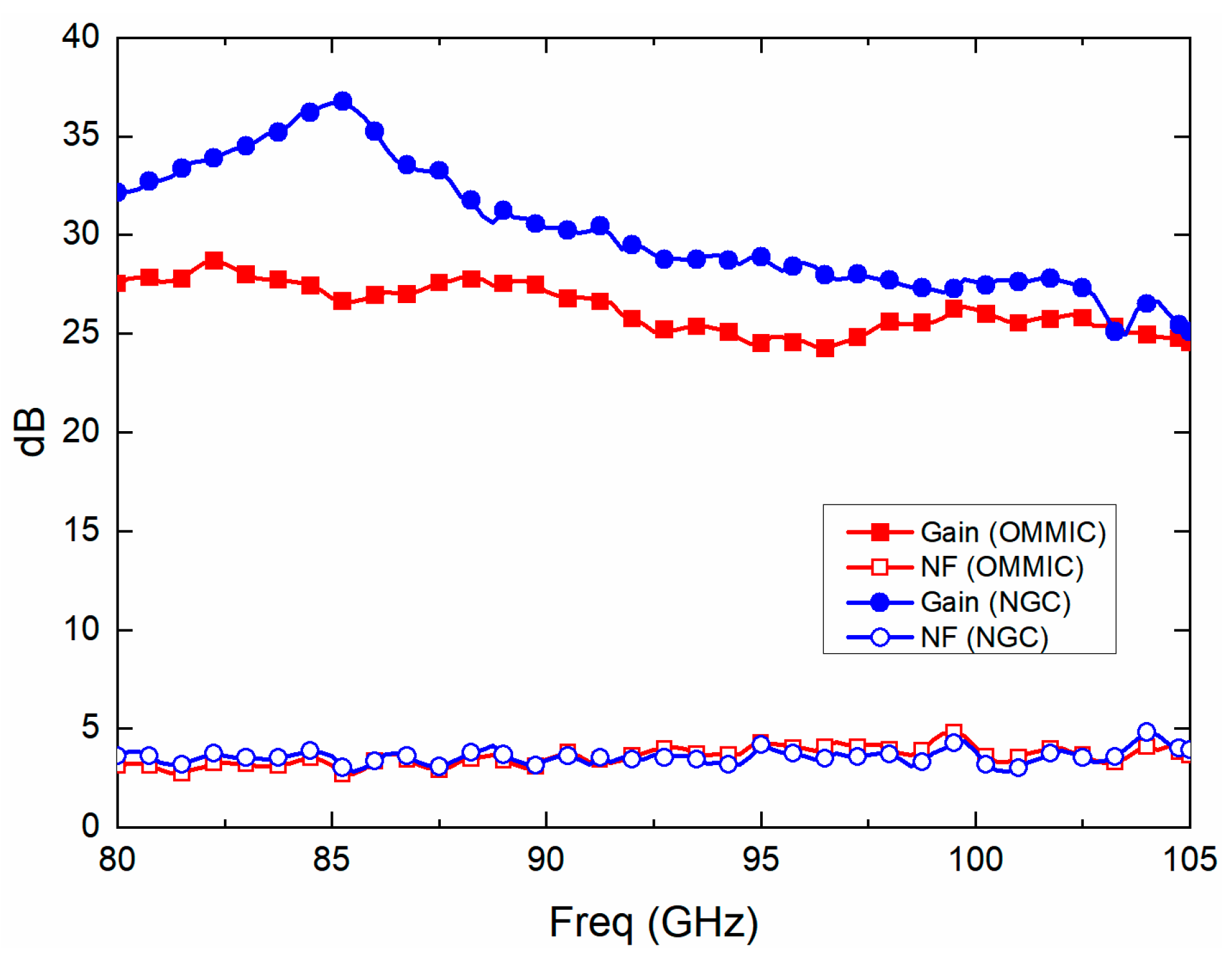
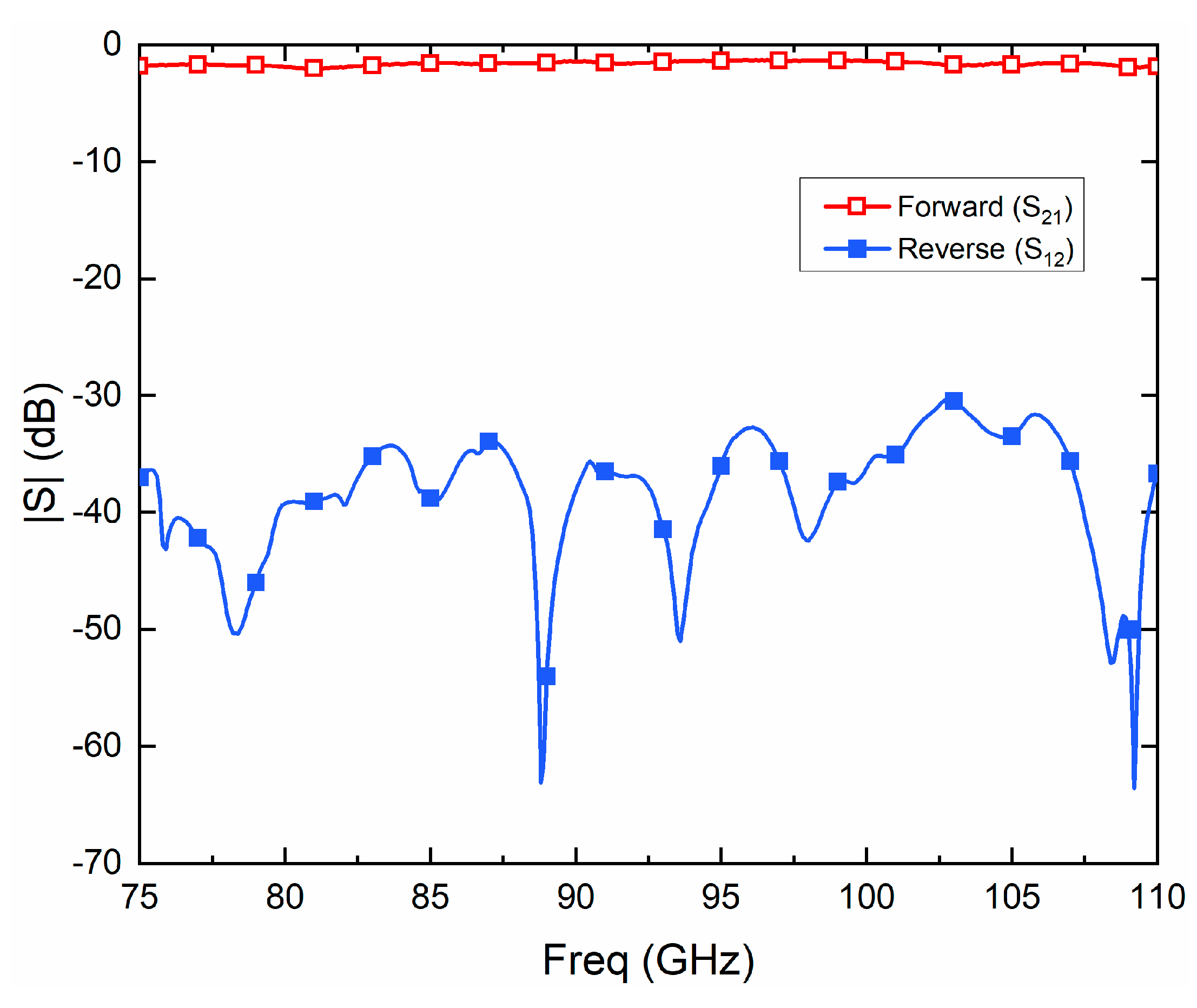
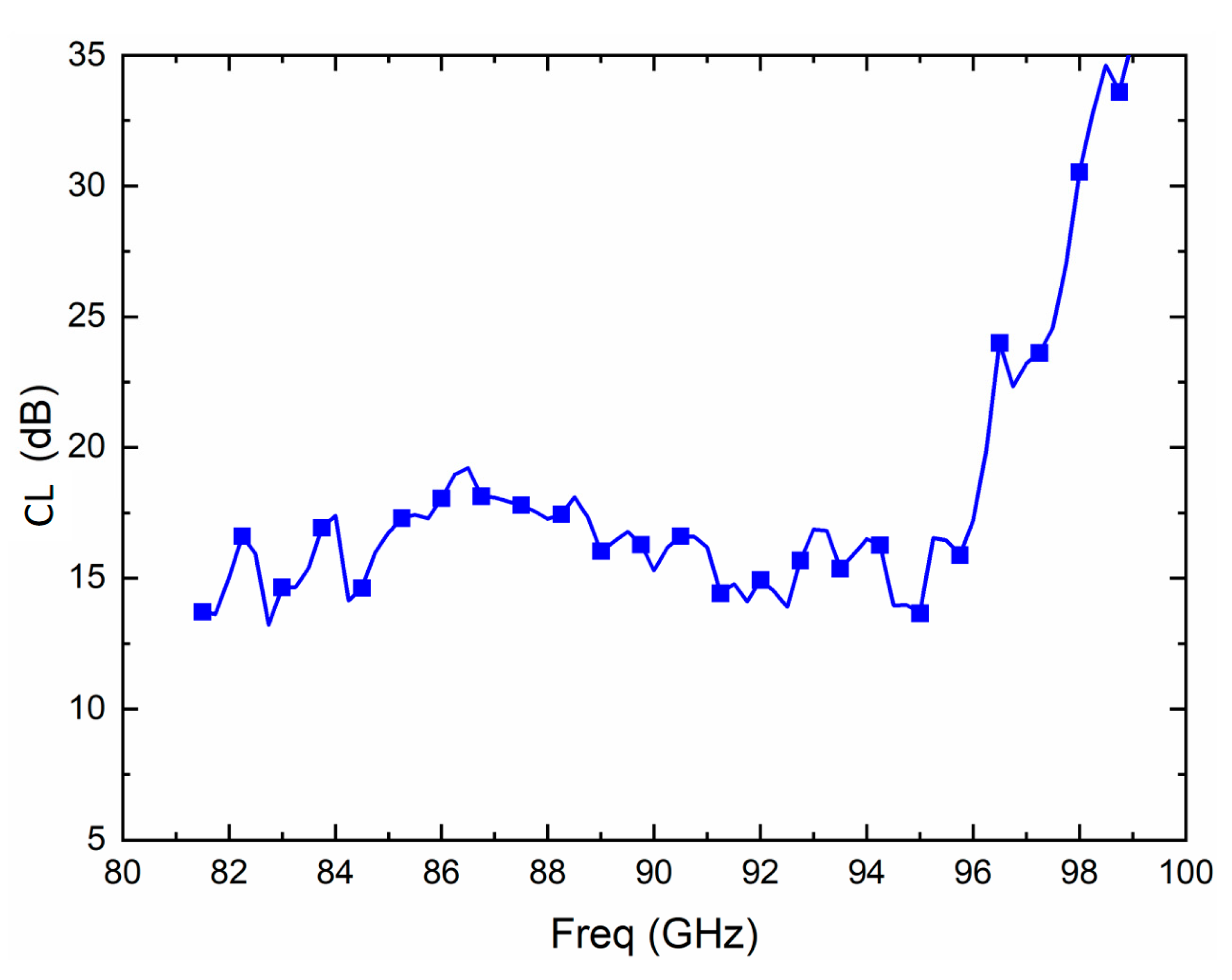

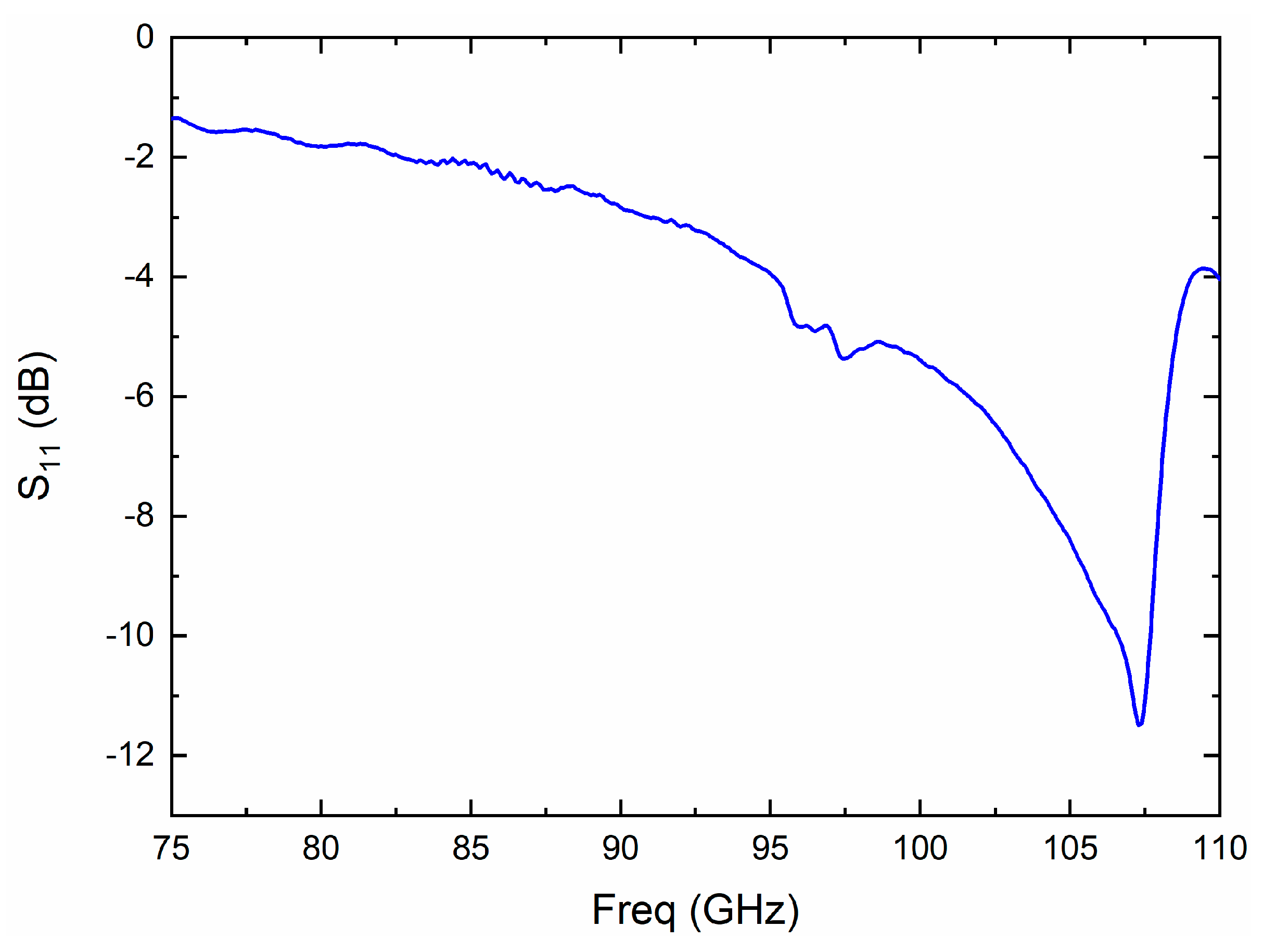
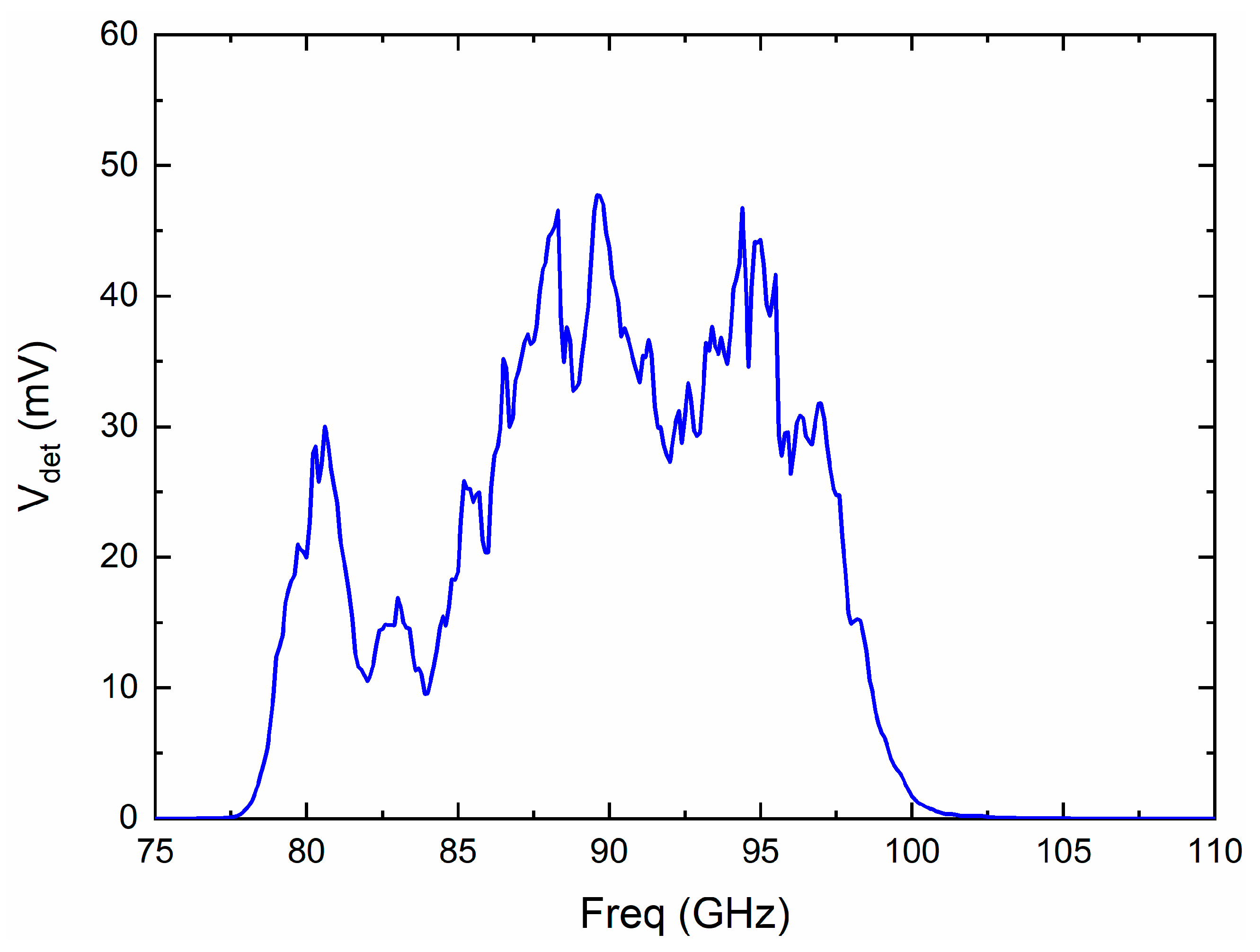
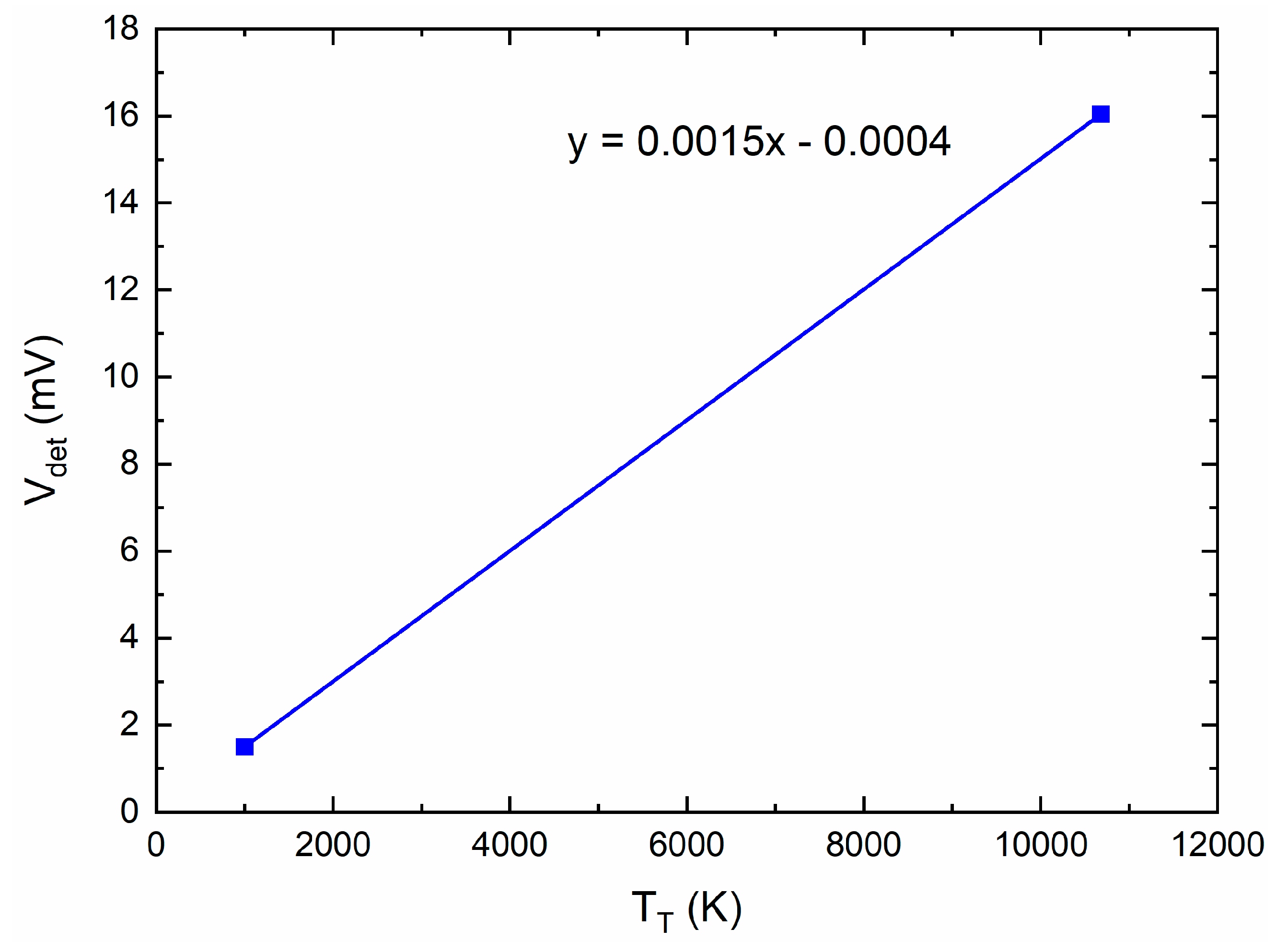
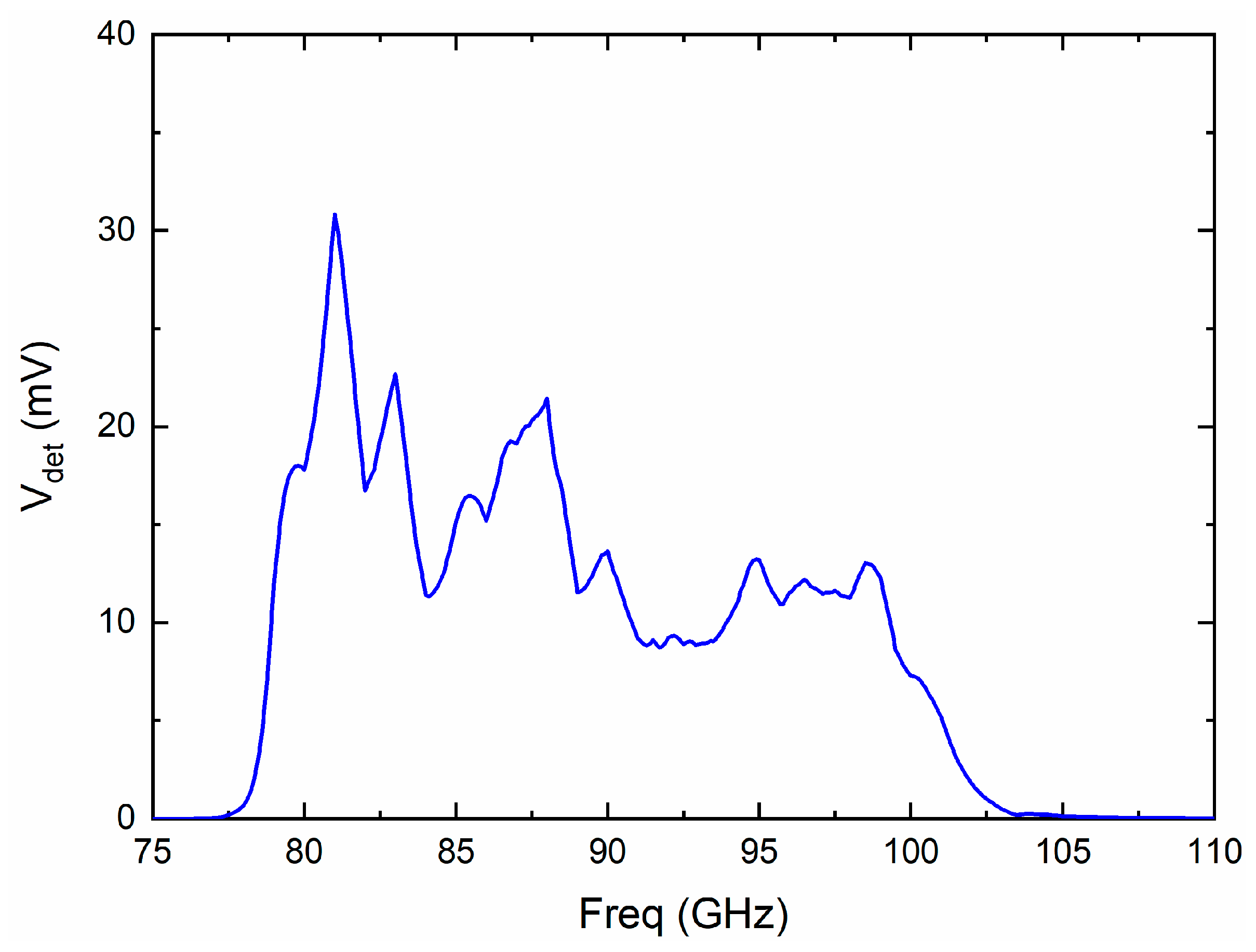
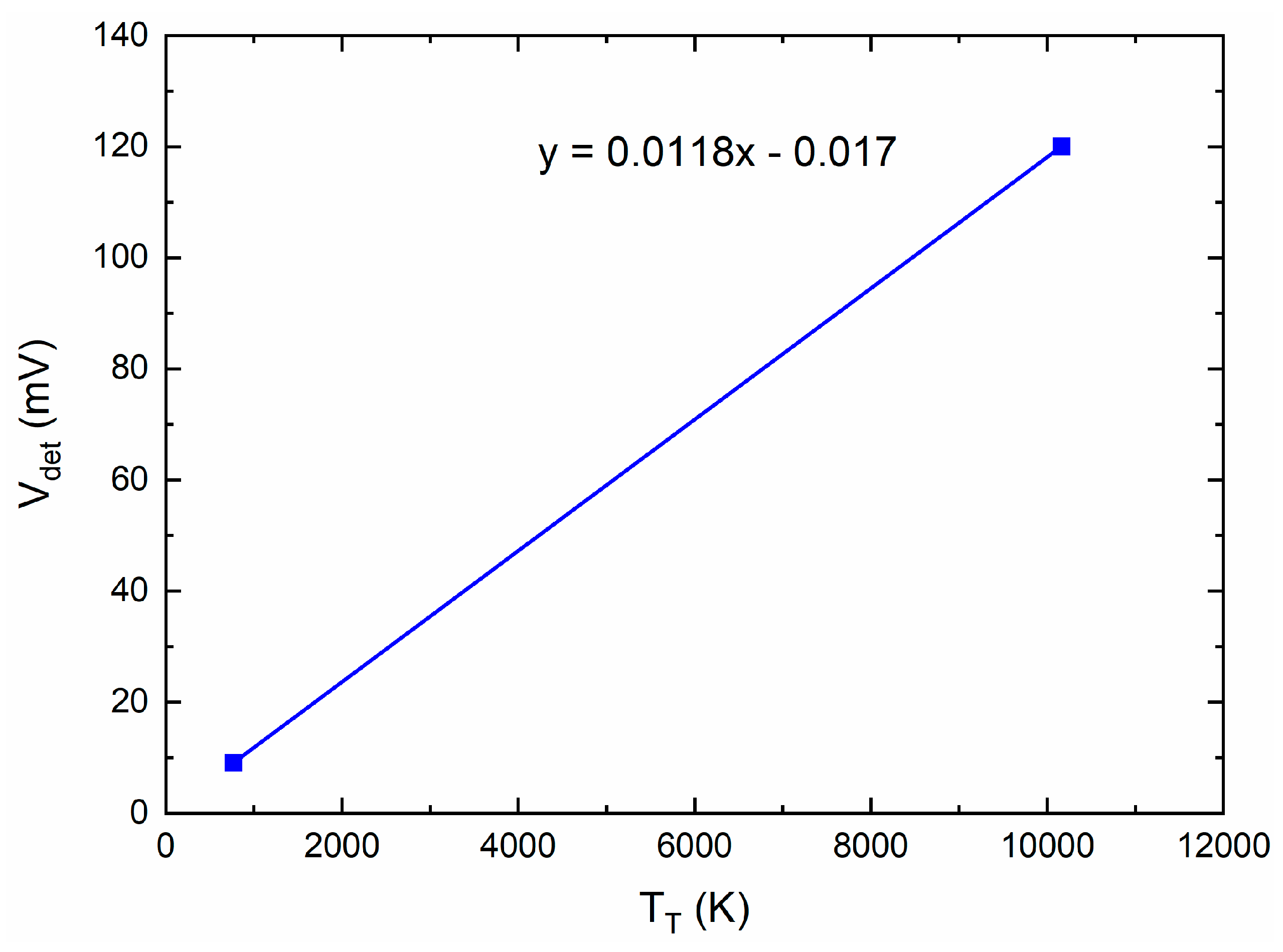
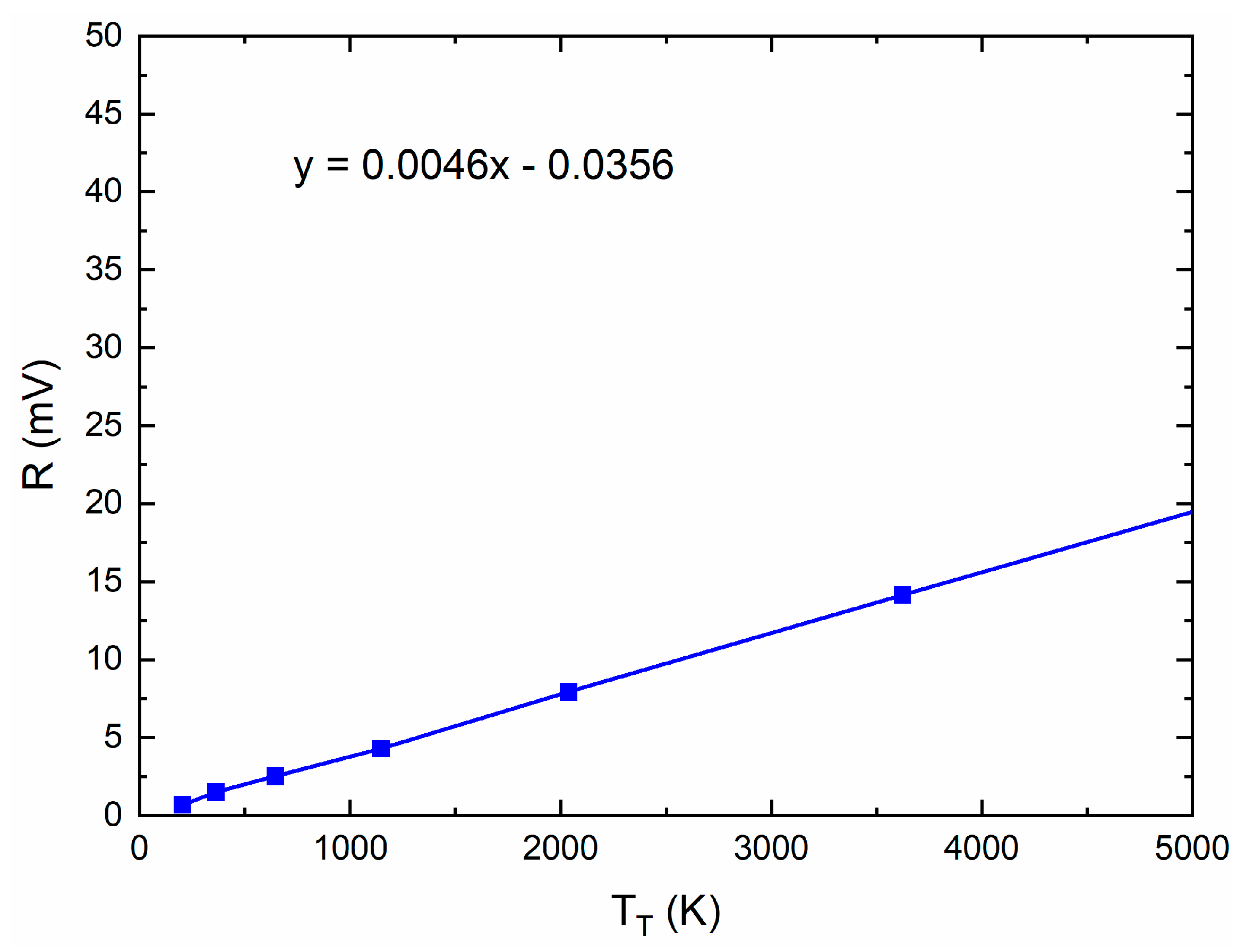
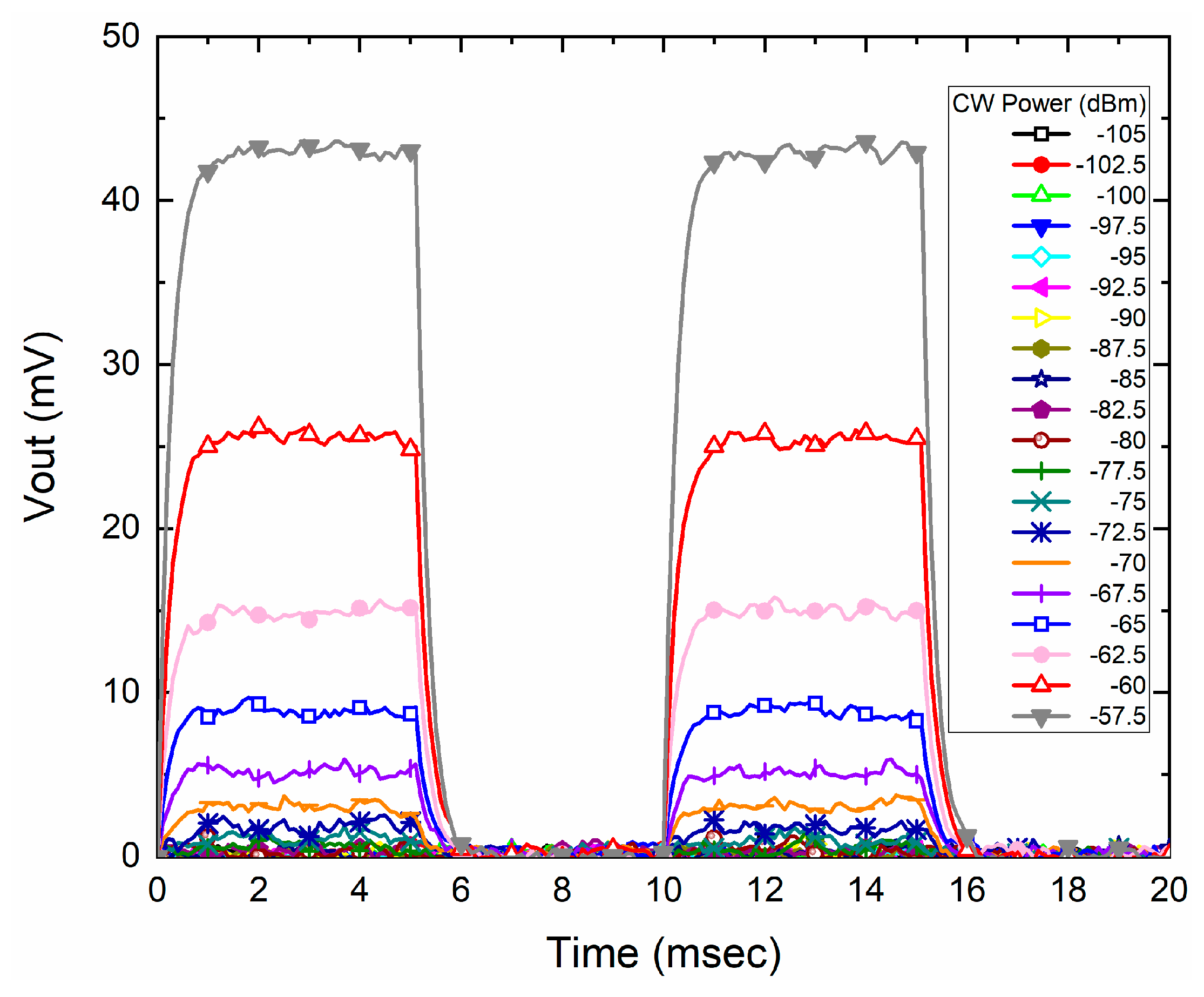
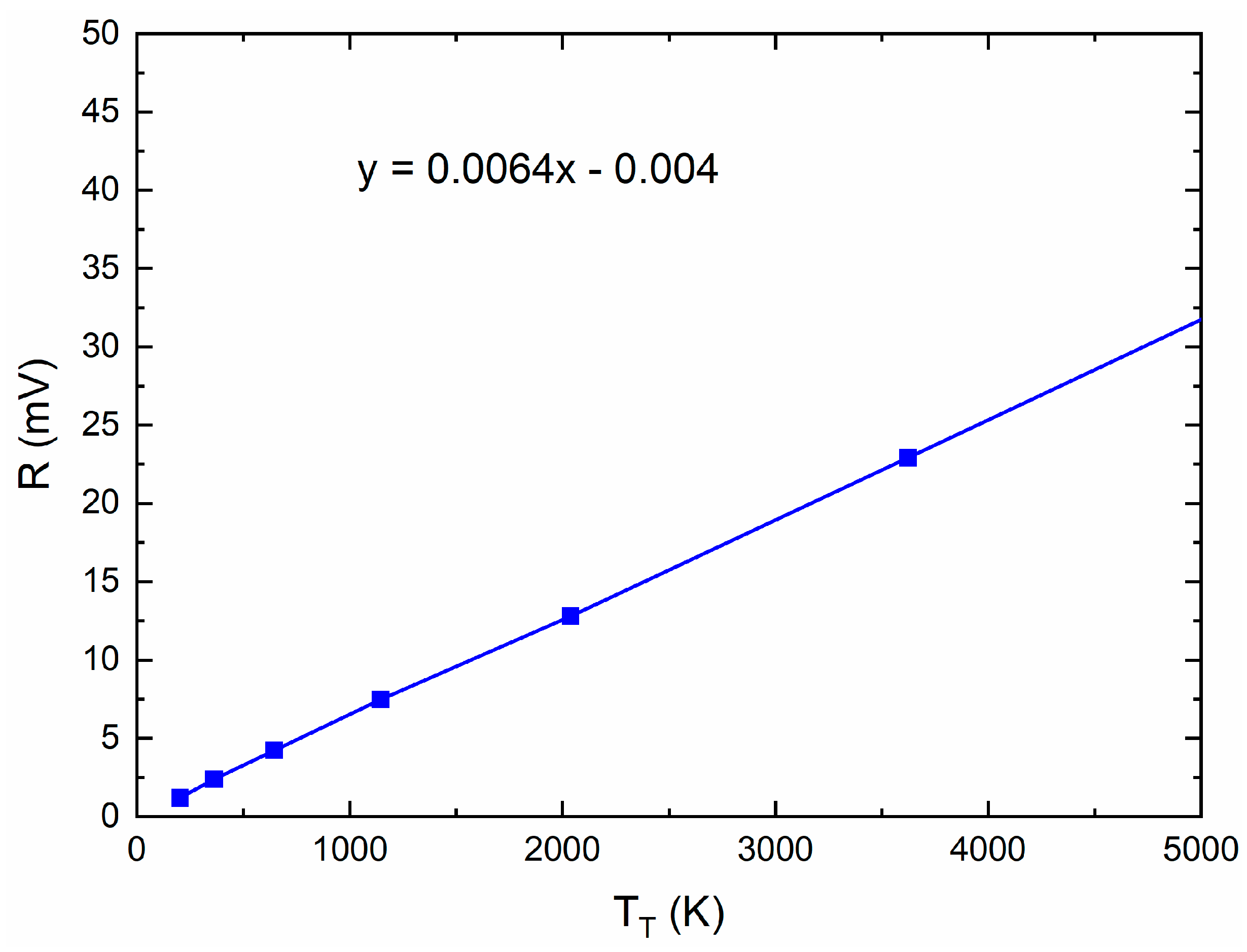
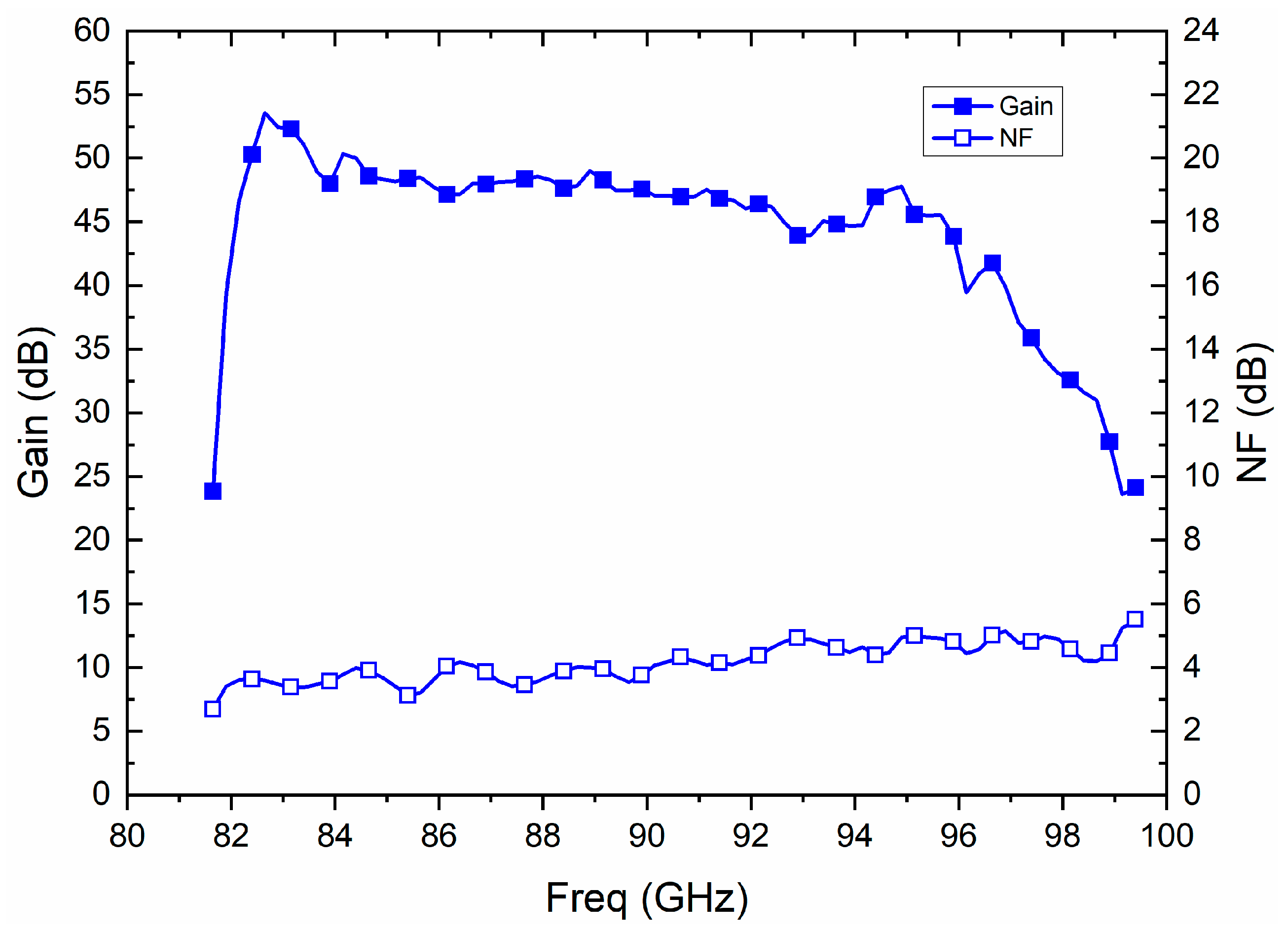

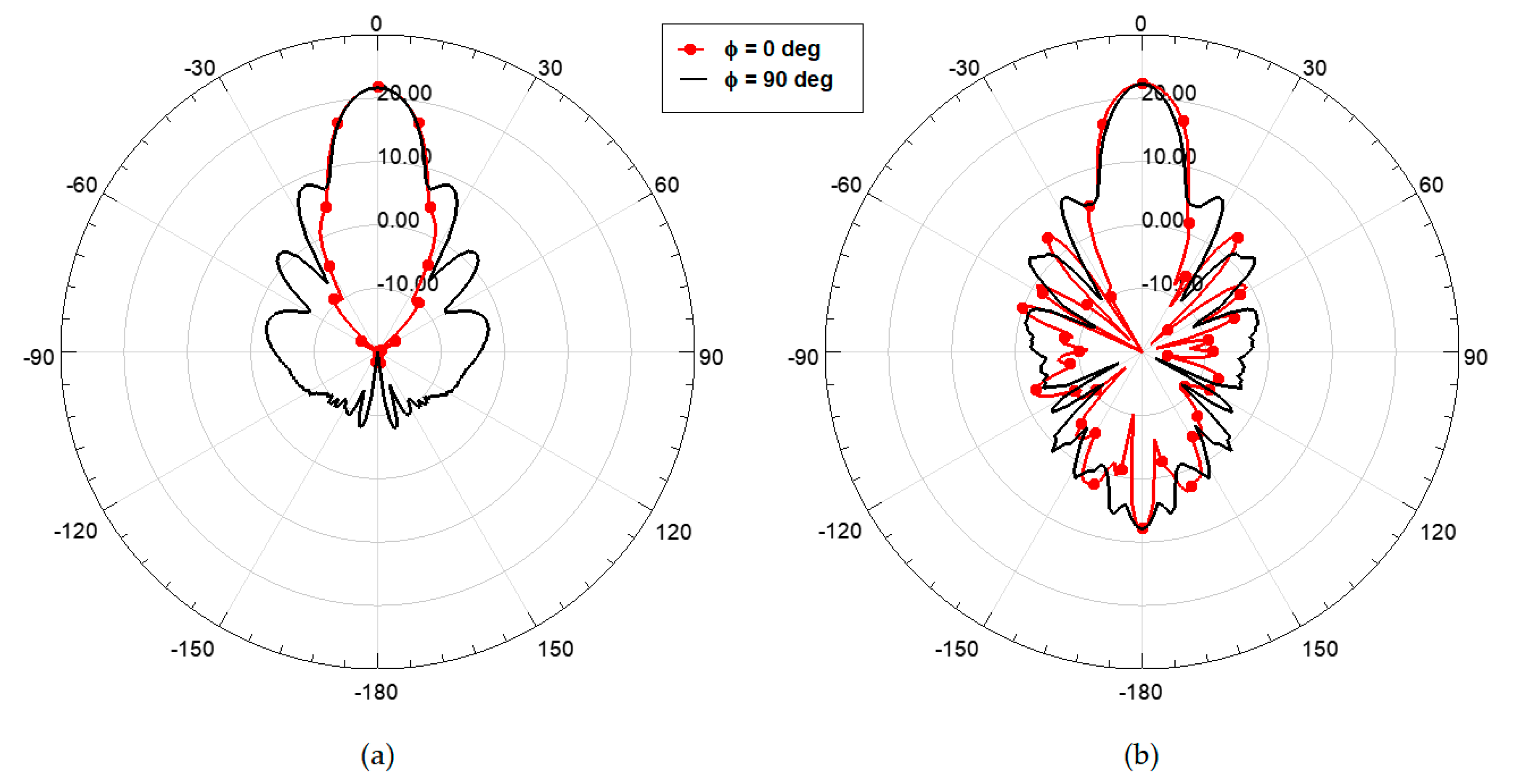


| Reference | Technology | B3dB (GHz) | NF (dB) | Gain | PDC mW |
|---|---|---|---|---|---|
| [16] | Ommic. Mounted | 75–105 | 4.4 | 14.9 | - |
| [17] | 0.13 µm SiGe | 70–87 | 4.2 | 22.3 | 8 |
| [18] | GaN | 86–98 | 3.8 | 20 | 128 |
| This work: Ommic CGY2190UH | 70 nm methamorphic HEMT mounted | 75–105 | 3.5 | 25 | 39.6 |
| This work: NGC ALP283 | 100 nm InP HEMT mounted | 80–100 | 3.5 | 35 | 30 |
| Topology | BHF (GHz) | NF (dB) | ΔT (mK) | Pin Cold (dBm) | Vmean Cold (mV) | Pin Hot (dBm) | Vmean Hot (mV) | Responsivity (mV/mW) | Responsivity (µV/K) |
|---|---|---|---|---|---|---|---|---|---|
| RF Chain | 20.91 | 3.5 | - | - | - | - | - | - | - |
| RF + mix IF + det IF | 17.8 | 5 | 27.72 | −66.3 | 1.5 | −56.01 | 16.04 | 6 × 106 | 1.5 |
| RF + det W | 20.56 | 4 | 18.39 | −66.73 | 9.1 | −55.52 | 120.03 | 4 × 107 | 11.8 |
| Topology | Responsivity Total Power (mV/mW) | Responsivity Total Power (µV/K) | Responsivity Dicke (µV/K) | ΔT Total Power (mK) | NEP pW/sqrt(Hz) | ΔT Dicke (mK) |
|---|---|---|---|---|---|---|
| Super-heterodyne: RF + mixIF + det | 6 × 106 | 1.5 | 4.6 | 27.72 | 0.0018 | 55.44 |
| Direct Det.: RF + det W | 4 × 107 | 11.8 | 6.4 | 18.39 | 0.0015 | 36.78 |
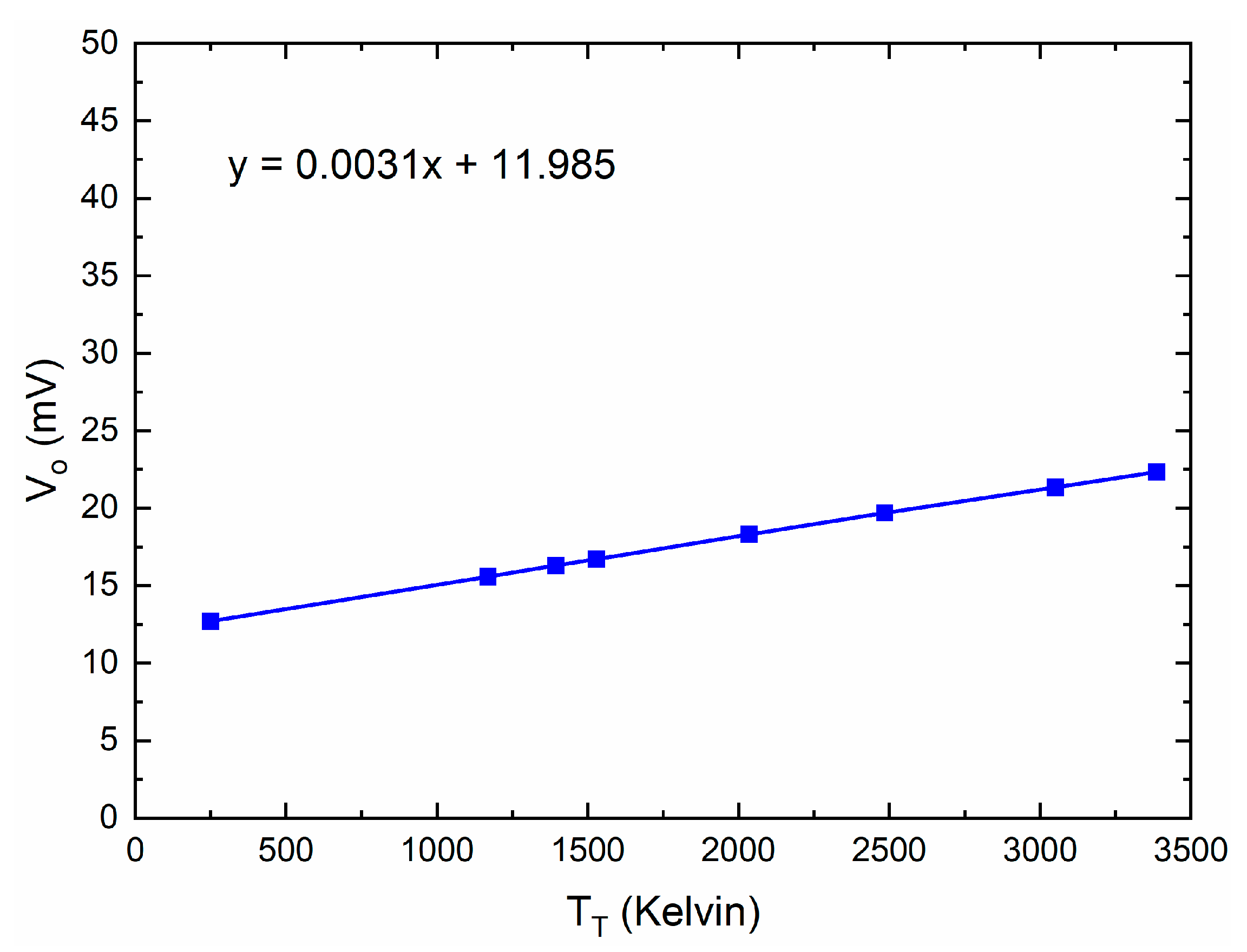
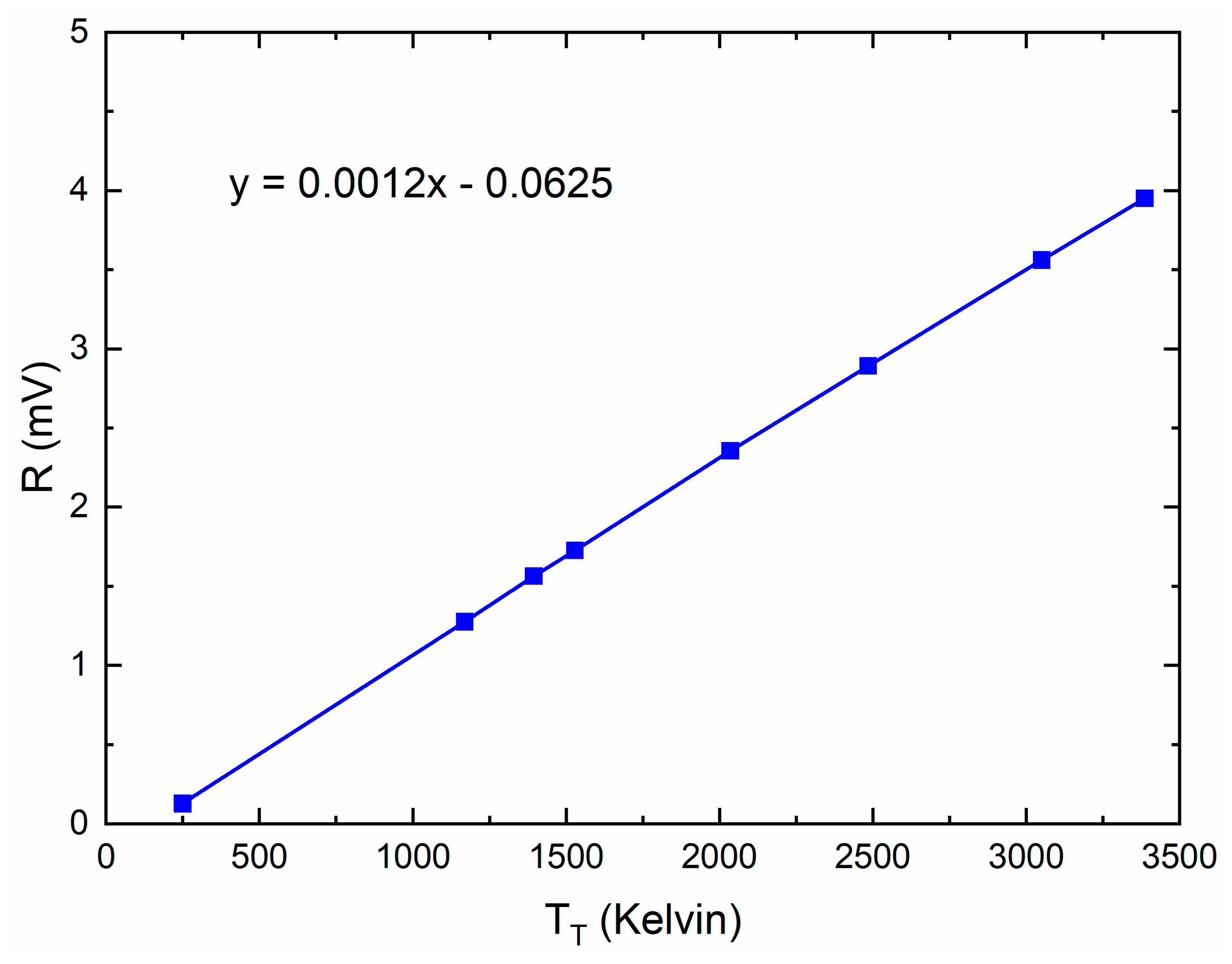
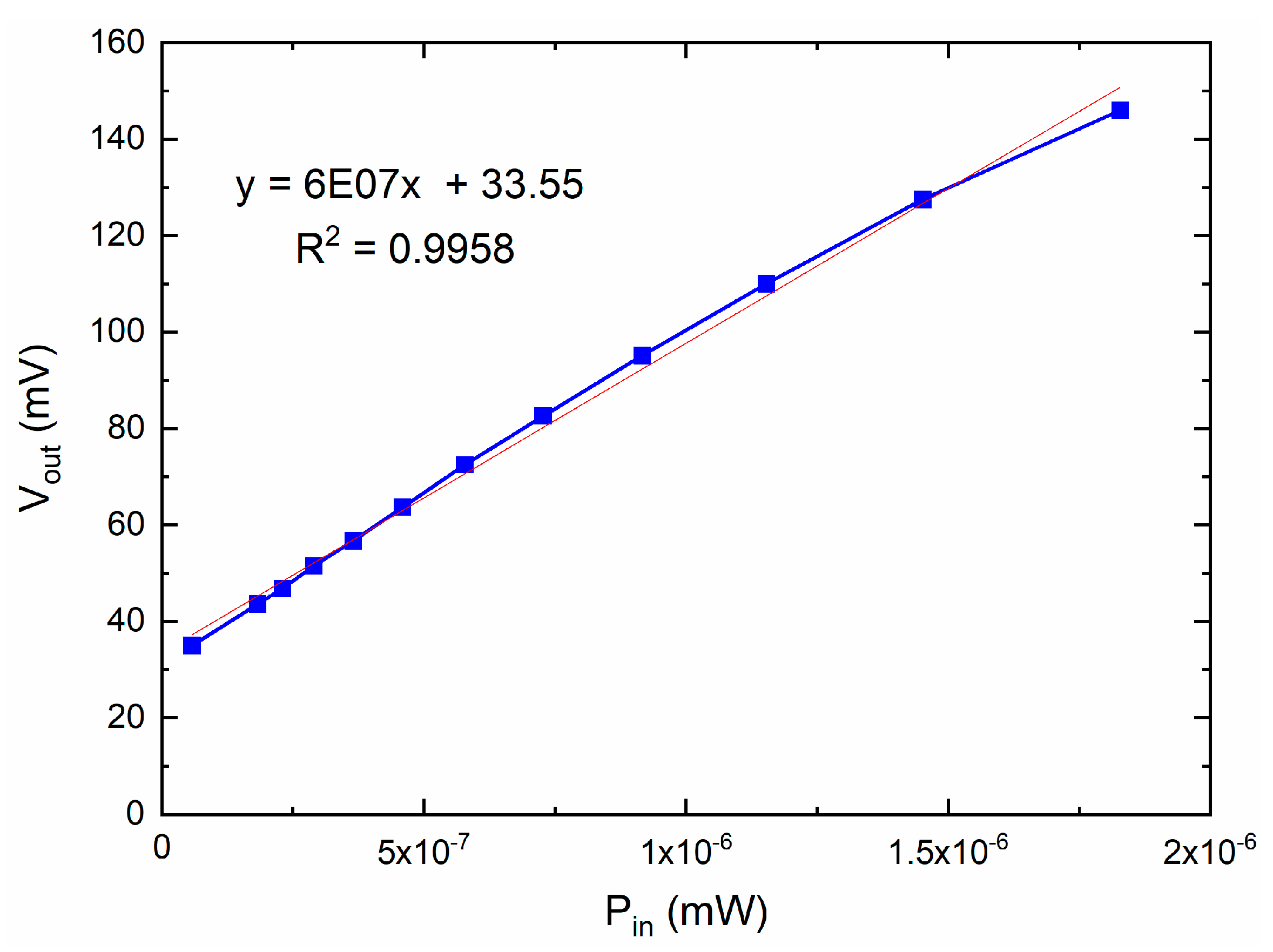
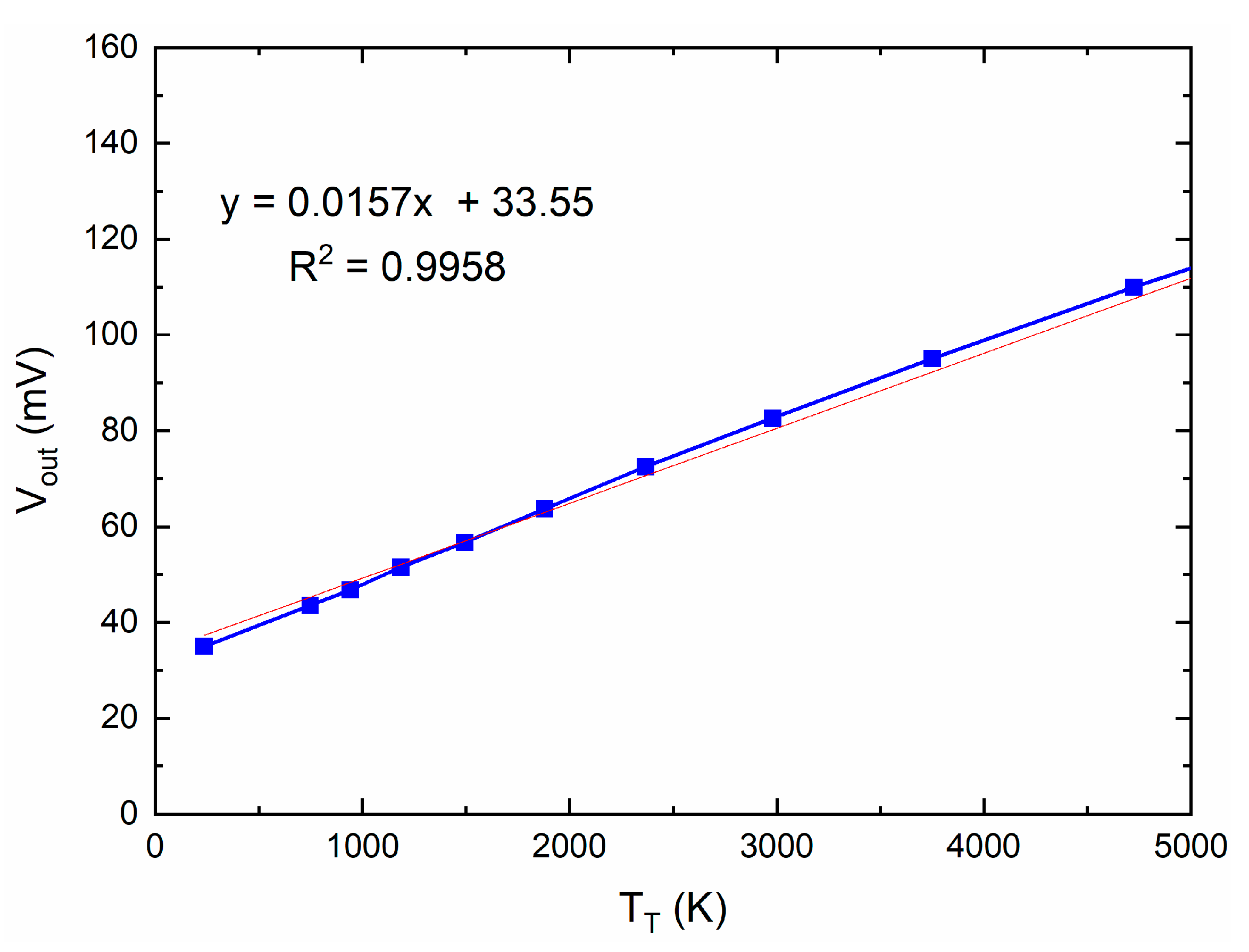
| Type of Configuration\Parameter | BHF (GHz) | Total Power Responsivity (mV/mW) | Total Power Responsivity (μV / K) | Offset (mV) | R (μVrms/K) | Sensitivity ΔT (mK) (τ = 30 ms) | NEP (pW/sqrt(Hz)) |
|---|---|---|---|---|---|---|---|
| Super-heterodyne total power | 10.7 | 1.18 × 107 | 3.1 | 11.98 | − | 152 | 0.0055 |
| Super-heterodyne Dicke | 10.7 | − | − | 1.2 | 305 | ||
| Direct detection total power | 19.9 | 6 × 107 | 15.7 | 33.55 | − | 58.49 | 0.0039 |
| Direct detection Dicke | 19.9 | − | − | 6 | 116.98 |
| Ref\Parameter | BHF (GHz) and (Frequency (GHz)) | Responsivity (mV/mW) | Sensitivity ΔT (mK) | NEP(pW/sqrt(Hz)) | NF (dB) |
|---|---|---|---|---|---|
| [23] | 20 (83–103) | 690 | |||
| [23] | 15 (84–99) | 2.5 × 106–5 × 106 | 830 | 0.021 | |
| [25] | 4 (89.5–93.5) | 500 | 11.5 | ||
| [26] | 22 (W band) | 1000 | 76 | ||
| [27] | 4 (W band) | 550 | 11.5 | ||
| [28] | 12 (W band) | 16.106 | 1000 | 0.009 | 8.9 |
| [29] | 10 (160–170) | 28 × 106 | 350 (τ = 3.125 ms) | 0.014/0.018 | 8.14 |
| [30] | 11.8 (136) | 5.2 x106 | 250 (τ = 3.125 ms) | 0.0014 | 7.9 |
| [32] | 11.5 (centered 82.5) | − | 650 | 0.0093 | 6.4 |
| [33] | centered 91 | − | 210 | − | 8.4 |
| [34] | 10.7 (center 56) | 61 × 106 | 0.0032 | 5.3 | |
| This work Super-heterodyne | 10.7 (W band) | 1.18 × 107 | 152 | 0.0055 | 4 |
| This work Direct Detec | 19.9 (W band) | 6 × 107 | 58.49 | 0.0039 | 3.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pascual, J.P.; Aja, B.; Villa, E.; Terán, J.V.; de la Fuente, L.; Artal, E. Performance Assessment of W-Band Radiometers: Direct versus Heterodyne Detections. Electronics 2021, 10, 2317. https://doi.org/10.3390/electronics10182317
Pascual JP, Aja B, Villa E, Terán JV, de la Fuente L, Artal E. Performance Assessment of W-Band Radiometers: Direct versus Heterodyne Detections. Electronics. 2021; 10(18):2317. https://doi.org/10.3390/electronics10182317
Chicago/Turabian StylePascual, Juan Pablo, Beatriz Aja, Enrique Villa, Jose Vicente Terán, Luisa de la Fuente, and Eduardo Artal. 2021. "Performance Assessment of W-Band Radiometers: Direct versus Heterodyne Detections" Electronics 10, no. 18: 2317. https://doi.org/10.3390/electronics10182317
APA StylePascual, J. P., Aja, B., Villa, E., Terán, J. V., de la Fuente, L., & Artal, E. (2021). Performance Assessment of W-Band Radiometers: Direct versus Heterodyne Detections. Electronics, 10(18), 2317. https://doi.org/10.3390/electronics10182317







