Study of an Attenuator Supporting Meander-Line Slow Wave Structure for Ka-Band TWT
Abstract
:1. Introduction
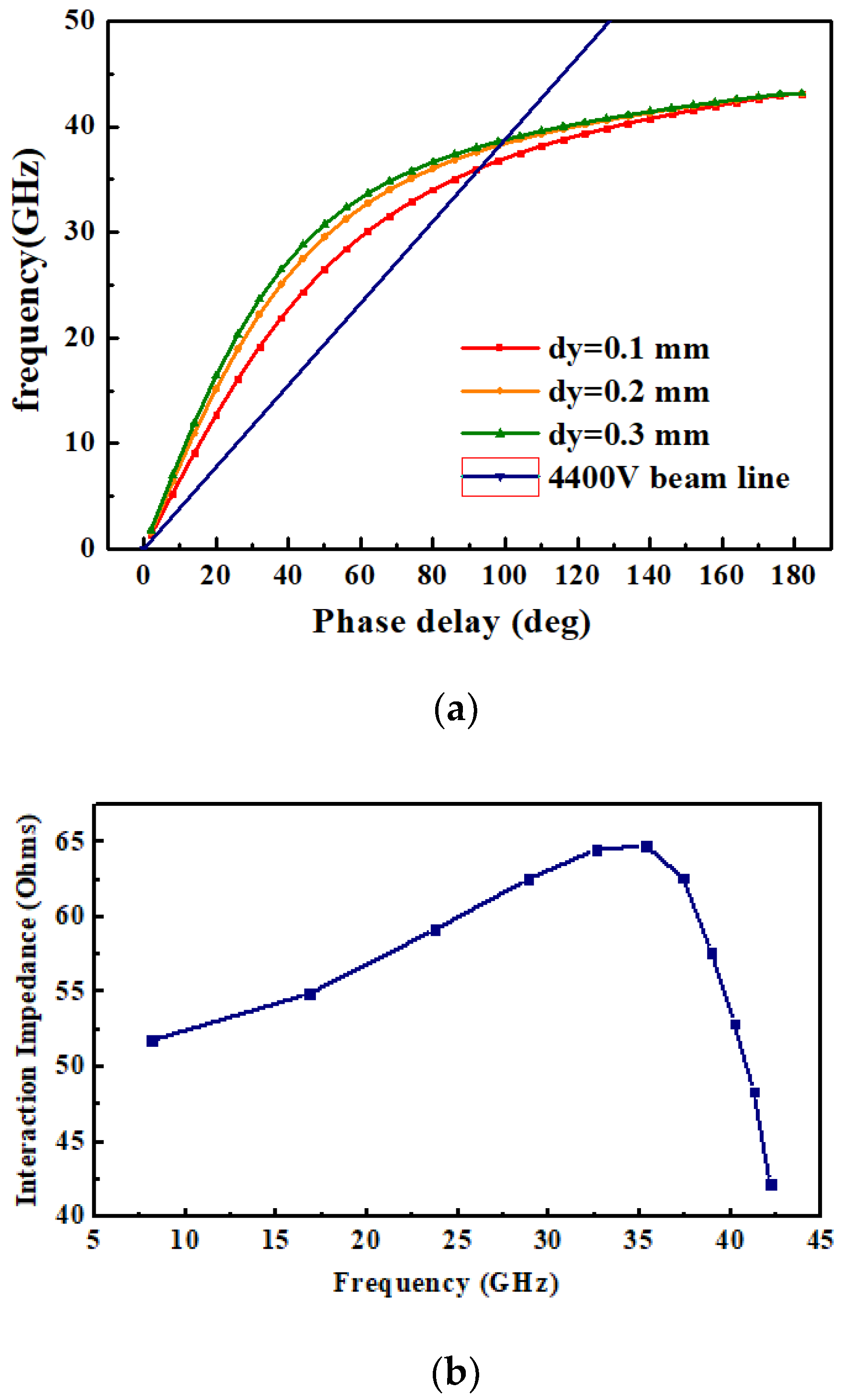
2. Structure Model and High Frequency Characteristics of the ASML SWS
3. Fabrication and Measurement Issues
3.1. Fabrication and Assembly
3.2. The Surface Roughness Measurement
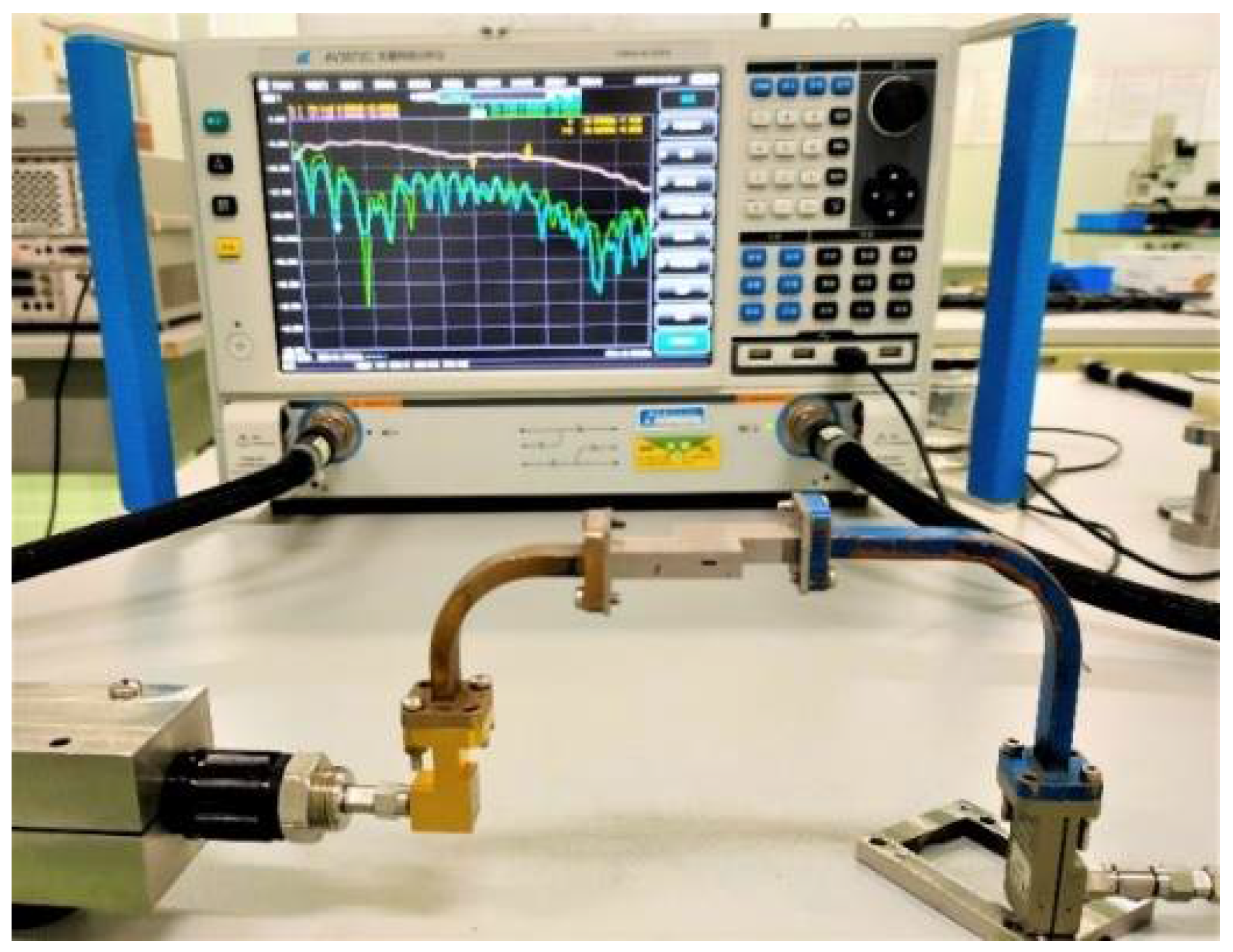
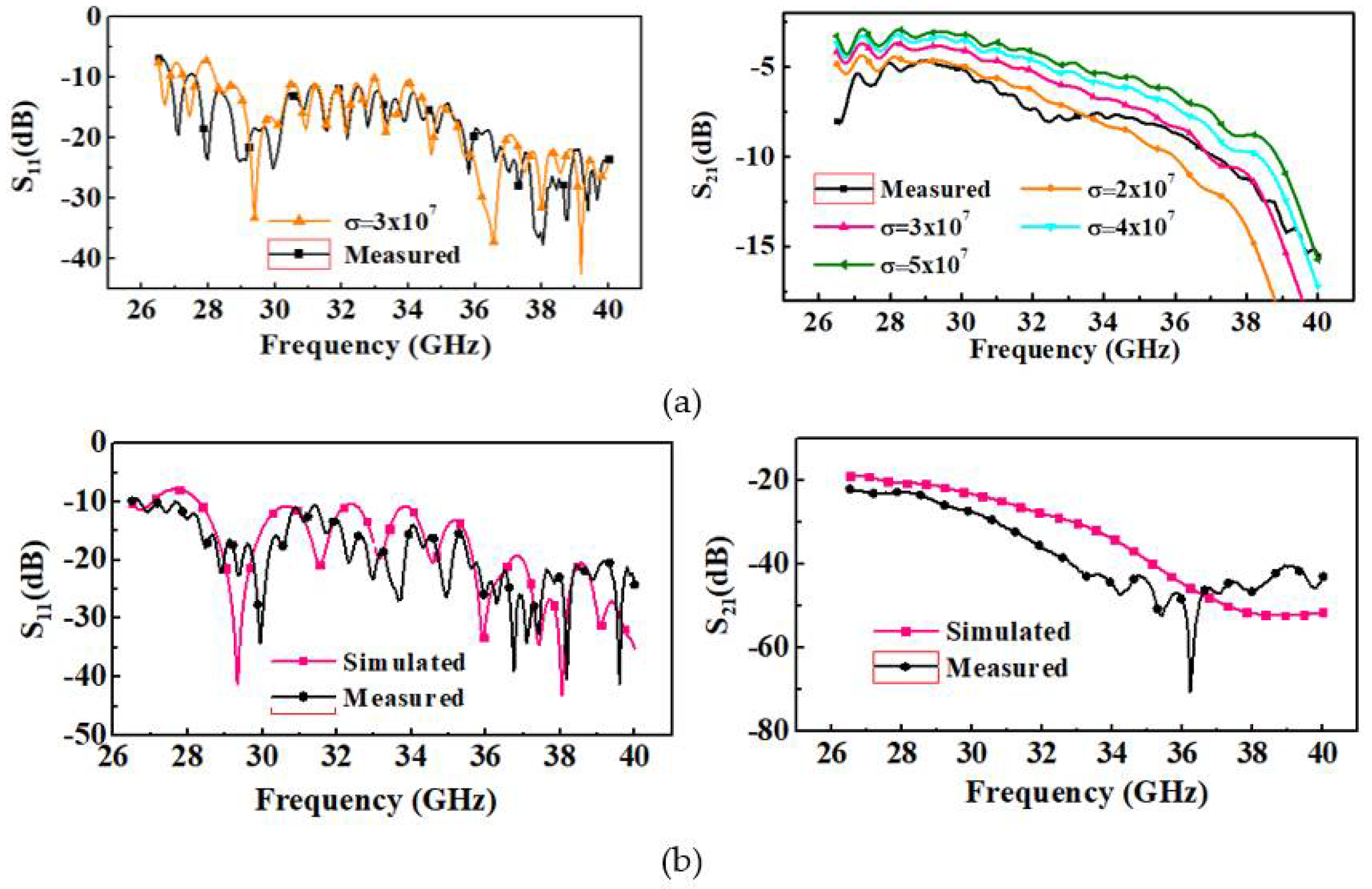
3.3. S-Parameters Measurements
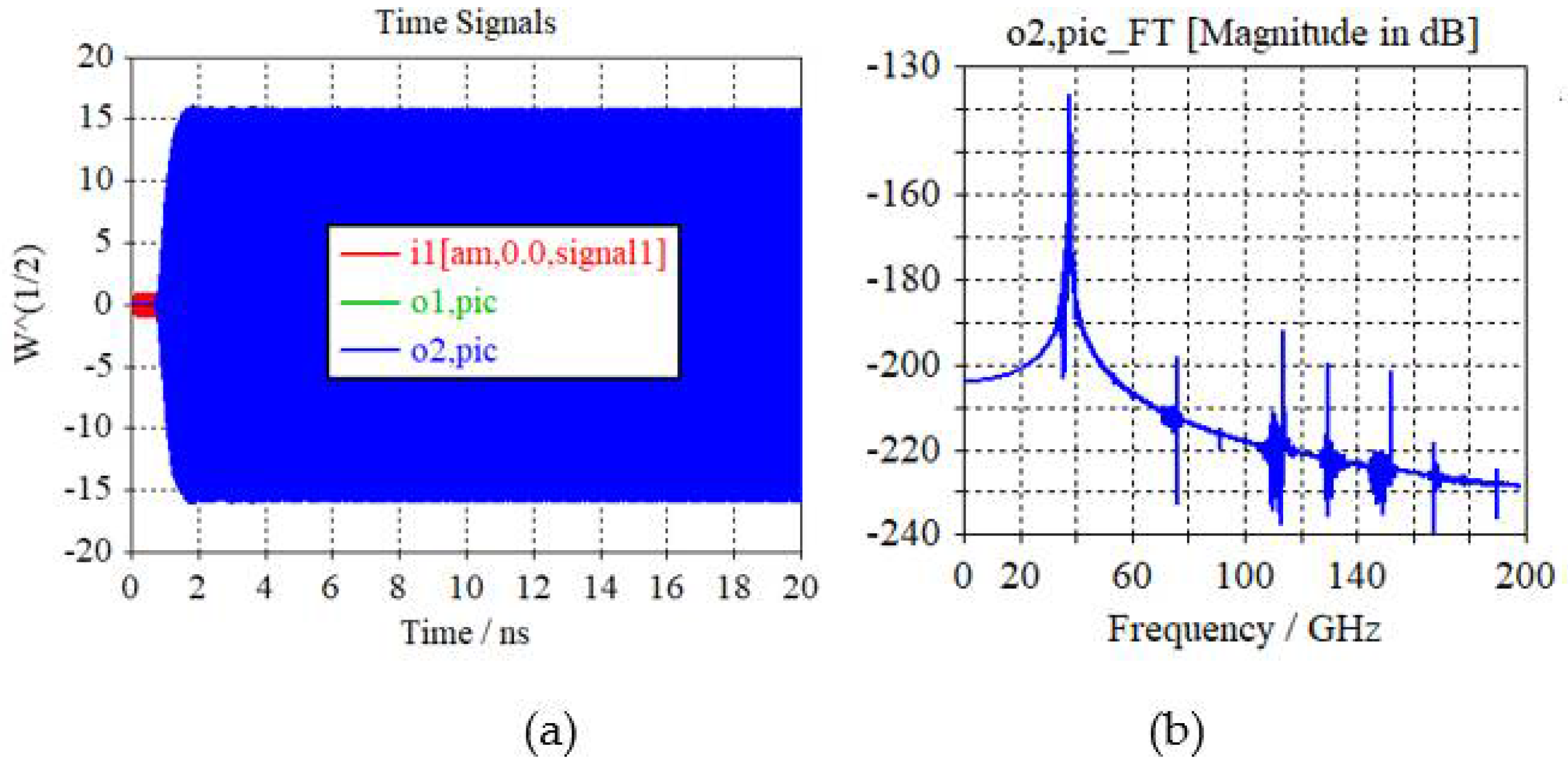
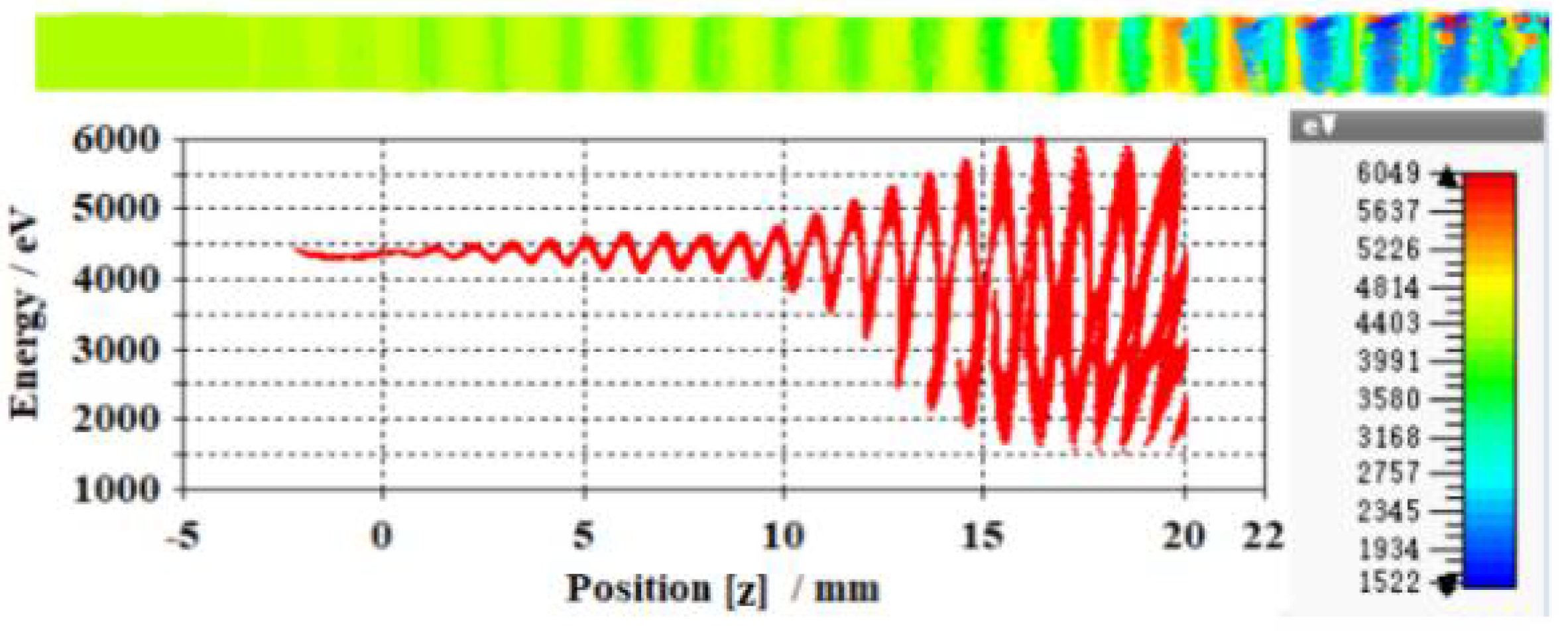
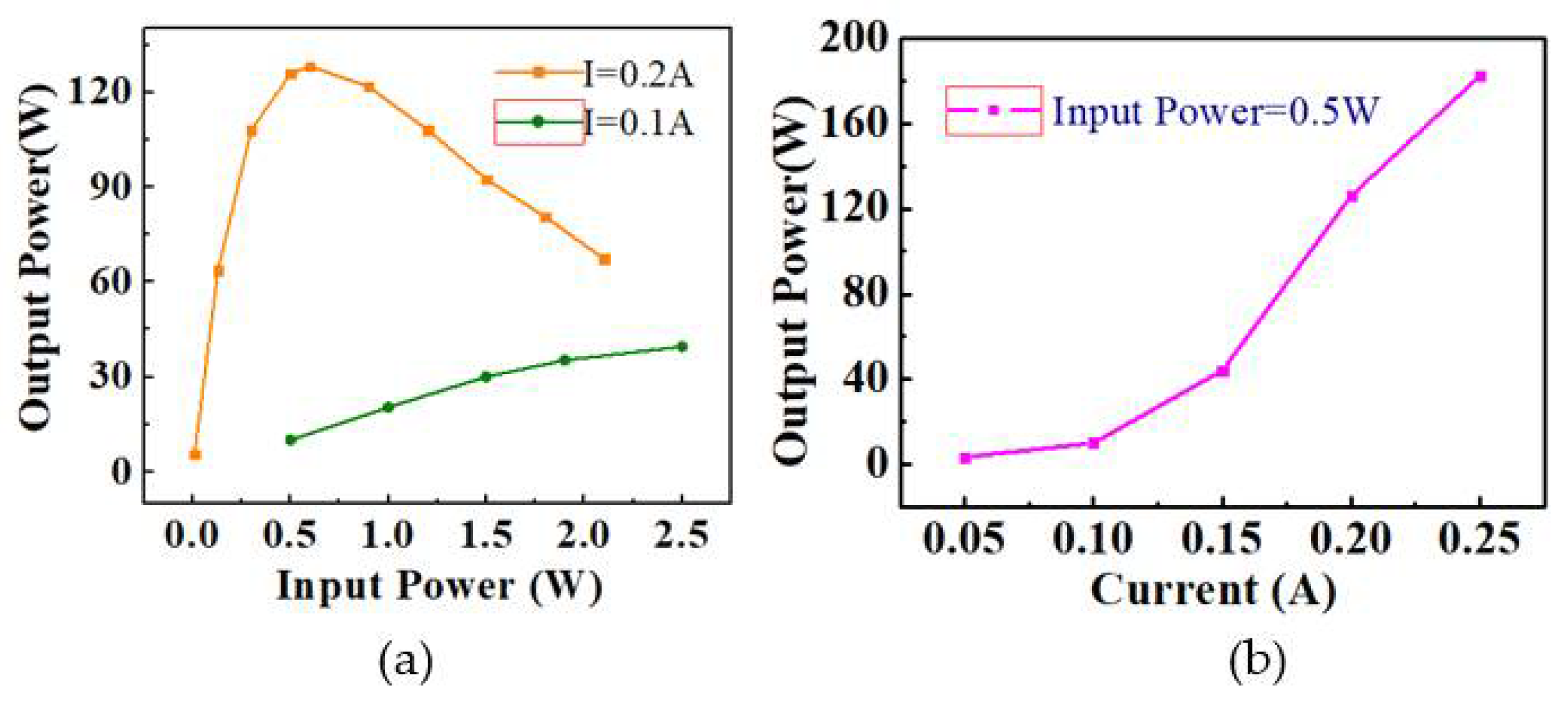
4. “Hot” Performance of the ASML TWT
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jiang, W.; Han, B.; Habibi, M.A.; Schotten, H.D. The Road Towards 6G: A Comprehensive Survey. IEEE Open J. Commun. Soc. 2021, 2, 334–366. [Google Scholar] [CrossRef]
- Hong, W.; Jiang, Z.H.; Yu, C.; Hou, D.; Wang, H.; Guo, C.; Hu, Y.; Kuai, L.; Yu, Y.; Jiang, Z.; et al. The Role of Millimeter-Wave Technologies in 5G/6G Wireless Communications. IEEE J. Microw. 2021, 1, 101–122. [Google Scholar] [CrossRef]
- Liu, Y.; Yuan, X.; Xiong, Z.; Kang, J.; Wang, X.; Niyato, D. Federated learning for 6G communications: Challenges, methods, and future directions. China Commun. 2020, 17, 9. [Google Scholar] [CrossRef]
- Chowdhury, M.Z.; Shahjalal, M.; Ahmed, S.; Jang, Y.M. 6G Wireless Communication Systems: Applications, Requirements, Technologies, Challenges, and Research Directions. IEEE Open J. Commun. Soc. 2020, 1, 957–975. [Google Scholar] [CrossRef]
- Dhillon, S.S.; Vitiello, M.S.; Linfield, E.H.; Davies, A.; Hoffmann, M.; Booske, J.; Paoloni, C.; Gensch, M.; Weightman, P.; Williams, G.P.; et al. The 2017 terahertz science and technology roadmap. J. Phys. D Appl. Phys. 2017, 50, 043001. [Google Scholar] [CrossRef]
- Basu, R.; Rao, J.M.; Le, T.; Letizia, R.; Paoloni, C. Development of a D-Band Traveling Wave Tube for High Data-Rate Wireless Links. IEEE Trans. Electron Devices 2021, 68, 9. [Google Scholar] [CrossRef]
- André, F.; Racamier, J.C.; Zimmermann, R.; Le, Q.T.; Krozer, V.; Ulisse, G.; Minenna, D.F.G.; Letizia, R.; Paoloni, C. Technology, Assembly, and Test of a W -Band Traveling Wave Tube for New 5G High-Capacity Networks. IEEE Trans. Electron Devices 2020, 67, 7. [Google Scholar] [CrossRef]
- Ulisse, G.; Krozer, V. $W$ -Band Traveling Wave Tube Amplifier Based on Planar Slow Wave Structure. IEEE Electron Device Lett. 2016, 38, 126–129. [Google Scholar] [CrossRef]
- Paoloni, C.; Gamzina, D.; Letizia, R.; Zheng, Y.; Luhmann, N.C., Jr. Millimeter wave traveling wave tubes for the 21st Century. J. Electromagn. Waves Appl. 2020, 35, 567–603. [Google Scholar] [CrossRef]
- Prakash, D.J.; Dwyer, M.M.; Argudo, M.M.; Debasu, M.L.; Dibaji, H.; Lagally, M.G.; Van Der Weide, D.W.; Cavallo, F. Self-Winding Helices as Slow-Wave Structures for Sub-Millimeter Traveling-Wave Tubes. ACS Nano 2020, 15, 1229–1239. [Google Scholar] [CrossRef] [PubMed]
- Shen, F.; Wei, Y.; Yin, H.; Gong, Y.; Xu, X.; Wang, S.; Wang, W.; Feng, J. A Novel V-Shaped Microstrip Meander-Line Slow-Wave Structure for W-band MMPM. IEEE Trans. Plasma Sci. 2011, 40, 463–469. [Google Scholar] [CrossRef]
- Shen, F.; Wei, Y.; Xu, X.; Liu, Y.; Huang, M.; Tang, T.; Gong, Y. U-shaped microstrip meander-line slow-wave structure for Ka-band traveling-wave tube. In Proceedings of the 2012 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Shenzhen, China, 5–8 May 2012. [Google Scholar] [CrossRef]
- Wang, S.; Gong, Y.; Hou, Y.; Wang, Z.; Wei, Y.; Duan, Z.; Cai, J. Study of a Log-Periodic Slow Wave Structure for Ka-band Radial Sheet Beam Traveling Wave Tube. IEEE Trans. Plasma Sci. 2013, 41, 2277–2282. [Google Scholar] [CrossRef]
- Zhao, C.; Aditya, S.; Wang, S. A Novel Coplanar Slow-Wave Structure for Millimeter-Wave BWO Applications. IEEE Trans. Electron Devices 2021, 68, 1924–1929. [Google Scholar] [CrossRef]
- Ryskin, N.M.; Torgashov, R.A.; Starodubov, A.V.; Rozhnev, A.G.; Serdobintsev, A.A.; Pavlov, A.M.; Galushka, V.V.; Bessonov, D.A.; Ulisse, G.; Krozer, V. Development of microfabricated planar slow-wave structures on dielectric substrates for miniaturized millimeter-band traveling-wave tubes. J. Vac. Sci. Technol. B 2021, 39, 013204. [Google Scholar] [CrossRef]
- Zhao, C.; Aditya, S.; Chua, C. A Microfabricated Planar Helix Slow-Wave Structure to Avoid Dielectric Charging in TWTs. IEEE Trans. Electron Devices 2015, 62, 1342–1348. [Google Scholar] [CrossRef]
- Wang, H.; Wang, Z.; Li, X.; He, T.; Xu, D.; Gong, H.; Tang, T.; Duan, Z.; Wei, Y.; Gong, Y. Study of a miniaturized dual-beam TWT with planar dielectric-rods-support uniform metallic meander line. Phys. Plasmas 2018, 25, 06. [Google Scholar] [CrossRef]
- Dong, Y.; Chen, Z.; Li, X.; Wang, H.; Wang, Z.; Wang, S.; Lu, Z.; Gong, H.; Duan, Z.; Feng, J.; et al. Ka-band dual sheet beam traveling wave tube using supported planar ring-bar slow wave structure. J. Electromagn. Waves Appl. 2020, 34, 1–15. [Google Scholar] [CrossRef]
- Wen, Z.; Luo, J.; Li, Y.; Guo, W.; Zhu, M. A Concentric Arc Meander Line Slow Wave Structure Applied on Low Voltage and High Efficiency Ka-Band TWT. IEEE Trans. Electron Devices 2021, 68, 1262–1266. [Google Scholar] [CrossRef]
- Wang, H.; Wang, S.; Wang, Z.; Li, X.; Xu, D.; Duan, Z.; Lu, Z.; Gong, H.; Aditya, S.; Gong, Y. Dielectric-Supported Staggered Dual Meander-Line Slow Wave Structure for an E-Band TWT. IEEE Trans. Electron Devices 2020, 68, 369–375. [Google Scholar] [CrossRef]
- Wang, Z.; Su, L.; Duan, Z.; Hu, Q.; Gong, H.; Lu, Z.; Feng, J.; Li, S.; Gong, Y. Investigation on a Ka Band Diamond-Supported Meander-Line SWS. J. Infrared Millim. Terahertz Waves 2020, 41, 1460–1468. [Google Scholar] [CrossRef]
- Wang, Z.; Du, F.; Li, S.; Hu, Q.; Duan, Z.; Gong, H.; Gong, Y.; Feng, J. Study on an X-Band Sheet Beam Meander-Line SWS. IEEE Trans. Plasma Sci. Devices 2020, 48, 12. [Google Scholar] [CrossRef]
- Starodubov, A.; Atkin, V.; Torgashov, R.; Navrotsky, I.A.; Ryskin, N. On the technological approach to microfabrication of a meander-line slow-wave structure for millimeter-band traveling-wave tubes with multiple sheet electron beams. In Proceedings of the Saratov Fall Meeting 2020: Laser Physics, Photonic Technologies, and Molecular Modeling, Saratov, Russia, 29 September–2 October 2020. [Google Scholar]
- Kirley, M.P.; Booske, J.H. Terahertz conductivity of coppersurfaces. IEEE Trans. THz Sci. Technol. 2015, 6, 1012–1020. [Google Scholar] [CrossRef]
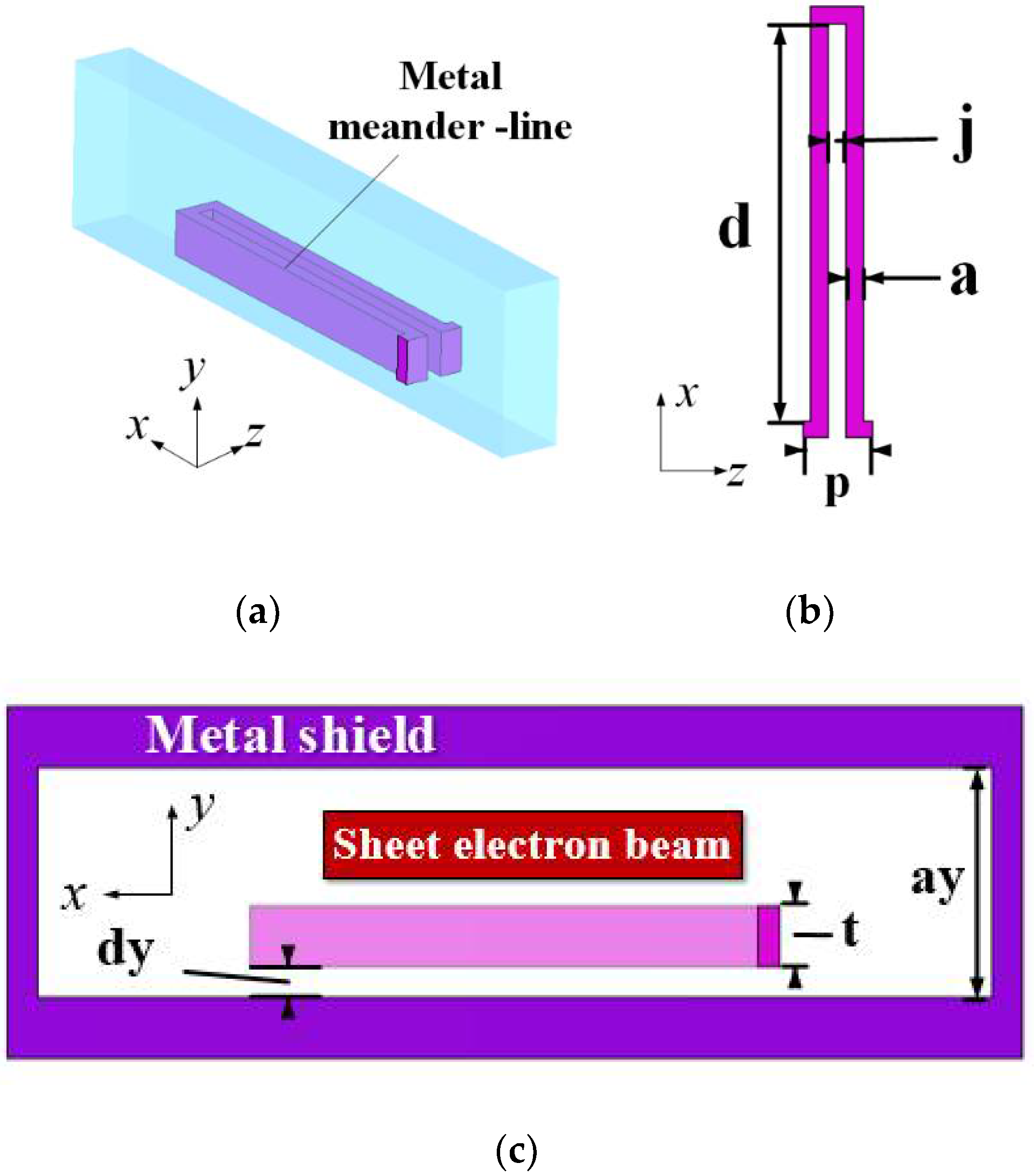
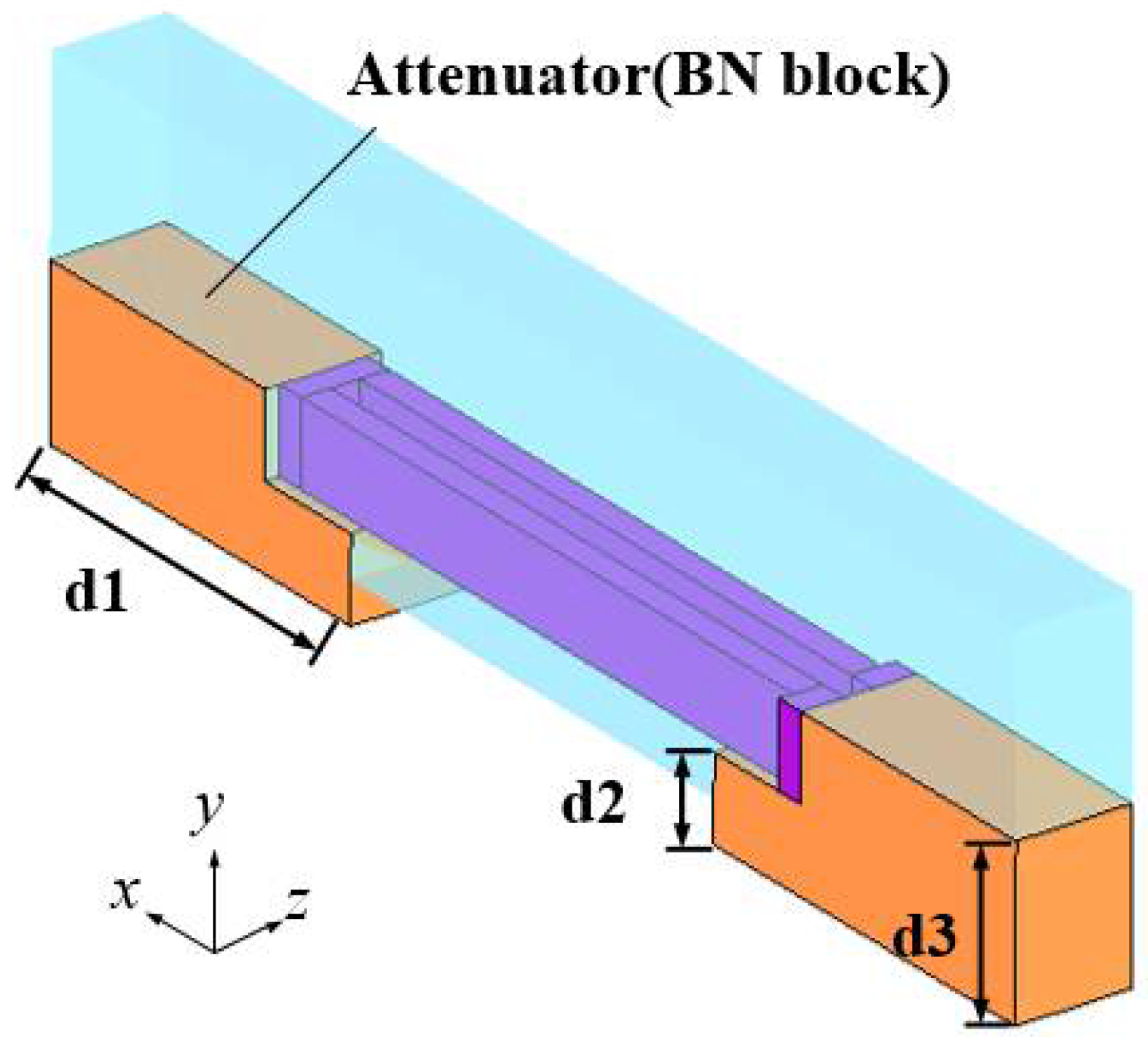




| Parameters | Value (mm) | Parameters | Value (mm) |
|---|---|---|---|
| d | 1.6 | ay | 0.756 |
| a | 0.07 | dy | 0.1 |
| j | 0.07 | d1 | 0.7 |
| p | 0.28 | d2 | 0.2 |
| t | 0.2 | d3 | 0.4 |
| Parameters | Values (mm) | Parameters | Values (mm) |
|---|---|---|---|
| dr1 | 6 | hr1 | 2.3 |
| dr2 | 2.55 | hr2 | 1.5 |
| dr3 | 3.5 | hr3 | 0.8 |
| dr4 | 2 | hr4 | 0.2 |
| wr | 1.1 | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Wang, S.; Wang, Z.; Li, X.; He, T.; Xu, D.; Duan, Z.; Lu, Z.; Gong, H.; Gong, Y. Study of an Attenuator Supporting Meander-Line Slow Wave Structure for Ka-Band TWT. Electronics 2021, 10, 2372. https://doi.org/10.3390/electronics10192372
Wang H, Wang S, Wang Z, Li X, He T, Xu D, Duan Z, Lu Z, Gong H, Gong Y. Study of an Attenuator Supporting Meander-Line Slow Wave Structure for Ka-Band TWT. Electronics. 2021; 10(19):2372. https://doi.org/10.3390/electronics10192372
Chicago/Turabian StyleWang, Hexin, Shaomeng Wang, Zhanliang Wang, Xinyi Li, Tenglong He, Duo Xu, Zhaoyun Duan, Zhigang Lu, Huarong Gong, and Yubin Gong. 2021. "Study of an Attenuator Supporting Meander-Line Slow Wave Structure for Ka-Band TWT" Electronics 10, no. 19: 2372. https://doi.org/10.3390/electronics10192372
APA StyleWang, H., Wang, S., Wang, Z., Li, X., He, T., Xu, D., Duan, Z., Lu, Z., Gong, H., & Gong, Y. (2021). Study of an Attenuator Supporting Meander-Line Slow Wave Structure for Ka-Band TWT. Electronics, 10(19), 2372. https://doi.org/10.3390/electronics10192372







