AC Current Ripple Harmonic Pollution in Three-Phase Four-Leg Active Front-End AC/DC Converter for On-Board EV Chargers
Abstract
:1. Introduction
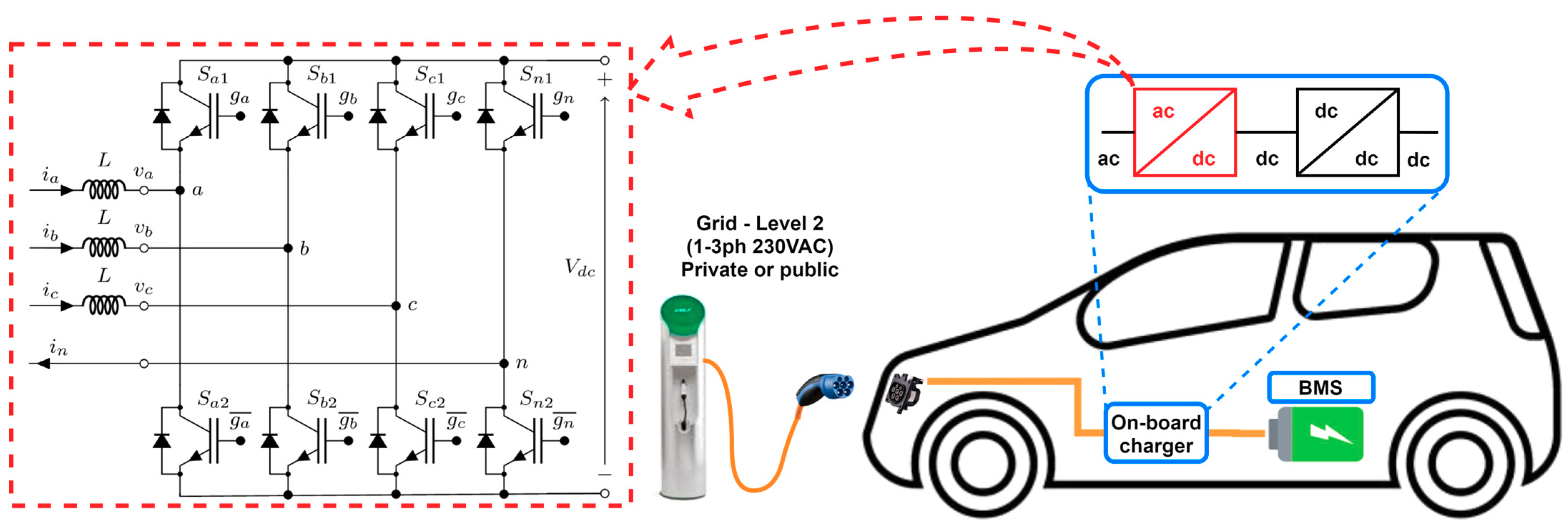
2. Basic Assumptions and Modulation Principle
2.1. Converter Model and Current Ripple Definition
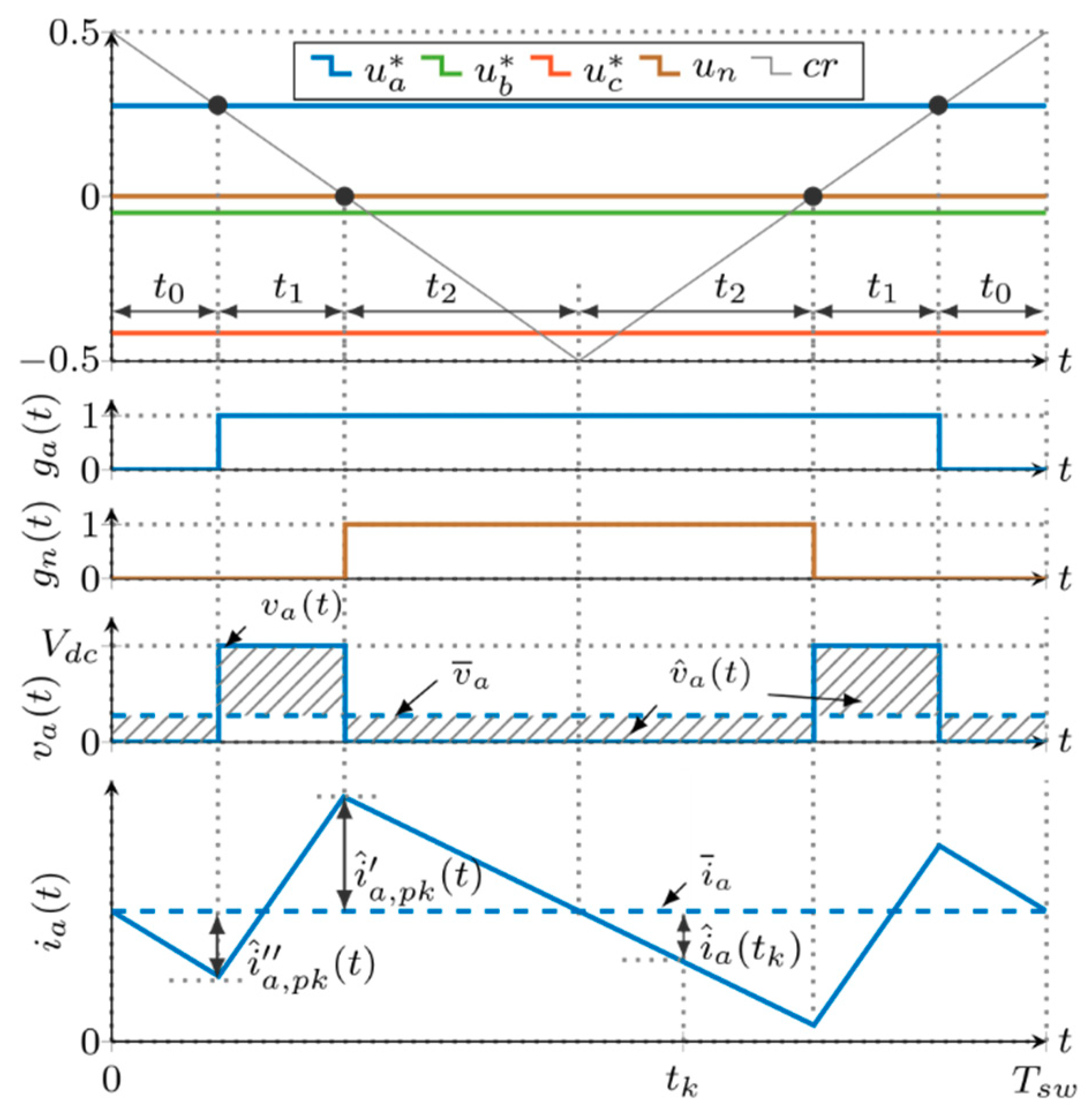
2.2. Carrier-Based Pulse-Width Modulation
3. Analysis of Phase Currents Ripple
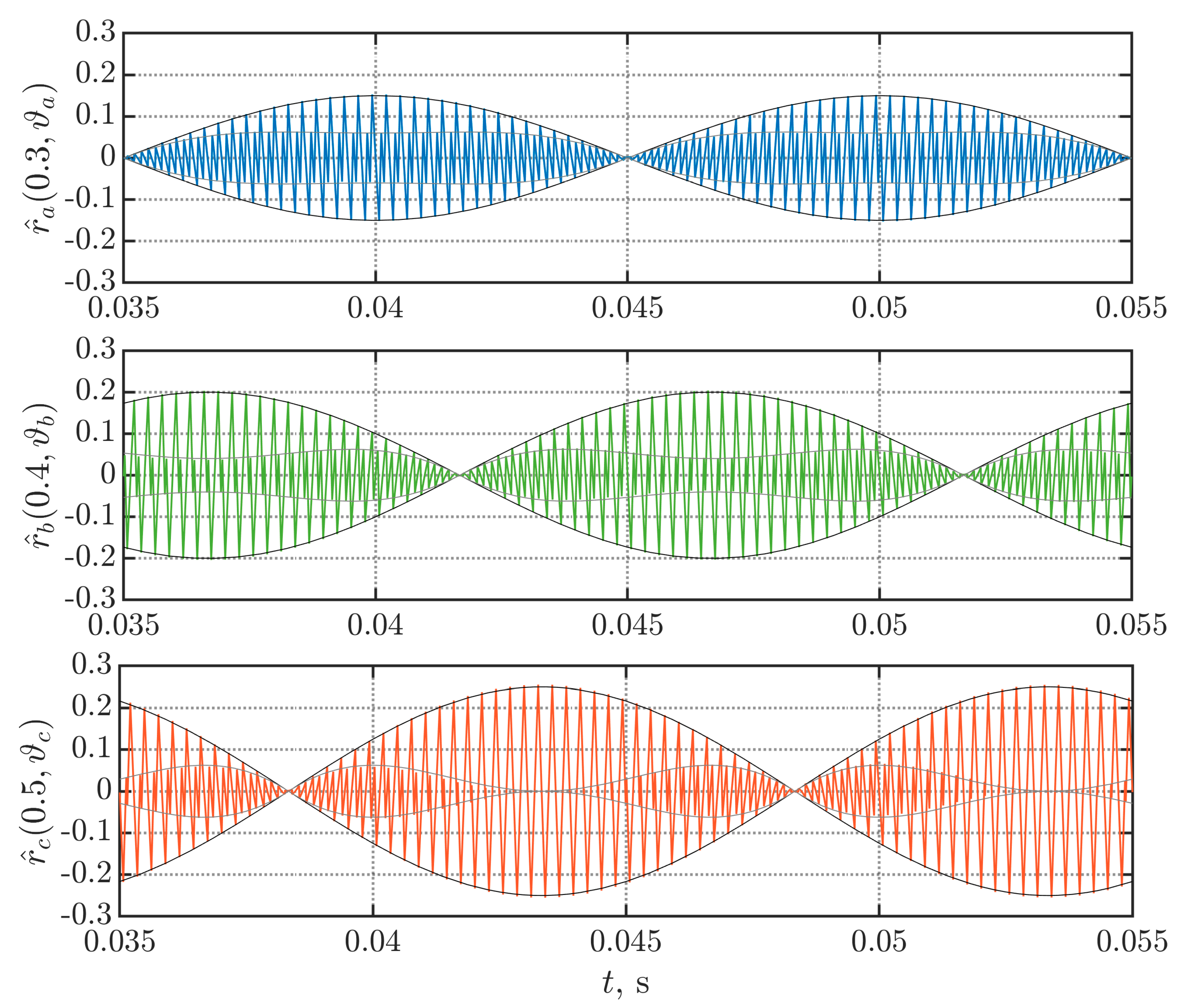
3.1. Phase Current Ripple Waveform
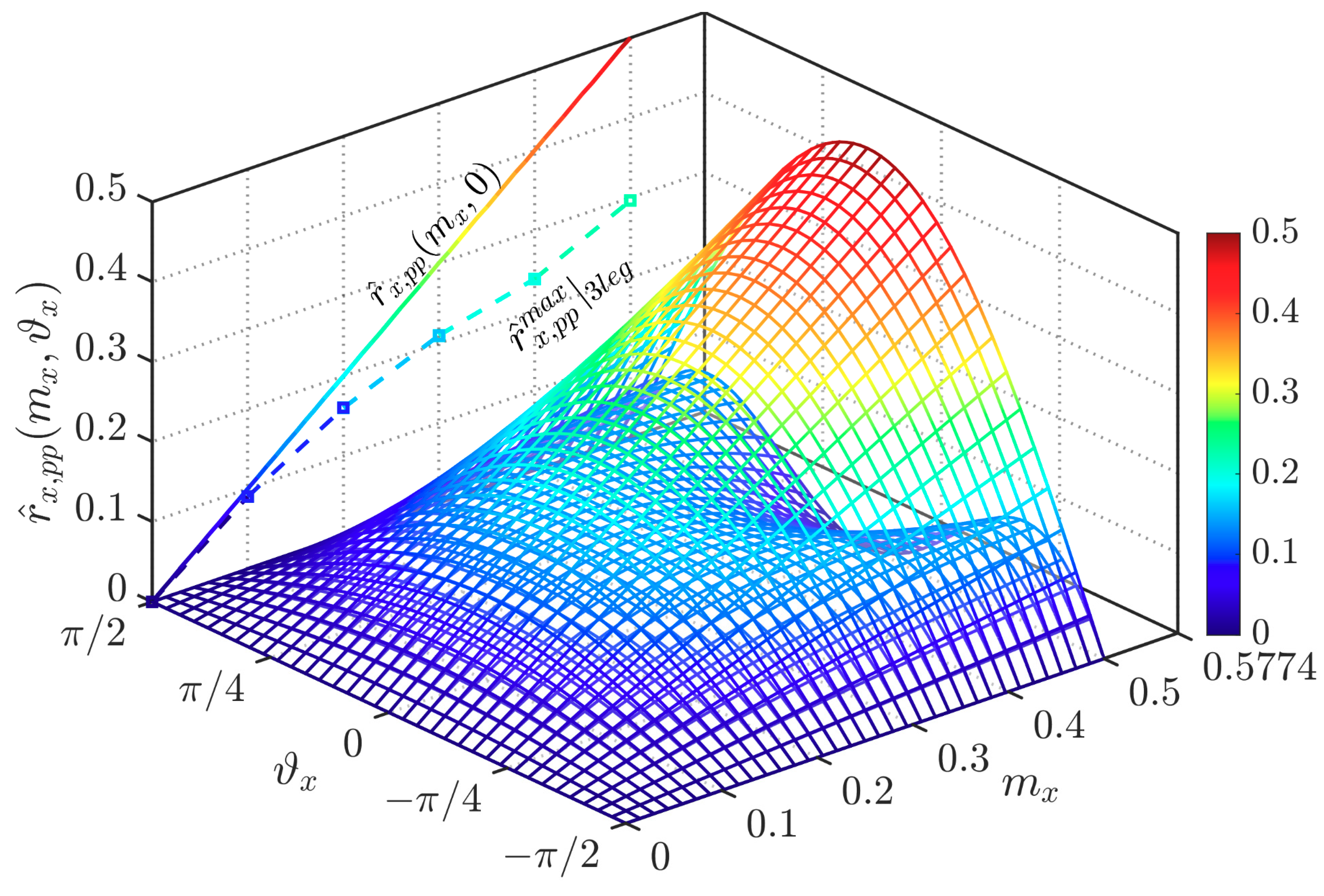
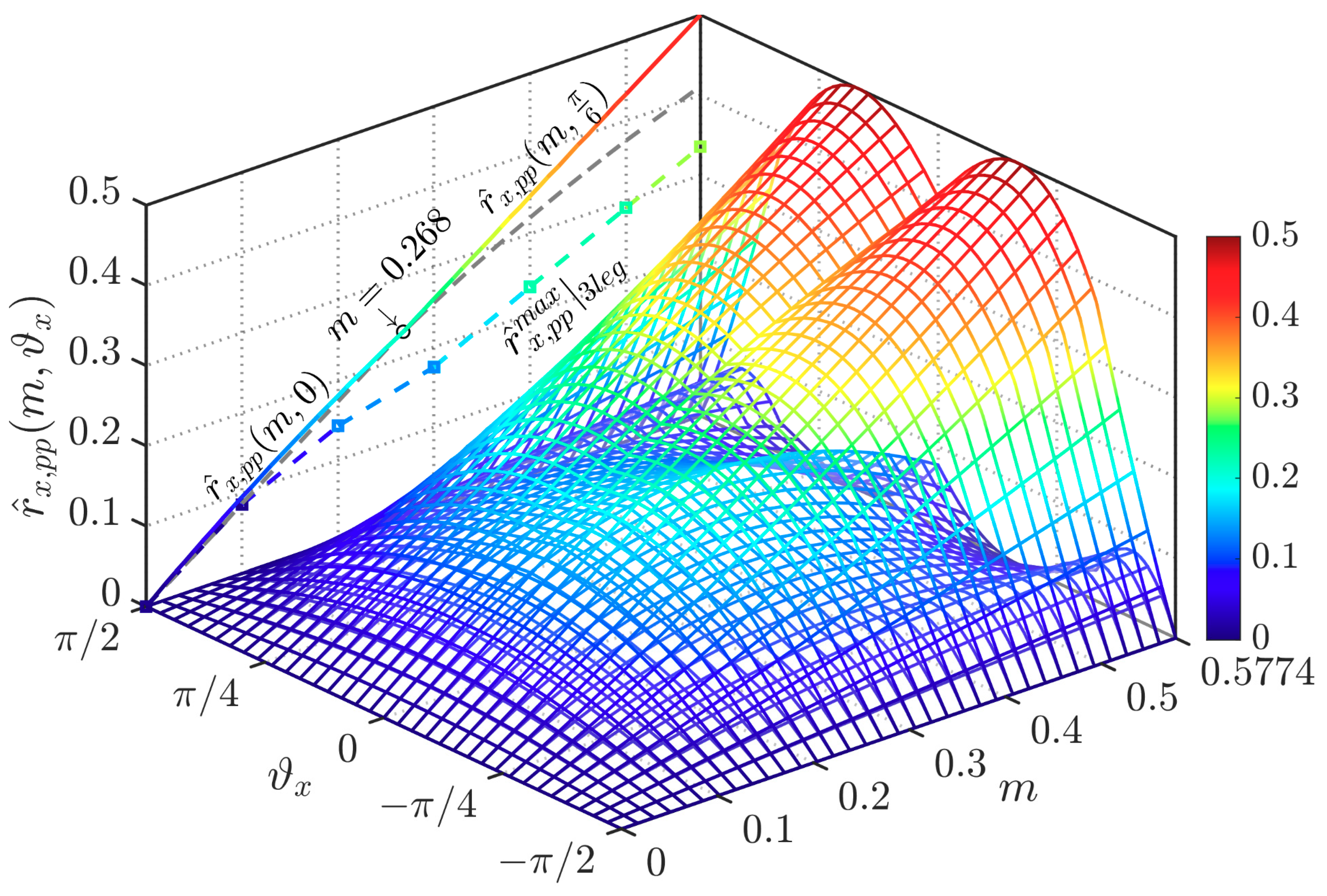
3.2. Phase Current Ripple RMS
4. Analysis of Neutral Current Ripple
4.1. Neutral Current Ripple Waveform
4.2. Neutral Current Ripple RMS
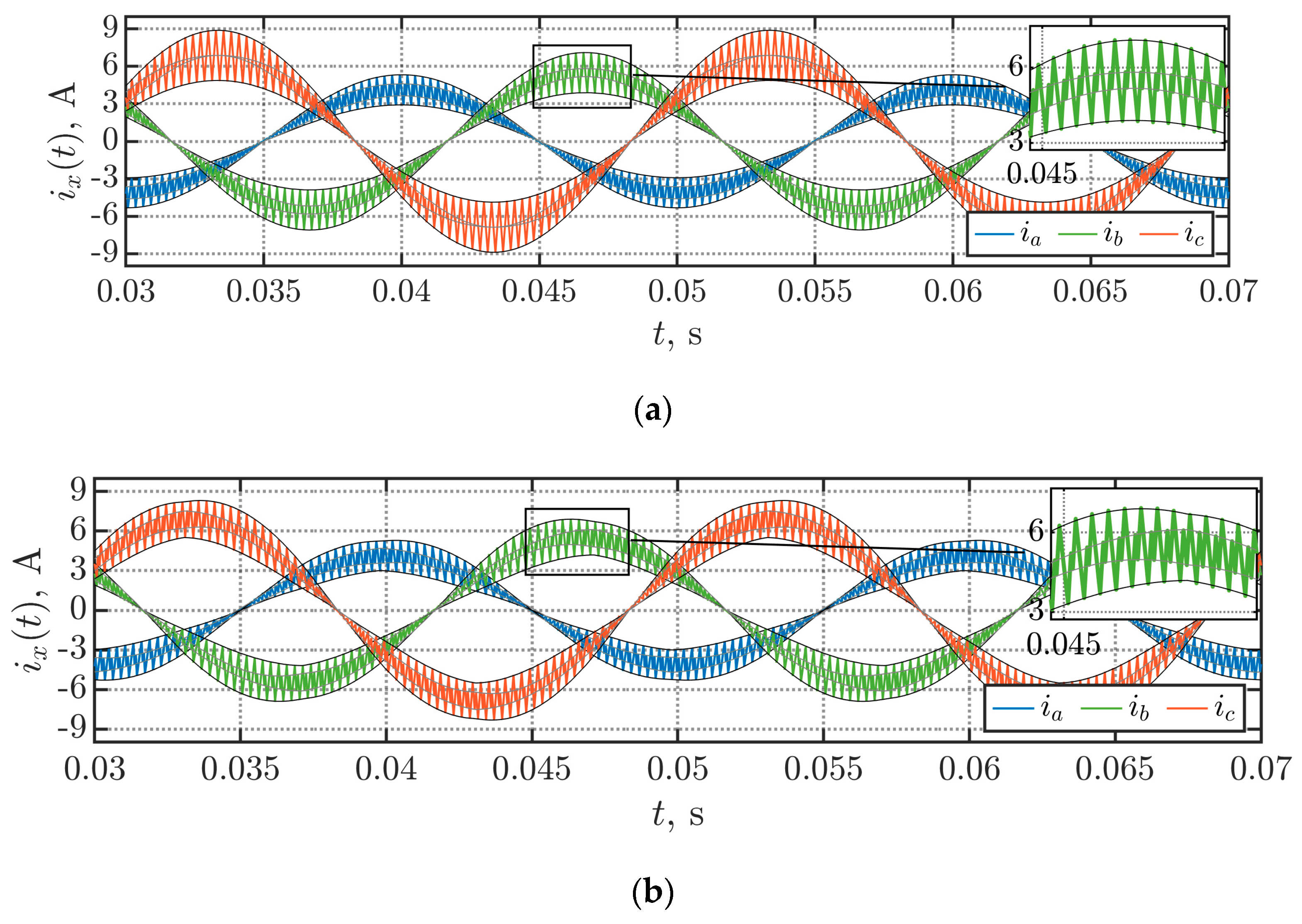
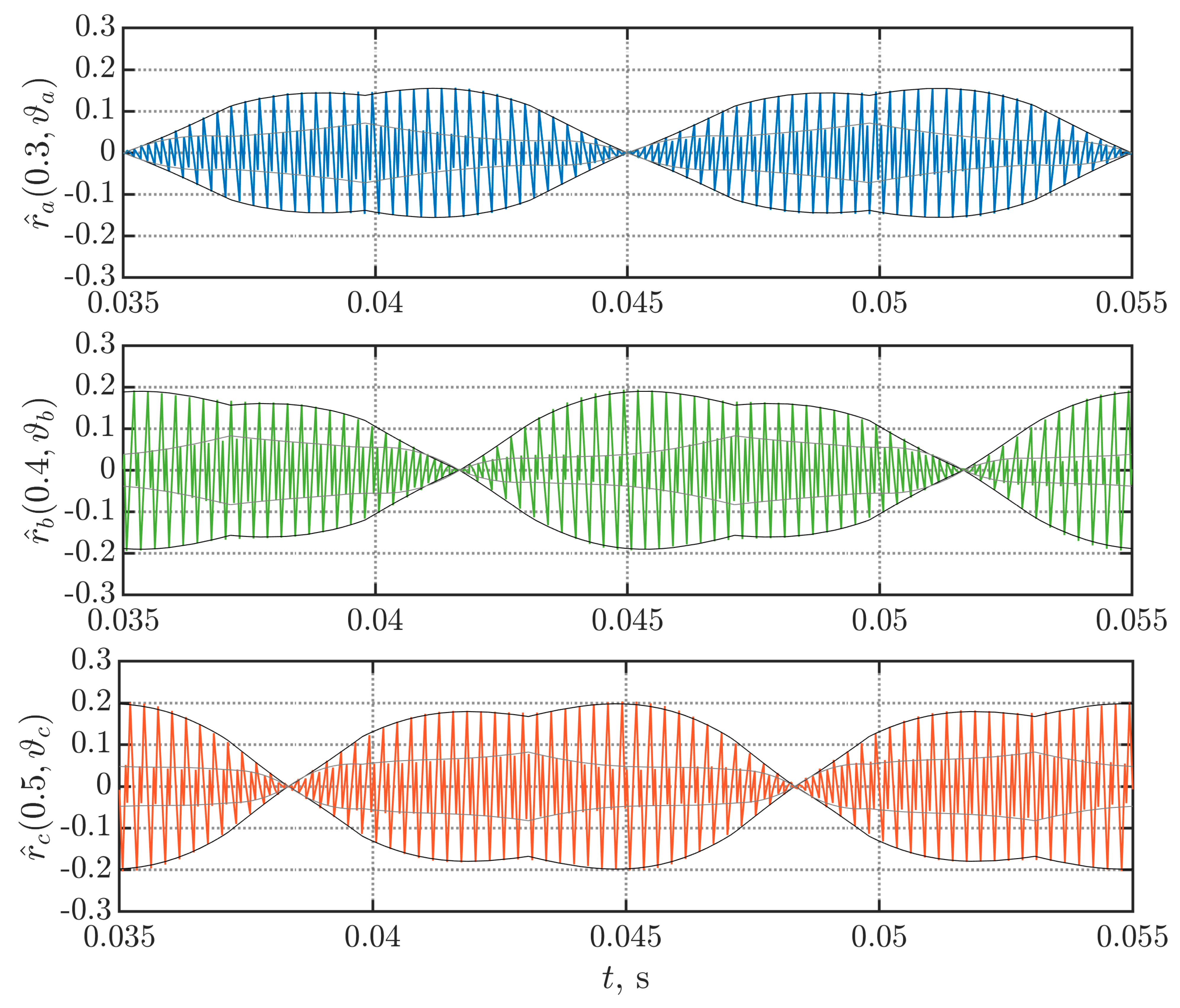
5. Experimental Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| x | Index for phases a, b, c, and neutral n, used as a subscript |
| , | Converter’s instantaneous voltage and current |
| , | Low-frequency components of instantaneous voltage and current (averaged over the switching period) |
| , | High-frequency (switching frequency) ripple components of instantaneous voltage and current |
| Modulating signals | |
| γ | Common-mode injection |
| mx | Modulation index (normalized by dc-link voltage Vdc) |
| ϑx | Phase power angle |
| , | Primary peak (pk) and primary peak-to-peak (pp) current ripple wrapping envelopes |
| , | Normalized primary peak (pk) and primary peak-to-peak (pp) current ripple wrapping envelopes |
| , | Secondary peak (pk) and secondary peak-to-peak (pp) current ripple wrapping envelopes |
| , | Normalized secondary peak (pk) and secondary peak-to-peak (pp) current ripple wrapping envelopes |
| Total current ripple RMS | |
| Normalized total current ripple RMS |
References
- De Freitas Takami, M.H.; da Silva, S.A.O.; Sampaio, L.P. Dynamic performance comparison involving grid-connected PV systems operating with active power-line conditioning and subjected to sudden solar irradiation changes. IET Renew. Power Gener. 2019, 13, 587–597. [Google Scholar] [CrossRef]
- Carrasco, G.; Silva, C.A.; Pena, R.; Cardenas, R. Control of a Four-Leg Converter for the Operation of a DFIG Feeding Stand-Alone Unbalanced Loads. IEEE Trans. Ind. Electron. 2015, 62, 4630–4640. [Google Scholar] [CrossRef]
- Khadkikar, V.; Chandra, A.; Singh, B. Digital signal processor implementation and performance evaluation of split capacitor, four-leg and three H-bridge-based three-phase four-wire shunt active filters. IET Power Electron. 2011, 4, 463–470. [Google Scholar] [CrossRef]
- Yaramasu, V.; Rivera, M.; Wu, B.; Rodriguez, J. Model Predictive Current Control of Two-Level Four-Leg Inverters—Part I: Concept, Algorithm, and Simulation Analysis. IEEE Trans. Power Electron. 2013, 28, 3459–3468. [Google Scholar] [CrossRef]
- Li, A.; Jiang, D.; Kong, W.; Qu, R. Four-Leg Converter for Reluctance Machine With DC-Biased Sinusoidal Winding Current. IEEE Trans. Power Electron. 2019, 34, 4569–4580. [Google Scholar] [CrossRef]
- Viatkin, A.; Hammami, M.; Grandi, G.; Ricco, M. Analysis of a Three-Phase Four-Leg Front-End Converter for EV Chargers with Balanced and Unbalanced Grid Currents. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; pp. 3442–3449. [Google Scholar]
- Fu, Y.; Li, Y.; Huang, Y.; Lu, X.; Zou, K.; Chen, C.; Bai, H. Imbalanced Load Regulation Based on Virtual Resistance of A Three-Phase Four-Wire Inverter for EV Vehicle-to-Home Applications. IEEE Trans. Transp. Electrif. 2019, 5, 162–173. [Google Scholar] [CrossRef]
- Lin, Z.; Ruan, X.; Jia, L.; Zhao, W.; Liu, H.; Rao, P. Optimized Design of the Neutral Inductor and Filter Inductors in Three-Phase Four-Wire Inverter with Split DC-Link Capacitors. IEEE Trans. Power Electron. 2019, 34, 247–262. [Google Scholar] [CrossRef]
- Hammami, M.; Ricco, M.; Viatkin, A.; Mandrioli, R.; Grandi, G. Evaluation of AC Current Ripple in case of Split-Capacitor Three-Phase Four Wires Inverters. In Proceedings of the 2020 6th IEEE International Energy Conference (ENERGYCon), Gammarth, Tunisia, 28 September–1 October 2020; pp. 128–132. [Google Scholar]
- Hammami, M.; Mandrioli, R.; Viatkin, A.; Ricco, M.; Grandi, G. Analysis of Input Voltage Switching Ripple in Three-Phase Four-Wire Split Capacitor PWM Inverters. Energies 2020, 13, 5076. [Google Scholar] [CrossRef]
- Hintz, A.; Prasanna, R.; Rajashekara, K. Comparative Study of Three-phase Grid Connected Inverter Sharing Unbalanced Three-phase and/or Single-phase systems. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 6491–6496. [Google Scholar]
- Zhao, W.; Ruan, X.; Yang, D.; Chen, X.; Jia, L. Neutral Point Voltage Ripple Suppression for a Three-Phase Four-Wire Inverter with an Independently Controlled Neutral Module. IEEE Trans. Ind. Electron. 2017, 64, 2608–2619. [Google Scholar] [CrossRef]
- Fu, Y.; Li, Y.; Huang, Y.; Bai, H.; Zou, K.; Lu, X.; Chen, C. Design Methodology of a Three-Phase Four-Wire EV Charger Operated at the Autonomous Mode. IEEE Trans. Transp. Electrif. 2019, 5, 1169–1181. [Google Scholar] [CrossRef]
- Wong, M.C.; Zhao, Z.Y.; Han, Y.D.; Zhao, L.B. Three-dimensional pulse-width modulation technique in three-level power inverters for three-phase four-wired system. IEEE Trans. Power Electron. 2011, 16, 418–427. [Google Scholar] [CrossRef] [Green Version]
- Golwala, H.; Chudamani, R. New Three-Dimensional Space Vector-Based Switching Signal Generation Technique without Null Vectors and with Reduced Switching Losses for a Grid-Connected Four-Leg Inverter. IEEE Trans. Power Electron. 2016, 31, 1026–1035. [Google Scholar] [CrossRef]
- Kim, J.H.; Sul, S.K. A Carrier-Based PWM Method for Three-Phase Four-Leg Voltage Source Converters. IEEE Trans. Power Electron. 2004, 19, 66–75. [Google Scholar] [CrossRef]
- Hava, A.M.; Kerkman, R.J.; Lipo, T.A. Carrier-based PWM-VSI overmodulation strategies: Analysis, comparison, and design. IEEE Trans. Power Electron. 1998, 13, 674–689. [Google Scholar] [CrossRef] [Green Version]
- Grandi, G.; Loncarski, J. Evaluation of current ripple amplitude in three-phase PWM voltage source inverters. In Proceedings of the 2013 International Conference-Workshop Compatibility and Power Electronics, Ljubljana, Slovenia, 5–7 June 2013; pp. 156–161. [Google Scholar]
- Grandi, G.; Loncarski, J.; Dordevic, O. Analysis and Comparison of Peak-to-Peak Current Ripple in Two-Level and Multilevel PWM Inverters. IEEE Trans. Ind. Electron. 2015, 62, 2721–2730. [Google Scholar] [CrossRef]
- Jiang, D.; Wang, F. Study of analytical current ripple of three-phase PWM converter. In Proceedings of the 2012 Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 5–9 February 2020; pp. 1568–1575. [Google Scholar]
- Grandi, G.; Loncarski, J.; Seebacher, R. Effects of current ripple on dead-time distortion in three-phase voltage source inverters. In Proceedings of the 2012 IEEE International Energy Conference and Exhibition (ENERGYCON), Florence, Italy, 9–12 September 2012; pp. 207–212. [Google Scholar]
- Cai, W.; Shen, Y.; Xiao, X.; Wang, W.; Zhang, W.; Li, K.; Zhang, C.; Zhao, Z. Design of the Neutral Line Inductor for Three-phase Four-leg Inverters. In Proceedings of the 2019 IEEE Sustainable Power and Energy Conference (iSPEC), Beijing, China, 21–23 November 2019; pp. 2455–2460. [Google Scholar]
- Viatkin, A.; Mandrioli, R.; Hammami, M.; Ricco, M.; Grandi, G. Theoretical Analysis of the AC Current Ripple in Three-Phase Four-Leg Sinusoidal PWM Inverters. In Proceedings of the 2020 IEEE 29th International Symposium on Industrial Electronics (ISIE), Delft, Netherlands, 17–19 June 2020; pp. 796–801. [Google Scholar]
- Bouarfa, A.; Bodson, M.; Fadel, M. An optimization formulation of converter control and its general solution for the four-leg Two-level inverter. IEEE Trans. Control. Syst. Technol. 2018, 26, 1901–1908. [Google Scholar] [CrossRef]
- Hou, C.; Wang, P.; Chen, C.; Chang, C. Common Mode Voltage Reduction in Four-Leg Inverter with Multicarrier PWM Scheme. In Proceedings of the 2019 10th International Conference on Power Electronics and ECCE Asia (ICPE 2019—ECCE Asia), Busan, Korea, 27–30 May 2019; pp. 3223–3228. [Google Scholar]
- Mandrioli, R.; Viatkin, A.; Hammami, M.; Ricco, M.; Grandi, G. A Comprehensive AC Current Ripple Analysis and Performance Enhancement via Discontinuous PWM in Three-Phase Four-Leg Grid-Connected Inverters. Energies 2020, 13, 4352. [Google Scholar] [CrossRef]
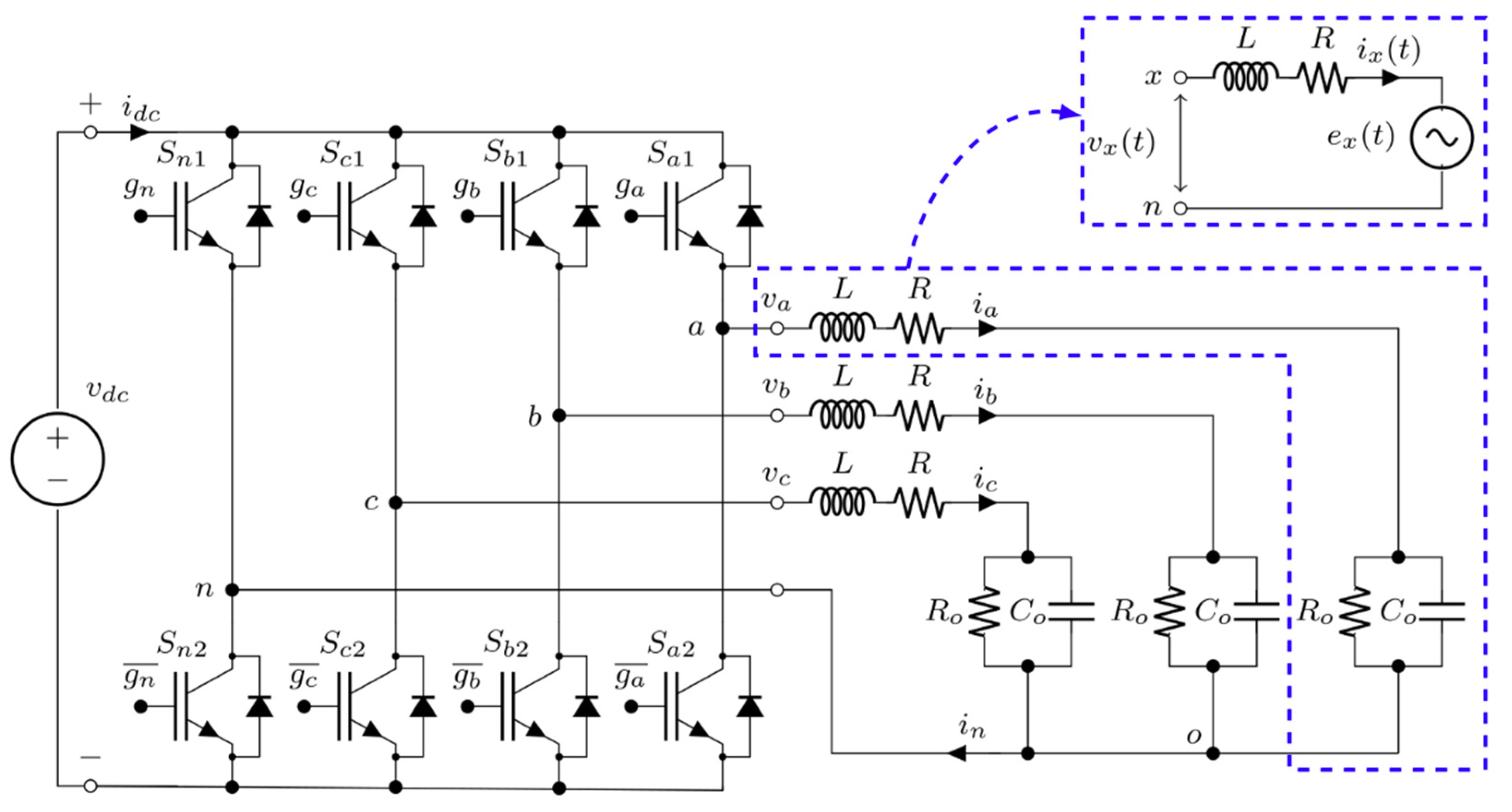
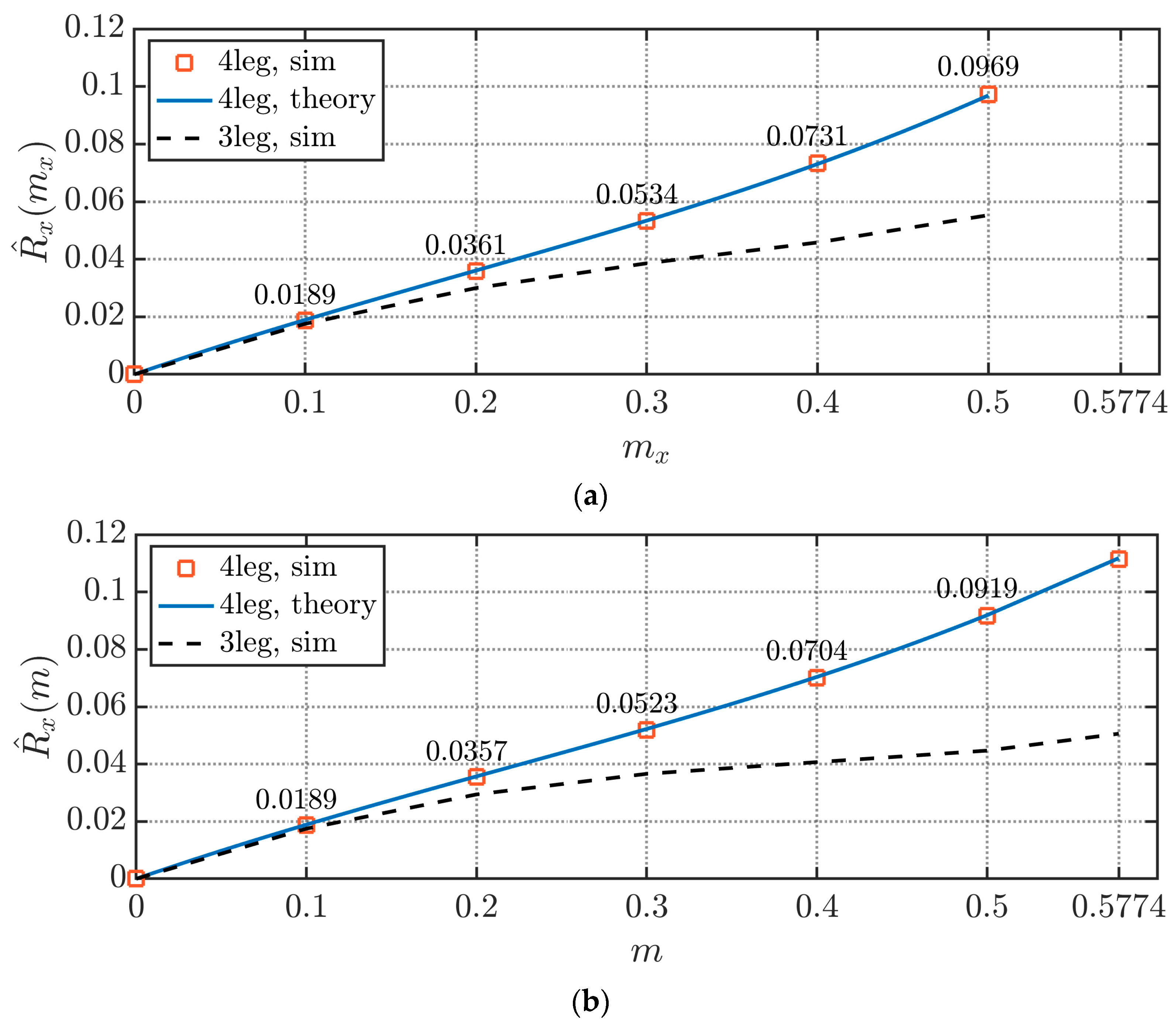
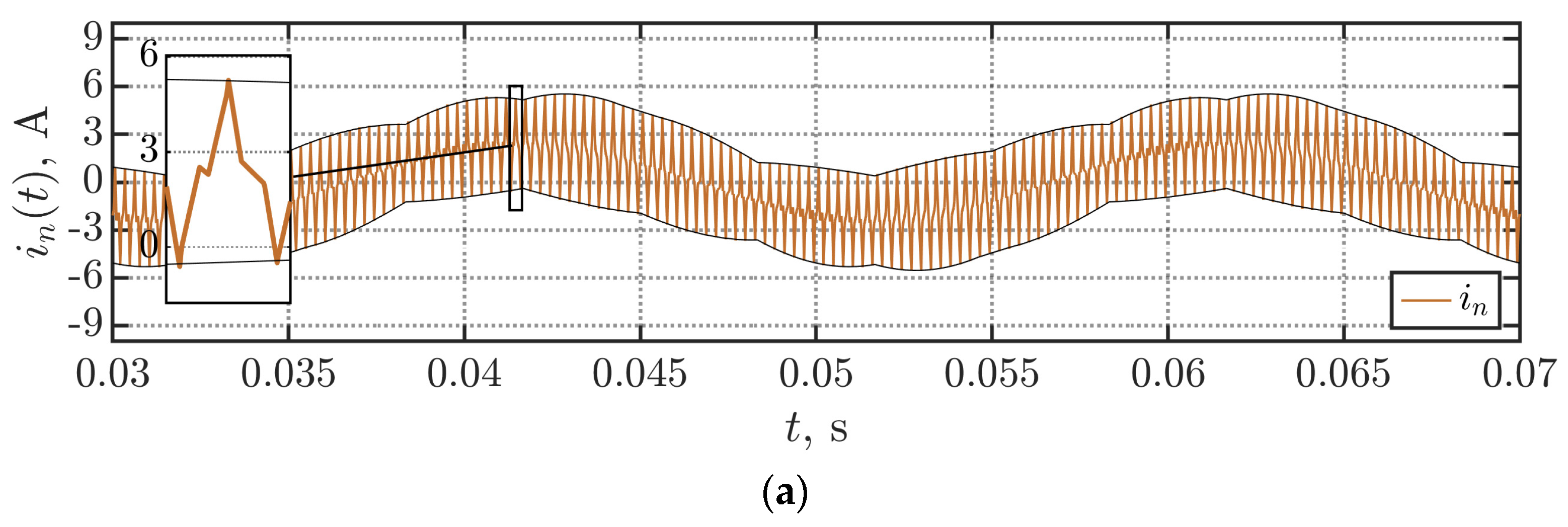
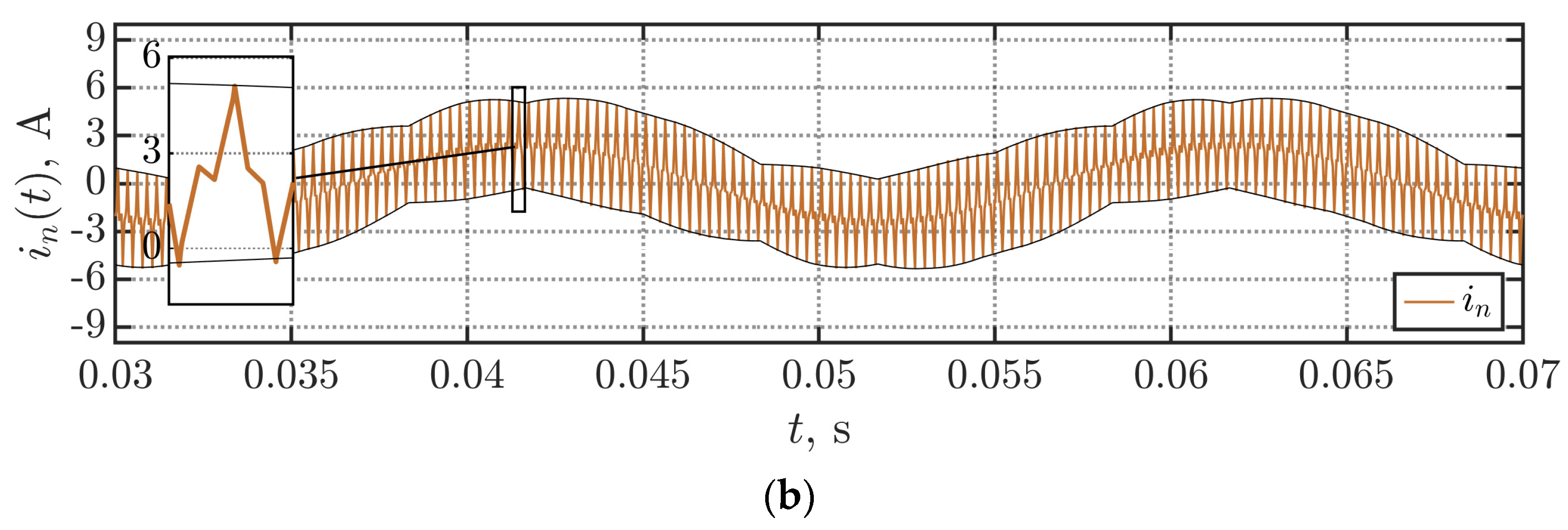
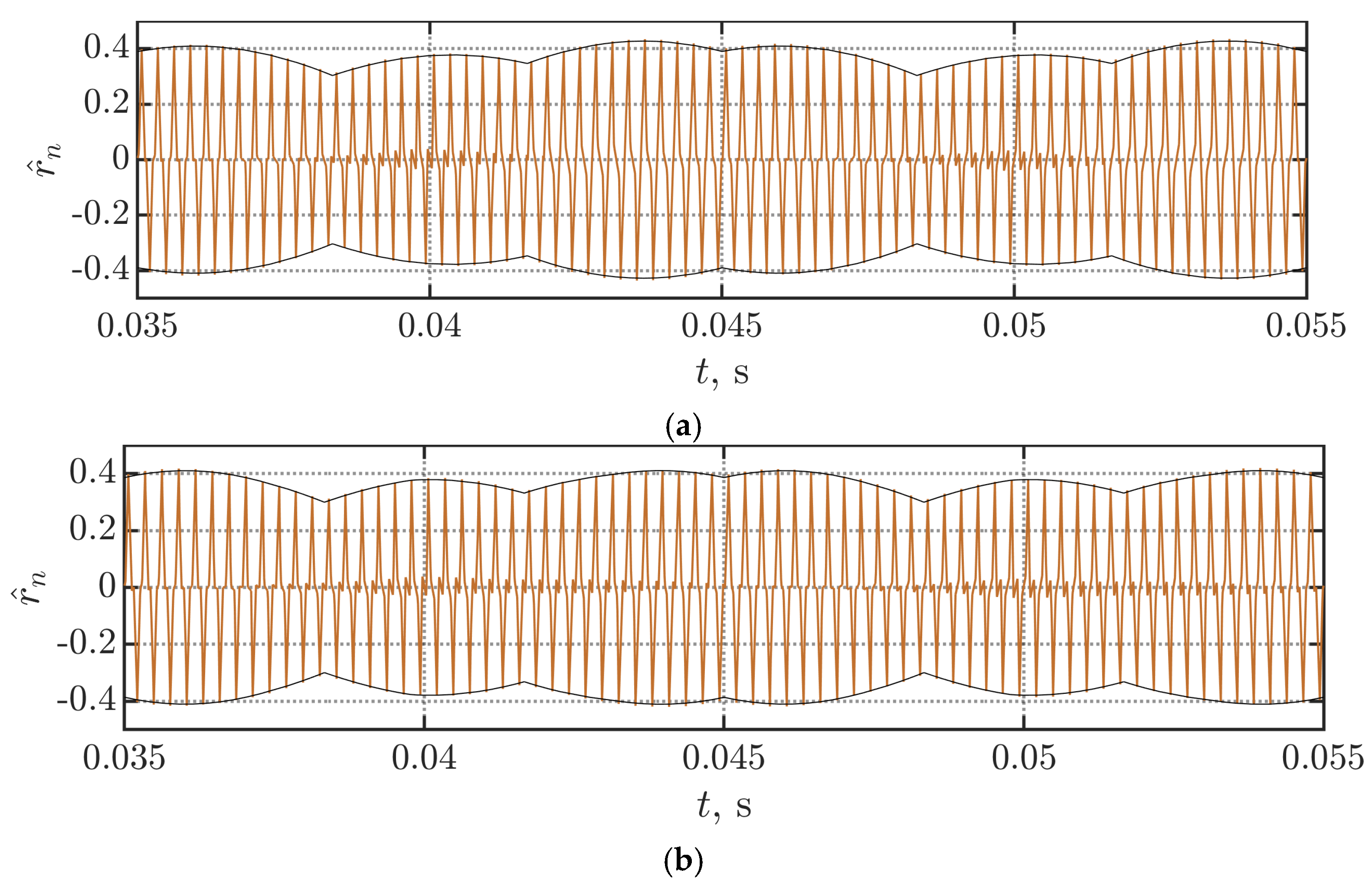
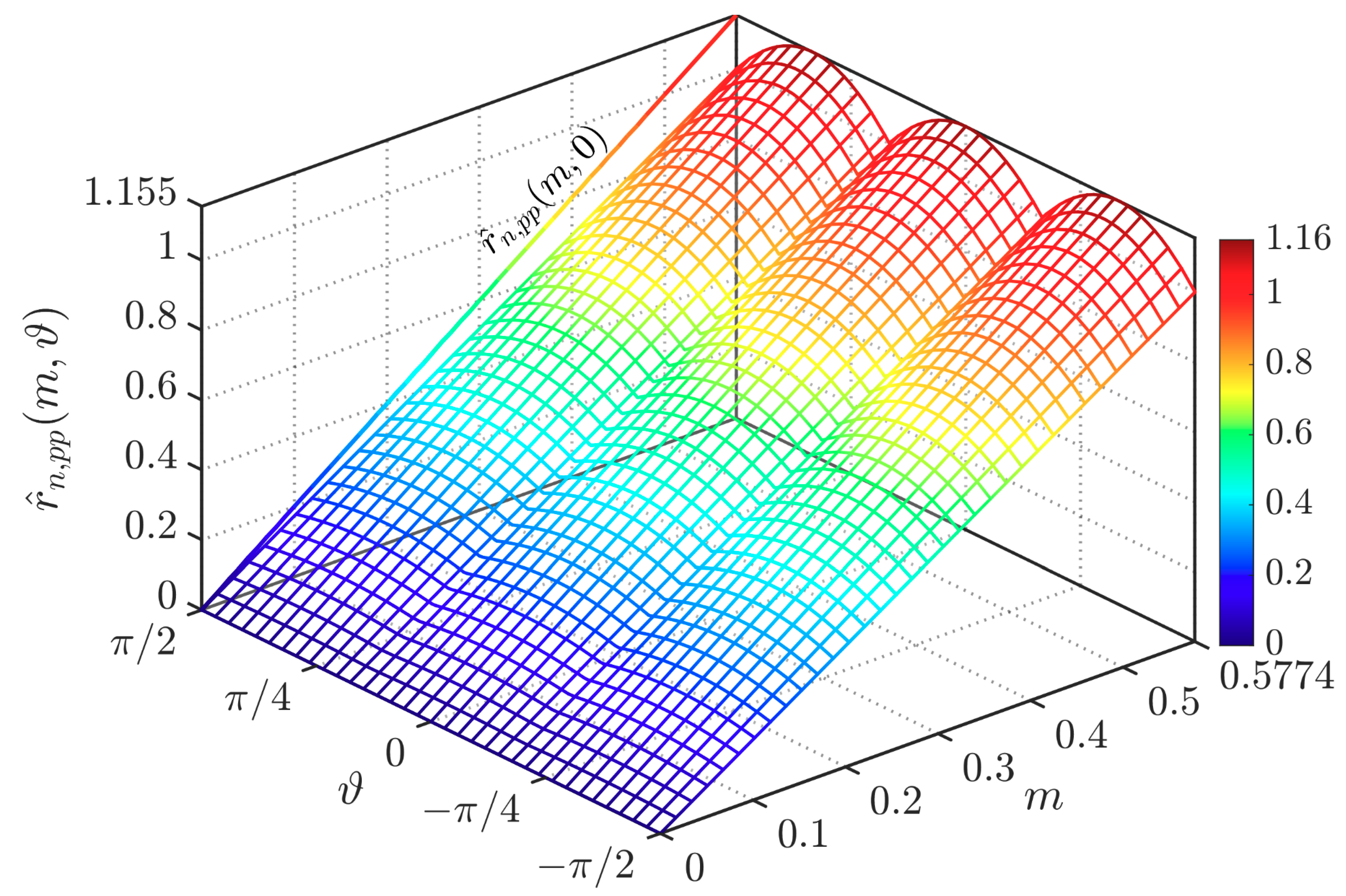



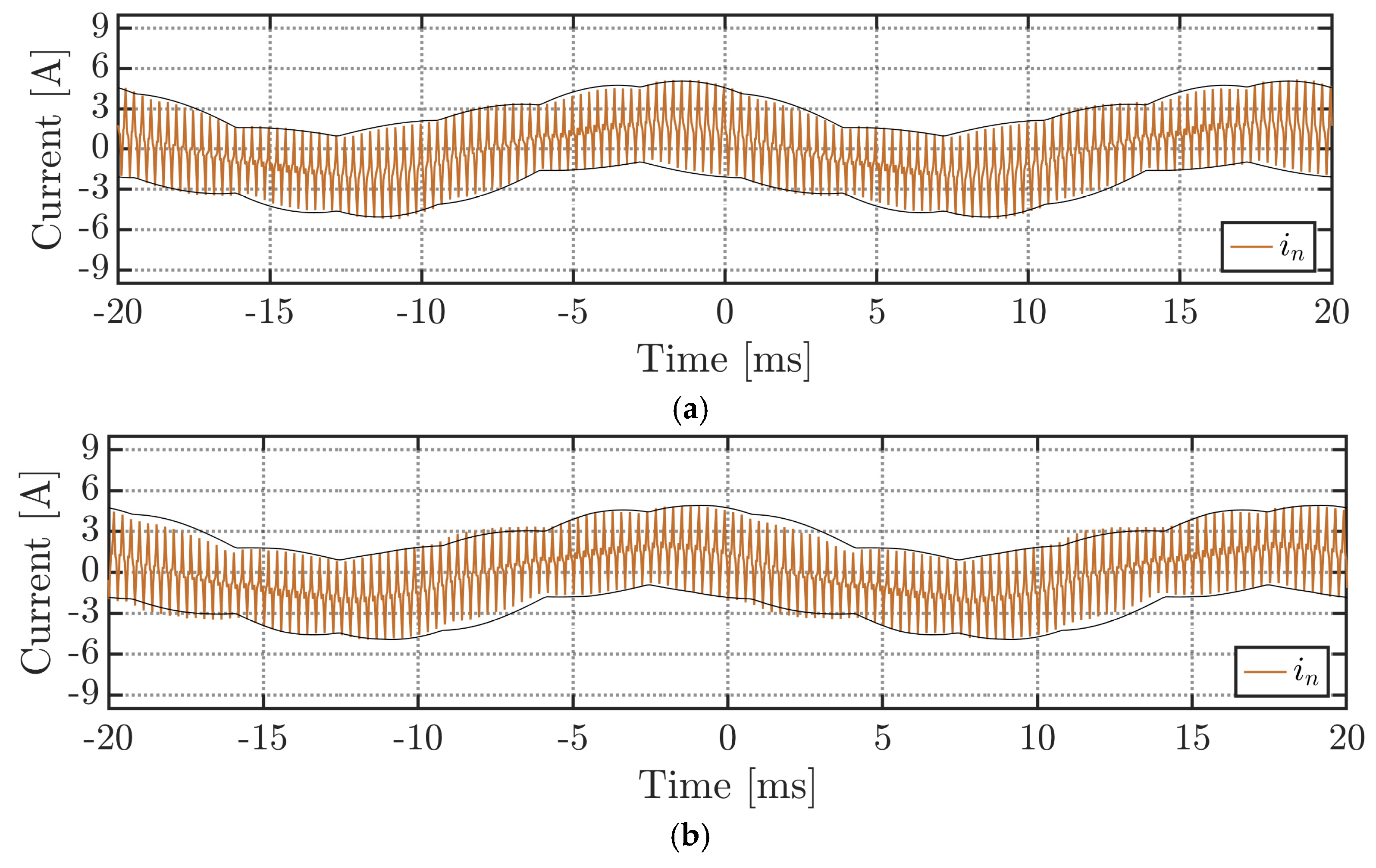
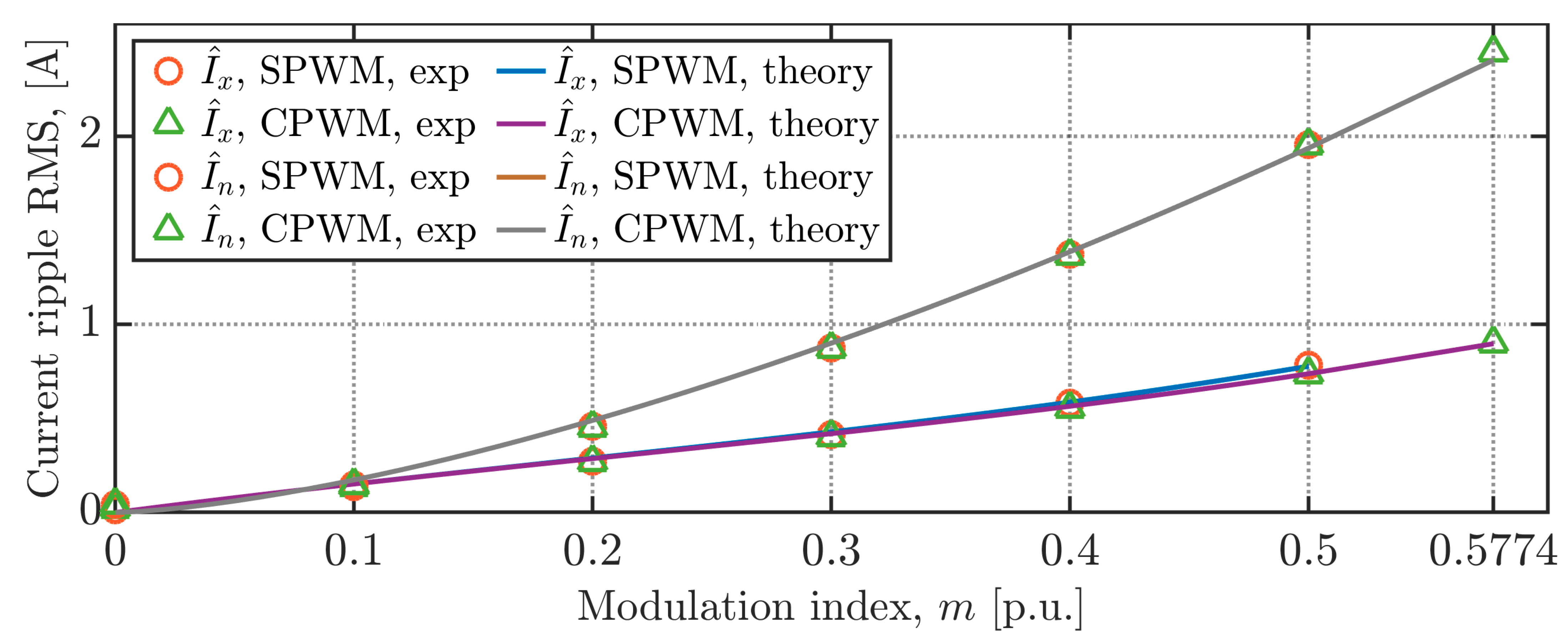

| Parameter | Value |
|---|---|
| Rated DC voltage, Vdc (V) | 100 |
| AC-link inductor parameters: L (mH), R (Ω) | 1.73, 0.727 |
| Passive load parameters: Co (μF), Ro (Ω) | 45, 6.6 |
| Power factor (@ 50 Hz) | 1 |
| Switching frequency, fsw (kHz) | 3.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Viatkin, A.; Mandrioli, R.; Hammami, M.; Ricco, M.; Grandi, G. AC Current Ripple Harmonic Pollution in Three-Phase Four-Leg Active Front-End AC/DC Converter for On-Board EV Chargers. Electronics 2021, 10, 116. https://doi.org/10.3390/electronics10020116
Viatkin A, Mandrioli R, Hammami M, Ricco M, Grandi G. AC Current Ripple Harmonic Pollution in Three-Phase Four-Leg Active Front-End AC/DC Converter for On-Board EV Chargers. Electronics. 2021; 10(2):116. https://doi.org/10.3390/electronics10020116
Chicago/Turabian StyleViatkin, Aleksandr, Riccardo Mandrioli, Manel Hammami, Mattia Ricco, and Gabriele Grandi. 2021. "AC Current Ripple Harmonic Pollution in Three-Phase Four-Leg Active Front-End AC/DC Converter for On-Board EV Chargers" Electronics 10, no. 2: 116. https://doi.org/10.3390/electronics10020116
APA StyleViatkin, A., Mandrioli, R., Hammami, M., Ricco, M., & Grandi, G. (2021). AC Current Ripple Harmonic Pollution in Three-Phase Four-Leg Active Front-End AC/DC Converter for On-Board EV Chargers. Electronics, 10(2), 116. https://doi.org/10.3390/electronics10020116








