A Mixed-Integer Conic Formulation for Optimal Placement and Dimensioning of DGs in DC Distribution Networks
Abstract
:1. Introduction
- ✓
- The guarantee of reaching the global optimum for the problem of the optimal siting and dimensioning of constant power sources in DC grids via an MI-SOCP model solved through B&B and interior-point methods.
- ✓
- The verification of the complexity that the original MINLP model presents in finding the optimal solution using powerful optimization tools available in GAMS. Numerical results in the 21-bus test feeder are optimal based on the GAMS solutions. However, in the 69-bus test feeder case, most of the solvers available in GAMS are stuck in local optimum solutions. This is not the case with the proposed MI-SOCP model, in which global solutions are reached for both test systems.
2. Exact MINLP Model
3. MI-SOCP Reformulation
4. Strategy of Solution
5. Test Feeders
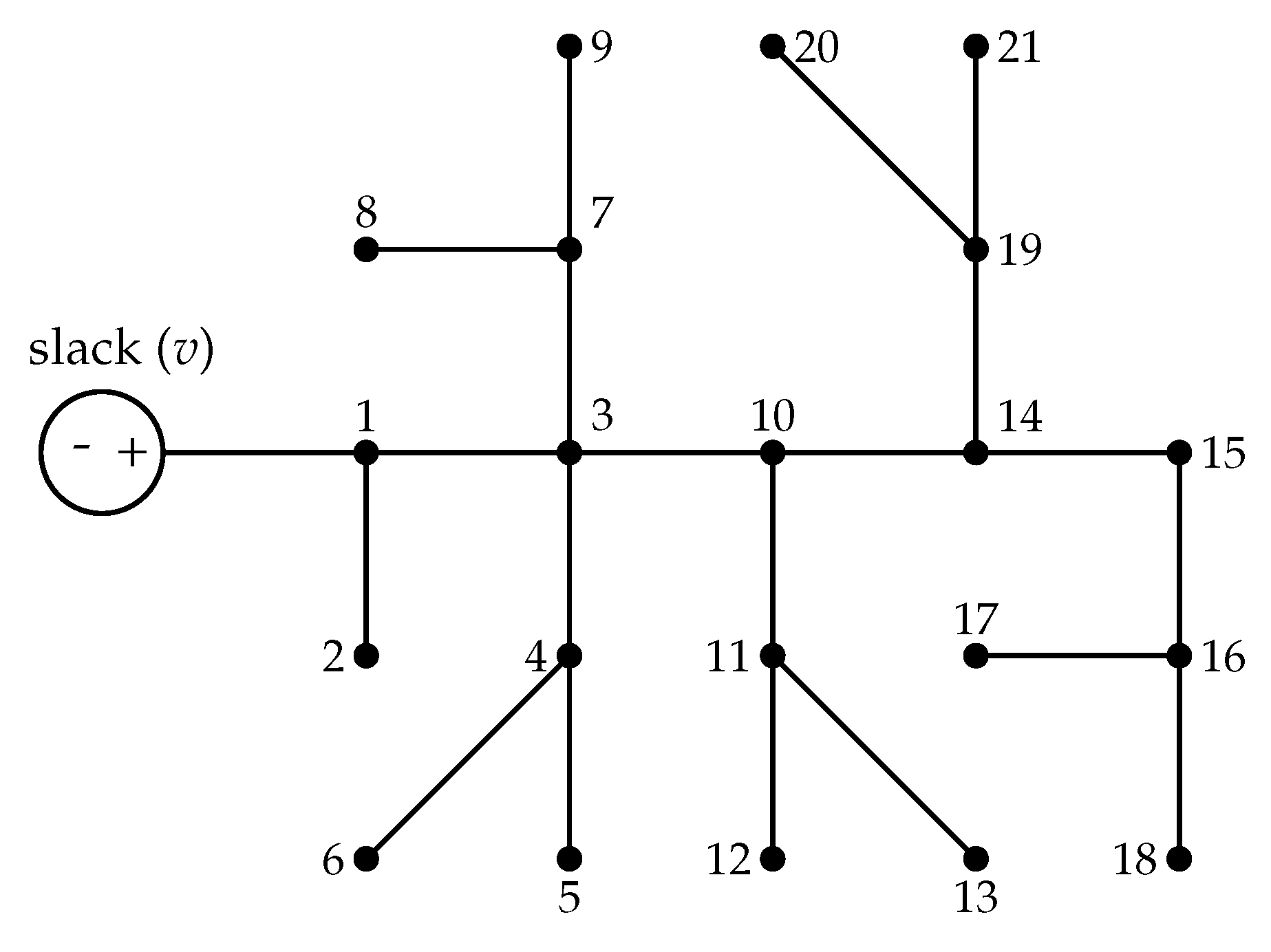
5.1. 21-Bus Test Feeder
5.2. 69-Bus Test Feeder
5.3. Implementation Characteristics of the Test Feeders
6. Computational Implementation
6.1. Solution under the Peak Load Condition
- ✓
- All the comparative solvers in the 21-bus test system reach the same numerical solution reported by the proposed MI-SOCP model, which corresponds to the final power losses of about kW. This confirms that nodes 9, 12 and 16 are the ones nodes associated with the global solution of the problem of siting and dimensioning of DGs in DC grids.
- ✓
- For the 69-bus test feeder, we can highlight that the proposed MI-SOCP reformulation finds the global solution with kW of final power losses. The BONMIN solver is the only solver that reaches this solution since the other optimization tools in GAMS are trapped in local solutions. The best places for locating constant power sources in this test feeder correspond to the nodes 17, 61 and 64, with a total power injection of about kW.
- ✓
- As for the power losses improvement in the 21-bus test system regarding the base case (pu), this was about , while in the 69-bus test feeder (base case with pu) this reduction was about .
- ✓
- Even though the ANTIGONE solver reaches the global solution for the 21-bus test system, it fails in the 69-bus test system because it cannot find a combination of three nodes to minimize power losses; it only identifies one, leaving the other two options free. Therefore, this solver was not reported in the second test feeder.
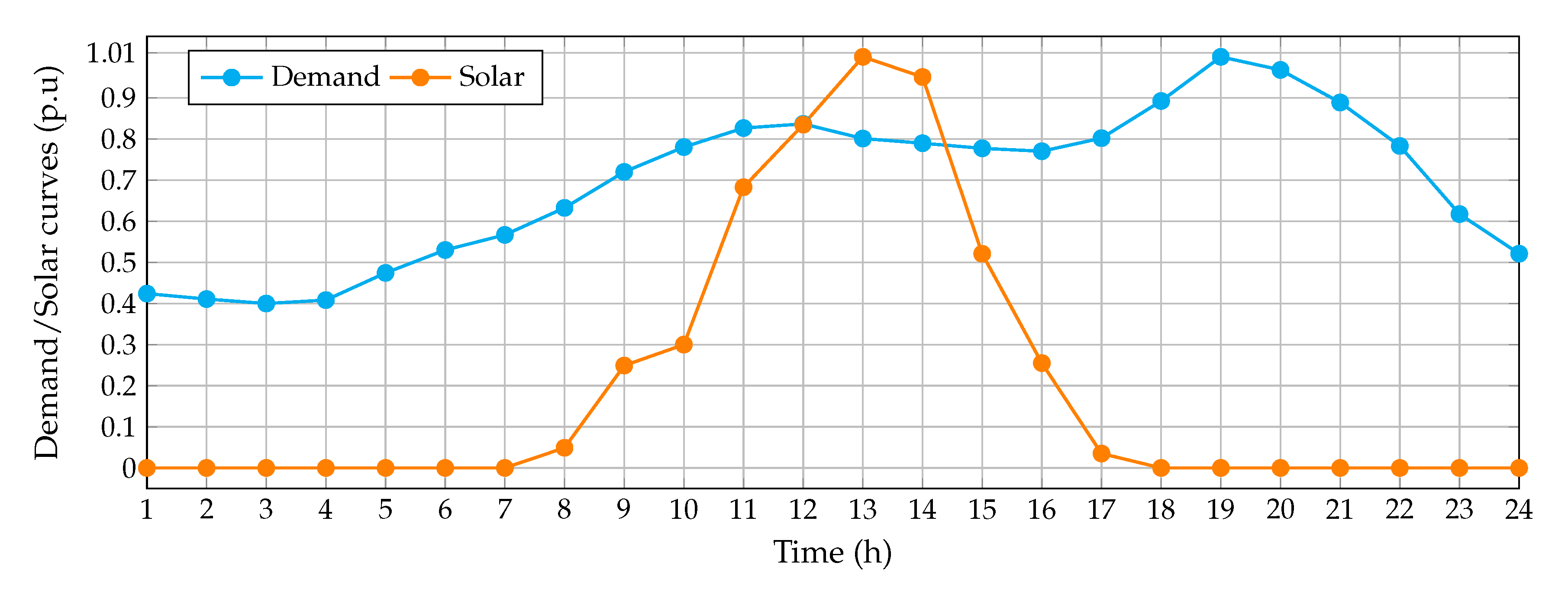
6.2. Solution Considering the Installation of Photovoltaic Generators
7. Conclusions and Future Works
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lotfi, H.; Khodaei, A. AC Versus DC Microgrid Planning. IEEE Trans. Smart Grid 2017, 8, 296–304. [Google Scholar] [CrossRef]
- Simiyu, P.; Xin, A.; Wang, K.; Adwek, G.; Salman, S. Multiterminal Medium Voltage DC Distribution Network Hierarchical Control. Electronics 2020, 9, 506. [Google Scholar] [CrossRef] [Green Version]
- Montoya, O.D.; Gil-González, W.; Grisales-Noreña, L. Relaxed convex model for optimal location and sizing of DGs in DC grids using sequential quadratic programming and random hyperplane approaches. Int. J. Electr. Power Energy Syst. 2020, 115, 105442. [Google Scholar] [CrossRef]
- Murillo-Yarce, D.; Garcés-Ruiz, A.; Escobar-Mejía, A. Passivity-Based Control for DC-Microgrids with Constant Power Terminals in Island Mode Operation. Rev. Fac. Ing. Univ. Antioq. 2018, 32–39. [Google Scholar] [CrossRef]
- Kumar, J.; Agarwal, A.; Agarwal, V. A review on overall control of DC microgrids. J. Energy Storage 2019, 21, 113–138. [Google Scholar] [CrossRef]
- Gao, F.; Kang, R.; Cao, J.; Yang, T. Primary and secondary control in DC microgrids: A review. J. Mod. Power Syst. Clean Energy 2018, 7, 227–242. [Google Scholar] [CrossRef] [Green Version]
- Garcés, A. On the Convergence of Newton’s Method in Power Flow Studies for DC Microgrids. IEEE Trans. Power Syst. 2018, 33, 5770–5777. [Google Scholar] [CrossRef] [Green Version]
- Montoya, O.D. A convex OPF approximation for selecting the best candidate nodes for optimal location of power sources on DC resistive networks. Eng. Sci. Technol. Int. J. 2020, 23, 527–533. [Google Scholar] [CrossRef]
- Montoya, O.D.; Garrido, V.M.; Grisales-Norena, L.F.; Gil-Gonzalez, W.; Garces, A.; Ramos-Paja, C.A. Optimal Location of DGs in DC Power Grids Using a MINLP Model Implemented in GAMS. In Proceedings of the 2018 IEEE 9th Power, Instrumentation and Measurement Meeting (EPIM), Salto, Uruguay, 14–16 November 2018. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W. A MIQP model for optimal location and sizing of dispatchable DGs in DC networks. Energy Syst. 2020. [Google Scholar] [CrossRef]
- Montoya, O.D.; Grisales-Noreña, L.F.; Gil-González, W.; Alcalá, G.; Hernandez-Escobedo, Q. Optimal Location and Sizing of PV Sources in DC Networks for Minimizing Greenhouse Emissions in Diesel Generators. Symmetry 2020, 12, 322. [Google Scholar] [CrossRef] [Green Version]
- Grisales-Noreña, L.F.; Garzon-Rivera, O.D.; Montoya, O.D.; Ramos-Paja, C.A. Hybrid Metaheuristic Optimization Methods for Optimal Location and Sizing DGs in DC Networks. In Communications in Computer and Information Science; Springer: Berlin/Heidelberg, Germany, 2019; pp. 214–225. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Grisales-Noreña, L.F. Hybrid GA-SOCP Approach for Placement and Sizing of Distributed Generators in DC Networks. Appl. Sci. 2020, 10, 8616. [Google Scholar] [CrossRef]
- Altun, T.; Madani, R.; Yadav, A.P.; Nasir, A.; Davoudi, A. Optimal Reconfiguration of DC Networks. IEEE Trans. Power Syst. 2020, 35, 4272–4284. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Hernández, J.C.; Giral-Ramírez, D.A.; Medina-Quesada, A. A Mixed-Integer Nonlinear Programming Model for Optimal Reconfiguration of DC Distribution Feeders. Energies 2020, 13, 4440. [Google Scholar] [CrossRef]
- Li, J.; Liu, F.; Wang, Z.; Low, S.H.; Mei, S. Optimal Power Flow in Stand-Alone DC Microgrids. IEEE Trans. Power Syst. 2018, 33, 5496–5506. [Google Scholar] [CrossRef] [Green Version]
- Gil-González, W.; Montoya, O.D.; Holguín, E.; Garces, A.; Grisales-Noreña, L.F. Economic dispatch of energy storage systems in dc microgrids employing a semidefinite programming model. J. Energy Storage 2019, 21. [Google Scholar] [CrossRef]
- Gil-González, W.; Montoya, O.D.; Grisales-Noreña, L.F.; Cruz-Peragón, F.; Alcalá, G. Economic Dispatch of Renewable Generators and BESS in DC Microgrids Using Second-Order Cone Optimization. Energies 2020, 13, 1703. [Google Scholar] [CrossRef] [Green Version]
- Jannesar, M.R.; Sedighi, A.; Savaghebi, M.; Anvari-Moghaddam, A.; Guerrero, J.M. Optimal probabilistic planning of passive harmonic filters in distribution networks with high penetration of photovoltaic generation. Int. J. Electr. Power Energy Syst. 2019, 110, 332–348. [Google Scholar] [CrossRef]
- Navidi, M.; Tafreshi, S.M.M.; Anvari-Moghaddam, A. A game theoretical approach for sub-transmission and generation expansion planning utilizing multi-regional energy systems. Int. J. Electr. Power Energy Syst. 2020, 118, 105758. [Google Scholar] [CrossRef]
- Khaligh, V.; Anvari-Moghaddam, A. Stochastic expansion planning of gas and electricity networks: A decentralized-based approach. Energy 2019, 186, 115889. [Google Scholar] [CrossRef]
- Montoya, O.D.; Serra, F.M.; Angelo, C.H.D. On the Efficiency in Electrical Networks with AC and DC Operation Technologies: A Comparative Study at the Distribution Stage. Electronics 2020, 9, 1352. [Google Scholar] [CrossRef]
- Garcés, A.; Montoya, O.D. A Potential Function for the Power Flow in DC Microgrids: An Analysis of the Uniqueness and Existence of the Solution and Convergence of the Algorithms. J. Control. Autom. Electr. Syst. 2019, 30, 794–801. [Google Scholar] [CrossRef]
- Gil-González, W.; Molina-Cabrera, A.; Montoya, O.D.; Grisales-Noreña, L.F. An MI-SDP Model for Optimal Location and Sizing of Distributed Generators in DC Grids That Guarantees the Global Optimum. Appl. Sci. 2020, 10, 7681. [Google Scholar] [CrossRef]
- Chen, Y.; Xiang, J.; Li, Y. SOCP Relaxations of Optimal Power Flow Problem Considering Current Margins in Radial Networks. Energies 2018, 11, 3164. [Google Scholar] [CrossRef] [Green Version]
- Hindi, H. A tutorial on convex optimization. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004. [Google Scholar] [CrossRef]
- Alizadeh, F.; Goldfarb, D. Second-order cone programming. Math. Program. 2003, 95, 3–51. [Google Scholar] [CrossRef]
- Jeyakumar, V.; Li, G. Exact Conic Programming Relaxations for a Class of Convex Polynomial Cone Programs. J. Optim. Theory Appl. 2016, 172, 156–178. [Google Scholar] [CrossRef]
- Montoya, O.D.; Molina-Cabrera, A.; Chamorro, H.R.; Alvarado-Barrios, L.; Rivas-Trujillo, E. A Hybrid Approach Based on SOCP and the Discrete Version of the SCA for Optimal Placement and Sizing DGs in AC Distribution Networks. Electronics 2020, 10, 26. [Google Scholar] [CrossRef]
- Gil-González, W.; Garces, A.; Montoya, O.D.; Hernández, J.C. A Mixed-Integer Convex Model for the Optimal Placement and Sizing of Distributed Generators in Power Distribution Networks. Appl. Sci. 2021, 11, 627. [Google Scholar] [CrossRef]
- Nesterov, Y. Lectures on Convex Optimization; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Tuy, H. Convex Analysis and Global Optimization; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar] [CrossRef]
- Benson, H.Y.; Ümit, S. Mixed-Integer Second-Order Cone Programming: A Survey. In Theory Driven by Influential Applications; INFORMS: Catonsville, MD, USA, 2013; pp. 13–36. [Google Scholar] [CrossRef] [Green Version]
- Lobo, M.S.; Vandenberghe, L.; Boyd, S.; Lebret, H. Applications of second-order cone programming. Linear Algebra Appl. 1998, 284, 193–228. [Google Scholar] [CrossRef] [Green Version]
- Nesterov, Y.; Nemirovskii, A. Interior-Point Polynomial Algorithms in Convex Programming; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1994. [Google Scholar] [CrossRef]
- Sturm, J.F. Using SeDuMi 1.02, A Matlab toolbox for optimization over symmetric cones. Optim. Methods Softw. 1999, 11, 625–653. [Google Scholar] [CrossRef]
- Toh, K.C.; Todd, M.J.; Tütüncü, R.H. SDPT3—A Matlab software package for semidefinite programming, Version 1.3. Optim. Methods Softw. 1999, 11, 545–581. [Google Scholar] [CrossRef]
- Grant, M.; Boyd, S. CVX: Matlab Software for Disciplined Convex Programming, Version 2.1. 2014. Available online: http://cvxr.com/cvx (accessed on 9 November 2020).
- Lavaei, J.; Low, S.H. Zero Duality Gap in Optimal Power Flow Problem. IEEE Trans. Power Syst. 2012, 27, 92–107. [Google Scholar] [CrossRef] [Green Version]
- Ridha, H.M.; Gomes, C.; Hizam, H. Estimation of photovoltaic module model’s parameters using an improved electromagnetic-like algorithm. Neural Comput. Appl. 2020, 32, 12627–12642. [Google Scholar] [CrossRef]
- Ćalasan, M.; Mujičić, D.; Rubežić, V.; Radulović, M. Estimation of Equivalent Circuit Parameters of Single-Phase Transformer by Using Chaotic Optimization Approach. Energies 2019, 12, 1697. [Google Scholar] [CrossRef] [Green Version]
- Ćalasan, M.; Micev, M.; Ali, Z.M.; Zobaa, A.F.; Aleem, S.H.E.A. Parameter Estimation of Induction Machine Single-Cage and Double-Cage Models Using a Hybrid Simulated Annealing–Evaporation Rate Water Cycle Algorithm. Mathematics 2020, 8, 1024. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Garces, A. Power flow approximation for DC networks with constant power loads via logarithmic transform of voltage magnitudes. Electr. Power Syst. Res. 2019, 175, 105887. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Orozco-Henao, C. Vortex search and Chu-Beasley genetic algorithms for optimal location and sizing of distributed generators in distribution networks: A novel hybrid approach. Eng. Sci. Technol. Int. J. 2020. [Google Scholar] [CrossRef]



| Bus i | Bus j | (pu) | (pu) | Bus i (pu) | Bus j (pu) | (pu) | (pu) |
|---|---|---|---|---|---|---|---|
| 1 | 2 | 0.0053 | 0.70 | 11 | 12 | 0.0079 | 0.68 |
| 1 | 3 | 0.0054 | 0.00 | 11 | 13 | 0.0078 | 0.10 |
| 3 | 4 | 0.0054 | 0.36 | 10 | 14 | 0.0083 | 0.00 |
| 4 | 5 | 0.0063 | 0.04 | 14 | 15 | 0.0065 | 0.22 |
| 4 | 6 | 0.0051 | 0.36 | 15 | 16 | 0.0064 | 0.23 |
| 3 | 7 | 0.0037 | 0.00 | 16 | 17 | 0.0074 | 0.43 |
| 7 | 8 | 0.0079 | 0.32 | 16 | 18 | 0.0081 | 0.34 |
| 7 | 9 | 0.0072 | 0.80 | 14 | 19 | 0.0078 | 0.09 |
| 3 | 10 | 0.0053 | 0.00 | 19 | 20 | 0.0084 | 0.21 |
| 10 | 11 | 0.0038 | 0.45 | 19 | 21 | 0.0082 | 0.21 |
| Bus i | Bus j | (pu) | (pu) | Bus i (pu) | Bus j (pu) | (pu) | (pu) |
|---|---|---|---|---|---|---|---|
| 1 | 2 | 0.0005 | 0 | 3 | 36 | 0.0044 | 26 |
| 2 | 3 | 0.0005 | 0 | 36 | 37 | 0.0640 | 26 |
| 3 | 4 | 0.0015 | 0 | 37 | 38 | 0.1053 | 0 |
| 4 | 5 | 0.0215 | 0 | 38 | 39 | 0.0304 | 24 |
| 5 | 6 | 0.3660 | 2.6 | 39 | 40 | 0.0018 | 24 |
| 6 | 7 | 0.3810 | 40.4 | 40 | 41 | 0.7283 | 102 |
| 7 | 8 | 0.0922 | 75 | 41 | 42 | 0.3100 | 0 |
| 8 | 9 | 0.0493 | 30 | 42 | 43 | 0.0410 | 6 |
| 9 | 10 | 0.8190 | 28 | 43 | 44 | 0.0092 | 0 |
| 10 | 11 | 0.1872 | 145 | 44 | 45 | 0.1089 | 39.22 |
| 11 | 12 | 0.7114 | 145 | 45 | 46 | 0.0009 | 39.22 |
| 12 | 13 | 1.0300 | 8 | 4 | 47 | 0.0034 | 0 |
| 13 | 14 | 1.0440 | 8 | 47 | 48 | 0.0851 | 79 |
| 14 | 15 | 1.0580 | 0 | 48 | 49 | 0.2898 | 384.7 |
| 15 | 16 | 0.1966 | 45 | 49 | 50 | 0.0822 | 384.7 |
| 16 | 17 | 0.3744 | 60 | 8 | 51 | 0.0928 | 40.5 |
| 17 | 18 | 0.0047 | 60 | 51 | 52 | 0.3319 | 3.6 |
| 18 | 19 | 0.3276 | 0 | 9 | 53 | 0.1740 | 4.35 |
| 19 | 20 | 0.2106 | 1 | 53 | 54 | 0.2030 | 26.4 |
| 20 | 21 | 0.3416 | 114 | 54 | 55 | 0.2842 | 24 |
| 21 | 22 | 0.0140 | 5 | 55 | 56 | 0.2813 | 0 |
| 22 | 23 | 0.1591 | 0 | 56 | 57 | 1.5900 | 0 |
| 23 | 24 | 0.3463 | 28 | 57 | 58 | 0.7837 | 0 |
| 24 | 25 | 0.7488 | 0 | 58 | 59 | 0.3042 | 100 |
| 25 | 26 | 0.3089 | 14 | 59 | 60 | 0.3861 | 0 |
| 26 | 27 | 0.1732 | 14 | 60 | 61 | 0.5075 | 1244 |
| 3 | 28 | 0.0044 | 26 | 61 | 62 | 0.0974 | 32 |
| 28 | 29 | 0.0640 | 26 | 62 | 63 | 0.1450 | 0 |
| 29 | 30 | 0.3978 | 0 | 63 | 64 | 0.7105 | 227 |
| 30 | 31 | 0.0702 | 0 | 64 | 65 | 1.0410 | 59 |
| 31 | 32 | 0.3510 | 0 | 65 | 66 | 0.2012 | 18 |
| 32 | 33 | 0.8390 | 10 | 66 | 67 | 0.0047 | 18 |
| 33 | 34 | 1.7080 | 14 | 67 | 68 | 0.7394 | 28 |
| 34 | 35 | 1.4740 | 4 | 68 | 69 | 0.0047 | 28 |
| 21-Bus Test Feeder | |||
|---|---|---|---|
| Solver | Location (Nodes) | Size(pu) | (pu) |
| ALPHAECP | |||
| ANTIGONE | |||
| BARON | |||
| BONMIN | |||
| DICOPT | |||
| SBB | |||
| MI-SOCP | |||
| 69-Bus Test Feeder | |||
| Solver | Location(Nodes) | Size (pu) | (pu) |
| ALPHAECP | |||
| BARON | |||
| BONMIN | |||
| COUENNE | |||
| DICOPT | |||
| SBB | |||
| MI-SOCP | |||
| No. of PVs | Location (Nodes) | Size (kW) | En. Losses (kWh/Day) | Proc. Time (s) |
|---|---|---|---|---|
| 0 | 1838.5218 | 63.73 | ||
| 1 | 1255.0827 | 75.70 | ||
| 2 | 1215.2164 | 95.22 | ||
| 3 | 1208.7995 | 233.16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Molina-Martin, F.; Montoya, O.D.; Grisales-Noreña, L.F.; Hernández, J.C. A Mixed-Integer Conic Formulation for Optimal Placement and Dimensioning of DGs in DC Distribution Networks. Electronics 2021, 10, 176. https://doi.org/10.3390/electronics10020176
Molina-Martin F, Montoya OD, Grisales-Noreña LF, Hernández JC. A Mixed-Integer Conic Formulation for Optimal Placement and Dimensioning of DGs in DC Distribution Networks. Electronics. 2021; 10(2):176. https://doi.org/10.3390/electronics10020176
Chicago/Turabian StyleMolina-Martin, Federico, Oscar Danilo Montoya, Luis Fernando Grisales-Noreña, and Jesus C. Hernández. 2021. "A Mixed-Integer Conic Formulation for Optimal Placement and Dimensioning of DGs in DC Distribution Networks" Electronics 10, no. 2: 176. https://doi.org/10.3390/electronics10020176
APA StyleMolina-Martin, F., Montoya, O. D., Grisales-Noreña, L. F., & Hernández, J. C. (2021). A Mixed-Integer Conic Formulation for Optimal Placement and Dimensioning of DGs in DC Distribution Networks. Electronics, 10(2), 176. https://doi.org/10.3390/electronics10020176








