Assessment of Cable Length Limit for Effective Protection by Z-Source Circuit Breakers in DC Power Networks
Abstract
:1. Introduction
1.1. DC Network Development and Protection Solutions
1.2. The State of the Art of Z-Source Circuit Breakers
2. Demonstration of ZCB’s Performance “with” and “without” Line Parameter Considerations
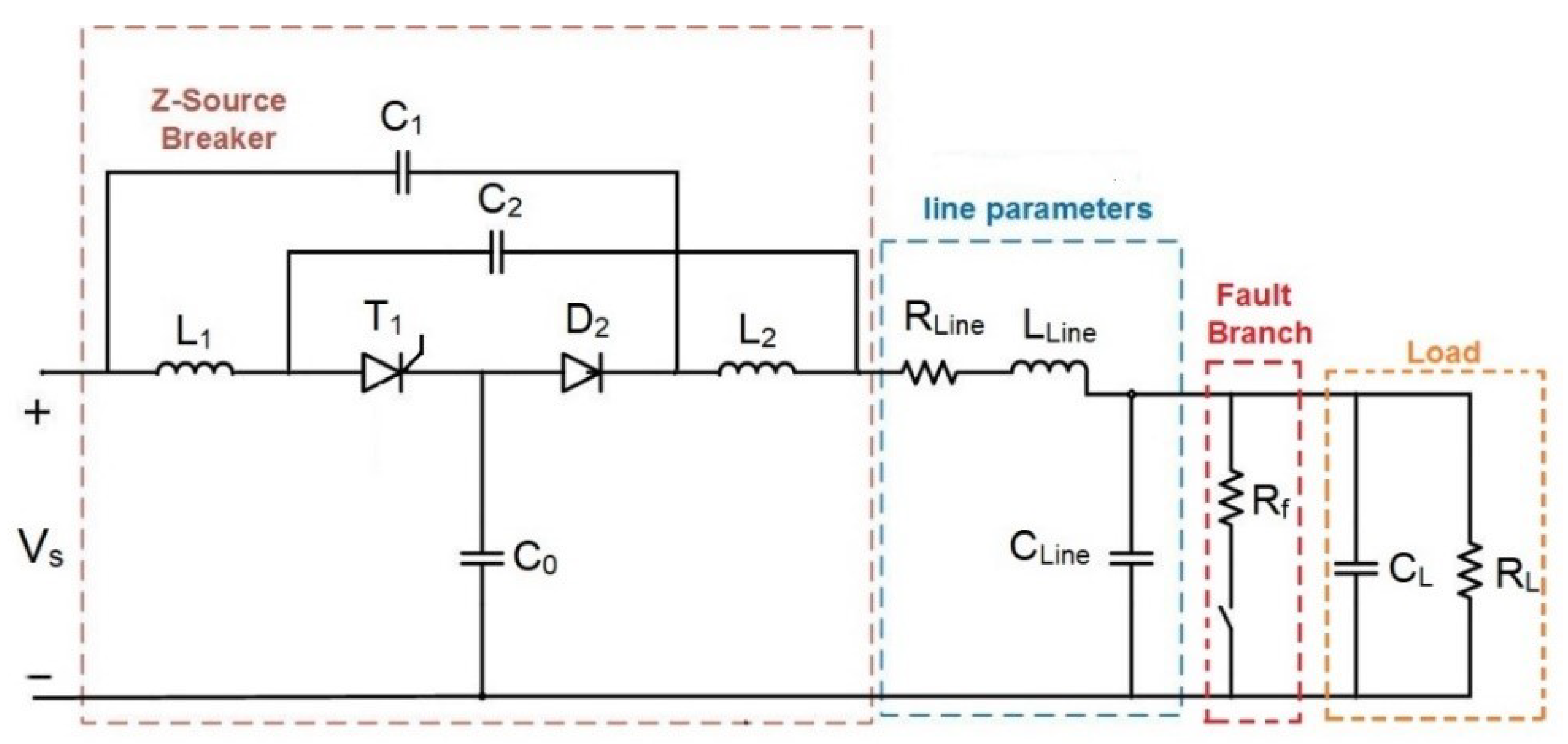
2.1. Specification of ZCB Parameters
- iscr is the current of SCR in amps;
- C is the Z-source capacitance for C0, C1, and C2, in farads;
- Iload is the load current, in amps;
- CL is the load capacitance, in farads;
- k is the minimum detectable fault ramp rate, in ;
- vs. is the source voltage, in volts;
- L is the Z-source inductance for L1 and L2, in henries;
- t is the time after a fault occurs, in seconds.
- Rf_max is the maximum detectable fault resistance in ;
- ttripping is the desired tripping time, in seconds.
2.2. Demonstration of Effects of Cable Length on ZCB’s Performance
- (1)
- The cable length does have an influence on the effectiveness of ZCBs, which can be observed in Figure 2b.
- (2)
- The fault current level has an impact on the ZCB’s performance. With the same cable length of 75 m, the ZCB does not turn off at Rf = 1.0 p.u., while it turns off in the other two cases.
2.3. Proposed Method of Cable Length Limit (CLL) Assessment
- (1)
- By applying the “Г” model of a power cable, the LLine can be combined into the L2 of the ZCB for the analysis of the ZCB’s operation. According to the numerical analysis in [22,26], there is a big margin in L2, and thus, the effect of LLine on the ZCB’s behavior is very limited and can be neglected for assessing the CLL.
- (2)
- (3)
- In addition, the RLine is connected in series in the fault circuit and would attenuate the resonance of an LC circuit, which contributes to the reverse current for the SCR’s turning off. Therefore, RLine has a negative effect on the ZCB’s operation and must be included in the assessment of the CLL too.
- Step 1:
- identify the ZCB parameters based on the prior-art methods, without considering the influence of the power cable.
- Step 2:
- build a model of the physical model (as shown Figure 1) in a simulation tool, e.g., the Matlab/Simulink environment applied here. Set the ZCB parameters from Step 1 in the simulation model. Set the cable parameters as a function of the cable length into the simulation model.
- Step 3:
- perform a number of simulations to check the impact of different quantities on the ZCB’s turnoff behavior. The quantities include the cable length, fault resistance (i.e., fault levels), and load amount (i.e., power delivery levels).
- Step 4:
- determine the CLL by analyzing the simulation results.
3. Assessing Cable Length Limit Depending on Fault Levels
4. Assessing Cable Length Limit Depending on Power Delivery Levels
4.1. Effective Protection for Various Power Delivery Conditions
- (a)
- As the value of Rf increases under a certain load, the effective protection by the breaker reduces accordingly. This is the same conclusion as the one from Section 3. This conclusion does not change with the power delivery level.
- (b)
- For a constant Rf, the breaker is able to respond to the fault at a longer distance in the case of a lower load-power requirement and vice versa. In other words, a lower power delivery level leads to a higher CLL. Therefore, for a long-distance, high-power condition, multi-line power delivery can be a solution for increasing the CLL and thus maintaining effective protection by ZCBs in DC networks.
4.2. Verification and Generation of CLL Curves
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Corzine, K.A.; Ashton, R.W. A new Z-source DC circuit breaker. IEEE Trans. Power Electron. 2012, 27, 2796–2804. [Google Scholar] [CrossRef]
- Chang, A.H.; Sennett, B.R.; Avestruz, A.-T.; Leeb, S.B.; Kirtley, J.L. Analysis and design of DC system protection using Z-source circuit breaker. IEEE Trans. Power Electron. 2016, 31, 1036–1049. [Google Scholar] [CrossRef]
- Cuzner, R.M.; Venkataramanan, G. The status of DC micro-grid protection. In Proceedings of the IEEE 2008 Industry Applications Society Annual Meeting (IAS’08), Edmonton, AB, Canada, 5–9 October 2008; pp. 1–8. [Google Scholar]
- Lee, S.; Kim, H. A study on Low-Voltage DC circuit breakers. In Proceedings of the IEEE 2013 International Symposium on Industrial Electronics (ISIE), Taipei, Taiwan, 28–31 May 2013; pp. 1–6. [Google Scholar]
- Ganhao, Z. Study on DC circuit breaker. In Proceedings of the IEEE 2014 Fifth International Conference on Intelligent Systems Design and Engineering Applications (ISDEA), Hunan, China, 15–16 June 2014; pp. 942–945. [Google Scholar]
- Ma, R.; Rong, M.; Yang, F.; Wu, Y.; Sun, H.; Yuan, D.; Wang, H.; Niu, C. Investigation on arc behavior during arc motion in air DC circuit breaker. IEEE Trans. Plasma Sci. 2013, 41, 2551–2560. [Google Scholar] [CrossRef]
- Lee, K.A.; Cho, Y.M.; Lee, H.J. Circuit Model and Analysis of Molded Case Circuit Breaker Interruption Phenomenon. Electronics 2020, 9, 2047. [Google Scholar] [CrossRef]
- Cho, Y.M.; Lee, K.A. Experimental Study on Splitter Plate for Improving the Dielectric Recovery Strength of Low-Voltage Circuit Breaker. Electronics 2020, 9, 2148. [Google Scholar] [CrossRef]
- Liljestrand, L.; Backman, M.; Jonsson, L.; Dullni, E.; Riva, M. Medium voltage DC vacuum circuit breaker. In Proceedings of the IEEE 2015 3rd International Conference on Electric Power Equipment–Switching Technology (ICEPE-ST), Busan, Korea, 25–28 October 2015; pp. 495–500. [Google Scholar]
- Polman, H.; Ferreira, J.A.; Kaanders, M.; Evenblij, B.H.; Gelder, P.V. Design of a bi-directional 600 V/6 kA ZVS hybrid DC switch using IGBTS. In Proceedings of the Conference Record of the 2001 IEEE Industry Applications Conference. 36th IAS Annual Meeting (Cat. No.01CH37248), Chicago, IL, USA, 30 September–4 October 2001; Volume 2, pp. 1052–1059. [Google Scholar]
- Meyer, J.M.; Rufer, A. A DC hybrid circuit breaker with ultrafast contact opening and integrated gate-commutated thyristors (IGCTS). IEEE Trans. Power Del. 2006, 21, 646–651. [Google Scholar] [CrossRef]
- Hassanpoor, A.; Hfner, J.; Jacobson, B. Technical assessment of load commutation switch in hybrid HVDC breaker. IEEE Trans. Power Electron. 2015, 30, 5393–5400. [Google Scholar] [CrossRef]
- Song, X.; Peng, C.; Huang, A. A medium voltage hybrid DC circuit breaker—Part I: Solid state main breaker based on 15 kV SiC Emitter Turn-off (ETO) thyristor. IEEE J. Emerg. Sel. Topics Power Electron. 2017, 5, 278–288. [Google Scholar] [CrossRef]
- Dring, D.; Ergin, D.; Wrflinger, K.; Dorn, J.; Schettler, F.; Spahic, E. System integration aspects of dc circuit breakers. IET Power Electron. 2016, 9, 219–227. [Google Scholar] [CrossRef]
- Bsche, D.; Wikening, E.D.; Kpf, H.; Kurrat, M. Hybrid dc circuit breaker feasibility study. IEEE Trans. Compon. Packag. Manuf. Technol. 2017, 7, 354–362. [Google Scholar]
- Shen, Z.J.; Miao, Z.; Roshandeh, A.M. Solid state circuit breakers for DC micrgrids: Current status and future trends. In Proceedings of the IEEE 2015 First International Conference on DC Microgrids (ICDCM), Atlanta, GA, USA, 7–10 June 2015; pp. 228–233. [Google Scholar]
- Peng, F.Z. Z-source inverter. In Proceedings of the Conference Record of the 2002 IEEE Industry Applications Conference. 37th IAS Annual Meeting (Cat. No.02CH37344), Pittsburgh, PA, USA, 13–18 October 2002; Volume 2, pp. 775–781. [Google Scholar]
- Nozadian, M.H.B.; Babaei, E.; Hosseini, S.H.; Asl, E.S. Switched Z-soirce networks: A review. IET Power Electron. 2019, 12, 1616–1633. [Google Scholar]
- Corzine, K.A.; Ashton, R.W. Structure and analysis of the Z-source MVDC breaker. In Proceedings of the IEEE 2011 Electric Ship Technologies Symposium (ESTS), Alexandria, VA, USA, 10–13 April 2011; pp. 334–338. [Google Scholar]
- Ryan, D.J.; Torresan, H.D.; Bahrani, B. A Bi-Directional Series Z-Source Circuit Breaker. IEEE Trans. Power Electron. 2017, 33, 7609–7621. [Google Scholar]
- Savaliya, S.G.; Fernandes, B.G. Analysis and Experimental Validation of Bidirectional Z-Source DC Circuit Breakers. IEEE Trans. Ind. Electron. 2019, 67, 4613–4622. [Google Scholar] [CrossRef]
- Keshavarzi, D.; Ghanbari, T.; Farjah, E. A Z-Source-Based Bidirectional DC Circuit Breaker with Fault Current Limitation and Interruption Capabilities. IEEE Trans. Power Electron. 2017, 32, 6813–6822. [Google Scholar] [CrossRef]
- Bhatta, S.; Fu, R.; Zhang, Y. A New Method of Detecting & Interrupting High-Impedance Faults by Specifying the Z-Source Breaker in Modern Power Systems. Electronics 2020, 9, 1654. [Google Scholar] [CrossRef]
- Bhatta, S.; Fu, R.; Zhang, Y. Detecting High-Impedance Fault with Z-Source Circuit Breakers in Smart Grids. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC 2020), New Orleans, LA, USA, 15–19 March 2020; pp. 1755–1761. [Google Scholar]
- Bhatta, S.; Zhang, Y.; Fu, R. Comparative Analysis of Power Loss Associated with Topology of Bi-Directional Z-Source Circuit Breakers. In Proceedings of the IEEE 2018 SoutheastCon 2018, St. Petersburg, FL, USA, 19–22 April 2018; pp. 1–5. [Google Scholar]
- Bhatta, S.; Zhang, Y.; Fu, R. Relationship of Steady-State Power Loss and Configurable Tripping Time in Z-Source Circuit Breakers. In Proceedings of the IEEE 2019 Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 3483–3489. [Google Scholar]
- Teppoz, L.; Bornard, G.; Besancon, G. Discrete-time control design for an hvdc transmission between two infinite buses. IFAC Proc. 2004, 37, 1057–1062. [Google Scholar] [CrossRef]
- Thomas, J.L.; Poullain, S.; Benchaib, A. Analysis of a robust DC-bus voltage control system for a VSC transmission scheme. In Proceedings of the IEE International Conf. on AC-DC Power Transmission, London, UK, 28–30 November 2001; pp. 119–124. [Google Scholar]
- Sabatier, J.; Youssef, T.; Pellet, M. An HVDC line parameters estimation method without optimization. Int. J. Electr. Power Energy Syst. 2016, 83, 541–546. [Google Scholar] [CrossRef]





| Parameters | Value | Remarks | |
|---|---|---|---|
| Z-Source Breaker Components | C0 = C1 = C2 = CZCB | 369 µF | Z-Source Capacitors |
| L1 = L2 = LZCB | 76.9 µH | Z-Source Inductors | |
| Source and Load Parameters | VS | 5 kV | Source Voltage |
| PL | 5 MW | Load Power | |
| RL | 5 Ω | Load Resistance | |
| CL | 20.25 µF | Load Capacitance | |
| Cable Line Parameters | r | 3.0 × 10−2 Ω km−1 | Line Series Resistance |
| l | 1.05 × 10−3 H km−1 | Line Series Inductance | |
| c | 11 × 10−9 F km−1 | Line Shunt Capacitance | |
| Fault Branch | Rf_Base | 5 Ω | Fault Resistance Base |
| Model | Rated Power | Rated Voltage | Rated Current |
|---|---|---|---|
| Prysmian Group DC Power Cables (XLPE, P-Laser, MI-paper, and MI-PPL paper) | 2400 MW–4000 MW | 525 kV–800 kV | 4.57 kA–5.6 kA |
| Phoenix Contact DC Cables | 2 kW–200 kW | 600 kV–1.0 kV | 2 A–200 A |
| Amphenol SINE Systems DC Power Cords | 7.8 kW–18 kW | 600 V | 13 A–30 A |
| Molex Power Cables | 3 kW–40 kW | 600 kV–1.0 kV | 5 A–40 A |
| Rf (in p.u.) | Rf_Actual (in Ω) | Cable Length Limit (CLL, in m) | Actual Line Parameters | ||
|---|---|---|---|---|---|
| RLine (in mΩ) | CLine (in nF) | LLine (in mH) | |||
| 0.10 | 0.50 | 485.80 | 14.55 | 5.34 | 0.51 |
| 0.20 | 1.00 | 375.52 | 11.25 | 4.13 | 0.39 |
| 0.50 | 2.50 | 200.45 | 6.00 | 2.20 | 0.21 |
| 0.80 | 4.00 | 115.64 | 3.45 | 1.27 | 0.12 |
| 1.00 | 5.00 | 70.25 | 2.10 | 0.77 | 0.07 |
| Power Delivery Level (PL) | Load Current (IL) | C0 = C1 = C2 = CZCB | L1 = L2 = LZCB | RF_base |
|---|---|---|---|---|
| 75 kW | 15 A | 5.54 μF | 5.13 mH | 333.33 Ω |
| 100 kW | 20 A | 7.38 μF | 3.85 mH | 250.00 Ω |
| 500 kW | 100 A | 36.90 μF | 0.77 mH | 50.00 Ω |
| 5000 kW | 1000 A | 369.00 μF | 0.07 mH | 5.00 Ω |
| RF (p.u) | RF_Actual (Ω) | Cable Length Limit (CLL, in km) | ||||||
|---|---|---|---|---|---|---|---|---|
| 75 kW | 100 kW | 500 kW | 5 MW | 75 kW | 100 kW | 500 kW | 5 MW | |
| 0.05 | 16.67 | 12.50 | 2.50 | 0.25 | 35.67 | 26.75 | 5.35 | 0.54 |
| 0.25 | 83.33 | 62.50 | 12.50 | 1.25 | 23.80 | 17.85 | 3.57 | 0.36 |
| 0.50 | 166.67 | 125.00 | 25.00 | 2.50 | 14.54 | 10.90 | 2.18 | 0.22 |
| 0.75 | 250.00 | 187.50 | 37.50 | 3.75 | 8.67 | 6.50 | 1.30 | 0.13 |
| 0.88 | 291.67 | 218.75 | 43.75 | 4.37 | 6.53 | 4.90 | 0.98 | 0.10 |
| 1.00 | 333.33 | 250.00 | 50.00 | 5.00 | 4.67 | 3.50 | 0.70 | 0.07 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, R.; Bhatta, S.; Keller, J.M.; Zhang, Y. Assessment of Cable Length Limit for Effective Protection by Z-Source Circuit Breakers in DC Power Networks. Electronics 2021, 10, 183. https://doi.org/10.3390/electronics10020183
Fu R, Bhatta S, Keller JM, Zhang Y. Assessment of Cable Length Limit for Effective Protection by Z-Source Circuit Breakers in DC Power Networks. Electronics. 2021; 10(2):183. https://doi.org/10.3390/electronics10020183
Chicago/Turabian StyleFu, Ruiyun, Sagar Bhatta, Joseph M. Keller, and Yucheng Zhang. 2021. "Assessment of Cable Length Limit for Effective Protection by Z-Source Circuit Breakers in DC Power Networks" Electronics 10, no. 2: 183. https://doi.org/10.3390/electronics10020183
APA StyleFu, R., Bhatta, S., Keller, J. M., & Zhang, Y. (2021). Assessment of Cable Length Limit for Effective Protection by Z-Source Circuit Breakers in DC Power Networks. Electronics, 10(2), 183. https://doi.org/10.3390/electronics10020183




