Two-Stage Modulation Study for DAB Converter
Abstract
:1. Introduction
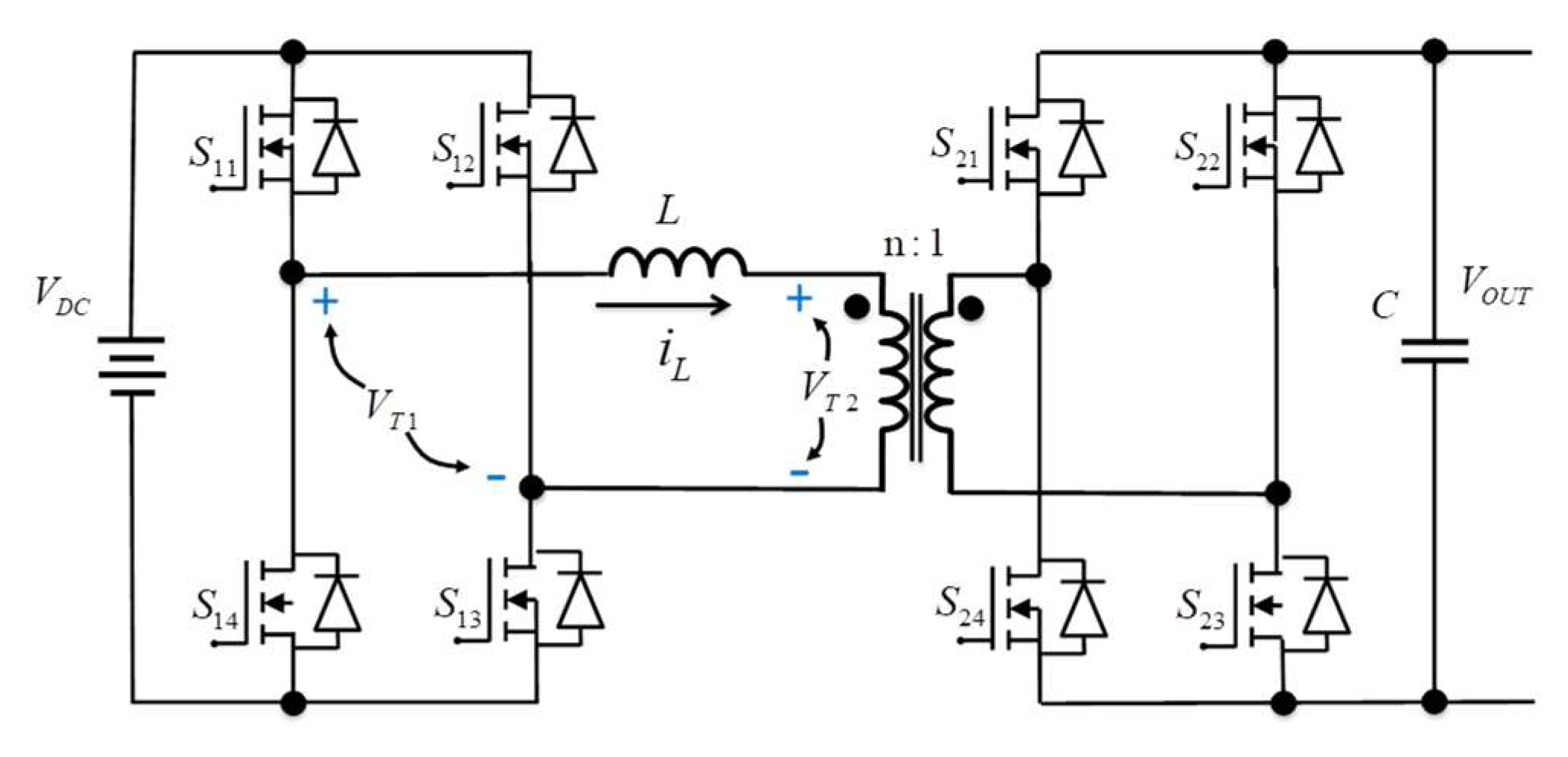
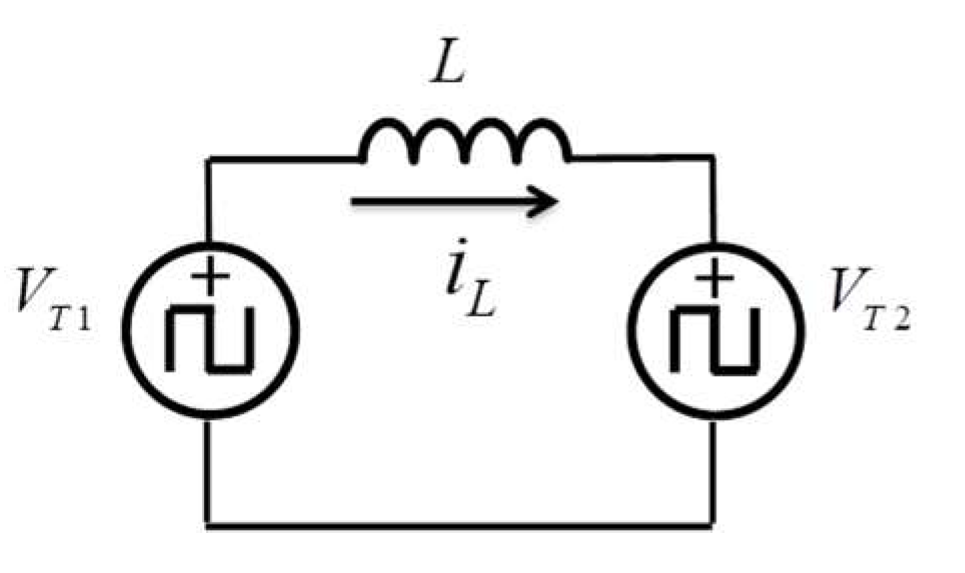
2. Dual Active Bridge Converter
Traditional Single-Phase-Shift Modulation
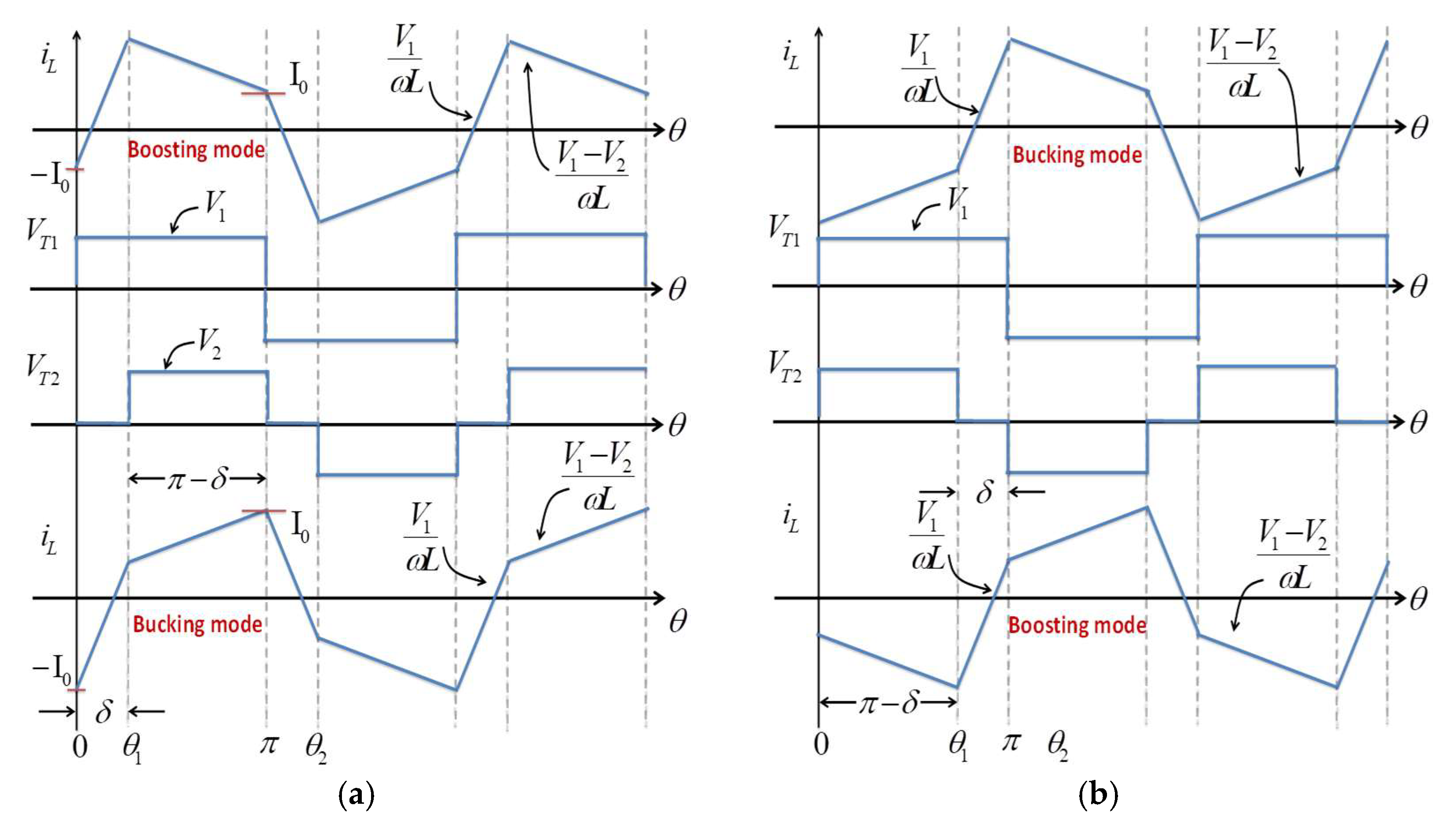
- From 0 < θ < δ. The output of VT1 is positive (VDC), but the output of VT2 is negative (-nVOUT). During this time, the inductor current will increase.
- From δ < θ < π. The output of VT1 is still positive (VDC), but the output of VT2 is now positive (nVOUT) as well. During this time, the inductor current will increase if the bucking mode happens or will decrease if the boosting mode occurs.
3. Two-Stage Modulations
3.1. Boost Modulation
- From 0 < θ < δ. The output of VT1 is positive (VDC), but the output of VT2 is zero. During this time, the inductor current will be increased.
- From δ < θ < π. The output of VT1 is again positive (VDC), but the output of VT2 is now positive (nVOUT). During this time, the inductor current will be increased if the bucking mode happens or will be decreased if the boosting mode occurs.
3.2. Bidirectional Power
- From 0 < θ < δ. The output of VT1 and VT2 are both positive (VDC and nVOUT). During this time, the inductor current will be increased if the bucking mode happens or will be decreased if the boosting mode occurs.
- From δ < θ < π. The output of VT1 is positive (VDC), but the output of VT2 is now zero. During this time, the inductor current will be increased.
3.3. Steady-State Analysis
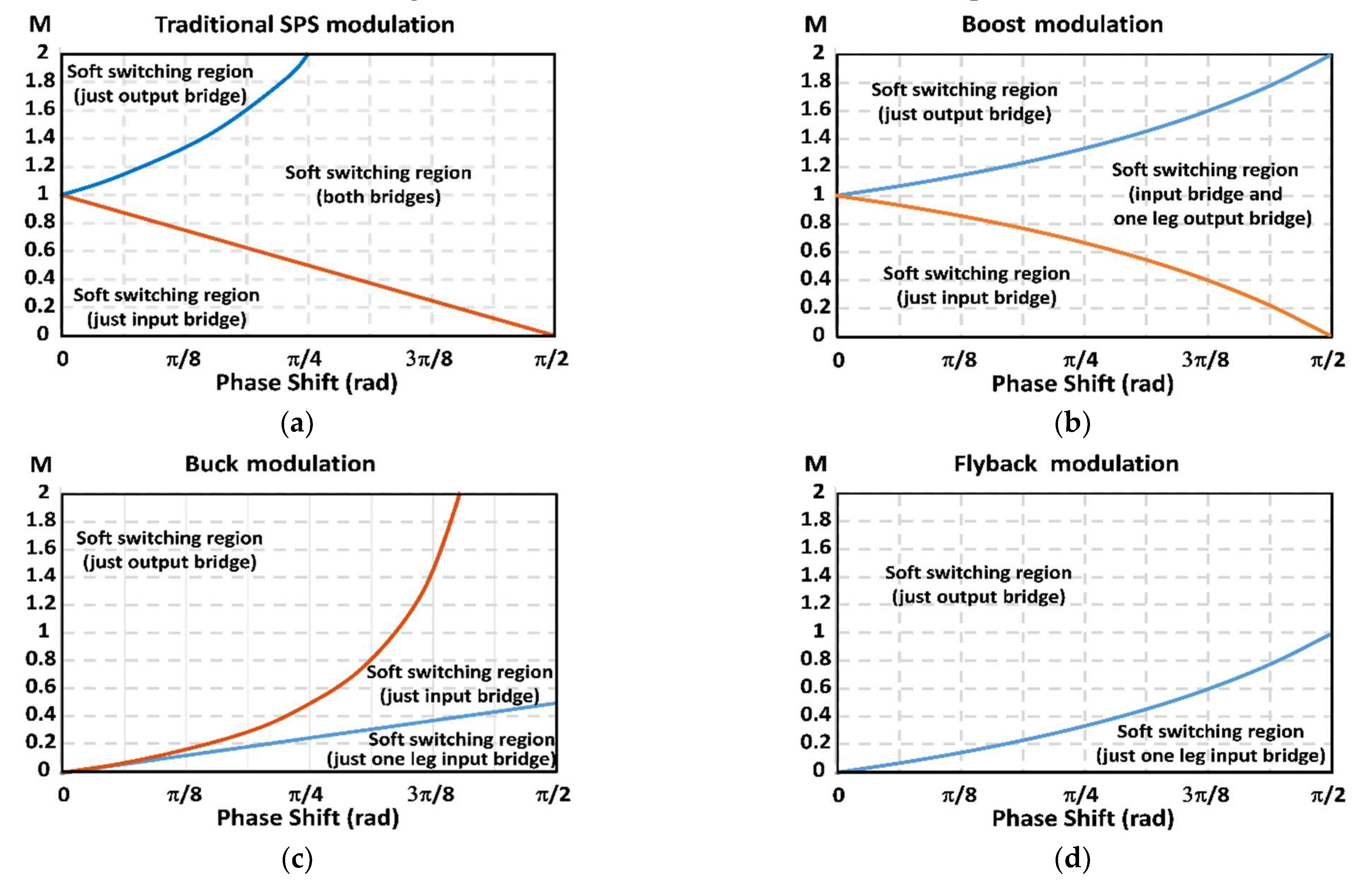
3.4. Soft-Switching
3.5. Discussion on Two-Stage Modulation
4. Experimental Results
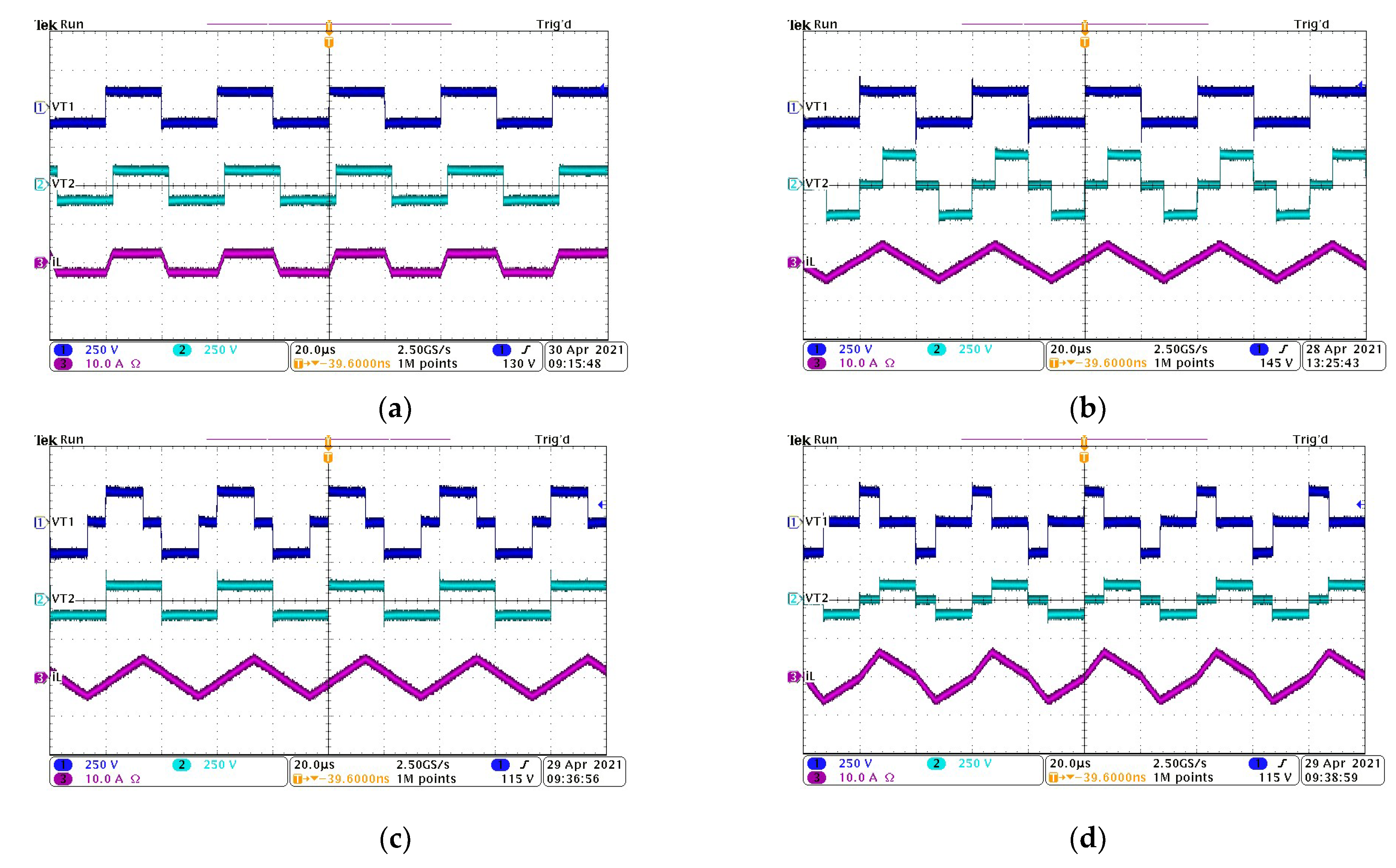
4.1. Steady-State Waveforms
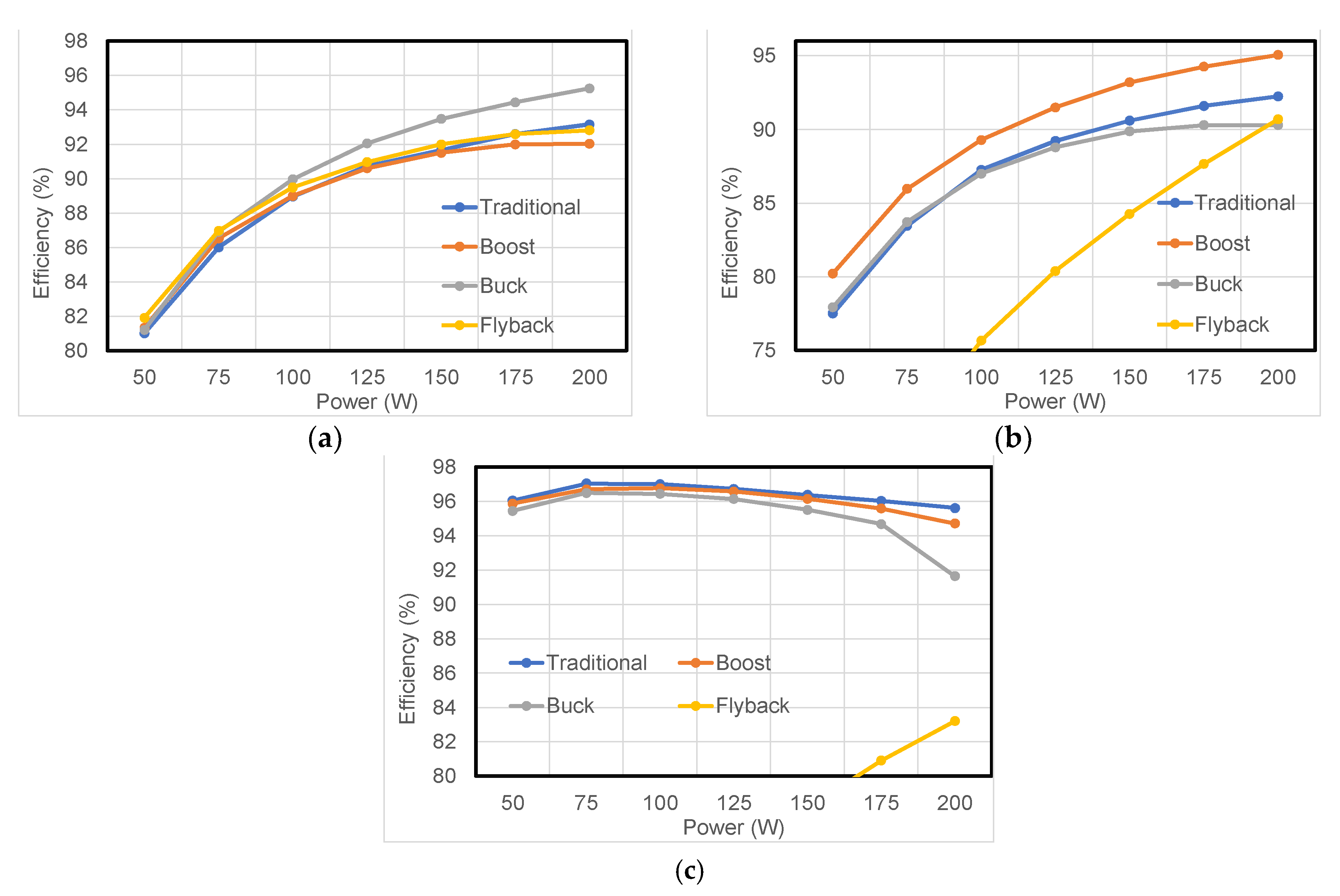
4.2. Efficiency
4.3. RMS Inductor Current
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Das, D.; Hrishikesan, V.M.; Kumar, C.; Liserre, M. Smart Transformer-Enabled Meshed Hybrid Distribution Grid. IEEE Trans. Ind. Electron. 2020, 68, 282–292. [Google Scholar] [CrossRef]
- Ruiz, F.; Perez, M.A.; Espinosa, J.R.; Gajowik, T.; Stynski, S.; Malinowski, M. Surveying Solid-State Transformer Structures and Controls: Providing Highly Efficient and Controllable Power Flow in Distribution Grids. IEEE Ind. Electron. Mag. 2020, 14, 56–70. [Google Scholar] [CrossRef]
- Liserre, M.; Buticchi, G.; Andresen, M.; De Carne, G.; Costa, L.; Zou, Z.-X. The Smart Transformer: Impact on the Electric Grid and Technology Challenges. IEEE Ind. Electron. Mag. 2016, 10, 46–58. [Google Scholar] [CrossRef] [Green Version]
- Buticchi, G.; Costa, L.F.; Barater, D.; Liserre, M.; Amarillo, E.D. A Quadruple Active Bridge Converter for the Storage Integration on the More Electric Aircraft. IEEE Trans. Power Electron. 2017, 33, 8174–8186. [Google Scholar] [CrossRef] [Green Version]
- Krismer, F.; Kolar, J.W. Accurate power loss model derivation of a high-current dual active bridge converter for an auto-motive application. IEEE Trans. Ind. Electron. 2010, 57, 881–891. [Google Scholar] [CrossRef]
- Naayagi, R.; Shuttleworth, R.; Forsyth, A. Bidirectional control of a dual active bridge DC–DC converter for aerospace applications. IET Power Electron. 2012, 5, 1104–1118. [Google Scholar] [CrossRef]
- Shi, Y.; Li, R.; Xue, Y.; Li, H. Optimized Operation of Current-Fed Dual Active Bridge DC–DC Converter for PV Applications. IEEE Trans. Ind. Electron. 2015, 62, 6986–6995. [Google Scholar] [CrossRef]
- Zhu, R.; de Carne, G.; Deng, F.; Liserre, M. Integration of large photovoltaic and wind system by means of smart trans-former. IEEE Trans. Ind. Electron. 2017, 64, 8928–8938. [Google Scholar] [CrossRef] [Green Version]
- Hou, N.; Li, Y.W. Overview and Comparison of Modulation and Control Strategies for a Nonresonant Single-Phase Dual-Active-Bridge DC–DC Converter. IEEE Trans. Power Electron. 2019, 35, 3148–3172. [Google Scholar] [CrossRef]
- Oggier, G.G.; García, G.O.; Oliva, A.R. Switching Control Strategy to Minimize Dual Active Bridge Converter Losses. IEEE Trans. Power Electron. 2009, 24, 1826–1838. [Google Scholar] [CrossRef]
- Oggier, G.G.; García, G.; Oliva, A.R. Modulation strategy to operate the dual active bridge DC–DC converter under soft switching in the whole operating range. IEEE Trans. Power Electron. 2010, 26, 1228–1236. [Google Scholar] [CrossRef]
- Oggier, G.G.; Ordonez, M. High-Efficiency DAB Converter Using Switching Sequences and Burst Mode. IEEE Trans. Power Electron. 2015, 31, 2069–2082. [Google Scholar] [CrossRef]
- Rodriguez-Rodrıguez, J.R.; Moreno-Goytia, E.L.; Venegas-Rebollar, V.; Ugalde-Caballero, L.E.; Anaya-Ruiz, G.A. The Pro-portional-Values Modulation (PVM), a technique for improving efficiency and power density of bidirectional DAB converters. Electr. Power Syst. Res. 2017, 144, 280–289. [Google Scholar] [CrossRef]
- Shi, H.; Wen, H.; Chen, J.; Hu, Y.; Jiang, L.; Chen, G. Minimum-Reactive-Power Scheme of Dual-Active-Bridge DC–DC Converter with Three-Level Modulated Phase-Shift Control. IEEE Trans. Ind. Appl. 2017, 53, 5573–5586. [Google Scholar] [CrossRef] [Green Version]
- Hou, N.; Song, W.; Li, Y.W.; Zhu, Y.; Zhu, Y. A Comprehensive Optimization Control of Dual-Active-Bridge DC–DC Converters Based on Unified-Phase-Shift and Power-Balancing Scheme. IEEE Trans. Power Electron. 2018, 34, 826–839. [Google Scholar] [CrossRef]
- Byen, B.J.; Ban, C.H.; Lim, Y.B.; Choe, G.H. An Efficiency-Optimized Modulation Strategy for Dual-Active-Bridge DC–DC Converters Using Dual-Pulse-Width-Modulation in the Low Power Region. J. Power Electron. 2017, 17, 1413–1421. [Google Scholar]
- Yaqoob, M.; Loo, K.-H.; Lai, Y.M. Fully Soft-Switched Dual-Active-Bridge Series-Resonant Converter with Switched-Impedance-Based Power Control. IEEE Trans. Power Electron. 2018, 33, 9267–9281. [Google Scholar] [CrossRef]
- Wu, F.; Feng, F.; Gooi, H.B. Cooperative Triple-Phase-Shift Control for Isolated DAB DC–DC Converter to Improve Current Characteristics. IEEE Trans. Ind. Electron. 2019, 66, 7022–7031. [Google Scholar] [CrossRef]
- Mou, D.; Luo, Q.; Li, J.; Wei, Y.; Chen, J. The Novel Single Phase-Shift Modulation Scheme for Dual Active Bridge Converter. Proceedings of 2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), Nanjing, China, 29 November–2 December 2020; pp. 2686–2690. [Google Scholar] [CrossRef]
- An, F.; Song, W.S.; Yang, K.X. Optimized power control with extended phase shift in dual-active-bridge dc–dc converters. Electron. Lett. 2018, 54, 651–653. [Google Scholar] [CrossRef]
- Zhao, B.; Yu, Q.; Sun, W. Extended-Phase-Shift Control of Isolated Bidirectional DC–DC Converter for Power Distribution in Microgrid. IEEE Trans. Power Electron. 2012, 27, 4667–4680. [Google Scholar] [CrossRef]
- Gu, Q.; Yuan, L.; Nie, J.; Sun, J.; Zhao, Z. Current Stress Minimization of Dual-Active-Bridge DC–DC Converter Within the Whole Operating Range. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 7, 129–142. [Google Scholar] [CrossRef]
- Dutta, S.; Hazra, S.; Bhattacharya, S. A Digital Predictive Current-Mode Controller for a Single-Phase High-Frequency Transformer-Isolated Dual-Active Bridge DC-to-DC Converter. IEEE Trans. Ind. Electron. 2016, 63, 5943–5952. [Google Scholar] [CrossRef]

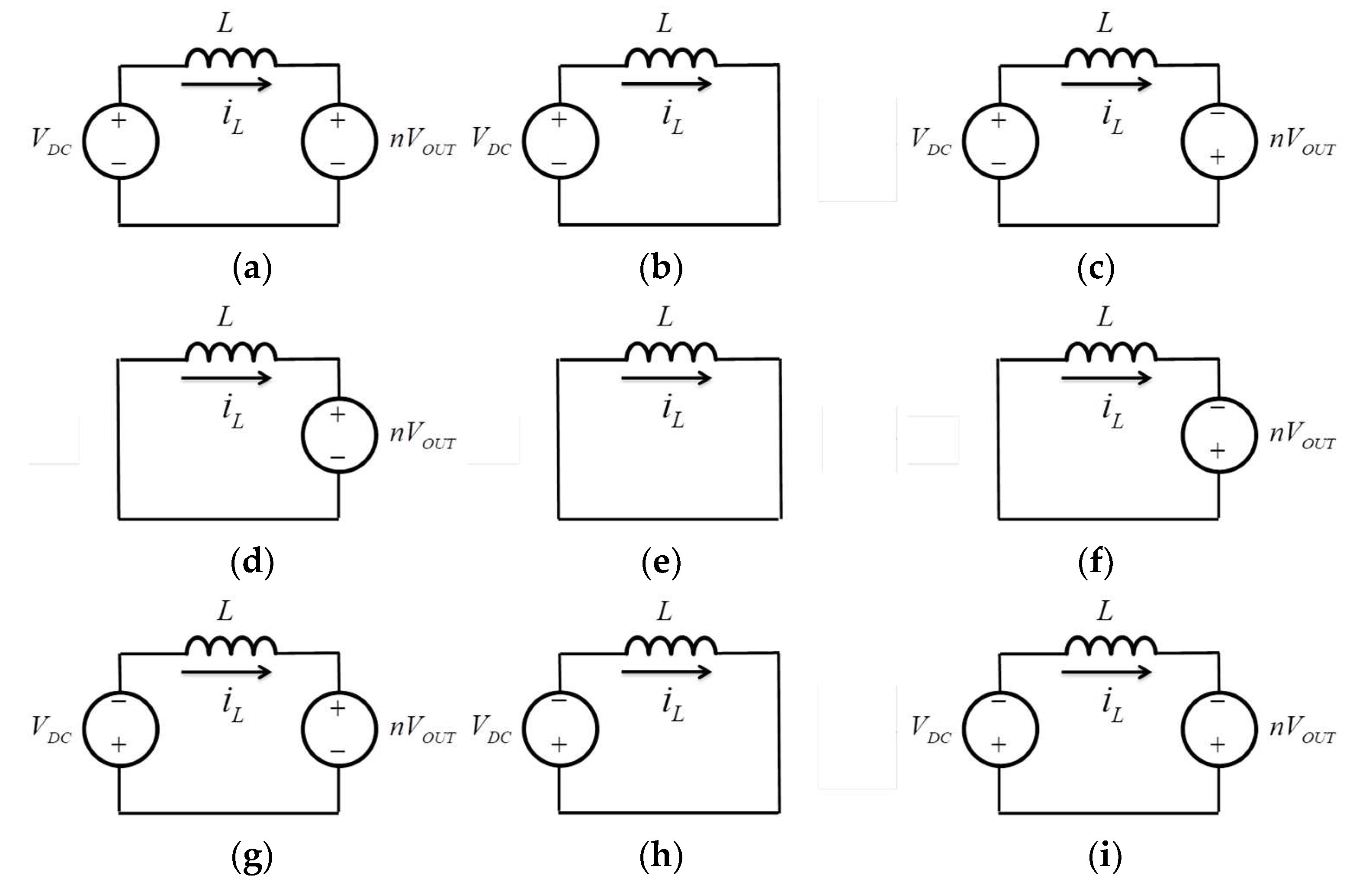


| Positive Semi-Cycle | Negative Semi-Cycle |
|---|---|
| Stage a | Stage i |
| Stage b | Stage h |
| Stage c | Stage g |
| Stage d | Stage f |
| Stage e | Stage e |
| Modulation | Switching States | |
|---|---|---|
| Positive Semi-Cycle | Negative Semi-Cycle | |
| SPS | c, a | g, i |
| Boost | b, a | h, i |
| Buck | a, d | i, f |
| Flyback | b, d | h, f |
| Modulation | Inductor Current | Output Power | ILrms and Power Factor |
|---|---|---|---|
| SPS | where: | ||
| Boost | where: | ||
| Buck | where: | ||
| Flyback | where: |
| Modulation | Input Bridge | Output Bridge |
|---|---|---|
| SPS | ||
| Boost | , | |
| Buck | , | |
| Flyback | , | , |
| Parameter | M = 0.5 | M = 2 | M = 1 |
|---|---|---|---|
| Output power | 200 W | ||
| Input voltage | 200 V | 100 V | 100 V |
| Output voltage | 100 V | 200 V | 100 V |
| Switching frequency | 25 kHz | ||
| Series inductor | 244 μH | 114 μH | |
| Transformer ratio | n = 1 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guzmán, P.; Vázquez, N.; Liserre, M.; Orosco, R.; Pinto Castillo, S.E.; Hernández, C. Two-Stage Modulation Study for DAB Converter. Electronics 2021, 10, 2561. https://doi.org/10.3390/electronics10212561
Guzmán P, Vázquez N, Liserre M, Orosco R, Pinto Castillo SE, Hernández C. Two-Stage Modulation Study for DAB Converter. Electronics. 2021; 10(21):2561. https://doi.org/10.3390/electronics10212561
Chicago/Turabian StyleGuzmán, Pablo, Nimrod Vázquez, Marco Liserre, Rodolfo Orosco, Sergio Enrique Pinto Castillo, and Claudia Hernández. 2021. "Two-Stage Modulation Study for DAB Converter" Electronics 10, no. 21: 2561. https://doi.org/10.3390/electronics10212561
APA StyleGuzmán, P., Vázquez, N., Liserre, M., Orosco, R., Pinto Castillo, S. E., & Hernández, C. (2021). Two-Stage Modulation Study for DAB Converter. Electronics, 10(21), 2561. https://doi.org/10.3390/electronics10212561







