Mathematical Modeling and Performance Evaluation of Switched-Capacitor-Based Battery Equalization Systems
Abstract
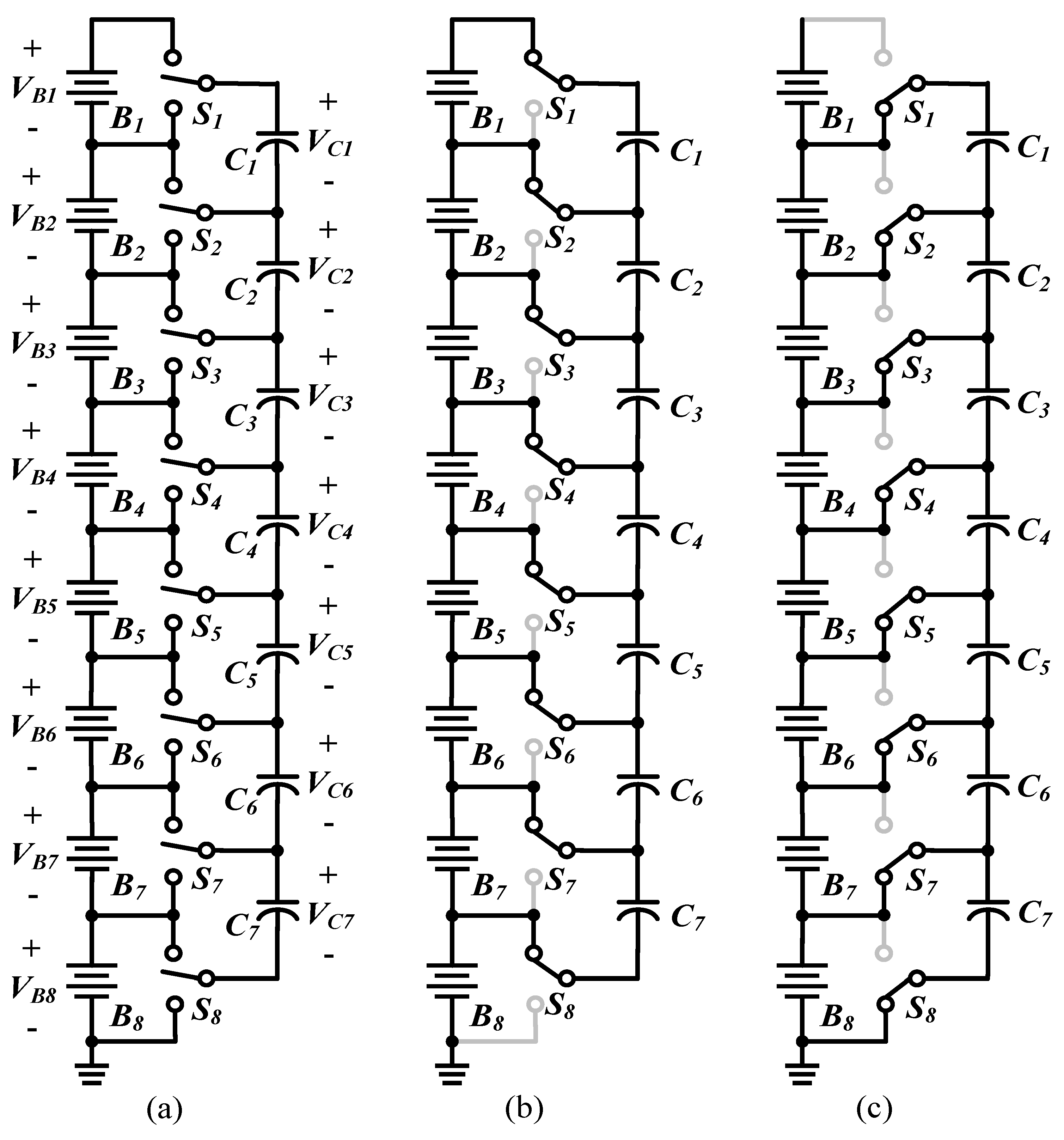
:1. Introduction
2. Description of the Compared SC-Based BEs
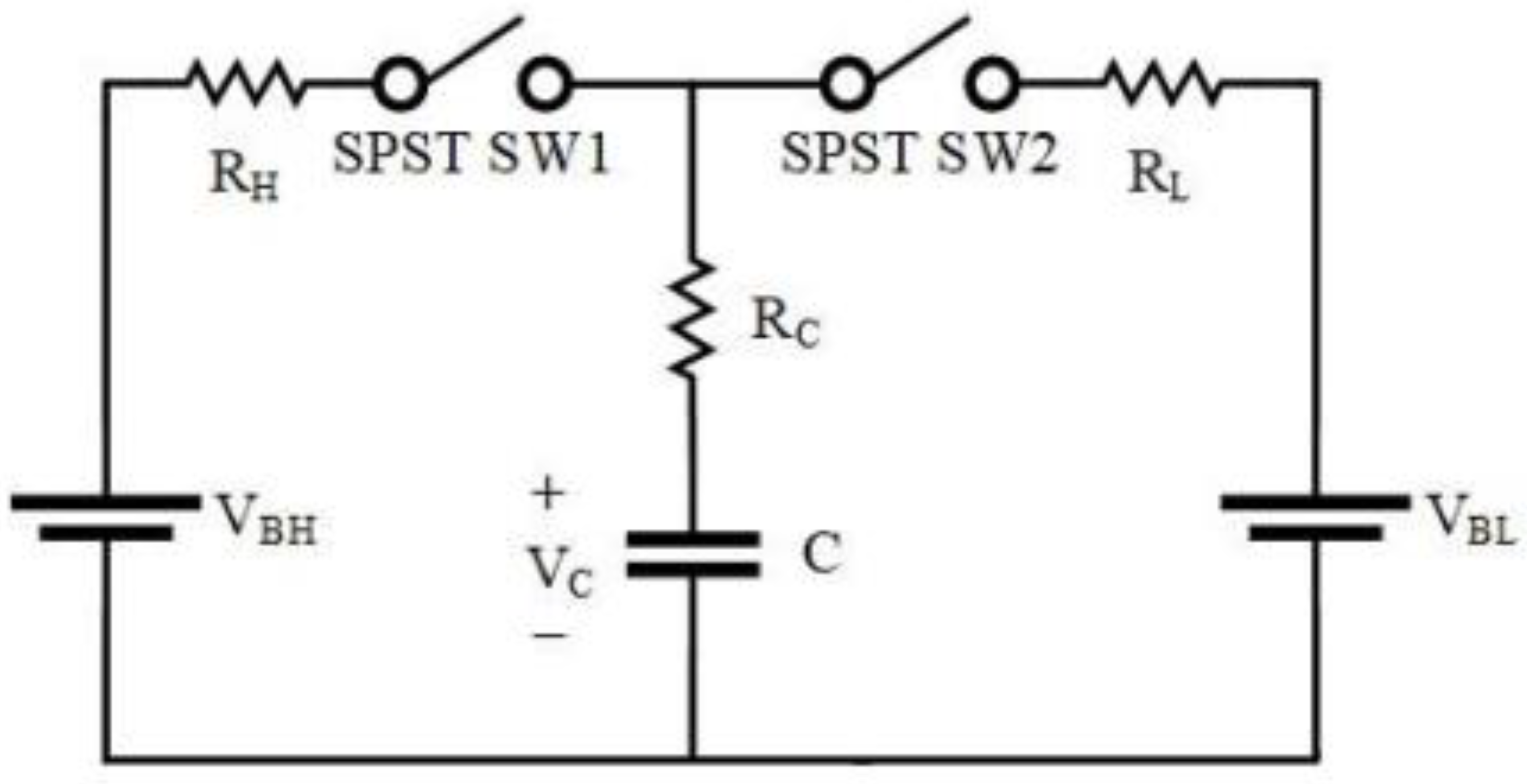
2.1. Conventional SC-Based BE
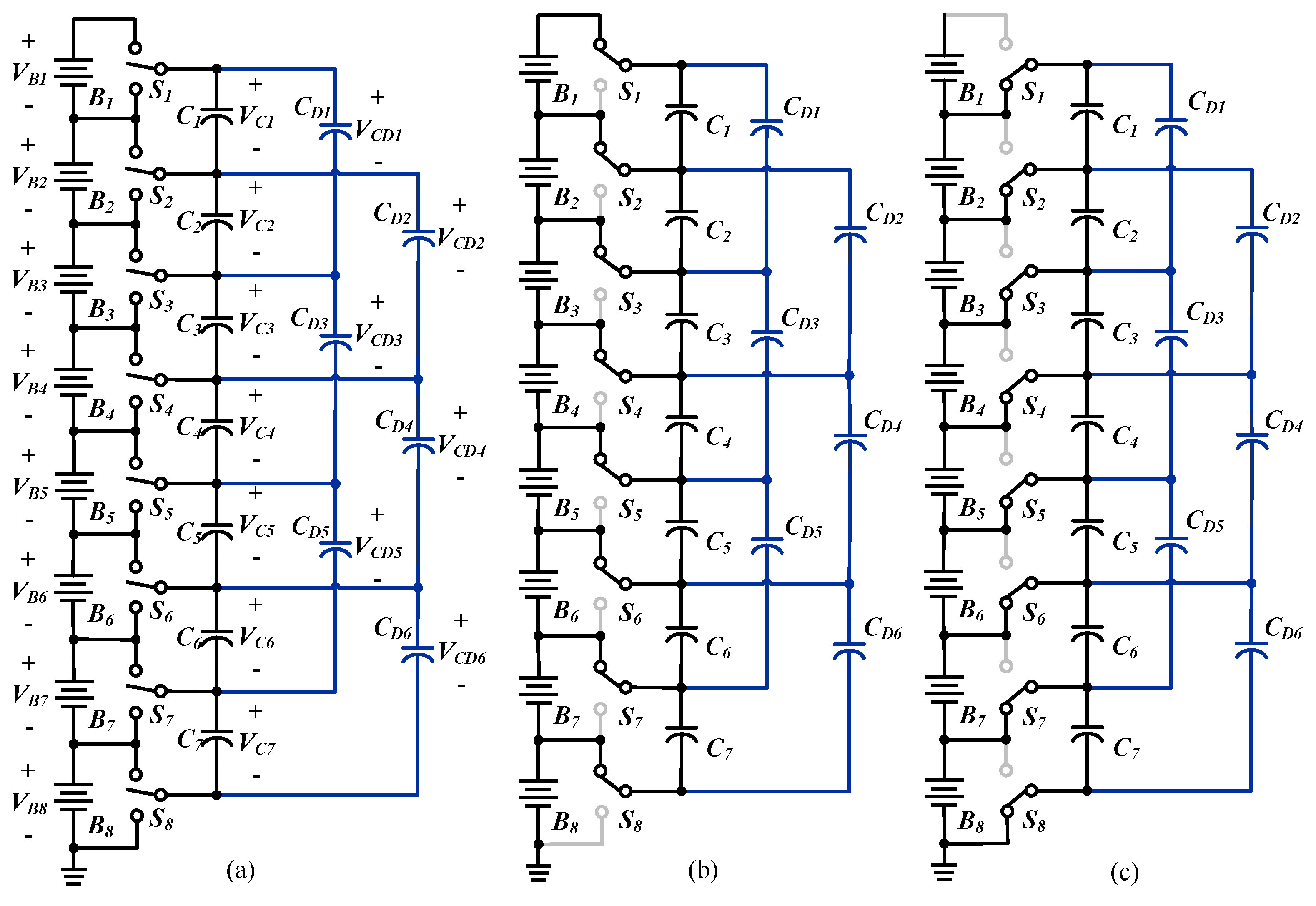
2.2. Double-Tiered SC-Based BE
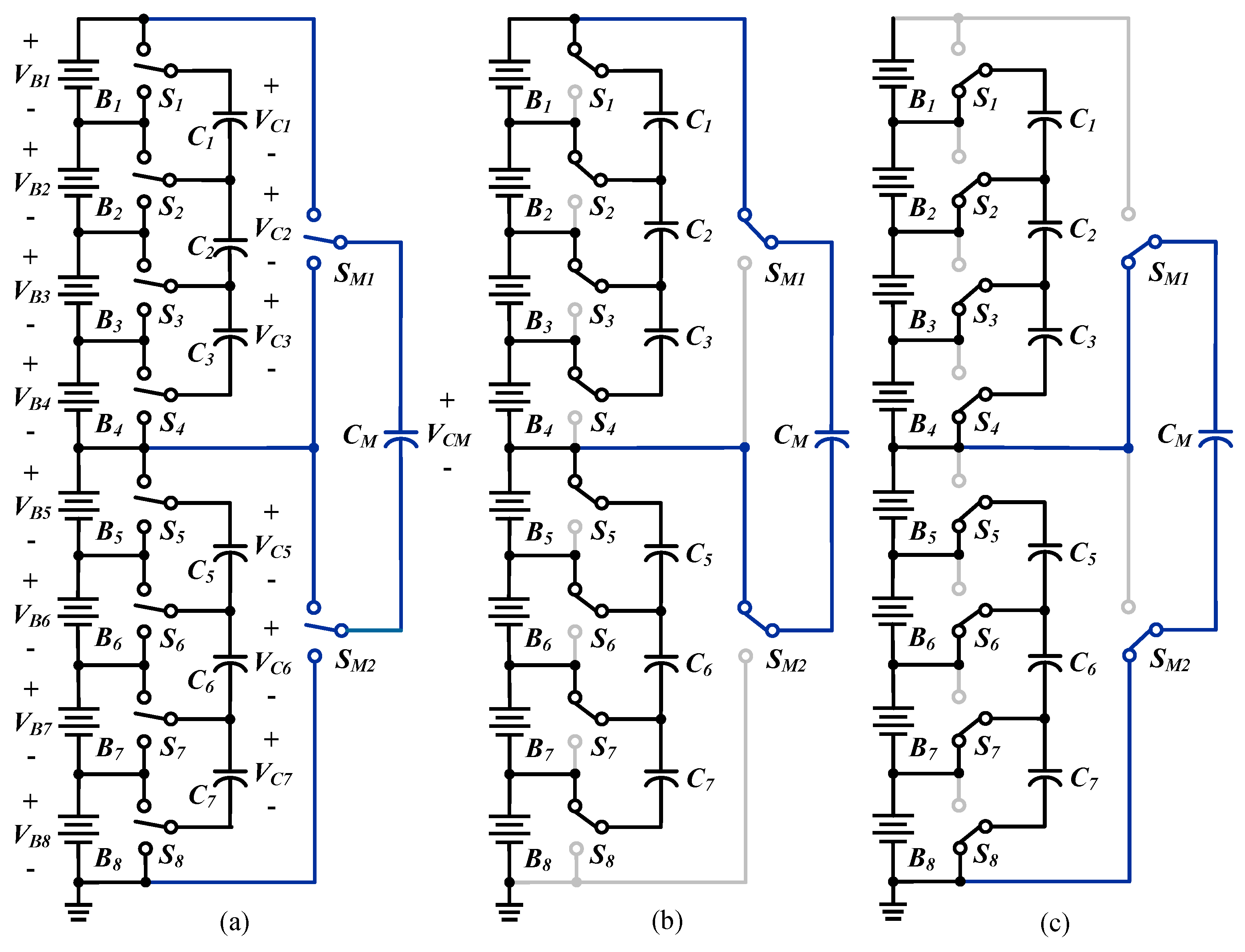
2.3. Modularized SC-Based BE
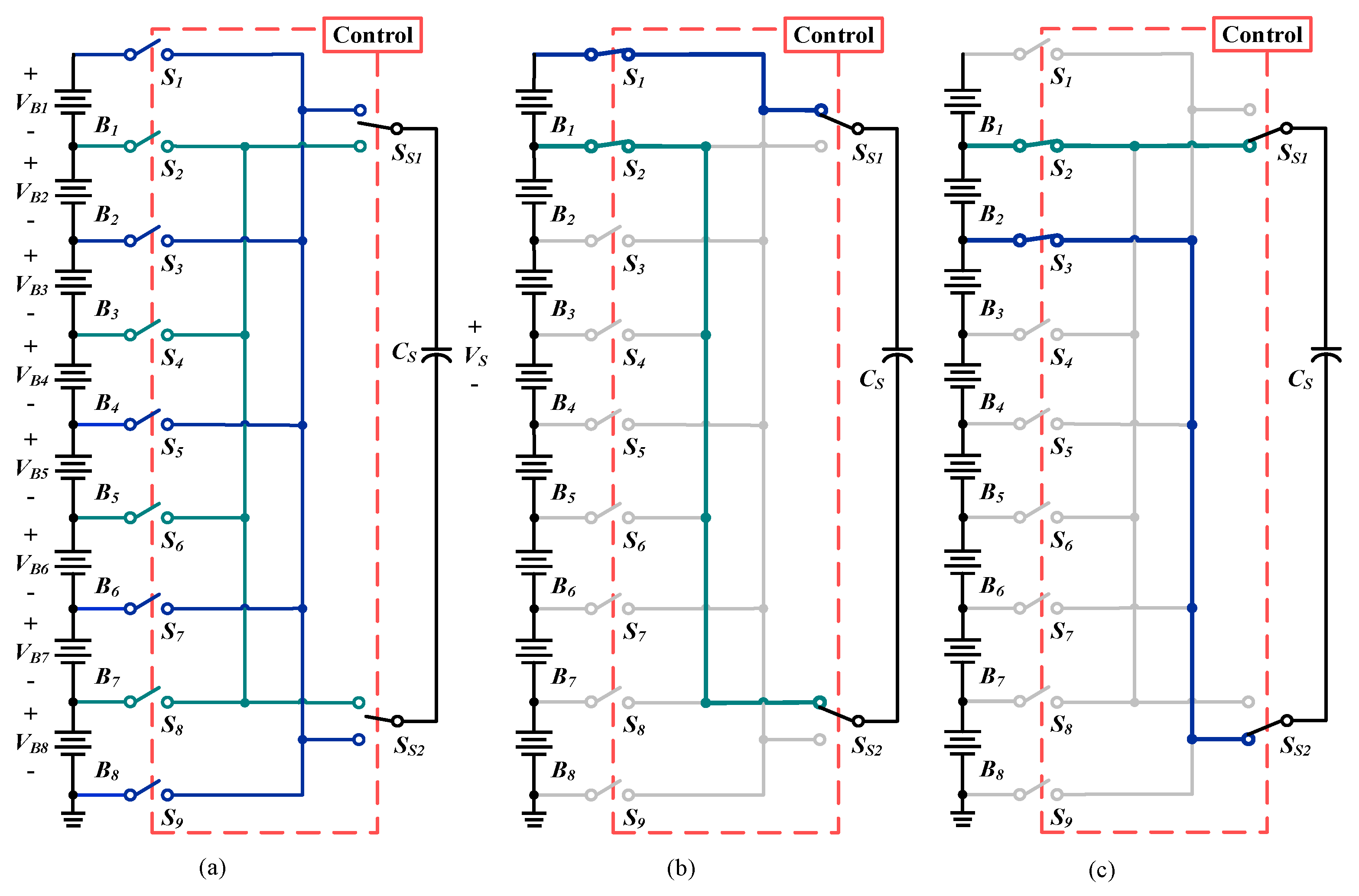
2.4. Chain Structure of SC-Based BE Type I
2.5. Chain Structure of SC-Based BE Type II
2.6. Series-Parallel SC-Based BE
2.7. Single-SC-Based BE
2.8. Comparison of the Number of Components in Each SC-Based BE
3. Mathematical Model of the Battery Equalization System
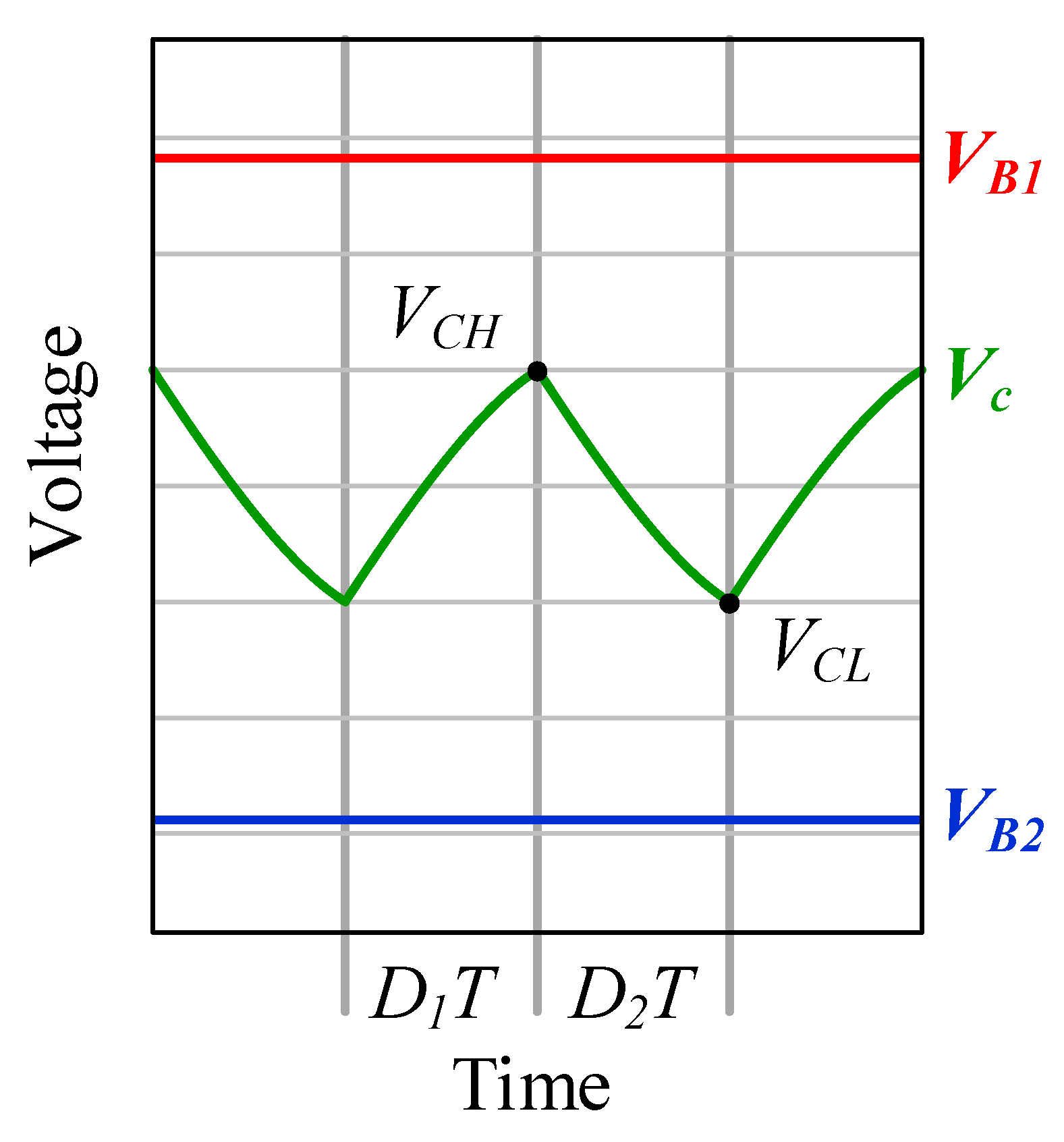
3.1. Calculation of Energy Transferred between Batteries
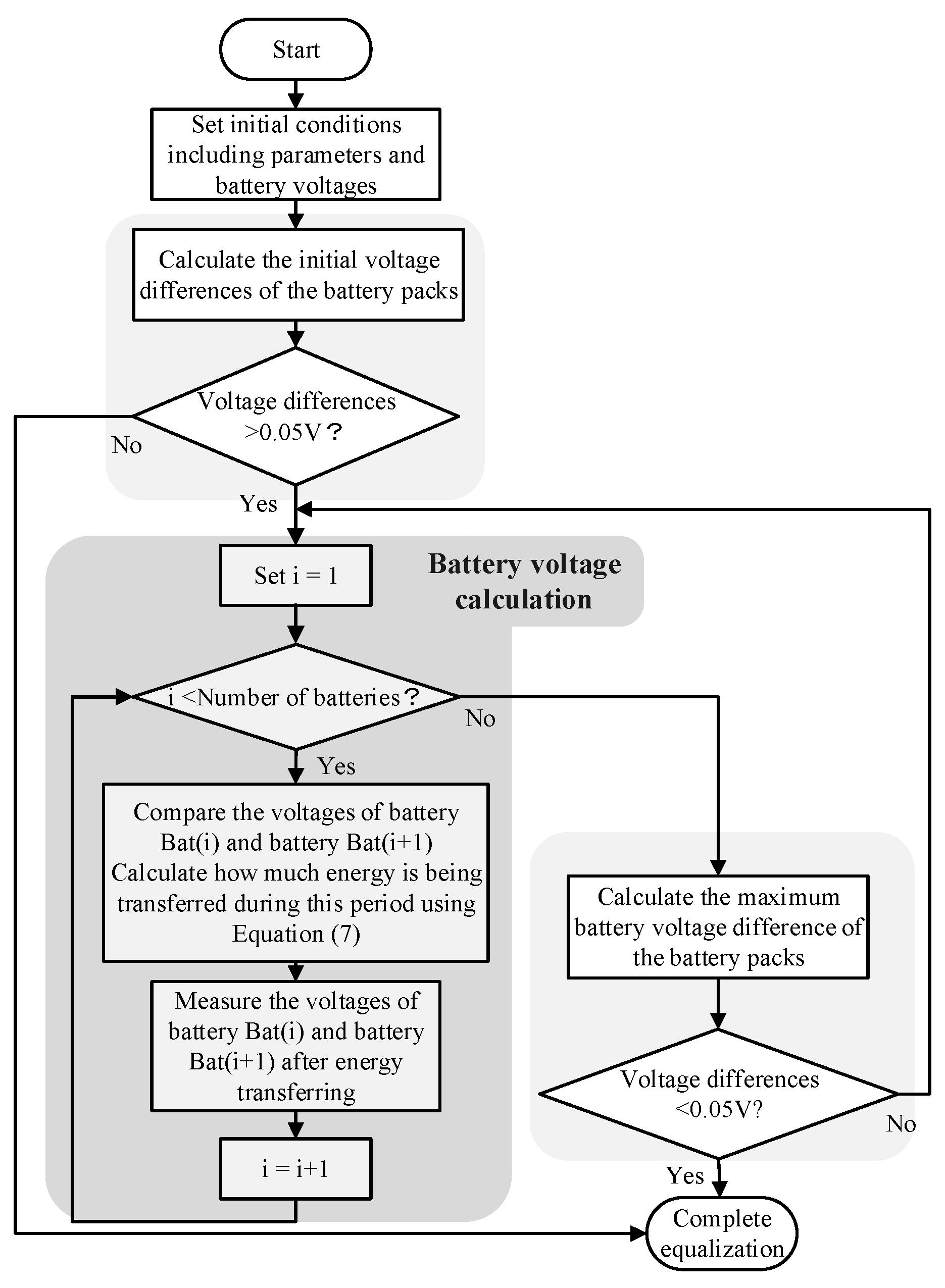
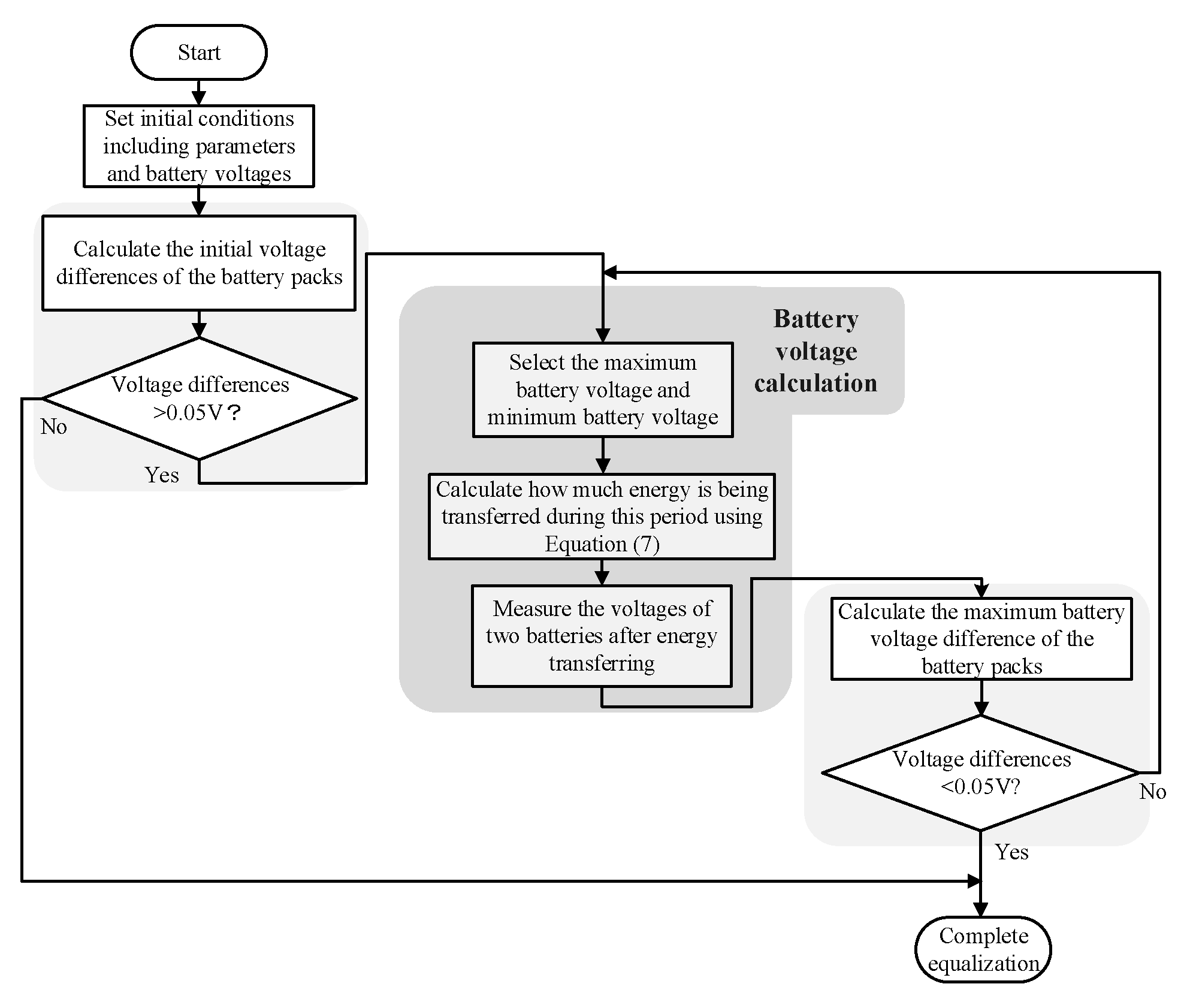
3.2. The Simulation Flow Chart of the Conventional SC-Based BE
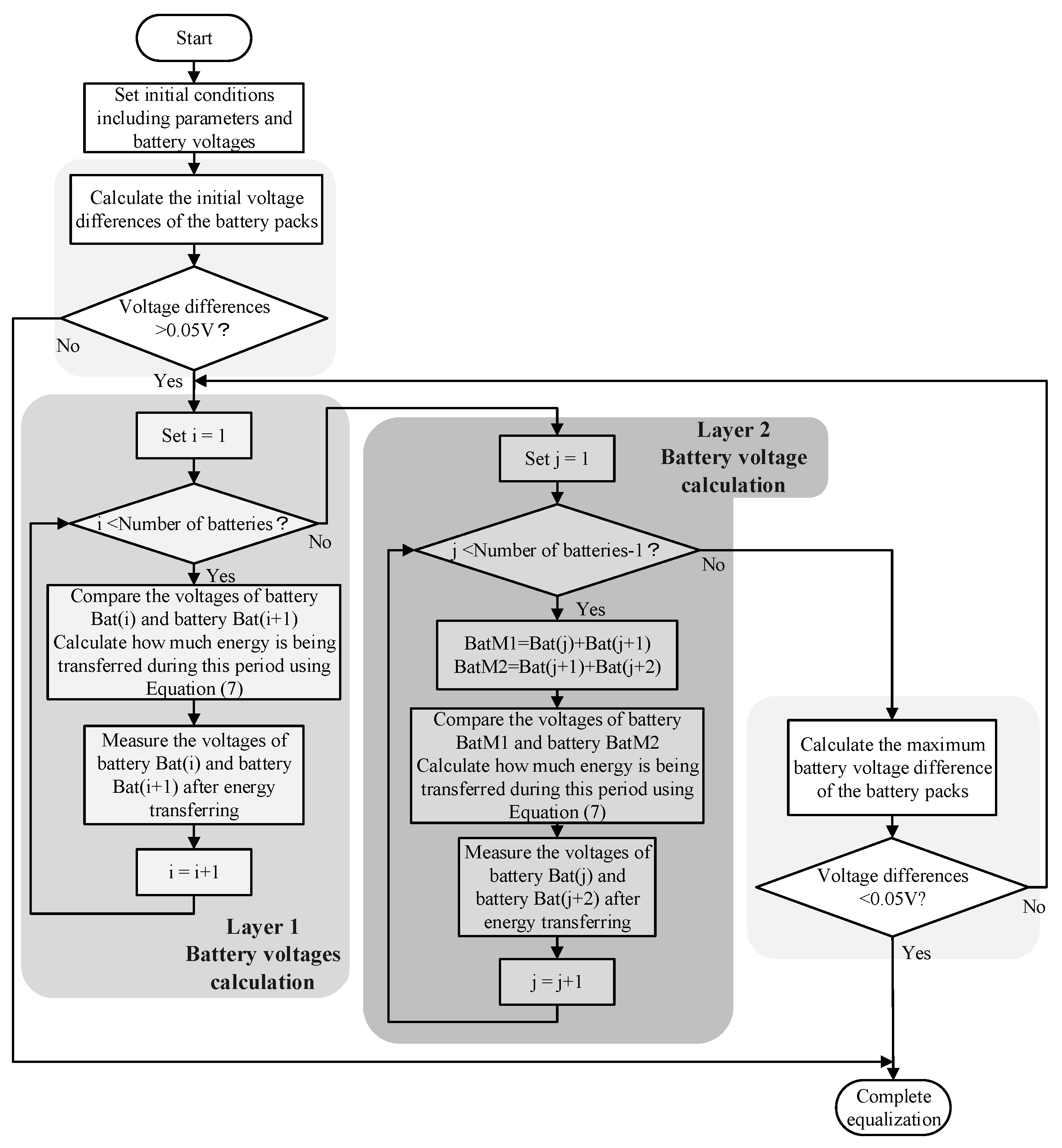
3.3. The Simulation Flow Chart of the Double-Tiered SC-Based BE
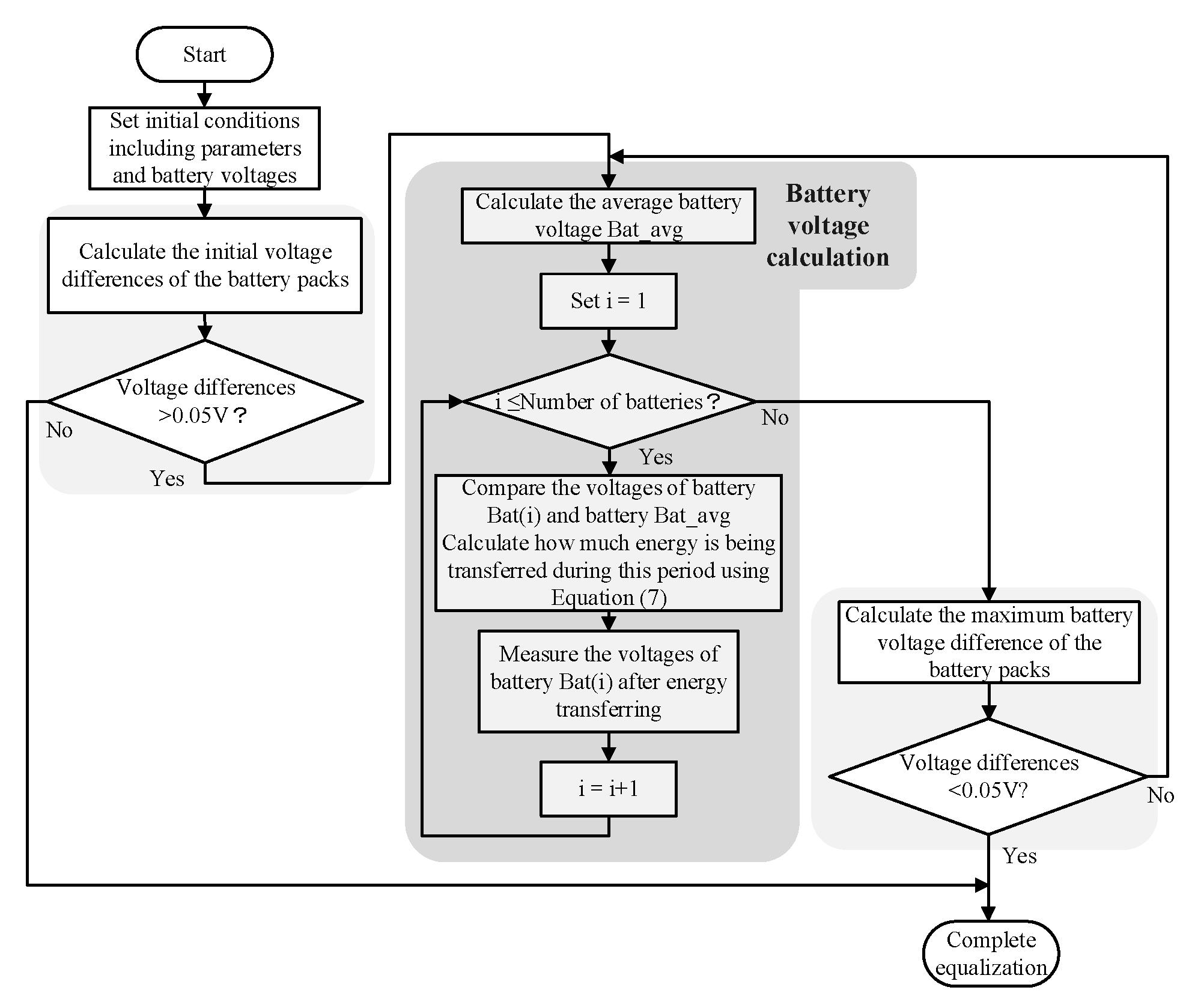
3.4. The Simulation Flow Chart of the Modularized SC-Based BE
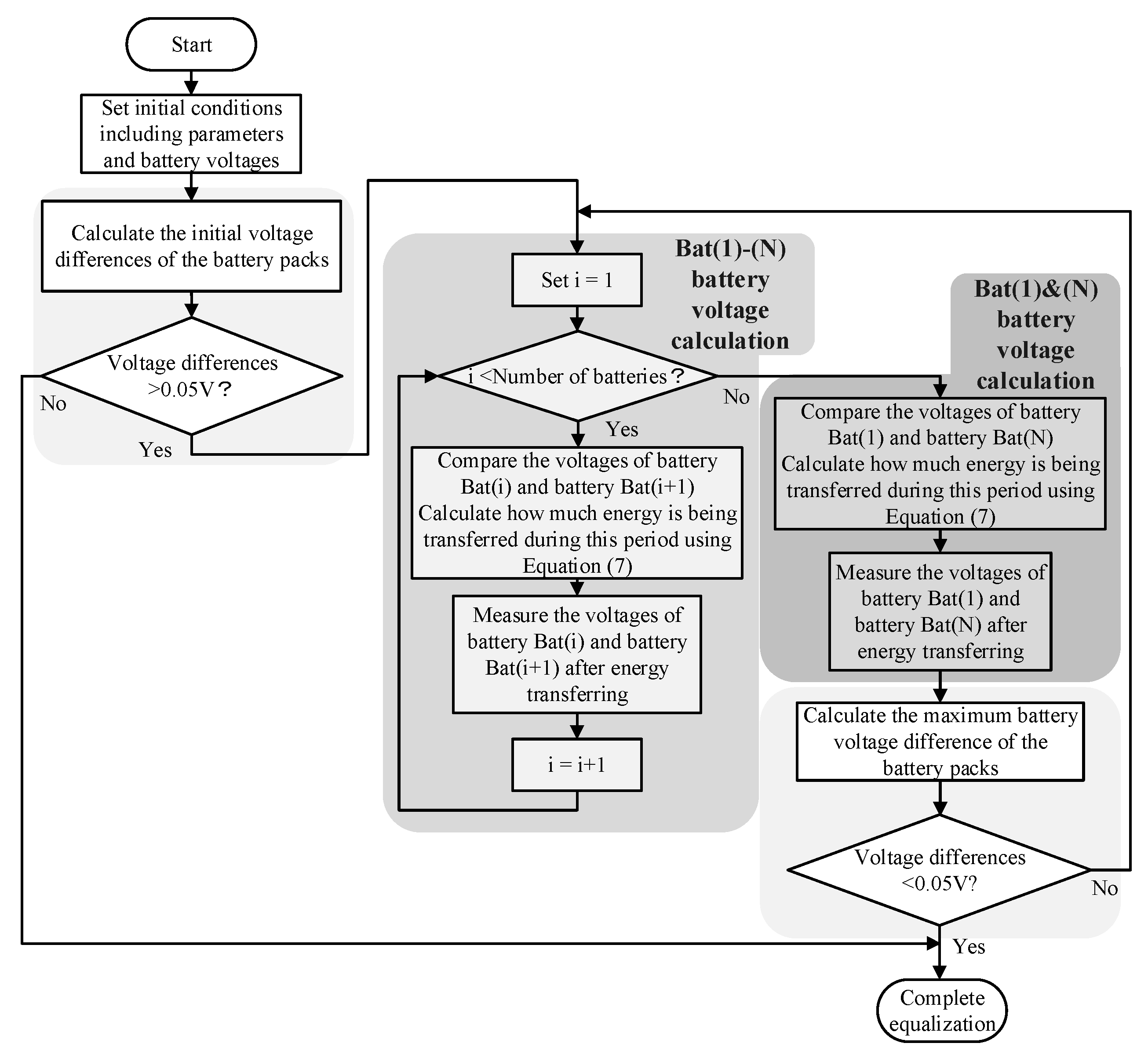
3.5. The Simulation Flow Chart of the Chain Structure of SC-Based BE Type I
3.6. The Simulation Flow Chart of the Chain Structure of SC-Based BE Type II
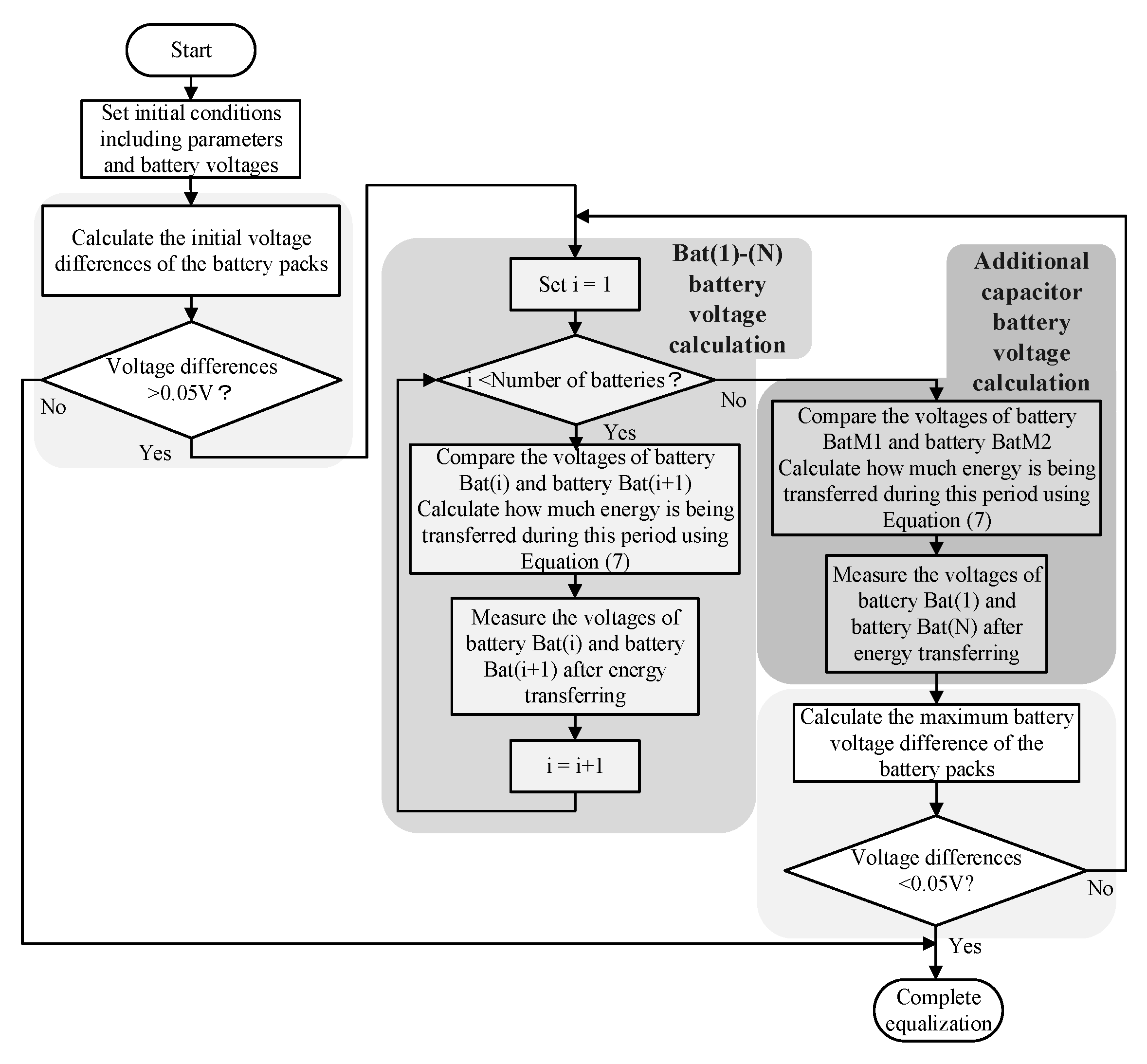
3.7. The Simulation Flow Chart of the Series-Parallel SC-Based BE
3.8. The Simulation Flow Chart of the Modularized SC-Based BE
3.9. Validation of the Simulation Platform
4. Analysis and Comparison of Balancing Performance
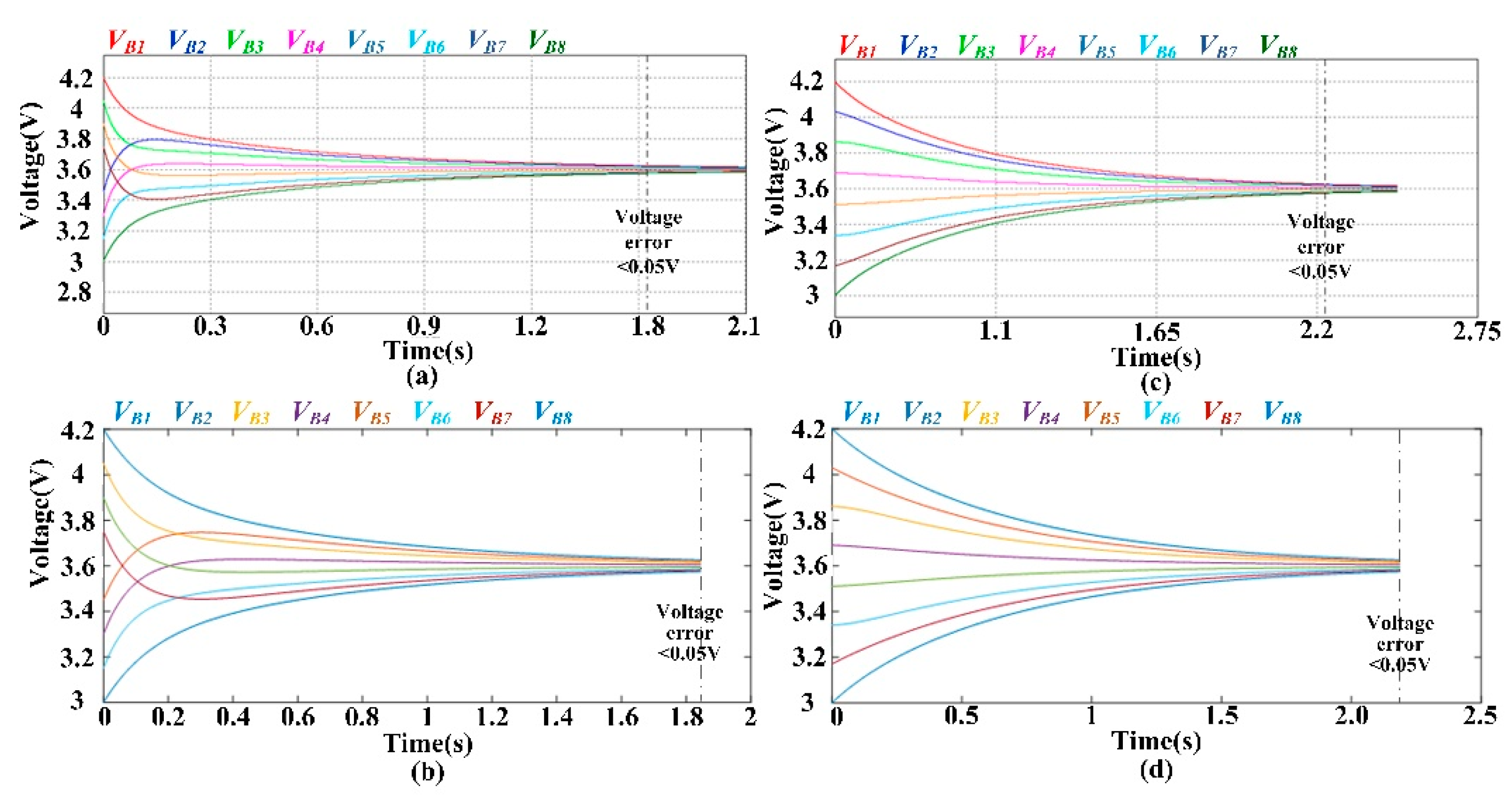
4.1. Equalization Results for Four Battery Cells
4.2. Equalization Results for Eight Battery Cells
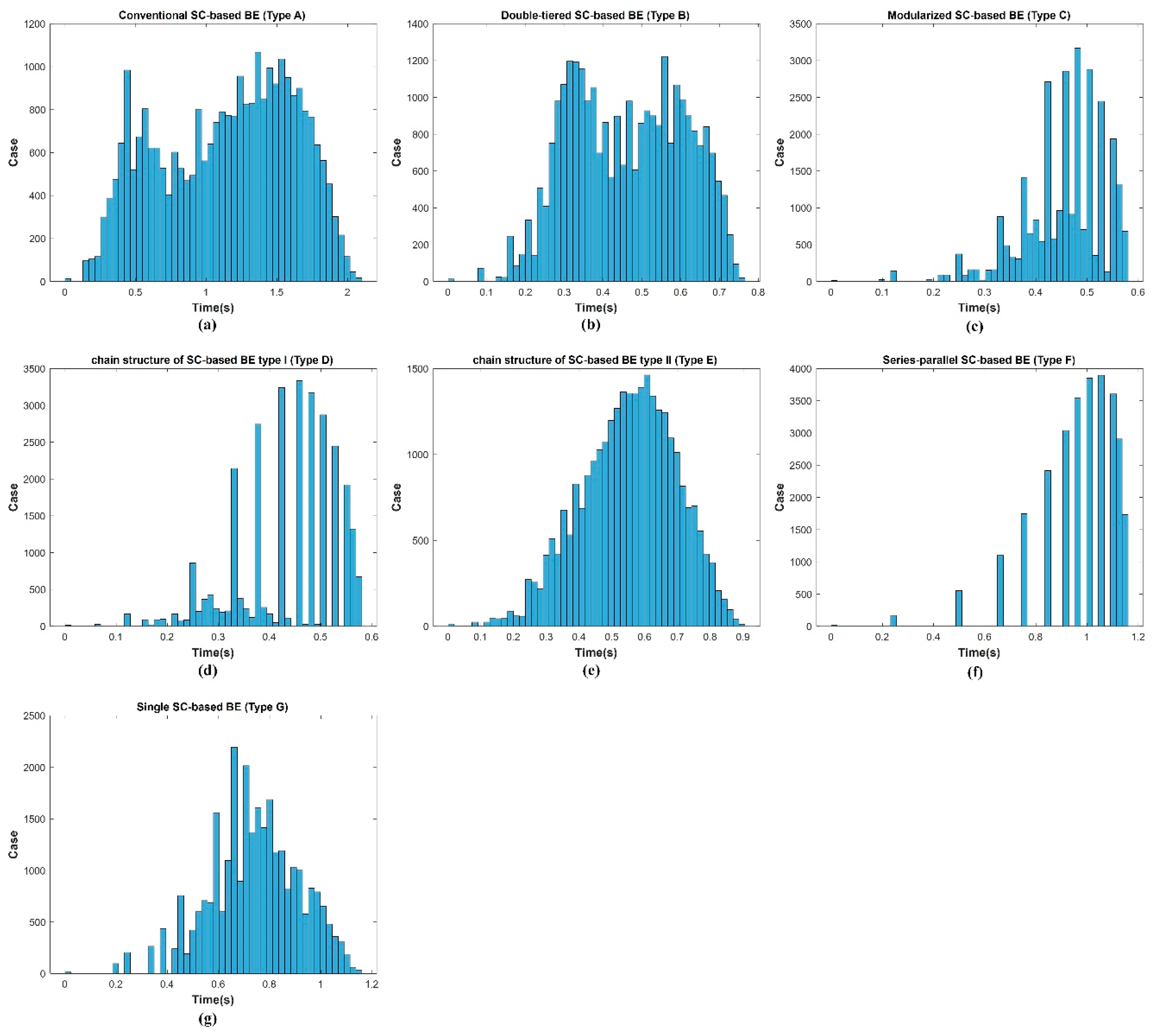
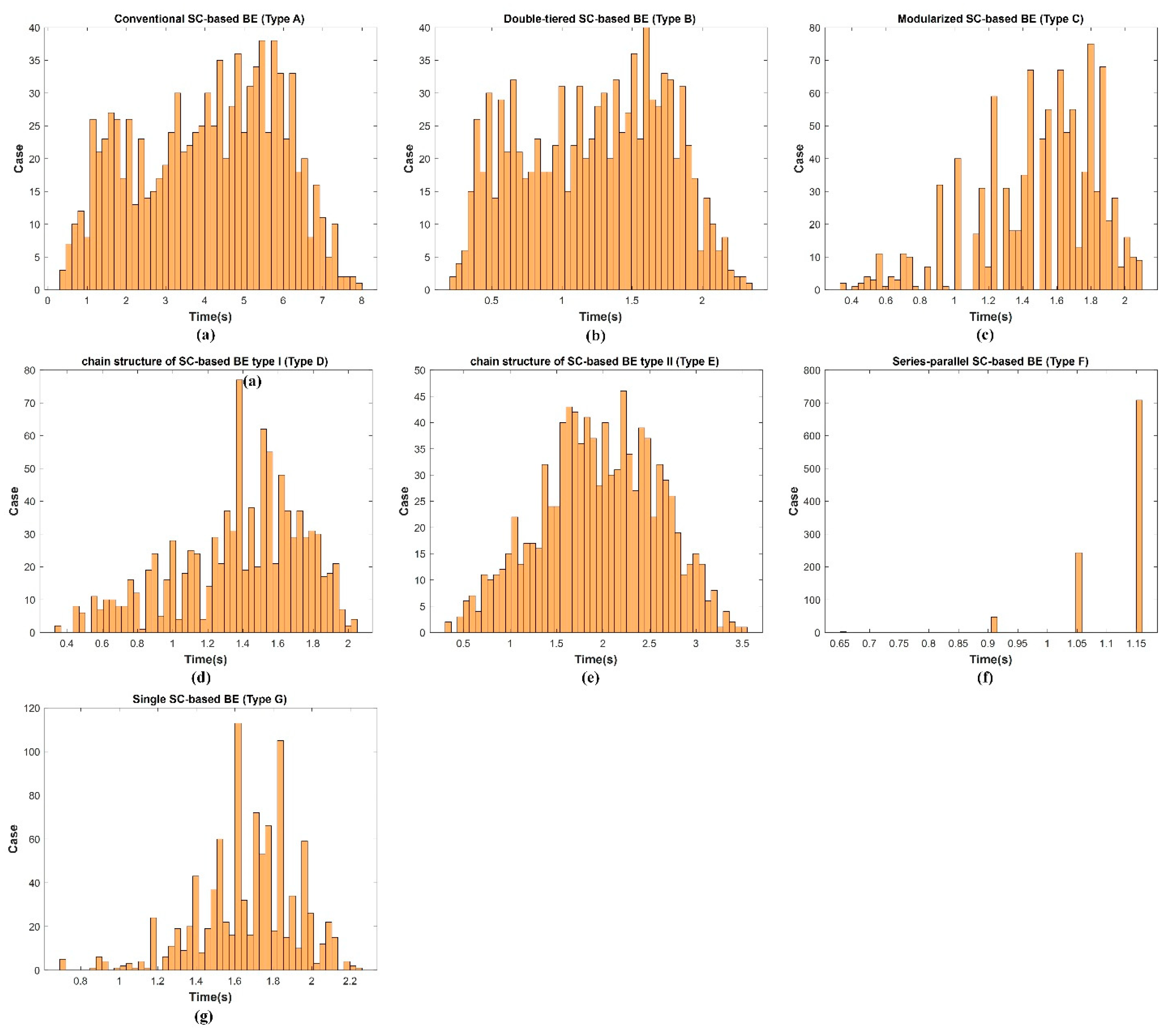
4.3. Analysis of the Balancing Performance for Different Numbers of Battery Cells
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ouyang, Q.; Wang, Z.; Liu, K.; Xu, G.; Li, Y. Optimal charging control for lithium-ion battery packs: A distributed average tracking approach. IEEE Trans. Ind. Inform. 2019, 16, 3430–3438. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, X.; Guo, B.; Zhu, C.; Wiedemann, J.; Wang, L.; Cao, J. Health-Aware Multiobjective Optimal Charging Strategy With Coupled Electrochemical-Thermal-Aging Model for Lithium-Ion Battery. IEEE Trans. Ind. Inform. 2019, 16, 3417–3429. [Google Scholar] [CrossRef]
- Xiong, R.; Yang, R.; Chen, Z.; Shen, W.; Sun, F. Online fault diagnosis of external short circuit for lithium-ion battery pack. IEEE Trans. Ind. Electron. 2019, 67, 1081–1091. [Google Scholar] [CrossRef]
- Lu, X.; Wang, H. Optimal sizing and energy management for cost-effective PEV hybrid energy storage systems. IEEE Trans. Ind. Inform. 2019, 16, 3407–3416. [Google Scholar] [CrossRef]
- Ding, L.; Han, Q.L.; Ning, B.; Yue, D. Distributed resilient finite-time secondary control for heterogeneous battery energy storage systems under denial-of-service attacks. IEEE Trans. Ind. Inform. 2019, 16, 4909–4919. [Google Scholar] [CrossRef]
- Chekired, D.A.; Khoukhi, L.; Mouftah, H.T. Fog-Computing-Based Energy Storage in Smart Grid: A Cut-Off Priority Queuing Model for Plug-In Electrified Vehicle Charging. IEEE Trans. Ind. Inform. 2019, 16, 3470–3482. [Google Scholar] [CrossRef]
- Yang, Y.D.; Hu, K.Y.; Tsai, C.H. Digital Battery Management Design for Point-of-Load Applications with Cell Balancing. IEEE Trans. Ind. Electron. 2019, 67, 6365–6375. [Google Scholar] [CrossRef]
- Zahedmanesh, A.; Muttaqi, K.M.; Sutanto, D. A Sequential Decision-Making Process for Optimal Techno-Economic Operation of a Grid Connected Electrical Traction Substation Integrated with Solar PV and BESS. IEEE Trans. Ind. Electron. 2020, 68, 1353–1364. [Google Scholar] [CrossRef]
- Ouyang, Q.; Han, W.; Zou, C.; Xu, G.; Wang, Z. Cell Balancing Control For Lithium-Ion Battery Packs: A Hierarchical Optimal Approach. IEEE Trans. Ind. Inform. 2019, 16, 5065–5075. [Google Scholar] [CrossRef]
- Vulligaddala, V.B.; Vernekar, S.; Singamla, S.; Adusumalli, R.K.; Ele, V.; Brandl, M.; Srinivas, M.B. A 7-Cell, Stackable, Li-Ion Monitoring and Active/Passive Balancing IC With In-Built Cell Balancing Switches for Electric and Hybrid Vehicles. IEEE Trans. Ind. Inform. 2019, 16, 3335–3344. [Google Scholar] [CrossRef]
- Shang, Y.; Zhao, S.; Fu, Y.; Han, B.; Hu, P.; Mi, C.C. A Lithium-ion battery balancing circuit based on synchronous rectification. IEEE Trans. Power Electron. 2019, 35, 1637–1648. [Google Scholar] [CrossRef]
- Raeber, M.; Heinzelmann, A.; Abdeslam, D.O. Analysis of an active charge balancing method based on a single non-isolated DC/DC converter. IEEE Trans. Ind. Electron. 2021, 68, 2257–2265. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Y.; Qi, H.; Zhang, J. Active battery equalization method based on redundant battery for electric vehicles. IEEE Trans. Veh. Technol. 2019, 68, 7531–7543. [Google Scholar] [CrossRef]
- Narayanaswamy, S.; Steinhorst, S.; Lukasiewycz, M.; Kauer, M.; Chakraborty, S. Optimal Dimensioning and Control of Active Cell Balancing Architectures. IEEE Trans. Veh. Technol. 2019, 68, 9632–9646. [Google Scholar] [CrossRef]
- Gallardo-Lozano, J.; Romero-Cadaval, E.; Milanes-Montero, M.I.; Guerrero-Martinez, M.A. Battery equalization active methods. J. Power Sources 2014, 246, 934–949. [Google Scholar] [CrossRef]
- Pascual, C.; Krein, P.T. Switched capacitor system for automatic series battery equalization. In Proceedings of the IEEE Annual Applied Power Electronics Conference and Exposition (APEC), Atlanta, GA, USA, 27 February 1997; pp. 848–854. [Google Scholar]
- Kobzev, G.A. Switched-capacitor systems for battery equalization. In Proceedings of the IEEE International Scientific and Practical Conference of Students, Post-graduates and Young Scientists. Modern Techniques and Technology, Tomsk, Russia, 3 March 2000; pp. 57–59. [Google Scholar]
- Baughman, A.C.; Ferdowsi, M. Double-tiered switched-capacitor battery charge equalization technique. IEEE Trans. Ind. Electron. 2008, 55, 2277–2285. [Google Scholar] [CrossRef]
- Park, H.S.; Kim, C.H.; Park, K.B.; Moon, G.W.; Lee, J.H. Design of a charge equalizer based on battery modularization. IEEE Trans. Veh. Technol. 2009, 58, 3216–3223. [Google Scholar] [CrossRef]
- Kim, M.Y.; Kim, C.H.; Kim, J.H.; Moon, G.W. A chain structure of switched capacitor for improved cell balancing speed of lithium-ion batteries. IEEE Trans. Ind. Electron. 2013, 61, 3989–3999. [Google Scholar] [CrossRef]
- Ye, Y.; Cheng, K.W.E. Modeling and analysis of series–parallel switched-capacitor voltage equalizer for battery/supercapacitor strings. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 977–983. [Google Scholar] [CrossRef]
- Daowd, M.; Antoine, M.; Omar, N.; Van den Bossche, P.; Van Mierlo, J. Single switched capacitor battery balancing system enhancements. Energies 2013, 6, 2149–2174. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Zhang, L.; Han, Y. System-theoretic analysis of a class of battery equalization systems: Mathematical modeling and performance evaluation. IEEE Trans. Veh. Technol. 2015, 64, 1445–1457. [Google Scholar] [CrossRef]




| n | GC | HVC | TC | GS | HVS | TS |
|---|---|---|---|---|---|---|
| Type A | n − 1 | 0 | n − 1 | 2n | 0 | 2n |
| Type B | n − 1 | n − 2 (2VB) | 2n − 3 | 2n | 0 | 2n |
| Type C | n − 1 | 1 | n | 2n | 4 | 2n + 4 |
| Type D | n | 0 | n | 2n | 4 | 2n + 4 |
| Type E | n − 1 | 1 (NVB) | n | 2n | 0 | 2n |
| Type F | n | 0 | n | 4n | 0 | 4n |
| Type G | 1 | 0 | 1 | 2(n + 1) | 8 | 2n + 10 |
| Parameter | Value |
|---|---|
| Cell voltage(VC) | 3–4.2 V |
| Cell capacity (CB) | 1 F |
| Cell internal resistance (RB) | 50 mΩ |
| Switch resistance (RSW) | 3 mΩ |
| Capacitor (C) | 330 μF |
| Capacitor ESR (ESR) | 30 mΩ |
| Switching frequency (f) | 25 kHz |
| Duty cycle (D) | 50% |
| Dead time | 400 ns (1%) |
| Initial Voltage (V) | VB1 | VB2 | VB3 | VB4 | VB5 | VB6 | VB7 | VB8 |
|---|---|---|---|---|---|---|---|---|
| Scenario 1 | 4.20 | 3.45 | 4.05 | 3.30 | 3.90 | 3.15 | 3.75 | 3.00 |
| Scenario 2 | 4.20 | 4.03 | 3.86 | 3.69 | 3.51 | 3.34 | 3.17 | 3.00 |
| Averaged Balance Time (Sec) | 500 Case 1 | 500 Case 2 | 500 Case 3 | 500 Case 4 | 500 Case AVG | 28,561 Case | Error (%) |
|---|---|---|---|---|---|---|---|
| Type A | 1.1460 | 1.1308 | 1.1403 | 1.1283 | 1.1364 | 1.1442 | 0.682 |
| Type B | 0.4619 | 0.4611 | 0.4632 | 0.4561 | 0.4606 | 0.4608 | 0.043 |
| Type C | 0.4535 | 0.4620 | 0.4574 | 0.4552 | 0.4570 | 0.4559 | −0.241 |
| Type D | 0.4329 | 0.4362 | 0.4373 | 0.4332 | 0.4349 | 0.4351 | 0.046 |
| Type E | 0.5503 | 0.5491 | 0.5517 | 0.5478 | 0.5497 | 0.5508 | 0.200 |
| Type F | 0.9701 | 0.9798 | 0.9744 | 0.9704 | 0.9737 | 0.9785 | 0.491 |
| Type G | 0.7349 | 0.7516 | 0.7491 | 0.7492 | 0.7462 | 0.7402 | −0.811 |
| Averaged Balance Time(Sec) | 1000 Case 1 | 1000 Case 2 | 1000 Case 3 | 1000 Case AVG | Case 1 Error(%) | Case 2 Error(%) | Case 3 Error(%) |
|---|---|---|---|---|---|---|---|
| Type A | 4.0646 | 3.9778 | 4.0772 | 4.0399 | −0.611 | 1.537 | −0.923 |
| Type B | 1.2296 | 1.2090 | 1.2320 | 1.2235 | −0.499 | 1.185 | −0.695 |
| Type C | 1.4984 | 1.4919 | 1.4870 | 1.4924 | −0.402 | 0.034 | 0.362 |
| Type D | 1.3779 | 1.3712 | 1.3714 | 1.3735 | −0.320 | 0.167 | 0.153 |
| Type E | 1.9533 | 1.9210 | 1.9570 | 1.9438 | −0.489 | 1.173 | −0.679 |
| Type F | 1.1211 | 1.1166 | 1.1219 | 1.1199 | −0.107 | 0.295 | −0.179 |
| Type G | 1.6675 | 1.6771 | 1.6777 | 1.6741 | 0.394 | −0.179 | −0.215 |
| Item | n = 4 | n = 8 | |||
|---|---|---|---|---|---|
| Structure | Balance Time (s) | Rank | Balance Time (s) | Rank | |
| Type A | 1.1364 | 7 | 4.0399 | 7 | |
| Type B | 0.4606 | 3 | 1.2235 | 2 | |
| Type C | 0.4570 | 2 | 1.4924 | 4 | |
| Type D | 0.4349 | 1 | 1.3735 | 3 | |
| Type E | 0.5497 | 4 | 1.9438 | 6 | |
| Type F | 0.9737 | 6 | 1.1199 | 1 | |
| Type G | 0.7462 | 5 | 1.6741 | 5 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ho, K.-C.; Liu, Y.-H.; Ye, S.-P.; Chen, G.-J.; Cheng, Y.-S. Mathematical Modeling and Performance Evaluation of Switched-Capacitor-Based Battery Equalization Systems. Electronics 2021, 10, 2629. https://doi.org/10.3390/electronics10212629
Ho K-C, Liu Y-H, Ye S-P, Chen G-J, Cheng Y-S. Mathematical Modeling and Performance Evaluation of Switched-Capacitor-Based Battery Equalization Systems. Electronics. 2021; 10(21):2629. https://doi.org/10.3390/electronics10212629
Chicago/Turabian StyleHo, Kun-Che, Yi-Hua Liu, Song-Pei Ye, Guan-Jhu Chen, and Yu-Shan Cheng. 2021. "Mathematical Modeling and Performance Evaluation of Switched-Capacitor-Based Battery Equalization Systems" Electronics 10, no. 21: 2629. https://doi.org/10.3390/electronics10212629
APA StyleHo, K.-C., Liu, Y.-H., Ye, S.-P., Chen, G.-J., & Cheng, Y.-S. (2021). Mathematical Modeling and Performance Evaluation of Switched-Capacitor-Based Battery Equalization Systems. Electronics, 10(21), 2629. https://doi.org/10.3390/electronics10212629






