Artificial Neural Networks Based Optimization Techniques: A Review
Abstract
1. Introduction
2. Materials and Methods
3. Challenges and Motivations for ANN-Based Optimization
- Ability to accept unlimited inputs and outputs; this unique advantage makes ANNs more important and popular than other AI methods, making them suitable for small or huge dataset analysis.
- Skills to learn and model non-linear and complex relationships, the ANNs can handle various real-life applications in different fields that are complicated and non-linear; this is a very significant advantage.
- Skills of training without complete information and the data may produce output, and the performance depends on the importance of the missing data.
- Distinct from the other deep learning prediction techniques, ANNs do not need any enforcement restrictions on the input variables, such as how the data need to be distributed.
- Skills to create ML: ANNs can learn events and sort wise decisions via commenting to reach similar events better.
- Multi-processing capability, the ANNs can assure numerical efficiency with their power of performing several duties simultaneously.
- Ability to tolerate faults, whereby ANNs can produce output results even if some cells are corrupted, and this advantage allows ANNs to tolerate faults.
- Ability to generalize; as soon as the ANNs learn from the initial input relations, they can conjecture unknown relationships in anonymous data, thus making the model generalized and allowing it to predict unknown data.
- In using distributed memory during the ANN learning, an essential process is adjusting samples and indoctrinating the network according to the desired output by viewing these samples to the network. This process allows the network to achieve and select the instance straight proportionally and by failing to show the event to the network in its full features, and the network may yield false outputs.
- Mysterious network behavior, After the ANN produces an analytical result, it is unexplained why or how selecting these outputs and rejecting the others may make it untrusted in the network.
- Appropriate network architecture design. ANNs have no exact law to determine the best structure design or a proper network structure must be achieved by experience and trial and error.
- Obscure duration time for the network; the optimum results may be produced during the training phase as expected because the network minimizes to a certain level the error on the sample to allow the training completion.
- Depending on the hardware, ANNs need powerful dual processors and ANN structures. This drawback is called the realization that the whole approach is equipment-dependent.
- Gradual corruption slows down the process over time and it suffers relative degradation, and the network problems do not immediately degrade directly.
- Difficulty recognizing network problems if they exist since ANNs are based on numerical data that explain the difficulties in numerical values before being introduced to the ANNs. This could depend on the researcher’s ability to display the mechanism and influence the network’s performance.
4. Review of Optimization Algorithms
5. Neural Networks in Deep Learning
6. Neural Networks Structure Types
6.1. Artificial Neural Networks
6.2. Recurrent Neural Network
6.3. Convolution Neural Network
7. Overview of Neural Networks Enhanced by Optimization Algorithms
7.1. Artificial Neural Networks Based Particle Swarm Optimization
7.2. Artificial Neural Networks-Based Genetic Algorithms
7.3. Artificial Neural Networks-Based Artificial Bee Colony
7.4. Artificial Neural Networks Based Evolutionary Algorithm
7.5. Artificial Neural Networks-Based Backtracking Search Algorithm
7.6. Artificial Neural Networks Based Other Optimization Search Algorithms
7.7. Optimization Search Algorithm-Based Artificial Neural Networks
8. Application on Artificial Neural Networks Based Optimization Algorithms
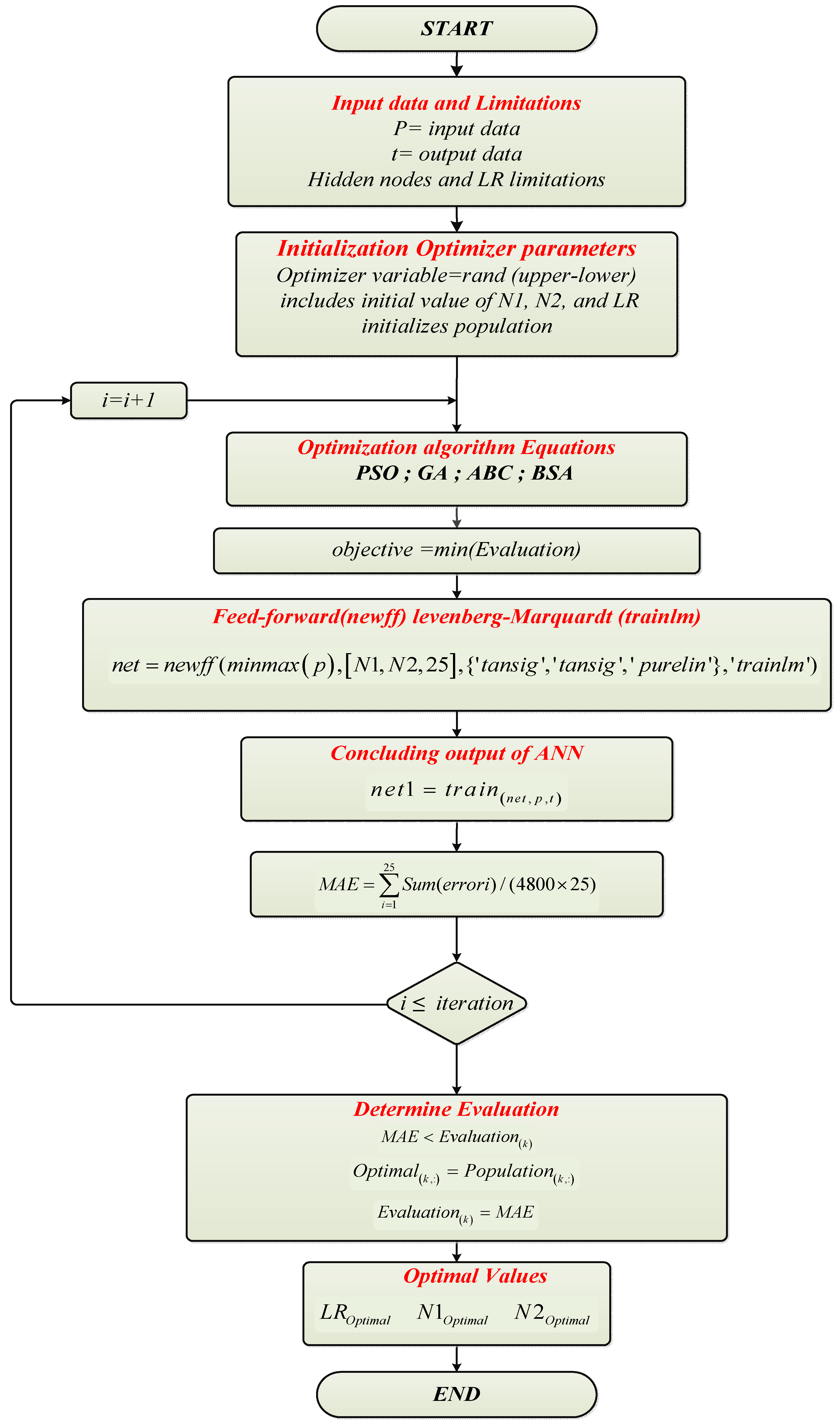
9. Artificial Neural Network Training-Based Optimized Parameters
| Algorithm 1. Pseudocode of ANN training based on optimized parameters obtained from optimization algorithms. |
| 1: Input: (solar irradiances, wind speed, energy price, battery status, gird status, and diesel fuel status) 2: Output: ANN-Net of the binary matrix of (24 × 25) 3: N1 = optimal value obtained 4: N2 = optimal value obtained we can call this net an intelligent binary controller 5: LR = optimal value obtained 6: // ANN 7: Applying Feed-Forward neural network () and Levenberg-Marquardt () 8: 9: 10: 11: 12: 13: 14: Output is an ANN-Net with input data and 25 outputs |
10. Conclusions and Future Work
- Generally, ANN intelligent methods are associated with powerful optimization tools, such as PSO, ABC, BSA, and GA techniques, in various engineering applications, such as electromagnetism, signal processing, and pattern recognition and classification, robotics. Nevertheless, they have a problem with constancy and cost. Thus, future research should be conducted on the appropriate optimization method selection, finding the system’s optimal value, such as cost-effect components with high accuracy.
- The conventional NN technologies create issues; for example, the human brain is highly complex, non-linear, and sensitive [212]. Therefore, additional investigation is needed on human brain monitoring optimization to obtain high accuracy. The low timing loss under the high-risk, complex situation to achieve high reliability, modularity, efficiency, and performance; further investigation of the system’s proper optimization selection is needed.
- Despite the benefits of optimization algorithms in reducing technical loss, low error, and cost, their use in ANN has been very limited. Only computational intelligence optimization algorithms have made significant progress toward optimizing the controller design and the price. As a result, advanced optimization algorithms will be better choices for ANN design.
- Enhancement of ANN parameters with optimization could result from new algorithms that save more time adjusting the ANN toward optimal architectures by avoiding trial and error or random selection. Like this, the optimal solution is considered as a smaller network, a straightforward calculation method, and less time could be achieved.
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
Abbreviations
| ABC | Artificial bee colony |
| ACO | Ant colony optimization |
| ACS | Artificial cooperative search algorithm |
| ADNN | Adadelta deep neural networks |
| ADPSO | Adaptive dynamic particle swarm optimization |
| AFSA | Artificial fish swarm optimization |
| AI | Artificial intelligence |
| AMARM | Adaptive memetic algorithm with a rank-based mutation |
| AMSG | Adam optimization stochastic gradient descent |
| ANFIS | Adaptive neuro-fuzzy inference systems |
| ANN | Artificial neural networks |
| ANN-ABC | Artificial neural networks-based artificial bee colony |
| ANN-BSA | Artificial neural networks-based backtracking search algorithm |
| ANN-BABC | Artificial neural networks-based bainary artificial bee colony |
| ANN-BBSA | Artificial neural networks-based binary backtracking search algorithm |
| ANN-BGA | Artificial neural networks-based binary genetic algorithm |
| ANN-BPSO | Artificial neural networks-based binary particle swarm optimization |
| ANN-GA | Artificial neural networks-based genetic algorithm |
| ANN-PSO | Artificial neural networks-based particle swarm optimization |
| Aop | Airblast-overpressure |
| AP | Affinity propagation |
| BABC | Binary artificial bee colony |
| BBBC | Big bang big crunch |
| BBO | Biogeography-based optimization |
| BBSA | Binary backtracking search algorithm |
| BCA | Bee colony algorithm |
| BFGS | Limited memory Broyden Fletcher Goldfarb Shannon |
| BFO | Bacteria foraging optimization |
| BGA | Binary genetic algorithm |
| BMO | Bird mating optimizer |
| BP | Backpropagation |
| BPNN | Backpropagation neural network |
| BPNN-PSO | Backpropagation neural network-based particle swarm optimization |
| BPSO | Binary particle swarm optimization |
| BSA | Backtracking search algorithm |
| CCG-BP | Correntropy-based conjugate gradient-backpropagation |
| CCPSO | Cultural cooperative particle swarm optimization |
| CNN | Convolutional neural networks |
| COA | Chaotic optimization algorithm |
| CRO | Chemical reaction optimization |
| CS | Cuckoo search |
| CSA | Cuckoo search algorithm |
| CSO | Cat swarm optimization |
| DBBO | Differential biogeography-based optimization |
| DCNN | Deep convolutional neural networks |
| DG | Distributed generation |
| DL | Deep learning |
| DMLP | Deep multilayer perceptron |
| DNN | Deep neural networks |
| DOP | Dynamic optimization problem |
| DSA | Dolphin swarm algorithm |
| EA | Evolutionary algorithms |
| EBP | Elman backpropagation algorithm |
| EFA | Electromagnetism-based firefly algorithm |
| ENN | Elman neural network |
| FA | Firefly algorithm |
| FLANN | Functional link artificial neural networks |
| FLNFN | Functional-link-based neural fuzzy network |
| FNN | Optimize feedforward NN |
| GA | Genetic algorithm |
| GAN | Generative adversarial network |
| GNN | Graph Neural Networks |
| GRNN | Generalized regression neural network |
| GSA | Gravitational search algorithm |
| GWO | Grey wolf algorithm |
| HSA | Harmony search algorithm |
| IT2FNN | Interval type-2 fuzzy neural networks |
| LR | Learning Rate |
| LSA | Lightning search algorithm |
| LSA-ANN | Lightning search algorithm-based particle swarm optimization |
| LSTM | Long short-term memory |
| MAE | Mean absolute error |
| MBSA | Modified backtracking search algorithm |
| MISO | Multiple-input single-output |
| ML | Machine learning |
| MLP | Multilayer perceptron |
| MNN | Modular neural network |
| MOA | Microcanonical optimization algorithm |
| MSE | Mean squire error |
| MVO | Multiverse optimizer |
| NN | Neural networks |
| NNA | Neural network algorithm |
| NNIT | Neural network-based information transfer |
| NNRW | Neural network with random weights |
| NSGA | Non-dominated sorting GA |
| OBD | Optimal brain damage |
| OPSONN | Opposition-based PSO neural network |
| PI | Proportional integral |
| PID | Proportional integral derivative |
| PL | Path Loss |
| PMS | Periodic mutation strategy |
| PNN | Probabilistic neural network |
| PSO | Particle swarm optimization |
| PSO-DNN | Particle swarm optimization-based deep neural network |
| PV | Photovoltaic |
| QLSA | Quantum-inspired lightning search algorithm |
| RBF | Radial basis functions |
| RBFNN | Radial basis functions neural network |
| RNN | Recurrent neural networks |
| RSW | Resistance spot welding optimization |
| SAPSO | Simulation annealing algorithm with particle swarm optimization |
| SGD | Stochastic gradient descent |
| SLFN | Single-layer feed-forward network |
| SOS | Symbiotic organisms search |
| SPS-PSO | Self-adaptive parameters and strategy-based PSO |
| SSO | Simplified swarm optimization |
| TCPSO | Tent-map chaotic particle swarm optimization |
| TLBO | Teaching–learning-based optimization algorithm |
| TO | Optimization topology |
| TPSO | Taguchi particle swarm optimization |
| TSEMO | Thompson sampling efficient multi-objective optimization |
| UCI | University of California Irvine |
| UCS | Unconfined compressive strength |
| WEC | Wave energy converters |
| WOA | Whale optimization algorithm |
References
- Oliver, J.M.; Esteban, M.D.; López-Gutiérrez, J.-S.; Negro, V.; Neves, M.G. Optimizing Wave Overtopping Energy Converters by ANN Modelling: Evaluating the Overtopping Rate Forecasting as the First Step. Sustainability 2021, 13, 1483. [Google Scholar] [CrossRef]
- Mosavi, A.; Salimi, M.; Ardabili, S.F.; Rabczuk, T.; Shamshirband, S.; Varkonyi-Koczy, A.R. State of the Art of Machine Learning Models in Energy Systems, a Systematic Review. Energies 2019, 12, 1301. [Google Scholar] [CrossRef]
- Zhou, H.; Sun, G.; Fu, S.; Liu, J.; Zhou, X.; Zhou, J. A big data mining approach of PSO-Based BP neural network for financial risk management with IoT. IEEE Access 2019, 7, 154035–154043. [Google Scholar] [CrossRef]
- Schweidtmann, A.M.; Mitsos, A. Deterministic Global Optimization with Artificial Neural Networks Embedded. J. Optim. Theory Appl. 2019, 180, 925–948. [Google Scholar] [CrossRef]
- Li, T.; Chan, Y.H.; Lun, D.P.K. Improved Multiple-Image-Based Reflection Removal Algorithm Using Deep Neural Networks. IEEE Trans. Image Process. 2021, 30, 68–79. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Ardabili, S.; Mosavi, A.; Dehghani, M.; Várkonyi-Kóczy, A.R. Deep Learning and Machine Learning in Hydrological Processes Climate Change and Earth Systems a Systematic Review. In Engineering for Sustainable Future; Springer: Berlin/Heidelberg, Germany, 2019; Volume 101, pp. 52–62. [Google Scholar] [CrossRef]
- Rani, P.; Kavita; Verma, S.; Nguyen, G.N. Mitigation of Black Hole and Gray Hole Attack Using Swarm Inspired Algorithm with Artificial Neural Network. IEEE Access 2020, 8, 121755–121764. [Google Scholar] [CrossRef]
- Milad, A.; Adwan, I.; Majeed, S.A.; Yusoff, N.I.M.; Al-Ansari, N.; Yaseen, Z.M. Emerging Technologies of Deep Learning Models Development for Pavement Temperature Prediction. IEEE Access 2021, 9, 23840–23849. [Google Scholar] [CrossRef]
- Moayedi, H.; Bui, D.T.; Gör, M.; Pradhan, B.; Jaafari, A. The feasibility of three prediction techniques of the artificial neural network, adaptive neuro-fuzzy inference system, and hybrid particle swarm optimization for assessing the safety factor of cohesive slopes. ISPRS Int. J. Geo-Inform. 2019, 8, 391. [Google Scholar] [CrossRef]
- Sasaki, H.; Igarashi, H. Topology optimization accelerated by deep learning. IEEE Trans. Magn. 2019, 55, 1–5. [Google Scholar] [CrossRef]
- Shamshirband, S.; Mosavi, A.; Rabczuk, T.; Nabipour, N.; Chau, K. Prediction of significant wave height; comparison between nested grid numerical model, and machine learning models of artificial neural networks, extreme learning and support vector machines. Eng. Appl. Comput. Fluid Mech. 2020, 14, 805–817. [Google Scholar] [CrossRef]
- Gonçalves, R.; Ribeiro, V.M.; Pereira, F.L.; Rocha, A.P. Deep learning in exchange markets. Inf. Econ. Policy 2019, 47, 38–51. [Google Scholar] [CrossRef]
- Mosavi, A.; Ardabili, S.; Várkonyi-Kóczy, A.R. List of Deep Learning Models. In Engineering for Sustainable Future; Springer: Berlin/Heidelberg, Germany, 2019; Volume 101, pp. 202–214. [Google Scholar] [CrossRef]
- Kim, K.G. Deep learning book review. Nature 2019, 29, 1–73. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Cecchetti, R.; de Paulis, F.; Olivieri, C.; Orlandi, A.; Buecker, M. Effective PCB Decoupling Optimization by Combining an Iterative Genetic Algorithm and Machine Learning. Electronics 2020, 9, 1243. [Google Scholar] [CrossRef]
- Mijwil, M.M. Artificial Neural Networks Advantages and Disadvantages. Linkedin 2018, 1–2. Available online: https://www.linkedin.com/pulse/artificial-neural-networks-advantages-disadvantages-maad-m-mijwel/ (accessed on 2 April 2021).
- Nabipour, N.; Dehghani, M.; Mosavi, A.; Shamshirband, S. Short-Term Hydrological Drought Forecasting Based on Different Nature-Inspired Optimization Algorithms Hybridized with Artificial Neural Networks. IEEE Access 2020, 8, 15210–15222. [Google Scholar] [CrossRef]
- Jafarian, F.; Taghipour, M.; Amirabadi, H. Application of artificial neural network and optimization algorithms for optimizing surface roughness, tool life and cutting forces in turning operation. J. Mech. Sci. Technol. 2013, 27, 1469–1477. [Google Scholar] [CrossRef]
- Askarzadeh, A.; Rezazadeh, A. Artificial neural network training using a new efficient optimization algorithm. Appl. Soft Comput. J. 2013, 13, 1206–1213. [Google Scholar] [CrossRef]
- Zappone, A.; Di Renzo, M.; Debbah, M.; Lam, T.T.; Qian, X. Model-Aided Wireless Artificial Intelligence: Embedding Expert Knowledge in Deep Neural Networks for Wireless System Optimization. IEEE Veh. Technol. Mag. 2019, 14, 60–69. [Google Scholar] [CrossRef]
- Jiang, J.; Fan, J.A. Simulator-based training of generative neural networks for the inverse design of metasurfaces. Nanophotonics 2019, 9, 1059–1069. [Google Scholar] [CrossRef]
- Mutlag, A.H.; Shareef, H.; Mohamed, A.; Hannan, M.A.; Abd Ali, J. An improved fuzzy logic controller design for PV inverters utilizing differential search optimization. Int. J. Photoenergy 2014, 2014. [Google Scholar] [CrossRef]
- Aljarah, I.; Al-Zoubi, A.M.; Faris, H.; Hassonah, M.A.; Mirjalili, S.; Saadeh, H. Simultaneous Feature Selection and Support Vector Machine Optimization Using the Grasshopper Optimization Algorithm. Cogn. Comput. 2018, 10, 478–495. [Google Scholar] [CrossRef]
- Ghazvinei, P.T.; Darvishi, H.H.; Mosavi, A.; bin Wan Yusof, K.; Alizamir, M.; Shamshirband, S.; Chau, K. Sugarcane growth prediction based on meteorological parameters using extreme learning machine and artificial neural network. Eng. Appl. Comput. Fluid Mech. 2018, 12, 738–749. [Google Scholar] [CrossRef]
- Ardabili, S.; Mosavi, A.; Várkonyi-Kóczy, A.R. Systematic Review of Deep Learning and Machine Learning Models in Biofuels Research. Engineering for Sustainable Future 2019, Volume 101, 19–32. [Google Scholar] [CrossRef]
- Taghizadeh-Mehrjardi, R.; Emadi, M.; Cherati, A.; Heung, B.; Mosavi, A.; Scholten, T. Bio-Inspired Hybridization of Artificial Neural Networks: An Application for Mapping the Spatial Distribution of Soil Texture Fractions. Remote Sens. 2021, 13, 1025. [Google Scholar] [CrossRef]
- Gharghan, S.K.; Nordin, R.; Ismail, M.; Ali, J.A. Accurate Wireless Sensor Localization Technique Based on Hybrid PSO-ANN Algorithm for Indoor and Outdoor Track Cycling. IEEE Sens. J. 2016, 16, 529–541. [Google Scholar] [CrossRef]
- Ahmed, M.; Mohamed, A.; Homod, R.; Shareef, H. Hybrid LSA-ANN Based Home Energy Management Scheduling Controller for Residential Demand Response Strategy. Energies 2016, 9, 716. [Google Scholar] [CrossRef]
- Yu, J.; Xi, L.; Wang, S. An improved particle swarm optimization for evolving feedforward artificial neural networks. Neural Process. Lett. 2007, 26, 217–231. [Google Scholar] [CrossRef]
- Dineva, A.; Mosavi, A.; Ardabili, S.F.; Vajda, I.; Shamshirband, S.; Rabczuk, T.; Chau, K.-W. Review of Soft Computing Models in Design and Control of Rotating Electrical Machines. Energies 2019, 12, 1049. [Google Scholar] [CrossRef]
- Ayub, S.; Guan, B.H.; Ahmad, F.; Oluwatobi, Y.A.; Nisa, Z.U.; Javed, M.F.; Mosavi, A. Graphene and Iron Reinforced Polymer Composite Electromagnetic Shielding Applications: A Review. Polymers 2021, 13, 2580. [Google Scholar] [CrossRef] [PubMed]
- Ayub, S.; Guan, B.H.; Ahmad, F.; Javed, M.F.; Mosavi, A.; Felde, I. Preparation Methods for Graphene Metal and Polymer Based Composites for EMI Shielding Materials: State of the Art Review of the Conventional and Machine Learning Methods. Metals 2021, 11, 1164. [Google Scholar] [CrossRef]
- Moayedi, H.; Mosavi, A. An Innovative Metaheuristic Strategy for Solar Energy Management through a Neural Networks Framework. Energies 2021, 14, 1196. [Google Scholar] [CrossRef]
- Nosratabadi, S.; Mosavi, A.; Duan, P.; Ghamisi, P.; Filip, F.; Band, S.S.; Reuter, U.; Gama, J.; Gandomi, A.H. Data Science in Economics: Comprehensive Review of Advanced Machine Learning and Deep Learning Methods. Mathematics 2020, 8, 1799. [Google Scholar] [CrossRef]
- Mosavi, A.; Faghan, Y.; Ghamisi, P.; Duan, P.; Ardabili, S.F.; Salwana, E.; Band, S.S. Comprehensive Review of Deep Reinforcement Learning Methods and Applications in Economics. Mathematics 2020, 8, 1640. [Google Scholar] [CrossRef]
- Chen, H.; Heidari, A.A.; Chen, H.; Wang, M.; Pan, Z.; Gandomi, A.H. Multi-population differential evolution-assisted Harris hawks optimization: Framework and case studies. Futur. Gener. Comput. Syst. 2020, 111, 175–198. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, B.; Wang, J.; Chen, C. Networked microgrids for self-healing power systems. IEEE Trans. Smart Grid 2016, 7, 310–319. [Google Scholar] [CrossRef]
- Tian, Y.; Peng, S.; Zhang, X.; Rodemann, T.; Tan, K.C.; Jin, Y. A Recommender System for Metaheuristic Algorithms for Continuous Optimization Based on Deep Recurrent Neural Networks. IEEE Trans. Artif. Intell. 2020, 1, 5–18. [Google Scholar] [CrossRef]
- Balachennaiah, P.; Suryakalavathi, M.; Nagendra, P. Optimizing real power loss and voltage stability limit of a large transmission network using firefly algorithm. Eng. Sci. Technol. Int. J. 2016, 19, 800–810. [Google Scholar] [CrossRef]
- Wong, L.A.; Shareef, H.; Mohamed, A.; Ibrahim, A.A. Novel quantum-inspired firefly algorithm for optimal power quality monitor placement. Front. Energy 2014, 8, 254–260. [Google Scholar] [CrossRef]
- Ramli, L.; Sam, Y.M.; Mohamed, Z.; Khairi Aripin, M.; Fahezal Ismail, M.; Ramli, L. Composite nonlinear feedback control with multi-objective particle swarm optimization for active front steering system. J. Teknol. 2015, 72, 13–20. [Google Scholar] [CrossRef][Green Version]
- Lin, M.H.; Tsai, J.F.; Yu, C.S. A review of deterministic optimization methods in engineering and management. Math. Probl. Eng. 2012, 2012, 756023. [Google Scholar] [CrossRef]
- Bui, D.K.; Nguyen, T.N.; Ngo, T.D.; Nguyen-Xuan, H. An artificial neural network (ANN) expert system enhanced with the electromagnetism-based firefly algorithm (EFA) for predicting the energy consumption in buildings. Energy 2020, 190, 116370. [Google Scholar] [CrossRef]
- Hannan, M.A.; Ali, J.A.; Hossain Lipu, M.S.; Mohamed, A.; Ker, P.J.; Indra Mahlia, T.M.; Mansor, M.; Hussain, A.; Muttaqi, K.M.; Dong, Z.Y. Role of optimization algorithms based fuzzy controller in achieving induction motor performance enhancement. Nat. Commun. 2020, 11, 3792. [Google Scholar] [CrossRef]
- Hannan, M.A.; Ali, J.A.; Mohamed, A.; Hussain, A. Optimization techniques to enhance the performance of induction motor drives: A review. Renew. Sustain. Energy Rev. 2018, 81, 1611–1626. [Google Scholar] [CrossRef]
- Miao, K.; Feng, Q.; Kuang, W. Particle Swarm Optimization Combined with Inertia-Free Velocity and Direction Search. Electronics 2021, 10, 597. [Google Scholar] [CrossRef]
- Garro, B.A.; Vázquez, R.A. Designing Artificial Neural Networks Using Particle Swarm Optimization Algorithms. Comput. Intell. Neurosci. 2015, 2015. [Google Scholar] [CrossRef] [PubMed]
- Conforth, M.; Meng, Y. Toward evolving Neural networks using Bio-inspired algorithms. In Proceedings of the Artificial Intelligence and Soft Computing—ICAISC 2008, Zakopane, Poland, 22–26 June 2008; pp. 413–419. [Google Scholar]
- Garro, B.A.; Sossa, H.; Vázquez, R.A. Back-Propagation vs Particle Swarm Optimization Algorithm: Which Algorithm is better to adjust the Synaptic Weights of a Feed-Forward ANN? Int. J. Artif. Intell. 2011, 7, 208–218. [Google Scholar]
- Rosli, A.D.; Adenan, N.S.; Hashim, H.; Abdullah, N.E.; Sulaiman, S.; Baharudin, R. Application of Particle Swarm Optimization Algorithm for Optimizing ANN Model in Recognizing Ripeness of Citrus. IOP Conf. Ser. Mater. Sci. Eng. 2018, 340. [Google Scholar] [CrossRef]
- Lazzús, J.A. Neural network-particle swarm modeling to predict thermal properties. Math. Comput. Model. 2013, 57, 2408–2418. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Do, Q.H. A hybrid Gravitational Search Algorithm and back-propagation for training feedforward neural networks. In Proceedings of the Advances in Intelligent Systems and Computing; Springer: Berlin/Heidelberg, Germany, 2015; Volume 326, pp. 381–392. [Google Scholar]
- Chaitanya, S.M.K.; Rajesh Kumar, P. Oppositional Gravitational Search Algorithm and Artificial Neural Network-based Classification of Kidney Images. J. Intell. Syst. 2020, 29, 485–496. [Google Scholar] [CrossRef]
- Momeni, E.; Yarivand, A.; Dowlatshahi, M.B.; Armaghani, D.J. An efficient optimal neural network based on gravitational search algorithm in predicting the deformation of geogrid-reinforced soil structures. Transp. Geotech. 2021, 26, 100446. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, Z.; Chen, Y. Hybrid teaching–learning-based optimization and neural network algorithm for engineering design optimization problems. Knowl.-Based Syst. 2020, 187. [Google Scholar] [CrossRef]
- Sun, Y.; Cao, M.; Sun, Y.; Gao, H.; Lou, F.; Liu, S.; Xia, Q. Uncertain data stream algorithm based on clustering RBF neural network. Microprocess. Microsyst. 2021, 81, 103731. [Google Scholar] [CrossRef]
- Faris, H.; Aljarah, I.; Al-Madi, N.; Mirjalili, S. Optimizing the Learning Process of Feedforward Neural Networks Using Lightning Search Algorithm. Int. J. Artif. Intell. Tools 2016, 25, 1650033. [Google Scholar] [CrossRef]
- Sarker, M.R.; Mohamed, R.; Saad, M.H.M.; Mohamed, A. DSPACE Controller-based enhanced piezoelectric energy harvesting system using PI-lightning search algorithm. IEEE Access 2019, 7, 3610–3626. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; He, K.; Li, D.; Xu, X.; Gong, Y. Intelligent feature recognition for STEP-NC-compliant manufacturing based on artificial bee colony algorithm and back propagation neural network. J. Manuf. Syst. 2021. [Google Scholar] [CrossRef]
- Li, C. Biodiversity assessment based on artificial intelligence and neural network algorithms. Microprocess. Microsyst. 2020, 79, 103321. [Google Scholar] [CrossRef]
- Civicioglu, P. Backtracking Search Optimization Algorithm for numerical optimization problems. Appl. Math. Comput. 2013, 219, 8121–8144. [Google Scholar] [CrossRef]
- Guha, D.; Roy, P.K.; Banerjee, S. Application of backtracking search algorithm in load frequency control of multi-area interconnected power system. Ain Shams Eng. J. 2018, 9, 257–276. [Google Scholar] [CrossRef]
- Abdolrasol, M.G.M.; Mohamed, A.; Hannan, M.A. Virtual power plant and microgrids controller for energy management based on optimization techniques. J. Electr. Syst. 2017, 13, 285–294. [Google Scholar]
- Shareef, H.; Ibrahim, A.A.; Mutlag, A.H. Lightning search algorithm. Appl. Soft Comput. J. 2015, 36, 315–333. [Google Scholar] [CrossRef]
- Abd Ali, J.; Hannan, M.; Mohamed, A. A Novel Quantum-Behaved Lightning Search Algorithm Approach to Improve the Fuzzy Logic Speed Controller for an Induction Motor Drive. Energies 2015, 8, 13112–13136. [Google Scholar] [CrossRef]
- Liu, L.; Liu, W.; Cartes, D.A. Particle swarm optimization-based parameter identification applied to permanent magnet synchronous motors. Eng. Appl. Artif. Intell. 2008, 21, 1092–1100. [Google Scholar] [CrossRef]
- Tabassum, M.; Mathew, K. A Genetic Algorithm Analysis towards Optimization solutions. Int. J. Digit. Inf. Wirel. Commun. 2014, 4, 124–142. [Google Scholar] [CrossRef]
- Chao, K.-H.; Hsieh, C.-C. Photovoltaic Module Array Global Maximum Power Tracking Combined with Artificial Bee Colony and Particle Swarm Optimization Algorithm. Electronics 2019, 8, 603. [Google Scholar] [CrossRef]
- Xue, Y.; Tang, T.; Liu, A.X. Large-scale feedforward neural network optimization by a self-adaptive strategy and parameter based particle swarm optimization. IEEE Access 2019, 7, 52473–52483. [Google Scholar] [CrossRef]
- Chen, D.; Zou, F.; Lu, R.; Li, S. Backtracking search optimization algorithm based on knowledge learning. Inf. Sci. 2019, 473, 202–226. [Google Scholar] [CrossRef]
- Sahu, R.K.; Panda, S.; Padhan, S. A novel hybrid gravitational search and pattern search algorithm for load frequency control of nonlinear power system. Appl. Soft Comput. J. 2015, 29, 310–327. [Google Scholar] [CrossRef]
- Yang, X.S.; He, X. Firefly algorithm: Recent advances and applications. Int. J. Swarm Intell. 2013, 1, 36. [Google Scholar] [CrossRef]
- Hassan, L.; Abdel-Nasser, M.; Saleh, A.; Omer, O.A.; Puig, D. Efficient Stain-Aware Nuclei Segmentation Deep Learning Framework for Multi-Center Histopathological Images. Electronics 2021, 10, 954. [Google Scholar] [CrossRef]
- Arora, V.; Mahla, S.K.; Leekha, R.S.; Dhir, A.; Lee, K.; Ko, H. Intervention of Artificial Neural Network with an Improved Activation Function to Predict the Performance and Emission Characteristics of a Biogas Powered Dual Fuel Engine. Electronics 2021, 10, 584. [Google Scholar] [CrossRef]
- Ketkar, N. Convolutional Neural Networks. In Deep Learning with Python; Apress: Berkeley, CA, USA, 2017; pp. 63–78. [Google Scholar]
- Medsker, L.R.; Jain, L.C. Recurrent Neural Networks Design and Applications. J. Chem. Inf. Model. 2013, 53, 1689–1699. [Google Scholar]
- Liu, J.; Gong, M.; Miao, Q.; Wang, X.; Li, H. Structure Learning for Deep Neural Networks Based on Multiobjective Optimization. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 2450–2463. [Google Scholar] [CrossRef]
- Rusek, K.; Suarez-Varela, J.; Almasan, P.; Barlet-Ros, P.; Cabellos-Aparicio, A. RouteNet: Leveraging Graph Neural Networks for Network Modeling and Optimization in SDN. IEEE J. Sel. Areas Commun. 2020, 38, 2260–2270. [Google Scholar] [CrossRef]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The graph neural network model. IEEE Trans. Neural Netw. 2009, 20, 61–80. [Google Scholar] [CrossRef]
- Takayama, K.; Morva, A.; Fujikawa, M.; Hattori, Y.; Obata, Y.; Nagai, T. Formula optimization of theophylline controlled-release tablet based on artificial neural networks. J. Control. Release 2000, 68, 175–186. [Google Scholar] [CrossRef]
- Wu, H.; Zhou, Y.; Luo, Q.; Basset, M.A. Training feedforward neural networks using symbiotic organisms search algorithm. Comput. Intell. Neurosci. 2016, 2016. [Google Scholar] [CrossRef]
- Alsenwi, M.; Yaqoob, I.; Pandey, S.R.; Tun, Y.K.; Bairagi, A.K.; Kim, L.W.; Hong, C.S. Towards coexistence of cellular and WiFi networks in unlicensed spectrum: A neural networks based approach. IEEE Access 2019, 7, 110023–110034. [Google Scholar] [CrossRef]
- Kusy, M.; Zajdel, R. Application of Reinforcement Learning Algorithms for the Adaptive Computation of the Smoothing Parameter for Probabilistic Neural Network. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 2163–2175. [Google Scholar] [CrossRef]
- Suganthi, L.; Iniyan, S.; Samuel, A.A. Applications of fuzzy logic in renewable energy systems—A review. Renew. Sustain. Energy Rev. 2015, 48, 585–607. [Google Scholar] [CrossRef]
- Na, W.; Feng, F.; Zhang, C.; Zhang, Q.J. A Unified Automated Parametric Modeling Algorithm Using Knowledge-Based Neural Network and l1 Optimization. IEEE Trans. Microw. Theory Tech. 2017, 65, 729–745. [Google Scholar] [CrossRef]
- Guo, S.; Pei, H.; Wu, F.; He, Y.; Liu, D. Modeling of solar field in direct steam generation parabolic trough based on heat transfer mechanism and artificial neural network. IEEE Access 2020, 8, 78565–78575. [Google Scholar] [CrossRef]
- Do Nascimento, E.O.; De Oliveira, L.N. Numerical Optimization of Flight Trajectory for Rockets via Artificial Neural Networks. IEEE Lat. Am. Trans. 2017, 15, 1556–1565. [Google Scholar] [CrossRef]
- Rayas-Sánchez, J.E. EM-based optimization of microwave circuits using artificial neural networks: The state-of-the-art. IEEE Trans. Microw. Theory Tech. 2004, 52, 420–435. [Google Scholar] [CrossRef]
- Chaffart, D.; Ricardez-Sandoval, L.A. Optimization and control of a thin film growth process: A hybrid first principles/artificial neural network based multiscale modelling approach. Comput. Chem. Eng. 2018, 119, 465–479. [Google Scholar] [CrossRef]
- Zhang, Z.; Cheng, Q.S.; Chen, H.; Jiang, F. An Efficient Hybrid Sampling Method for Neural Network-Based Microwave Component Modeling and Optimization. IEEE Microw. Wirel. Components Lett. 2020, 30, 625–628. [Google Scholar] [CrossRef]
- Deodhare, D.; Vidyasagar, M.; Sathiya Keerthi, S. Synthesis of fault-tolerant feedforward neural networks using minimax optimization. IEEE Trans. Neural Netw. 1998, 9, 891–900. [Google Scholar] [CrossRef]
- Song, X.; Kong, F.; Zhan, C.; Han, J. Hybrid Optimization Rainfall-Runoff Simulation Based on Xinanjiang Model and Artificial Neural Network. J. Hydrol. Eng. 2012, 17, 1033–1041. [Google Scholar] [CrossRef]
- Tian, W.; Liao, Z.; Zhang, J. An optimization of artificial neural network model for predicting chlorophyll dynamics. Ecol. Modell. 2017, 364, 42–52. [Google Scholar] [CrossRef]
- Ochoa-Estopier, L.M.; Jobson, M.; Smith, R. Operational optimization of crude oil distillation systems using artificial neural networks. Comput. Chem. Eng. 2013, 59, 178–185. [Google Scholar] [CrossRef]
- Cui, S. Artificial neural network-based optimization of extraction of anthocyanins in black rice. Food Sci. Technol. 2012, 1. Available online: https://en.cnki.com.cn/Article_en/CJFDTotal-SSPJ201201057.htm (accessed on 18 March 2021).
- De Oliveira, M.B.W.; De Almeida Neto, A. Optimization of traffic lights timing based on Artificial Neural Networks. In Proceedings of the 2014 17th IEEE International Conference on Intelligent Transportation Systems, ITSC 2014, Qingdao, China, 8–11 October 2014; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2014; pp. 1921–1922. [Google Scholar]
- Mukherjee, A.; Jain, D.K.; Goswami, P.; Xin, Q.; Yang, L.; Rodrigues, J.J.P.C. Back Propagation Neural Network Based Cluster Head Identification in MIMO Sensor Networks for Intelligent Transportation Systems. IEEE Access 2020, 8, 28524–28532. [Google Scholar] [CrossRef]
- Rusydi, M.I.; Anandika, A.; Rahmadya, B.; Fahmy, K.; Rusydi, A. Implementation of Grading Method for Gambier Leaves Based on Combination of Area, Perimeter, and Image Intensity Using Backpropagation Artificial Neural Network. Electronics 2019, 8, 1308. [Google Scholar] [CrossRef]
- Yang, F.; Moayedi, H.; Mosavi, A. Predicting the Degree of Dissolved Oxygen Using Three Types of Multi-Layer Perceptron-Based Artificial Neural Networks. Sustainability 2021, 13, 9898. [Google Scholar] [CrossRef]
- Dubey, S.R.; Chakraborty, S.; Roy, S.K.; Mukherjee, S.; Singh, S.K.; Chaudhuri, B.B. DiffGrad: An Optimization Method for Convolutional Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 4500–4511. [Google Scholar] [CrossRef]
- Zhao, L.; Hu, Z. Detection of Wildfire Smoke Images Based on a Densely Dilated Convolutional Network. Electronics 2019, 8, 1131. [Google Scholar] [CrossRef]
- Zhao, E.; Liu, Y.; Zhang, J.; Tian, Y. Forest Fire Smoke Recognition Based on Anchor Box Adaptive Generation Method. Electronics 2021, 10, 566. [Google Scholar] [CrossRef]
- Marini, F.; Walczak, B. Particle swarm optimization (PSO). A tutorial. Chemom. Intell. Lab. Syst. 2015, 149, 153–165. [Google Scholar] [CrossRef]
- Kerdphol, T.; Fuji, K.; Mitani, Y.; Watanabe, M.; Qudaih, Y. Optimization of a battery energy storage system using particle swarm optimization for stand-alone microgrids. Int. J. Electr. Power Energy Syst. 2016, 81, 32–39. [Google Scholar] [CrossRef]
- Momeni, E.; Jahed Armaghani, D.; Hajihassani, M.; Mohd Amin, M.F. Prediction of uniaxial compressive strength of rock samples using hybrid particle swarm optimization-based artificial neural networks. Meas. J. Int. Meas. Confed. 2015, 60, 50–63. [Google Scholar] [CrossRef]
- Xiao, G.; Juan, Z.; Zhang, C. Detecting trip purposes from smartphone-based travel surveys with artificial neural networks and particle swarm optimization. Transp. Res. Part C Emerg. Technol. 2016, 71, 447–463. [Google Scholar] [CrossRef]
- Li, N.; Chen, J.; Yuan, Y.; Tian, X.; Han, Y.; Xia, M. A Wi-Fi Indoor Localization Strategy Using Particle Swarm Optimization Based Artificial Neural Networks. Int. J. Distrib. Sens. Netw. 2016, 12, 4583147. [Google Scholar] [CrossRef]
- Qiao, J.F.; Lu, C.; Li, W.J. Design of dynamic modular neural network based on adaptive particle swarm optimization algorithm. IEEE Access 2018, 6, 10850–10857. [Google Scholar] [CrossRef]
- Yadav, N.; Yadav, A.; Kumar, M.; Kim, J.H. An efficient algorithm based on artificial neural networks and particle swarm optimization for solution of nonlinear Troesch’s problem. Neural Comput. Appl. 2017, 28, 171–178. [Google Scholar] [CrossRef]
- Das, G.; Pattnaik, P.K.; Padhy, S.K. Artificial Neural Network trained by Particle Swarm Optimization for non-linear channel equalization. Expert Syst. Appl. 2014, 41, 3491–3496. [Google Scholar] [CrossRef]
- Serizawa, T.; Fujita, H. Optimization of convolutional neural network using the linearly decreasing weight particle swarm optimization. arXiv 2020, arXiv:2001.05670. [Google Scholar]
- Shi, W.; Liu, D.; Cheng, X.; Li, Y.; Zhao, Y. Particle Swarm Optimization-Based Deep Neural Network for Digital Modulation Recognition. IEEE Access 2019, 7, 104591–104600. [Google Scholar] [CrossRef]
- Aljanad, A.; Tan, N.M.L.; Agelidis, V.G.; Shareef, H. Neural Network Approach for Global Solar Irradiance Prediction at Extremely Short-Time-Intervals Using Particle Swarm Optimization Algorithm. Energies 2021, 14, 1213. [Google Scholar] [CrossRef]
- Wu, S.; Yang, J.; Zhang, R.; Ono, H. Prediction of Endpoint Sulfur Content in KR Desulfurization Based on the Hybrid Algorithm Combining Artificial Neural Network with SAPSO. IEEE Access 2020, 8, 33778–33791. [Google Scholar] [CrossRef]
- Zhang, G.; Tan, F.; Wu, Y. Ship Motion Attitude Prediction Based on an Adaptive Dynamic Particle Swarm Optimization Algorithm and Bidirectional LSTM Neural Network. IEEE Access 2020, 8, 90087–90098. [Google Scholar] [CrossRef]
- Wang, J.; Kumbasar, T. Parameter optimization of interval Type-2 fuzzy neural networks based on PSO and BBBC methods. IEEE/CAA J. Autom. Sin. 2019, 6, 247–257. [Google Scholar] [CrossRef]
- Abdolrasol, M.G.M.; Mohamed, R.; Hannan, M.A.; Al-Shetwi, A.Q.; Mansor, M.; Blaabjerg, F.G. Artificial Neural Network Based Particle Swarm Optimization for Microgrid Optimal Energy Scheduling. IEEE Trans. Power Electron. 2021. [Google Scholar] [CrossRef]
- Roy, P.; Mahapatra, G.S.; Dey, K.N. Forecasting of software reliability using neighborhood fuzzy particle swarm optimization based novel neural network. IEEE/CAA J. Autom. Sin. 2019, 6, 1365–1383. [Google Scholar] [CrossRef]
- Lin, H.; Zhao, B.; Liu, D.; Alippi, C. Data-based fault tolerant control for affine nonlinear systems through particle swarm optimized neural networks. IEEE/CAA J. Autom. Sin. 2020, 7, 954–964. [Google Scholar] [CrossRef]
- Hajihassani, M.; Jahed Armaghani, D.; Sohaei, H.; Tonnizam Mohamad, E.; Marto, A. Prediction of airblast-overpressure induced by blasting using a hybrid artificial neural network and particle swarm optimization. Appl. Acoust. 2014, 80, 57–67. [Google Scholar] [CrossRef]
- Gaur, S.; Ch, S.; Graillot, D.; Chahar, B.R.; Kumar, D.N. Application of Artificial Neural Networks and Particle Swarm Optimization for the Management of Groundwater Resources. Water Resour. Manag. 2013, 27, 927–941. [Google Scholar] [CrossRef]
- Chan, K.Y.; Dillon, T.; Chang, E.; Singh, J. Prediction of short-term traffic variables using intelligent swarm-based neural networks. IEEE Trans. Control Syst. Technol. 2013, 21, 263–274. [Google Scholar] [CrossRef]
- Lin, C.J.; Chen, C.H.; Lin, C.T. A hybrid of cooperative particle swarm optimization and cultural algorithm for neural fuzzy networks and its prediction applications. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2009, 39, 55–68. [Google Scholar] [CrossRef]
- Volkan Pehlivanoglu, Y. A new particle swarm optimization method enhanced with a periodic mutation strategy and neural networks. IEEE Trans. Evol. Comput. 2013, 17, 436–452. [Google Scholar] [CrossRef]
- Kalani, H.; Sardarabadi, M.; Passandideh-Fard, M. Using artificial neural network models and particle swarm optimization for manner prediction of a photovoltaic thermal nanofluid based collector. Appl. Therm. Eng. 2017, 113, 1170–1177. [Google Scholar] [CrossRef]
- Song, Y.; Chen, Z.; Yuan, Z. New chaotic PSO-based neural network predictive control for nonlinear process. IEEE Trans. Neural Netw. 2007, 18, 595–600. [Google Scholar] [CrossRef]
- Chen, J.F.; Do, Q.H.; Hsieh, H.N. Training artificial neural networks by a hybrid PSO-CS Algorithm. Algorithms 2015, 8, 292–308. [Google Scholar] [CrossRef]
- Chou, P.Y.; Tsai, J.T.; Chou, J.H. Modeling and Optimizing Tensile Strength and Yield Point on a Steel Bar Using an Artificial Neural Network with Taguchi Particle Swarm Optimizer. IEEE Access 2016, 4, 585–593. [Google Scholar] [CrossRef]
- Chai, R.; Ling, S.H.; Hunter, G.P.; Tran, Y.; Nguyen, H.T. Brain-Computer Interface Classifier for Wheelchair Commands Using Neural Network with Fuzzy Particle Swarm Optimization. IEEE J. Biomed. Health Inform. 2014, 18, 1614–1624. [Google Scholar] [CrossRef]
- Bangyal, W.H.; Ahmad, J.; Rauf, H.T.; Shakir, R. Evolving artificial neural networks using opposition based particle swarm optimization neural network for data classification. In Proceedings of the 2018 International Conference on Innovation and Intelligence for Informatics, Computing, and Technologies, 3ICT 2018, Zallaq, Bahrain, 18–19 November 2018; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2018. [Google Scholar]
- Darrel, W. A Genetic Algorithm Tutorial. Stat. Comput. 1994, 4, 65–85. [Google Scholar] [CrossRef]
- Daraban, S.; Petreus, D.; Morel, C. A novel MPPT (maximum power point tracking) algorithm based on a modified genetic algorithm specialized on tracking the global maximum power point in photovoltaic systems affected by partial shading. Energy 2014, 74, 374–388. [Google Scholar] [CrossRef]
- Irshad, M.; Khalid, S.; Hussain, M.Z.; Sarfraz, M. Outline capturing using rational functions with the help of genetic algorithm. Appl. Math. Comput. 2016, 274, 661–678. [Google Scholar] [CrossRef]
- Gomes, H.M.; Awruch, A.M.; Lopes, P.A.M. Reliability based optimization of laminated composite structures using genetic algorithms and Artificial Neural Networks. Struct. Saf. 2011, 33, 186–195. [Google Scholar] [CrossRef]
- Kim, H.J.; Jo, N.O.; Shin, K.S. Optimization of cluster-based evolutionary undersampling for the artificial neural networks in corporate bankruptcy prediction. Expert Syst. Appl. 2016, 59, 226–234. [Google Scholar] [CrossRef]
- Baykasoǧlu, A.; Baykasoǧlu, C. Multiple objective crashworthiness optimization of circular tubes with functionally graded thickness via artificial neural networks and genetic algorithms. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 2005–2016. [Google Scholar] [CrossRef]
- Erzurum Cicek, Z.I.; Kamisli Ozturk, Z. Optimizing the artificial neural network parameters using a biased random key genetic algorithm for time series forecasting. Appl. Soft Comput. 2021, 102, 107091. [Google Scholar] [CrossRef]
- Dharmistha, M.; Vishwakarma, D. Genetic Algorithm based Weights Optimization of Artificial Neural Network. Int. J. Adv. Res. Electr. Electron. Instrum. Energy 2013, 1, 206–211. [Google Scholar]
- Zhang, T.; Wang, J.; Liu, Q.; Zhou, J.; Dai, J.; Han, X.; Zhou, Y.; Xu, K. Efficient spectrum prediction and inverse design for plasmonic waveguide systems based on artificial neural networks. Photonics Res. 2019, 7, 368–380. [Google Scholar] [CrossRef]
- Chidambaram, B.; Ravichandran, M.; Seshadri, A.; Muniyandi, V. Computational Heat Transfer Analysis and Genetic Algorithm-Artificial Neural Network-Genetic Algorithm-Based Multiobjective Optimization of Rectangular Perforated Plate Fins. IEEE Trans. Components Packag. Manuf. Technol. 2017, 7, 208–216. [Google Scholar] [CrossRef]
- Efosa, C.I.; Kingsley, C.U. Architecture Optimization Model for the Deep Neural Network for Binary Classification Problems. i-Manags. J. Softw. Eng. 2019, 14, 18. [Google Scholar] [CrossRef]
- Sales de Menezes, L.H.; Carneiro, L.L.; Maria de Carvalho Tavares, I.; Santos, P.H.; Pereira das Chagas, T.; Mendes, A.A.; Paranhos da Silva, E.G.; Franco, M.; Rangel de Oliveira, J. Artificial neural network hybridized with a genetic algorithm for optimization of lipase production from Penicillium roqueforti ATCC 10110 in solid-state fermentation. Biocatal. Agric. Biotechnol. 2021, 31, 101885. [Google Scholar] [CrossRef]
- Abdullah, S.; Pradhan, R.C.; Pradhan, D.; Mishra, S. Modeling and optimization of pectinase-assisted low-temperature extraction of cashew apple juice using artificial neural network coupled with genetic algorithm. Food Chem. 2021, 339, 127862. [Google Scholar] [CrossRef] [PubMed]
- Rashidi, M.M.; Bég, O.A.; Parsa, A.B.; Nazari, F. Analysis and optimization of a transcritical power cycle with regenerator using artificial neural networks and genetic algorithms. Proc. Inst. Mech. Eng. Part A J. Power Energy 2011, 225, 701–717. [Google Scholar] [CrossRef]
- Safikhani, H.; Abbassi, A.; Khalkhali, A.; Kalteh, M. Multi-objective optimization of nanofluid flow in flat tubes using CFD, Artificial Neural Networks and genetic algorithms. Adv. Powder Technol. 2014, 25, 1608–1617. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Li, Y.; Zhou, R.; Lin, Z. An Artificial Neural Network Assisted Optimization System for Analog Design Space Exploration. IEEE Trans. Comput. Des. Integr. Circuits Syst. 2020, 39, 2640–2653. [Google Scholar] [CrossRef]
- Qu, Z.; Yuan, S.; Chi, R.; Chang, L.; Zhao, L. Genetic optimization method of pantograph and catenary comprehensive monitor status prediction model based on adadelta deep neural network. IEEE Access 2019, 7, 23210–23221. [Google Scholar] [CrossRef]
- Jiang, Q.; Huang, R.; Huang, Y.; Chen, S.; He, Y.; Lan, L.; Liu, C. Application of BP neural network based on genetic algorithm optimization in evaluation of power grid investment risk. IEEE Access 2019, 7, 154827–154835. [Google Scholar] [CrossRef]
- Abeyrathna, K.D.; Jeenanunta, C. Hybrid particle swarm optimization with genetic algorithm to train artificial neural networks for short-term load forecasting. Int. J. Swarm Intell. Res. 2019, 10, 1–14. [Google Scholar] [CrossRef]
- Barzegar, R.; Asghari Moghaddam, A. Combining the advantages of neural networks using the concept of committee machine in the groundwater salinity prediction. Model. Earth Syst. Environ. 2016, 2, 26. [Google Scholar] [CrossRef]
- Kayabasi, A. An Application of ANN Trained by ABC Algorithm for Classification of Wheat Grains. Int. J. Intell. Syst. Appl. Eng. 2018, 6, 85–91. [Google Scholar] [CrossRef]
- Awan, S.M.; Aslam, M.; Khan, Z.A.; Saeed, H. An efficient model based on artificial bee colony optimization algorithm with Neural Networks for electric load forecasting. Neural Comput. Appl. 2014, 25, 1967–1978. [Google Scholar] [CrossRef]
- Hajimirzaei, B.; Navimipour, N.J. Intrusion detection for cloud computing using neural networks and artificial bee colony optimization algorithm. ICT Express 2019, 5, 56–59. [Google Scholar] [CrossRef]
- Badem, H.; Basturk, A.; Caliskan, A.; Yuksel, M.E. A new efficient training strategy for deep neural networks by hybridization of artificial bee colony and limited–memory BFGS optimization algorithms. Neurocomputing 2017, 266, 506–526. [Google Scholar] [CrossRef]
- Zhuo-Ming, C.; Yun-Xia, W.; Wei-Xin, L.; Zhen, X.; Han-Lin-Wei, X. Artificial Bee Colony Algorithm for Modular Neural Network; Springer: Berlin/Heidelberg, Germany, 2013; pp. 350–356. [Google Scholar]
- Ding, S.; Li, H.; Su, C.; Yu, J.; Jin, F. Evolutionary artificial neural networks: A review. Artif. Intell. Rev. 2013, 39, 251–260. [Google Scholar] [CrossRef]
- Kılıç, F.; Yılmaz, İ.H.; Kaya, Ö. Adaptive Co-Optimization of Artificial Neural Networks using Evolutionary Algorithm for Global Radiation Forecasting. Renew. Energy 2021. [Google Scholar] [CrossRef]
- Benmessahel, I.; Xie, K.; Chellal, M. A new evolutionary neural networks based on intrusion detection systems using multiverse optimization. Appl. Intell. 2018, 48, 2315–2327. [Google Scholar] [CrossRef]
- Chai, Z.; Yang, X.; Liu, Z.; Lei, Y.; Zheng, W.; Ji, M.; Zhao, J. Correlation Analysis-Based Neural Network Self-Organizing Genetic Evolutionary Algorithm. IEEE Access 2019, 7, 135099–135117. [Google Scholar] [CrossRef]
- Nassif, N. Modeling and optimization of HVAC systems using artificial neural network and genetic algorithm. Build. Simul. 2014, 7, 237–245. [Google Scholar] [CrossRef]
- Goudos, S.K.; Tsoulos, G.V.; Athanasiadou, G.; Batistatos, M.C.; Zarbouti, D.; Psannis, K.E. Artificial Neural Network Optimal Modeling and Optimization of UAV Measurements for Mobile Communications Using the L-SHADE Algorithm. IEEE Trans. Antennas Propag. 2019, 67, 4022–4031. [Google Scholar] [CrossRef]
- Yu, J.J.Q.; Lam, A.Y.S.; Li, V.O.K. Evolutionary artificial neural network based on Chemical Reaction Optimization. In Proceedings of the 2011 IEEE Congress of Evolutionary Computation, CEC 2011, New Orleans, LA, USA, 5–8 June 2011; pp. 2083–2090. [Google Scholar]
- Pakdaman, M.; Ahmadian, A.; Effati, S.; Salahshour, S.; Baleanu, D. Solving differential equations of fractional order using an optimization technique based on training artificial neural network. Appl. Math. Comput. 2017, 293, 81–95. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Saad, M.H.; Ayob, A. Neural network approach for estimating state of charge of lithium-ion battery using backtracking search algorithm. IEEE Access 2018, 6, 10069–10079. [Google Scholar] [CrossRef]
- Wang, B.; Wang, L.; Yin, Y.; Xu, Y.; Zhao, W.; Tang, Y. An Improved Neural Network with Random Weights Using Backtracking Search Algorithm. Neural Process. Lett. 2016, 44, 37–52. [Google Scholar] [CrossRef]
- Chen, D.; Lu, R.; Zou, F.; Li, S.; Wang, P. A learning and niching based backtracking search optimisation algorithm and its applications in global optimisation and ANN training. Neurocomputing 2017, 266, 579–594. [Google Scholar] [CrossRef]
- Wu, S.; Wang, Z.; Ling, D. Echo state network prediction based on backtracking search optimization algorithm. In Proceedings of the 2019 IEEE 3rd Information Technology, Networking, Electronic and Automation Control Conference, ITNEC 2019, Chengdu, China, 15–17 March 2019; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2019; pp. 661–664. [Google Scholar]
- Hannan, M.A.; Mohamed, R.; Abdolrasol, M.G.M.; Al-Shetwi, A.Q.; Ker, P.J.; Begum, R.A.; Muttaqi, K.M. ANN based binary backtracking search algorithm for virtual power plant scheduling and cost-effective evaluation. In Proceedings of the 2021 IEEE Texas Power and Energy Conference, College Station, TX, USA, 2–5 February 2021. [Google Scholar]
- Meng, A.; Ge, J.; Yin, H.; Chen, S. Wind speed forecasting based on wavelet packet decomposition and artificial neural networks trained by crisscross optimization algorithm. Energy Convers. Manag. 2016, 114, 75–88. [Google Scholar] [CrossRef]
- Lehký, D.; Slowik, O.; Novák, D. Reliability-based design: Artificial neural networks and double-loop reliability-based optimization approaches. Adv. Eng. Softw. 2018, 117, 123–135. [Google Scholar] [CrossRef]
- Uzlu, E.; Kankal, M.; Akpinar, A.; Dede, T. Estimates of energy consumption in Turkey using neural networks with the teaching-learning-based optimization algorithm. Energy 2014, 75, 295–303. [Google Scholar] [CrossRef]
- Shi, H.; Li, W. Artificial neural networks with ant colony optimization for assessing performance of residential buildings. In Proceedings of the FBIE 2009—2009 International Conference on Future BioMedical Information Engineering, Sanya, China, 13–14 December 2009; pp. 379–382. [Google Scholar]
- Pereira, L.A.M.; Rodrigues, D.; Ribeiro, P.B.; Papa, J.P.; Weber, S.A.T. Social-spider optimization-based artificial neural networks training and its applications for Parkinson’s Disease identification. In Proceedings of the IEEE Symposium on Computer-Based Medical Systems, New York, NY, USA, 27–29 May 2014; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2014; pp. 14–17. [Google Scholar]
- Liu, X.F.; Zhan, Z.H.; Gu, T.L.; Kwong, S.; Lu, Z.; Duh, H.B.L.; Zhang, J. Neural Network-Based Information Transfer for Dynamic Optimization. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 1557–1570. [Google Scholar] [CrossRef] [PubMed]
- Kouhalvandi, L.; Ceylan, O.; Ozoguz, S. Automated Deep Neural Learning-Based Optimization for High Performance High Power Amplifier Designs. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 4420–4433. [Google Scholar] [CrossRef]
- Heravi, A.R.; Abed Hodtani, G. A new correntropy-based conjugate gradient backpropagation algorithm for improving training in neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 6252–6263. [Google Scholar] [CrossRef] [PubMed]
- Yun, S.; Kang, J.M.; Kim, I.M.; Ha, J. Deep Artificial Noise: Deep Learning-Based Precoding Optimization for Artificial Noise Scheme. IEEE Trans. Veh. Technol. 2020, 69, 3465–3469. [Google Scholar] [CrossRef]
- Su, H.; Qi, W.; Yang, C.; Aliverti, A.; Ferrigno, G.; De Momi, E. Deep neural network approach in human-like redundancy optimization for anthropomorphic manipulators. IEEE Access 2019, 7, 124207–124216. [Google Scholar] [CrossRef]
- Ma, Y.; Han, R.; Wang, W. Prediction-Based Portfolio Optimization Models Using Deep Neural Networks. IEEE Access 2020, 8, 115393–115405. [Google Scholar] [CrossRef]
- Pourdaryaei, A.; Mokhlis, H.; Illias, H.A.; Kaboli, S.H.A.; Ahmad, S.; Ang, S.P. Hybrid ANN and artificial cooperative search algorithm to forecast short-term electricity price in de-regulated electricity market. IEEE Access 2019, 7, 125369–125386. [Google Scholar] [CrossRef]
- Yeh, W.C. New parameter-free simplified swarm optimization for artificial neural network training and its application in the prediction of time series. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 661–665. [Google Scholar] [CrossRef]
- Kumaran, J.; Ravi, G. Long-term sector-wise electrical energy forecasting using artificial neural network and biogeography-based optimization. Electr. Power Components Syst. 2015, 43, 1225–1235. [Google Scholar] [CrossRef]
- Yang, T.; Asanjan, A.A.; Faridzad, M.; Hayatbini, N.; Gao, X.; Sorooshian, S. An enhanced artificial neural network with a shuffled complex evolutionary global optimization with principal component analysis. Inf. Sci. 2017, 418–419, 302–316. [Google Scholar] [CrossRef]
- Lu, T.C.; Yu, G.R.; Juang, J.C. Quantum-based algorithm for optimizing artificial neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 1266–1278. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, F. Effective Neural Network Training with a New Weighting Mechanism-Based Optimization Algorithm. IEEE Access 2019, 7, 72403–72410. [Google Scholar] [CrossRef]
- Sun, W.Z.; Wang, J.S. Elman Neural Network Soft-Sensor Model of Conversion Velocity in Polymerization Process Optimized by Chaos Whale Optimization Algorithm. IEEE Access 2017, 5, 13062–13076. [Google Scholar] [CrossRef]
- Aljarah, I.; Faris, H.; Mirjalili, S. Optimizing connection weights in neural networks using the whale optimization algorithm. Soft Comput. 2018, 22. [Google Scholar] [CrossRef]
- Kumar, M.; Mishra, S.K.; Sahu, S.S. Cat Swarm Optimization Based Functional Link Artificial Neural Network Filter for Gaussian Noise Removal from Computed Tomography Images. Appl. Comput. Intell. Soft Comput. 2016, 2016, 1–6. [Google Scholar] [CrossRef]
- Yusiong, J.P.T. Optimizing Artificial Neural Networks using Cat Swarm Optimization Algorithm. Int. J. Intell. Syst. Appl. 2012, 5, 69–80. [Google Scholar] [CrossRef]
- Le, P.N.; Kang, H.J. Robot Manipulator Calibration Using a Model Based Identification Technique and a Neural Network with the Teaching Learning-Based Optimization. IEEE Access 2020, 8, 105447–105454. [Google Scholar] [CrossRef]
- Manngård, M.; Kronqvist, J.; Böling, J.M. Structural learning in artificial neural networks using sparse optimization. Neurocomputing 2018, 272, 660–667. [Google Scholar] [CrossRef]
- Ma, J.-w. Optimization of Feed-Forward Neural Networks based on Artificial Fish-Swarm Algorithm. 2004. Available online: https://www.semanticscholar.org/paper/Optimization-of-feed-forward-neural-networks-based-Jian-wei/663ea00fe44a17a89da2838c774ebe665dedcabf (accessed on 15 March 2021).
- Kim, T.; Lee, J.; Choe, Y. Bayesian optimization-based global optimal rank selection for compression of convolutional neural networks. IEEE Access 2020, 8, 17605–17618. [Google Scholar] [CrossRef]
- Petro, B.; Kasabov, N.; Kiss, R.M. Selection and Optimization of Temporal Spike Encoding Methods for Spiking Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 358–370. [Google Scholar] [CrossRef] [PubMed]
- Gulcu, A.; Kus, Z. Hyper-Parameter Selection in Convolutional Neural Networks Using Microcanonical Optimization Algorithm. IEEE Access 2020, 8, 52528–52540. [Google Scholar] [CrossRef]
- Wang, H.; Luo, Y.; An, W.; Sun, Q.; Xu, J.; Zhang, L. PID Controller-Based Stochastic Optimization Acceleration for Deep Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 5079–5091. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.J.; Ling, H.F.; Chen, S.Y.; Xue, J.Y. A Hybrid Neuro-Fuzzy Network Based on Differential Biogeography-Based Optimization for Online Population Classification in Earthquakes. IEEE Trans. Fuzzy Syst. 2015, 23, 1070–1083. [Google Scholar] [CrossRef]
- Sheng, W.; Shan, P.; Mao, J.; Zheng, Y.; Chen, S.; Wang, Z. An Adaptive Memetic Algorithm with Rank-Based Mutation for Artificial Neural Network Architecture Optimization. IEEE Access 2017, 5, 18895–18908. [Google Scholar] [CrossRef]
- Wu, L.; He, D.; Ai, B.; Wang, J.; Qi, H.; Guan, K.; Zhong, Z. Artificial Neural Network Based Path Loss Prediction for Wireless Communication Network. IEEE Access 2020, 8, 199523–199538. [Google Scholar] [CrossRef]
- Naserbegi, A.; Aghaie, M.; Mahmoudi, S.M. PWR core pattern optimization using grey wolf algorithm based on artificial neural network. Prog. Nucl. Energy 2020, 129, 103505. [Google Scholar] [CrossRef]
- Arunchai, T.; Sonthipermpoon, K.; Apichayakul, P.; Tamee, K. Resistance Spot Welding Optimization Based on Artificial Neural Network. Int. J. Manuf. Eng. 2014, 2014. [Google Scholar] [CrossRef]
- Abdolrasol, M.G.M.; Hannan, M.A.; Hussain, S.M.S.; Ustun, T.S.; Sarker, M.R.; Ker, P.J. Energy Management Scheduling for Microgrids in the Virtual Power Plant System Using Artificial Neural Networks. Energies 2021, 14, 6507. [Google Scholar] [CrossRef]
- Hannan, M.A.; Abdolrasol, M.G.M.; Faisal, M.; Ker, P.J.; Begum, R.A.; Hussain, A. Binary Particle Swarm Optimization for Scheduling MG Integrated Virtual Power Plant Toward Energy Saving. IEEE Access 2019, 7, 107937–107951. [Google Scholar] [CrossRef]
- Ahmed, M.S.; Mohamed, A.; Khatib, T.; Shareef, H.; Homod, R.Z.; Ali, J.A. Real time optimal schedule controller for home energy management system using new binary backtracking search algorithm. Energy Build. 2017, 138, 215–227. [Google Scholar] [CrossRef]
- Abdolrasol, M.G.M.; Hannan, M.A.; Mohamed, A.; Amiruldin, U.A.U.; Abidin, I.B.Z.; Uddin, M.N. An Optimal Scheduling Controller for Virtual Power Plant and Microgrid Integration Using the Binary Backtracking Search Algorithm. IEEE Trans. Ind. Appl. 2018, 54, 2834–2844. [Google Scholar] [CrossRef]
- Roslan, M.F.; Hannan, M.A.; Jern Ker, P.; Begum, R.A.; Indra Mahlia, T.M.; Dong, Z.Y. Scheduling controller for microgrids energy management system using optimization algorithm in achieving cost saving and emission reduction. Appl. Energy 2021, 292, 116883. [Google Scholar] [CrossRef]
- Hannan, M.A.; Begum, R.A.; Abdolrasol, M.G.; Hossain Lipu, M.S.; Mohamed, A.; Rashid, M.M. Review of baseline studies on energy policies and indicators in Malaysia for future sustainable energy development. Renew. Sustain. Energy Rev. 2018, 94, 551–564. [Google Scholar] [CrossRef]
- Safari, A.; Babaei, F.; Farrokhifar, M. A load frequency control using a PSO-based ANN for micro-grids in the presence of electric vehicles. Int. J. Ambient. Energy 2021, 42, 688–700. [Google Scholar] [CrossRef]
- Shabbir, J.; Anwer, T. Artificial Intelligence and its Role in Near Future. arXiv 2018, arXiv:1804.01396. [Google Scholar]
- Wang, M.; Chen, H. Chaotic multi-swarm whale optimizer boosted support vector machine for medical diagnosis. Appl. Soft Comput. 2020, 88, 105946. [Google Scholar] [CrossRef]
- Shan, W.; Qiao, Z.; Heidari, A.A.; Chen, H.; Turabieh, H.; Teng, Y. Double adaptive weights for stabilization of moth flame optimizer: Balance analysis, engineering cases, and medical diagnosis. Knowl.-Based Syst. 2021, 214, 106728. [Google Scholar] [CrossRef]
- Tu, J.; Chen, H.; Liu, J.; Heidari, A.A.; Zhang, X.; Wang, M.; Ruby, R.; Pham, Q.V. Evolutionary biogeography-based whale optimization methods with communication structure: Towards measuring the balance. Knowl.-Based Syst. 2021, 212, 106642. [Google Scholar] [CrossRef]














| Technique | Advantages | Disadvantages |
|---|---|---|
| PSO [62] |
|
|
| GA [63] |
|
|
| NNA [52] |
|
|
| ABC [64] |
|
|
| LSA [58] |
|
|
| EA [65] |
|
|
| BSA [73] |
|
|
| GSA [67] |
|
|
| FA [68] |
|
|
| Neural Networks | Optimizer | Optimizer Problem | Application Improved |
|---|---|---|---|
| dynamic MNN [111] | Adaptive PSO | To calculate the weights | Design of dynamic modular neural network |
| DNN [115] | PSO | To optimize the number of hidden layer nodes | Digital modulation recognition |
| ANN [117] | Simulation annealled PSO | initial weights and biases of the neural network are optimized | Endpoint sulfur content in Kambara reactor desulfurization |
| BiLSTM NN [118] | ADPSO | To optimize the hyperparameters of BiLSTM neural network | Ship motion attitude prediction |
| IT2FNNs [119] | PSO & BBBC | For parameter optimization for Takagi-Sugeno-Kang TSK type IT2FNNs | Design interval type-2 fuzzy neural networks IT2FNNs |
| FNN [72] | SPS-PSO | Weight optimization problem parameters | For parameter and self-adaptive mechanism strategies. |
| ANN [49] | PSO | Train a set of synaptic weights | To evaluate the fitness of each solution and find the best ANN design |
| ANN [113] | PSO | Find the optimal weights of the network | Non-linear channel equalization |
| ANN [116] | PSO | For optimizing the number of hidden layers and neurons used and the learning rate | Global solar irradiance prediction at extremely short-time-intervals |
| CNN [114] | PSO | For hyperparameter optimization with linearly decreasing weights | CNN architecture design |
| ANN [120] | PSO | For an optimal number of hidden layers and learning rate | Microgrid scheduling and management |
| Neural Networks | Optimizer | Optimizer Problem | Application Improved |
|---|---|---|---|
| ANN [123] | PSO | To predict airblast-overpressure (AOp) in quarry blasting | Airblast-overpressure induced influential parameters in four granite quarry sites in Malaysia |
| ANN [124] | PSO | To minimize pumping cost and solve ground management issues | Management of groundwater of the Dore river basin in France |
| ANN [125] | PSO | To solve traffic flow predictors problems | Forecast traffic flow conditions on a freeway in Australia |
| Neural fuzzy Network [126] | CCPSO | To increase the global search capacity using the belief space | Several predictive applications |
| ANN [127] | PSO & PMS | A periodic mutation application strategy with diversity variety for six benchmark test functions | Airfoil in transonic flow |
| ANN [128] | PSO | To identify a complex non-linear relationship between input and output parameters | Photovoltaic thermal nanofluid |
| ANN [129] | tent-map chaotic PSO (TCPSO) | To perform the nonlinear optimization to enhance the convergence and accuracy | Numerical simulations of two benchmark functions |
| ANN [130] | Hybrid PSO-CS Algorithm | To investigate the algorithm performance with two benchmark problems | Benchmark classification for ANN structures. |
| ANN [121] | neighborhood fuzzy PSO | To enhance forecasting of software reliability | Forecasting of software reliability |
| Critic NN [122] | PSO | Solve the Hamilton-Jacobi-Bellman equation more efficiently. | Data-based fault-tolerant control |
| ANN [29] | PSO | To improve the distance estimation accuracy of mobile nodes | Wireless sensor localization technique |
| ANN [131] | Taguchi PSO (TPSO) | To solve high-dimensional global numerical optimization problems. | Optimize the chemical composition of a steel bar |
| ANN [112] | PSO | To obtain the numerical solution of Troesch’s problem | Non-linear Troesch’s problem |
| ANN [110] | Affinity Propagation (AP) & PSO | To reduce the maximum location error and enhance the prediction performance | Wi-Fi-based indoor localization system |
| ANN [108] | PSO | To predict unconfined compressive strength (UCS) of rocks | Predicting UCS rocks from different states in Malaysia |
| ANN [31] | PSO | To evolve the structure and weights of ANNs | Evaluated on several benchmarks |
| ANN [132] | Fuzzy PSO | Classification of a three-class mental task-based brain-computer interface | Brain-computer interface for wheelchair commands |
| ANN [133] | PSO | For training on opposition based PSO neural network (OPSONN) algorithm | Data classification |
| Neural Networks | Optimizer | Optimizer Problem | Application Improved |
|---|---|---|---|
| ANN [152] | PSO &GA | To overcome the training issue of local minima traps | Short-term load forecasting |
| ANN [137] | GA | To overcome high computational cost by using multilayer perceptron NN | Design of anisotropic laminated composite structures |
| ANN [143] | GA | To determine suitable parameters for maximum weight reduction | Heat transfer analysis in perforated plate fins |
| ANN [138] | GA | To solve the data imbalance problem caused by simultaneous ANN optimization. | Corporate bankruptcy prediction |
| DNN [144] | GA | To select optimal network parameters of the Deep-NN | Binary classification for university student admissions |
| ANN [139] | Crashworthiness optimization and GA | To design parameter alternatives and determine optimal combinations. | Circular tubes having a functionally graded thickness |
| ANN [140] | GA | To find the number of hidden neurons, bias values of hidden neurons, and the connection weights between nodes. | Time-series forecasting for real-life data |
| ANN [145] | GA | To optimize lipase production through the ANN model | Lipase production from Penicillium roqueforti ATCC 10110 in solid-state fermentation |
| ANN [146] | GA | Optimum extraction parameters | Low-temperature extraction of cashew apple juice |
| ANN [147] | GA | To optimize the thermal efficiency, exergy efficiency, and specific network. | Transcritical power cycle with regenerator |
| ANN [148] | Non-dominated Sorting GA | To numerically solve problems in various flat tubes for nanofluid flow analysis and regime | Nanofluid flow in flat tubes |
| ANN [17] | GA | To minimize the number of decoupling capacitors for reducing the differences between the input impedance | PCB decoupling |
| ANN [149] | GA | For analog circuit optimization system automated sizing of integrated circuits | Analog design space exploration |
| ADNN [150] | GA | To prevent prediction models from falling into local optimum and a comprehensive catenary model | Pantograph and catenary |
| ANN [151] | GA | To optimize the weight and threshold of a BP neural network | Power grid investment risk problems |
| ANN [141] | GA | For weight optimization in a pre-specified neural network | Applied on a mobile ad-hoc network |
| ANN [142] | GA | To design the network architecture and select the hyperparameters for ANNs | Plasmonic waveguide systems |
| MLP, RBFNN & GRNN [153] | GA | Search for optimal weights | Predicting groundwater salinity |
| Neural Networks | Optimizer | Optimizer Problem | Application Improved |
|---|---|---|---|
| ANN [155] | ABC | To optimized set of neuron connection weights | Electric load forecasting |
| Modular NN [158] | ABC | For synaptic weights optimization | Classifier designed for NN |
| MLP network [156] | ABC & Fuzzy clustering algorithms | To optimize linkage weights and biases | Intrusion detection for cloud computing |
| DNN [8] | swarm-based ABC | To optimize DNN parameter protection against dual attacks | Mobile ad hoc network for mitigation of black and gray holes attacks |
| DNN [157] | ABC & BFGS | For hybridization parameters of deep neural networks | Data classification of dimensions and sizes |
| Neural Networks | Optimizer | Optimizer Problem | Application Improved |
|---|---|---|---|
| ANN [160] | EA | To co-optimize the ANN properties | Global radiation forecasting |
| ANN [161] | Multiverse optimizer (MVO)/EA | To allow ENN to solve problems encountered by ANNs | Intrusion detection systems using multiverse optimization via a benchmark dataset |
| ANN [162] | Self-organized genetic EA | To improve the performance efficiency and structural efficiency of the built ANN | Structure of neural network and its implementation |
| ANN [163] | EA | For optimization and ANN for modeling | High voltage AC systems |
| ANN [164] | EAs | For self-adaptive control parameters and dynamically adjust the population size for ANN weight optimization | Unmanned aerial vehicle measurements for mobile communications |
| ANN [166] | EA | To adjust the weights to satisfy the differential equations | Differential equations of fractional order |
| ANN [165] | EA/CRO | To replace backpropagation in training neural networks | ANN architecture design |
| Neural Networks | Optimizer | Optimizer Problem | Application Improved |
|---|---|---|---|
| Back-propagation NN [167] | BSA | To find the optimal values of hidden layer neurons and learning rate | Estimating state of charge of lithium-ion batteries |
| SLFN [168] | BSA | To optimize the neural network with random weights, and derive the output layer weights. | Improve neural network design |
| ANN [169] | Modified BSA | For learning and niching strategies such as learning strategy, a niching strategy, and a mutation strategy | Chaotic time series prediction and benchmark functions |
| Echo State Network/RNN [170] | Adaptive BSA | To optimize the connection weights matrix of the echo state network reservoir | Echo state network architecture design |
| ANN [171] | Binary BSA | To optimize the number of nodes in hidden layers and learning rate | Energy management to reduce the cost |
| Neural Networks | Optimizer | Optimizer Problem | Application Improved |
|---|---|---|---|
| FNNs [84] | SOS | For training of FNNs | UCI machine learning repository |
| ANN [174] | TLBO | To replace the BP with TLBO | Estimates of energy consumption in Turkey |
| ANN [176] | Social-spider Optimization | To improve the training phase of ANN with multilayer perceptrons | Parkinson’s disease identification |
| DMLP, LSTM, CNN [182] | DNNs | DNNs to predict each stock’s future return also DNNs are applied to measure the risk of each stock | Portfolio optimization models utilizing the stocks market of China |
| ANN [177] | NNIT & EA | To solve dynamic optimization problems | Moving peaks benchmark |
| DNN [178] | TSEMO & DNN | To get the number of passive components in the input and output matching networks | Designing high power amplifier circuit topologies |
| RNN [40] | Metaheuristic Algorithms | For the objective analytic function of a continuous optimization problem | Estimate tree structures |
| ANN [179] | CCG-BP | Optimizing common correntropy-based BP algorithms based on MSE | Improving training in NNs for enhancing the signal-to-noise ratios |
| DNN [180] | Deep AN | For optimal precoding scheme | Artificial noise scheme wiretap channels |
| ANN [181] | DCNN | For reconstruction enhancement and reducing online prediction time | Anthropomorphic manipulators |
| ANN [183] | ACS | To select the input variables subsets for forecasting of electricity price | Forecasts of short-term electricity prices in a deregulated market |
| Neural Networks | Optimizer | Optimizer Problem | Application Improved |
|---|---|---|---|
| ANN [185] | BBO | To obtain the best global weight parameters | Long-term sector-wise power forecasting |
| ANN [186] | (SP-UCI) | To the weight-training process of a three-layer feed-forward ANN | Gradient-based optimization schemes |
| ANN [184] | SSO | To adjust the weights in ANNs | For ANN modeling |
| ANN [21] | BMO | For weight training of ANNs | Solving three real-world classification problems |
| ANN [187] | Quantum-based algorithm | Few connections and high classification performance using connection weights. | ANN design and structure |
| ANN [194] | sparse optimization | To simultaneously estimate the weights and model structure of an ANN | Model structure of ANN |
| ANN [188] | NWM-Adam | To resolve the undesirable convergence behavior by weighting mechanism-based first-order gradient descent optimization | For effective neural network training |
| Knowledge-based NN [88] | i1Optimizer | To force some weights of the NNs to zeros while leaving other weights as non-zeros. | For unified automated parametric modeling algorithm |
| Elman Neural Network [189] | WOA | To train the connection weights between the layers | Network soft-sensor model of conversion velocity in a polymerization process |
| ANN [190] | WOA | Optimizing connection weights of ANN controlling parameters weights and biases | ANN structure design |
| FLANN [191] | CSO | For the selection of an optimum weight of the neural network filter | Gaussian noise removal from tomography Images |
| ANN [192] | CSO & OBD | For optimization of the connection weights | ANN structure design |
| ANN [193] | TLBO | To optimize weights and bias of the NN | Robot manipulator |
| Neural Networks | Optimizer | Optimizer Problem | Application Improved |
|---|---|---|---|
| ANN [195] | AFSA | To obtain hidden layers trained by the back-propagation algorithm | Design of neural networks |
| ANN [202] | PL | To eliminate redundant information by impacts of the number of neurons in the hidden layer, number of hidden layers, number of training samples | Wireless communication network |
| DNN [80] | Multi-objective Optimization | To find the optimal structure with high representation ability and better generalization for each layer. | Structure of DNN model |
| CNN [103] | diffGrad | To adjust each parameter for faster gradient changing parameters | Image categorization experiments |
| ANN [30] | LSA | Using suitable learning rate value and number of nodes in the hidden layers | Home energy management scheduling |
| CNN [196] | BayesOpt | To utilize both a simple objective function and a proper optimization | low-rank decomposition |
| CNN [197] | Ben’s Spiker algorithm | For parameter optimization | Signal-to-noise ratio |
| CNN [198] | MOA | For hyper-parameter optimization and architecture selection for CNN | Using six widely-used image recognition datasets |
| DNN [199] | SGD-M | Use past and present gradients for DNN parameter updates | PID Controller |
| Hybrid neuro-fuzzy [200] | DBBO | For parameter optimization of both the main network and the subnetwork | Online population classification in earthquakes |
| ANN [201] | AMARM | To simultaneously fine-tune the number of hidden neurons and connection weights | Design ANN architectures. |
| Neural Networks Optimizer | Optimization Algorithm Enhanced | Optimizer Problem | Application Improved |
|---|---|---|---|
| ANN [203] | GWO | ANN is applied to estimate the fitness function value of GWO | Pressurized water reactor |
| ANN [204] | RSW | ANN as a tool in finding the parameter optimization of RSW | A sensitive to exact measurement of aluminum alloy |
| CNN [11] | TO | The trained CNN approximately evaluates individuals | Cross-sectional image of an interior permanent magnet motor |
| Symbol | Description |
|---|---|
| P | Controller input data |
| t | Controller output data |
| = 100 | Maximum iterations for ANN |
| Population size = 20 | Size of the population |
| = 0 | Min value of LR |
| = 1 | Max value of LR |
| = 6 | Min value of nodes in hidden layer1 |
| = 30 | Max value of nodes in hidden layer1 |
| = 6 | Min value of nodes in hidden layer2 |
| = 30 | Max value of nodes in hidden layer2 |
| Optimization Algorithm | No. of Nodes in Hidden Layer1 (N1) | No. of Nodes in Hidden Layer2 (N2) | Learning Rate Value (LR) | Training Time | Training Performance (MSE) |
|---|---|---|---|---|---|
| PSO | 18 | 30 | 0.7 | 20:00:48 | 3.99 × 10−6 |
| GA | 23 | 28 | 0.6 | 20:31:36 | 5.46 × 10−6 |
| ABC | 26 | 29 | 0.45 | 30:32:29 | 2.52 × 10−5 |
| BSA | 22 | 27 | 0.6 | 4:30:29 | 6.37 × 10−7 |
| Optimization Algorithm | Objective Function (MAE) | No. of Nodes in Hidden Layer 1 (N1) | No. of Nodes in Hidden Layer 2 (N2) | Learning Rate Value (LR) | No. of Input and Output | Regression (R) | Training Performance (MSE) |
|---|---|---|---|---|---|---|---|
| Hybrid LSA-ANN [30] | 9.128 × 10−9 | 6 | 4 | 0.6175 | 5 and 4 | 1 | 9.128 × 10−9 |
| PSO-DNN [115] | - | 20 | 60 | 0.1 | 12 | - | - |
| Hybrid ANN-PSO [29] | 0.1742 | 18 | 16 | 0.071 | 3 and 1 | 0.99991 | - |
| BPNN-PSO [116] | 0.1911 × 10−2, 0.2032 × 10−2 | 14 and 9 | 9 and 11 | 0.7373, 0.6481 | 7 and 1 | 0.99993, 0.99999 | 4.3 × 10−5 |
| ANN-PSO tested | 0.0144 | 18 | 30 | 0.7 | 6 and 25 | 0.99999 | 3.99 × 10−6 |
| ANN-GA tested | 0.0080 | 23 | 28 | 0.6 | 6 and 25 | 0.99999 | 5.46 × 10−6 |
| ANN-ABC tested | 0.0172 | 26 | 29 | 0.45 | 6 and 25 | 0.99995 | 2.52 × 10−5 |
| ANN-BSA tested | 0.0062 | 22 | 27 | 0.6 | 6 and 25 | 1 | 6.37 × 10−7 |
| Enhancement Method | Reference | Year | Application Enhanced |
|---|---|---|---|
| ANN-based GA | [140] | 2021 | Time-series forecasting for real-life data |
| ANN-based binary BSA | [171] | 2021 | Virtual power plant |
| ANN-based PSO | [120] | 2021 | Microgrid energy management |
| ANN-based LSA | [30] | 2016 | Home energy management |
| DNN-based PSO | [115] | 2019 | Digital modulation recognition |
| ANN-based AMARM | [201] | 2017 | Design ANN architectures. |
| BPNN-based PSO | [116] | 2021 | Global solar irradiance prediction |
| ANN-based BSA | [167] | 2018 | Estimating state of charge of lithium-Ion battery |
| ANN-based PSO | [211] | 2016 | Wireless sensor localization for cycling tracking |
| ANN-based PL | [202] | 2020 | Wireless communication network |
| ANN-based ABC | [155] | 2014 | Electric load forecasting |
| ANN-based SAPSO | [117] | 2020 | Kambara reactor desulfurization |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdolrasol, M.G.M.; Hussain, S.M.S.; Ustun, T.S.; Sarker, M.R.; Hannan, M.A.; Mohamed, R.; Ali, J.A.; Mekhilef, S.; Milad, A. Artificial Neural Networks Based Optimization Techniques: A Review. Electronics 2021, 10, 2689. https://doi.org/10.3390/electronics10212689
Abdolrasol MGM, Hussain SMS, Ustun TS, Sarker MR, Hannan MA, Mohamed R, Ali JA, Mekhilef S, Milad A. Artificial Neural Networks Based Optimization Techniques: A Review. Electronics. 2021; 10(21):2689. https://doi.org/10.3390/electronics10212689
Chicago/Turabian StyleAbdolrasol, Maher G. M., S. M. Suhail Hussain, Taha Selim Ustun, Mahidur R. Sarker, Mahammad A. Hannan, Ramizi Mohamed, Jamal Abd Ali, Saad Mekhilef, and Abdalrhman Milad. 2021. "Artificial Neural Networks Based Optimization Techniques: A Review" Electronics 10, no. 21: 2689. https://doi.org/10.3390/electronics10212689
APA StyleAbdolrasol, M. G. M., Hussain, S. M. S., Ustun, T. S., Sarker, M. R., Hannan, M. A., Mohamed, R., Ali, J. A., Mekhilef, S., & Milad, A. (2021). Artificial Neural Networks Based Optimization Techniques: A Review. Electronics, 10(21), 2689. https://doi.org/10.3390/electronics10212689











