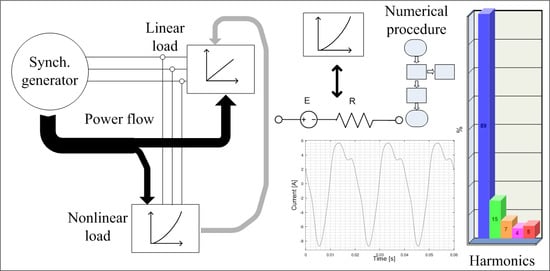
Method for the Analysis of Three-Phase Networks Containing Nonlinear Circuit Elements in View of an Efficient Power Flow Computation
Abstract
:1. Introduction
2. Equivalent Source Voltage Correction
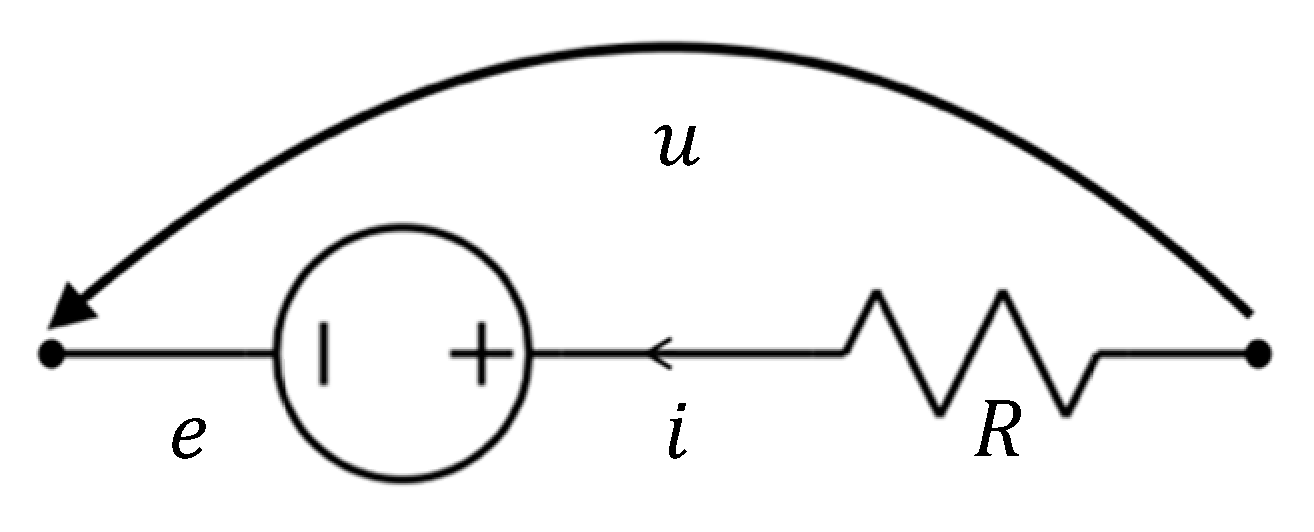
- —the equivalent voltage source of the nonlinear element at iteration n in the time domain;
- —the vector of complex phasors of the source harmonics ;
- —the vector of complex phasors of the voltage at the nonlinear element terminals;
- F—the Fourier transform;
- F−1—the inverse Fourier transform.
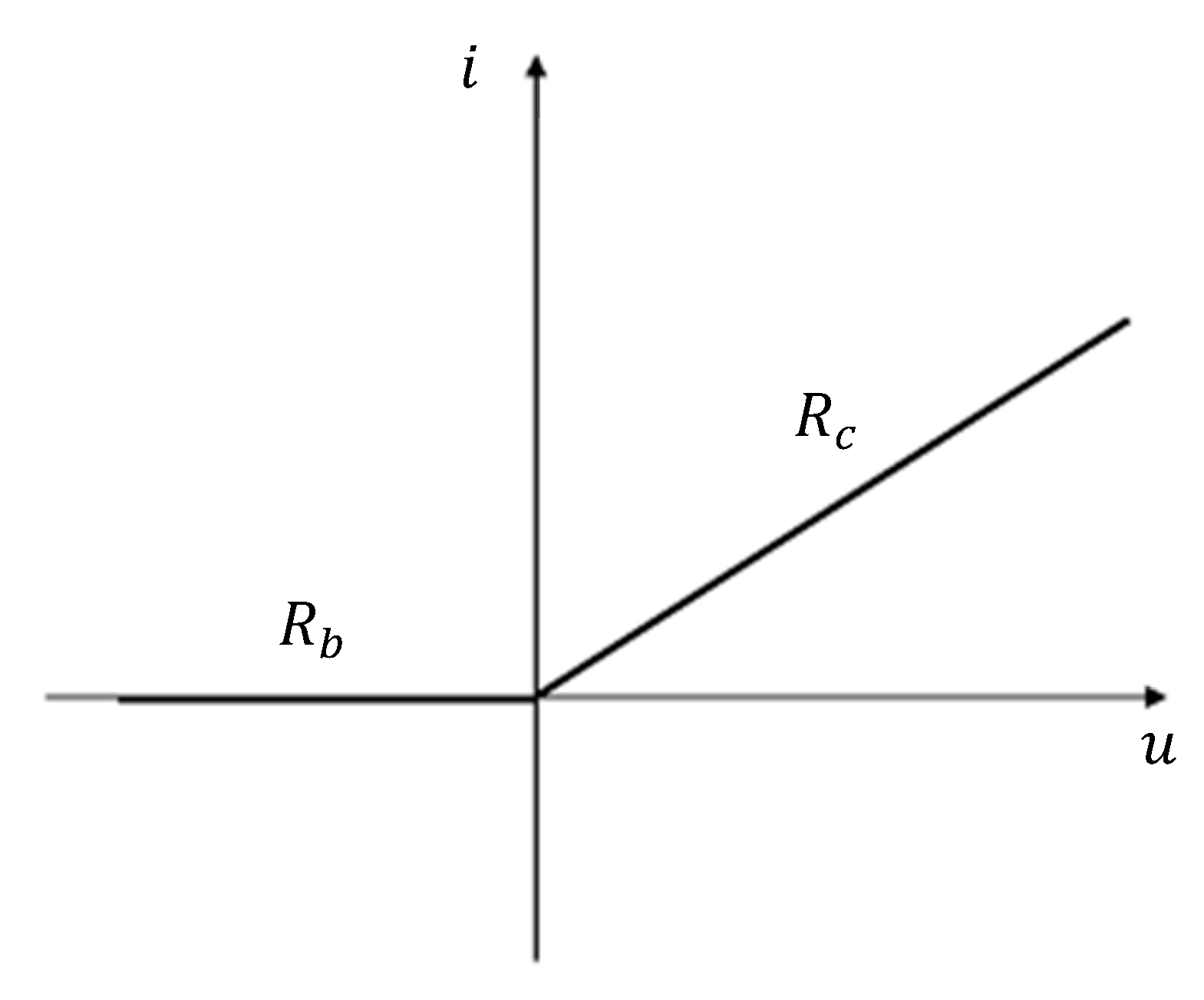
- Nonlinear circuit elements are substituted with real sources whose ideal internal sources are dependent on the voltages at the terminals of the generators themselves (through function g).
- Circuits are defined for each harmonic and sequence in the complex.
- Having the time values of the equivalent sources (zero ones may be considered to start with), the harmonic spectrum of these equivalent sources is computed (using the Fourier series transform, F).
- The circuit is solved in complex, on each harmonic and sequence, and the complex voltages at the equivalent generators’ terminals are obtained (using function h).
- The time-domain values of voltages, previously determined at point 4, are computed (using the inverse Fourier series transform, F−1).
- The equivalent sources voltages are corrected (via function g).
- The Fourier transform F is non-expansive when truncated to a finite number of terms [28];
- For the inverse Fourier transform F−1, we take into account only the harmonics computed in the previous step of the iterative procedure.
3. Equivalent Source Current Correction
4. The Conservation of Complex Powers (Balance of Power)
5. Illustrative Example 1—Cylindrical (Non-Salient) Pole Power Generator of Equal Reactances per Sequence
5.1. Equivalent Source Voltage Correction Solution
5.2. Comparison of the Proposed Algorithm Results against LTspice Simulation Software
5.3. Power Computation and Validity Check—Balance of Powers
6. Illustrative Example 2—Salient Pole Power Generator of Different Reactances per Sequence
6.1. Equivalent Source Voltage Correction Solution
6.2. Comparison against LTspice Software Results
6.3. Balance of Powers
7. Conclusions
- To our best knowledge, it is the only method that can be efficiently applied to nonlinear circuits, comprising three-phase generators presenting different sequence reactance values. In these cases, the inductances are a function of the rotor position; hence, they are also a function of time. This significantly complicates the time-domain analysis, besides the fact that the entire three-phase circuit must be solved.
- The circuit analysis is performed for each frequency harmonic.
- A single phase can be utilized for the three-phase circuit analysis. The method features an enormous computation effort in the case of large-scale circuits.
- We point out that the sources corresponding to the nonlinear elements are decomposed on positive, negative and zero sequences. Obviously, the computation time is reduced significantly. The most time-consuming software component is harmonic analysis. Nonetheless, in the context of the necessity of repeating this analysis during iterations, quantities and are determined only once at the beginning of the procedure (by reducing the argument in the first quadrant).
- The nonlinearity of the resistive circuit elements is taken into account only through the correction made to the equivalent sources’ values.
- Compared to the Harmonic Balance method, the presented method here has the advantage that convergence is always guaranteed without being necessary to recurse to under-relaxation. Moreover, the method even admits the use of over-relaxation. Compared to the Harmonic Balance Method the computation requires processing a smaller number of data, demanding less memory, and thus more harmonics may be considered in the analysis.
- Compared to the behavioral frequency-domain models, the presented method is more accurate, being based on a nonlinear time-domain characteristic, which is easier to determine and use. Moreover, it has the advantage of being able to process a significantly greater number of harmonics (at the user’s choice). The method presented in our paper may use a reduced number and/or a selection of harmonics (e.g., up to rank 25, or odd harmonics, which are not multiples of 3: 1, 5, 7, 11, 13, 17, 19, 23, 25), all by keeping a satisfactory degree of accuracy in a short computation time [28].
- It is also worth mentioning that the proposed method is equally efficient even when harmonic resonance is occurring on certain harmonics.
- Similar to all methods based on harmonic analysis, the proposed method is affected by the Gibbs effect, but the obtained result is sufficiently exact to a satisfactory degree.
- We mention that LTspice, one of the most efficient circuit analysis softwares, solves nonlinear circuits in the time domain, with the periodic regime solution being obtained through the symptotic behavior method (in the time domain). LTspice is unable to solve three-phase networks powered by generators exhibiting different sequence reactances. The internal inductances of the phases are coupled and time-dependent (upon the rotor’s position). LTspice cannot separate a single phase to perform the entire three-phase network analysis. Conversely, the time domain analysis avoids the Gibbs effect, which manifests itself when the present paper’s method is applied. That would represent a downside of the method.
- This paper’s method allows for easy complex-power computation and transfer throughout the network, for each circuit element, including the nonlinear elements, and permits identifying the harmonic frequencies where the circuit elements absorb power, as well as the ones they “deliver” power. The balance of powers (computed with the proposed algorithm) is in accordance with Tellegen’s theorem and confirms Țugulea’s power theory (and its subsequent developments), regarding the power flow in three-phase circuits affected by nonlinear elements. The generators of the network always deliver complex power only on the fundamental frequency and on positive sequences. Nonlinear loads (alongside linear ones) absorb power on the fundamental frequency. Part of the absorbed power is retained by the nonlinear elements, while the rest of the power is reinjected throughout the network as delivered power on the higher harmonics. Although apparently purely resistive, the nonlinear loads also absorb/deliver internally reactive power, not only active power.
Author Contributions
Funding
Conflicts of Interest
References
- Da Silva, R.P.B.; Quadros, R.; Shaker, H.R.; da Silva, L.C.P. Analysis of the Electrical Quantities Measured by Revenue Meters Under Different Voltage Distortions and the Influences on the Electrical Energy Billing. Energies 2019, 12, 4757. [Google Scholar] [CrossRef] [Green Version]
- Tabora, J.M.; Tostes, M.E.D.L.; De Matos, E.O.; Soares, T.M.; Bezerra, U.H. Voltage Harmonic Impacts on Electric Motors: A Comparison between IE2, IE3 and IE4 Induction Motor Classes. Energies 2020, 13, 3333. [Google Scholar] [CrossRef]
- Lumbreras, D.; Gálvez, E.; Collado, A.; Zaragoza, J. Trends in Power Quality, Harmonic Mitigation and Standards for Light and Heavy Industries: A Review. Energies 2020, 13, 5792. [Google Scholar] [CrossRef]
- Mboving, C.A. Investigation on the Work Efficiency of the LC Passive Harmonic Filter Chosen Topologies. Electronics 2021, 10, 896. [Google Scholar] [CrossRef]
- Petrushyn, V.; Horoshko, V.; Plotkin, J.; Almuratova, N.; Toigozhinova, Z. Power Balance and Power Factors of Distorted Electrical Systems and Variable Speed Asynchronous Electric Drives. Electronics 2021, 10, 1676. [Google Scholar] [CrossRef]
- Junior, O.D.B.; Amorim, T.S.; Carletti, D.; Neto, A.F.; Encarnação, L.F. Design of an Enhanced FLC-Based Controller for Selective Harmonic Compensation in Active Power Filters. Electronics 2020, 9, 2052. [Google Scholar] [CrossRef]
- Gonçalves, J.; Valtchev, S.; Melicio, R.; Gonçalves, A.; Blaabjerg, F. Hybrid Three-Phase Rectifiers with Active Power Factor Correction: A Systematic Review. Electronics 2021, 10, 1520. [Google Scholar] [CrossRef]
- Sušin, D.; Nemec, M.; Ambrožič, V.; Nedeljković, D. Limitations of Harmonics Control in Power Converters. Electronics 2019, 8, 739. [Google Scholar] [CrossRef] [Green Version]
- Gutiérrez, F.E.R.; Castillo, O.C.; Rivas, J.J.R.; González, R.O.; Sánchez, E.P.; Morales, L.G.G. Harmonics Reduction and Reactive Power Injection in Wind Generation Systems. Electronics 2021, 10, 1964. [Google Scholar] [CrossRef]
- Mahmoudian, M.; Rodrigues, E.M.G.M.G.; Pouresmaeil, E. An Efficient H7 Single-Phase Photovoltaic Grid Connected Inverter for CMC Conceptualization and Mitigation Method. Electronics 2020, 9, 1440. [Google Scholar] [CrossRef]
- Udovichenko, A.V.; Brovanov, S.V.; Grishanov, E.V.; Stennikova, S.M. A Five-Level Converter in a Three-Level Mode for Common-Mode Leakage Current Suppression in PV-Generation Systems. Electronics 2021, 10, 2382. [Google Scholar] [CrossRef]
- Ashique, R.H.; Maruf, H.; Sourov, K.M.S.H.; Islam, M.; Islam, A.; Rabbani, M.; Islam, R.; Khan, M.M.; Shihavuddin, A. A Comparative Performance Analysis of Zero Voltage Switching Class E and Selected Enhanced Class E Inverters. Electronics 2021, 10, 2226. [Google Scholar] [CrossRef]
- Wu, S.-T.; Chen, F.-Y.; Chien, M.-C.; Wang, J.-M.; Su, Y.-Y. A Hybrid Control Scheme with Fast Transient and Low Harmonic for Boost PFC Converter. Electronics 2021, 10, 1848. [Google Scholar] [CrossRef]
- Faifer, M.; Laurano, C.; Ottoboni, R.; Toscani, S.; Zanoni, M. Frequency-Domain Nonlinear Modeling Approaches for Power Systems Components—A Comparison. Energies 2020, 13, 2609. [Google Scholar] [CrossRef]
- Díaz-Araujo, M.H.; Medina-Rios, A.; Madrigal-Martínez, M.; Balderas, A.C. Analysis of Grid-Connected Photovoltaic Generation Systems in the Harmonic Domain. Energies 2019, 12, 4785. [Google Scholar] [CrossRef] [Green Version]
- Constantinescu, F.; Gheorghe, A.G.; Marin, M.E.; Taus, O.S. Harmonic balance analysis of home appliances power networks. In Proceedings of the 2017 14th International Conference on Engineering of Modern Electric Systems (EMES), Oradea, Romania, 1–7 June 2017; pp. 256–260. [Google Scholar]
- Constantinescu, F.; Rață, M.M.; Enache, F.R.; Vătășelu, G.; Ștefănescu, V.; Milici, D.; Aramă, I. Frequency domain models for nonlinear loads with firing angle control devices Part I—Measurements. In Proceedings of the 2019 15th International Conference on Engineering of Modern Electric Systems (ICEMES), Oradea, Romania, 13–14 June 2019. [Google Scholar]
- Constantinescu, F.; Gheorghe, A.G.; Marin, M.E.; Vătășelu, G.; Ștefănescu, V.; Bodescu, D. New models for frequency do-main simulation of home appliances networks. In Proceedings of the 11-th International Symposium on Advanced Topics in Electrical Engineering, Bucharest, Romania, 28–30 March 2019. [Google Scholar]
- Enache, F.R.; Constantinescu, F.; Rață, M.; Vătășelu, G.; Ștefănescu, V.; Milici, D.; Aramă, I. Frequency domain models for nonlinear loads with firing angle control devices, Part II—Modeling. In Proceedings of the 6th International Symposium on Electrical and Electronics Engineering, Galați, Romania, 18–20 October 2019. [Google Scholar]
- Liu, T.; Xu, L.; He, Y.; Wu, H.; Yang, Y.; Wu, N.; Yang, X.; Shi, X.; Wei, F. A Novel Simulation Method for Analyzing Diode Electrical Characteristics Based on Neural Networks. Electronics 2021, 10, 2337. [Google Scholar] [CrossRef]
- Ciuceanu, R.M.; Nemoianu, I.V.; Mănescu Păltânea, V.; Păltânea, G. On Professor Țugulea’s visionary power theory: A review, recent advances and perspectives. Rev. Roum. Sci. Techn. Électrotechn. Énerg. 2018, 63, 123–127. [Google Scholar]
- Nemoianu, I.V.; Dascalu, M.I.; Manescu, V.; Paltanea, G.; Ciuceanu, R.M.; Păltânea, V.M. In-deep First Assessment of the Influence of Nonlinear Elements in Three-Phase Networks with Neutral. In Proceedings of the 2019 11th International Symposium on Advanced Topics in Electrical Engineering (ATEE), Bucharest, Romania, 28–30 March 2019; pp. 1–6. [Google Scholar]
- Nemoianu, I.V.; Dascălu, M.I.; Mănescu Păltânea, V.; Păltânea, G.; Radulian, A. Detailed evaluation for the power flow effects of nonlinear circuit elements in three-phase networks without neutral. Rev. Roum. Sci. Techn. Électrotechn. Énerg. 2019, 64, 195–198. [Google Scholar]
- Nemoianu, I.V.; Paltanea, V.M.; Paltanea, G.; Ciuceanu, R.M. Insight into the Non-Symmetry and Residual Active and Reactive Power Flow in the case of Three-Phase Distorting Networks without Neutral. In Proceedings of the 2021 12th International Symposium on Advanced Topics in Electrical Engineering (ATEE), Bucharest, Romania, 25–27 March 2021; pp. 1–6. [Google Scholar]
- Hănțilă, I.F. A method for solving nonlinear resistive networks. Rev. Roum. Sci. Techn. Électrotechn. Énerg. 1979, 24, 217–226. [Google Scholar]
- Hănțilă, I.F.; Maricaru, M.; Ciuceanu, R.M.; Corlan, L. Harmonic analysis of circuits with nonlinear resistive elements. Rev. Roum. Sci. Techn. Électrotechn. Énerg. 2012, 57, 333–340. [Google Scholar]
- Vasilescu, G.M.; Hănțilă, I.F.; Maricaru, M.; Bârsan, I.; Stanciu, V. A new method for solving the periodic steady state of nonlinear circuits. Rev. Roum. Sci. Techn. Électrotechn. Énerg. 2014, 59, 339–349. [Google Scholar]
- Hănțilă, I.F.; Constantinescu, F.; Gheorghe, A.G.; Niţescu, M.; Maricaru, M. A new algorithm for frequency domain analysis of nonlinear circuits. Rev. Roum. Sci. Techn. Électrotechn. Énerg. 2009, 54, 57–66. [Google Scholar]
- Hănțilă, I.F.; Maricaru, M.; Stănculescu, M.; Vasilescu, G.M. Method for analyzing three-phase networks with nonlinear resistive elements. Rev. Roum. Sci. Techn. Électrotechn. Énerg. 2019, 64, 103–106. [Google Scholar]
- Hănțilă, I.F.; Vasile, N.; Demeter, E.; Marinescu, S.; Covrig, M. Câmpul Electromagnetic Staționar în Medii Neliniare; ICPE: București, Romania, 1998; pp. 46–51. ISBN 973-98322-0-2. [Google Scholar]














| Harmonic Order | |||||
|---|---|---|---|---|---|
| 0—DC component | 0 | −1.1012 × 103 | 1.1012 × 103 | 0 | |
| 1—fundamental | −3.1249 × 103 −2.2739 × 102j | 3.0979 × 101 +5.8394 × 102j | 1.5132 × 103 +1.1275 × 102j | 1.5806 × 103 −4.6929 × 102j | −6.8212 × 10−13 +2.8422 × 10−13j |
| 2 | 3.6912 +1.3916 × 102j | −3.0980 × 101 −1.2321 × 102j | 2.7288 × 101 −1.5950 × 101j | −1.4211 × 10−14 −5.6843 × 10−14j | |
| 3 | 0 | −5.4456 × 101 +4.6640 × 101j | 5.4456 × 101 −4.6640 × 101j | −1.4211 × 10−14 +2.1316 × 10−14j | |
| 4 | 2.2478 × 10−2 +1.6948j | −7.7229 × 10−1 −8.7408 × 10−1j | 7.4981 × 10−1 −8.2073 × 10−1j | −3.3307 × 10−16 −3.3307 × 10−16j | |
| 5 | 8.9241 × 10−2 +8.4107j | −5.2063 −1.7664j | 5.1170 −6.6443j | 0 +1.9984 × 10−15j | |
| 6 | 0 | −2.7754 × 10−1 +4.0435 × 10−1j | 2.7754 × 10−1 −4.0435 × 10−1j | −5.5511 × 10−17 −5.5511 × 10−17j | |
| 7 | 2.3962 × 10−3 +3.1617 × 10−1j | −3.5779 × 10−1 +2.3732 × 10−1j | 3.5539 × 10−1 −5.5349 × 10−1j | −2.2204 × 10−16 +5.5511 × 10−17j | |
| 8 | 1.5097 × 10−3 +2.2765 × 10−1j | −3.5625 × 10−1 +3.3775 × 10−1j | 3.5474 × 10−1 −5.6541 × 10−1j | 1.6653 × 10−16 −1.6653 × 10−16j | |
| 9 | 0 | −6.2792 × 10−3 +9.7711 × 10−3j | 6.2792 × 10−3 −9.7711 × 10−3j | −1.7347 × 10−18 +0j | |
| 10 | 2.0533 × 10−4 +3.8704 × 10−2j | −1.2991 × 10−1 +1.4732 × 10−1j | 1.2971 × 10−1 −1.8603 × 10−1j | 8.3267 × 10−17 −5.5511 × 10−17j | |
| … | … | … | … | … | |
| 999 | 0 | −1.4358 × 10−15 −2.2189 × 10−9j | 1.4358 × 10−15 +2.2189 × 10−9j | 3.2312 × 10−27 +4.1359 × 10−25j | |
| 1000 | 1.9794 × 10−14 +3.7311 × 10−10j | −2.1239 × 10−14 −2.6122 × 10−9j | 1.4446 × 10−15 +2.2391 × 10−9j | 3.8774 × 10−26 −1.2408 × 10−24j | |
| Total = | Total = | Total = | Total = | Overall Balance of Powers +++ | |
| Balance of powers for each network component (summing up all harmonic components) | −3.1249 × 103 −2.2739 × 102j | 3.4786 × 101 +7.3380 × 102j | 3.1932 × 102 +3.4637 × 101j | 2.7707 × 103 −5.4105 × 102j | −7.1091 × 10−13 +2.5015 × 10−13j |
| Harmonic Order | |||||
|---|---|---|---|---|---|
| DC component | 0 | −1.1823 × 103 | 1.1823 × 103 | 0 | |
| 1—fundamental | −3.2226 × 103 −7.3492 × 101j | 3.2790 × 101 +6.1807 × 102j | 1.5776 × 103 −6.5922 × 101j | 1.6122 × 103 −4.7866 × 102j | −2.2737 × 10−13 +1.4779 × 10−12j |
| 2 | 3.1786 +1.9971 × 101j | −3.8473 −1.9581 × 101j | 6.6880 × 10−1 −3.9091 × 10−1j | 0 | |
| 3 | 0 | −4.5309 × 101 +3.8806 × 101j | 4.5309 × 101 −3.8806 × 101j | −1.4211 × 10−14 +1.4211 × 10−14j | |
| 4 | 1.0834 × 10−01 +1.3615j | −2.0935 × 10−1 −1.2509j | 1.0101 × 10−1 −1.1056 × 10−1j | 4.4409 × 10−16 +4.4409 × 10−16j | |
| 5 | 2.3801 × 10−1 +3.7386j | −6.1859 × 10−1 −3.2444j | 3.8058 × 10−1 −4.9417 × 10−1j | 8.8818 × 10−16 −4.4409 × 10−16j | |
| 6 | 0 | −2.8656 +4.1749j | 2.8656 −4.1749j | 8.8818 × 10−16 −8.8818 × 10−16j | |
| 7 | 3.9572 × 10−2 +8.7022 × 10−1j | −2.0293 × 10−1 −6.1581 × 10−1j | 1.6336 × 10−1 −2.5442 × 10−1j | 0 +3.3307 × 10−16j | |
| 8 | 7.6495 × 10−2 +1.9225j | −5.7656 × 10−1 −1.1255j | 5.0007 × 10−1 −7.9704 × 10−1j | −2.2204 × 10−16 −8.8818 × 10−16j | |
| 9 | 0 | −1.8838 × 10−1 +2.9313 × 10−1j | 1.8838 × 10−1 −2.9313 × 10−1j | −1.6653 × 10−16 +5.5511 × 10−17j | |
| 10 | 4.0520 × 10−3 +1.2730 × 10−1j | −7.5223 × 10−2 −2.5223 × 10−2j | 7.1171 × 10−2 −1.0207 × 10−1j | −6.9389 × 10−17 +7.6328 × 10−17j | |
| ... | ... | ... | ... | ... | |
| 999 | 0 | −2.8261 × 10−15 −4.3674 × 10−9j | 2.8261 × 10−15 +4.3674 × 10−9j | −1.1309 × 10−25 +8.2718 × 10−25j | |
| 1000 | 1.5573 × 10−12 +4.8925 × 10−9j | −1.5605 × 10−12 −9.7861 × 10−9j | 3.1571 × 10−15 +4.8935 × 10−9j | 2.8434 × 10−25 +3.3087 × 10−24j | |
| = | = | = | = | Overall balance of powers | |
| Balance of powers for each network component (summing up all harmonic components) | −3.2226 × 103 −7.3492 × 101j | 3.6443 × 101 +6.4637 × 102j | 3.4103 × 102 −4.8642 × 101j | 2.8451 × 103 −5.2424 × 102j | −2.3970 × 10−13 +1.4909 × 10−12j |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tufan, C.; Nemoianu, I.V. Method for the Analysis of Three-Phase Networks Containing Nonlinear Circuit Elements in View of an Efficient Power Flow Computation. Electronics 2021, 10, 2710. https://doi.org/10.3390/electronics10212710
Tufan C, Nemoianu IV. Method for the Analysis of Three-Phase Networks Containing Nonlinear Circuit Elements in View of an Efficient Power Flow Computation. Electronics. 2021; 10(21):2710. https://doi.org/10.3390/electronics10212710
Chicago/Turabian StyleTufan, Claudiu, and Iosif Vasile Nemoianu. 2021. "Method for the Analysis of Three-Phase Networks Containing Nonlinear Circuit Elements in View of an Efficient Power Flow Computation" Electronics 10, no. 21: 2710. https://doi.org/10.3390/electronics10212710
APA StyleTufan, C., & Nemoianu, I. V. (2021). Method for the Analysis of Three-Phase Networks Containing Nonlinear Circuit Elements in View of an Efficient Power Flow Computation. Electronics, 10(21), 2710. https://doi.org/10.3390/electronics10212710