Adaptive Robust Control for Networked Strict-Feedback Nonlinear Systems with State and Input Quantization
Abstract
:1. Introduction
2. Problem Statement
3. Main Results
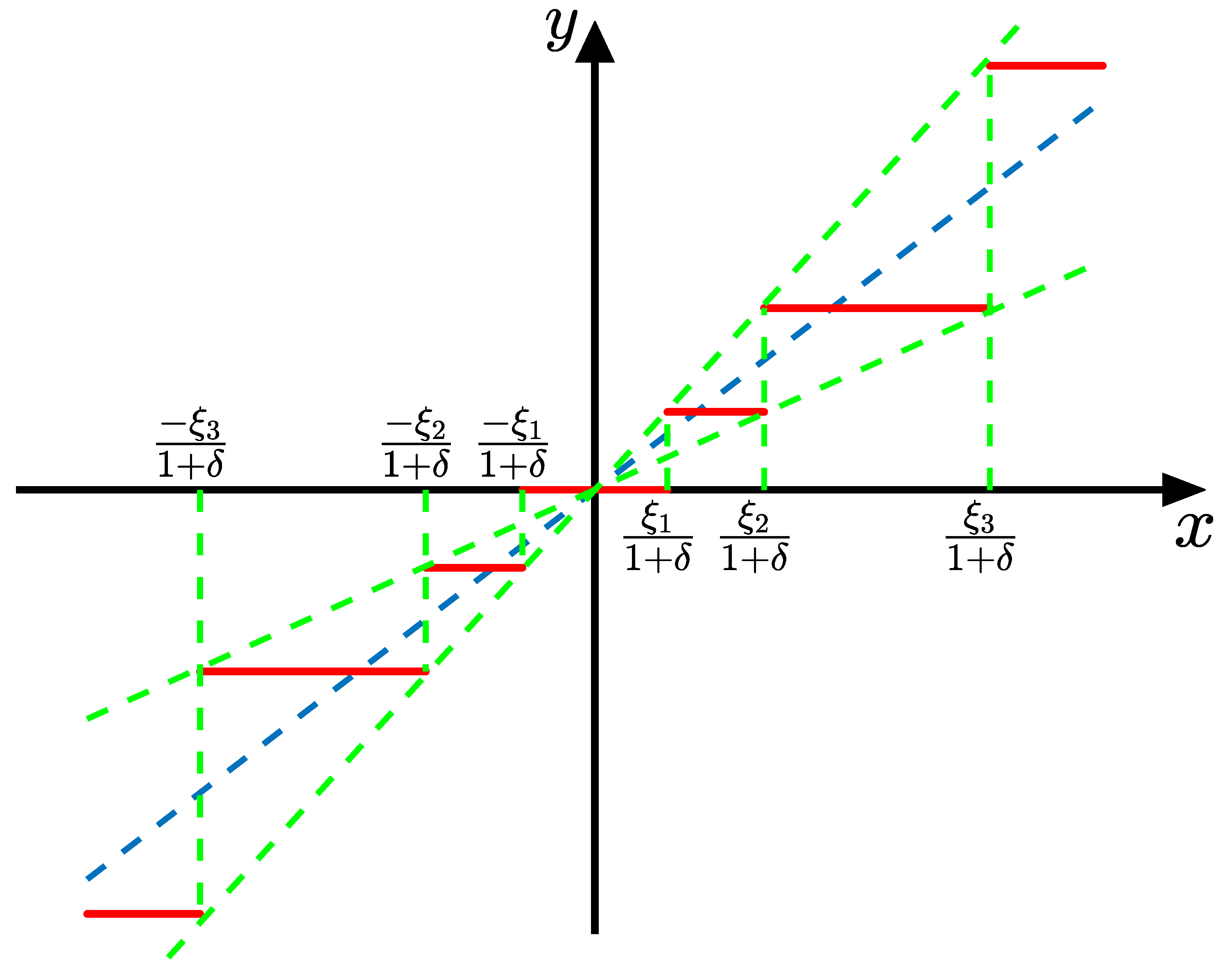
3.1. Backstepping Based Arc with Quantized States
3.2. Backstepping-Based Arc with Quantized States and Input
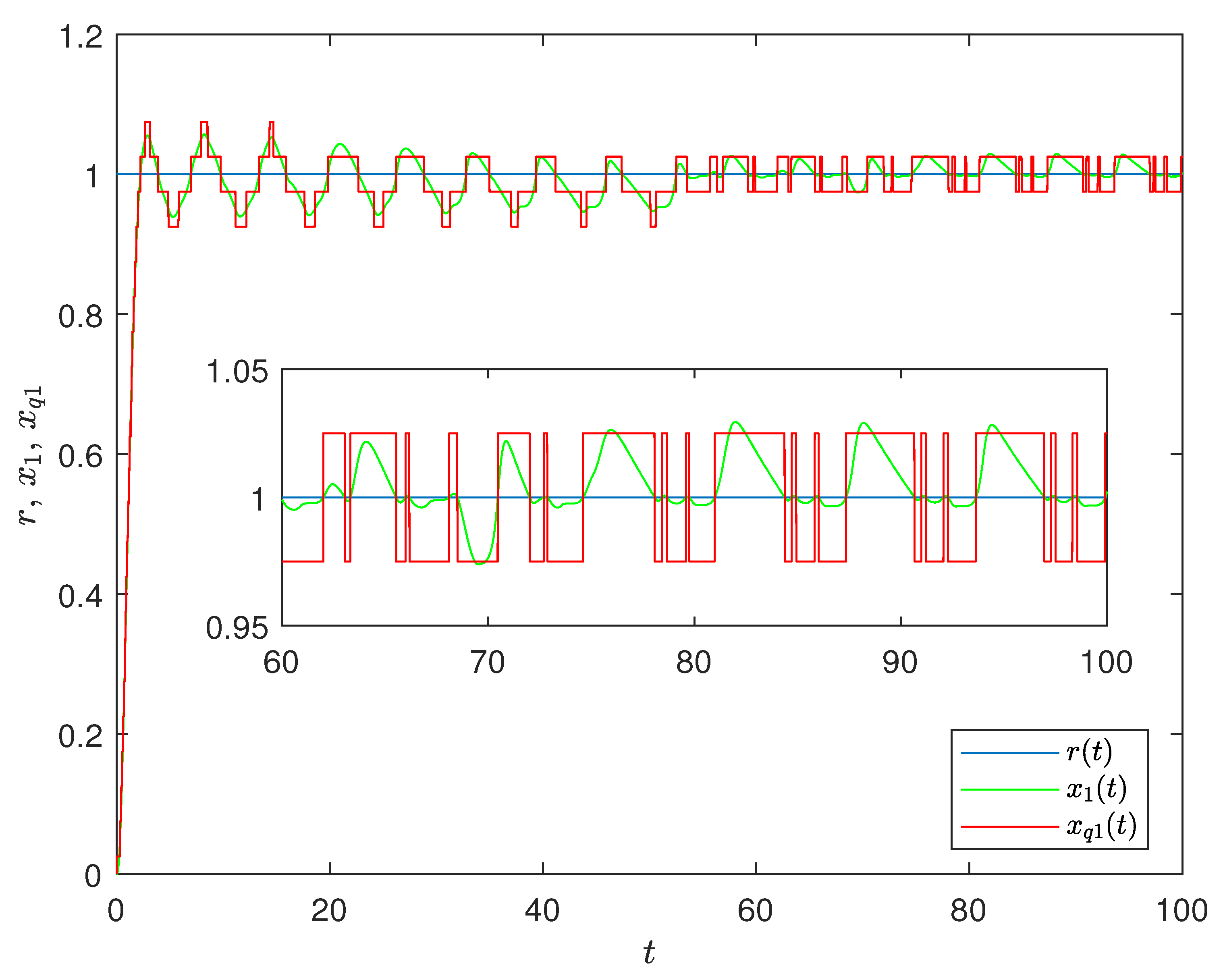
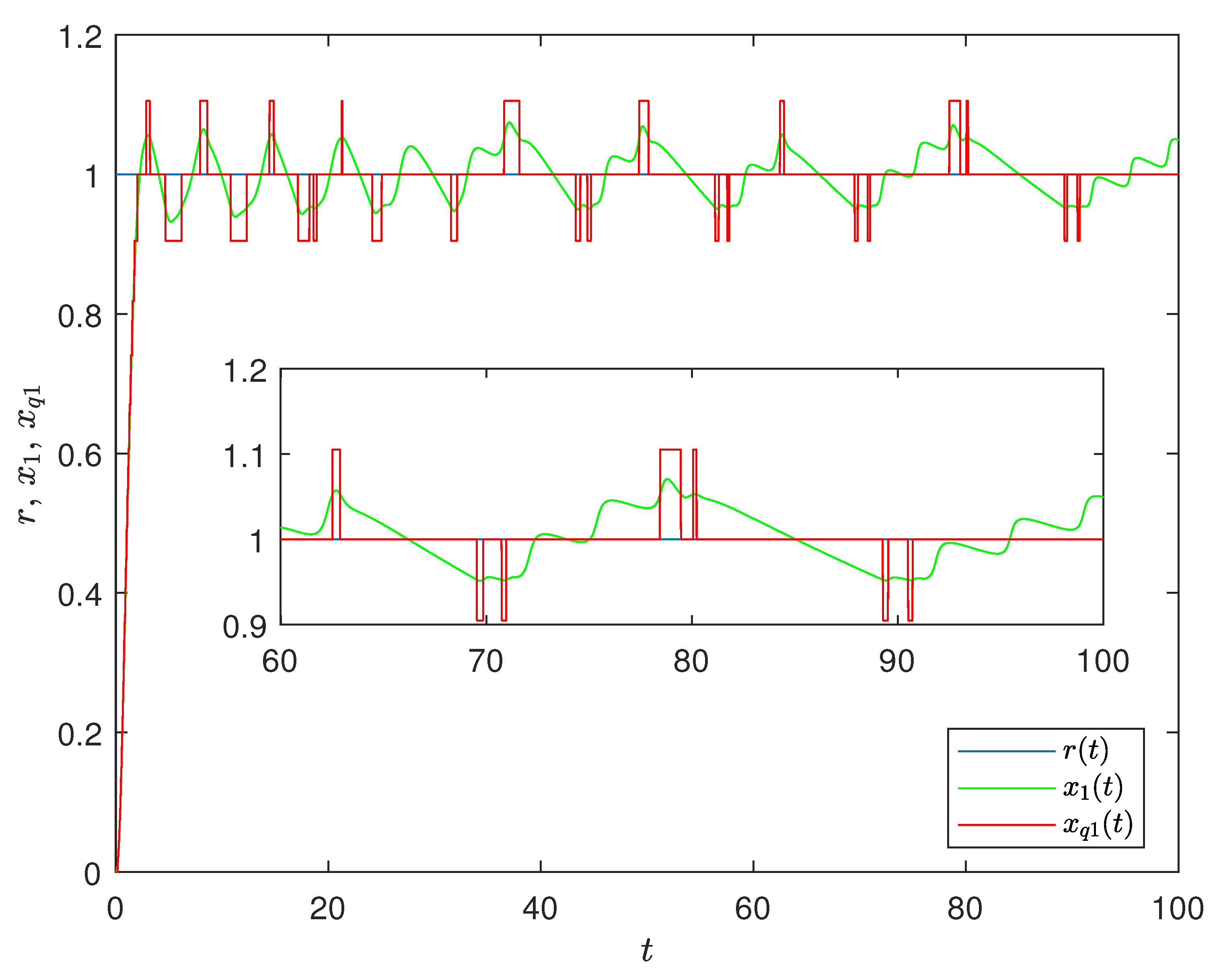
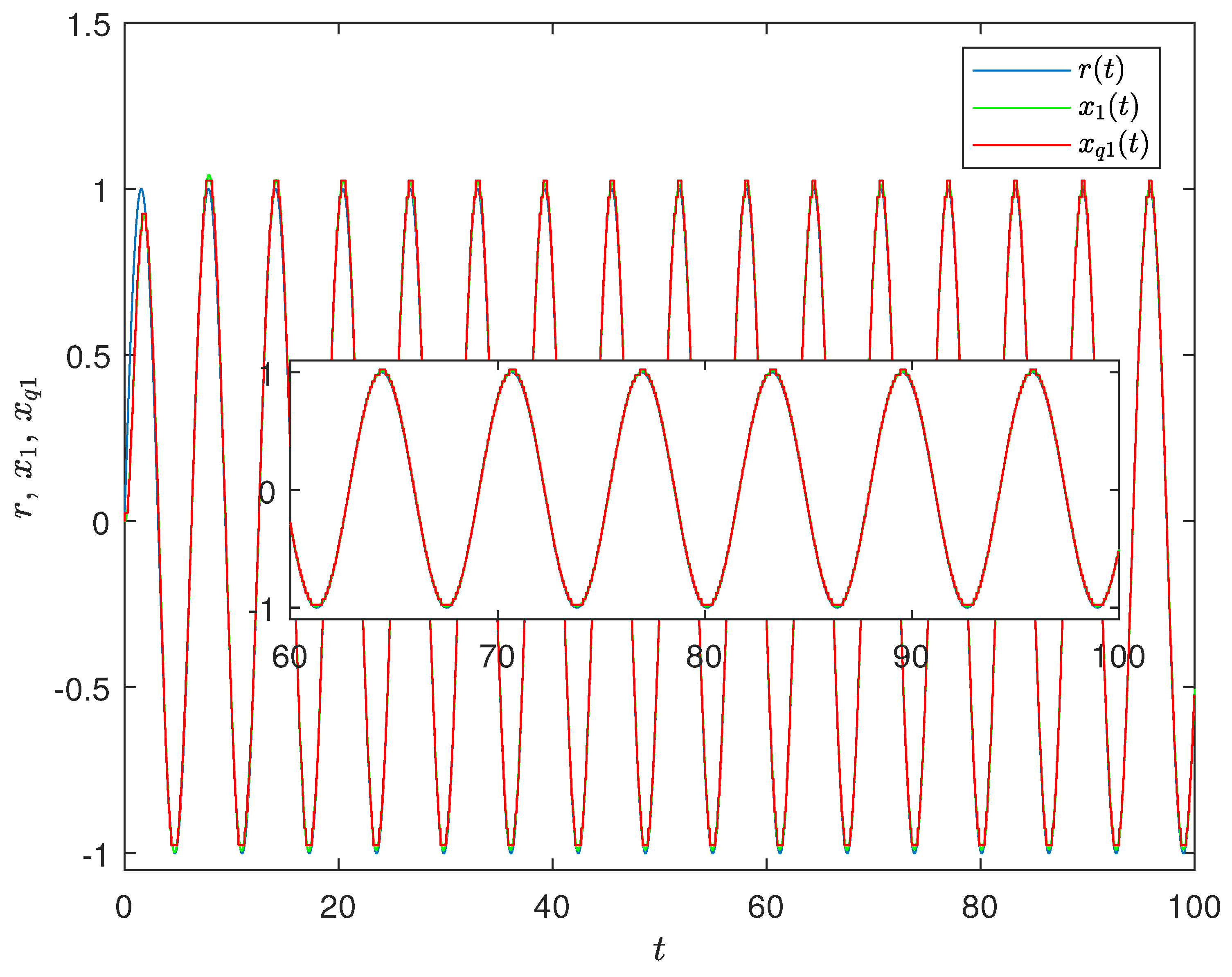
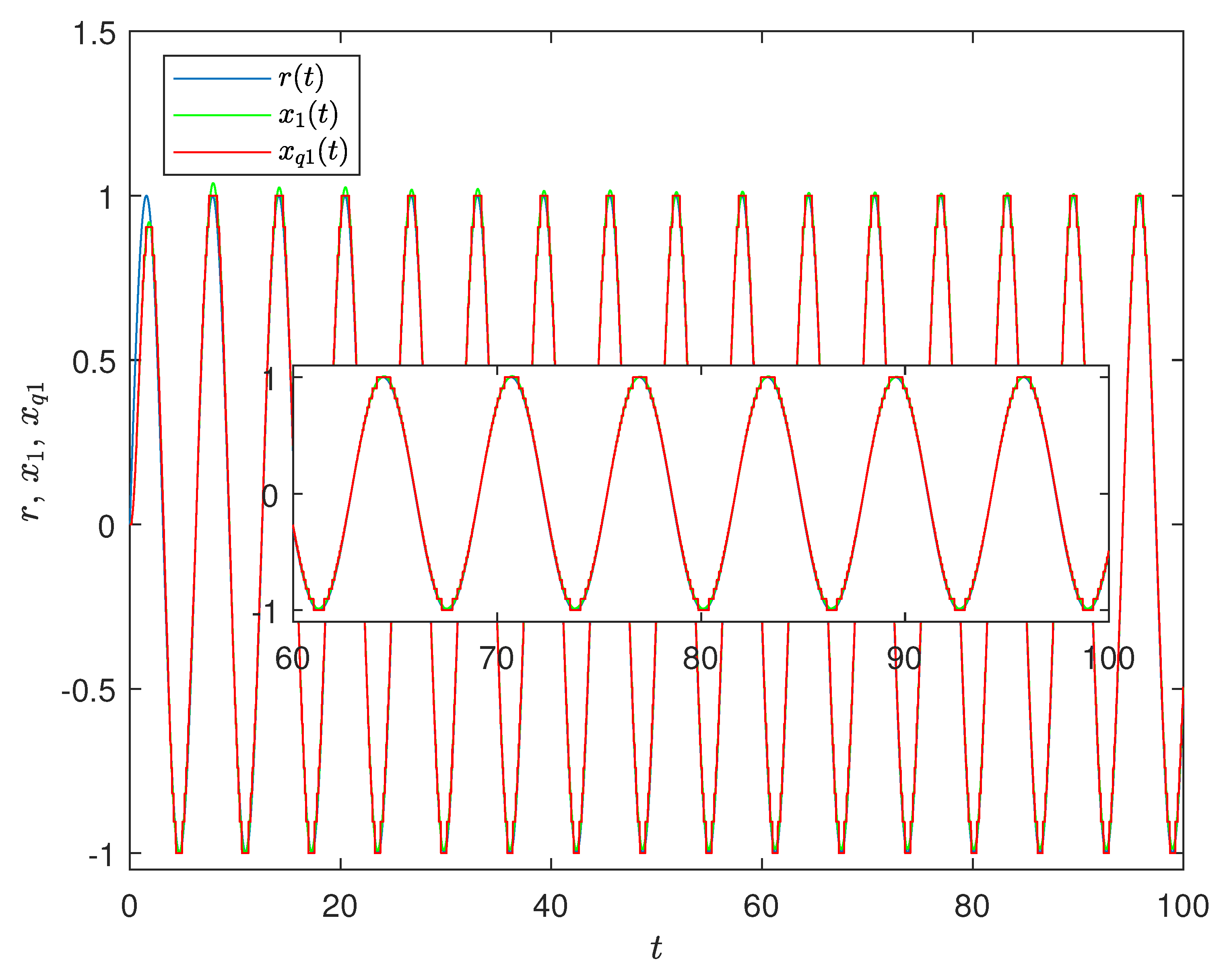
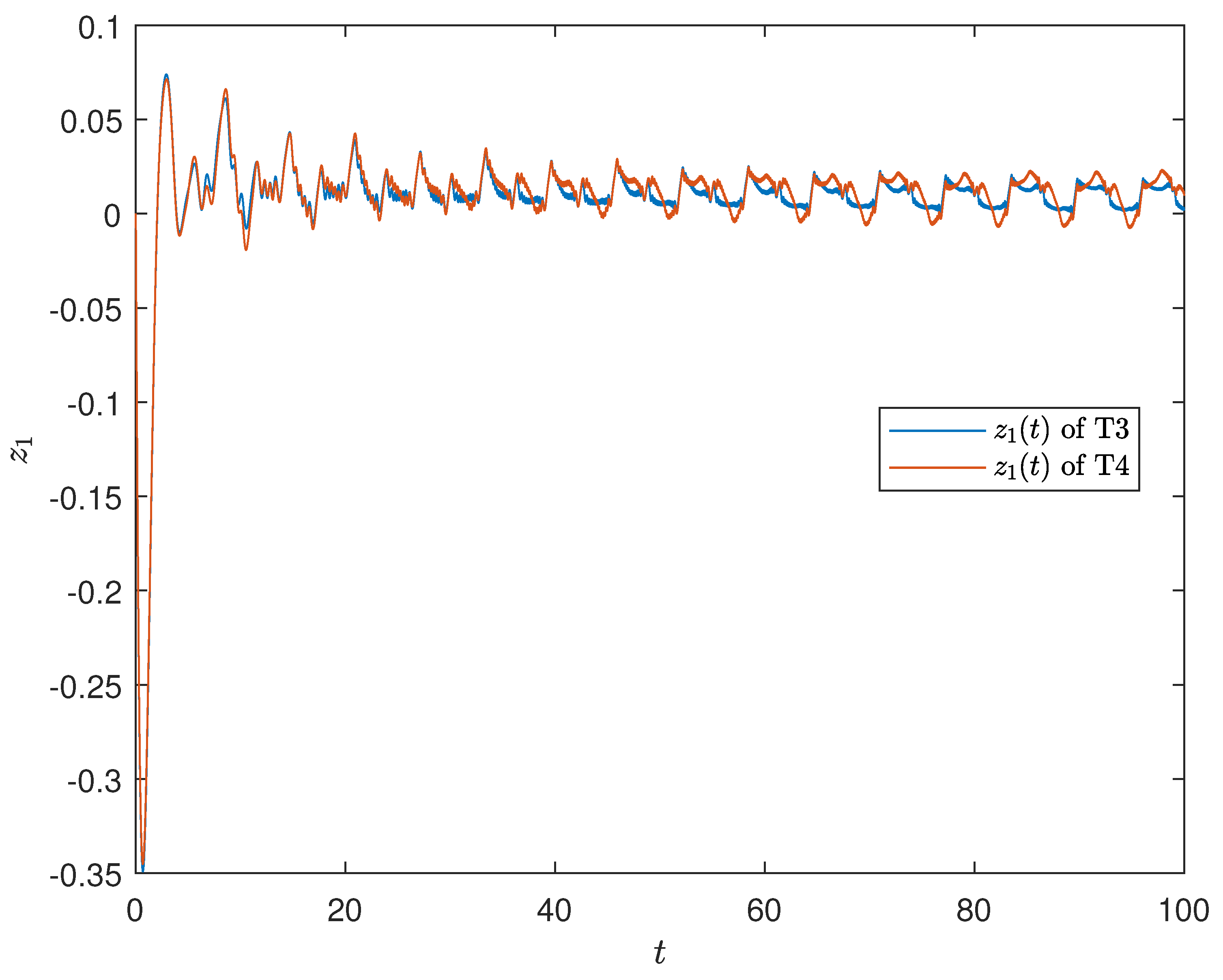
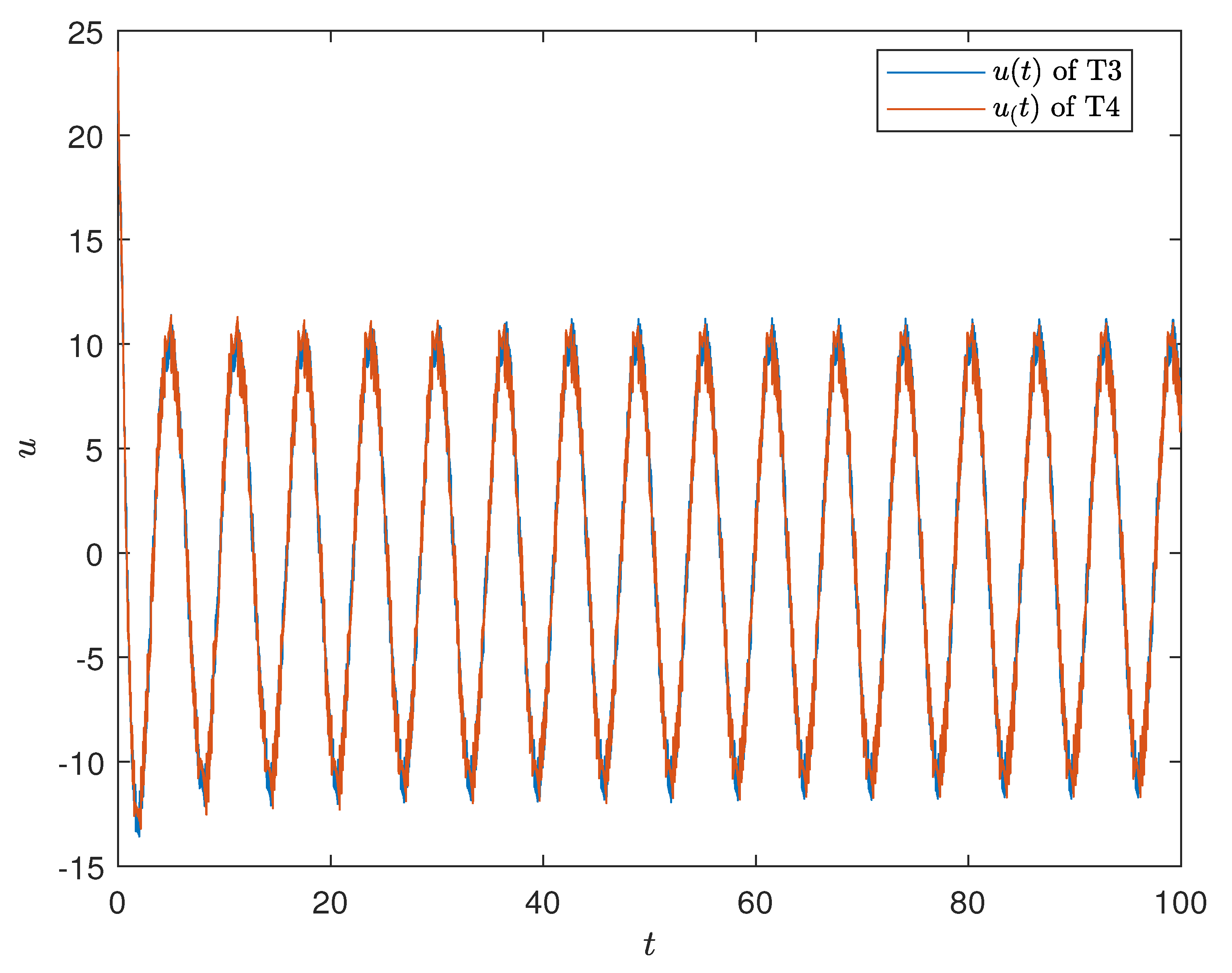
4. Results Validation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tong, S.; Li, Y. Adaptive fuzzy output feedback tracking backstepping control of strict-feedback nonlinear systems with unknown dead zones. IEEE Trans. Fuzzy Syst. 2012, 20, 168–180. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, W.; Feng, Z. Vehicle yaw stability control via H-infinity gain scheduling. Mech. Syst. Signal Process. 2018, 106, 62–75. [Google Scholar] [CrossRef]
- Doudou, S.; Khaber, F. Robust adaptive fuzzy control for a class of uncertain nonaffine nonlinear systems with unknown control directions. Trans. Inst. Meas. Control 2021, 43, 01423312211015114. [Google Scholar] [CrossRef]
- Di Ferdinando, M.; Castillo-Toledo, B.; Di Gennaro, S.; Pepe, P. Robust quantized sampled-data stabilization for a class of lipschitz nonlinear systems with time-varying uncertainties. IEEE Control Syst. Lett. 2021, 6, 1256–1261. [Google Scholar] [CrossRef]
- Kokotovic, P. The joy of feedback: Nonlinear and adaptive. IEEE Control Syst. 1992, 12, 7–17. [Google Scholar]
- Lozano, R.; Brogliato, B. Adaptive control of robot manipulators with flexible joints. IEEE Trans. Autom. Control 1992, 37, 174–181. [Google Scholar] [CrossRef]
- Corless, M.; Leitmann, G. Continuous state feedback guaranteeing uniform ultimate boundedness for uncertain dynamic systems. IEEE Trans. Autom. Control 1981, 26, 1139–1144. [Google Scholar] [CrossRef] [Green Version]
- Yao, B.; Tomizuka, M. Adaptive robust control of SISO nonlinear systems in a semi-strict feedback form. Automatica 1997, 33, 893–900. [Google Scholar] [CrossRef]
- Sun, W.; Wang, X.; Zhang, C. A Model-Free Control Strategy for Vehicle Lateral Stability with Adaptive Dynamic Programming. IEEE Trans. Ind. Electron. 2020, 67, 10693–10701. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, W.; Gao, H. High Precision Robust Control for Periodic Tasks of Linear Motor via B-Spline Wavelet Neural Network Observer. IEEE Trans. Ind. Electron. 2021. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, Y.; Huang, Y.; Gao, H.; Kaynak, O. Transient-performance-guaranteed robust adaptive control and its application to precision motion control systems. IEEE Trans. Ind. Electron. 2016, 63, 6510–6518. [Google Scholar] [CrossRef]
- Sun, W.; Liu, Y.; Gao, H. Constrained Sampled-Data ARC for a Class of Cascaded Nonlinear Systems With Applications to Motor-Servo Systems. IEEE Trans. Ind. Informatics 2019, 15, 766–776. [Google Scholar] [CrossRef]
- Mishra, S.K.; Jha, A.V.; Verma, V.K.; Appasani, B.; Abdelaziz, A.Y.; Bizon, N. An optimized triggering algorithm for event-triggered control of networked control systems. Mathematics 2021, 9, 1262. [Google Scholar] [CrossRef]
- He, Y.; Ji, M.D.; Zhang, C.K.; Wu, M. Global exponential stability of neural networks with time-varying delay based on free-matrix-based integral inequality. Neural Netw. 2016, 77, 80–86. [Google Scholar] [CrossRef]
- Nesic, D.; Teel, A. Input-output stability properties of networked control systems. IEEE Trans. Autom. Control 2004, 49, 1650–1667. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, F.; Ho, D.W.C.; Liu, X. Robust H∞ Control for Networked Systems With Random Packet Losses. IEEE Trans. Syst. Man Cybern. Part B 2007, 37, 916–924. [Google Scholar] [CrossRef] [PubMed]
- Quevedo, D.E.; Nesic, D. Input-to-state stability of packetized predictive control over unreliable networks affected by packet-dropouts. IEEE Trans. Autom. Control 2011, 56, 370–375. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Liu, G.; Rees, D. Actively compensating for data packet disorder in networked control systems. IEEE Trans. Circuits Syst. 2010, 57, 913–917. [Google Scholar] [CrossRef]
- Gao, H.; Chen, T. A new approach to quantized feedback control systems. Automatica 2008, 44, 534–542. [Google Scholar] [CrossRef]
- Chen, W.; Jiao, L.; Li, J.; Li, R. Adaptive NN Backstepping Output-Feedback Control for Stochastic Nonlinear Strict-Feedback Systems With Time-Varying Delays. IEEE Trans. Syst. Man Cybern. Part B 2010, 40, 939–950. [Google Scholar] [CrossRef]
- Zhang, J.; Xu, H.; Zheng, H. Adaptive sampled-data output tracking of parametric strict-feedback non-linear systems. IET Control Theory Appl. 2012, 6, 985–991. [Google Scholar] [CrossRef]
- Zeng, D.; Liu, Z.; Chen, C.L.; Zhang, Y. Adaptive neural tracking control for switched nonlinear systems with state quantization. Neurocomputing 2021, 454, 392–404. [Google Scholar] [CrossRef]
- Zhou, J.; Wen, C.; Wang, W.; Yang, F. Adaptive Backstepping Control of Nonlinear Uncertain Systems with Quantized States. IEEE Trans. Autom. Control 2019, 64, 4756–4763. [Google Scholar] [CrossRef]
- Aslmostafa, E.; Ghaemi, S.; Badamchizadeh, M.A.; Ghiasi, A.R. Adaptive backstepping quantized control for a class of unknown nonlinear systems. ISA Trans. 2021. [Google Scholar] [CrossRef]
- Sun, H.; Hovakimyan, N.; Basar, T. L1 adaptive controller for uncertain nonlinear multi-input multi-output systems with input quantization. IEEE Trans. Autom. Control 2012, 57, 565–578. [Google Scholar] [CrossRef]
- Zhou, J.; Wen, C.; Yang, G. Adaptive backsepping stabilization of nonlinear uncertain systems with quantized input signal. IEEE Trans. Autom. Control 2014, 59, 460–464. [Google Scholar] [CrossRef]
- Xing, L.; Wen, C.; Zhu, Y.; Su, H.; Liu, Z. Output feedback control for uncertain nonlinear systems with input quantization. Automatica 2016, 65, 191–202. [Google Scholar] [CrossRef]
- Liu, T.; Jiang, Z.; Hill, D. A sector bound approach to feedback control of nonlinear systems with state quantization. Automatica 2012, 48, 145–152. [Google Scholar] [CrossRef]
- Ceragioli, F.; De Persis, C.; Frasca, P. Discontinuities and Hystersis in Quantized Average Consensus. Automatica 2011, 47, 1919–1928. [Google Scholar] [CrossRef] [Green Version]



| B | E | R | |||||
|---|---|---|---|---|---|---|---|
| Value | 0.15 | 0.05 | 0.8 | 10 | 0.05 | 0.02 | 0.05 |
| Bound | [0.05,0.5] | [0.02,0.5] | [0.2,1] | [1,10] | - | - | - |
| Value | 0.1 | 0.1 | 1 | 5 | 0 | 0 | 0 |
| Uniform quantizer | State quantizer | |
| Input quantizer | ||
| Logarithmic quantizer | State quantizer | |
| Input quantizer | ||
| Parameter | Value | Parameter | Value | |
|---|---|---|---|---|
| Control law | 3 | 0.2 | ||
| 1 | 0.2 | |||
| 5 | 0.2 | |||
| Adaptive law | 0.02 | 0.01 | ||
| 0.02 | 0.01 | |||
| 0.02 | 0.01 | |||
| 5 | 0.1 |
| Testings | Quantizer | Trajectory |
|---|---|---|
| T1 | Uniform quantizer | |
| T2 | Logarithmic quantizer | |
| T3 | Uniform quantizer | |
| T4 | Logarithmic quantizer |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Wang, J.; Gomes, L.; Sun, W. Adaptive Robust Control for Networked Strict-Feedback Nonlinear Systems with State and Input Quantization. Electronics 2021, 10, 2783. https://doi.org/10.3390/electronics10222783
Liu Y, Wang J, Gomes L, Sun W. Adaptive Robust Control for Networked Strict-Feedback Nonlinear Systems with State and Input Quantization. Electronics. 2021; 10(22):2783. https://doi.org/10.3390/electronics10222783
Chicago/Turabian StyleLiu, Yanbin, Jue Wang, Luis Gomes, and Weichao Sun. 2021. "Adaptive Robust Control for Networked Strict-Feedback Nonlinear Systems with State and Input Quantization" Electronics 10, no. 22: 2783. https://doi.org/10.3390/electronics10222783






