Improved Hybrid Parameters Extraction of a PV Module Using a Moth Flame Algorithm
Abstract
:1. Introduction
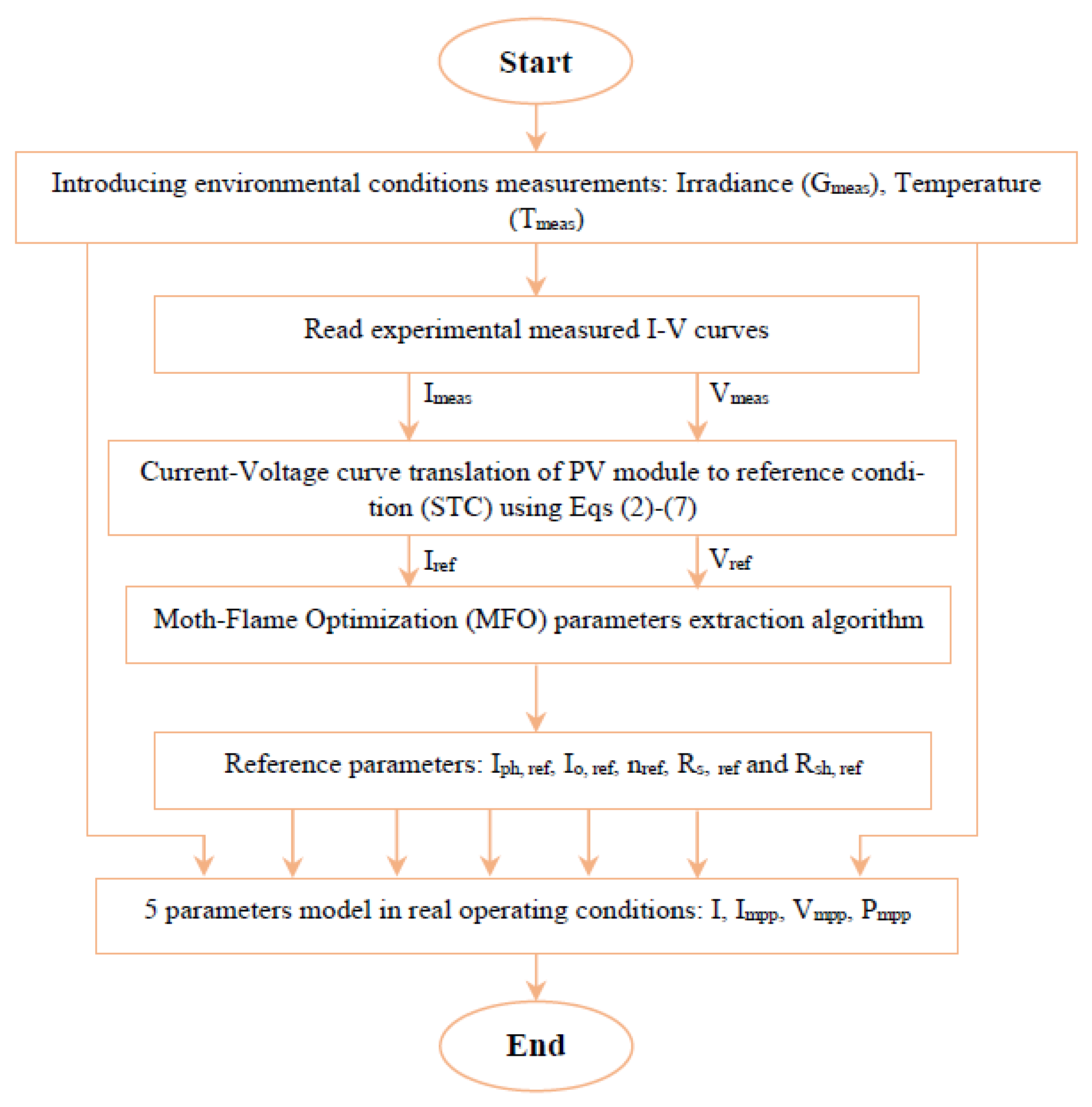
2. Modeling of a PV Array and Parameters Identification
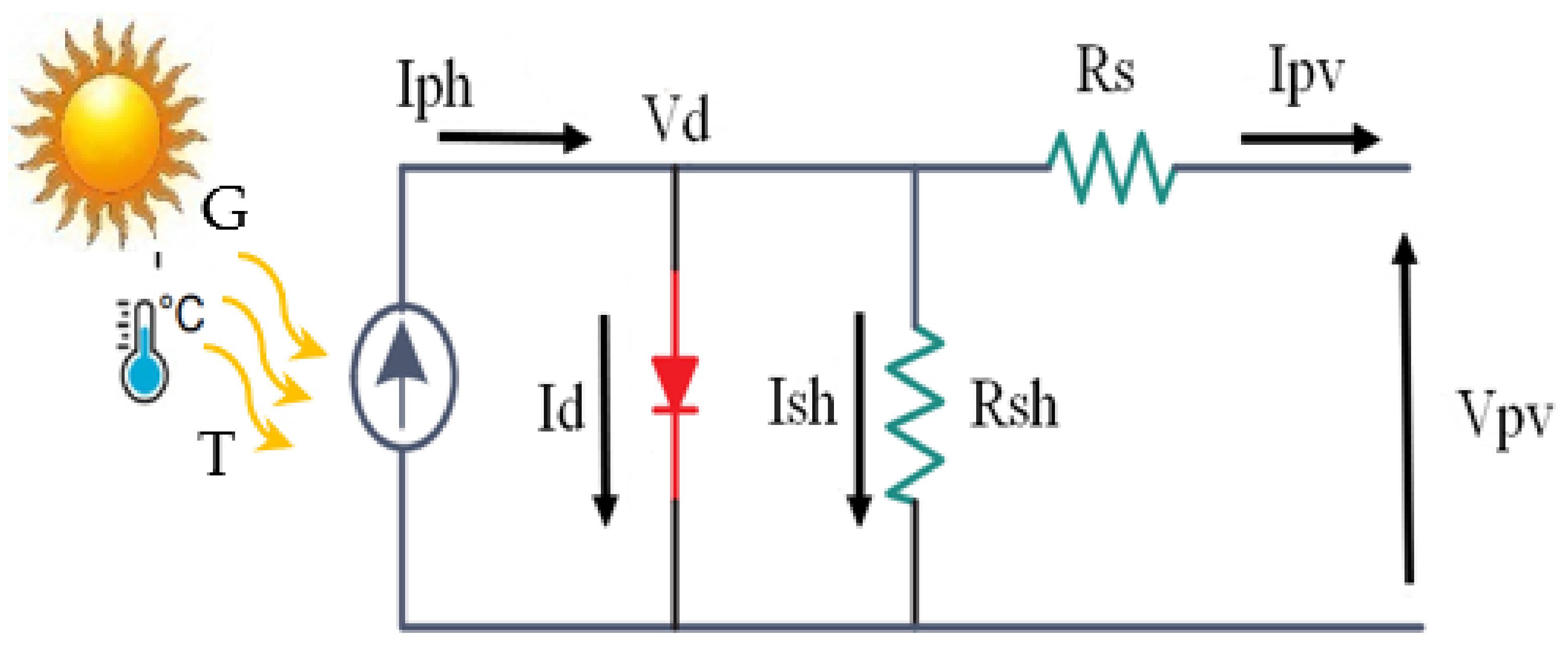
2.1. Modeling of a PV Array
2.2. Current-Voltage Translation to Reference Conditions
2.3. Identification of Reference Parameters
2.4. PV Module Parameter Extraction Based on the MFO Algorithm
| Algorithm 1: Moth flame optimization (MFO) for pv module parameters extraction |
 |
2.5. Five-Parameters under Actual Operating Conditions
3. Experimental Results and Validation
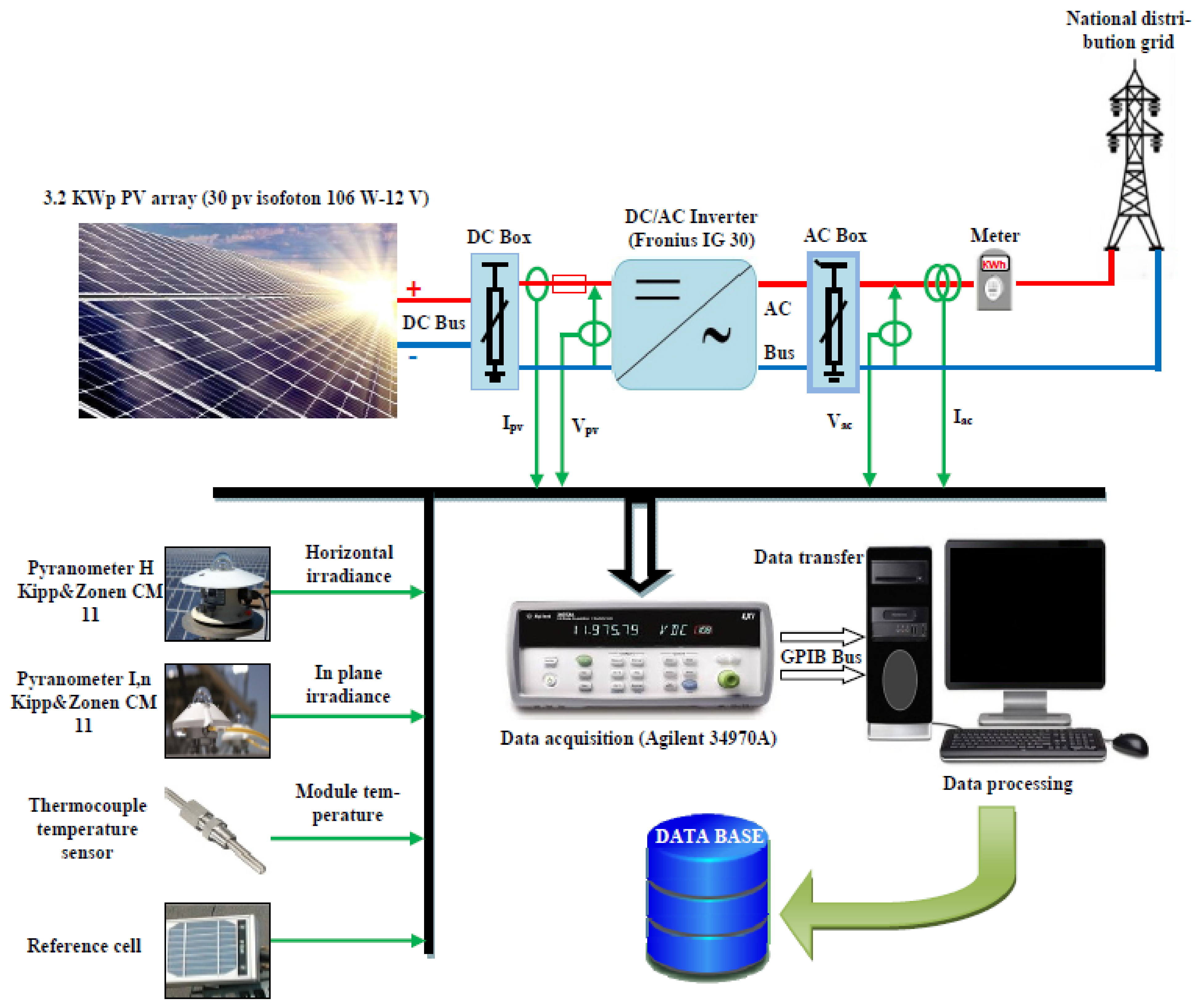
3.1. Grid-Connected PV System Description
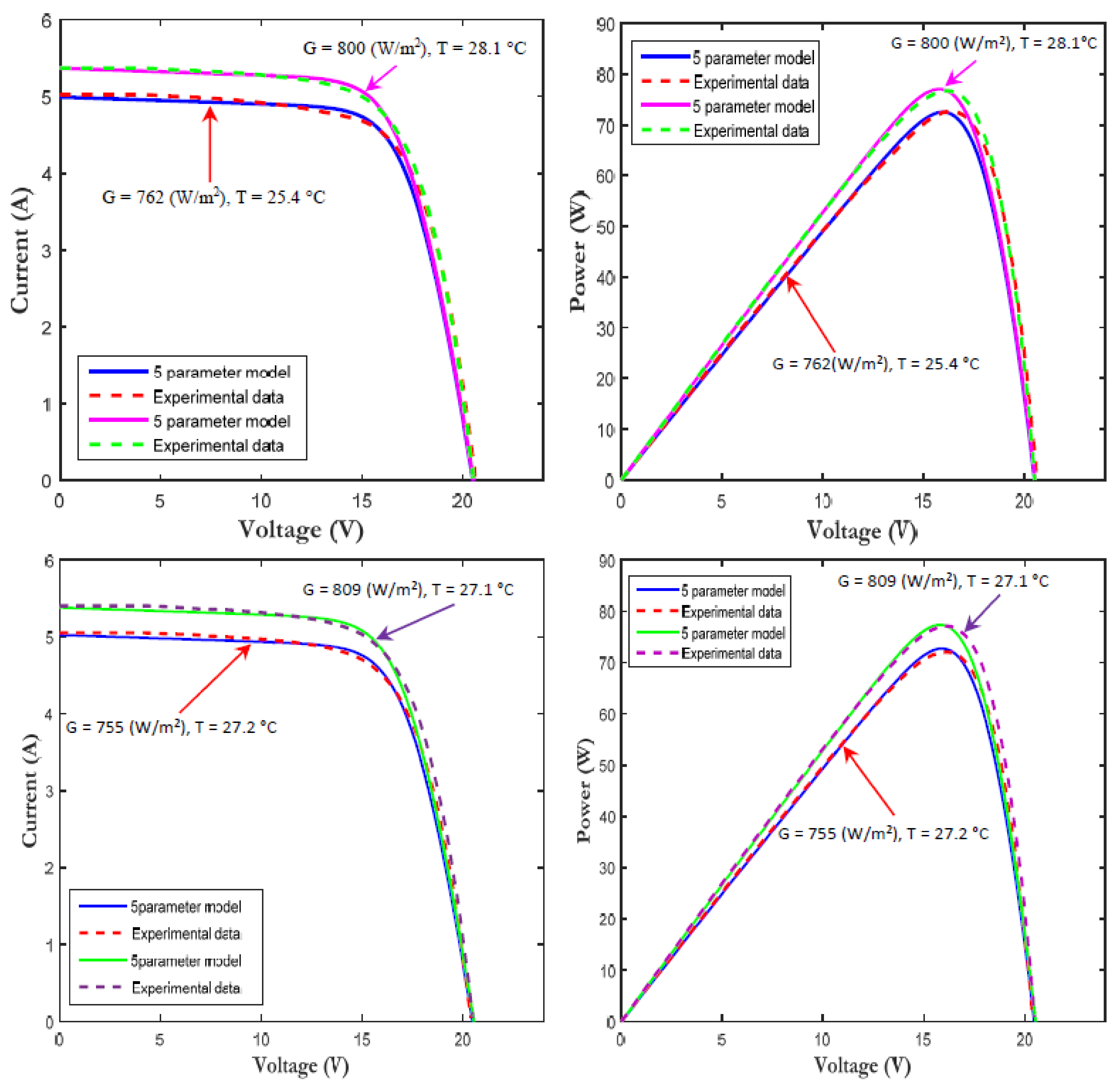
3.2. Reference Parameters Extraction Results
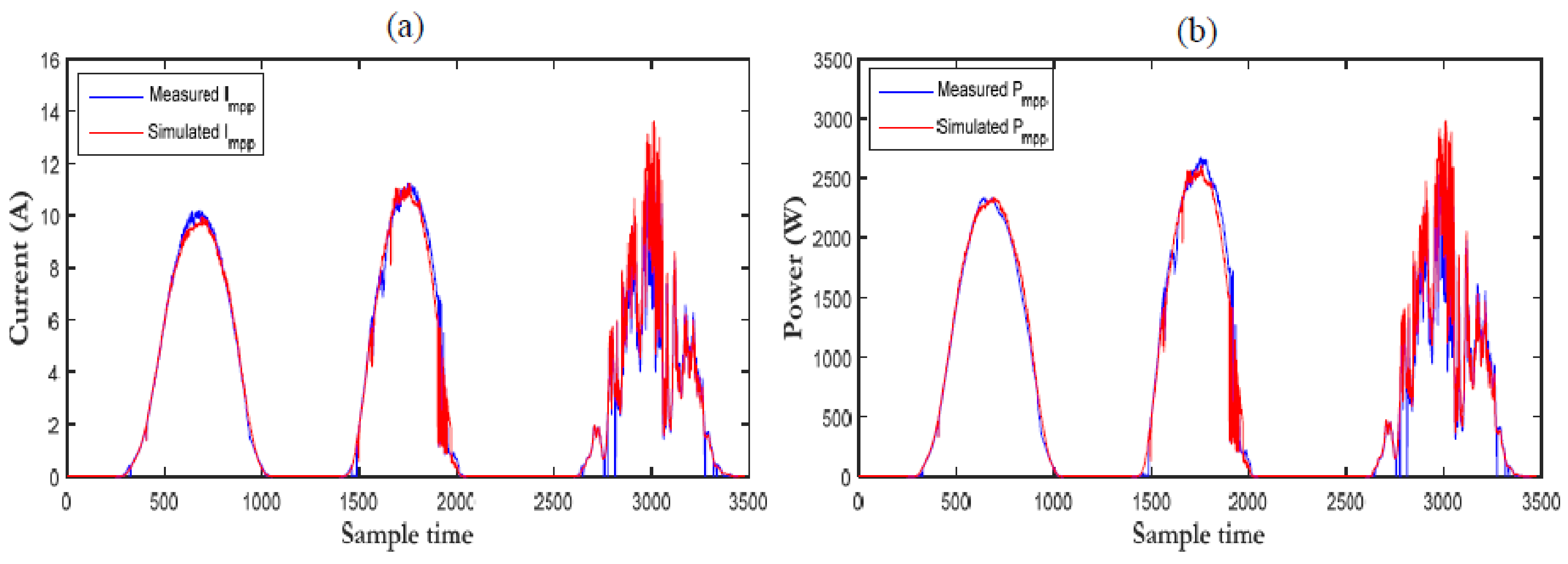
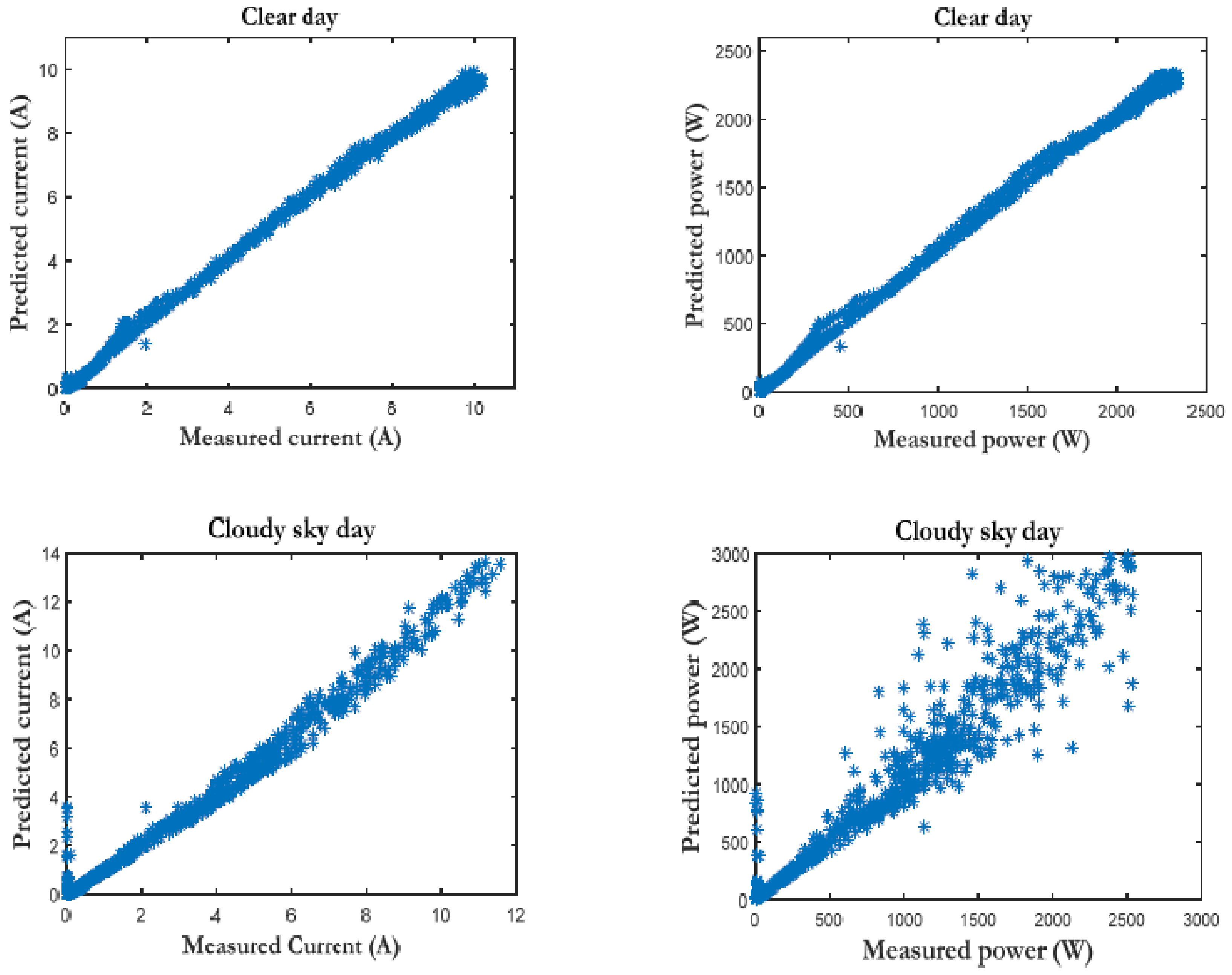
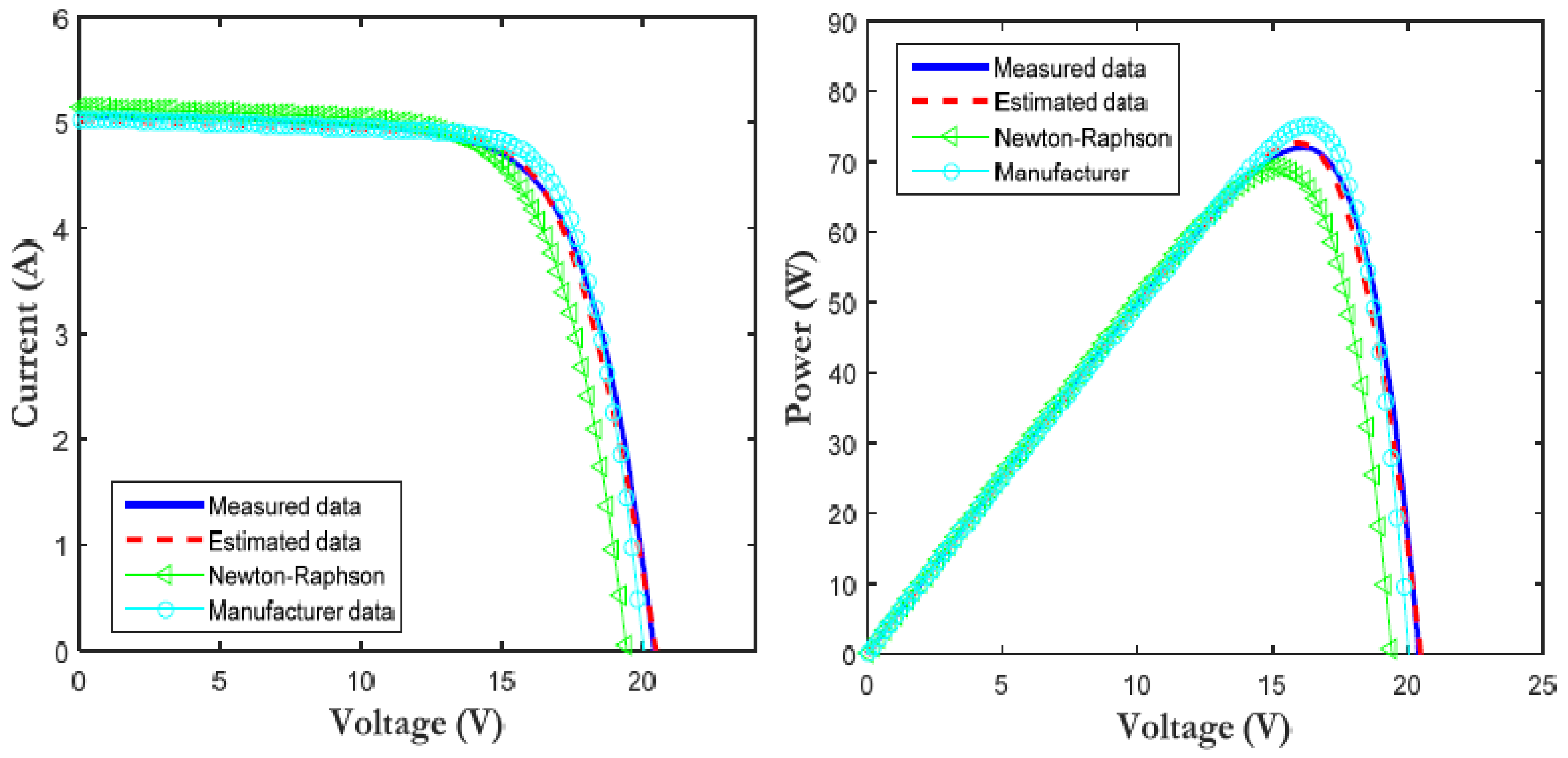
3.3. Accuracy of the Proposed Methodology
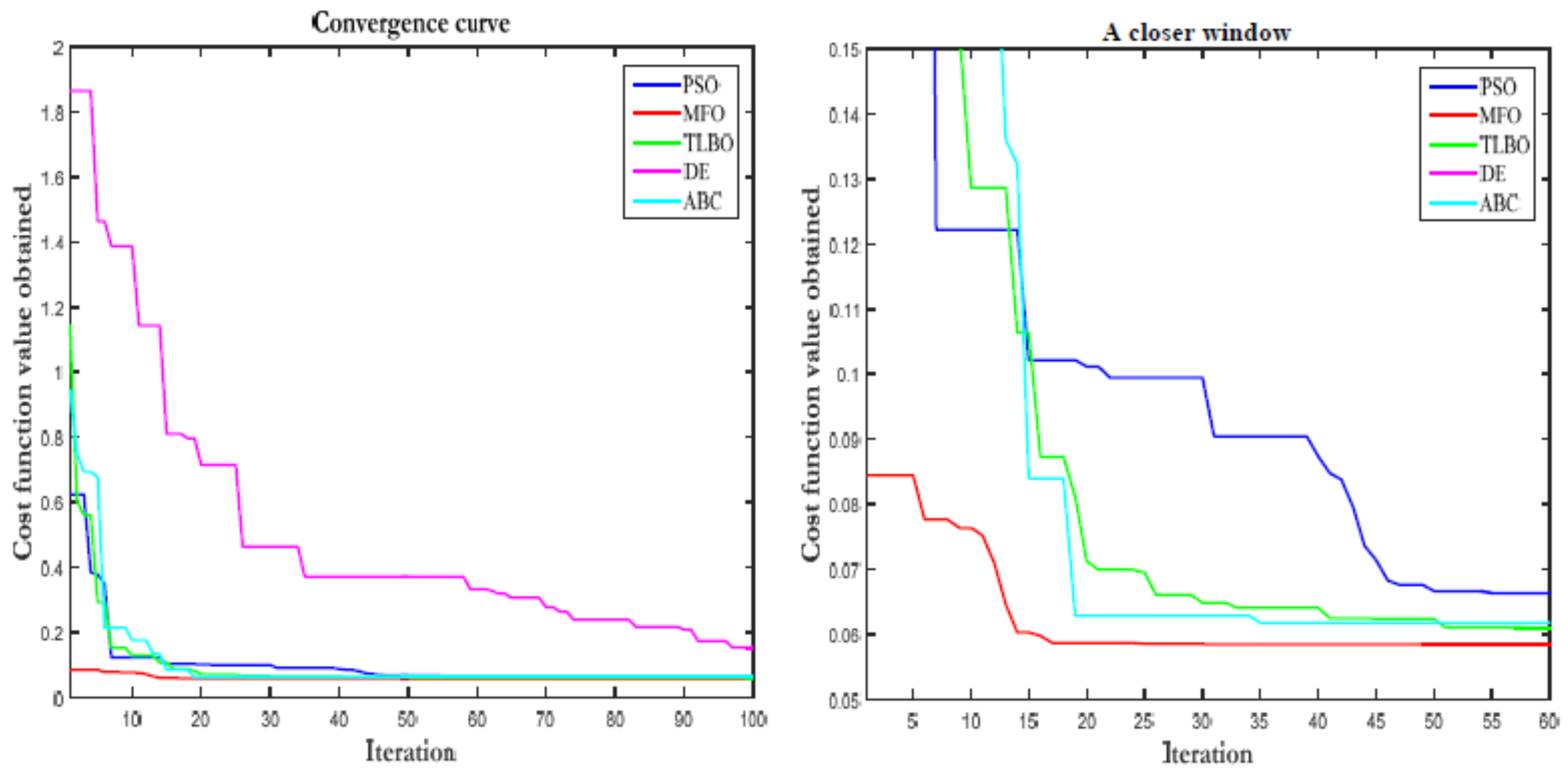
3.4. Comparison Study
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chaibi, Y.; Allouhi, A.; Salhi, M. A simple iterative method to determine the electrical parameters of photovoltaic cell. J. Clean. Prod. 2020, 269, 122363. [Google Scholar] [CrossRef]
- Mao, M.; Zhang, L.; Huang, H.; Chong, B.; Zhou, L. Maximum power exploitation for grid-connected PV system under fast-varying solar irradiation levels with modified salp swarm algorithm. J. Clean. Prod. 2020, 268, 122158. [Google Scholar] [CrossRef]
- Chouder, A.; Silvestre, S. Automatic supervision and fault detection of PV systems based on power losses analysis. Energy Convers. Manag. 2010, 51, 1929–1937. [Google Scholar] [CrossRef]
- Dhimish, M.; Holmes, V.; Mehrdadi, B.; Dales, M. Comparing Mamdani Sugeno fuzzy logic and RBF ANN network for PV fault detection. Renew. Energy 2018, 117, 257–274. [Google Scholar] [CrossRef] [Green Version]
- Kichou, S.; Silvestre, S.; Nofuentes, G.; Torres-Ramírez, M.; Chouder, A.; Guasch, D. Characterization of degradation and evaluation of model parameters of amorphous silicon photovoltaic modules under outdoor long term exposure. Energy 2016, 96, 231–241. [Google Scholar] [CrossRef]
- Dash, V.; Bajpai, P. Power management control strategy for a stand-alone solar photovoltaic-fuel cell-battery hybrid system. Sustain. Energy Technol. Assess. 2015, 9, 68–80. [Google Scholar] [CrossRef]
- Mahmoud, Y.A.; Xiao, W.; Zeineldin, H.H. A Parameterization Approach for Enhancing PV Model Accuracy. IEEE Trans. Ind. Electron. 2012, 60, 5708–5716. [Google Scholar] [CrossRef]
- Triki-Lahiani, A.; Bennani-Ben Abdelghani, A.; Slama-Belkhodja, I. Fault detection and monitoring systems for photovoltaic installations: A review. Renew. Sustain. Energy Rev. 2018, 82, 2680–2692. [Google Scholar] [CrossRef]
- Moshksar, E.; Ghanbari, T. Adaptive Estimation Approach for Parameter Identification of Photovoltaic Modules. IEEE J. Photovolt. 2017, 7, 614–623. [Google Scholar] [CrossRef]
- De Soto, W.; Klein, S.A.; Beckman, W.A. Improvement and validation of a model for photovoltaic array performance. Sol. Energy 2006, 80, 78–88. [Google Scholar] [CrossRef]
- Villalva, M.G.; Gazoli, J.R.; Filho, E.R. Comprehensive Approach to Modeling and Simulation of Photovoltaic Arrays. IEEE Trans. Power Electron. 2009, 24, 1198–1208. [Google Scholar] [CrossRef]
- Siddique, H.A.B.; Xu, P.; De Doncker, R.W. Parameter extraction algorithm for one-diode model of PV panels based on datasheet values. In Proceedings of the 2013 International Conference on Clean Electrical Power (ICCEP), Alghero, Italy, 11–13 June 2013; pp. 7–13. [Google Scholar] [CrossRef]
- Lo Brano, V.; Orioli, A.; Ciulla, G.; Di Gangi, A. An improved five-parameter model for photovoltaic modules. Sol. Energy Mater. Sol. Cells 2010, 94, 1358–1370. [Google Scholar] [CrossRef]
- Carrero, C.; Ramírez, D.; Rodríguez, J.; Platero, C.A. Accurate and fast convergence method for parameter estimation of PV generators based on three main points of the I–V curve. Renew. Energy 2011, 36, 2972–2977. [Google Scholar] [CrossRef]
- Zagrouba, M.; Sellami, A.; Bouaïcha, M.; Ksouri, M. Identification of PV solar cells and modules parameters using the genetic algorithms: Application to maximum power extraction. Sol. Energy 2010, 84, 860–866. [Google Scholar] [CrossRef]
- Low, K.S.; Soon, J.J. Photovoltaic model identification using particle swarm optimization with inverse barrier constraint. IEEE Trans. Power Electron. 2012, 27, 3975–3983. [Google Scholar]
- Jiang, L.L.; Maskell, D.L.; Patra, J.C. Parameter estimation of solar cells and modules using an improved adaptive differential evolution algorithm. Appl. Energy 2013, 112, 185–193. [Google Scholar] [CrossRef]
- Askarzadeh, A.; Rezazadeh, A. Artificial bee swarm optimization algorithm for parameters identification of solar cell models. Appl. Energy 2013, 102, 943–949. [Google Scholar] [CrossRef]
- Oliva, D.; Cuevas, E.; Pajares, G. Parameter identification of solar cells using artificial bee colony optimization. Energy 2014, 72, 93–102. [Google Scholar] [CrossRef]
- Patel, S.J.; Panchal, A.K.; Kheraj, V. Extraction of solar cell parameters from a single current-voltage characteristic using teaching learning based optimization algorithm. Appl. Energy 2014, 119, 384–393. [Google Scholar] [CrossRef]
- Askarzadeh, A.; Dos Santos Coelho, L. Determination of photovoltaic modules parameters at different operating conditions using a novel bird mating optimizer approach. Energy Convers. Manag. 2015, 89, 608–614. [Google Scholar] [CrossRef]
- Alam, D.F.; Yousri, D.A.; Eteiba, M.B. Flower Pollination Algorithm based solar PV parameter estimation. Energy Convers. Manag. 2015, 101, 410–422. [Google Scholar] [CrossRef]
- Kang, T.; Yao, J.; Jin, M.; Yang, S.; Duong, T. A novel improved cuckoo search algorithm for parameter estimation of photovoltaic (PV) models. Energies 2018, 11, 1060. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Yu, K.; Du, W.; Zhao, W.; Liu, G. Parameters identification of solar cell models using generalized oppositional teaching learning based optimization. Energy 2016, 99, 170–180. [Google Scholar] [CrossRef]
- Ben Messaoud, R. Extraction of uncertain parameters of double-diode model of a photovoltaic panel using Ant Lion Optimization. SN Appl. Sci. 2020, 2, 239. [Google Scholar] [CrossRef] [Green Version]
- Tatabhatla, V.M.R.; Agarwal, A.; Kanumuri, T. Performance enhancement by shade dispersion of Solar Photo-Voltaic array under continuous dynamic partial shading conditions. J. Clean. Prod. 2018, 213, 462–479. [Google Scholar] [CrossRef]
- Han, W.; Wang, H.; Chen, L. Parameters Identification for Photovoltaic Module Based on an Improved Artificial Fish Swarm Algorithm. Sci. World J. 2014, 2014, 12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jack, V.; Salam, Z.; Ishaque, K. Cell modelling and model parameters estimation techniques for photovoltaic simulator application: A review. Appl. Energy 2015, 154, 500–519. [Google Scholar] [CrossRef]
- Chine, W.; Mellit, A.; Lughi, V.; Malek, A.; Sulligoi, G.; Pavan, A.M. A novel fault diagnosis technique for photovoltaic systems based on artificial neural networks. Renew. Energy 2016, 90, 501–512. [Google Scholar] [CrossRef]
- Hadj Arab, A.; Chenlo, F.; Benghanem, M. Loss-of-load probability of photovoltaic water pumping systems. Sol. Energy 2004, 76, 713–723. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Garoudja, E.; Kara, K.; Chouder, A.; Silvestre, S. Parameters extraction of photovoltaic module for long-term prediction using artifical bee colony optimization. In Proceedings of the 2015 3rd International Conference on Control, Engineering & Information Technology (CEIT), Tlemcen, Algeria, 25–27 May 2015. [Google Scholar] [CrossRef]
- Chouder, A.; Silvestre, S.; Sadaoui, N.; Rahmani, L. Modeling and simulation of a grid connected PV system based on the evaluation of main PV module parameters. Simul. Model. Pract. Theory 2012, 20, 46–58. [Google Scholar] [CrossRef]
- Elkholy, A.; El-Ela, A.A. Optimal parameters estimation and modelling of photovoltaic modules using analytical method. Heliyon 2019, 5, e02137. [Google Scholar] [CrossRef] [PubMed]
- Tossa, A.K.; Soro, Y.M.; Azoumah, Y.; Yamegueu, D. A new approach to estimate the performance and energy productivity of photovoltaic modules in real operating conditions. Sol. Energy 2014, 110, 543–560. [Google Scholar] [CrossRef]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization. 2005. Available online: https://abc.erciyes.edu.tr/pub/tr06_2005.pdf (accessed on 1 January 2005).
- Kennedy, J.; Eberhart, R. Particle Swarm Optimisation. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar] [CrossRef]
- Rainer, S.; Kenneth, P. Differential Evolution: A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341. [Google Scholar]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching-Learning-Based Optimization: An optimization method for continuous non-linear large scale problems. Inf. Sci. 2012, 183, 1–15. [Google Scholar] [CrossRef]
- Yetayew, T.T.; Jyothsna, T.R. Parameter extraction of photovoltaic modules using Newton Raphson and simulated annealing techniques. In Proceedings of the 2015 IEEE Power, Communication and Information Technology Conference (PCITC), Bhubaneswar, India, 15–17 October 2016; pp. 229–234. [Google Scholar] [CrossRef]




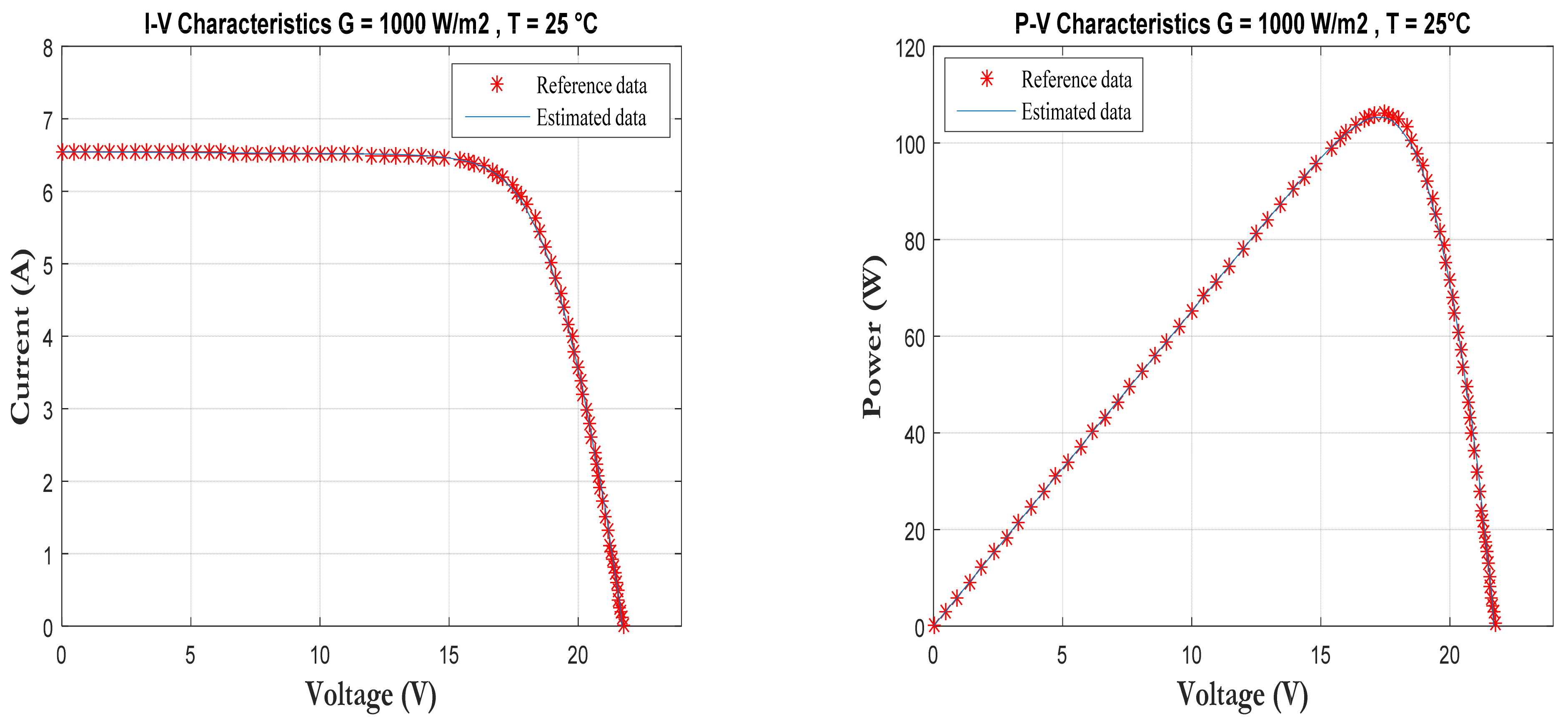



| Parameters | Value |
|---|---|
| Peak power (Pmpp) | 106 W |
| Voltage at maximum power point (Vmpp) | 17.4 V |
| Current at maximum power point (Impp) | 6.1 A |
| Open circuit voltage (Voc) | 21.8 V |
| Short circuit current (Isc) | 6.54 A |
| KIsc (α) | 0.06%/°C |
| KVoc (β) | −0.36%/°C |
| Electrical Parameters | Iph (A) | Io (A) | n | Rs (Ω) | Rsh (Ω) |
|---|---|---|---|---|---|
| Extracted value | 6.5497 | 4.4 × 10−9 | 1.0555 | 0.4503 | 200 |
| Algorithm | PSO | ABC | DE | TLBO | MFO |
|---|---|---|---|---|---|
| value | 0.06633 | 0.060355 | 0.096007 | 0.061811 | 0.058483 |
| Environmental Conditions: Irradiance (W/m2), Temperature (°C) | G = 755, T = 27.2 | G = 762, T = 25.4 | G = 800, T = 28.1 | G = 809, T = 27.1 |
|---|---|---|---|---|
| RMS error five parameter model (%) | 1.3019 | 1.3214 | 1.3019 | 1.3113 |
| RMSE | R2 | MAPE (%) | ||||
|---|---|---|---|---|---|---|
| Power (W) | Current (A) | Power (W) | Current (A) | Power (W) | Current (A) | |
| Clear sky | 0.018782 | 0.016813 | 0.99753 | 0.99797 | 1.0905 | 0.98862 |
| Semi-cloudy sky | 0.06494 | 0.060174 | 0.97069 | 0.9742 | 2.7066 | 2.4113 |
| Cloudy sky | 0.070958 | 0.043726 | 0.92747 | 0.96863 | 2.9426 | 1.8707 |
| Environmental Conditions | Clear Sky | Environmental Conditions | Cloudy Sky | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| G (W/m2) | T(°C) | Power (W) | Current (A) | G (W/m2) | T (°C) | Power (W) | Current (A) | ||||
| RMSE% | MAPE% | RMSE% | MAPE% | RMSE% | MAPE% | RMSE% | MAPE% | ||||
| 673.79 | 30.77 | 0.054637 | 5.4637 | 0.017583 | 1.7583 | 188.19 | 21.71 | 0.010086 | 1.0086 | 0.046736 | 4.6736 |
| 538.12 | 32.74 | 0.082229 | 8.2229 | 0.0093891 | 0.93891 | 357.54 | 23.66 | 0.24869 | 24.869 | 0.0041172 | 0.41172 |
| 817.88 | 26.80 | 0.013904 | 1.3904 | 0.026544 | 2.6544 | 502.01 | 26.06 | 0.046529 | 4.6529 | 0.023955 | 2.3955 |
| 796.62 | 27.78 | 0.017636 | 1.7636 | 0.027878 | 2.7878 | 726.73 | 34.39 | 0.0079556 | 0.79556 | 0.041621 | 4.1621 |
| 454.62 | 22.45 | 0.015602 | 1.5602 | 0.005936 | 0.5936 | 697.02 | 35.66 | 0.010388 | 1.0388 | 0.077301 | 7.7301 |
| 507.32 | 23.86 | 0.032526 | 3.2526 | 0.03363 | 3.363 | 645.4 | 36.22 | 0.10104 | 10.104 | 0.060013 | 6.0013 |
| 711.97 | 24.51 | 0.013365 | 1.3365 | 0.016809 | 1.6809 | 661.22 | 36.56 | 0.029775 | 2.9775 | 0.066183 | 6.6183 |
| 299.74 | 21.51 | 0.019952 | 1.9952 | 0.016826 | 1.6826 | 440.17 | 24.37 | 0.075597 | 7.5597 | 0.037356 | 3.7356 |
| 474.56 | 23.69 | 0.027675 | 2.7675 | 0.024634 | 2.4634 | 594.72 | 35.48 | 0.031403 | 3.1403 | 0.067343 | 6.7343 |
| 570.4 | 23.63 | 0.029903 | 2.9903 | 0.00010529 | 0.010529 | 645.4 | 36.22 | 0.10104 | 10.104 | 0.060013 | 6.0013 |
| 620.52 | 23.59 | 0.018597 | 1.8597 | 0.020909 | 2.0909 | 421.18 | 30.35 | 0.090537 | 9.0537 | 0.0090071 | 0.90071 |
| 695.2 | 24.88 | 0.017972 | 1.7972 | 0.0055639 | 0.55639 | 366.27 | 27.98 | 0.10943 | 10.943 | 0.0052539 | 0.52539 |
| 741.74 | 23.87 | 0.023456 | 2.3456 | 0.0086413 | 0.86413 | 305.02 | 27.82 | 0.05132 | 5.132 | 0.061044 | 6.1044 |
| 722.08 | 26.87 | 0.027109 | 2.7109 | 0.03948 | 3.948 | 962.34 | 45.24 | 0.14584 | 14.584 | 0.16242 | 16.242 |
| 836.05 | 24.03 | 0.0024489 | 0.24489 | 0.031237 | 3.1237 | 587.9 | 35.44 | 0.019116 | 1.9116 | 0.097721 | 9.7721 |
| 853.05 | 25.41 | 0.025509 | 2.5509 | 0.017009 | 1.7009 | 323.92 | 32.86 | 0.031559 | 3.1559 | 0.064599 | 6.4599 |
| Electrical Parameter | Iph (A) | Io (A) | n | Rs (Ω) | Rsh (Ω) | |
|---|---|---|---|---|---|---|
| value | Estimated | 6.5497 | 4.4 × 10−9 | 1.0555 | 0.4503 | 200 |
| Newton-Raphson | 6.69 | 1.097 × 10−5 | 1.601 | 0.157 | 200.371 | |
| Manufacturer | 6.548 | 4.44 × 10−9 | 1.033 | 0.23 | 199.771 |
| Environmental Conditions: Irradiance (W/m2), Temperature (°C) | Estimated | Newton-Raphson | Manufacturer |
|---|---|---|---|
| RMS error five parameter model (%) G = 755, T = 27.2 | 1.3019 | 1.4045 | 1.3795 |
| G = 762, T = 25.4 | 1.3214 | 1.4213 | 1.3974 |
| G = 800, T = 28.1 | 1.3019 | 1.3883 | 1.376 |
| G = 809, T = 27.1 | 1.3113 | 1.3954 | 1.3843 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamadi, S.A.; Chouder, A.; Rezaoui, M.M.; Motahhir, S.; Kaddouri, A.M. Improved Hybrid Parameters Extraction of a PV Module Using a Moth Flame Algorithm. Electronics 2021, 10, 2798. https://doi.org/10.3390/electronics10222798
Hamadi SA, Chouder A, Rezaoui MM, Motahhir S, Kaddouri AM. Improved Hybrid Parameters Extraction of a PV Module Using a Moth Flame Algorithm. Electronics. 2021; 10(22):2798. https://doi.org/10.3390/electronics10222798
Chicago/Turabian StyleHamadi, Safi Allah, Aissa Chouder, Mohamed Mounir Rezaoui, Saad Motahhir, and Ameur Miloud Kaddouri. 2021. "Improved Hybrid Parameters Extraction of a PV Module Using a Moth Flame Algorithm" Electronics 10, no. 22: 2798. https://doi.org/10.3390/electronics10222798
APA StyleHamadi, S. A., Chouder, A., Rezaoui, M. M., Motahhir, S., & Kaddouri, A. M. (2021). Improved Hybrid Parameters Extraction of a PV Module Using a Moth Flame Algorithm. Electronics, 10(22), 2798. https://doi.org/10.3390/electronics10222798







