A SPICE Model for IGBTs and Power MOSFETs Focusing on EMI/EMC in High-Voltage Systems
Abstract
:1. Introduction
- (1)
- A model accurately describing the operation of an IGBT that is as simple and universal as possible; and
- (2)
- A simple model illustrating only the basic parameters of transistors but capable of modeling EMC–EMI problems.
2. Methodology
- Construction of a simulation model for an IGBT for SPICE using the initial parameter values obtained from datasheets;
- Construction of a test bench for the IGBT;
- Measurements of input and output voltages;
- Construction of a simulation model of the test bench;
- Simulation of input and output voltages and adjustment of the IGBT parameters to fit the measurement results;
- Testing of the IGBT models for different levels of controlling signals;
- Testing of the IGBT models in the presence of different loads.
2.1. Equivalent Circuit Model of an IGBT
2.2. Procedure to Generate Parameters of the Equivalent Circuit Model of the IGBT
3. Model Verification
3.1. Modeling of SEMIKRON Module SKM200GB123D
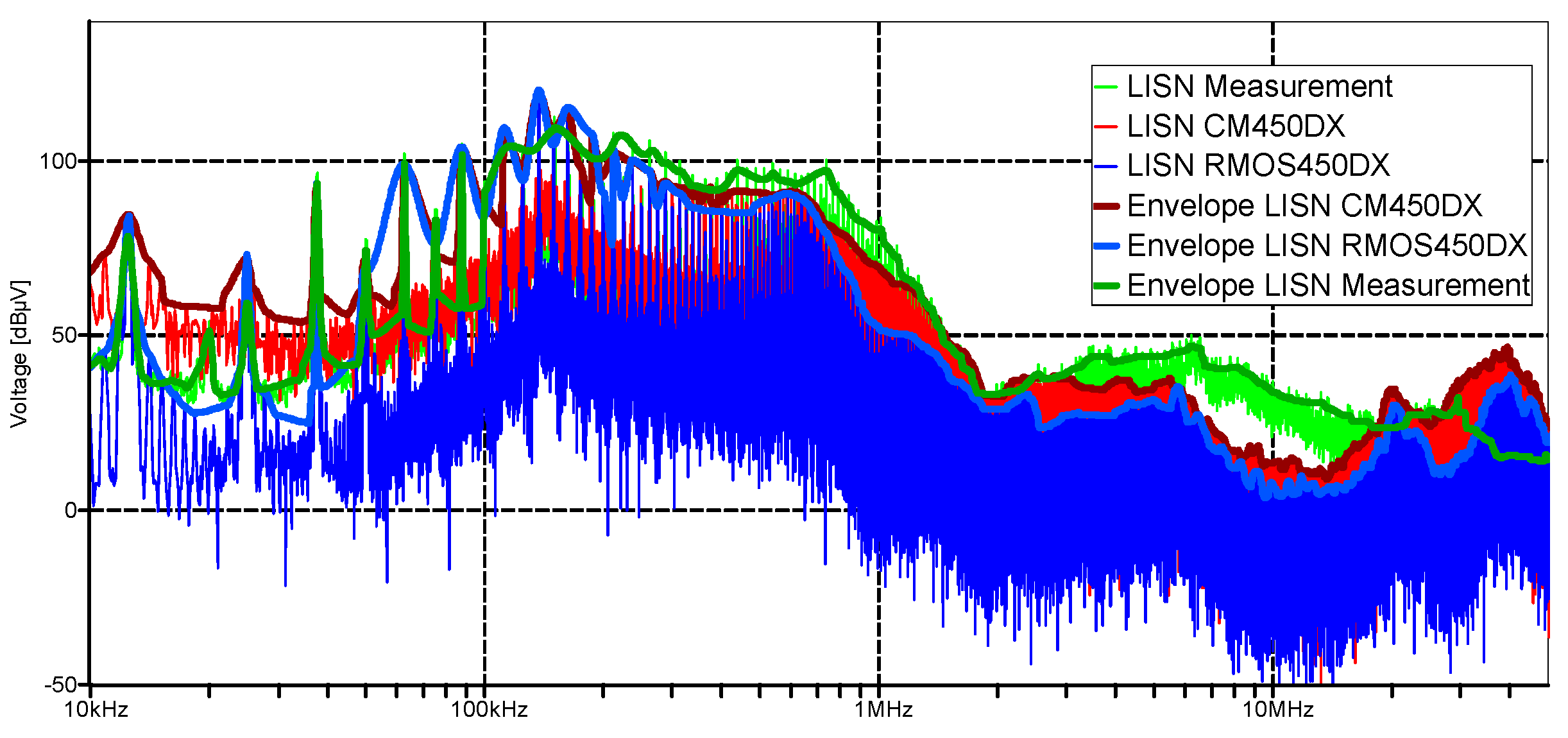
3.2. Modeling of Mitsubishi Electric Model CM450DX-24S
4. EMC-Oriented Model of IGBTS and MOSFETS
5. Calculation Times
6. EMC-Oriented Model of IGBT and MOSFET
7. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sheng, K.; Williams, B.; Finney, S. A review of IGBT models. IEEE Trans. Power Electron. 2000, 15, 1250–1266. [Google Scholar] [CrossRef]
- Hefner, A.R. Analytical modeling of device-circuit interactions for the power insulated gate bipolar transistor (IGBT). IEEE Trans. Ind. Appl. 1988, 1, 606–614. [Google Scholar] [CrossRef] [Green Version]
- Hefner, A.R. Modeling buffer layer IGBTs for circuit simulation. IEEE Trans. Power Electron. 1995, 10, 111–123. [Google Scholar] [CrossRef]
- Mitter, C.S.; Hefner, A.R.; Chen, D.Y.; Lee, F.C. Insulated gate bipolar transistor (IGBT) modeling using IG-SPICE. IEEE Trans. Ind. Appl. 1994, 30, 24–33. [Google Scholar] [CrossRef]
- Hefner, A.; Bouche, S. Automated parameter extraction software for advanced IGBT modeling. In Proceedings of the COMPEL 2000 7th Workshop on Computers in Power Electronics (Cat. No.00TH8535), Blacksburg, VA, USA, 16–18 July 2000; pp. 10–18. [Google Scholar] [CrossRef]
- Kuo, D.-S.; Choi, J.-Y.; Giandomenico, D.; Hu, C.; Sapp, S.; Sassaman, K.; Bregar, R. Modeling the turn-off characteristics of the bipolar-MOS transistor. IEEE Electron. Device Lett. 1985, 6, 211–214. [Google Scholar] [CrossRef]
- Kuo, D.-S.; Hu, C.; Sapp, S.P. An analytical model for the power bipolar-MOS transistor. Solid-State Electron. 1986, 29, 1229–1237. [Google Scholar] [CrossRef]
- McDonald, R.J.; Fossum, J.G. High-voltage device modeling for SPICE simulation of HVICs. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 1988, 7, 425–432. [Google Scholar] [CrossRef]
- Baliga, B.J. Analytical modeling of IGBTs: Challenges and solutions. IEEE Trans. Electron Devices 2013, 60, 535–543. [Google Scholar] [CrossRef]
- Strollo, A.G.M. A new IGBT circuit model for SPICE simulation. In Proceedings of the PESC97, Record 28th Annual IEEE Power Electronics Specialists Conference. Formerly Power Conditioning Specialists Conference 1970–71, Power Processing and Electronic Specialists Conference 1972, St. Louis, MO, USA, 27 June 1997; Volume 1, pp. 133–138. [Google Scholar] [CrossRef]
- Mihalic, F.; Jezernik, K.; Krischan, K.; Rentmeister, M. IGBT SPICE macro model. In Proceedings of the 1992 International Conference on Industrial Electronics, Control, Instrumentation, and Automation, San Diego, CA, USA, 13 November 1992; Volume 1, pp. 240–245. [Google Scholar]
- Kim, H.; Cho, Y.; Kim, S.-D.; Choi, Y.-I. Parameter extraction for the static and dynamic model of IGBT. In Proceedings of the IEEE Power Electronics Specialist Conference, Seattle, WA, USA, 20–24 June 1993; pp. 71–74. [Google Scholar] [CrossRef]
- Tzou, Y.-Y.; Hsu, L.-J. A practical SPICE macro model for the IGBT. In Proceedings of the IECON ‘93—19th Annual Conference of IEEE Industrial Electronics, Maui, HI, USA, 15–19 November 1993; Volume 2, pp. 762–766. [Google Scholar] [CrossRef]
- Shen, Z.; Chow, T. Modeling and characterization of the insulated gate bipolar transistor (IGBT) for SPICE simulation. In Proceedings of the 5th International Symposium on Power Semiconductor Devices and ICs, Monterey, CA, USA, 18–20 May 1993; pp. 165–170. [Google Scholar] [CrossRef]
- Hsu, J.T.; Ngo, K.D. Behavioral modeling of the IGBT using the Hammerstein configuration. IEEE Trans. Power Electron. 1996, 11, 746–754. [Google Scholar] [CrossRef]
- Musumeci, S.; Raciti, A.; Sardo, M.; Frisina, F.; Letor, R. PT-IGBT PSpice model with new parameter extraction for life-time and epy dependent behaviour simulation. In Proceedings of the PESC Record, 27th Annual IEEE Power Electronics Specialists Conference, Baveno, Italy, 23–27 June 1996; Volume 2, pp. 1682–1688. [Google Scholar] [CrossRef]
- Tichenor, J.L.; Sudhoff, S.D.; Drewniak, J.L. Behavioral IGBT modeling for predicting high frequency effects in motor drives. IEEE Trans. Power Electron. 2000, 15, 354–360. [Google Scholar] [CrossRef]
- Tone, A.; Miyaoku, Y.; Miura-Mattausch, M.; Kikuchihara, H.; Feldmann, U.; Saito, T.; Mizoguchi, T.; Yamamoto, T.; Mattausch, H.J. HiSIM_IGBT2: Modeling of the dynamically varying balance between MOSFET and BJT contributions during switching operations. IEEE Trans. Electron Devices 2019, 66, 3265–3272. [Google Scholar] [CrossRef]
- Meng, J.; Ning, P.; Wen, X. A novel method of gate capacitances extraction for IGBT physical models. In Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Sze, S.M. Karrier Transport Phenomena. In Physics of Semiconductor Devices; Wiley-Interscience: New York, NY, USA; John Wiley & Sons: Chichester, UK, 1981; pp. 27–38. [Google Scholar]
- Pspice Reference Guide, 2nd Online ed., PSpice Reference Guide ORCAD. 31 May 2000. Available online: https://www.seas.upenn.edu/~jan/spice/PSpice_ReferenceguideOrCAD.pdf (accessed on 15 September 2021).
- Khanna, V.K. Physics and Modeling of IGBT. In The Insulated Gate Bipolar Transistor Theory and Design; John Wiley & Sons Inc.: New Jersey, NJ, USA, 2003; pp. 239–302. [Google Scholar]
- Baliga, B.J. Physics-Baced circuit model. In The IGBT Device Physics, Design and Applications of the Insulated Gate Bipolar Transistor; Elsevier: Oxford, UK; Waltham, MA, USA, 2015; pp. 205–222. [Google Scholar]


























| Model | SIMetrix | LTspice |
|---|---|---|
| Calculation Time | Calculation Time | |
| RMOS450DX | 3 min 36 s | 3 min 58 s |
| CM450DX-24S | 10 min 12 s | 19 min 20 s |
| RGTVX6TS65D (Rohm model) | 8 min 57 s | Convergence problem |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khvitia, B.; Gheonjian, A.; Kutchadze, Z.; Jobava, R. A SPICE Model for IGBTs and Power MOSFETs Focusing on EMI/EMC in High-Voltage Systems. Electronics 2021, 10, 2822. https://doi.org/10.3390/electronics10222822
Khvitia B, Gheonjian A, Kutchadze Z, Jobava R. A SPICE Model for IGBTs and Power MOSFETs Focusing on EMI/EMC in High-Voltage Systems. Electronics. 2021; 10(22):2822. https://doi.org/10.3390/electronics10222822
Chicago/Turabian StyleKhvitia, Badri, Anna Gheonjian, Zviadi Kutchadze, and Roman Jobava. 2021. "A SPICE Model for IGBTs and Power MOSFETs Focusing on EMI/EMC in High-Voltage Systems" Electronics 10, no. 22: 2822. https://doi.org/10.3390/electronics10222822
APA StyleKhvitia, B., Gheonjian, A., Kutchadze, Z., & Jobava, R. (2021). A SPICE Model for IGBTs and Power MOSFETs Focusing on EMI/EMC in High-Voltage Systems. Electronics, 10(22), 2822. https://doi.org/10.3390/electronics10222822






