Analysis of Complex Solid-Gas Flow under the Influence of Gravity through Inclined Channel and Comparison with Real-Time Dual-Sensor System
Abstract
:1. Introduction
- The gas-solid flow, non-invasive, real-time measurement and monitoring are studied in this paper, including the mass flow rate (MFR) of solid particles.
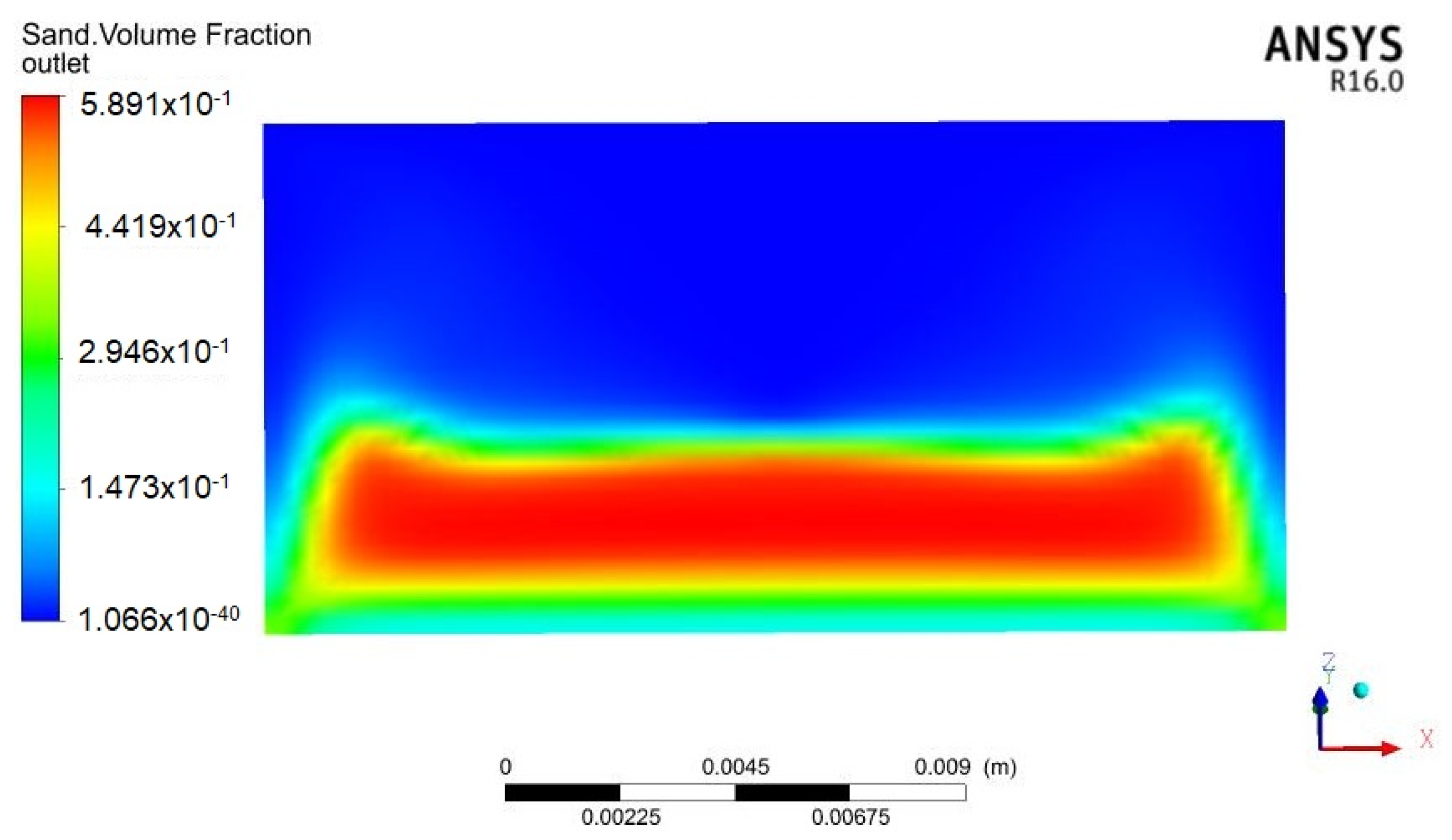
- Due to the bonding of solid particles, there is a serious problem of gas-solid flow pipe and conduit blockage in a large number of processing industries. In response to this problem, the paper uses specialized simulation tools (ANSYS R16.0 FLUENT) to study the effects of gravity on the flow of solid-state particles in the inclined channel [4] and to focus on the behavior of pneumatic sand flow in the tilt channel to provide insight into the problem of the gas-solid flow pipe and conduit blockage.
- This paper employed a dual-sensor approach (electrical and mechanical sensors) for invasive solid MFR measurement to complete a new measurement and monitoring system design using the advantages of both the sensors. Among these, the flow rate profile and volume flow concentration of solid particles are calculated based on the data collected by electrical sensors, while the MFR of solid particles is the responsibility of the mechanical load sensor.
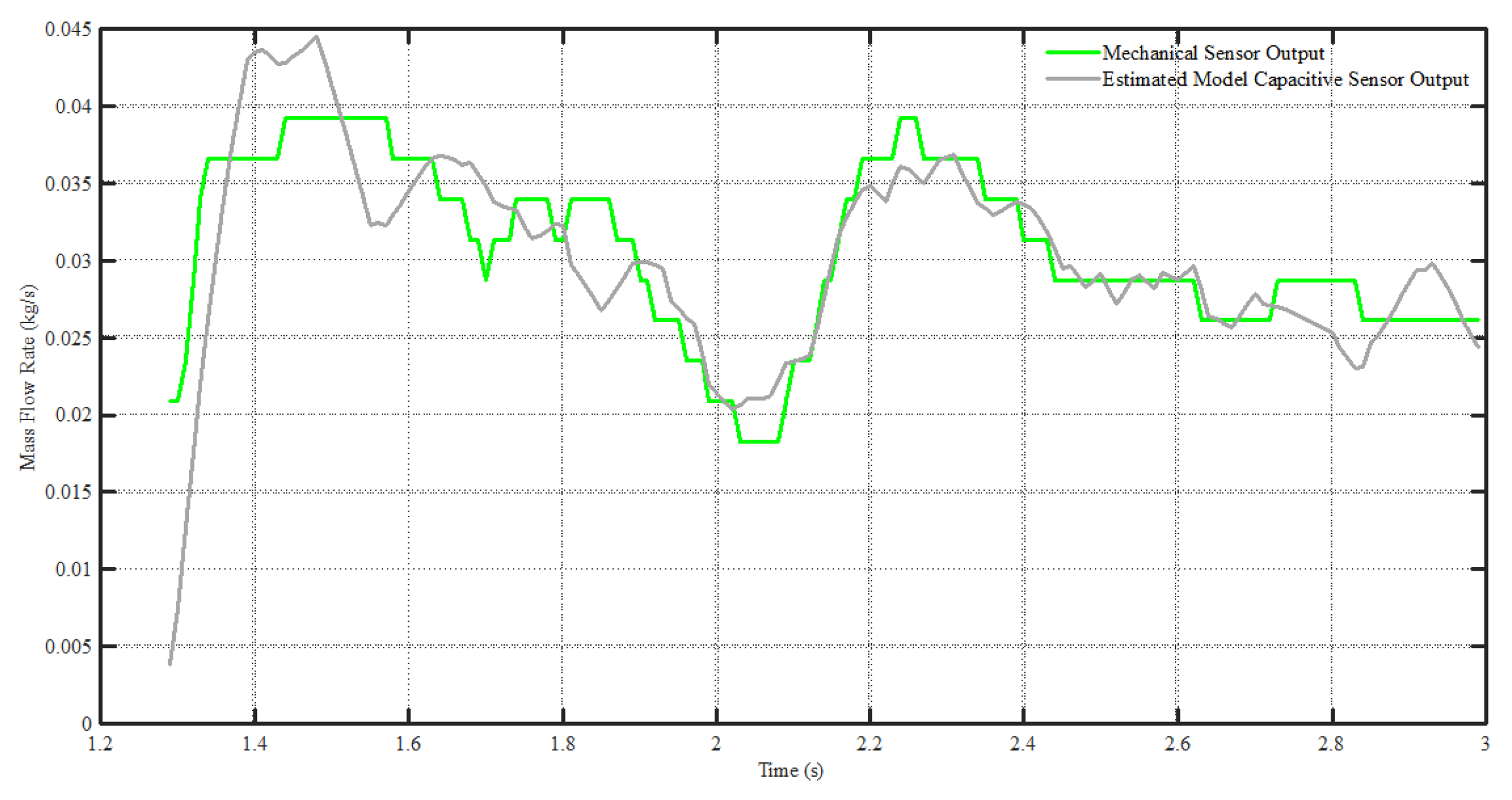
- Data fusion was applied to the results of both sensors to enhance the accuracy closer to the true values. This arrangement consists of a load cell connected at the lower side of the tube and two capacitive electrodes situated along the channel’s walls.
- Our proposed sensor architecture compares well to alternatives and is appropriate for the proposed application in the research field.
2. Measurement Principles
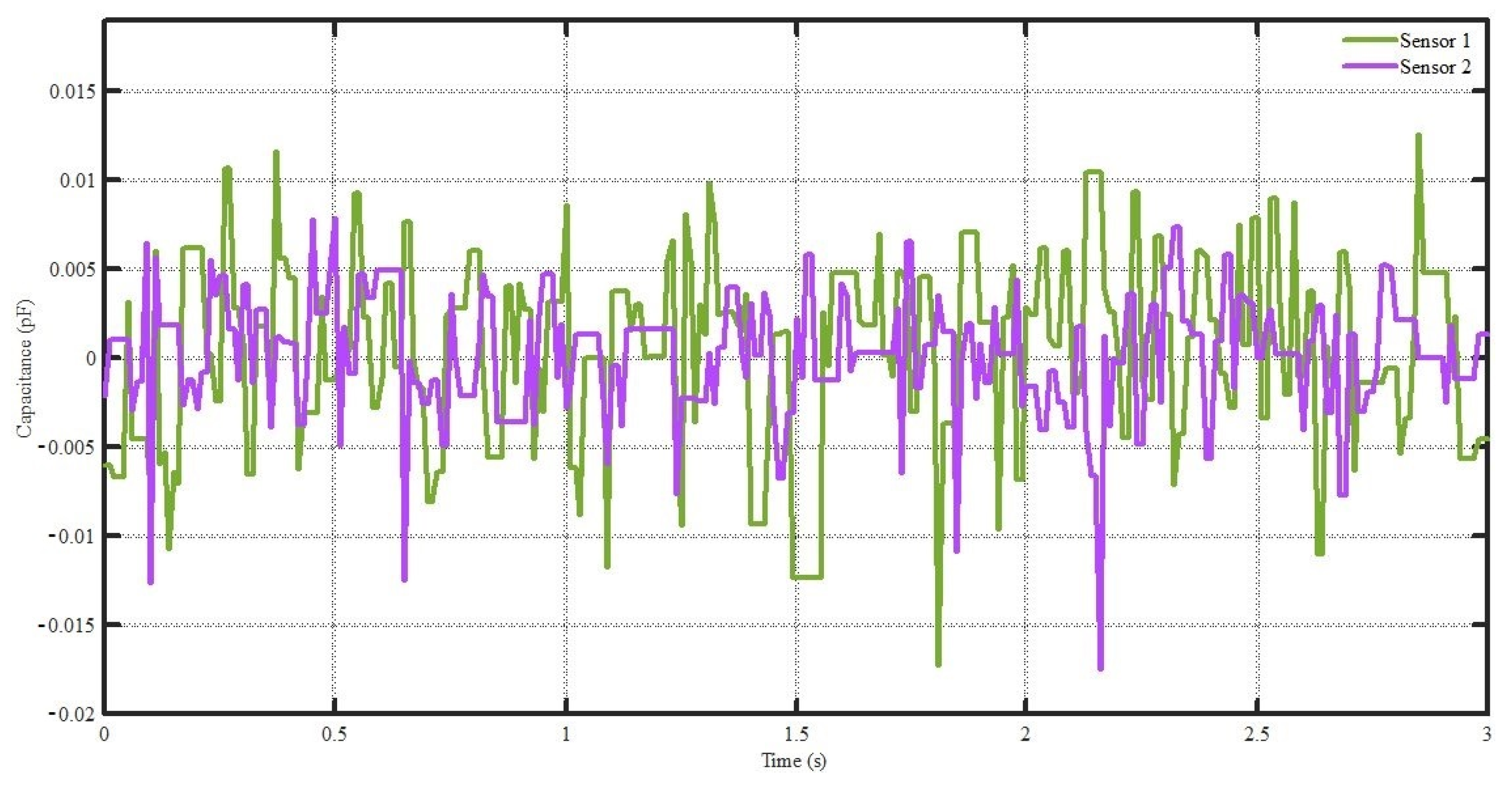
2.1. Indirect Measurement (by Electrical Sensor)
2.1.1. Measurement of Velocity
2.1.2. Concentration of Volumetric Flow
2.2. Direct Measurement (by Mechanical Sensor)
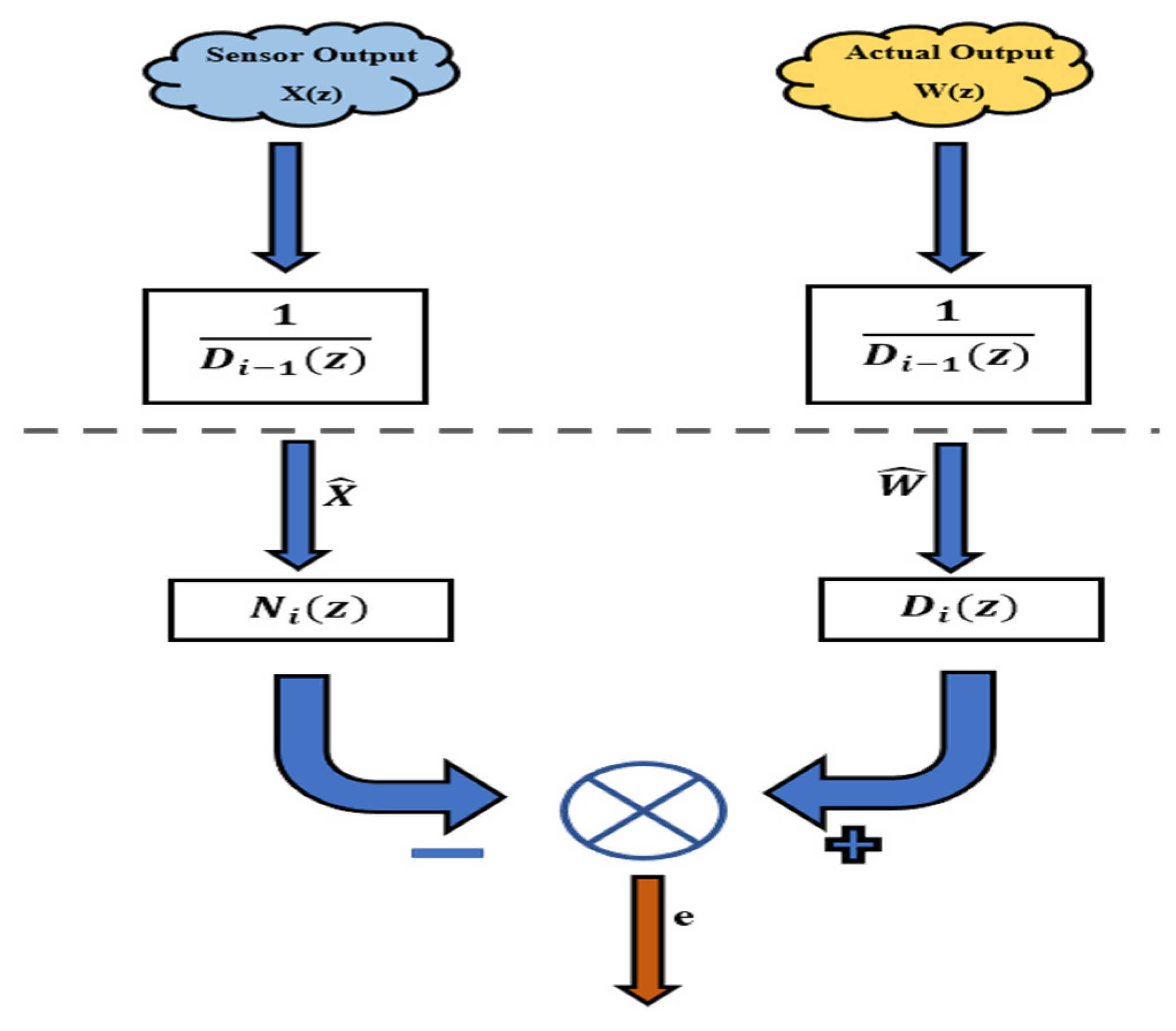
3. Data Fusion of the Sensors to the Actual Value
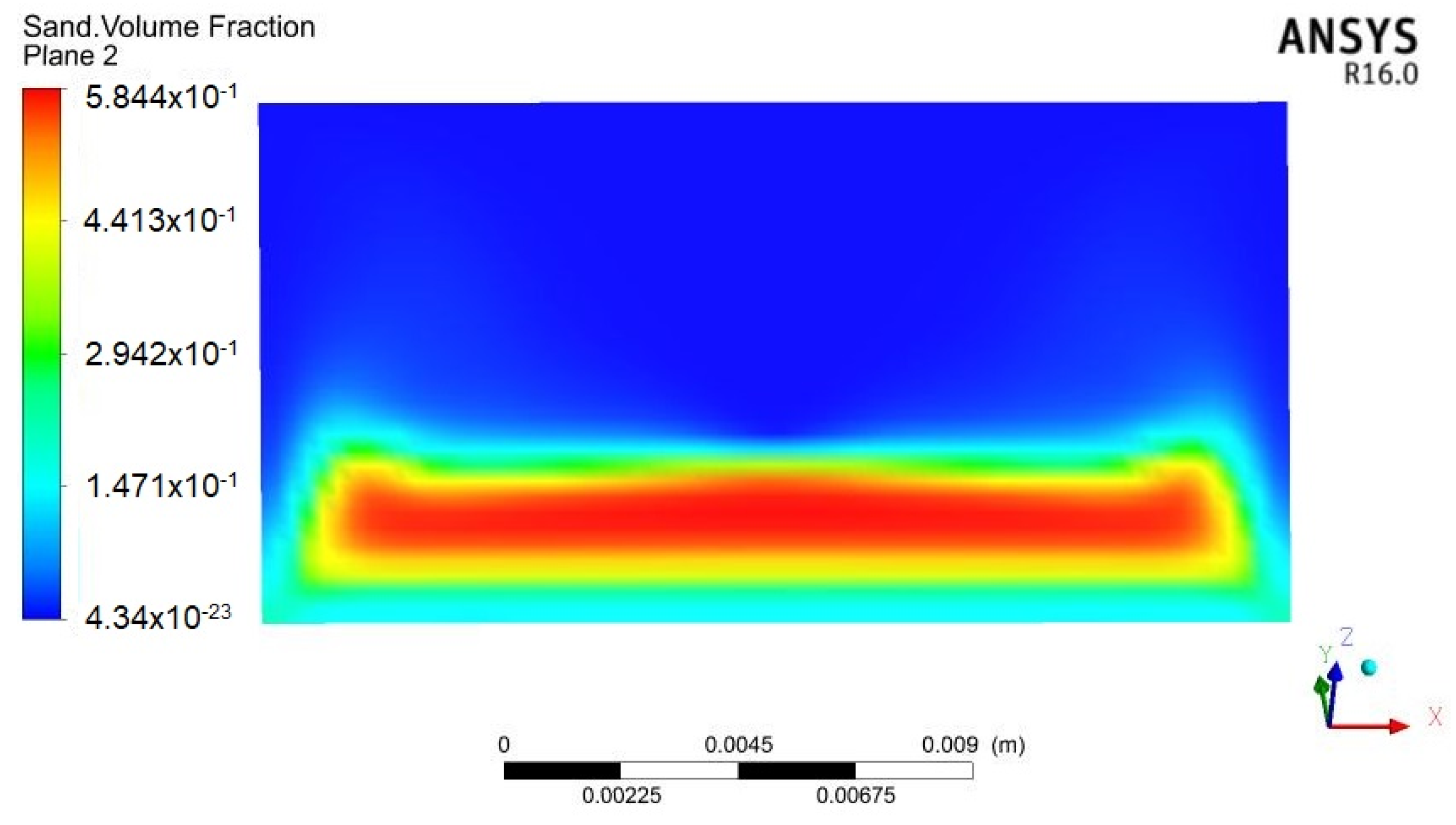
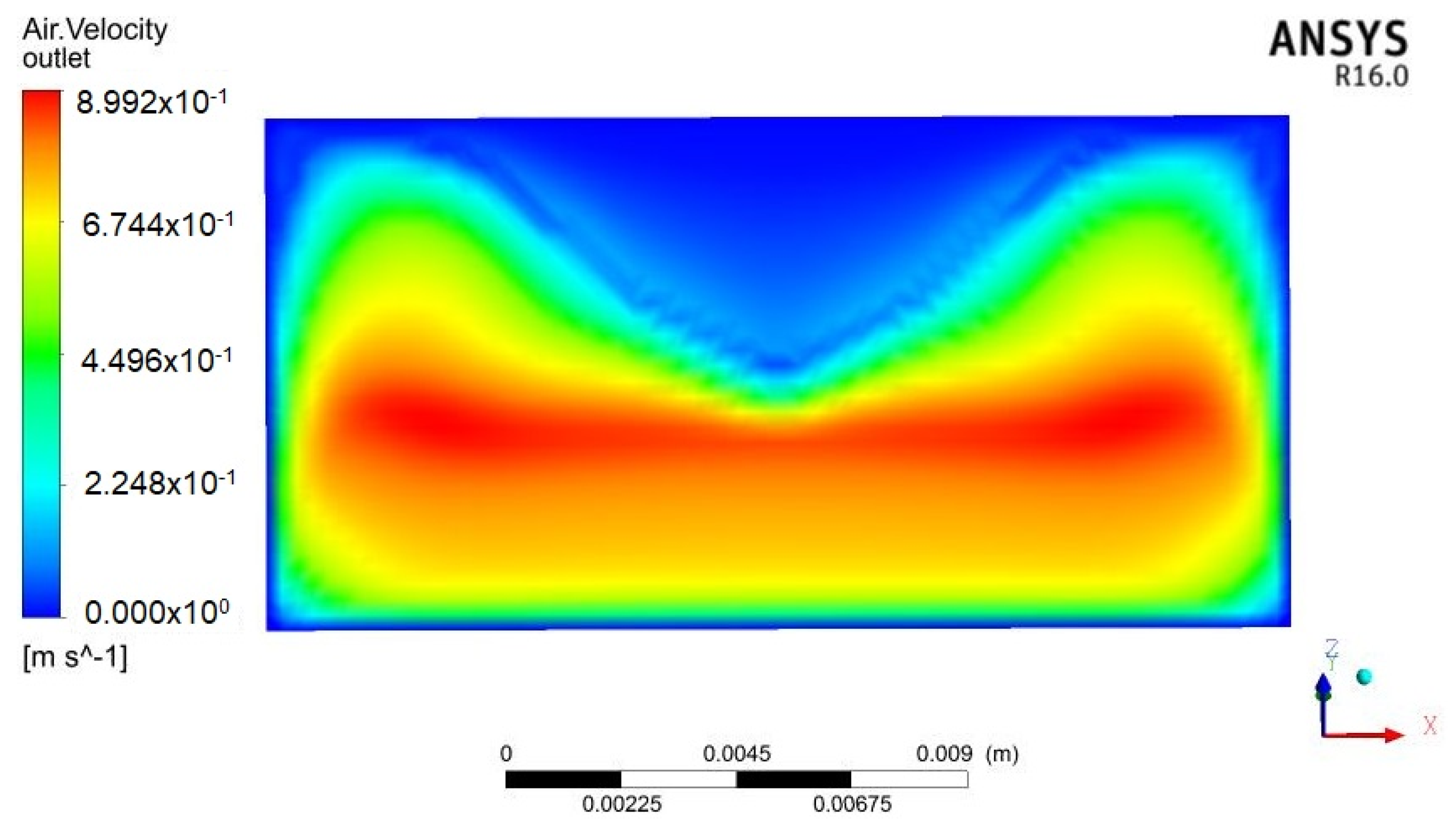
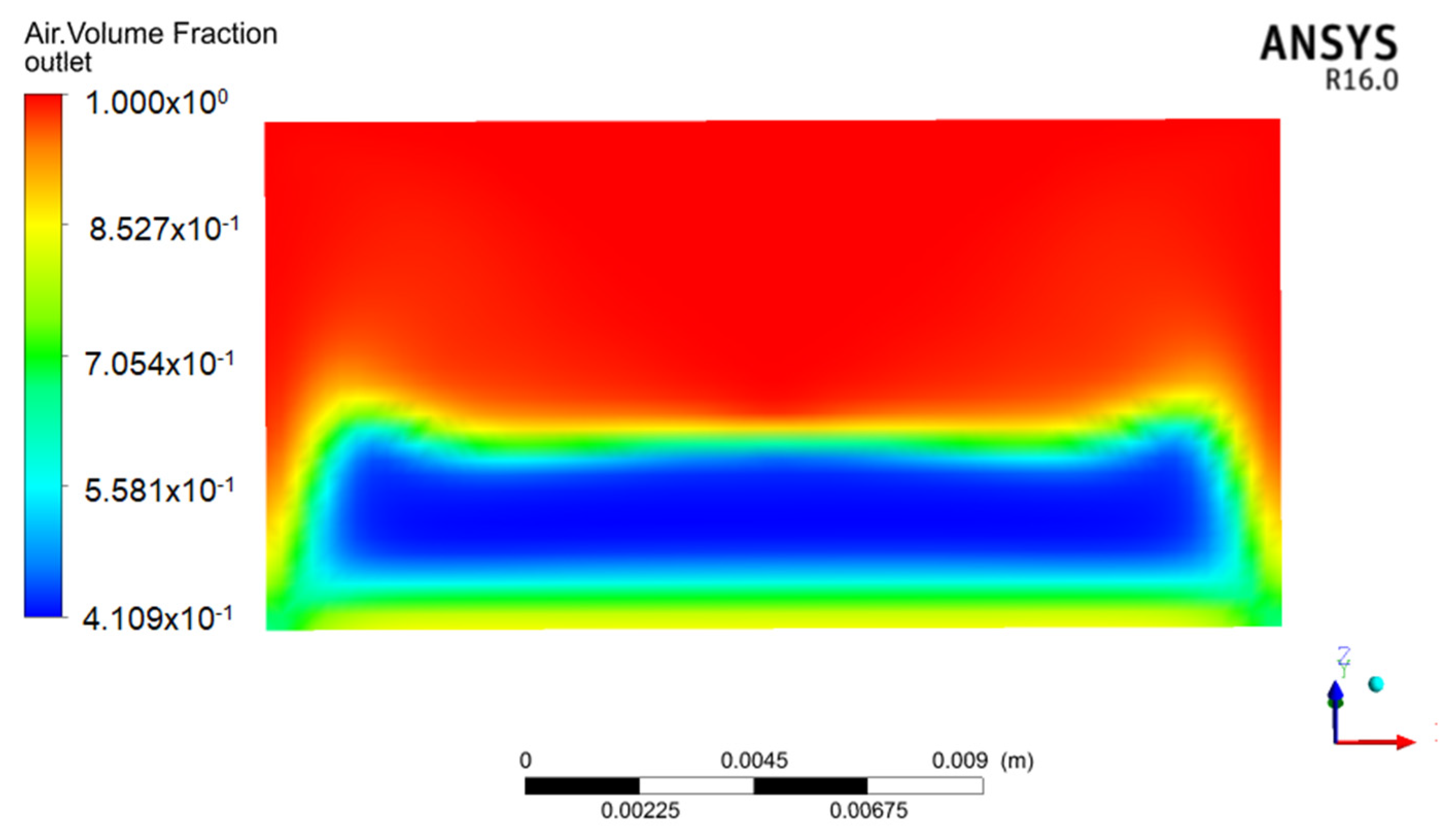
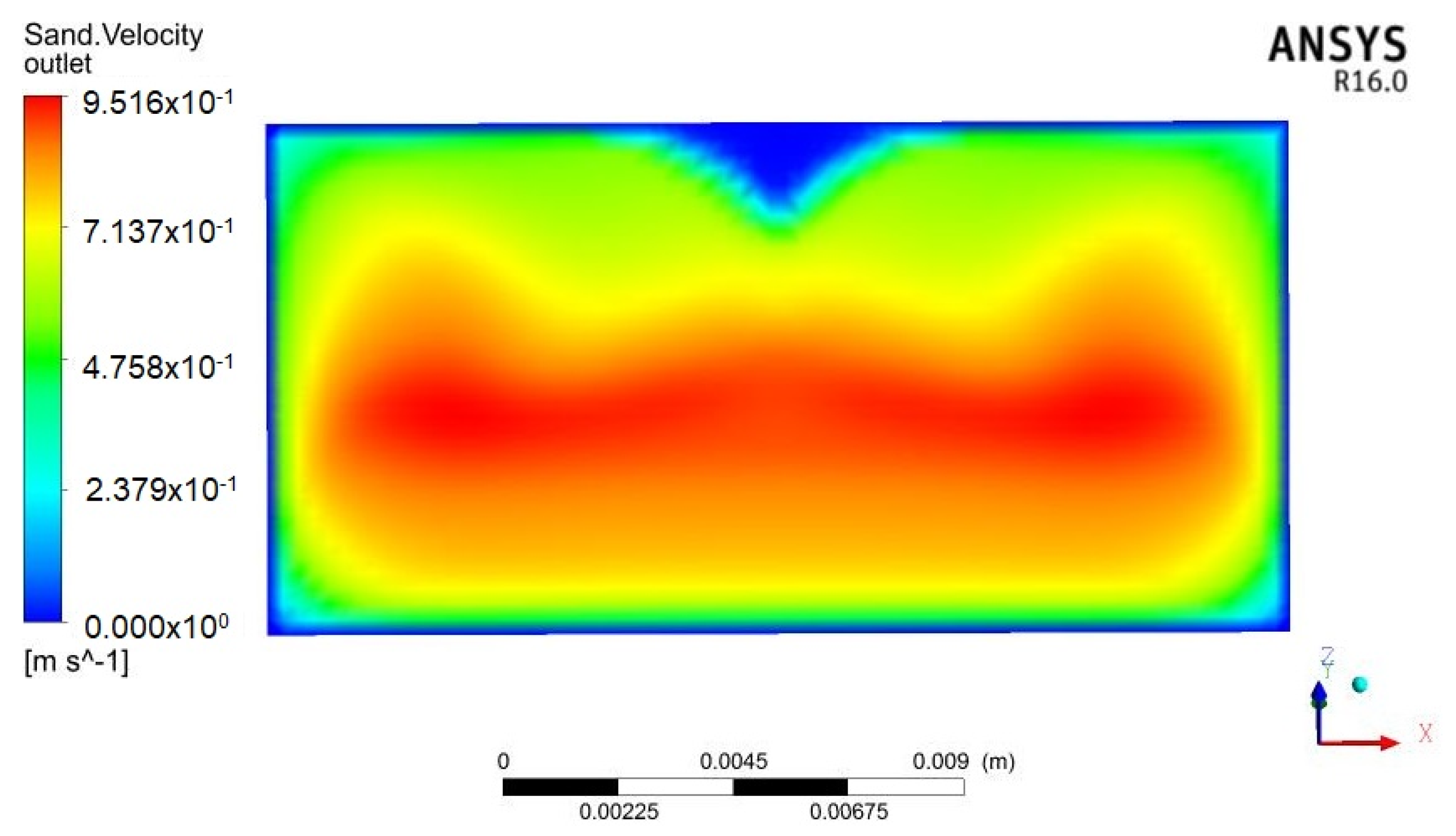
4. Solid Flow Simulation
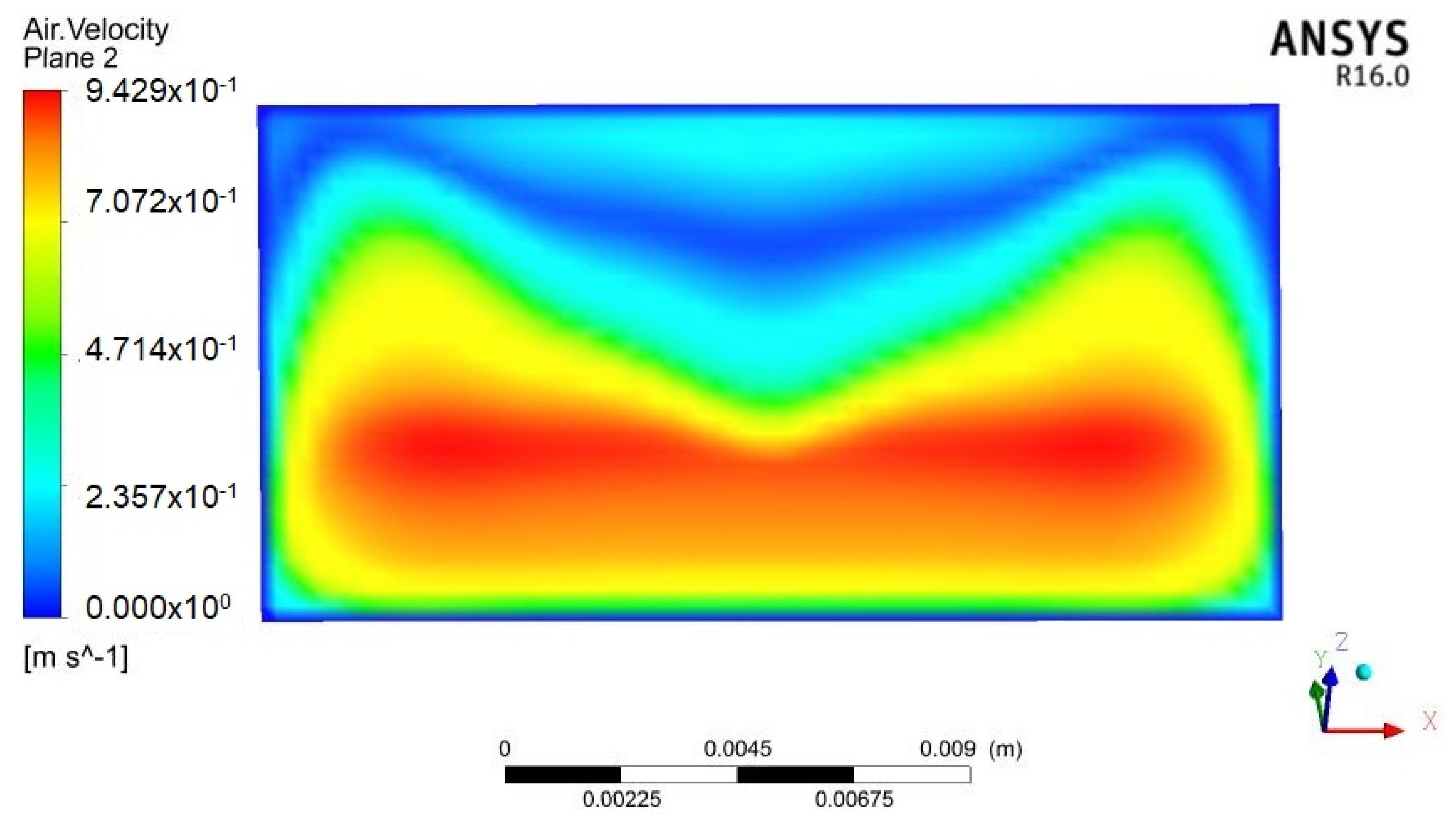
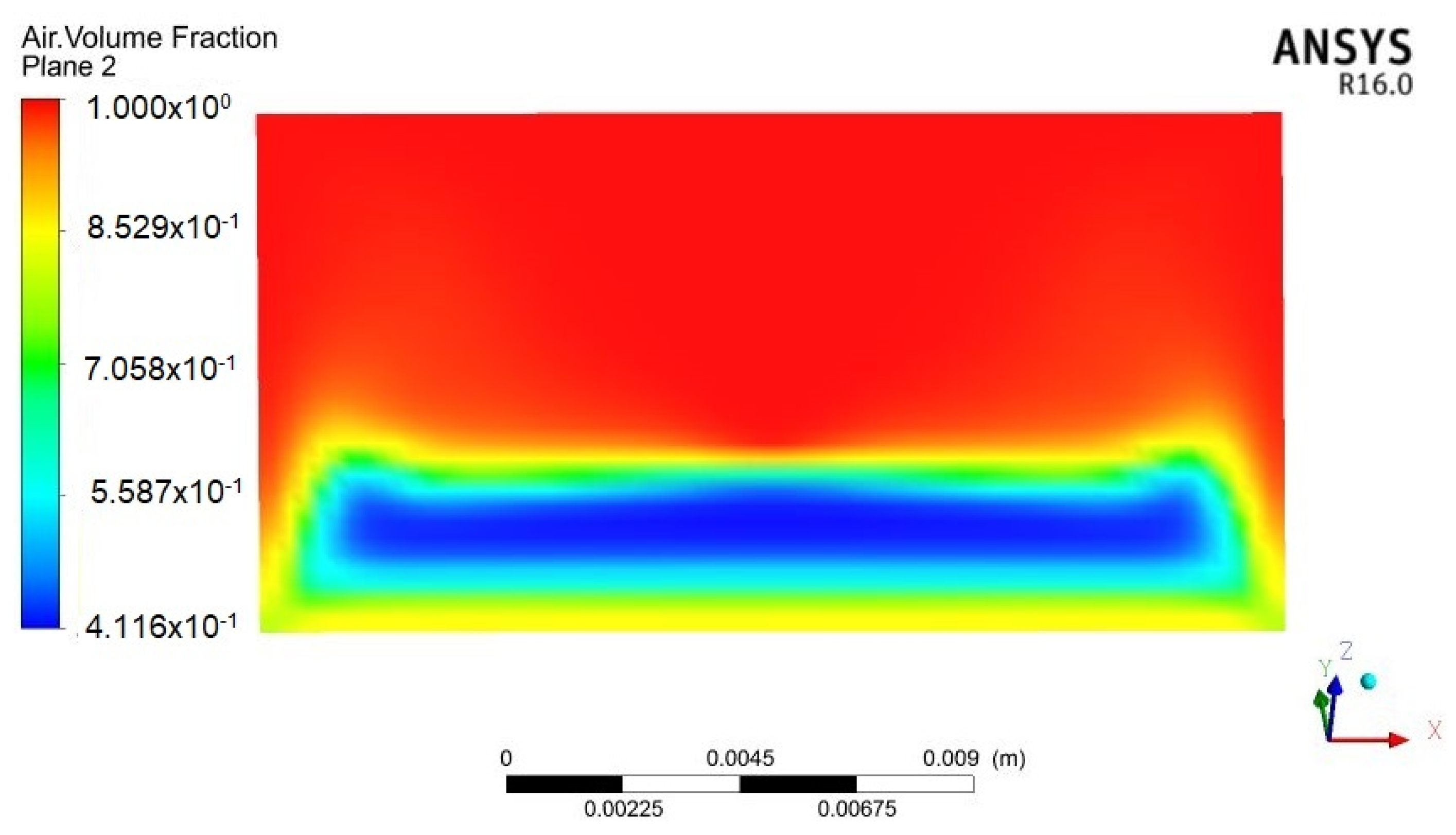
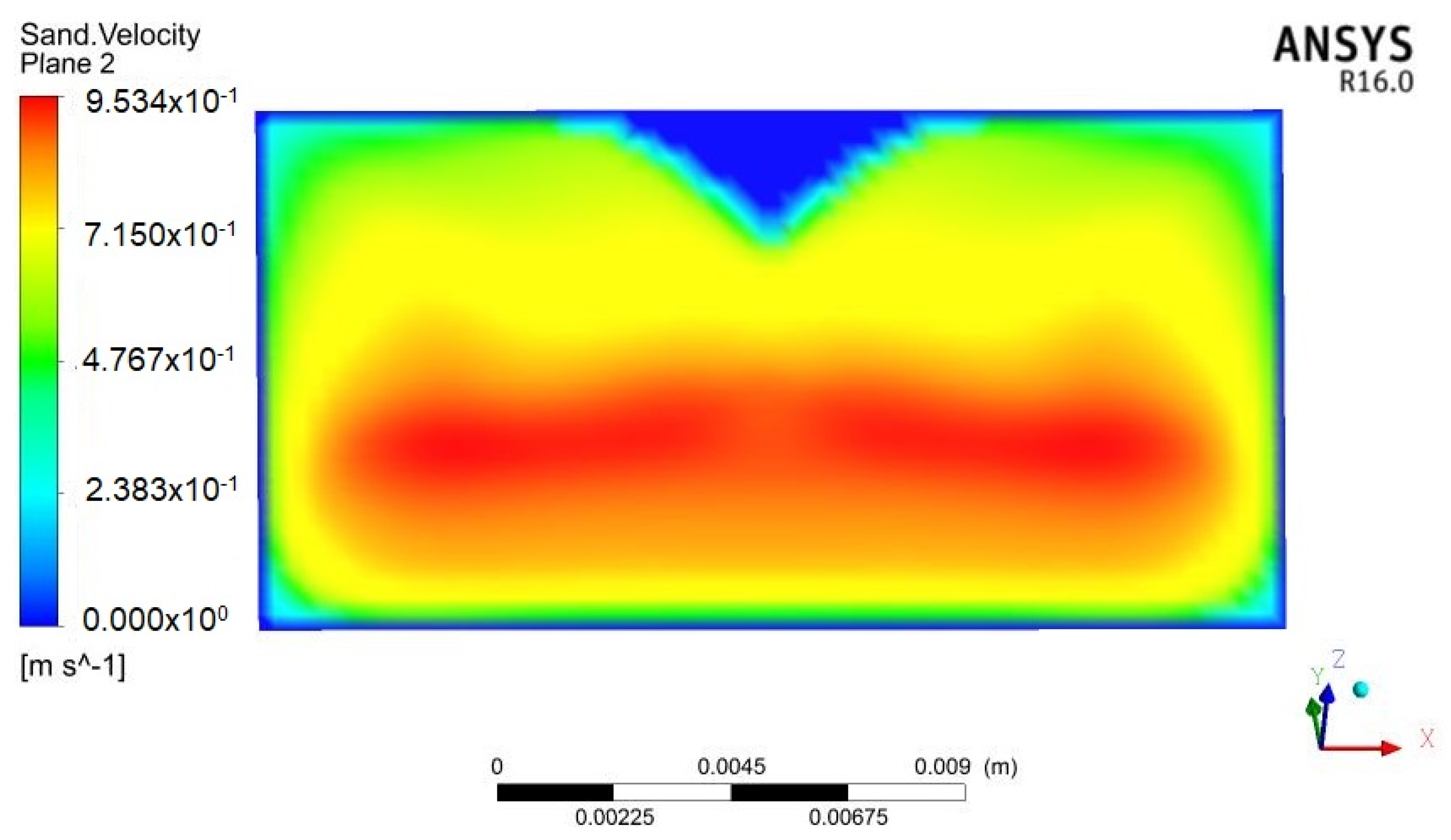
4.1. Simulation Analysis
4.2. Simulation Analysis
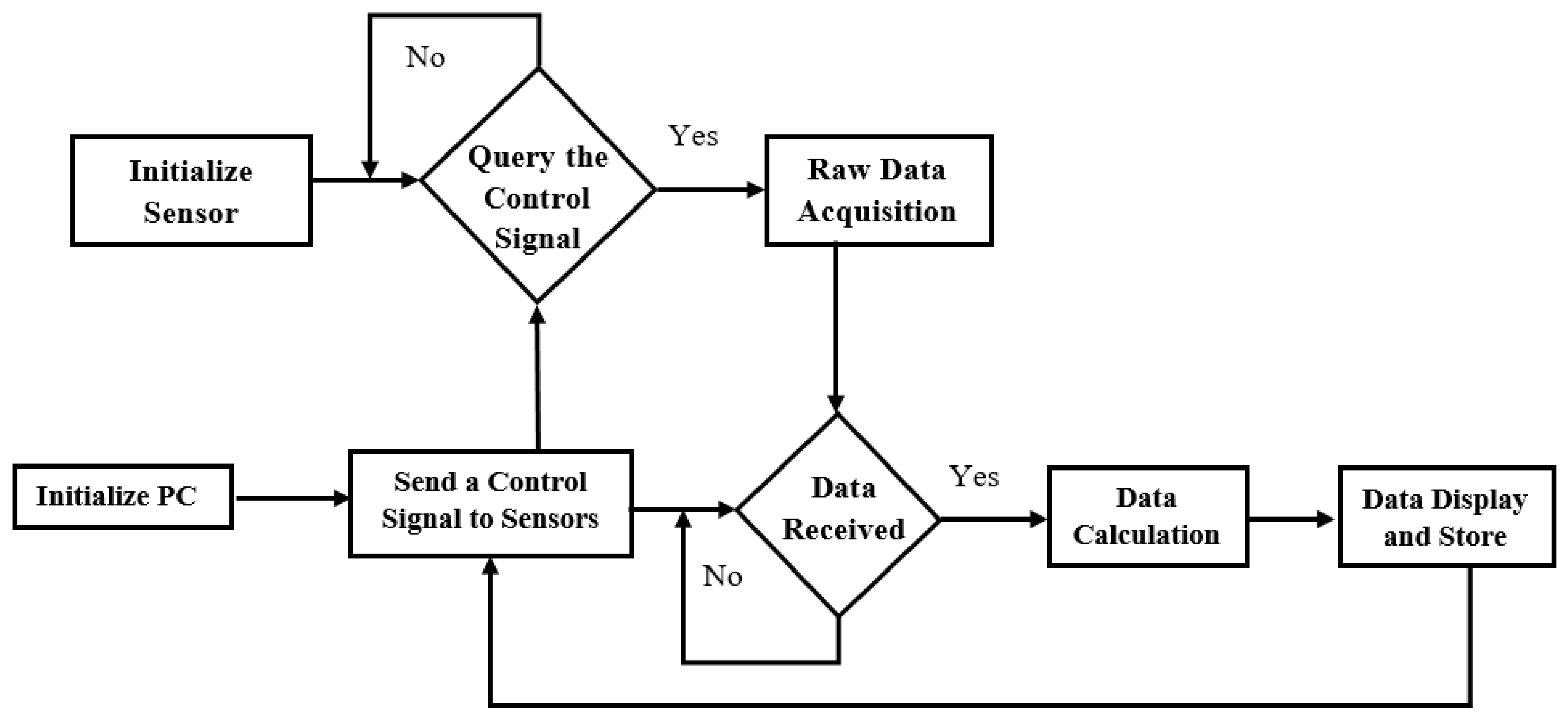
5. Measurement System
Design of Instrument
6. Results and Discussions
6.1. Design of Instrument
6.2. Concentration of Volumetric Flow
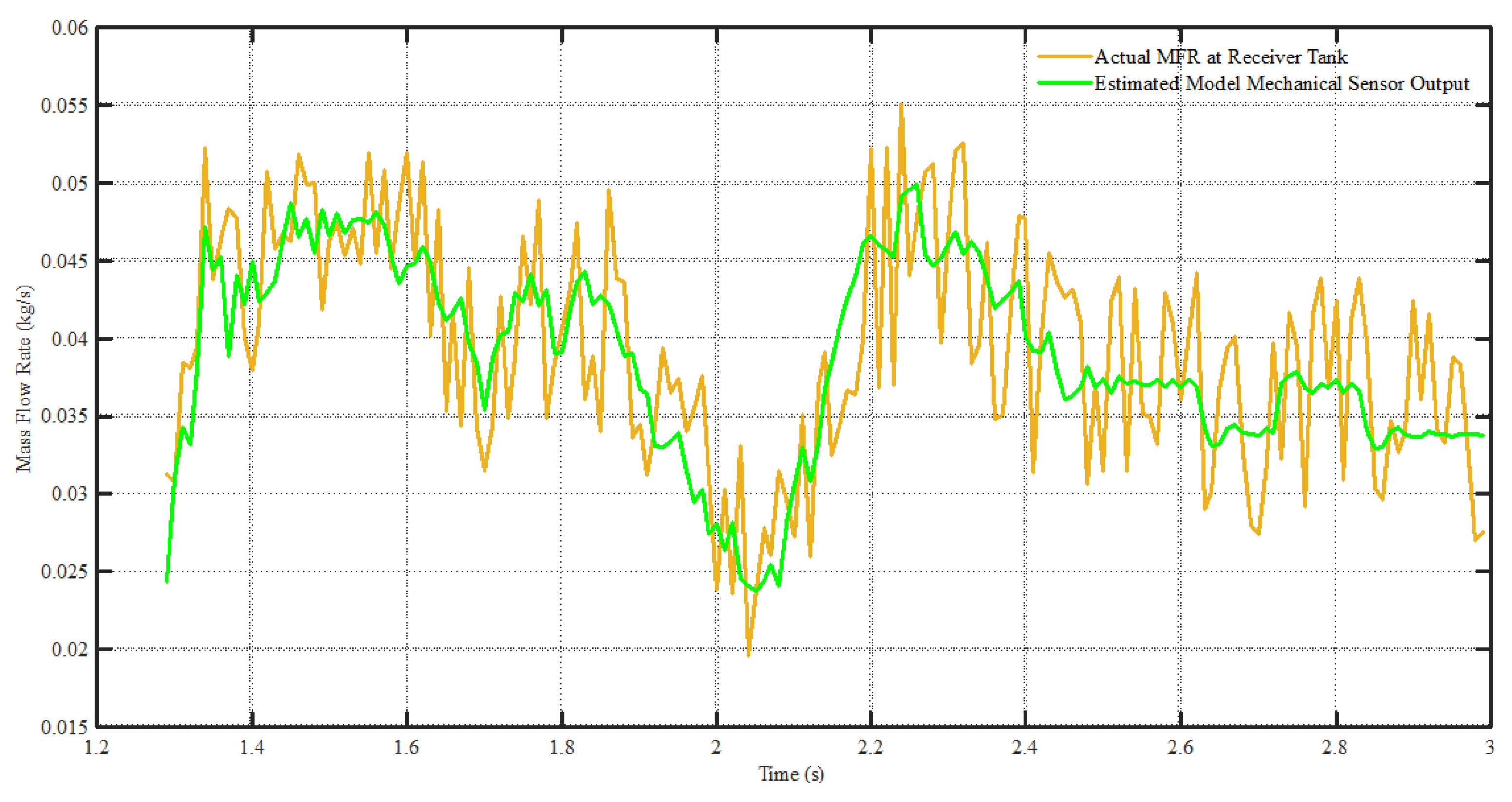
6.3. Measurements of Mechanical Sensor
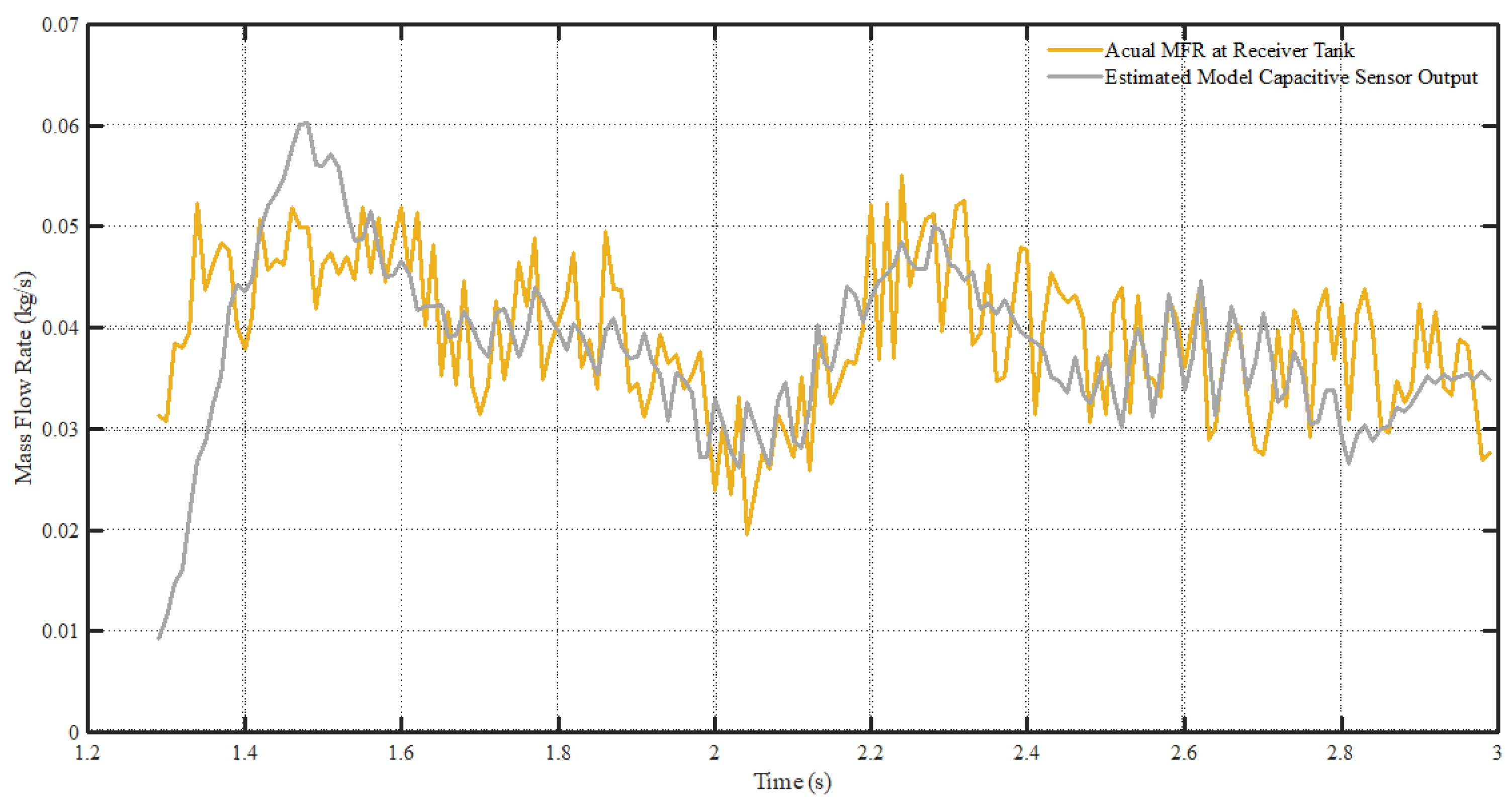
6.4. Data Fusion of Sensors to the Real MFR
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cui, H.; Grace, J.R. Pneumatic Conveying of Biomass Particles: A Review. China Particuology 2006, 4, 183–188. [Google Scholar] [CrossRef]
- Xie, H.; Tan, L.; Liu, J.; Chen, H.; Yang, H. Numerical and Experimental Investigation on Opening Direction Steady Axial Flow Force Compensation of Converged Flow Cartridge Proportional Valve. Flow Meas. Instrum. 2018, 62, 123–134. [Google Scholar] [CrossRef]
- Tominaga, Y.; Okaze, T.; Mochida, A. Wind Tunnel Experiment and CFD Analysis of Sand Erosion/Deposition Due to Wind around an Obstacle. J. Wind Eng. Ind. Aerodyn. 2018, 182, 262–271. [Google Scholar] [CrossRef]
- Zheng, Y.; Liu, Q. Review of Techniques for the Mass Flow Rate Measurement of Pneumatically Conveyed Solids. Meas. J. Int. Meas. Confed. 2011, 44, 589–604. [Google Scholar] [CrossRef]
- Sen, S.; Das, P.K.; Dutta, P.K.; Maity, B.; Chaudhuri, S.; Mandal, C.; Roy, S.K. PC-Based Gas-Solids Two-Phase Mass Flowmeter for Pneumatically Conveying Systems. Flow Meas. Instrum. 2000, 11, 205–212. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, C.; Yang, W.; Wang, C.H. Application of Electrical Capacitance Tomography in Particulate Process Measurement—A Review. Adv. Powder Technol. 2014, 25, 174–188. [Google Scholar] [CrossRef]
- McKee, S.L.; Dyakowski, T.; Williams, R.A.; Bell, T.A.; Allen, T. Solids Flow Imaging and Attrition Studies in a Pneumatic Conveyor. Powder Technol. 1995, 82, 105–113. [Google Scholar] [CrossRef]
- Xia, H.; Kan, R.; Xu, Z.; He, Y.; Liu, J.; Chen, B.; Yang, C.; Yao, L.; Wei, M.; Zhang, G. Two-Step Tomographic Reconstructions of Temperature and Species Concentration in a Flame Based on Laser Absorption Measurements with a Rotation Platform. Opt. Lasers Eng. 2017, 90, 10–18. [Google Scholar] [CrossRef]
- Hu, H.L.; Xu, T.M.; Hui, S.E.; Zhou, Q.L. A Novel Capacitive System for the Concentration Measurement of Pneumatically Conveyed Pulverized Fuel at Power Stations. Flow Meas. Instrum. 2006, 17, 87–92. [Google Scholar] [CrossRef]
- Ismail, B.; Ahmed, W. Innovative Techniques For Two-Phase Flow Measurements. Recent Patents Electr. Eng. 2010, 1, 1–13. [Google Scholar] [CrossRef]
- Holler, G.; Fuchs, A.; Hrach, D. Flow Velocity Determination in Cryogenic Media by Means of Capacitive Sensing. In Proceedings of the 3rd International Conference on Sensing Technology, Taipei, Taiwan, 30 November–3 December 2008; pp. 472–476. [Google Scholar]
- Brasseur, G.; Brandstätter, B.; Zangl, H. State of the Art of Robust Capacitive Sensors. In Proceedings of the 1st International Workshop on Robotic Sensing, 2003, ROSE’ 03, Oorebo, Sweden, 3–6 October 2003. [Google Scholar]
- Bretterklieber, T.; Zangl, H.; Holler, G.; Hrach, D.; Hammerschmidt, D.; Motz, M. Vielseitig Anwendbare Auswerteeinheit Für Robuste Kapazitive Sensoren. Elektrotechnik Inf. 2008, 125, 132–137. [Google Scholar] [CrossRef]
- Sun, M.; Liu, S.; Lei, J.; Li, Z. Mass Flow Measurement of Pneumatically Conveyed Solids Using Electrical Capacitance Tomography. Meas. Sci. Technol. 2008, 19, 19. [Google Scholar] [CrossRef]
- Abrar, U.; Shi, L.; Jaffri, N.R.; Short, M.; Hasham, K. Electrical and Mechanical Sensor-Based Mass Flow Rate Measurement System: A Comparative Approach. In Proceedings of the 2020 4th International Conference on Robotics and Automation Sciences (ICRAS), Wuhan, China, 12–14 June 2020; IEEE: Wuhan, China, 2020. [Google Scholar]
- Zheng, Y.; Liu, Q. Review of Certain Key Issues in Indirect Measurements of the Mass Flow Rate of Solids in Pneumatic Conveying Pipelines. Measurement 2010, 43, 727–734. [Google Scholar] [CrossRef]
- Yan, Y.; Byrne, B.; Woodhead, S.; Coulthard, J. Velocity Measurement of Pneumatically Conveyed Solids Using Electrodynamic Sensors. Meas. Sci. Technol. 1995, 6, 515–537. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, C.; Wang, Y. Parameter Selection in Cross-Correlation-Based Velocimetry Using Circular Electrostatic Sensors. IEEE Trans. Instrum. Meas. 2010, 59, 1268–1275. [Google Scholar] [CrossRef]
- Ortmanns, M.; Buhmann, A.; Manoli, Y.; Achour, H. Interface Circuits. In Reference Module in Materials Science and Materials Engineering; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Zhang, M.; Ma, L.; Soleimani, M. Magnetic Induction Tomography Guided Electrical Capacitance Tomography Imaging with Grounded Conductors. Meas. J. Int. Meas. Confed. 2014, 53, 171–181. [Google Scholar] [CrossRef] [Green Version]
- Jaffri, N.R.; Almogren, A.; Ahmad, A.; Abrar, U.; Radwan, A.; Khan, F.A. Iterative Algorithms for Deblurring of Images in Case of Electrical Capacitance Tomography. Math. Probl. Eng. 2021, 2021, 1–11. [Google Scholar] [CrossRef]
- Gajewski, J.B. Electrostatic Nonintrusive Method for Measuring the Electric Charge, Mass Flow Rate, and Velocity of Particulates in the Two-Phase Gas-Solid Pipe Flows–Its Only or as Many as 50 Years of Historical Evolution. IEEE Trans. Ind. Appl. 2008, 44, 1418–1430. [Google Scholar] [CrossRef]
- Li, J.; Fu, F.; Li, S.; Xu, C.; Wang, S. Velocity Characterization of Dense Phase Pneumatically Conveyed Solid Particles in Horizontal Pipeline through an Integrated Electrostatic Sensor. Int. J. Multiph. Flow 2015, 76, 198–211. [Google Scholar] [CrossRef]
- Steiglitz, K.; McBride, L. A Technique for the Identification of Linear Systems. IEEE Trans. Automat. Contr. 1965, 10, 461–464. [Google Scholar] [CrossRef]
- Jia, Y.; Chernyshev, V.; Skliar, M. Ultrasound Measurements of Segmental Temperature Distribution in Solids: Method and Its High-Temperature Validation. Ultrasonics 2016, 66, 91–102. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.; Chen, L.; Meng, Z.; Zhang, G. Numerical Research of Magnetohydrodynamics Buoyant Flow in Dual Functional Lead Lithium Fusion Blanket. Fusion Eng. Des. 2019, 149, 111331. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Y.; Yao, J.; Fairweather, M. Reynolds Number Dependence of Particle Resuspension in Turbulent Duct Flows. Chem. Eng. Sci. 2018, 187, 33–51. [Google Scholar] [CrossRef]
- Gerber, S.; Oevermann, M. A Two Dimensional Euler–Lagrangian Model of Wood Gasification in a Charcoal Bed—Part I: Model Description and Base Scenario. Fuel 2014, 115, 385–400. [Google Scholar] [CrossRef]
- Pietrzak, M.; Płaczek, M. Void Fraction Predictive Methods in Two-Phase Flow across a Small Diameter Channel. Int. J. Multiph. Flow 2019, 121, 103115. [Google Scholar] [CrossRef]
- Rao, S.M.; Zhu, K.; Wang, C.H.; Sundaresan, S. Electrical Capacitance Tomography Measurements on the Pneumatic Conveying of Solids. Ind. Eng. Chem. Res. 2001, 40, 4216–4226. [Google Scholar] [CrossRef]
- Orak, İ.; Koçyiğit, A. The Thickness Effect of Insulator Layer between the Semiconductor and Metal Contact on C-V Characteristics of Al/Si3N4/p-Si Device. Pamukkale Univ. J. Eng. Sci. 2017, 23, 536–542. [Google Scholar] [CrossRef] [Green Version]
- Huang, Z.; Zhu, J.; Lu, L. An AD7746-Based Data Acquisition System for Capacitive Pressure Sensor in Weather Detection Application. Key Eng. Mater. 2011, 483, 461–464. [Google Scholar] [CrossRef]
- Che, H.Q.; Wu, M.; Ye, J.M.; Yang, W.Q.; Wang, H.G. Monitoring a Lab-Scale Wurster Type Fluidized Bed Process by Electrical Capacitance Tomography. Flow Meas. Instrum. 2018, 62, 223–234. [Google Scholar] [CrossRef] [Green Version]
- Xul, L.; Carter, R.M.; Yan, Y. Mass Flow Measurement of Fine Particles in a Pneumatic Suspension Using Electrostatic Sensing and Neural Network Techniques. In Proceedings of the 2005 IEEE Instrumentationand Measurement Technology Conference Proceedings, Ottawa, ON, Canada, 16–19 May 2005; pp. 17–19. [Google Scholar]
- Szpica, D. The Determination of the Flow Characteristics of a Low-Pressure Vapor-Phase Injector with a Dynamic Method. Flow Meas. Instrum. 2018, 62, 44–55. [Google Scholar] [CrossRef]
- Yan, Y. Mass Flow Measurement of Bulk Solids in Pneumatic Pipelines. Meas. Sci. Technol. 1996, 7, 1687–1706. [Google Scholar] [CrossRef]
- Gagliano, S.; Stella, G.; Bucolo, M. Real-Time Detection of Slug Velocity in Microchannels. Micromachines 2020, 11, 241. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Klinzing, G.E. Historical Review of Pneumatic Conveying. Kona Powder Part. J. 2018, 2018, 150–159. [Google Scholar] [CrossRef] [Green Version]






| Dimension/Property | Value | |
|---|---|---|
| Channel | Length | 33 cm |
| Width | 2 cm | |
| Solid Particles | Height | 1 cm |
| Inclination | 50° | |
| Density | 2500 kg/m3 | |
| Viscosity | 0.001003 kg/m.s, | |
| Diameter | 0.111 mm | |
| Packing limit | 0.6 | |
| Velocity | 0.47 m/s |
| Measurement Points | Flow(kg/s) | |
|---|---|---|
| Sand-MFR | Inlet | 0.047 |
| Outlet | −0.06980251 | |
| Net | −0.02280251 | |
| Inlet | 9.212002 × 10−05 | |
| Air-MFR | Outlet | −8.094581 × 10−05 |
| Net | 1.1174421 × 10−05 |
| Capacitance (pF) | Mass (kg) | Volumetric Concentration (%) |
|---|---|---|
| 0.49501 | 0 | 0 |
| 0.79612 | 0.0031 | 28.851 |
| 1.20063 | 0.0053 | 48.081 |
| 1.38101 | 0.0082 | 76.921 |
| 1.40193 | 0.0101 | 96.151 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abrar, U.; Yousaf, A.; Jaffri, N.R.; Rehman, A.U.; Ahmad, A.; Gardezi, A.A.; Naseer, S.; Shafiq, M.; Choi, J.-G. Analysis of Complex Solid-Gas Flow under the Influence of Gravity through Inclined Channel and Comparison with Real-Time Dual-Sensor System. Electronics 2021, 10, 2849. https://doi.org/10.3390/electronics10222849
Abrar U, Yousaf A, Jaffri NR, Rehman AU, Ahmad A, Gardezi AA, Naseer S, Shafiq M, Choi J-G. Analysis of Complex Solid-Gas Flow under the Influence of Gravity through Inclined Channel and Comparison with Real-Time Dual-Sensor System. Electronics. 2021; 10(22):2849. https://doi.org/10.3390/electronics10222849
Chicago/Turabian StyleAbrar, Usama, Adnan Yousaf, Nasif Raza Jaffri, Ateeq Ur Rehman, Aftab Ahmad, Akber Abid Gardezi, Salman Naseer, Muhammad Shafiq, and Jin-Ghoo Choi. 2021. "Analysis of Complex Solid-Gas Flow under the Influence of Gravity through Inclined Channel and Comparison with Real-Time Dual-Sensor System" Electronics 10, no. 22: 2849. https://doi.org/10.3390/electronics10222849







