Estimation of Knee Joint Extension Force Using Mechanomyography Based on IGWO-SVR Algorithm
Abstract
:1. Introduction
- A new, improved swarm intelligence optimization algorithm (IGWO) combined with SVR is proposed. In the IGWO, a new nonlinear convergence factor and a new location update strategy are creatively proposed, which can effectively improve the estimation of knee joint extension force;
- The new nonlinear convergence factor and the new position update strategy are applied to IGWO for the first time;
- The first application of the proposed IGWO-SVR model in muscle force estimation;
- The proposed IGWO-SVR model is superior to other models in performance indexes of RMSE, MAPE, and R.
2. Methodology
2.1. Support Vector Regression
2.2. Traditional Gray Wolf Algorithm and Its Improvement
2.2.1. Traditional Gray Wolf Algorithm
2.2.2. Improved Gray Wolf Algorithm
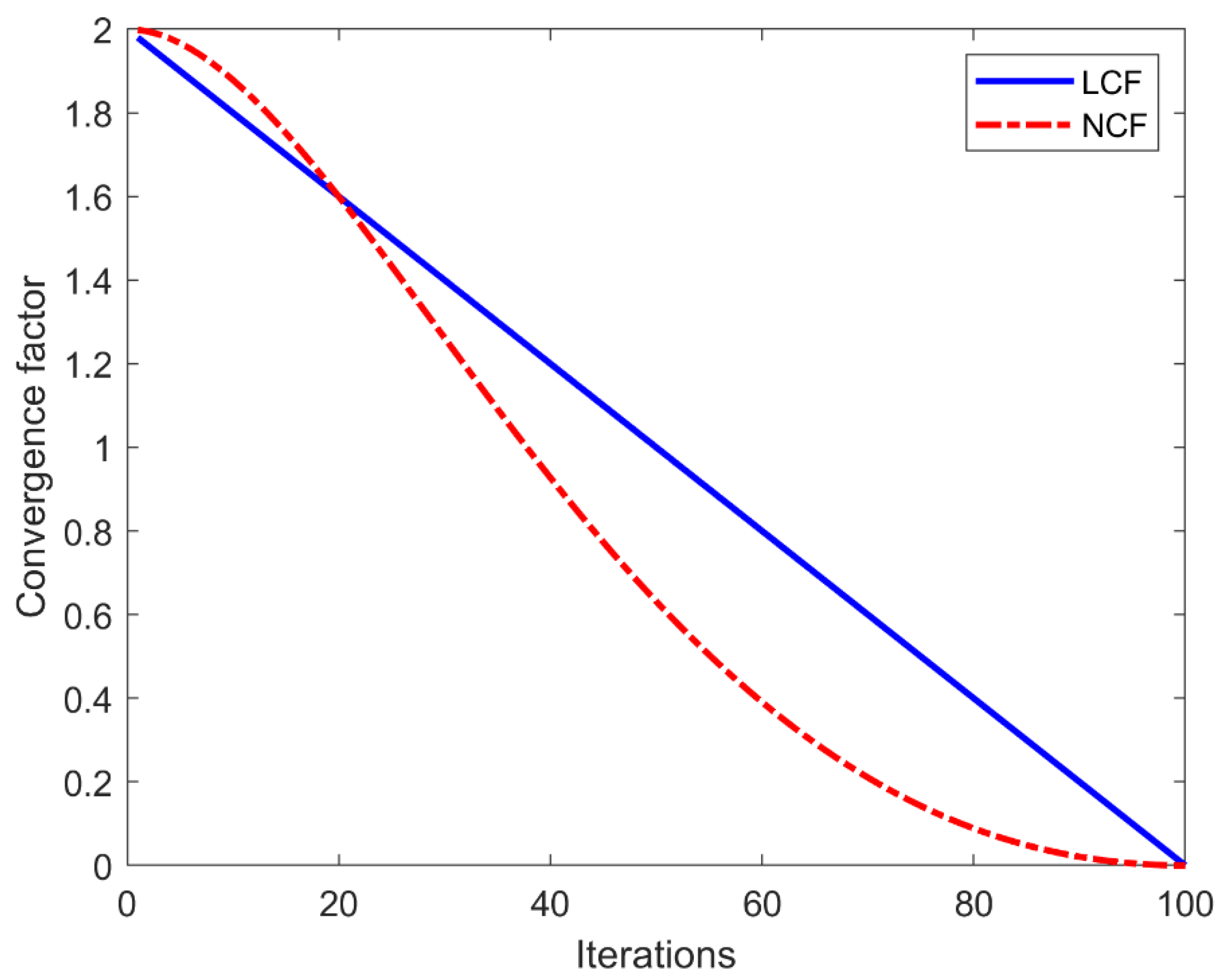
- Nonlinear convergence factor control strategy (NCF)
- 2.
- Update location strategy
2.3. IGWO-SVR Model Construction
- (1)
- The experimental data are divided into training samples and test samples. If the quantity level difference between data is too large, the estimation result of SVR will be adversely affected. In addition, SVR is very sensitive to data between [0, 1]. To improve efficiency, the experimental data are normalized to the range [0, 1], and the normalized equation is defined as follows:where represents the normalized data of each row, represents each original input data, and represent the minimum and maximum values of each row data, respectively;
- (2)
- Set related parameters such as group size N, the maximum number of iterations , and optimization parameter value range;
- (3)
- Initialize population randomly;
- (4)
- The fitness value of each wolf position is calculated and ranked in ascending order. The three leading wolves positions are denoted as , , and , respectively. The fitness value in this paper is expressed by mean square error (MSE);
- (5)
- The distances are calculated according to (13) by updating the nonlinear convergence factor . Then the new individual position is obtained according to (20); that is, the new SVR parameter values are obtained;
- (6)
- If the number of iterations reaches the maximum, the iteration is terminated, and the optimal parameters C and are output; Otherwise, return to (3) and continue the iteration;
- (7)
- The optimized parameters C and are used to establish the SVR estimation model.
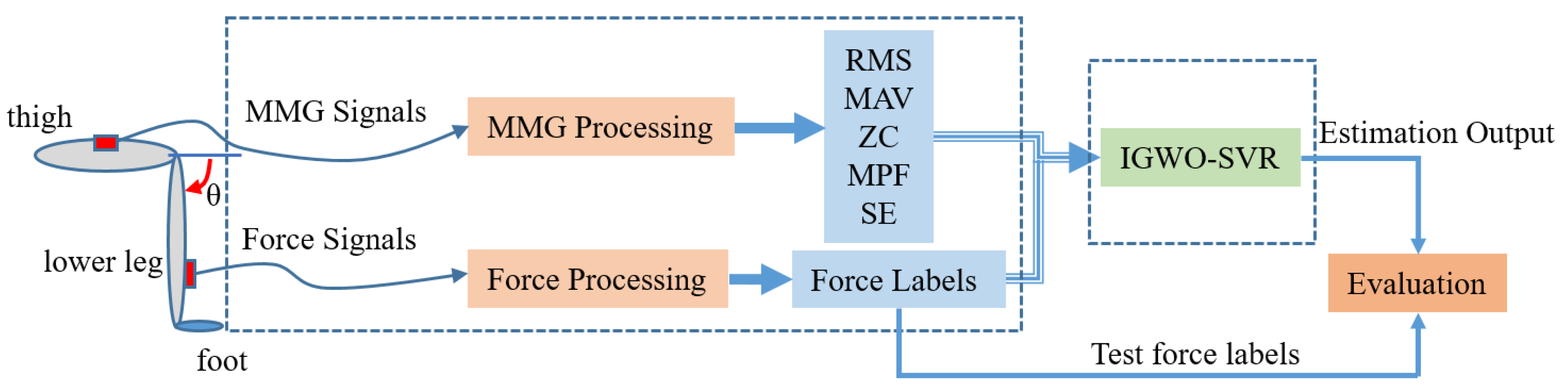
2.4. IGWO-SVR for Knee Joint Extension Force Estimation
3. Experimental
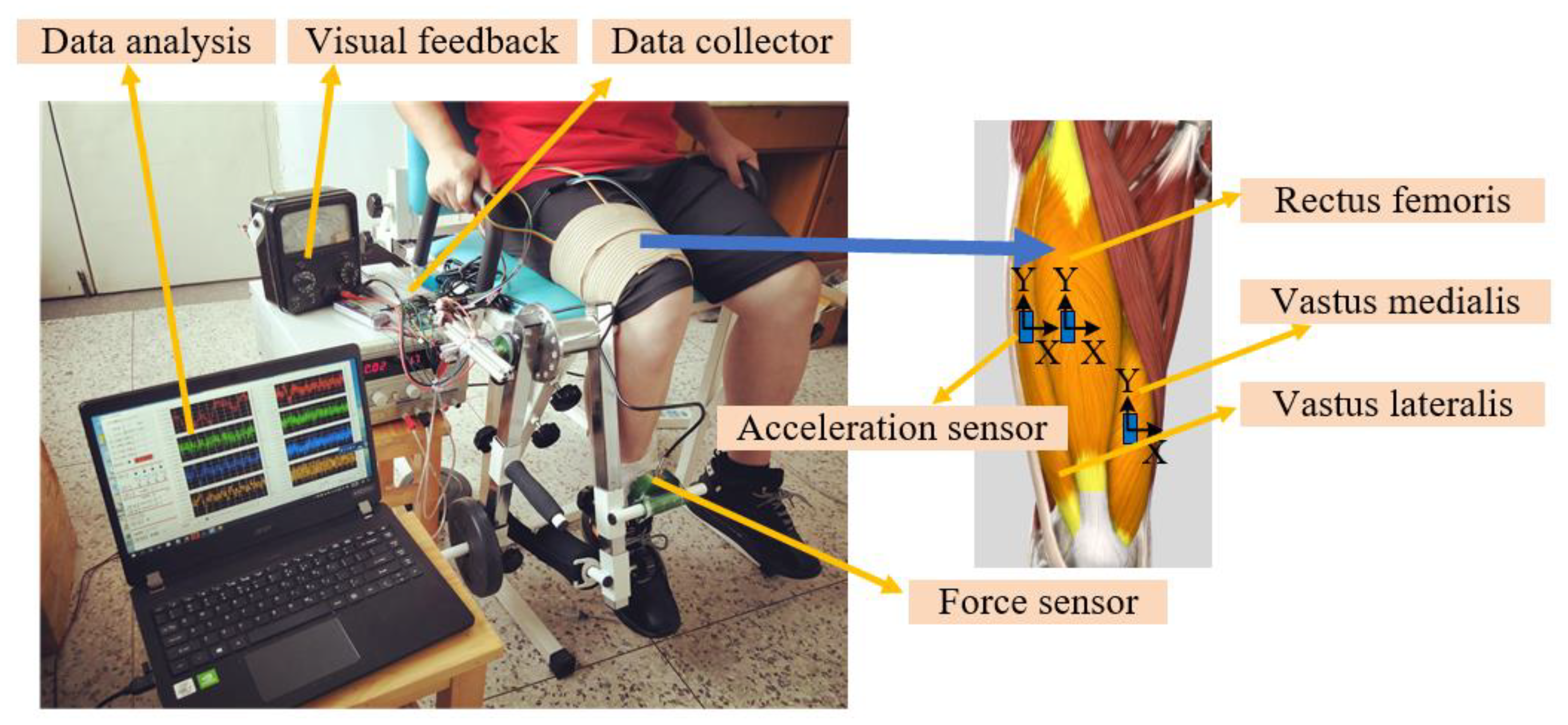
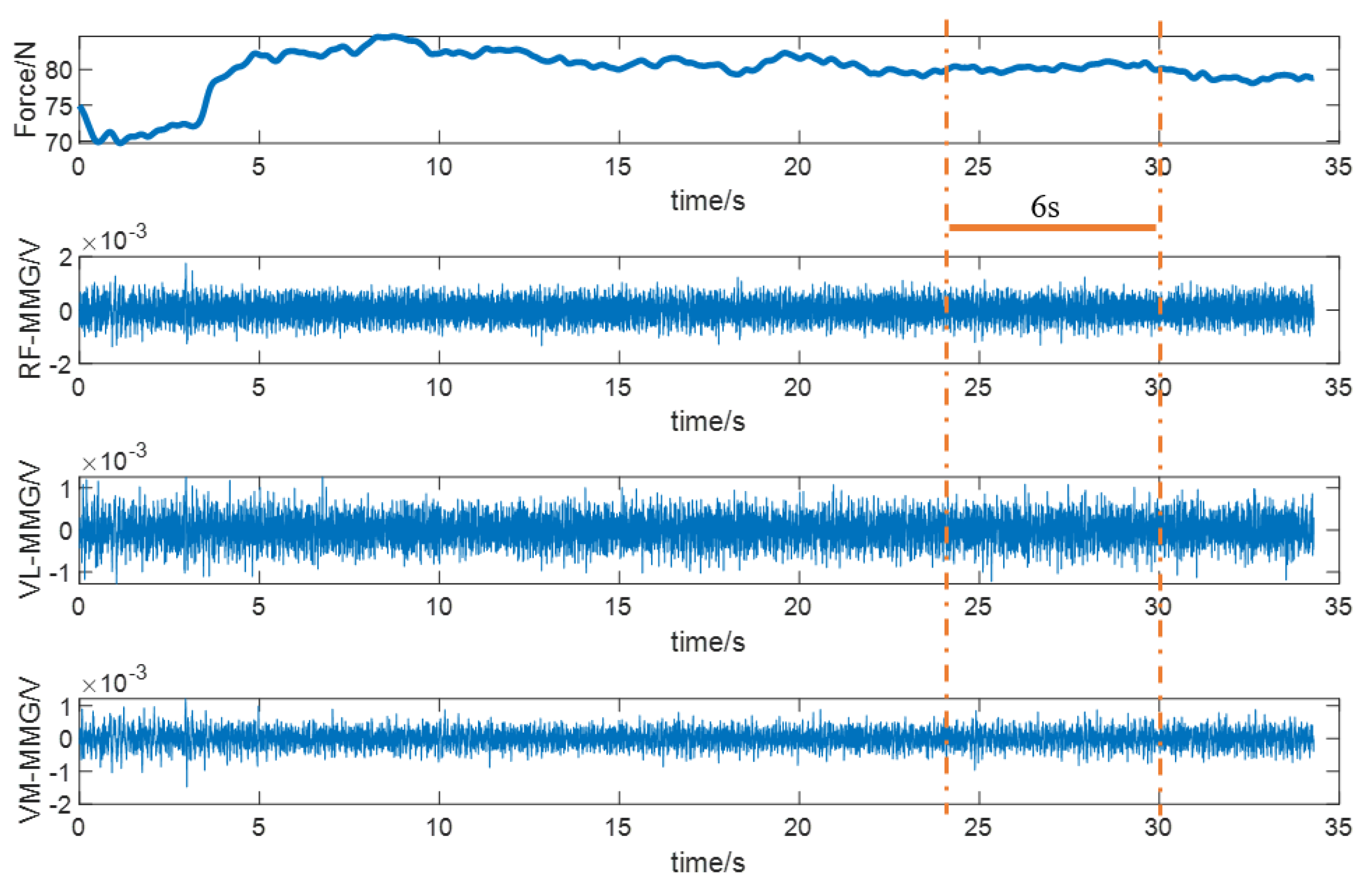
3.1. Signal Acquisition and Processing
3.2. Model Evaluation Index
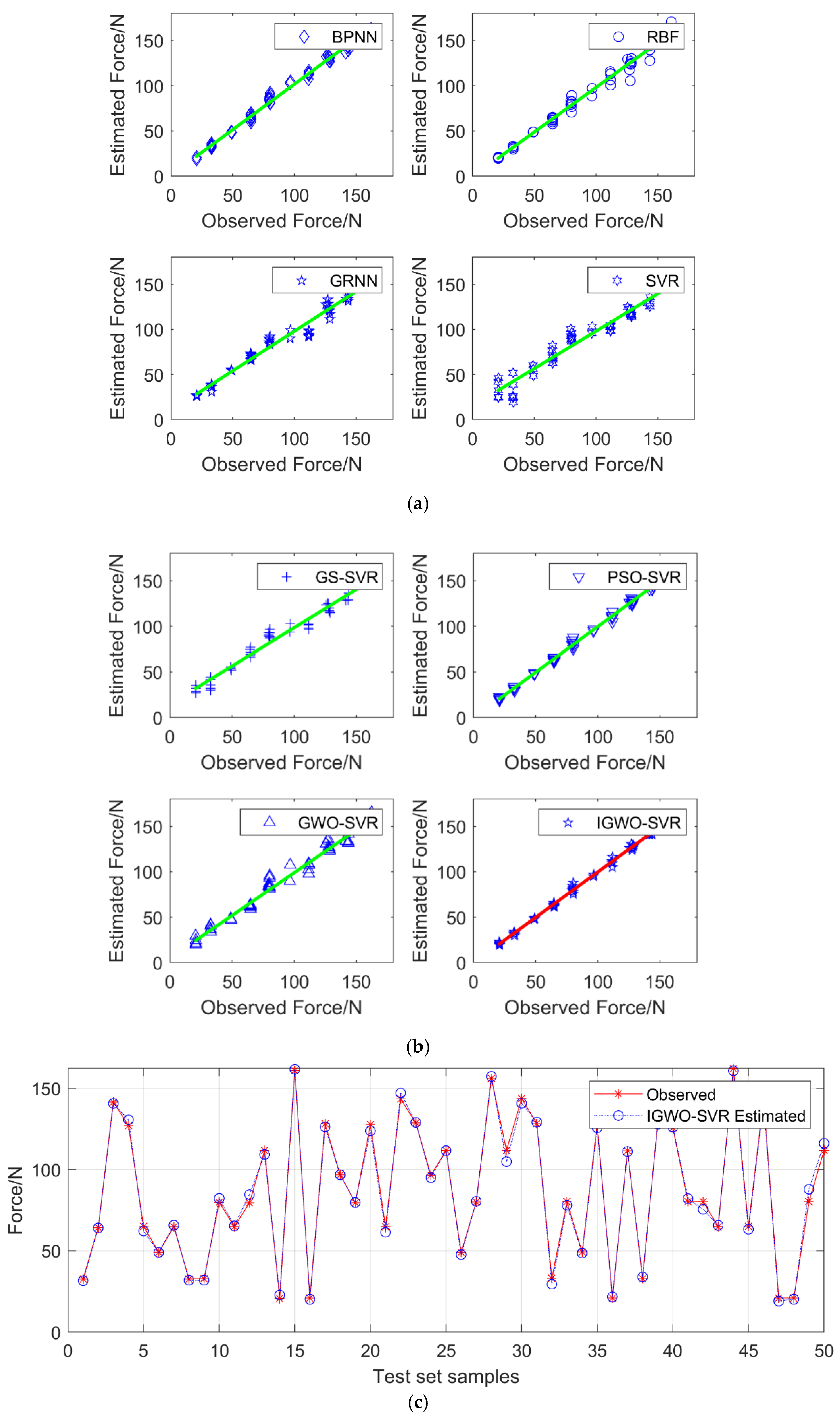
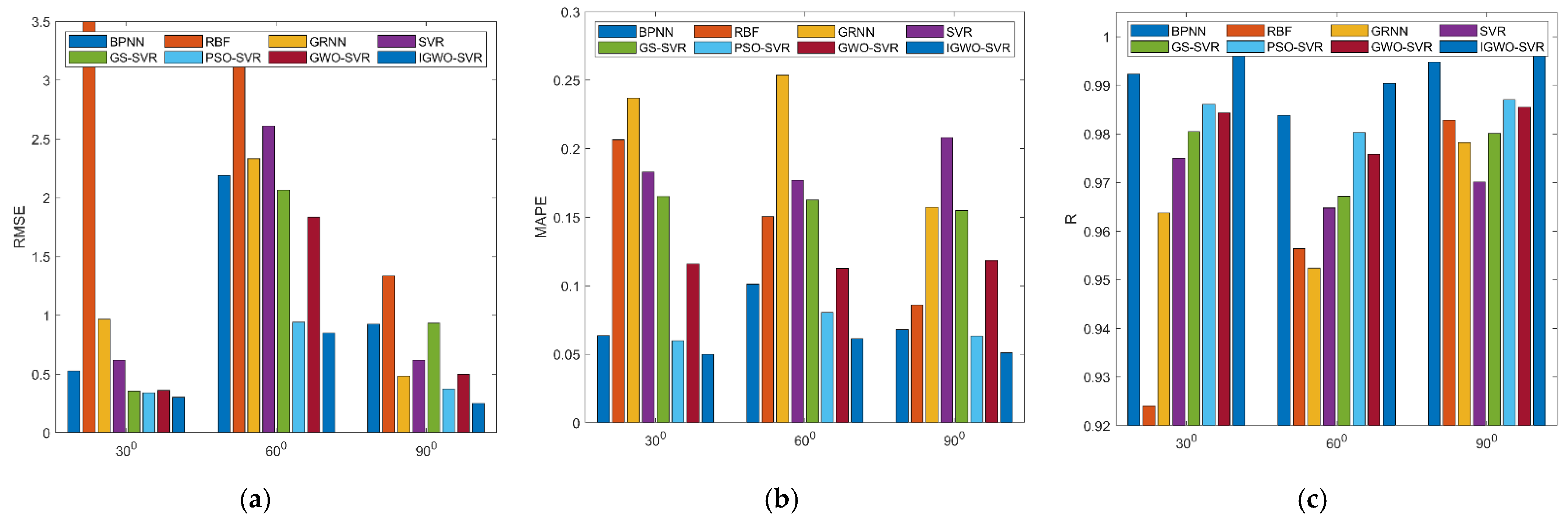
3.3. Results and Discussion
4. Application and Limitation
5. Conclusions and Future Outlook
- (1)
- In consideration of the influence of other lower limb motion parameters, such as motion angular velocity and body posture, on the estimation of lower limb muscle force;
- (2)
- Consider other improved swarm intelligence algorithms to optimize machine learning and further improve the accuracy of muscle force estimation;
- (3)
- Apply the estimation results to the recognition of human lower limb motion intention and the compliant control of the intelligent portable wearable robot.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rathor, R.; Singh, A.K.; Choudhary, H.; Goswami, C.; Fekete, G. A systematic review on gait analysis methods and assistive devices in lower limb prosthetics. Mater. Today Proc. 2021, 44, 4251–4255. [Google Scholar] [CrossRef]
- Asheghabadi, A.S.; Moqadam, S.B.; Xu, J. Multichannel finger pattern recognition using single-site mechanomyography. IEEE Sens. J. 2021, 21, 8184–8193. [Google Scholar] [CrossRef]
- Jafarzadeh, M.; Hussey, D.C.; Tadesse, Y. Deep learning approach to control of prosthetic hands with electromyography signals. In Proceedings of the IEEE International Symposium on Measurement and Control in Robotics (ISMCR 2019), Houston, TX, USA, 19–21 September 2019; pp. A1-4-1–A1-4-11. [Google Scholar]
- Song, Y.; Du, Y.; Wu, X.; Chen, X.; Xie, P. A synchronous and multi-domain feature extraction method of EEG and sEMG in power-assist rehabilitation robot. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA 2014), Hong Kong, China, 31 May–7 June 2014; pp. 4940–4945. [Google Scholar]
- Na, Y.; Choi, C.; Lee, H.; Kim, J. A study on estimation of joint force through isometric index finger abduction with the help of semg peaks for biomedical applications. IEEE Trans. Cybern. 2016, 46, 2–8. [Google Scholar] [CrossRef]
- Liang, X.; Wang, W.; Hou, Z.; Ren, S.; Peng, L.; Hu, J. Interactive control methods for rehabilitation robot. Sci. Sin. Inf. 2018, 48, 24–46. [Google Scholar] [CrossRef]
- Vidovic, M.M.C.; Hwang, H.J.; Amsüss, S.; Hahne, J.M.; Farina, D.; Müller, K.R. Improving the robustness of myoelectric pattern recognition for upper limb prostheses by covariate shift adaptation. IEEE T. Neur. Sys. Reh. 2016, 24, 961–970. [Google Scholar] [CrossRef]
- Oster, G.; Jaffe, J.S. Low frequency sounds from sustained contraction of human skeletal muscle. Biophys. J. 1980, 30, 119–127. [Google Scholar] [CrossRef] [Green Version]
- Barry, D.T. Acoustic signals from frog skeletal muscle. Biophys. J. 1987, 51, 769–773. [Google Scholar] [CrossRef] [Green Version]
- Posatskiy, A.O.; Chau, T. The effects of motion artifact on mechanomyography: A comparative study of microphones and accelerometers. J. Electromyogr. Kinesiol. 2012, 22, 320–324. [Google Scholar] [CrossRef] [PubMed]
- Tarata, M.T. Mechanomyography versus Electromyography, in monitoring the muscular fatigue. Biomed. Eng. Online 2003, 2, 3. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.; Pang, M.; Yu, P. Effect of muscle fatigue on surface electromyography-based hand grasp force estimation. Appl. Bionics. Biomech. 2021, 2021, 8817480. [Google Scholar] [CrossRef]
- Ibitoye, M.O.; Hamzaid, N.A.; Zuniga, J.M.; Wahab, A.K.A. Mechanomyography and muscle function assessment: A review of current state and prospects. Clin. Biomech. 2014, 29, 691–704. [Google Scholar] [CrossRef]
- Naeem, J.; Hamzaid, N.A.; Islam, M.A.; Azman, A.W.; Bijak, M. Mechanomyography-based muscle fatigue detection during electrically elicited cycling in patients with spinal cord injury. Med. Biol. Eng. Comput. 2019, 57, 1199–1211. [Google Scholar] [CrossRef]
- Cè, E.; Rampichini, S.; Limonta, E.; Esposito, F. Torque and mechanomyogram correlations during muscle relaxation: Effects of fatigue and time-course of recovery. J. Electromyogr. Kinesiol. 2013, 23, 1295–1303. [Google Scholar] [CrossRef]
- Kasuya, M.; Seki, M.; Kawamura, K.; Fujie, M.G. Subtle grip force estimation from EMG and muscle stiffness—Relationship between muscle character frequency and grip force. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC 2011), Boston, MA, USA, 30 August–3 September 2011; pp. 4116–4119. [Google Scholar]
- Meng, W.; Ding, B.; Zhou, Z.; Liu, Q.; Ai, Q. An EMG-based force prediction and control approach for robot-assisted lower limb rehabilitation. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics (SMC 2014), San Diego, CA, USA, 5–8 October 2014; pp. 2198–2203. [Google Scholar]
- Anwar, T.; Jumaily, A.A. ANFIS to estimate damping coefficient from EMG to optimize the interaction force. In Proceedings of the International Conference on Microelectronics, Computing and Communications (MicroCom 2016), Durgapur, India, 23–25 January 2016; pp. 1–6. [Google Scholar]
- Sepulveda, F.; Wells, D.M.; Vaughan, C.L. A neural network representation of electromyography and joint dynamics in human gait. J. Biomech. 1993, 26, 101–109. [Google Scholar] [CrossRef]
- Li, Q.L.; Song, Y.; Hou, Z.G. Estimation of lower limb periodic motions from sEMG using least squares support vector regression. Neural Process. Lett. 2015, 41, 371–388. [Google Scholar] [CrossRef]
- Wang, C.; Li, J.; Guo, C.; Huang, Q.; Yang, B.; Liu, H. sEMG-based estimation of human arm force using regression model. In Proceedings of the IEEE International Conference on Robotics and Biomimetics (ROBIO), Macau, China, 5–8 December 2017; pp. 1044–1049. [Google Scholar]
- Akataki, K.; Mita, K.; Watakabe, M.; Itoh, K. Mechanomyogram and force relationship during voluntary isometric ramp contractions of the biceps brachii muscle. Eur. J. Appl. Physiol. 2001, 84, 19–25. [Google Scholar] [CrossRef] [PubMed]
- Beck, T.W.; Defreitas, J.M.; Stock, M.S. The linearity and reliability of the mechanomyographic amplitude versus submaximal isometric force relationship. Physiol. Meas. 2009, 30, 1009–1016. [Google Scholar] [CrossRef] [PubMed]
- Youn, W.; Kim, J. Estimation of elbow flexion force during isometric muscle contraction from mechanomyography and electromyography. Med. Biol. Eng. Comput. 2010, 48, 1149–1157. [Google Scholar] [CrossRef] [Green Version]
- Youn, W.; Kim, J. Feasibility of using an artificial neural network model to estimate the elbow flexion force from mechanomyography. J. Neurosci. Methods. 2011, 194, 386–393. [Google Scholar] [CrossRef]
- Lei, K.F.; Cheng, S.C.; Lee, M.Y.; Lin, W.Y. Measurement and estimation of muscle contraction strength using mechanomyography based on artificial neural network algorithm. Biomed. Eng. Appl. Basis. Commun. 2013, 25, 1350020. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, X.; Zhu, X.; Gao, X.; Chen, X.; Chen, X. A regression-based framework for quantitative assessment of muscle spasticity using combined EMG and inertial data from wearable sensors. Front. Neurosci. 2019, 13, 398. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Yu, J.; Xia, C.; Yang, K.; Cao, H.; Wu, Q. Research on GA-SVM based head-motion classification via mechanomyography feature analysis. Sensors 2019, 19, 1986. [Google Scholar] [CrossRef] [Green Version]
- Ibitoye, M.O.; Hamzaid, N.A.; Wahab, A.K.A.; Hasnan, N.; Olatunji, S.O.; Davis, G.M. Estimation of electrically-evoked knee torque from mechanomyography using support vector regression. Sensors 2016, 16, 1115. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Xie, C.; Wu, H.; Hu, D.; Zhang, Q.; Gao, L. Estimation of knee extension force using mechanomyography signals detected through clothing. In International Conference on Intelligent Robotics and Applications (ICIRA 2019); Springer: Cham, Switzerland, 2019; pp. 3–14. [Google Scholar]
- Ibitoye, M.O.; Hamzaid, N.A.; Wahab, A.K.A.; Hasnan, N.; Olatunji, S.O.; Davis, G.M. SVR modelling of mechanomyographic signals predicts neuromuscular stimulation-evoked knee torque in paralyzed quadriceps muscles undergoing knee extension exercise. Comput. Biol. Med. 2020, 117, 103614. [Google Scholar] [CrossRef]
- Huang, X.; Huang, X.; Wang, B.; Xie, Z. Fault diagnosis of transformer based on modified grey wolf optimization algorithm and support vector machine. IEEJ Trans. Electr. Electron. Eng. 2020, 15, 409–417. [Google Scholar] [CrossRef]
- Xie, Q.; Guo, Z.; Liu, D.; Chen, C.; Shen, Z.; Wang, X. Optimization of heliostat field distribution based on improved gray wolf optimization algorithm. Renew. Energ. 2021, 176, 447–458. [Google Scholar] [CrossRef]
- Deris, A.M.; Zain, A.M.; Sallehuddin, R. A note of hybrid GR-SVM for prediction of surface roughness in abrasive water jet machining: A response. Meccanica 2017, 52, 1993–1994. [Google Scholar] [CrossRef]
- Jiang, F.; Peng, Z.; He, J. Short-term load forecasting based on support vector regression with improved grey wolf optimizer. In Proceedings of the 10th International Conference on Advanced Computational Intelligence (ICACI 2018), Xiamen, China, 29–31 March 2018; pp. 807–812. [Google Scholar]
- Zhou, Z.; Zhang, R.; Wang, Y.; Zhu, Z.; Zhang, J. Color difference classification based on optimization support vector machine of improved grey wolf algorithm. Optik 2018, 170, 17–29. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Zhu, A.; Xu, C.; Li, Z.; Wu, J.; Liu, Z. Hybridizing grey wolf optimization with differential evolution for global optimization and test scheduling for 3D stacked SoC. J. Syst. Eng. Electron. 2015, 26, 317–328. [Google Scholar] [CrossRef]
- Zhou, Y.; Yang, X.; Tao, L.; Li, Y. Transformer fault diagnosis model based on improved gray wolf optimizer and probabilistic neural network. Energies 2021, 14, 3029. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, W.; Pan, Y. Enhancing electronic nose performance by feature selection using an improved grey wolf optimization based algorithm. Sensors 2020, 20, 4065. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Yang, B.; Ma, C.; Wang, S.; Yang, W. Thermal error modeling of gear hobbing machine based on IGWO-GRNN. Int. J. Adv. Manuf. Technol. 2020, 106, 5001–5016. [Google Scholar] [CrossRef]


| LUS1 | LUS2 | |||||
|---|---|---|---|---|---|---|
| RMSE | MAPE | R | RMSE | MAPE | R | |
| LCF | 0.2962 | 0.0277 | 0.9972 | 0.2165 | 0.0274 | 0.9979 |
| NCF | 0.2050 | 0.0265 | 0.9980 | 0.1938 | 0.0256 | 0.9983 |
| Subject | Age (Years) | Height (m) | Body Weight (kg) | Joint Angle (°) |
|---|---|---|---|---|
| S1 | 42 | 1.74 | 72.6 | 0~90 |
| S2 | 29 | 1.70 | 68.0 | 0~90 |
| S3 | 21 | 1.70 | 68.5 | 0~90 |
| S4 | 21 | 1.72 | 66.5 | 0~90 |
| Models | Evaluation Index | Models | Evaluation Index | ||||
|---|---|---|---|---|---|---|---|
| RMSE | MAPE | R | RMSE | MAPE | R | ||
| BPNN | 1.1841 | 0.0463 | 0.9958 | GS-SVR | 0.6712 | 0.1347 | 0.9842 |
| RBF | 1.5942 | 0.0389 | 0.9917 | PSO-SVR | 0.2817 | 0.0569 | 0.9883 |
| GRNN | 0.3278 | 0.1037 | 0.9849 | GWO-SVR | 0.2868 | 0.0748 | 0.9883 |
| SVR | 0.4006 | 0.1744 | 0.9715 | IGWO-SVR | 0.1938 | 0.0256 | 0.9983 |
| Models | Evaluation Index | Models | Evaluation Index | ||||
|---|---|---|---|---|---|---|---|
| RMSE | MAPE | R | RMSE | MAPE | R | ||
| BPNN | 0.9233 | 0.068 | 0.9948 | GS-SVR | 0.9346 | 0.1549 | 0.9801 |
| RBF | 1.3367 | 0.0859 | 0.9828 | PSO-SVR | 0.3738 | 0.0634 | 0.9871 |
| GRNN | 0.4854 | 0.1572 | 0.9782 | GWO-SVR | 0.4989 | 0.1183 | 0.9855 |
| SVR | 0.6194 | 0.2081 | 0.9701 | IGWO-SVR | 0.2492 | 0.0509 | 0.9967 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Gao, L.; Lu, W.; Wang, D.; Xie, C.; Cao, H. Estimation of Knee Joint Extension Force Using Mechanomyography Based on IGWO-SVR Algorithm. Electronics 2021, 10, 2972. https://doi.org/10.3390/electronics10232972
Li Z, Gao L, Lu W, Wang D, Xie C, Cao H. Estimation of Knee Joint Extension Force Using Mechanomyography Based on IGWO-SVR Algorithm. Electronics. 2021; 10(23):2972. https://doi.org/10.3390/electronics10232972
Chicago/Turabian StyleLi, Zebin, Lifu Gao, Wei Lu, Daqing Wang, Chenlei Xie, and Huibin Cao. 2021. "Estimation of Knee Joint Extension Force Using Mechanomyography Based on IGWO-SVR Algorithm" Electronics 10, no. 23: 2972. https://doi.org/10.3390/electronics10232972
APA StyleLi, Z., Gao, L., Lu, W., Wang, D., Xie, C., & Cao, H. (2021). Estimation of Knee Joint Extension Force Using Mechanomyography Based on IGWO-SVR Algorithm. Electronics, 10(23), 2972. https://doi.org/10.3390/electronics10232972







