Sliding Mode Robust Active Disturbance Rejection Control for Single-Link Flexible Arm with Large Payload Variations
Abstract
:1. Introduction
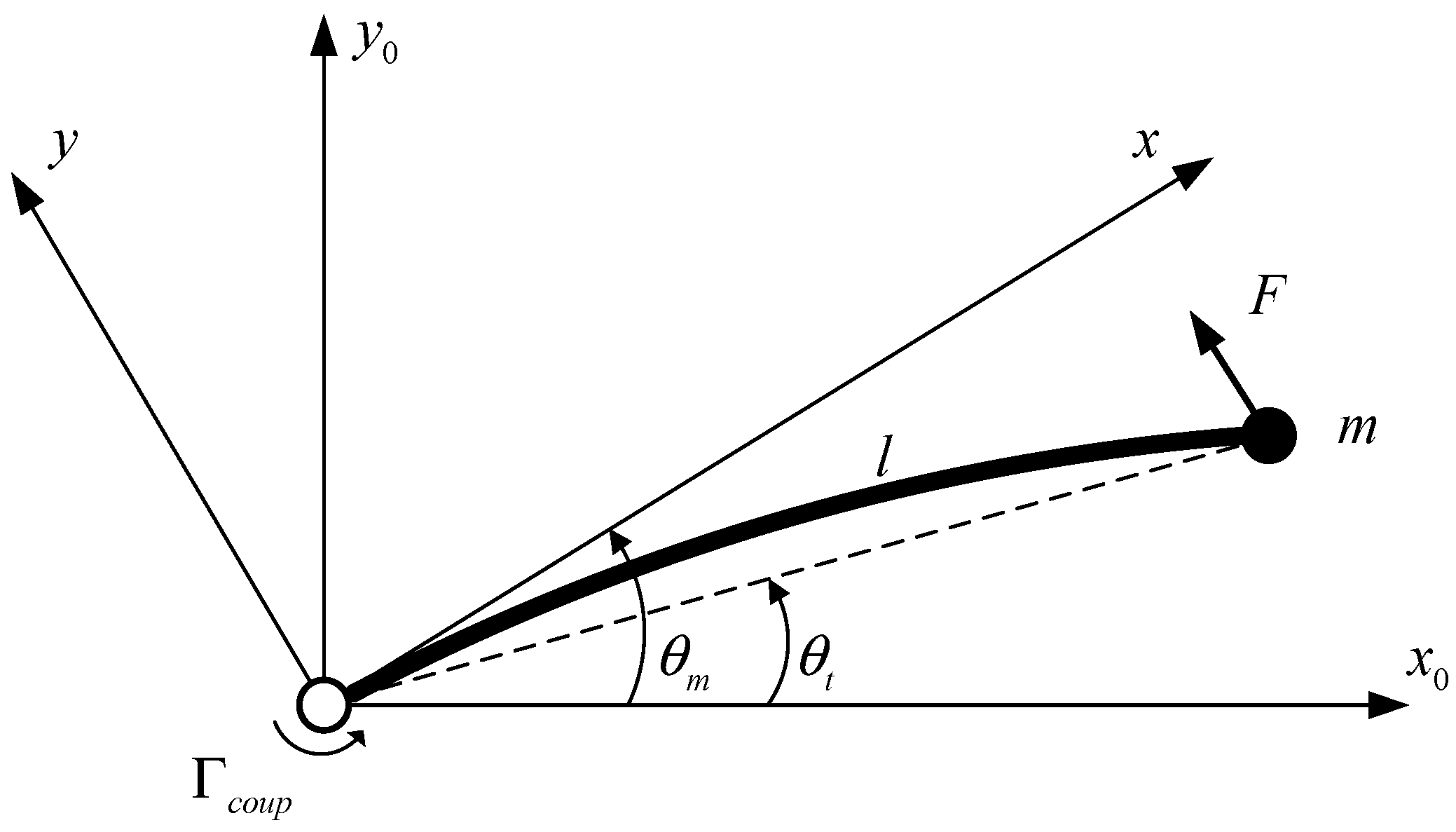
2. Modeling of Single-Link Flexible Arm
3. General Control Scheme
3.1. Inner Loop Controller
3.2. Outer Loop Controller
3.2.1. Extended State Observer
3.2.2. Feedback Control Law
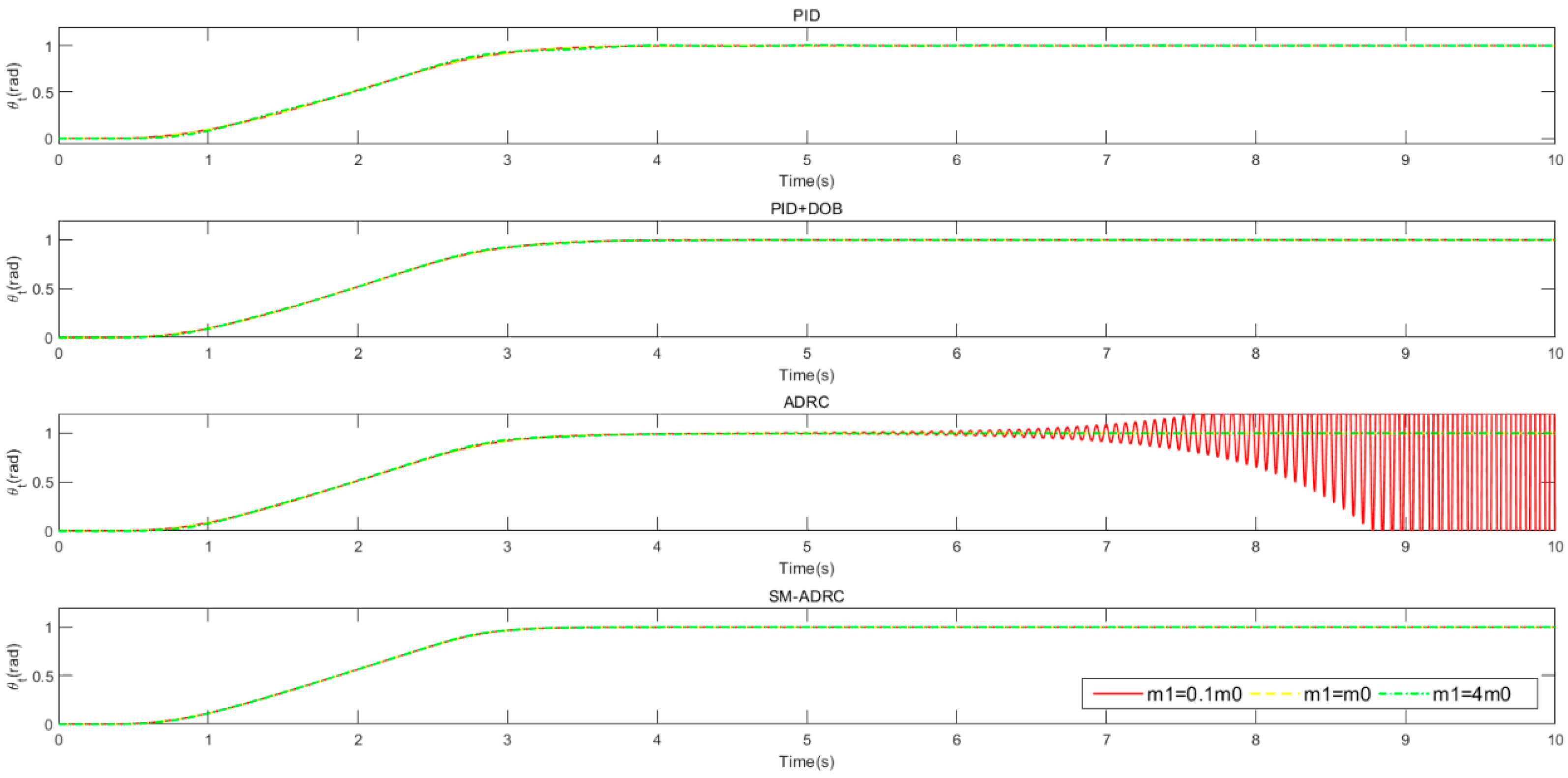
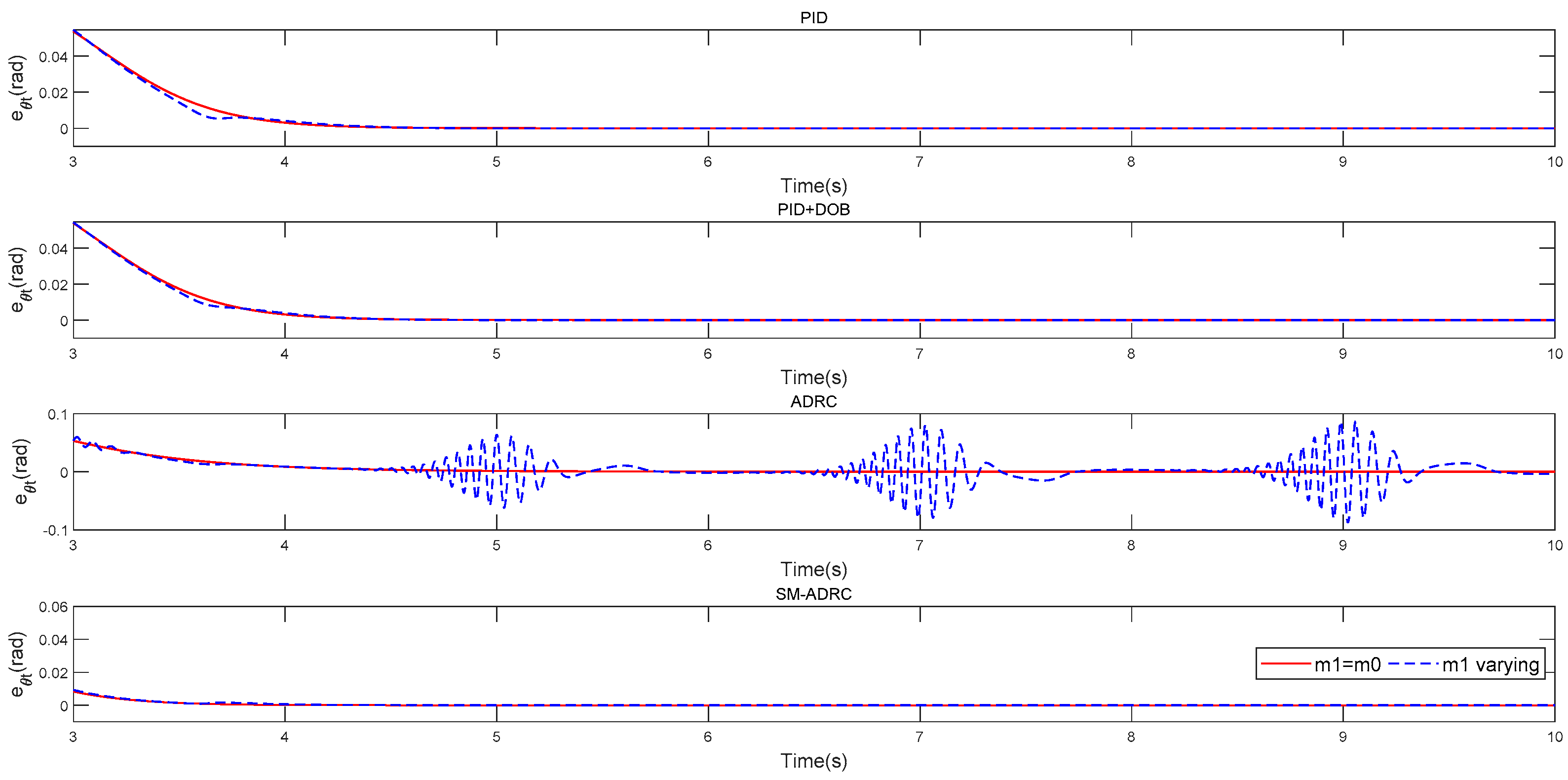
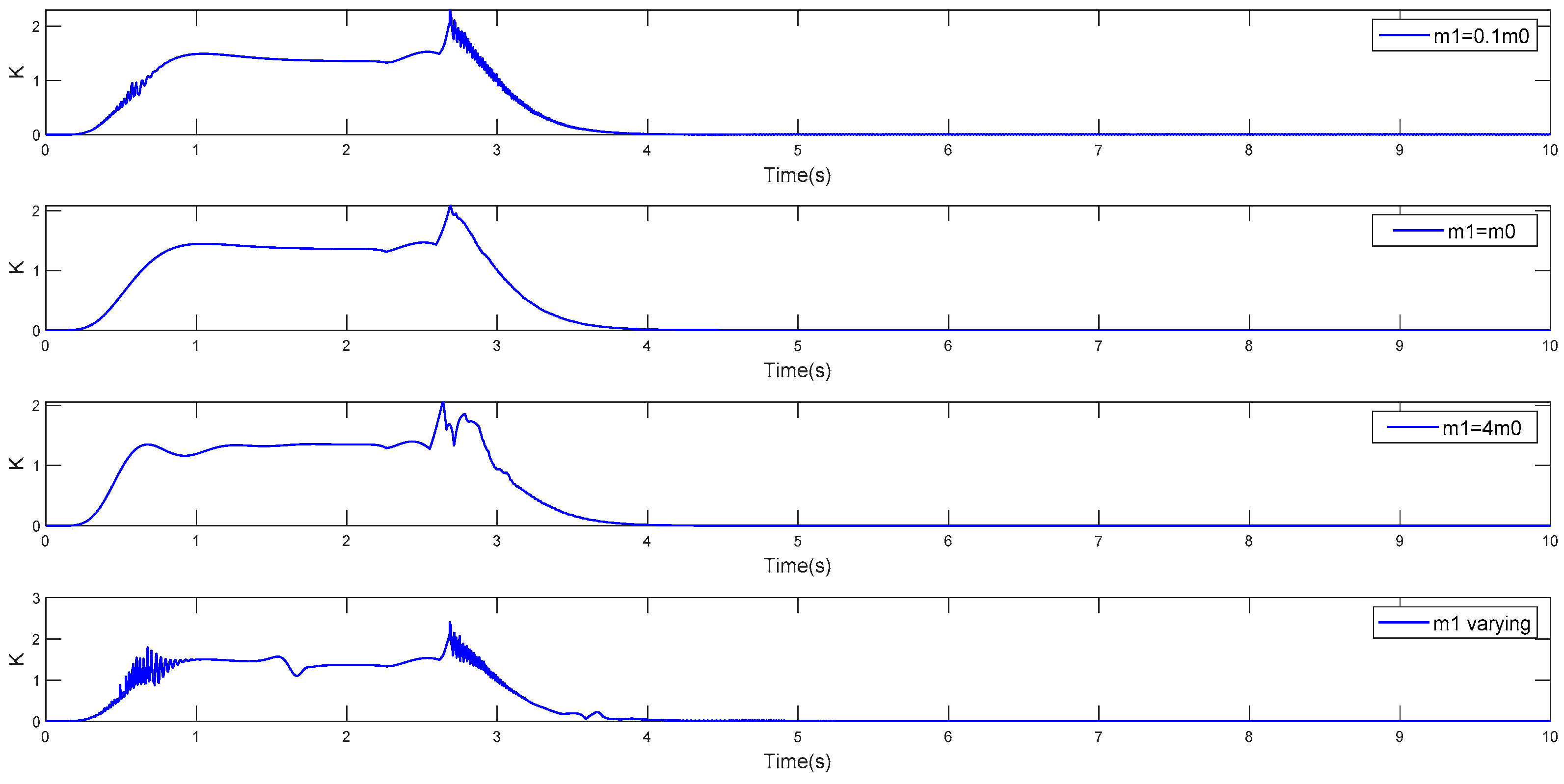
4. Simulation Results
4.1. Simulation Results with
4.2. Robustness Test
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Feliu, V.; Ramos, F. Strain gauge based control of single-link flexible very lightweight robots robust to payload changes. Mechatronics 2005, 15, 547–571. [Google Scholar] [CrossRef]
- Feliu, V.; Castillo, F.J.; Ramos, F.; Somolinos, J.A. Robust tip trajectory tracking of a very lightweight single-link flexible arm in presence of large payload changes. Mechatronics 2012, 22, 594–613. [Google Scholar] [CrossRef]
- Morales, R.; Feliu, V.; Jaramillo, V. Position control of very lightweight single-link flexible arms with large payload variations by using disturbance observers. Robot. Auton. Syst. 2012, 60, 532–547. [Google Scholar] [CrossRef]
- Feliu-Talegon, D.; Feliu-Batlle, V. Passivity-based control of a single-link flexible manipulator using fractional controllers. Nonlinear Dyn. 2019, 95, 2415–2441. [Google Scholar] [CrossRef]
- Yang, J.H.; Lian, F.L.; Fu, L.C. Nonlinear adaptive control for flexible-link manipulators. IEEE Trans. Robot Autom. 1997, 13, 140–148. [Google Scholar] [CrossRef]
- Becedas, J.; Trapero, J.R.; Feliu, V.; Sira-Ramírez, H. Adaptive controller for single-link flexible manipulators based on algebraic identification and generalized proportional integral control. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2009, 39, 735–751. [Google Scholar] [CrossRef]
- Corradini, M.L.; Giantomassi, A.; Ippoliti, G.; Longhi, S.; Orlando, G. Robust control of robot arms via quasi sliding modes and neural networks. Stud. Comput. Intell. 2015, 576, 79–105. [Google Scholar]
- Sun, C.; Wei, H.; Jie, H. Neural network control of a flexible robotic manipulator using the lumped spring-mass model. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 1863–1874. [Google Scholar] [CrossRef]
- Zhang, H.; Gao, X.; Xu, G. Research on improved PD control of flexible manipulator. In Proceedings of the 2019 Chinese Control and Decision Conference, Nanchang, China, 3–5 June 2019. [Google Scholar]
- Sayahkarajy, M.; Mohamed, Z.; Faudzi, A.; Supriyanto, E. Hybrid vibration and rest-to-rest control of a two-link flexible robotic arm using H∞ loop-shaping control design. Forum. Math. 2016, 18, 171–191. [Google Scholar] [CrossRef]
- Zhang, L.; Li, X.; Liu, H.; Wang, A.; Cao, X. Backstepping-based H∞ tracking control for single-link flexible joint manipulators. In Proceedings of the 2019 Chinese Control Conference, Guangzhou, China, 27–30 July 2019. [Google Scholar]
- O’Connor, W.J.; de la Flor, F.R.; McKeown, D.J.; Feliu, V. Wave-based control of non-linear flexible mechanical systems. Nonlinear Dyn. 2009, 57, 113. [Google Scholar] [CrossRef]
- Pereira, E.; Aphale, S.S.; Feliu, V.; Moheimani, S.R. Integral resonant control for vibration damping and precise tip-positioning of a single-link flexible manipulator. IEEE/ASME Trans. Mechatron. 2010, 16, 232–240. [Google Scholar] [CrossRef] [Green Version]
- Han, J. Active disturbance rejection controller and its applications (in Chinese). Control Decis. 1998, 13, 19–23. [Google Scholar]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Gao, Z. Scaling and bandwidth-parameterization based controller tuning. In Proceedings of the American Control Conference, Denver, CO, USA, 4–6 June 2003; Volume 6, pp. 4989–4996. [Google Scholar]
- Yang, H.; Yang, Y.; Yuan, Y.; Fan, X. Back-stepping control of two-link flexible manipulator based on an extended state observer. Adv. Space Res. 2015, 56, 2312–2322. [Google Scholar] [CrossRef]
- Fareh, R. Control of a single flexible link manipulator using fractional active disturbance rejection control. In Proceedings of the 6th International Conference on Control, Decision and Information Technologies, Paris, France, 23–26 April 2019. [Google Scholar]
- Li, R.; Li, T.; Bu, R.; Zheng, Q.; Chen, C. Active disturbance rejection with sliding mode control based course and path following for underactuated ships. Math. Probl. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- Chen, C.F.; Du, Z.J.; He, L.; Wang, J.; Wu, D.; Dong, W. Active disturbance rejection with fast terminal sliding mode control for a lower limb exoskeleton in swing phase. IEEE Access 2019, 7, 72343–72357. [Google Scholar] [CrossRef]
- Karami, M.; Kazemi, A.; Vatankhah, R.; Khosravifard, A. Adaptive fractional-order backstepping sliding mode controller design for an electrostatically actuated size-dependent microplate. J. Vib. Control. 2021, 27, 1353–1369. [Google Scholar] [CrossRef]
- Tuwa, P.R.N.; Woafo, P. Suppression of the noise-induced effects in an electrostatic micro-plate using an adaptive back-stepping sliding mode control. ISA Trans. 2018, 72, 100–109. [Google Scholar] [CrossRef]
- Takougang, S.; Kingni, A.; Cheukem, P.R.; Nwagoum Tuwa, A.C.; Chamgoué, V.; Pham, T.; Jafari, S. Synchronous reluctance motor with load vibration perturbation: Analysis, electronic implementation and adaptive backstepping sliding mode control. Iran. J. Sci. Technol. Trans. Electr. Eng. 2021, 45, 645–654. [Google Scholar]
- Faraji, B.; Gheisarnejad, M.; Yalsavar, M.; Khooban, M.H. An adaptive ADRC control for parkinson’s patients using machine learning. IEEE Sens. J. 2020, 21, 8670–8678. [Google Scholar] [CrossRef]
- Liu, W.; Zhao, T. An active disturbance rejection control for hysteresis compensation based on Neural Networks adaptive control. ISA Trans. 2021, 109, 81–88. [Google Scholar] [CrossRef]
- Wu, D.; Ren, F.; Qiao, L.; Zhang, W. Active disturbance rejection controller design for dynamically positioned vessels based on adaptive hybrid biogeography-based optimization and differential evolution. ISA Trans. 2018, 78, 56–65. [Google Scholar] [CrossRef]
- Qiao, H.; Meng, H.; Ke, W.; Gao, Q.; Wang, S. Adaptive control of missile attitude based on BP–ADRC. Aircr. Eng. Aerosp. Technol. 2020, 92, 1475–1481. [Google Scholar] [CrossRef]
- Du, C.; Yin, Z.; Zhang, Y.; Liu, J.; Sun, X.; Zhong, Y. Research on active disturbance rejection control with parameter autotune mechanism for induction motors based on adaptive particle swarm optimization algorithm with dynamic inertia weight. IEEE Trans. Power Electron. 2018, 34, 2841–2855. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, Z.; Yan, M. An Optimization design of adaptive cruise control system based on MPC. and ADRC. Actuators 2021, 10, 110. [Google Scholar] [CrossRef]
- Nie, Z.; Zhang, B.; Wang, Q.; Liu, R.; Luo, J. Adaptive active disturbance rejection control guaranteeing uniformly ultimate boundedness and simplicity. Int. J. Robust Nonlinear Control. 2020, 30, 7278–7294. [Google Scholar] [CrossRef]
- Feliu, V.; Rattan, K.S.; Brown, H.B. Adaptive control of a single-link flexible manipulator. IEEE Control Syst. Mag. 1990, 10, 29–33. [Google Scholar] [CrossRef]
- Feliu, V.; Rattan, K.S.; Brown, H.B. Control of flexible arms with friction in the joints. IEEE Trans. Robot. Autom. 1993, 9, 467–475. [Google Scholar] [CrossRef]
- Rosas Almeida, D.I.; Alvarez, J.; Cantu Cardenas, J.A. Application of the active disturbance rejection control structure to improve the controller performance of uncertain pneumatic actuators. Asian J. Control. 2019, 21, 99–113. [Google Scholar] [CrossRef] [Green Version]
- Gandhi, R.V.; Adhyaru, D.M. Hybrid extended state observer based control for systems with matched and mismatched disturbances. ISA Trans. 2020, 106, 61–73. [Google Scholar] [CrossRef]
- Liu, A.; Li, T.; Gu, Y.; Dai, H. Cooperative extended state observer based control of vehicle platoons with arbitrarily small time headway. Automatica 2021, 129, 109678. [Google Scholar] [CrossRef]
- Guo, B.Z.; Zhao, Z.L. On the convergence of an extended state observer for nonlinear systems with uncertainty. Syst. Control Lett. 2011, 60, 420–430. [Google Scholar] [CrossRef]
- Fareh, R.; Al-Shabi, M.; Bettayeb, M.; Ghommam, J. Robust active disturbance rejection control for flexible link manipulator. Robotica 2020, 38, 118–135. [Google Scholar] [CrossRef]





| DC Motor Parameters | ||
| Motor inertia | 6.87 × 10−5 (kg m2) | |
| Viscous friction | 1.041 × 10−3 (N m s) | |
| Electromechanical constant | 0.21 ((N m)/V) | |
| Motor Coulomb friction torque | 119.7 × 10−3 (N m) | |
| Flexible Manipulator Parameters | ||
| Nominal mass | 0.05 (kg) | |
| Length | 0.7 (m) | |
| Flexural rigidity | 0.325 (N m2) | |
| Stiffness | 1.395 (N m) | |
| Nominal natural frequency | 7.546 (rad/s) |
| Control Parameters | ||
|---|---|---|
| Location closed loop poles (Inner loop) | 300 | |
| Controller bandwidth (Outer loop) | 5 (rad/s) | |
| Observer bandwidth (Outer loop) | 40 (rad/s) | |
| Nominal control gain (Outer loop) | 56.94 | |
| SM part Parameters | 5 | |
| 0.02 | ||
| Sample time | 0.001 |
| Tracking Error | PID | PID+DOB | ADRC | SM-ADRC |
|---|---|---|---|---|
| 338.7690 | 335.5991 | 385.8804 | 119.9095 | |
| 6.5293 | 3.4917 | 3.9336 | 1.4116 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Liu, P.; Jing, F.; Liu, B.; Peng, W.; Guo, M.; Xie, M. Sliding Mode Robust Active Disturbance Rejection Control for Single-Link Flexible Arm with Large Payload Variations. Electronics 2021, 10, 2995. https://doi.org/10.3390/electronics10232995
Wang F, Liu P, Jing F, Liu B, Peng W, Guo M, Xie M. Sliding Mode Robust Active Disturbance Rejection Control for Single-Link Flexible Arm with Large Payload Variations. Electronics. 2021; 10(23):2995. https://doi.org/10.3390/electronics10232995
Chicago/Turabian StyleWang, Fan, Peng Liu, Feng Jing, Bo Liu, Wei Peng, Min Guo, and Meilin Xie. 2021. "Sliding Mode Robust Active Disturbance Rejection Control for Single-Link Flexible Arm with Large Payload Variations" Electronics 10, no. 23: 2995. https://doi.org/10.3390/electronics10232995
APA StyleWang, F., Liu, P., Jing, F., Liu, B., Peng, W., Guo, M., & Xie, M. (2021). Sliding Mode Robust Active Disturbance Rejection Control for Single-Link Flexible Arm with Large Payload Variations. Electronics, 10(23), 2995. https://doi.org/10.3390/electronics10232995






