Explainable Convolutional Neural Network to Investigate Age-Related Changes in Multi-Order Functional Connectivity
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Apparatus
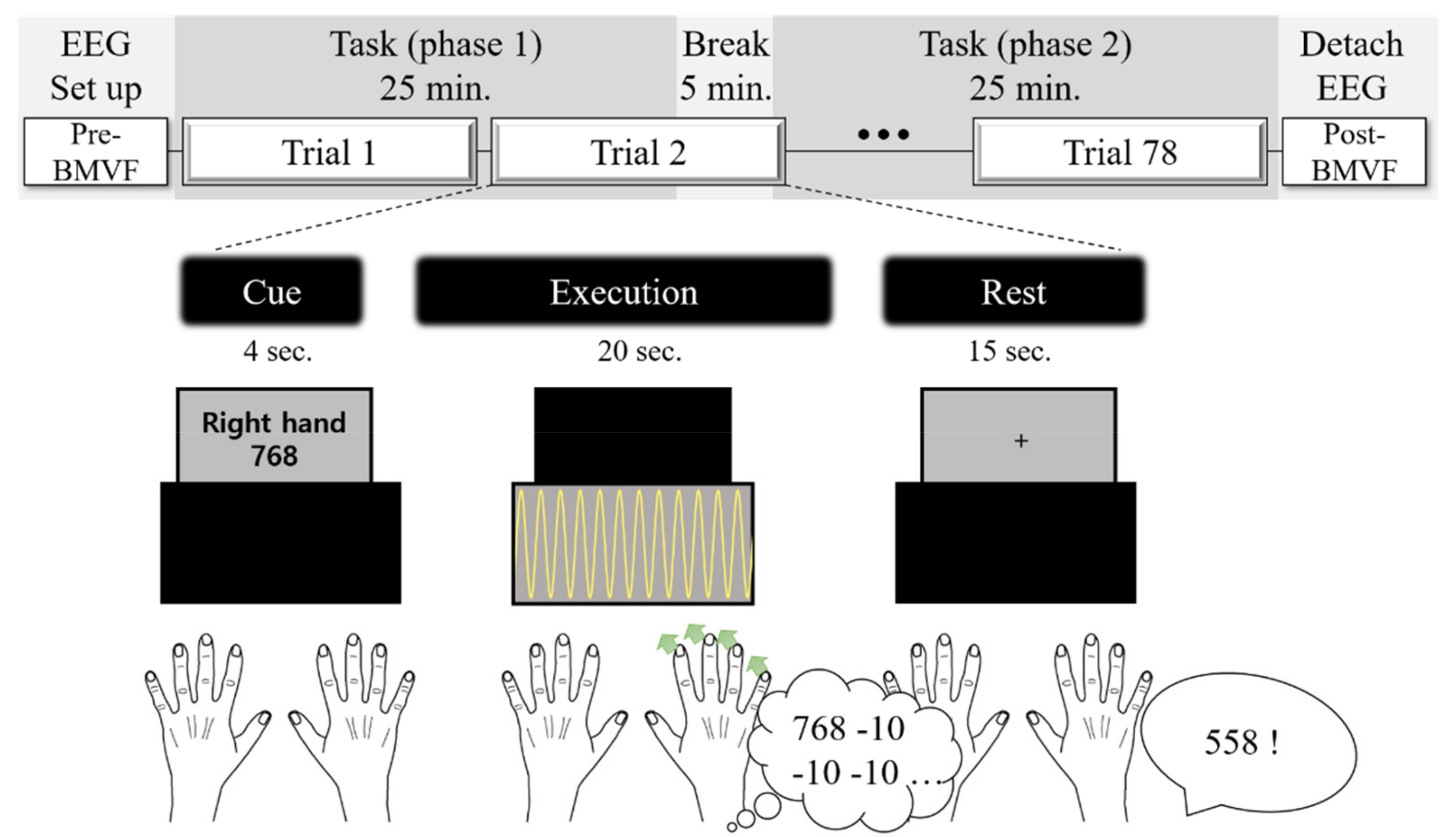
2.3. Experimental Paradigm
2.4. Preprocessing
2.5. Estimation of Low- and High-Order Functional Connectivity Values
2.6. Explainable CNN
2.7. Filter Bank Common Spatial Pattern
2.8. Analysis of LRP-Derived Relevance Value by Brain Hemispheres and Regions
3. Results
3.1. Behavior Results
3.2. Classification Accuracy: CNN Results
3.3. Relationship between Classification Accuracies and Behavior Performances
3.4. LRP Results
3.5. Comparison of LRP-Derived Relevance in Intra- and Inter-Hemispheric FC between Age Groups
3.6. Comparison of LRP-Derived Relevance in Intra- and Inter-Regional FCs between Age Groups
4. Discussion
4.1. Higher Classification Accuracy in the Elderly Group Than in the Young Adult Group
4.2. Age-Related Compensatory Overactivation in the Prefrontal Cortex
4.3. Age-Related Increase in Functional Connectivity within Hemispheres Rather Than across Hemispheres
4.4. Compensatory Overactivity in Higher-Order FC
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Doniec, R.J.; Sieciński, S.; Duraj, K.M.; Piaseczna, N.J.; Mocny-Pachońska, K.; Tkacz, E.J. Recognition of Drivers’ Activity Based on 1D Convolutional Neural Network. Electronics 2020, 9, 2002. [Google Scholar] [CrossRef]
- Lee, T.-S.; Goh, S.J.A.; Quek, S.Y.; Phillips, R.; Guan, C.; Cheung, Y.B.; Feng, L.; Teng, S.S.W.; Wang, C.C.; Chin, Z.Y. A brain-computer interface based cognitive training system for healthy elderly: A randomized control pilot study for usability and preliminary efficacy. PLoS ONE 2013, 8, e79419. [Google Scholar] [CrossRef] [Green Version]
- Smith, G.E.; Housen, P.; Yaffe, K.; Ruff, R.; Kennison, R.F.; Mahncke, H.W.; Zelinski, E.M. A Cognitive Training Program Based on Principles of Brain Plasticity: Results from the Improvement in Memory with Plasticity-based Adaptive Cognitive Training (IMPACT) Study. J. Am. Geriatr. Soc. 2009, 57, 594–603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schal, G.K.; McFarland, D.J.; Hinterberger, T.; Birbaumer, N.; Wolpaw, J.R. BCI2000: A general-purpose brain-computer interface (BCI) system. IEEE Trans. Biomed. Eng. 2004, 51, 1034–1043. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Xu, D.; Cheng, M.; Gao, S. A BCI-based environmental controller for the motion-disabled. IEEE Trans. Neural Syst. Rehabil. Eng. 2003, 11, 137–140. [Google Scholar] [CrossRef]
- Bak, S.; Park, J.; Shin, J.; Jeong, J. Open-Access fNIRS Dataset for Classification of Unilateral Finger-and Foot-Tapping. Electronics 2019, 8, 1486. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.J.; Hong, M.J.; Ehong, K.-S. Decoding of four movement directions using hybrid NIRS-EEG brain-computer interface. Front. Hum. Neurosci. 2014, 8, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.J.; Ghafoor, U.; Hong, K.-S. Early detection of hemodynamic responses using EEG: A hybrid EEG-fNIRS study. Front. Human Neurosci. 2018, 12, 479. [Google Scholar] [CrossRef]
- Hong, K.-S.; Khan, M.J. Hybrid brain–computer interface techniques for improved classification accuracy and increased number of commands: A review. Front. Neurorobotics 2017, 11, 35. [Google Scholar] [CrossRef] [Green Version]
- Park, S.-M.; Yeom, H.-G.; Sim, K.-B. User State Classification Based on Functional Brain Connectivity Using a Convolutional Neural Network. Electronics 2021, 10, 1158. [Google Scholar] [CrossRef]
- Saeed, U.; Shah, S.Y.; Shah, S.A.; Ahmad, J.; Alotaibi, A.A.; Althobaiti, T.; Ramzan, N.; Alomainy, A.; Abbasi, Q.H. Discrete Human Activity Recognition and Fall Detection by Combining FMCW RADAR Data of Heterogeneous Environments for Independent Assistive Living. Electronics 2021, 10, 2237. [Google Scholar] [CrossRef]
- Herweg, A.; Gutzeit, J.; Kleih, S.; Kübler, A. Wheelchair control by elderly participants in a virtual environment with a brain-computer interface (BCI) and tactile stimulation. Biol. Psychol. 2016, 121, 117–124. [Google Scholar] [CrossRef]
- Calero-García, M.D.; Navarro-González, E. Effectiveness of a memory training programme in the maintenance of status in elderly people with and without cognitive decline. Clin. Y Salud 2006, 17, 187–202. [Google Scholar]
- Yu, H.; Sunderraj, C.M.A.A.; Chang, C.K.; Wong, J. Emotion Aware System for the Elderly; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Volosyak, I.; Gembler, F.; Stawicki, P. Age-related differences in SSVEP-based BCI performance. Neurocomputing 2017, 250, 57–64. [Google Scholar] [CrossRef]
- Park, D.C. The basic mechanisms accounting for age-related decline in cognitive function. In Cognitive Aging: A Primer; Psychology Press: New York, NY, USA, 2000; pp. 3–19. [Google Scholar]
- Salthouse, T.A. The processing-speed theory of adult age differences in cognition. Psychol. Rev. 1996, 103, 403–428. [Google Scholar] [CrossRef] [Green Version]
- Hasher, L.; Zacks, R.T. Working memory, comprehension, and aging: A review and a new view. In Psychology of Learning and Motivation; Academic Press: Cambridge, MA, USA, 1998; pp. 193–225. [Google Scholar] [CrossRef]
- Raz, N. Aging of the brain and its impact on cognitive performance: Integration of structural and functional findings. In The Handbook of Aging and Cognition; Lawrence Erlbaum Associates Publishers: Mahwah, NJ, USA, 2000; pp. 1–90. [Google Scholar]
- Kemper, T.L. Neuroanatomical and neuropathological changes during aging and dementia. In The Handbook of Aging and Cognition; Lawrence Erlbaum Associates Publishers: Mahwah, NJ, USA, 1994; pp. 1–9. [Google Scholar]
- Logan, J.M.; Sanders, A.L.; Snyder, A.Z.; Morris, J.C.; Buckner, R.L. Under-Recruitment and Nonselective Recruitment: Dissociable neural mechanisms associated with aging. Neuron 2002, 33, 827–840. [Google Scholar] [CrossRef] [Green Version]
- Cabeza, R. Hemispheric asymmetry reduction in older adults: The HAROLD model. Psychol. Aging 2002, 17, 85–100. [Google Scholar] [CrossRef]
- Chen, M.L.; Fu, D.; Boger, J.; Jiang, N. Age-Related Changes in Vibro-Tactile EEG Response and Its Implications in BCI Applications: A Comparison Between Older and Younger Populations. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 603–610. [Google Scholar] [CrossRef]
- Reuter-Lorenz, P.A.; Cappell, K.A. Neurocognitive Aging and the Compensation Hypothesis. Curr. Dir. Psychol. Sci. 2008, 17, 177–182. [Google Scholar] [CrossRef]
- Reuter-Lorenz, P.A.; Stanczak, L.; Miller, A.C. Neural Recruitment and Cognitive Aging: Two Hemispheres Are Better Than One, Especially as You Age. Psychol. Sci. 1999, 10, 494–500. [Google Scholar] [CrossRef]
- Grady, C.L.; Maisog, J.M.; Horwitz, B.; Ungerleider, L.G.; Mentis, M.J.; Salerno, J.A.; Pietrini, P.; Wagner, E.; Haxby, J.V. Age-related changes in cortical blood flow activation during visual processing of faces and location. J. Neurosci. 1994, 14, 1450–1462. [Google Scholar] [CrossRef] [Green Version]
- Cappell, K.A.; Gmeindl, L.; Reuter-Lorenz, P.A. Age differences in prefontal recruitment during verbal working memory maintenance depend on memory load. Cortex 2010, 46, 462–473. [Google Scholar] [CrossRef] [Green Version]
- McIntosh, A.R.; Sekuler, A.B.; Penpeci, C.; Rajah, M.N.; Grady, C.L.; Sekuler, R.; Bennett, P.J. Recruitment of unique neural systems to support visual memory in normal aging. Curr. Biol. 1999, 9, 1275-S2. [Google Scholar] [CrossRef] [Green Version]
- Persson, J.; Nyberg, L.; Lind, J.; Larsson, A.; Nilsson, L.-G.; Ingvar, M.; Buckner, R.L. Structure–Function Correlates of Cognitive Decline in Aging. Cereb. Cortex 2005, 16, 907–915. [Google Scholar] [CrossRef]
- Cabeza, R.; Kingstone, A. Functional neuroimaging of cognitive aging. In Handbook of Functional Neuroimaging of Cognition; Cabeza, R., Kingstone, A., Eds.; Mit Press: Cambridge, MA, USA, 2006; pp. 379–419. [Google Scholar]
- Reuter-Lorenz, P.A. New visions of the aging mind and brain. Trends Cogn. Sci. 2002, 6, 394–400. [Google Scholar] [CrossRef]
- Velanova, K.; Lustig, C.; Jacoby, L.L.; Buckner, R.L. Evidence for Frontally Mediated Controlled Processing Differences in Older Adults. Cereb. Cortex 2006, 17, 1033–1046. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lu, Q.; Bi, K.; Liu, C.; Luo, G.; Tang, H.; Yao, Z. Predicting depression based on dynamic regional connectivity: A windowed Granger causality analysis of MEG recordings. Brain Res. 2013, 1535, 52–60. [Google Scholar] [CrossRef] [PubMed]
- Daly, I.; Nasuto, S.; Warwick, K. Brain computer interface control via functional connectivity dynamics. Pattern Recognit. 2012, 45, 2123–2136. [Google Scholar] [CrossRef]
- Tiwari, A.; Falk, T.H. Fusion of Motif-and spectrum-related features for improved EEG-based emotion recognition. Comput. Intell. Neurosci. 2019, 2019, 3076324. [Google Scholar] [CrossRef]
- Gupta, R.; Falk, T.H. Relevance vector classifier decision fusion and EEG graph-theoretic features for automatic affective state characterization. Neurocomputing 2016, 174, 875–884. [Google Scholar] [CrossRef]
- Sengupta, A.; Tiwari, A.; Chaudhuri, A.; Routray, A. Analysis of loss of alertness due to cognitive fatigue using motif synchronization of eeg records. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 1652–1655. [Google Scholar]
- Chu, C.; Hsu, A.-L.; Chou, K.-H.; Bandettini, P.; Lin, C.; Alzheimer’s Disease Neuroimaging Initiative. Does feature selection improve classification accuracy? Impact of sample size and feature selection on classification using anatomical magnetic resonance images. Neuroimage 2012, 60, 59–70. [Google Scholar] [CrossRef]
- Sun, X.; Qian, C.; Chen, Z.; Wu, Z.; Luo, B.; Pan, G. Remembered or Forgotten?—An EEG-Based Computational Prediction Approach. PLoS ONE 2016, 11, e0167497. [Google Scholar] [CrossRef] [Green Version]
- Schirrmeister, R.T.; Springenberg, J.T.; Fiederer, L.D.J.; Glasstetter, M.; Eggensperger, K.; Tangermann, M.; Hutter, F.; Burgard, W.; Ball, T. Deep learning with convolutional neural networks for EEG decoding and visualization. Human Brain Mapp. 2017, 38, 5391–5420. [Google Scholar] [CrossRef] [Green Version]
- Lawhern, V.J.; Solon, A.J.; Waytowich, N.R.; Gordon, S.M.; Hung, C.P.; Lance, B.J. EEGNet: A compact convolutional neural network for EEG-based brain–computer interfaces. J. Neural Eng. 2018, 15, 056013. [Google Scholar] [CrossRef] [Green Version]
- Sakhavi, S.; Guan, C.; Yan, S. Learning temporal information for brain-computer interface using convolutional neural networks . IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5619–5629. [Google Scholar] [CrossRef]
- Han, C.; Jo, S.A.; Jo, I.; Kim, E.; Park, M.H.; Kang, Y. An adaptation of the Korean mini-mental state examination (K-MMSE) in elderly Koreans: Demographic influence and population-based norms (the AGE study). Arch. Gerontol. Geriatr. 2008, 47, 302–310. [Google Scholar] [CrossRef]
- Salvo, P.; Raedt, R.; Carrette, E.; Schaubroeck, D.; Vanfleteren, J.; Cardon, L. A 3D printed dry electrode for ECG/EEG recording. Sens. Actuators A-Phys. 2012, 174, 96–102. [Google Scholar] [CrossRef]
- Van Diessen, E.; Numan, T.; van Dellen, E.; van der Kooi, A.; Boersma, M.; Hofman, D.; van Lutterveld, R.; van Dijk, B.; van Straaten, E.; Hillebrand, A. Opportunities and methodological challenges in EEG and MEG resting state functional brain network research. Clin. Neurophysiol. 2015, 126, 1468–1481. [Google Scholar] [CrossRef]
- Sakkalis, V. Review of advanced techniques for the estimation of brain connectivity measured with EEG/MEG. Comput. Biol. Med. 2011, 41, 1110–1117. [Google Scholar] [CrossRef]
- Zhou, Y.; Qiao, L.; Li, W.; Zhang, L.; Shen, D. Simultaneous Estimation of Low- and High-Order Functional Connectivity for Identifying Mild Cognitive Impairment. Front. Neuroinf. 2018, 12, 3. [Google Scholar] [CrossRef] [Green Version]
- Gupta, A.K.; Nagar, D.K. Matrix Variate Distributions; Chapman & Hall: Boca Raton, UK, 2000. [Google Scholar]
- Dutilleul, P. The MLE algorithm for the matrix normal distribution. J. Stat. Comput. Simul. 1999, 64, 105–123. [Google Scholar] [CrossRef]
- Zhang, Y.; Schneider, J.G. Learning multiple tasks with a sparse matrix-normal penalty. Proc. NIPS 2010, 6, 2550–2558. [Google Scholar]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. Proc. CVPR 2017, 1, 1251–1258. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, B. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Bach, S.; Binder, A.; Montavon, G.; Klauschen, F.; Müller, K.-R.; Samek, W. On Pixel-Wise Explanations for Non-Linear Classifier Decisions by Layer-Wise Relevance Propagation. PLoS ONE 2015, 10, e0130140. [Google Scholar] [CrossRef] [Green Version]
- Tangermann, M.; Müller, K.-R.; Aertsen, A.; Birbaumer, N.; Braun, C.; Brunner, C.; Leeb, R.; Mehring, C.; Miller, K.J.; Müller-Putz, G. Review of the BCI Competition IV. Front. Neurosci. 2012, 6, 1–31. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ramoser, H.; Muller-Gerking, J.; Pfurtscheller, G. Optimal spatial filtering of single trial EEG during imagined hand movement. IEEE Trans. Rehabil. Eng. 2000, 8, 441–446. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yong, X.; Menon, C. EEG Classification of Different Imaginary Movements within the Same Limb. PLoS ONE 2015, 10, e0121896. [Google Scholar] [CrossRef] [PubMed]
- Diestel, R. Extremal Graph Theory. In Graph Theory. Graduate Texts in Mathematics; Springer: Berlin/Heidelberg, Germany, 2005; Volume 173. [Google Scholar] [CrossRef]
- Cohen, J. A Coefficient of Agreement for Nominal Scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Landis, J.R.; Koch, G.G. The Measurement of Observer Agreement for Categorical Data. Biometrics 1977, 33, 159–174. [Google Scholar] [CrossRef] [Green Version]
- Rychwalska, A. Understanding cognition through functional connectivity. In Complex Human Dynamics; Springer: Berlin/Heidelberg, Germany, 2013; pp. 21–34. [Google Scholar] [CrossRef]
- Hong, K.-S.; Khan, M.J.; Hong, M.J. Feature extraction and classification methods for hybrid fNIRS-EEG brain-computer interfaces. Front. Hum. Neurosci. 2018, 12, 246. [Google Scholar] [CrossRef]
- Yang, D.; Hong, K.-S.; Yoo, S.-H.; Kim, C.-S. Evaluation of Neural Degeneration Biomarkers in the Prefrontal Cortex for Early Identification of Patients With Mild Cognitive Impairment: An fNIRS Study. Front. Hum. Neurosci. 2019, 13, 317. [Google Scholar] [CrossRef] [Green Version]
- Naseer, N.; Qureshi, N.K.; Noori, F.M.; Hong, K.-S. Analysis of Different Classification Techniques for Two-Class Functional Near-Infrared Spectroscopy-Based Brain-Computer Interface. Comput. Intell. Neurosci. 2016, 2016, 5480760. [Google Scholar] [CrossRef] [Green Version]
- Tang, Z.; Li, C.; Sun, S. Single-trial EEG classification of motor imagery using deep convolutional neural networks. Opt. Int. J. Light Electron Opt. 2017, 130, 11–18. [Google Scholar] [CrossRef]
- Reuter-Lorenz, P.A.; Jonides, J.; Smith, E.E.; Hartley, A.; Miller, A.; Marshuetz, C.; Koeppe, R.A. Age Differences in the Frontal Lateralization of Verbal and Spatial Working Memory Revealed by PET. J. Cogn. Neurosci. 2000, 12, 174–187. [Google Scholar] [CrossRef]
- Cabeza, R.; Daselaar, S.M.; Dolcos, F.; Prince, S.; Budde, M.; Nyberg, L. Task-independent and Task-specific Age Effects on Brain Activity during Working Memory, Visual Attention and Episodic Retrieval. Cereb. Cortex 2004, 14, 364–375. [Google Scholar] [CrossRef]
- Mather, M.; Carstensen, L.L. Aging and motivated cognition: The positivity effect in attention and memory. Trends Cogn. Sci. 2005, 9, 496–502. [Google Scholar] [CrossRef]
- Deiber, M.-P.; Passingham, R.E.; Colebatch, J.; Friston, K.; Nixon, P.D.; Frackowiak, R. Cortical areas and the selection of movement: A study with positron emission tomography. Exp. Brain Res. 1991, 84, 393–402. [Google Scholar] [CrossRef]
- Goble, D.J.; Coxon, J.P.; Van Impe, A.; De Vos, J.; Wenderoth, N.; Swinnen, S.P. The neural control of bimanual movements in the elderly: Brain regions exhibiting age-related increases in activity, frequency-induced neural modulation, and task-specific compensatory recruitment. Hum. Brain Mapp. 2010, 31, 1281–1295. [Google Scholar] [CrossRef]
- Weissman, D.H.; Banich, M.T. The cerebral hemispheres cooperate to perform complex but not simple tasks. Neuropsychology 2000, 14, 41–59. [Google Scholar] [CrossRef]
- Cabeza, R.; Grady, C.L.; Nyberg, L.; McIntosh, A.; Tulving, E.; Kapur, S.; Jennings, J.M.; Houle, S.; Craik, F. Age-Related Differences in Neural Activity during Memory Encoding and Retrieval: A Positron Emission Tomography Study. J. Neurosci. 1997, 17, 391–400. [Google Scholar] [CrossRef] [Green Version]
- Ray, W.J.; Cole, H.W. EEG Alpha Activity Reflects Attentional Demands, and Beta Activity Reflects Emotional and Cognitive Processes. Science 1985, 228, 750–752. [Google Scholar] [CrossRef]
- Wang, L.; Wang, W.; Yan, T.; Song, J.; Yang, W.; Wang, B.; Go, R.; Huang, Q.; Wu, J. Beta-Band Functional Connectivity Influences Audiovisual Integration in Older Age: An EEG Study. Front. Aging Neurosci. 2017, 9, 239. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, H.; Chen, X.; Lee, S.-W.; Shen, D. Hybrid High-order Functional Connectivity Networks Using Resting-state Functional MRI for Mild Cognitive Impairment Diagnosis. Sci. Rep. 2017, 7, 6530. [Google Scholar] [CrossRef] [Green Version]







| Calculation Speed (Subtraction per Trial) | |||||
|---|---|---|---|---|---|
| Age | Task | Value | Average | Value | Average |
| Young | 0.18 ± 0.02 | - | - | ||
| 0.20 ± 0.02 | 0.19 ± 0.02 | ||||
| 0.20 ± 0.01 | |||||
| 0.19 ± 0.02 | 20.0 ± 1.24 | ||||
| 0.20 ± 0.02 | 0.21 ± 0.02 | 18.5 ± 1.13 | 19.4 ± 1.15 | ||
| 0.23 ± 0.02 | 19.8 ± 0.98 | ||||
| Old | 0.57 ± 0.07 | ||||
| 0.55 ± 0.07 | 0.57 ± 0.08 | ||||
| 0.60 ± 0.11 | |||||
| 0.59 ± 0.09 | 16.8 ± 1.28 | ||||
| 0.57 ± 0.09 | 0.60 ± 0.08 | 15.4 ± 1.31 | 15.9 ± 1.30 | ||
| 0.63 ± 0.08 | 16.6 ± 1.33 | ||||
| LoFC | Single Both | Single Right | Single Left | Dual Both | Dual Right | Dual Left | |
|---|---|---|---|---|---|---|---|
| PF | 3 | 2 | 2 | 2 | 0 | 0 | |
| F | 2 | 1 | 1 | 3 | 0 | 0 | |
| C | 1 | 0 | 0 | 2 | 0 | 0 | |
| P | 2 | 2 | 0 | 1 | 0 | 0 | |
| LT | 2 | 1 | 1 | 1 | 0 | 0 | |
| RT | 0 | 0 | 0 | 1 | 0 | 0 | |
| O | 0 | 0 | 0 | 1 | 0 | 0 | |
| 1.43 | 0.86 | 0.57 | 1.57 | 0 | 0 | ||
| HiFC | Single Both | Single Right | Single Left | Dual Both | Dual Right | Dual Left | |
| PF | 5 | 3 | 4 | 2 | 0 | 0 | |
| F | 3 | 1 | 2 | 2 | 0 | 0 | |
| C | 2 | 1 | 3 | 1 | 0 | 0 | |
| P | 3 | 0 | 4 | 1 | 0 | 1 | |
| LT | 2 | 0 | 1 | 4 | 0 | 0 | |
| RT | 0 | 0 | 1 | 0 | 0 | 0 | |
| O | 2 | 1 | 3 | 0 | 0 | 0 | |
| 2.43 | 0.86 | 2.57 | 1.43 | 0 | 0.29 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, S.; Jin, Y.; Bak, S.; Yoon, B.; Jeong, J. Explainable Convolutional Neural Network to Investigate Age-Related Changes in Multi-Order Functional Connectivity. Electronics 2021, 10, 3020. https://doi.org/10.3390/electronics10233020
Dong S, Jin Y, Bak S, Yoon B, Jeong J. Explainable Convolutional Neural Network to Investigate Age-Related Changes in Multi-Order Functional Connectivity. Electronics. 2021; 10(23):3020. https://doi.org/10.3390/electronics10233020
Chicago/Turabian StyleDong, Sunghee, Yan Jin, SuJin Bak, Bumchul Yoon, and Jichai Jeong. 2021. "Explainable Convolutional Neural Network to Investigate Age-Related Changes in Multi-Order Functional Connectivity" Electronics 10, no. 23: 3020. https://doi.org/10.3390/electronics10233020
APA StyleDong, S., Jin, Y., Bak, S., Yoon, B., & Jeong, J. (2021). Explainable Convolutional Neural Network to Investigate Age-Related Changes in Multi-Order Functional Connectivity. Electronics, 10(23), 3020. https://doi.org/10.3390/electronics10233020







