Novel Step-Up Topologies of Zigzag Autotransformer
Abstract
:1. Introduction
2. Three Step-Up Topologies of Zigzag Autotransformer
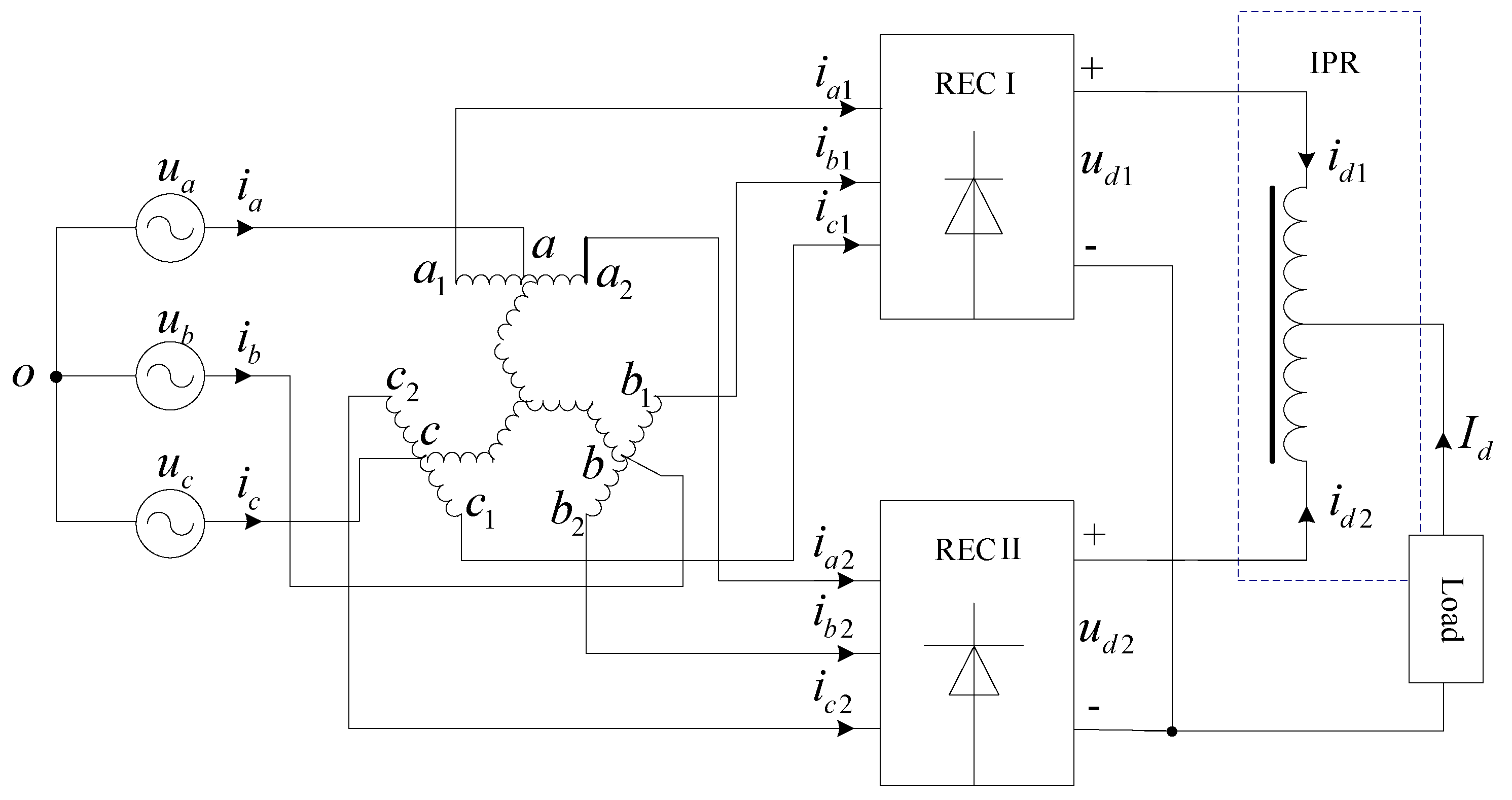
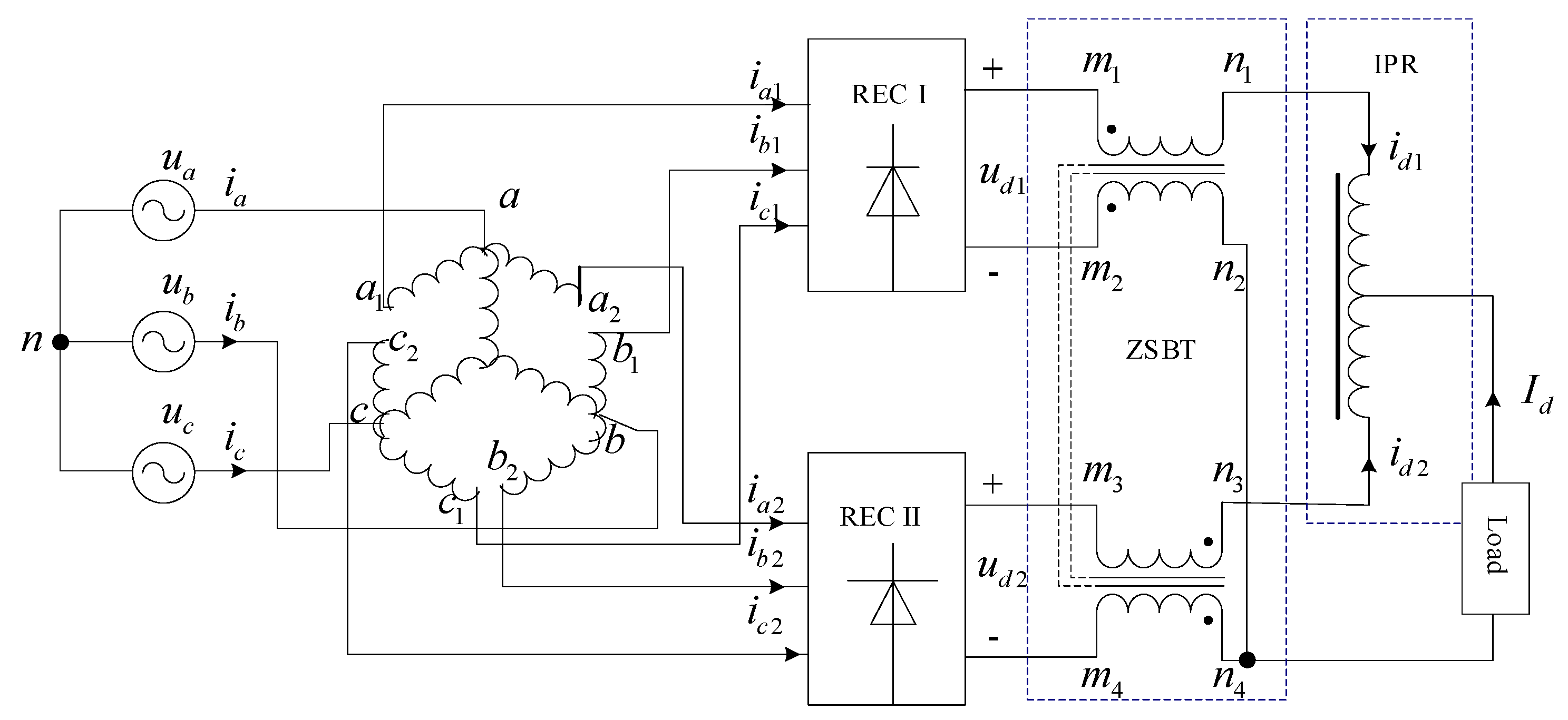
2.1. 12-Pulse Rectifier System
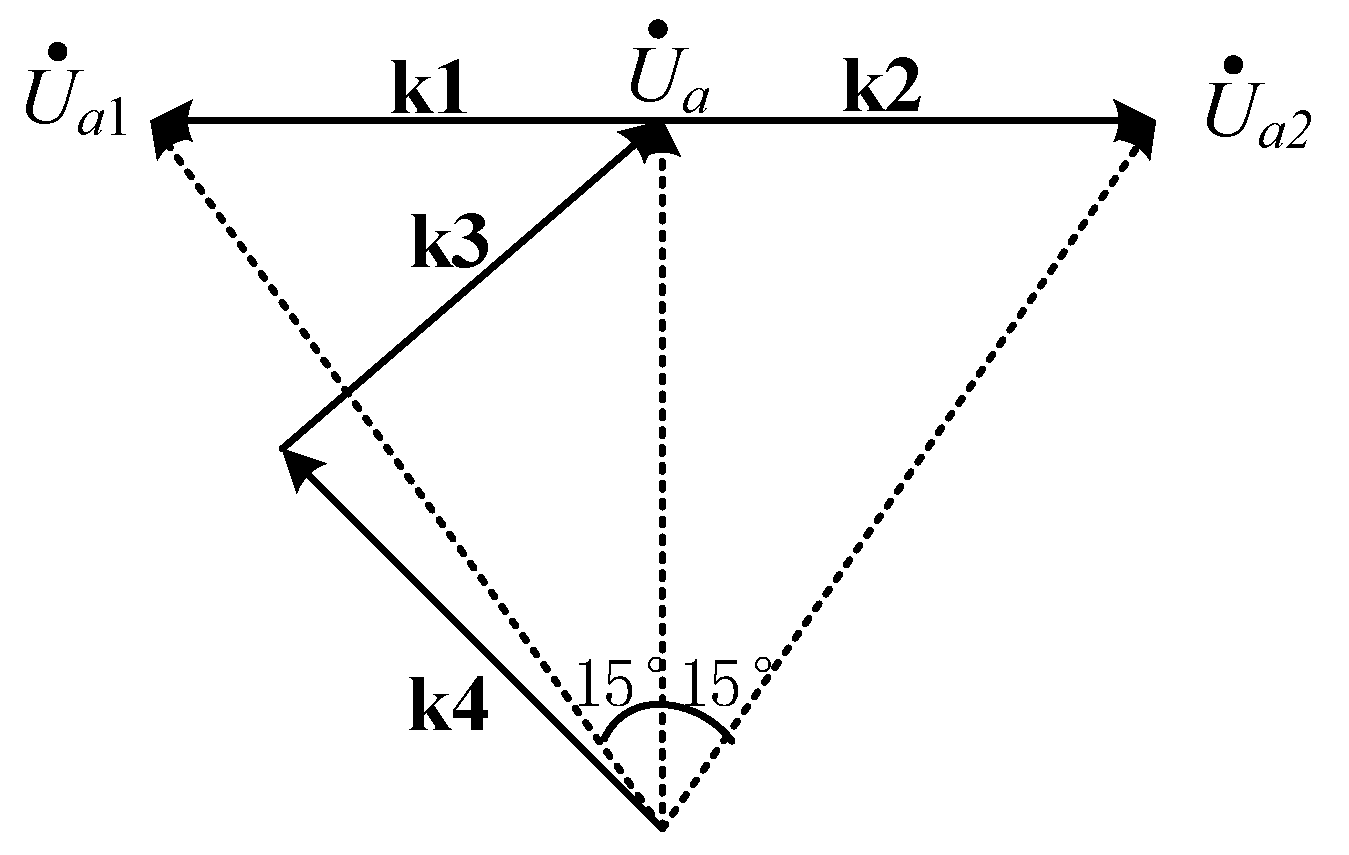
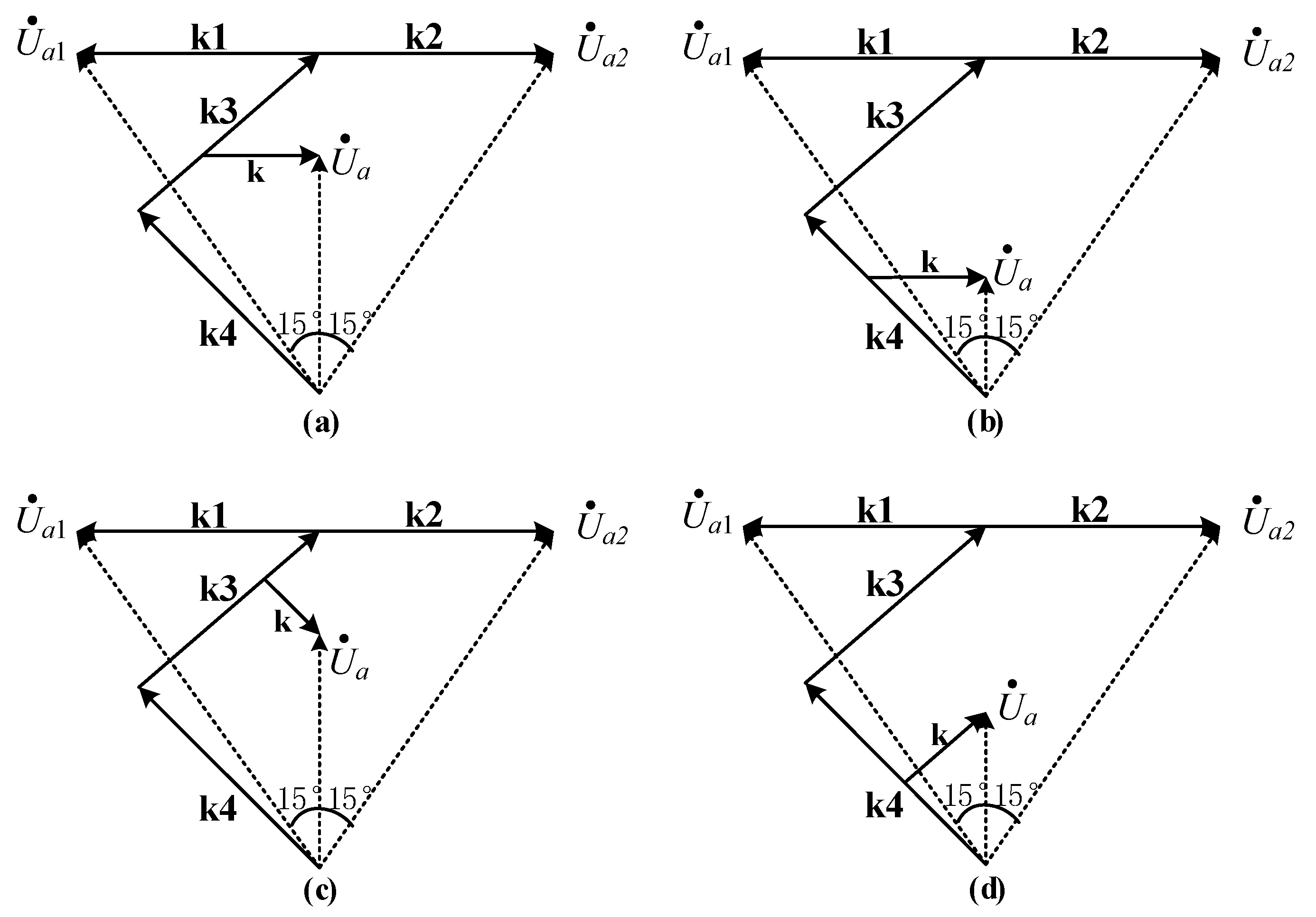
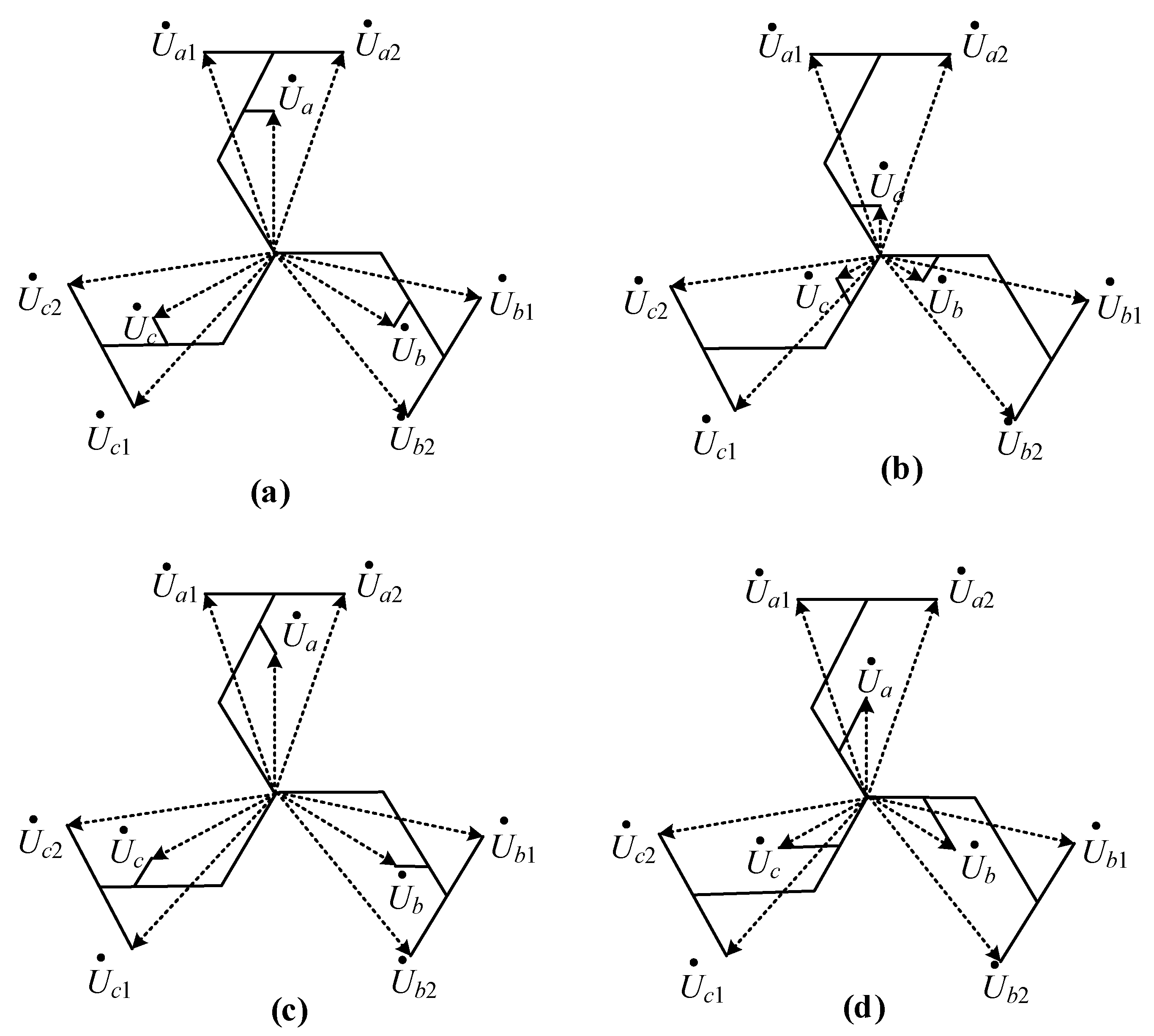
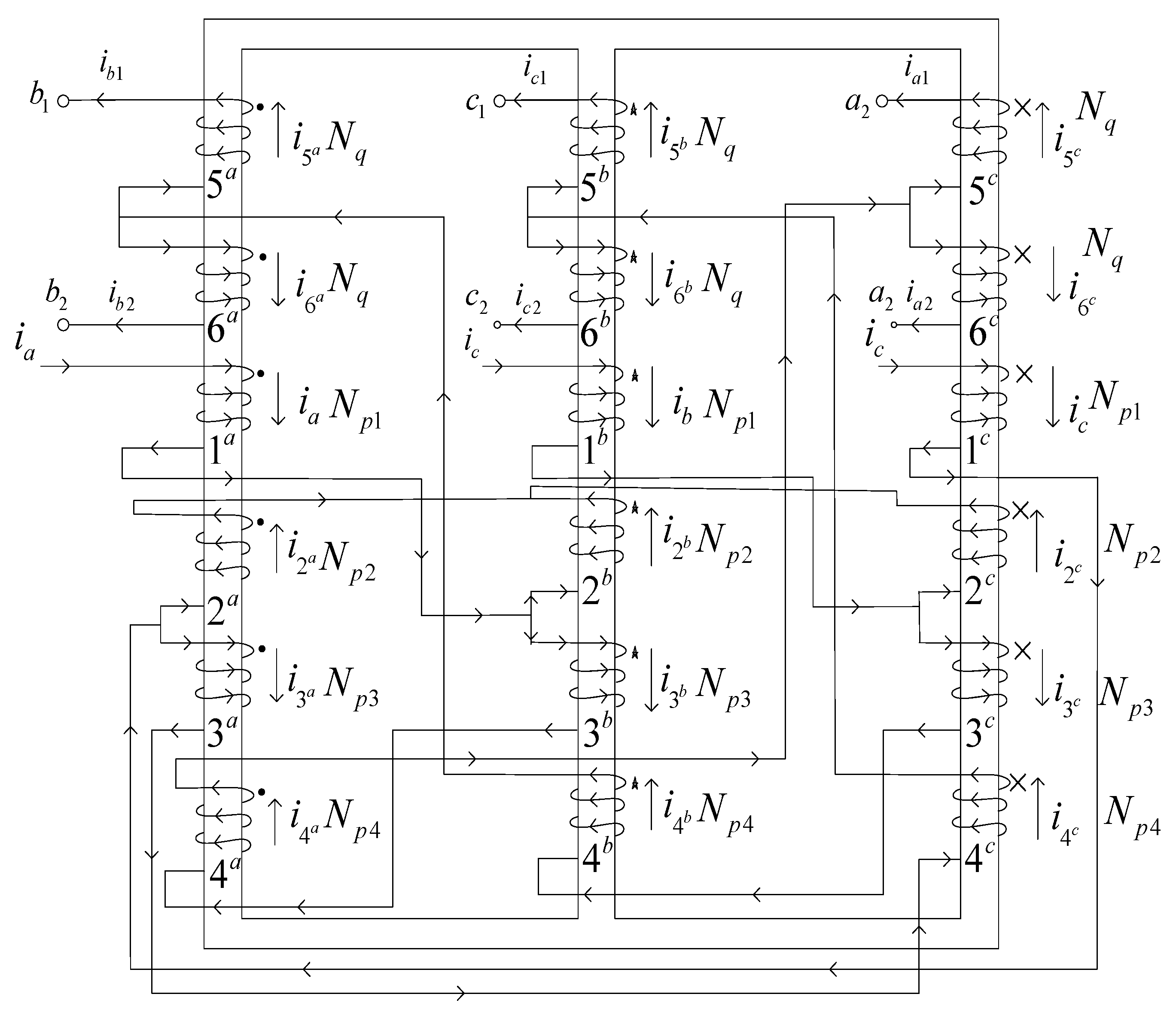
2.2. Step-Up Topology Design of Zigzag Autotransformer
3. Equivalent Capacity of Autotransformer
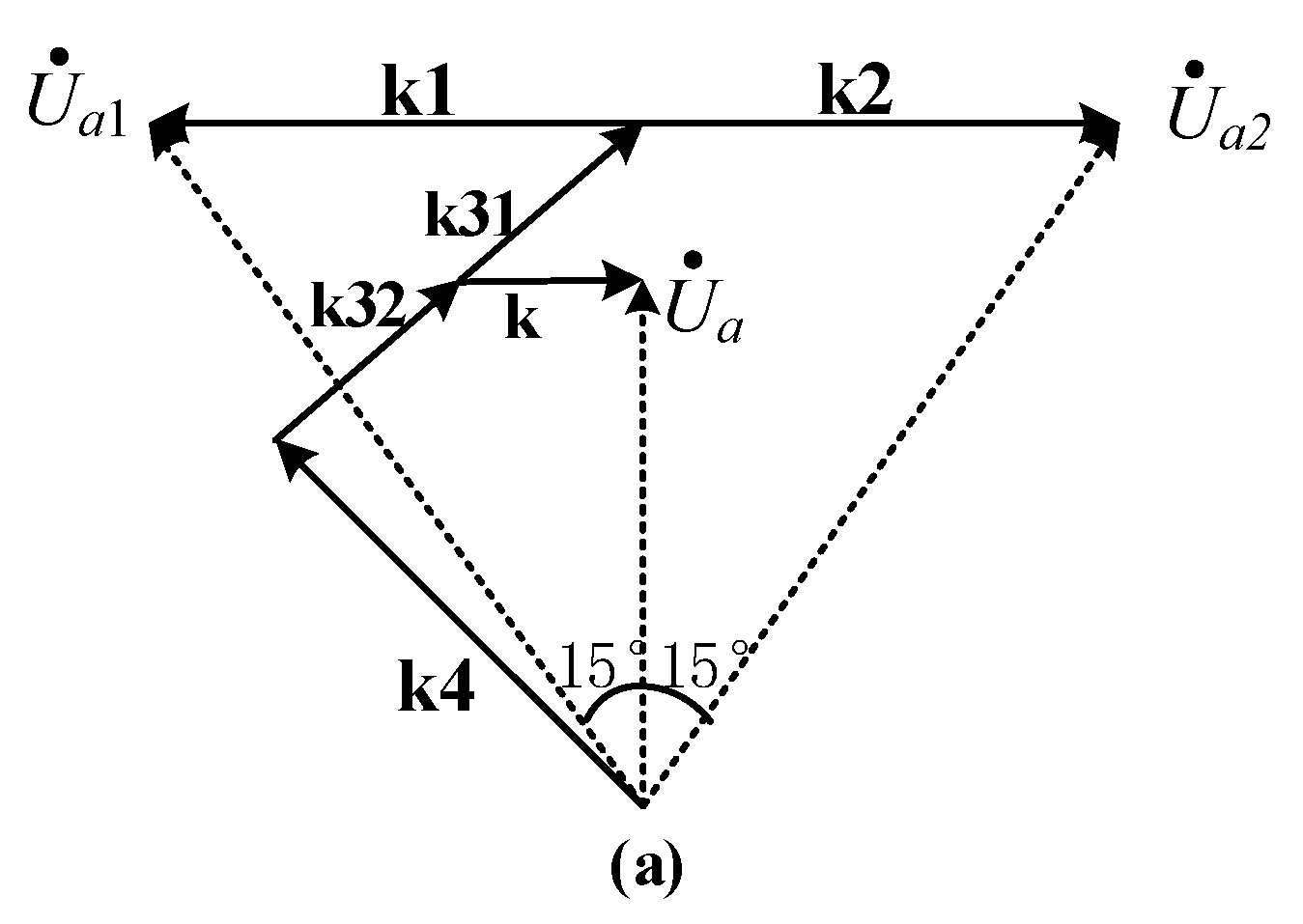
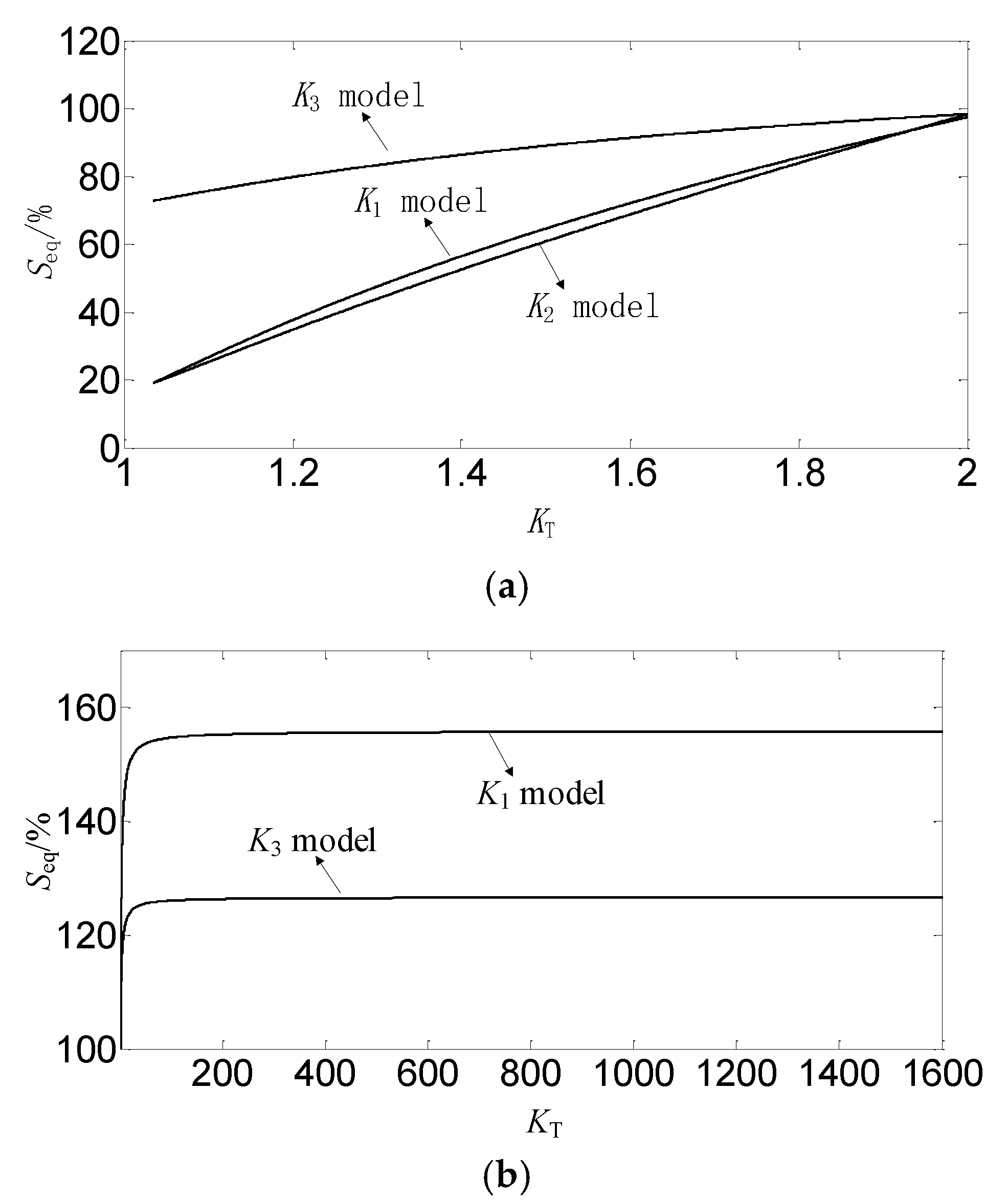
3.1. K1 Topology
3.2. K2 and K3 Topologies
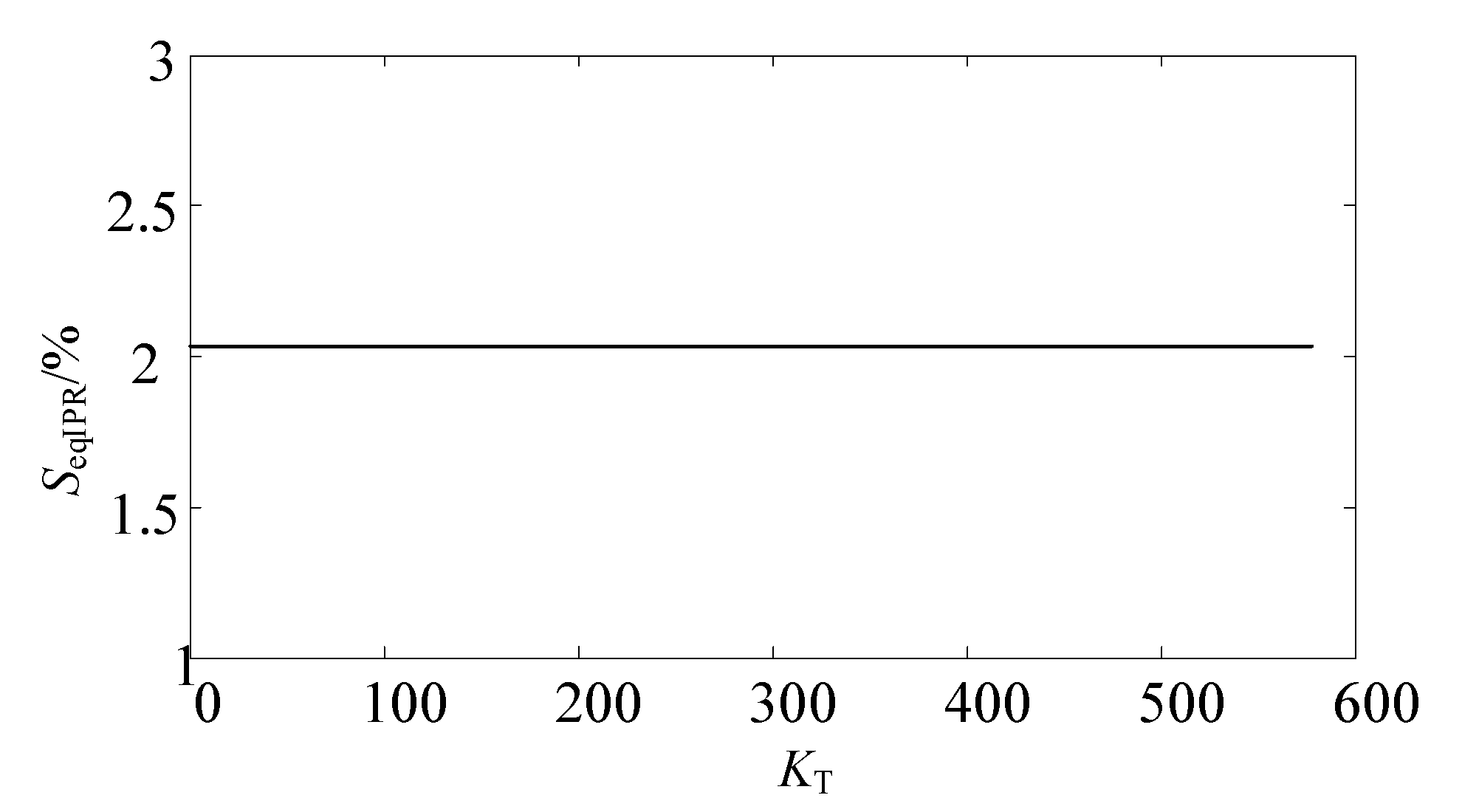
4. Equivalent Capacity of Balance Reactor
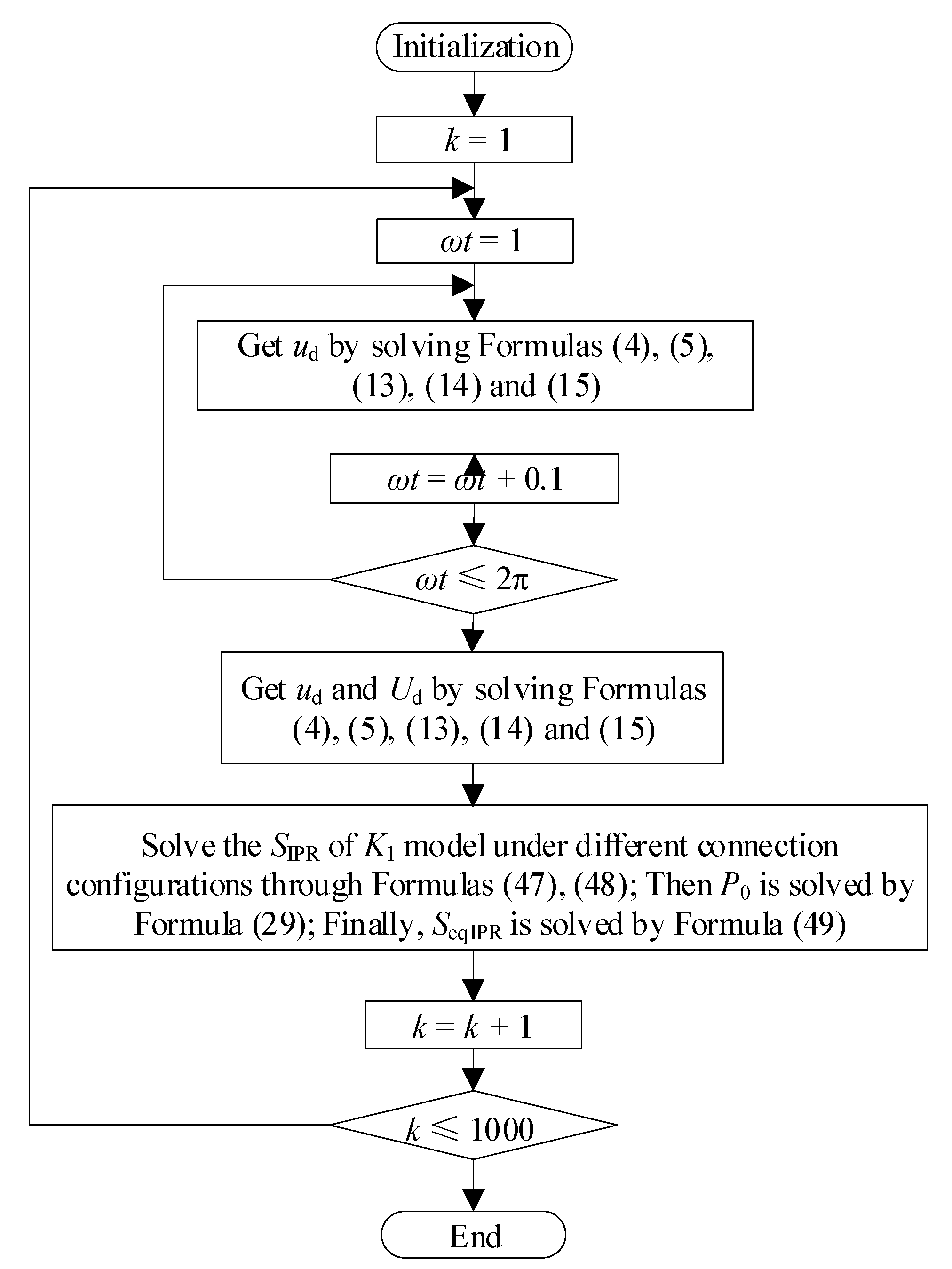
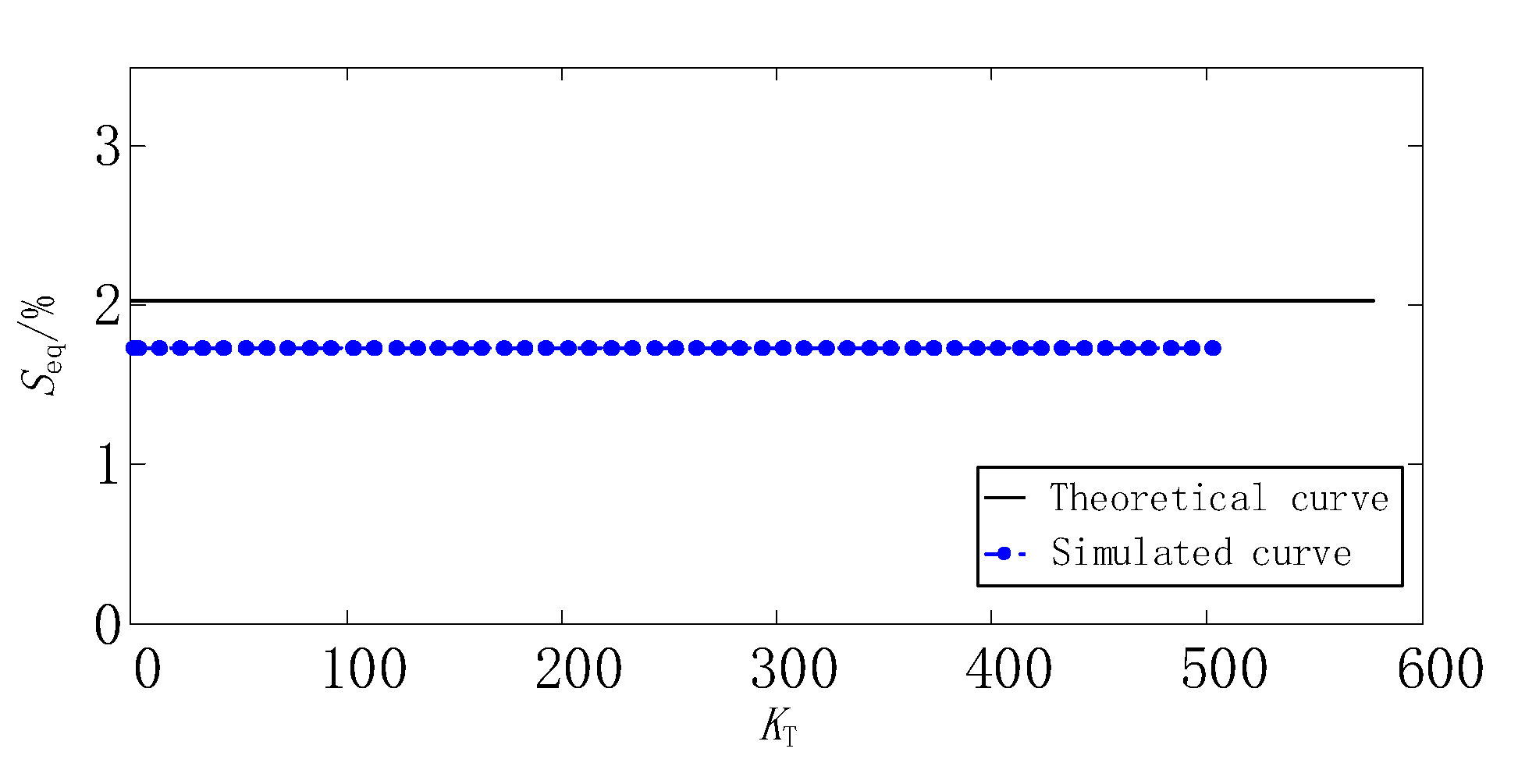
5. Simulation
6. Comparison
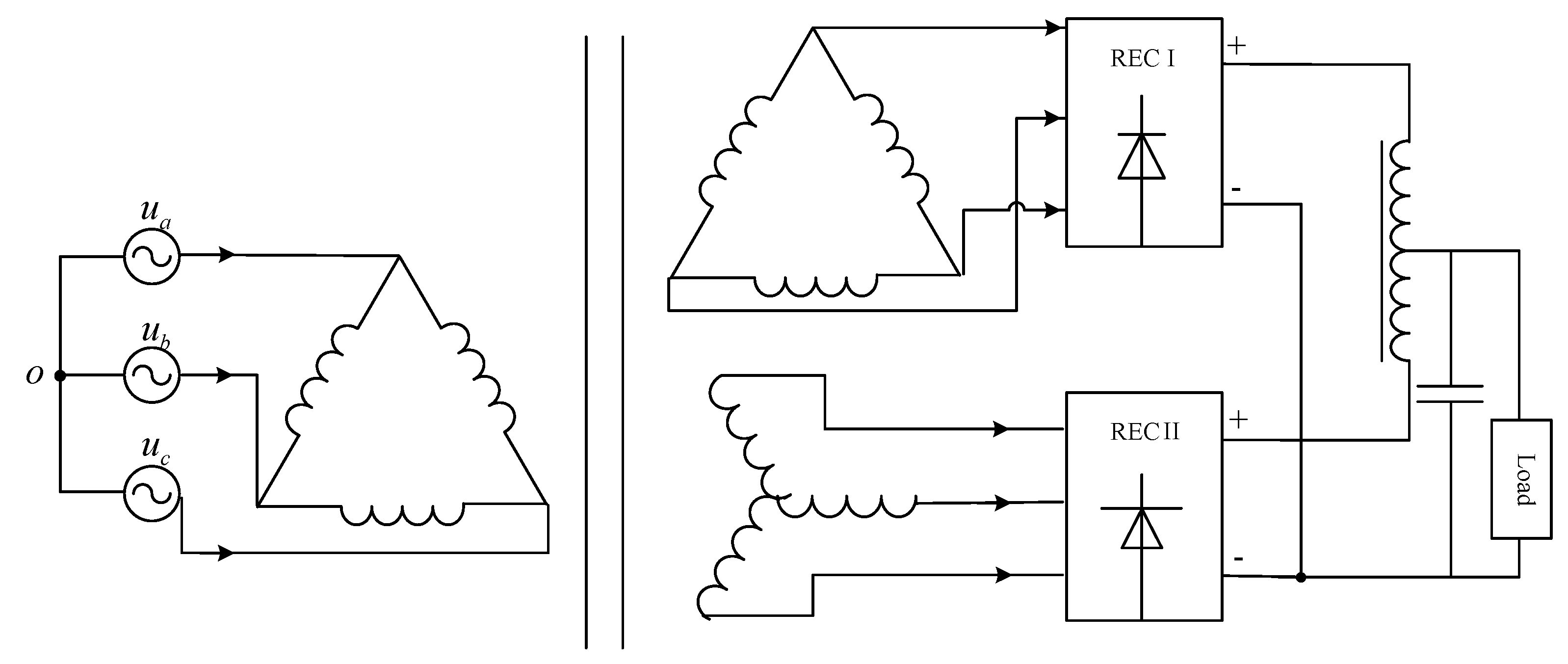
6.1. Comparison with Star Autotransformer
6.2. Comparison with Isolated Autotransformer
6.3. Comparison with Phase-Shift Angle Step-Up Mode
7. Conclusions
- (1)
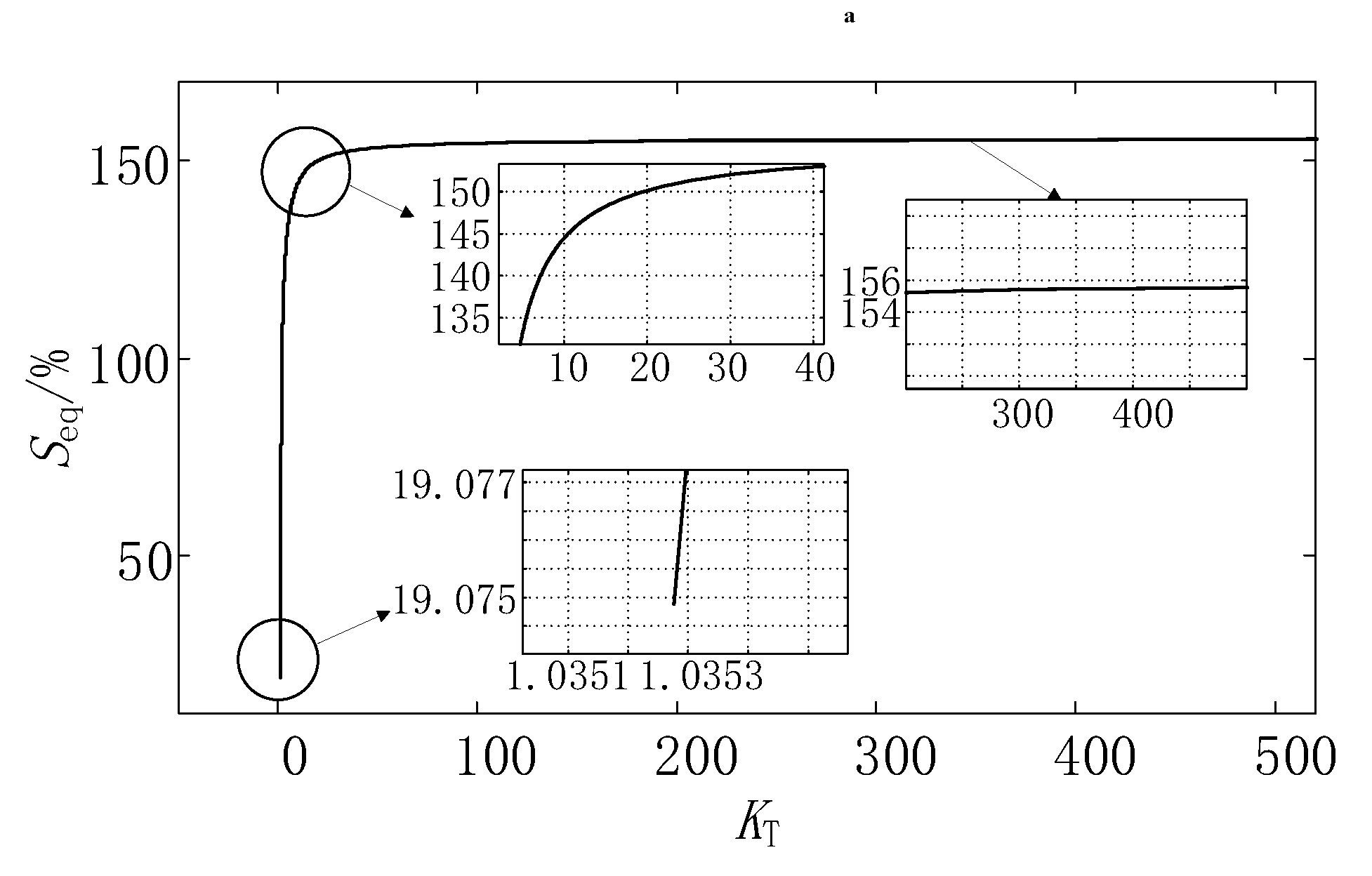
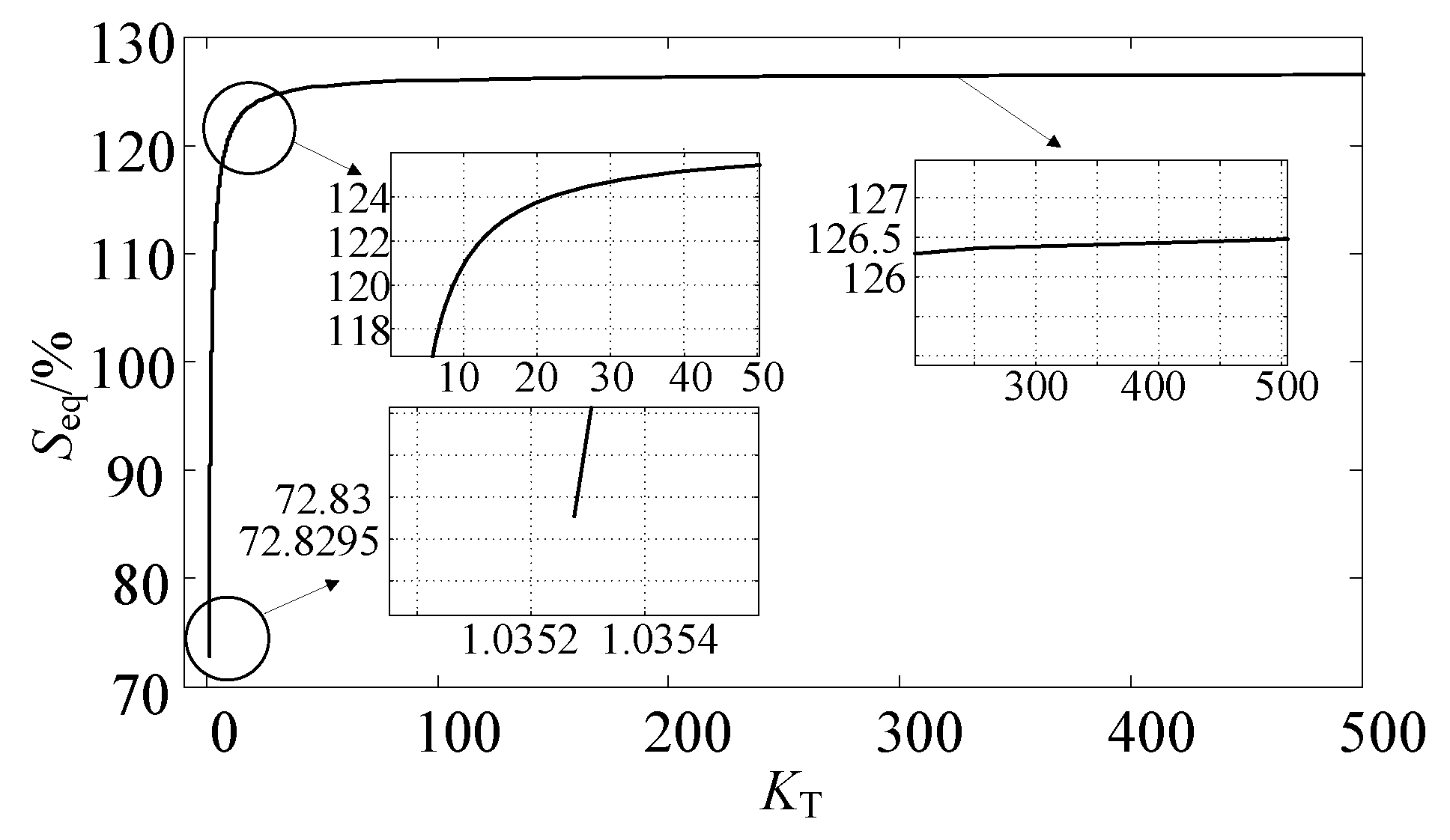
- When the transformation ratio of autotransformer is greater than or equal to 1.0353 and less than 2.0705, the equivalent capacity of balance reactor is basically maintained at about 2.017%. At this time, the equivalent capacity of K2 topology transformer is the smallest of the three topologies. Therefore, K2 topology is the best choice among the three topologies.
- (2)
- When the transformation ratio of autotransformer is greater than 2.0705, the equivalent capacity of balance reactor is basically maintained at about 2.017%. At this time, the equivalent capacity of K3 topology transformer is the smallest of the three topologies. Therefore, K3 topology is the best choice among the three topologies.
- (3)
- Compared with the star autotransformer, the DC side of the zigzag autotransformer rectifier circuit presents a high resistance state to the zero-sequence current, which can reduce the use of the DC side zero sequence current suppressor, system complexity and cost of the DC side circuit. Compared with isolated autotransformer, zigzag autotransformer has the advantages of high-power transmission efficiency and small capacity. Finally, for the phase-shifting angle transformer, the voltage step-up range can be expanded by optimizing the structure transformer. To sum up, the zigzag autotransformer step-up topology designed in this paper has the advantages of small volume, low system cost and wide step-up range compared with other step-up structures and step-up methods.
8. Suggestions
- (1)
- Research on the transformer structure of other autotransformer structures. There are many kinds of autotransformers, and there are still few studies on step-up and step-down of other autotransformers. Therefore, further exploration is still needed in this regard.
- (2)
- Experimental exploration of theoretical analysis. In the current research, it mainly focuses on its theoretical rationality. The experimental results may not be optimal, but they should be sufficient to draw the conclusions mentioned in the paper. It is necessary to build the corresponding experimental environment to verify the effectiveness of theoretical analysis.
- (3)
- Research on the relationship between transformer with asymmetric structure, transformation ratio and magnetic flux leakage inductance of autotransformer. The current research mainly focuses on the voltage transformation part of the symmetrical autotransformer, but the asymmetric autotransformer structure also exists in the application. At this time, the transformer will have problems such as magnetic flux leakage, inductance leakage and harmonic injection. In this case, it is also necessary to explore the transformation ratio, the harmonic content on the AC side of the system and the equivalent capacity of devices on the DC side of the system.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abdollahi, R.; Gharehpetian, G.B.; Anvari-Moghaddam, A.; Blaabjerg, F. Pulse Tripling Circuit and Twelve Pulse Rectifier Combination for Sinusoidal Input Current. IEEE Access 2021, 9, 103588–103599. [Google Scholar] [CrossRef]
- Zhang, Y.; Xia, J.; Zhang, X.; Chen, Z.; Li, B.; Luo, Q.; He, Y. Modeling and Prediction of the Reliability Analysis of an 18-Pulse Rectifier Power Supply for Aircraft Based Applications. IEEE Access 2020, 8, 47063–47071. [Google Scholar] [CrossRef]
- Ch, X.-Q.; Hao, C.-L.; Qiu, H.; Li, M. Thirty-six pulse rectifier scheme based on zigzag auto-connected transformer. Arch. Electr. Eng. 2016, 65, 117–132. [Google Scholar]
- Kalpana, R.; Bhuvaneswari, G.; Singh, B.; Singh, S.; Gairola, S. Autoconnected-Transformer-Based 20-Pulse AC–DC Converter for Telecommunication Power Supply. IEEE Trans. Ind. Electron. 2012, 60, 4178–4190. [Google Scholar] [CrossRef]
- Pan, Q.; Ma, W.; Liu, D.; Zhao, Z.; Meng, J. A New Critical Formula and Mathematical Topology of Double-Tap Interphase Reactor in a Six-Phase Tap-Changer Diode Rectifier. IEEE Trans. Ind. Electron. 2007, 54, 479–485. [Google Scholar]
- Abdollahi, R. Pulse doubling in zigzag-connected autotransformer-based 12-pulse ac-dc converter for power quality improvement. J. Electr. Eng. 2012, 63, 357–364. [Google Scholar] [CrossRef] [Green Version]
- Jiang, L.L.; Mao, L.; Chen, Q.H.; Tang, D.P. Design and Optimization of 12 kW P Type 18-pulse autotransformer Rectifier Units. Power Electron. 2012, 46, 4–6. [Google Scholar]
- Chen, J.; Shen, J.; Chen, J.; Shen, P.; Song, Q.; Gong, C. Investigation on the selection and design of step-Up/Down 18-pulse ATRUs for more electric aircrafts. IEEE Trans. Transp. Electrif. 2019, 5, 795–811. [Google Scholar] [CrossRef]
- Fernandes, R.C.; da Silva Oliveira, P.; de Seixas, F.J.M. A family of autoconnected transformers for 12-and 18-pulse converters—Generalization for delta and wye topologies. IEEE Trans. Power Electron. 2010, 26, 2065–2078. [Google Scholar] [CrossRef]
- Abdollahi, R.; Jalilian, A. Application of Pulse Doubling in Star-Connected Autotransformer Based 12-Pulse AC-DC Converter for Power Quality Improvement. World Acad. Sci. Eng. Technol. 2013, 5, 280–288. [Google Scholar]
- Zhang, Y.; Zhang, X.; Chen, Z.; Li, B.; He, Y. Engineering Application Research of Aircraft Power Supply Characteristics Based on 18-Pulse Rectifier Power System. IEEE Access 2019, 7, 22026–22034. [Google Scholar] [CrossRef]
- Xu, Y.; Li, P.; Lu, C.; He, X.; Li, D.; Fang, Y. Waveform Control of Multi-Pulse Flat-Top High Magnetic Field Based on Pulsed Generator System. IEEE Trans. Appl. Supercond. 2020, 30, 1–5. [Google Scholar] [CrossRef]
- Lucia, O.; Maussion, P.; Dede, E.J.; Burdio, J.M. Induction Heating Technology and Its Applications: Past Developments, Current Technology, and Future Challenges. IEEE Trans. Ind. Electron. 2014, 61, 2509–2520. [Google Scholar] [CrossRef] [Green Version]
- Yilmaz, I.; Ermis, M.; Cadirci, I. Medium-Frequency Induction Melting Furnace as a Load on the Power System. IEEE Trans. Ind. Appl. 2011, 48, 1203–1214. [Google Scholar] [CrossRef]
- Perise, J.S.; Bakkar, M.; Rodriguez, S.B. Open-Circuit Fault Diagnosis and Maintenance in Multi-Pulse Parallel and Series TRU Topologies. IEEE Trans. Power Electron. 2020, 35, 10906–10916. [Google Scholar] [CrossRef]
- Singh, B.; Gairola, S.; Singh, B.N.; Chandra, A.; Al-Haddad, K. Multipulse AC–DC converters for improving power quality: A review. IEEE Trans. Power Electron. 2008, 23, 260–281. [Google Scholar] [CrossRef]
- Li, Q.; Meng, F.; Gao, L.; Zhang, H.; Du, Q. A 30-Pulse Rectifier Using Passive Voltage Harmonic Injection Method at DC Link. IEEE Trans. Ind. Electron. 2019, 67, 9273–9291. [Google Scholar] [CrossRef]
- Hao, C.L.; Chen, X.Q.; Qiu, H. Delta-Polygon autotransformer based 24-Pulse rectifier for switching mode power supply. Telkomnika 2016, 14, 431. [Google Scholar] [CrossRef] [Green Version]
- Meng, F.; Gao, L.; Yang, S.; Yang, W. Effect of Phase-Shift Angle on a Delta-Connected Autotransformer Applied to a 12-Pulse Rectifier. IEEE Trans. Ind. Electron. 2015, 62, 4678–4690. [Google Scholar] [CrossRef]
- Burgos, R.; Uan-Zo-li, A.; Lacaux, F.; Roshan, A.; Wang, F.; Boroyevich, D. New step-up and step-down 18-pulse direct asymmetric autotransformer rectifier units. In Proceedings of the 2005 IEEE 36th Power Electronics Specialists Conference, Dresden, Germany, 16 June 2015; pp. 1149–1155. [Google Scholar]
- Xiao-qiang, C.; Hao, Q. Zigzag connected autotransformer-based 24-pulse AC-DC converter. Int. J. Emerg. Electr. Power Syst. 2015, 16, 23–32. [Google Scholar] [CrossRef]
- Singh, B.; Gairola, S. A Zigzag Connected autotransformer Based 24-Pulse AC-DC Converter. J. Electr. Eng. Technol. 2006, 3, 183–187. [Google Scholar]


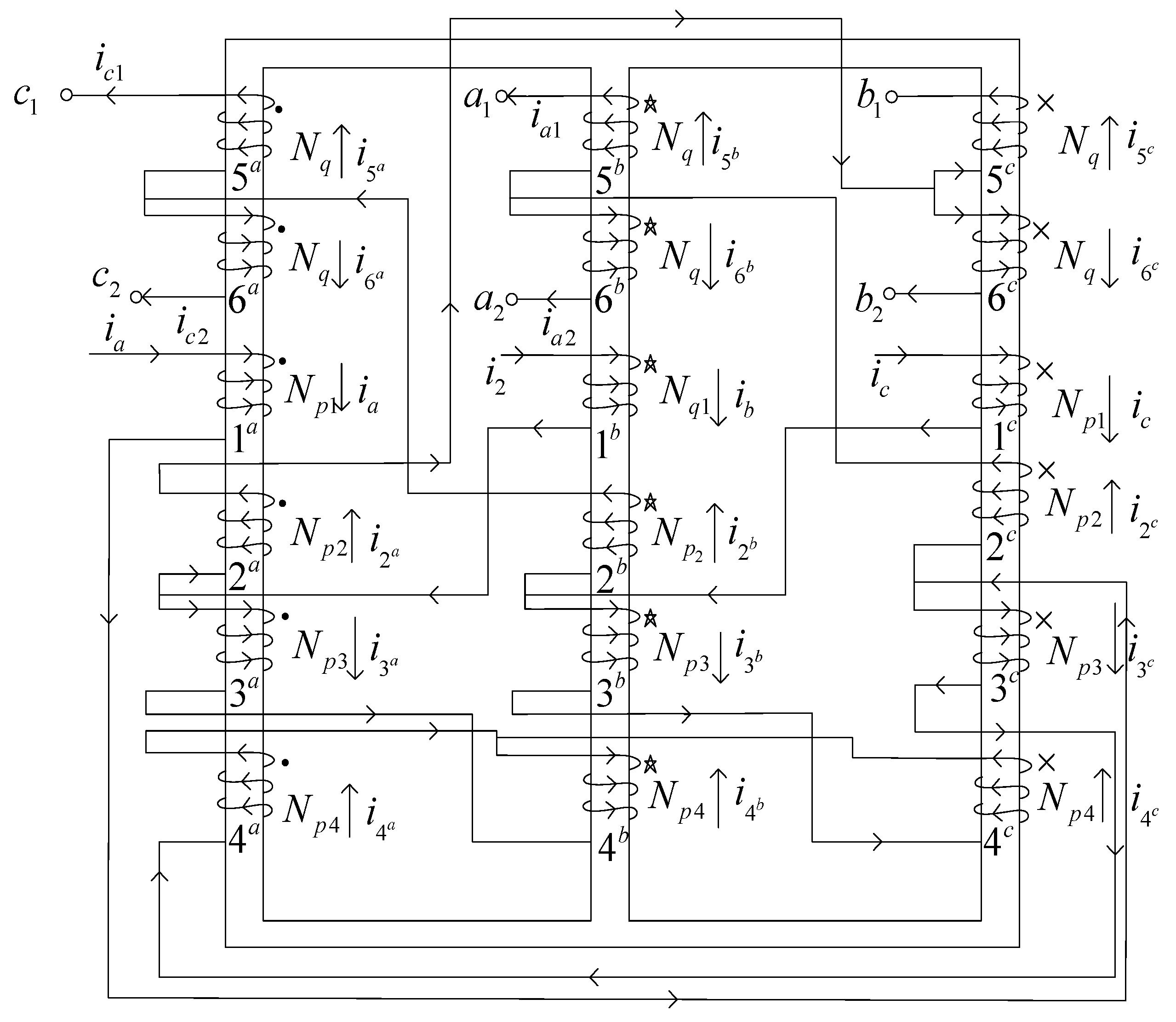

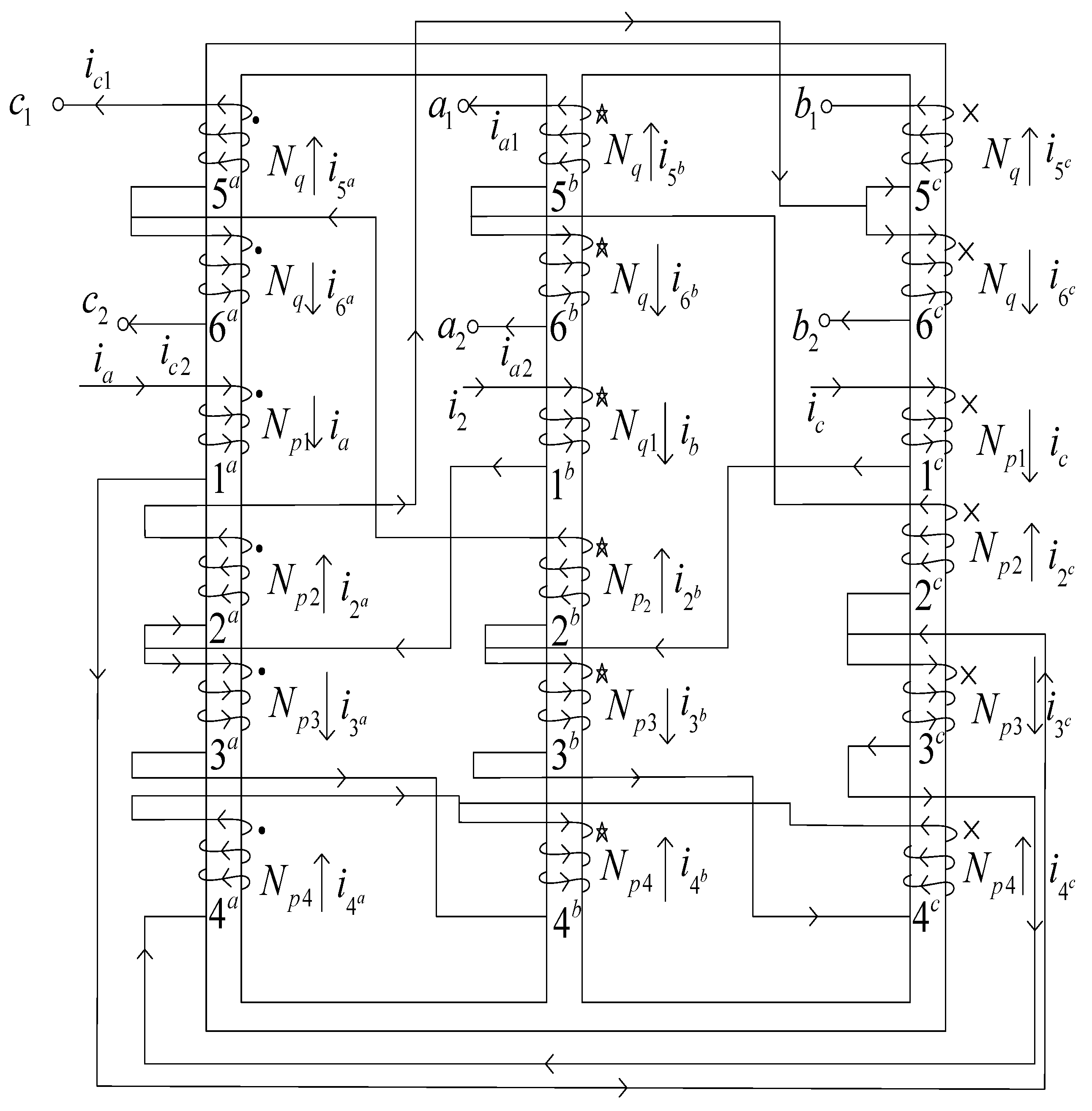





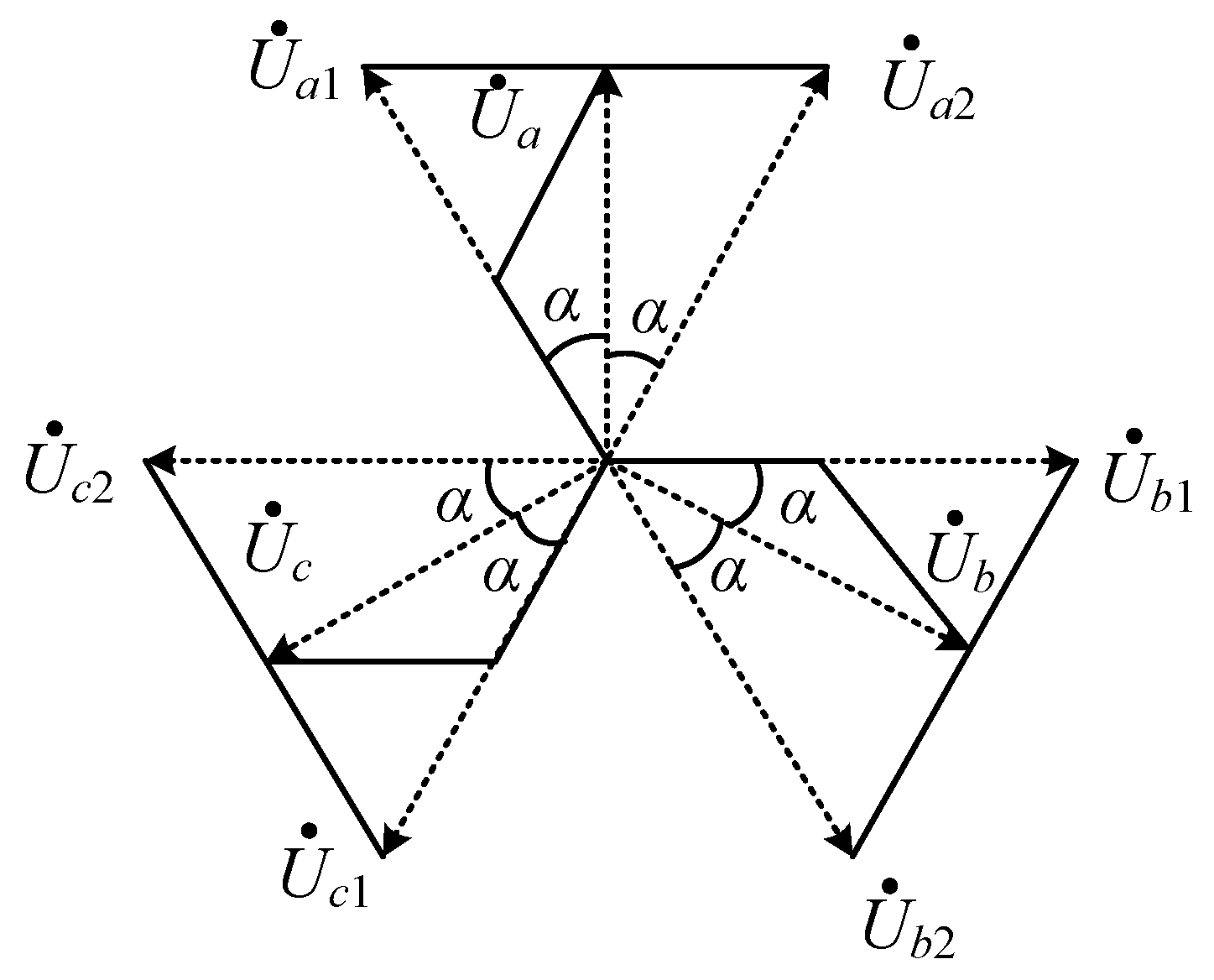
| Units: | pu |
|---|---|
| Nominal power and frequency | [75e3VA, 50 Hz] |
| Winding resistances [R1 R2… Rn] | [0 Ω, 0 Ω, 0 Ω, 0 Ω, 0 Ω] |
| Winding leakage inductances [L1 L2… Ln] | [0 H, 0 H, 0 H, 0 H, 0.00 H] |
| Magnetization resistance Rm | 50 Ω |
| Magnetization inductance Lm | 50 H |
| Saturation characteristic [i1, phi1; i2, phi2;…] | [0, 0, 0.0024, 1.2; 1.0, 1.52] |
| Number of Bridge Arms: | 3 |
|---|---|
| Snubber resistance Rs | 1 × 105 Ω |
| Snubber capacitance Cs | Inf F |
| Power Electronic device | diodes |
| Ron | 1 × 10−3 Ω |
| Lon | 0 H |
| Forward voltage Vf | 0 V |
| Type of Mutual Inductance: | Two or Three Windings with Equal Mutual Terms |
|---|---|
| Winding 1 self-impedance [R1 L1]: | [0.7 Ω 0.7 × 10−3 H] |
| Winding 2 self-impedance [R2 L2]: | [0.7 Ω 0.7 × 10−3 H] |
| Mutual impedance [Rm Lm]: | [1.0 Ω 1.0 × 10−3 H] |
| Step-Up Structure | Blocking Zero Sequence Current | Manufacturing Difficulty | Transformer Symmetry | Will Non Characteristic Harmonics Be Generated |
|---|---|---|---|---|
| Star connected autotransformer | No | High | Symmetrical structure | No |
| Isolated transformer | No | Low | Asymmetric structure | Yes |
| Phase shift angle transformer | No | High | Asymmetric structure | Yes |
| Zigzag autotransformer | Yes | High | Symmetrical structure | No |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; He, B. Novel Step-Up Topologies of Zigzag Autotransformer. Electronics 2021, 10, 3071. https://doi.org/10.3390/electronics10243071
Wang J, He B. Novel Step-Up Topologies of Zigzag Autotransformer. Electronics. 2021; 10(24):3071. https://doi.org/10.3390/electronics10243071
Chicago/Turabian StyleWang, Jiarong, and Bo He. 2021. "Novel Step-Up Topologies of Zigzag Autotransformer" Electronics 10, no. 24: 3071. https://doi.org/10.3390/electronics10243071





