Hat-Top Beams for Generating Tunable THz Radiations Using a Medium of Conducting Nanocylinders
Abstract
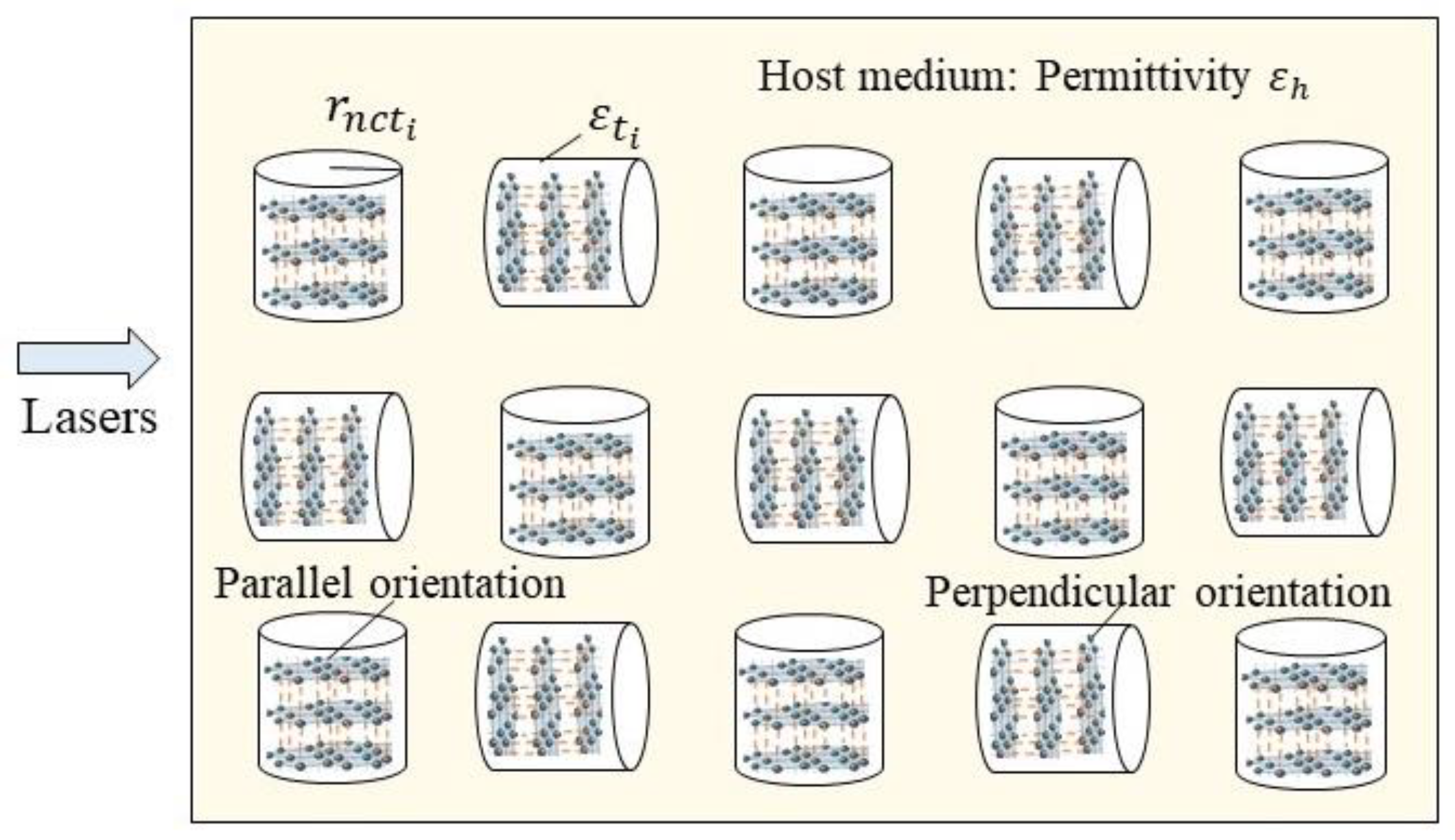
:1. Introduction
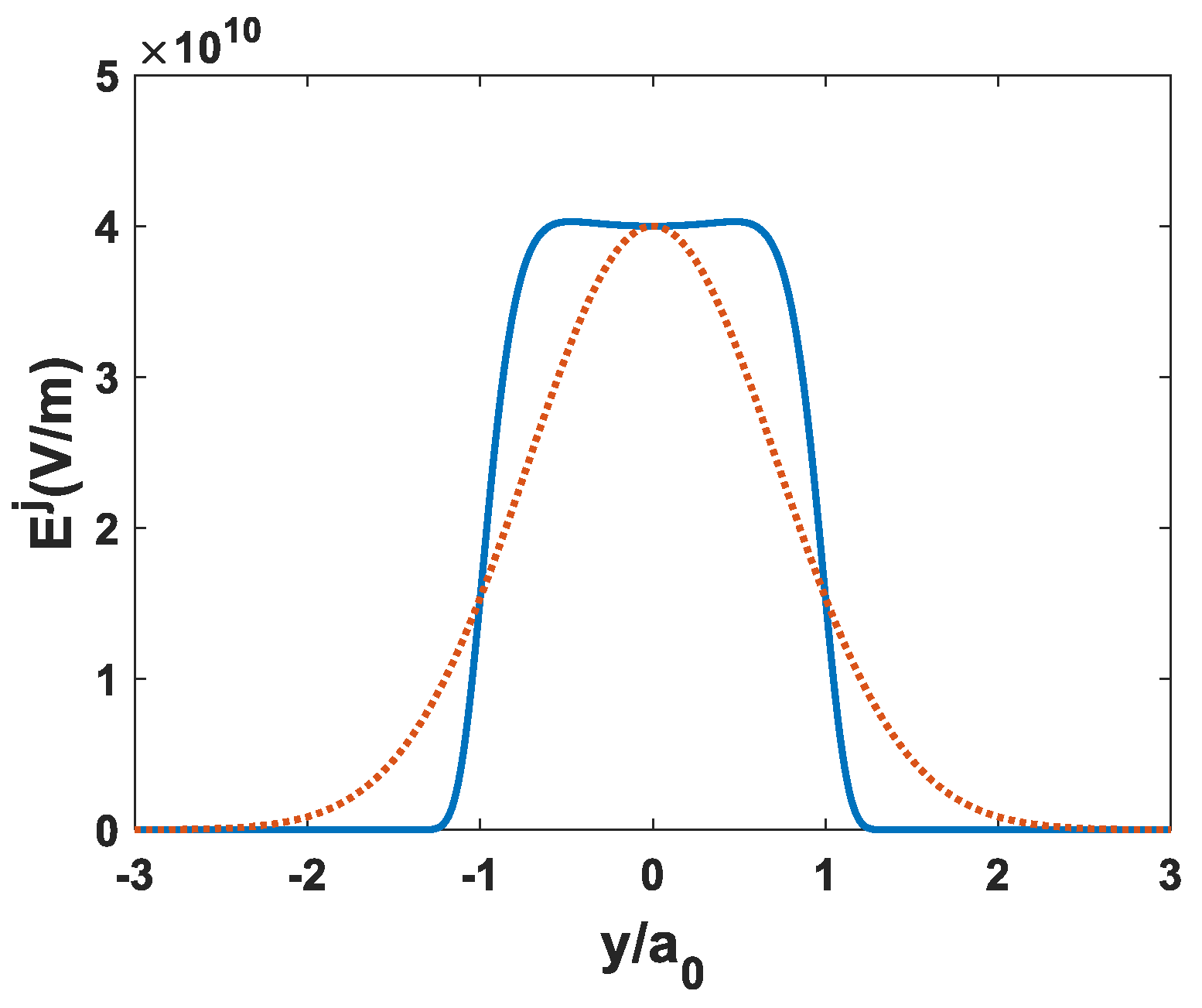
2. Hat-Top Laser Beams
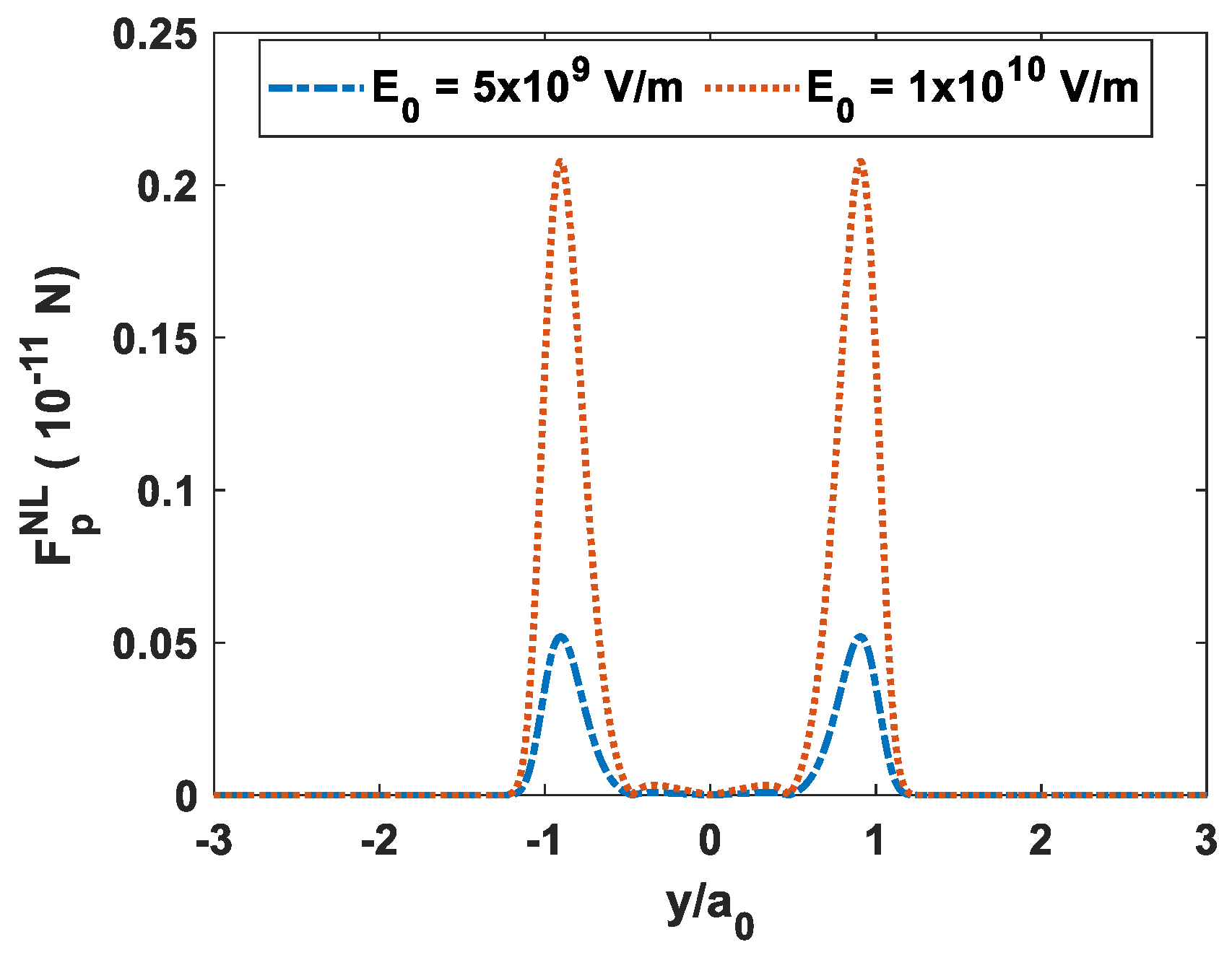
3. Origination of Ponderomotive Force
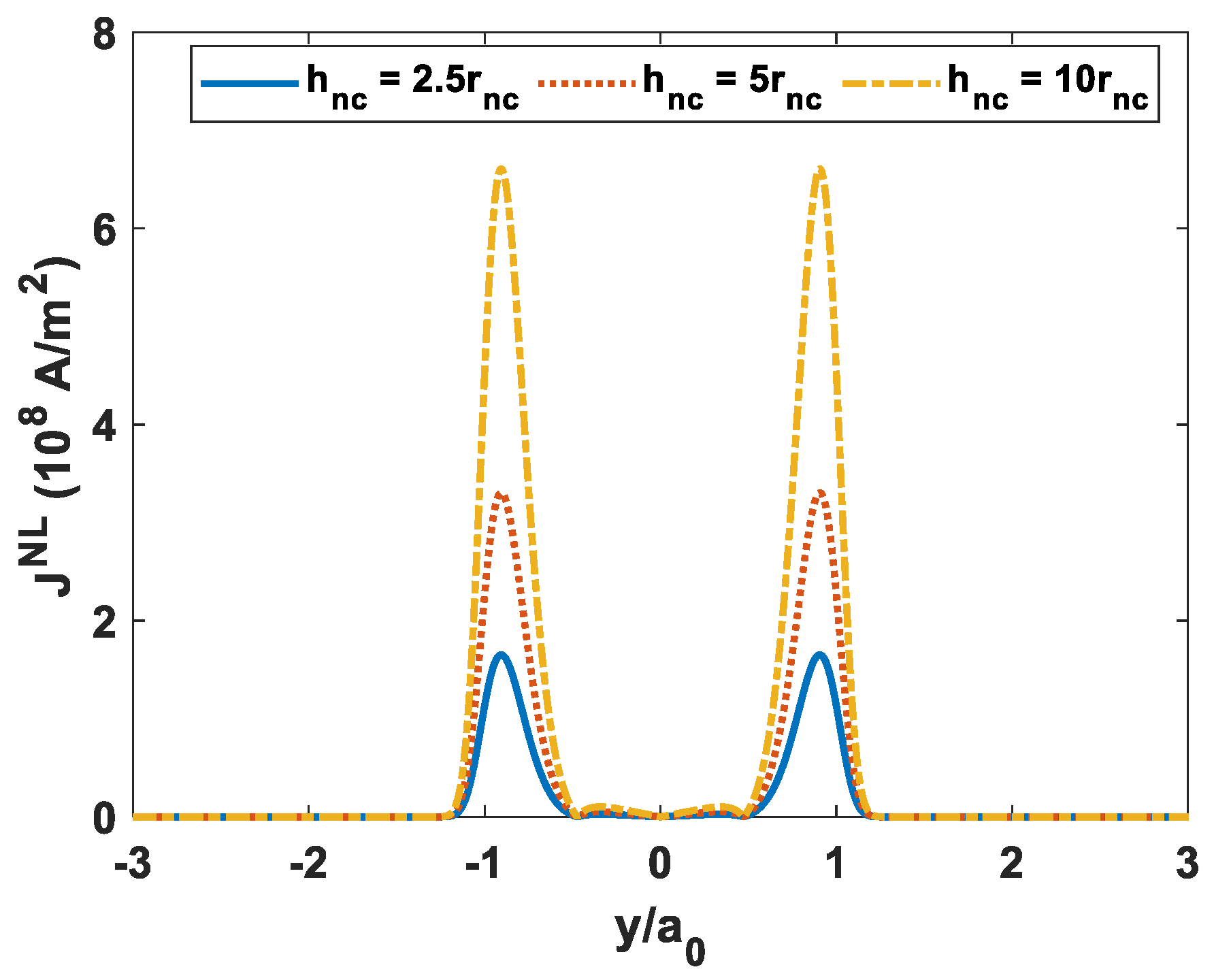
4. Nonlinear Current and THz Generation
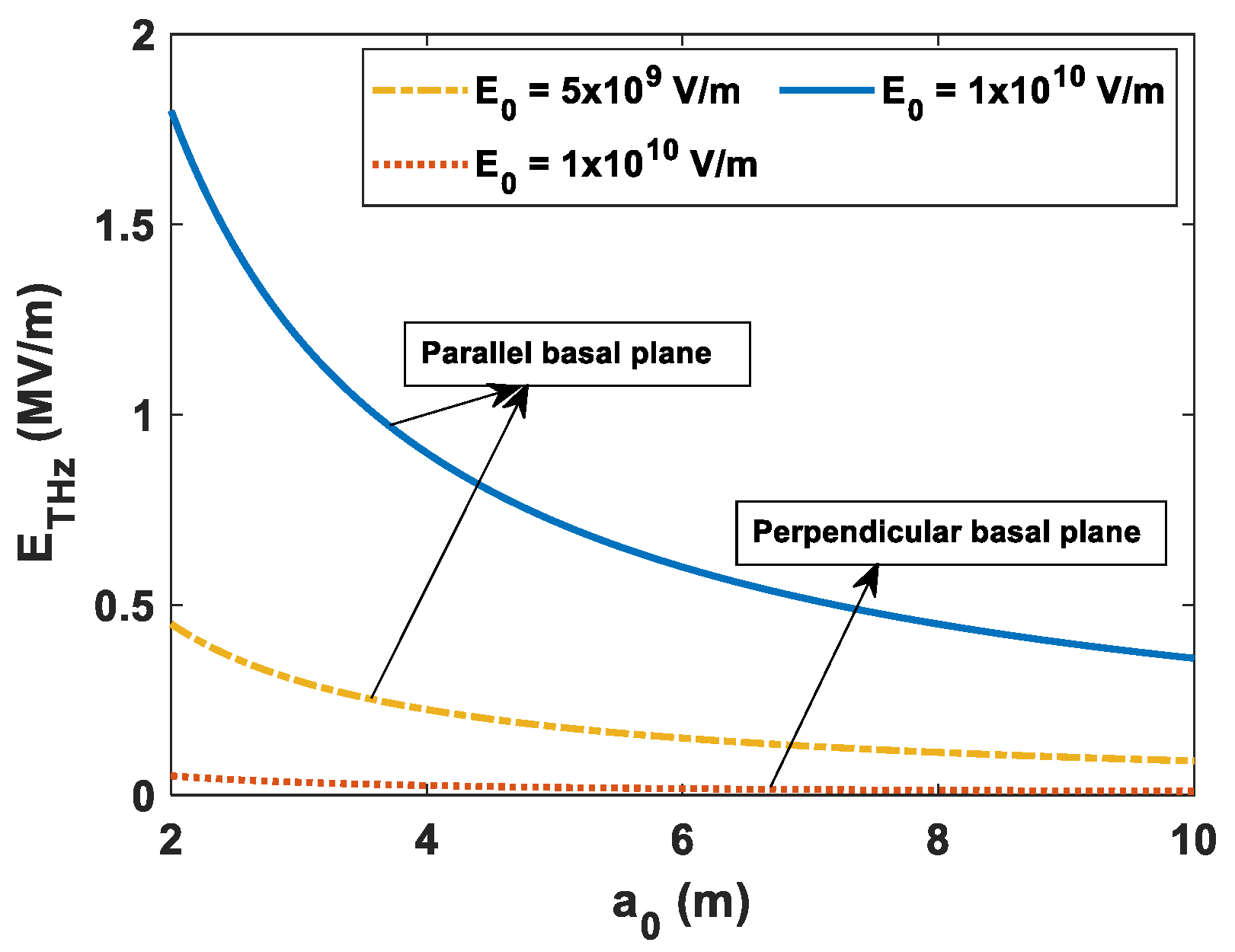
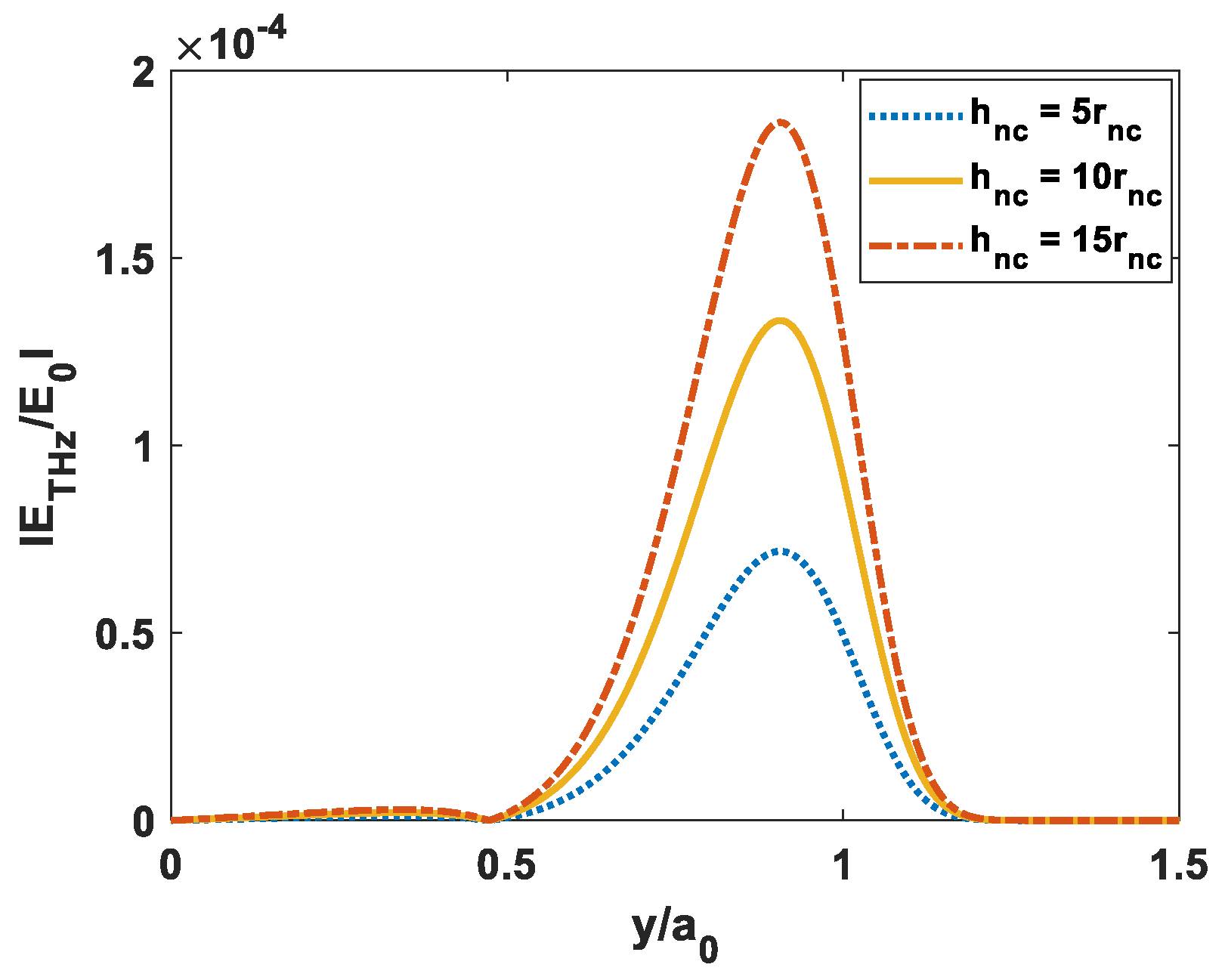
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dragoman, D.; Dragoman, M. Terahertz fields and applications. Prog. Quantum Electron. 2004, 28, 1–66. [Google Scholar] [CrossRef]
- Tonouchi, M. Cutting-edge terahertz technology. Nat. Photonics 2007, 1, 97–105. [Google Scholar] [CrossRef]
- Krumbholz, N.; Gerlach, K.; Rutz, F.; Koch, M.; Piesiewicz, R.; Kürner, T.; Mittleman, D. Omnidirectional terahertz mirrors: A key element for future terahertz communication systems. Appl. Phys. Lett. 2006, 88, 3–5. [Google Scholar] [CrossRef]
- Ebbinghaus, S.; Schröck, K.; Schauer, J.C.; Bründermann, E.; Heyden, M.; Schwaab, G.; Böke, M.; Winter, J.; Tani, M.; Havenith, M. Terahertz time-domain spectroscopy as a new tool for the characterization of dust forming plasmas. Plasma Sources Sci. Technol. 2006, 15, 72–77. [Google Scholar] [CrossRef]
- Nishizawa, S.; Sakai, K.; Hangyo, M.; Nagashima, T.; Takeda, M.W.; Tominaga, K.; Oka, A.; Tanaka, K.; Morikawa, O. Terahertz time-domain spectroscopy. Terahertz Optoelectron. 2005, 203–270. [Google Scholar] [CrossRef]
- Yan, Z.-K.; Zhang, H.-J.; Ying, Y.-B. Research progress of terahertz wave technology in quality measurement of food and agricultural products. Guang pu xue yu Guang pu fen xi= Guang pu 2007, 27, 2228–2234. [Google Scholar]
- Qin, J.; Ying, Y.; Xie, L. The detection of agricultural products and food using terahertz spectroscopy: A review. Appl. Spectrosc. Rev. 2013, 48, 439–457. [Google Scholar] [CrossRef]
- Sizov, F. THz radiation sensors. Opto-Electron. Rev. 2010, 18, 10–36. [Google Scholar] [CrossRef] [Green Version]
- Ulbricht, R.; Hendry, E.; Shan, J.; Heinz, T.F.; Bonn, M. Carrier dynamics in semiconductors studied with time-resolved terahertz spectroscopy. Rev. Mod. Phys. 2011, 83, 543–586. [Google Scholar] [CrossRef] [Green Version]
- Carr, G.L.; Martin, M.C.; McKinney, W.R.; Jordan, K.; Neil, G.R.; Williams, G.P. High-power terahertz radiation from relativistic electrons. Nature 2002, 420, 153–156. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.C.; Upadhya, P.C.; Beere, H.E.; Linfield, E.H.; Davies, A.G.; Gregory, I.S.; Baker, C.; Tribe, W.R.; Evans, M.J. Generation and detection of ultrabroadband terahertz radiation using photoconductive emitters and receivers. Appl. Phys. Lett. 2004, 85, 164–166. [Google Scholar] [CrossRef] [Green Version]
- Glyavin, M.Y.; Luchinin, A.G.; Golubiatnikov, G.Y. Generation of 1.5-kW, 1-THz coherent radiation from a gyrotron with a pulsed magnetic field. Phys. Rev. Lett. 2008, 100, 1–3. [Google Scholar] [CrossRef]
- Cook, A.M.; Tikhoplav, R.; Tochitsky, S.Y.; Travish, G.; Williams, O.B.; Rosenzweig, J.B. Observation of narrow-band terahertz coherent cherenkov radiation from a cylindrical dielectric-lined waveguide. Phys. Rev. Lett. 2009, 103, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Malik, H.K. Generalized treatment of skew-cosh-Gaussian lasers for bifocal terahertz radiation. Phys. Lett. Sect. A Gen. At. Solid State Phys. 2020, 384, 126304. [Google Scholar] [CrossRef]
- Malik, H.K. Laser-Matter Interaction for Radiation and Energy; CRC Press: Boca Raton, FL, USA, 2021; ISBN 1315396009. [Google Scholar]
- Gill, R.; Singh, D.; Malik, H.K. Multifocal terahertz radiation by intense lasers in rippled plasma. J. Theor. Appl. Phys. 2017, 11, 103–108. [Google Scholar] [CrossRef] [Green Version]
- Punia, S.; Malik, H.K. THz radiation generation in axially magnetized collisional pair plasma. Phys. Lett. Sect. A Gen. At. Solid State Phys. 2019, 383, 1772–1777. [Google Scholar] [CrossRef]
- Malik, A.K.; Malik, H.K.; Stroth, U. Strong terahertz radiation by beating of spatial-triangular lasers in a plasma. Appl. Phys. Lett. 2011, 99, 2–4. [Google Scholar] [CrossRef]
- Jepsen, P.U.; Jacobsen, R.H.; Keiding, S.R. Generation and detection of terahertz pulses from biased semiconductor antennas. J. Opt. Soc. Am. B 1996, 13, 2424. [Google Scholar] [CrossRef]
- Althuwayb, A.A. On-Chip Antenna Design Using the Concepts of Metamaterial and SIW Principles Applicable to Terahertz Integrated Circuits Operating over 0.6-0.622 THz. Int. J. Antennas Propag. 2020, 2020. [Google Scholar] [CrossRef]
- Alibakhshikenari, M.; Virdee, B.S.; Salekzamankhani, S.; Aïssa, S.; See, C.H.; Soin, N.; Fishlock, S.J.; Althuwayb, A.A.; Abd-Alhameed, R.; Huynen, I.; et al. High-isolation antenna array using SIW and realized with a graphene layer for sub-terahertz wireless applications. Sci. Rep. 2021, 11, 1–14. [Google Scholar] [CrossRef]
- Alibakhshikenari, M.; Virdee, B.S.; Althuwayb, A.A.; Aïssa, S.; See, C.H.; Abd-Alhameed, R.A.; Falcone, F.; Limiti, E. Study on on-Chip Antenna Design Based on Metamaterial-Inspired and Substrate-Integrated Waveguide Properties for Millimetre-Wave and THz Integrated-Circuit Applications. J. Infrared Millim. Terahertz Waves 2021, 42, 17–28. [Google Scholar] [CrossRef]
- Alibakhshikenari, M.; Virdee, B.S.; Khalily, M.; See, C.H.; Abd-Alhameed, R.; Falcone, F.; Denidni, T.A.; Limiti, E. High-Gain On-Chip Antenna Design on Silicon Layer with Aperture Excitation for Terahertz Applications. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 1576–1580. [Google Scholar] [CrossRef]
- Dorranian, D.; Starodubtsev, M.; Kawakami, H.; Ito, H.; Yugami, N.; Nishida, Y. Radiation from high-intensity ultrashort-laser-pulse and gas-jet magnetized plasma interaction. Phys. Rev. E—Stat. Nonlinear, Soft Matter Phys. 2003, 68, 026409/1–026409/7. [Google Scholar] [CrossRef] [PubMed]
- Dorranian, D.; Ghoranneviss, M.; Starodubtsev, M.; Ito, H.; Yugami, N.; Nishida, Y. Generation of short pulse radiation from magnetized wake in gas-jet plasma and laser interaction. Phys. Lett. Sect. A Gen. At. Solid State Phys. 2004, 331, 77–83. [Google Scholar] [CrossRef]
- Malik, A.K.; Malik, H.K.; Nishida, Y. Terahertz radiation generation by beating of two spatial-Gaussian lasers. Phys. Lett. Sect. A Gen. At. Solid State Phys. 2011, 375, 1191–1194. [Google Scholar] [CrossRef]
- Malik, A.K.; Malik, H.K. Tuning and focusing of terahertz radiation by dc magnetic field in a laser beating process. IEEE J. Quantum Electron. 2013, 49, 232–237. [Google Scholar] [CrossRef]
- Ghaem, E.N.; Dorranian, D.; Sari, A.H. External magnetic field effects on the characteristics of cobalt nanoparticles prepared by pulsed laser ablation. Opt. Quantum Electron. 2021, 53, 1–14. [Google Scholar] [CrossRef]
- Gildenburg, V.B.; Vvedenskii, N.V. Optical-to-THz wave conversion via excitation of plasma oscillations in the tunneling-ionization process. Phys. Rev. Lett. 2007, 98, 1–4. [Google Scholar] [CrossRef]
- Chen, Z.Y.; Li, X.Y.; Yu, W. Intense terahertz emission from relativistic circularly polarized laser pulses interaction with overdense plasmas. Phys. Plasmas 2013, 20, 1–6. [Google Scholar] [CrossRef]
- Malik, H.K.; Singh, D.; Kumar, R. Strong Terahertz radiation generation via wakefield in collisional plasma. J. Taibah Univ. Sci. 2020, 14, 1279–1287. [Google Scholar] [CrossRef]
- Kumar, M.; Tripathi, V.K.; Jeong, Y.U. Laser driven terahertz generation in hot plasma with step density profile. Phys. Plasmas 2015, 22, 1–3. [Google Scholar] [CrossRef]
- Bhasin, L.; Tripathi, V.K. Terahertz generation from laser filaments in the presence of a static electric field in a plasma. Phys. Plasmas 2011, 18, 18–21. [Google Scholar] [CrossRef]
- Chen, M.K.; Kim, J.H.; Yang, C.E.; Yin, S.S.; Hui, R.; Ruffin, P. Terahertz generation in multiple laser-induced air plasmas. Appl. Phys. Lett. 2008, 93, 3–5. [Google Scholar] [CrossRef] [Green Version]
- Polyushkin, D.K.; Márton, I.; Rácz, P.; Dombi, P.; Hendry, E.; Barnes, W.L. Mechanisms of THz generation from silver nanoparticle and nanohole arrays illuminated by 100 fs pulses of infrared light. Phys. Rev. B—Condens. Matter Mater. Phys. 2014, 89, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Welsh, G.H.; Hunt, N.T.; Wynne, K. Terahertz-pulse emission through laser excitation of surface plasmons in a metal grating. Phys. Rev. Lett. 2007, 98, 3–6. [Google Scholar] [CrossRef]
- Zhang, L.; Mu, K.; Zhou, Y.; Wang, H.; Zhang, C.; Zhang, X.C. High-power THz to IR emission by femtosecond laser irradiation of random 2D metallic nanostructures. Sci. Rep. 2015, 5, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Kajikawa, K.; Nagai, Y.; Uchiho, Y.; Ramakrishnan, G.; Kumar, N.; Ramanandan, G.K.P.; Planken, P.C.M. Terahertz emission from surface-immobilized gold nanospheres. Opt. Lett. 2012, 37, 4053. [Google Scholar] [CrossRef] [Green Version]
- Sepehri Javan, N.; Rouhi Erdi, F. Theoretical study of the generation of terahertz radiation by the interaction of two laser beams with graphite nanoparticles. J. Appl. Phys. 2017, 122, 1–7. [Google Scholar] [CrossRef]
- Sharma, D.; Singh, D.; Malik, H.K. Shape-Dependent Terahertz Radiation Generation Through Nanoparticles. Plasmonics 2020, 15, 177–187. [Google Scholar] [CrossRef]
- Homburg, O.; Mitra, T. Gaussian-to-top-hat beam shaping: An overview of parameters, methods, and applications. In Proceedings of the Laser Resonators, Microresonators, and Beam Control XIV. Int. Soc. Opt. Photonics 2012, 8236, 82360A. [Google Scholar] [CrossRef]
- Le, H.; Penchev, P.; Henrottin, A.; Bruneel, D.; Nasrollahi, V.; Ramos-de-Campos, J.A.; Dimov, S. Effects of top-hat laser beam processing and scanning strategies in laser micro-structuring. Micromachines 2020, 11, 221. [Google Scholar] [CrossRef] [Green Version]
- Malik, L.; Escarguel, A. Role of the temporal profile of femtosecond lasers of two different colours in holography. EPL 2018, 124, 64002. [Google Scholar] [CrossRef]
- Malik, L.; Escarguel, A.; Kumar, M.; Tevatia, A.; Singh Sirohi, R. Uncovering the remarkable contribution of lasers peak intensity region in holography. Laser Phys. Lett. 2021, 18, 086003. [Google Scholar] [CrossRef]
- Malik, L. Dark hollow lasers may be better candidates for holography. Opt. Laser Technol. 2020, 132, 106485. [Google Scholar] [CrossRef]
- Sihvola, A.H. Electromagnetic Mixing Formulas and Applications; IET: London, UK, 1999; ISBN 0852967721. [Google Scholar]
- Johnson, L.G.; Dresselhaus, G. Optical properies of graphite. Phys. Rev. B 1973, 7, 2275–2285. [Google Scholar] [CrossRef]
- Taft, E.A.; Philipp, H.R. Optical properties of graphite. Phys. Rev. 1965, 138, A197. [Google Scholar] [CrossRef]
- Rothwell, E.J.; Cloud, M.J. Electromagnetics; CRC Press: Boca Raton, FL, USA, 2018; ISBN 1439878188. [Google Scholar]
- Wang, T.J.; Marceau, C.; Chen, Y.; Yuan, S.; Théberge, F.; Châteauneuf, M.; Dubois, J.; Chin, S.L. Terahertz emission from a dc-biased two-color femtosecond laser-induced filament in air. Appl. Phys. Lett. 2010, 96, 2–4. [Google Scholar] [CrossRef]
- Jana, N.R.; Gearheart, L.; Murphy, C.J. Wet chemical synthesis of high aspect ratio cylindrical gold nanorods. J. Phys. Chem. B 2001, 105, 4065–4067. [Google Scholar] [CrossRef]
- Varshney, P.; Gopal, K.; Upadhyay, A. Terahertz emission from nonlinear interaction of laser beat wave with nanoparticles. Laser Phys. Lett. 2020, 17, 126002. [Google Scholar] [CrossRef]
- Thakur, V.; Kant, N.; Vij, S. Effect of cross-focusing of two laser beams on THz radiation in graphite nanoparticles with density ripple. Phys. Scr. 2020, 95, 45602. [Google Scholar] [CrossRef]
- Sepehri Javan, N.; Rouhi Erdi, F.; Najafi, M.N. Magnetic field effect on the self-focusing of an intense laser pulse interacting with a bulk medium of graphite nanoparticles. Phys. Plasmas 2017, 24, 052301. [Google Scholar] [CrossRef]
- Chou, J.; Han, Y.; Jalali, B. Adaptive RF-photonic arbitrary waveform generator. IEEE Photonics Technol. Lett. 2003, 15, 581–583. [Google Scholar] [CrossRef]
- Cherezova, T.Y.; Chesnokov, S.S.; Kaptsov, L.N.; Kudryashov, A.V. Super-Gaussian output laser beam formation by bimorph adaptive mirror. Opt. Commun. 1998, 155, 99–106. [Google Scholar] [CrossRef]
- Ye, J.; Yan, L.; Pan, W.; Luo, B.; Zou, X.; Yi, A.; Yao, S. Photonic generation of triangular-shaped pulses based on frequency-to-time conversion. Opt. Lett. 2011, 36, 1458. [Google Scholar] [CrossRef]
- Wang, H.; Latkin, A.I.; Boscolo, S.; Harper, P.; Turitsyn, S.K. Generation of triangular-shaped optical pulses in normally dispersive fibre. J. Opt. 2010, 12, 035205. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malik, H.K.; Punia, T.; Sharma, D. Hat-Top Beams for Generating Tunable THz Radiations Using a Medium of Conducting Nanocylinders. Electronics 2021, 10, 3134. https://doi.org/10.3390/electronics10243134
Malik HK, Punia T, Sharma D. Hat-Top Beams for Generating Tunable THz Radiations Using a Medium of Conducting Nanocylinders. Electronics. 2021; 10(24):3134. https://doi.org/10.3390/electronics10243134
Chicago/Turabian StyleMalik, Hitendra K., Tamanna Punia, and Dimple Sharma. 2021. "Hat-Top Beams for Generating Tunable THz Radiations Using a Medium of Conducting Nanocylinders" Electronics 10, no. 24: 3134. https://doi.org/10.3390/electronics10243134
APA StyleMalik, H. K., Punia, T., & Sharma, D. (2021). Hat-Top Beams for Generating Tunable THz Radiations Using a Medium of Conducting Nanocylinders. Electronics, 10(24), 3134. https://doi.org/10.3390/electronics10243134





