Implementation and Validation of Hybrid Control for a DFIG Wind Turbine Using an FPGA Controller Board
Abstract
:1. Introduction
2. System Modeling
2.1. Wind Turbine
2.2. DFIG
3. Hybrid Control
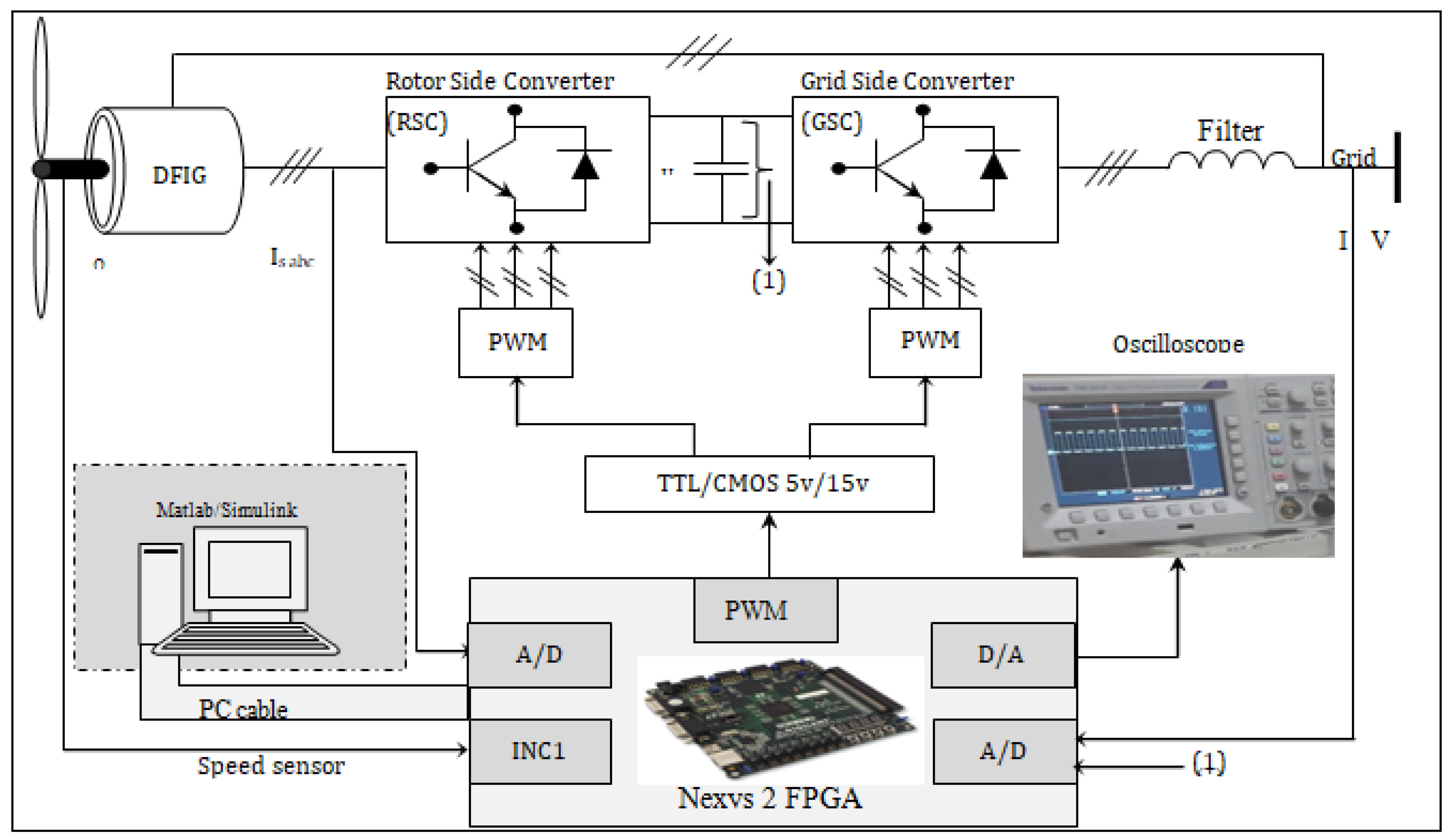
4. FPGA Implementation
- Backstepping control blocks: The first block is for controlling the active and reactive power of the stator and the second for the control laws Vrd and Vrq.
- Calculation block: This block is used to calculate from the measured currents and voltages: the active power, the reactive power, the magnetic fluxes of the stator, the rotor pulsation, and the stator pulsation.
- Measuring block: This block contains ADC interfaces that allow the connection between the FPGA and the analog-to-digital converter, which allows the currents to be acquired from a Hall Effect sensor.
- PWM block: This block is used to generate the control signals Sa, Sb, and Sc of the rotor side converters. The Timing block controls the start and end of each block, which makes it possible to refresh the reference voltages at the start of each sampling period.
5. Hardware Co-Simulation
6. Experimental Results and Discussions
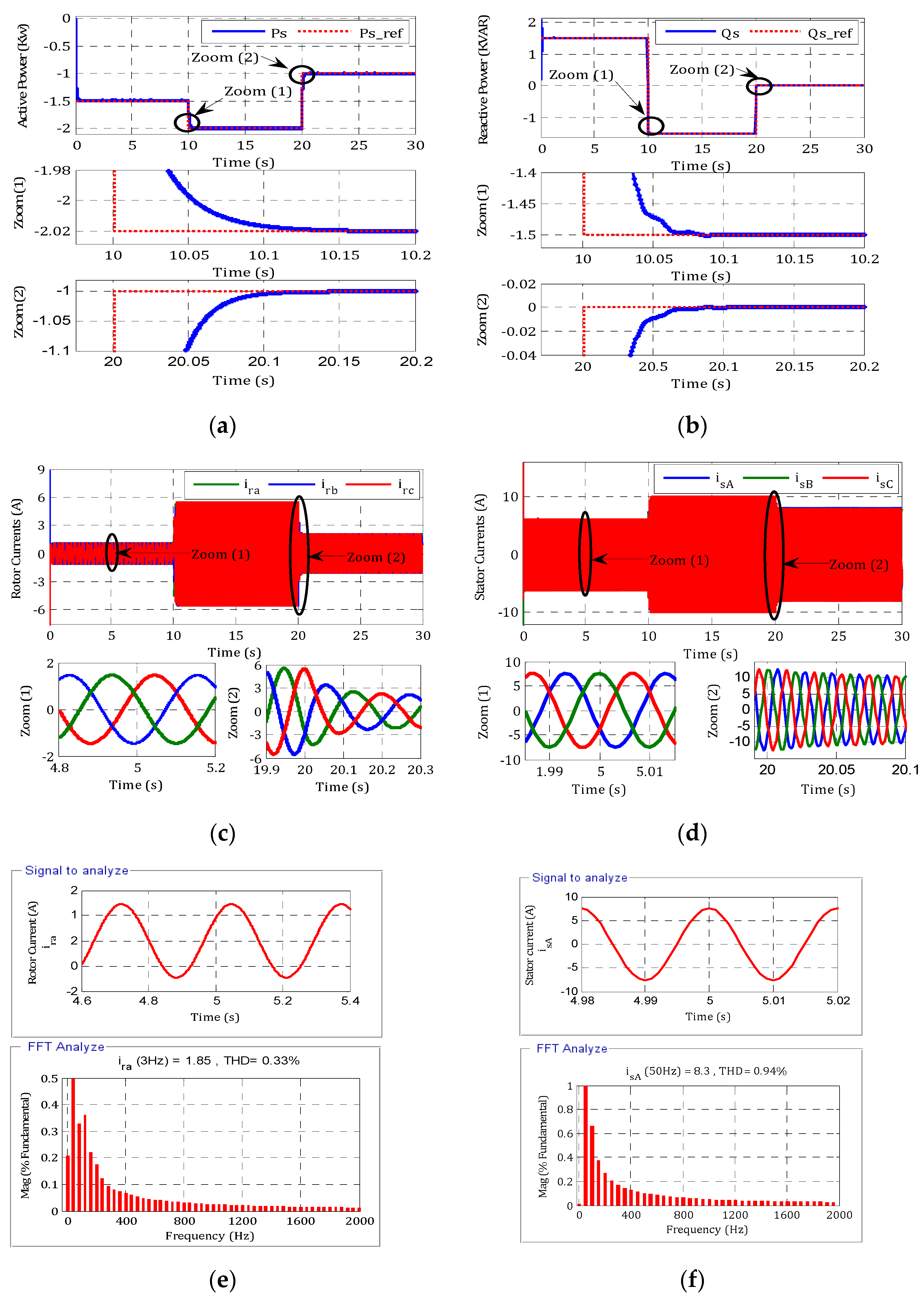
6.1. Performance Test Static
- The active and reactive power tracking test is always carried out with high performance.
- The active power is always negative, which means that the MADA is operating in generator mode and is supplying power to the network.
- The reactive power control allows us to have either negative or positive reactive power (capacitive or inductive behavior). The sizes ordered perfectly follow their references with a static error of εs = 0.067%.
- The response of the active and reactive power is aperiodic, with:
- ➢
- Response time of tr(Ps) = 170 ms and tr(Qs) = 50 ms
- ➢
- Variation band of ∆Ps = ±5 W and ∆Qs = ±5 VAR.
- The three-phase stator and rotor currents respond effectively to the torque variations; they are proportional to the active power provided.
- The current has a sinusoidal form with a frequency of 50 Hz for the stator current alongside the rotor current frequency, which is stabilized at 3 Hz at time t = 4.8 s to an imposed speed of 1800 tr/min.
- The harmonic distortion is related to 0.33% for the rotor current and 0.94% for the stator current.
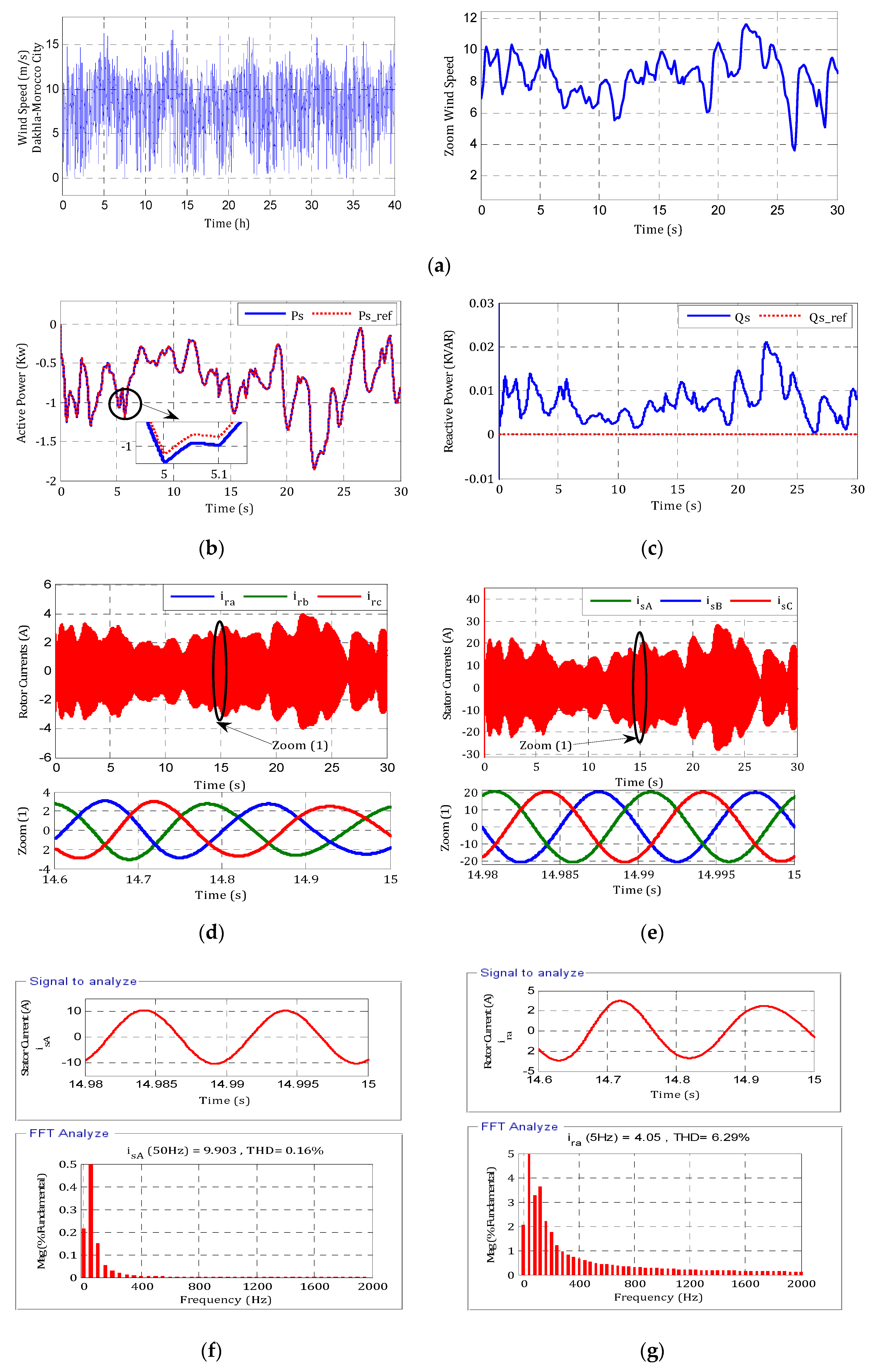
6.2. Performance Test Dynamic
- The active and reactive power perfectly follows the generated setpoints, the unit power factor obtained after the end of its transient regime.
- The quality of the energy is much improved; the evolution of the currents is indeed sinusoidal, with a frequency of 50 Hz.
- The harmonic distortion is significant (6.29%) for the current rotor and only 0.16% for the stator current.
6.3. Robustness Test
- Variations in stator (Rs) and rotor (Rr) resistances result in a small increase in response time, with almost zero static error and less oscillation.
- The fluctuations of the rotor and stator inductances (Lr) and (Ls) show the same response time in the beginning, with low sensitivity in the dynamics of the reference, which always maintains the decoupling between the active and reactive powers.
6.4. Hardware Test
6.5. Comparison Study
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Symbol | Quantity | Values |
|---|---|---|
| Ps | Stator power | 1.5 KW |
| p | Pole number | 2 |
| Rs | Stator resistance | 4.85 Ω |
| Rr | Rotor resistance | 3.805 Ω |
| Ls | Stator inductance | 274 mH |
| Lr | Rotor inductance | 258 mH |
| Tem | Electromagnetic torque | 32 Nm |
| Symbol | Quantity | Values |
|---|---|---|
| R | Radius of the turbine blade | 20 m |
| J | Turbine and generator moment | 1000 N.m |
| ρ | Specific density of air | 1.22 kg/m3 |
| λopt | Tip–speed ratio | 8 |
| Cp | Optimal power coefficient | 0.45 |
References
- Kazemia, M.V.; Moradib, M.; Kazemi, R.V. Minimization of powers ripple of direct power controlled DFIG by fuzzy controller and improved discrete space vector modulation. Electr. Power Syst. Res. 2012, 89, 23–30. [Google Scholar] [CrossRef]
- Yung-Tsai, W.; Yuan-Yih, H. Reactive power control strategy for a wind farm with DFIG. Renew. Energy 2016, 94, 383–390. [Google Scholar]
- Yao, J.; Li, H.; Chen, Z.; Xia, X.; Chen, X.; Li, Q.; Liao, Y. Operation of Wind Turbine-Driven DFIG Systems Under Distorted Grid Voltage Conditions: Analysis and Experimental Validations. IEEE Trans. Power Electr. 2013, 28, 3167–3181. [Google Scholar]
- Ebrahimkhani, S. Robust fractional order sliding mode control of doubly-fed induction generator (DFIG)-based wind turbines. ISA Trans. 2016, 63, 343–354. [Google Scholar] [CrossRef] [PubMed]
- Ademi, S.; Jovanovic, M. High-efficiency control of brushless doubly-fed machines for wind turbines and pump drives. Energy Conv. Manag. 2014, 81, 120–132. [Google Scholar] [CrossRef]
- Kaloi, G.S.; Wanga, J.; Baloch, M.H. Active and reactive power control of the doubly fed induction generator based on wind energy conversion system. Energy Rep. 2016, 2, 194–200. [Google Scholar] [CrossRef] [Green Version]
- Bouderbala, M.; Bossoufi, B.; Deblecker, O.; Alami Aroussi, H.; Taoussi, M.; Lagrioui, A.; Motahhir, S.; Masud, M.; Alraddady, F.A. Experimental Validation of Predictive Current Control for DFIG: FPGA Implementation. Electronics 2021, 10, 2670. [Google Scholar] [CrossRef]
- Aroussi, H.A.; Ziani, E.; Bouderbala, M.; Bossoufi, B. Enhancement of the direct power control applied to DFIG-WECS. Int. J. Electr. Comput. Eng. 2020, 10, 35. [Google Scholar] [CrossRef]
- Bossoufi, B.; Karim, M.; Lagrioui, A.; Taoussi, M.; EL Hafyani, M.L. Backstepping Adaptive Control of DFIG-Generators for Variable-Speed Wind Turbines. Int. J. Comput. Technol. 2014, 12, 3719–3733. [Google Scholar] [CrossRef]
- Taoussi, M.; Karim, M.; Bossoufi, B.; Hammoumi, D.; Lagrioui, A. Speed Backstepping control of the doubly-fed induction machine drive. J. Appl. Inf. Technol. 2015, 74, 189–199. [Google Scholar]
- Saady, I.; Bossoufi, B.; Karim, M.; Motahhir, S.; Adouairi, M.S.; Majout, B.; Lamnadi, M.; Masud, M.; Al-Amri, J.F. Optimisation for a photovoltaic pumping system using indirect Field Oriented Control of Induction Motor. Electronics 2021, 10, 3076. [Google Scholar] [CrossRef]
- Zhou, D.; Blaabjerg, F.; Lau, M.; Tonnes, M. Optimized Reactive Power Flux of DFIG Power Converters for Better Reliability Performance Considering Grid Codes. IEEE Trans. Ind. Electr. 2015, 62, 1552–1562. [Google Scholar] [CrossRef]
- Alami Aroussi, H.; Ziani, E.M.; Bossoufi, B. Robust control of a power wind system based on the double fed induction generator (DFIG). J. Autom. Syst. Eng. JASE 2015, 9, 156–166. [Google Scholar]
- Taoussi, M.; Karim, M.; Bossoufi, B.; Lagrioui, A.; El Mahfoud, M. The Fuzzy Control for Rotor Flux Orientation of the doubly-fed asynchronous generator Drive. Int. J. Computers Technol. 2014, 13, 4707–4722. [Google Scholar] [CrossRef]
- Bossoufi, B.; Karim, M.; Taoussi, M.; Aroussi, H.A.; Bouderbala, M.; Deblecker, O. Rooted Tree Optimization for Backstepping Power Control of DFIG Wind Turbine: dSPACE Implementation. IEEE Access 2021, 9, 26512–26522. [Google Scholar] [CrossRef]
- Bossoufi, B.; Karim, M.; Lagrioui, A.; Taoussi, M. FPGA-Based Implementation nonlinear Backstepping control of a PMSM Drive. IJPEDS Int. J. Power Electr. Drive Syst. 2014, 4, 12–23. [Google Scholar]
- Hu, J.; Yuan, X. VSC-based direct torque and reactive power control of doubly fed induction generator. Renew. Energy 2012, 40, 13–23. [Google Scholar] [CrossRef]
- Bossoufi, B.; Taoussi, M.; Alami Aroussi, H.; Bouderbala, M.; Motahhir, S.; Camara, M.B. DSPACE-Based Implementation for Observer Backstepping Power Control of DFIG Wind Turbine. IET Electr. Power Appl. 2020, 14, 2395–2403. [Google Scholar] [CrossRef]
- Mellit, A.; Mekki, H.; Messai, A.; Kalogirou, S.A. FPGA-based implementation of intelligent predictor for global solar irradiation, Part I: Theory and simulation. Expert Syst. Appl. 2011, 38, 2668–2685. [Google Scholar] [CrossRef]
- Bossoufi, B.; Karim, M.; Lagrioui, A.; Taoussi, M.; Derouich, A. Observer Backstepping control of DFIG-Generators for Wind Turbines Variable-Speed: FPGA-Based Implementation. Renew. Energy J. 2015, 81, 903–917. [Google Scholar] [CrossRef]
- Orosz, T.; Rassõlkin, A.; Kallaste, A.; Arsénio, P.; Pánek, D.; Kaska, J.; Karban, P. Robust Design Optimization and Emerging Technologies for Electrical Machines: Challenges and Open Problems. Appl. Sci. 2020, 10, 6653. [Google Scholar] [CrossRef]





| Publication | Technique | Performances | Robustness | |||
|---|---|---|---|---|---|---|
| Response Time | Error Ɛs (%) | Overshot (%) | Power Ripple | |||
| [9] | DTC-classical | --- | 0.32% | 5% | --- | Moderate |
| DTC-GA-based PI | --- | 0.12% | 1% | --- | Moderate | |
| [10] | High-order sliding mode | 130 ms | 0.2% | 0% | ±17 w | High |
| Fuzzy siding mode | 150 ms | 0.14% | 0% | ±15 w | High | |
| [11] | DPC | 200 ms | --- | 0% | ±19 w | Moderate |
| [12] | Fuzzy-Pi | 230 ms | 0.15% | 5% | ±23 w | Low |
| Proposal technique | Hybrid control | 170 ms | 0.12% | 0% | ±5 w | High |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taoussi, M.; Bossoufi, B.; Bouderbala, M.; Motahhir, S.; Alkhammash, E.H.; Masud, M.; Zinelaabidine, N.; Karim, M. Implementation and Validation of Hybrid Control for a DFIG Wind Turbine Using an FPGA Controller Board. Electronics 2021, 10, 3154. https://doi.org/10.3390/electronics10243154
Taoussi M, Bossoufi B, Bouderbala M, Motahhir S, Alkhammash EH, Masud M, Zinelaabidine N, Karim M. Implementation and Validation of Hybrid Control for a DFIG Wind Turbine Using an FPGA Controller Board. Electronics. 2021; 10(24):3154. https://doi.org/10.3390/electronics10243154
Chicago/Turabian StyleTaoussi, Mohammed, Badre Bossoufi, Manale Bouderbala, Saad Motahhir, Eman H. Alkhammash, Mehedi Masud, Nada Zinelaabidine, and Mohammed Karim. 2021. "Implementation and Validation of Hybrid Control for a DFIG Wind Turbine Using an FPGA Controller Board" Electronics 10, no. 24: 3154. https://doi.org/10.3390/electronics10243154
APA StyleTaoussi, M., Bossoufi, B., Bouderbala, M., Motahhir, S., Alkhammash, E. H., Masud, M., Zinelaabidine, N., & Karim, M. (2021). Implementation and Validation of Hybrid Control for a DFIG Wind Turbine Using an FPGA Controller Board. Electronics, 10(24), 3154. https://doi.org/10.3390/electronics10243154










