Multi-Monostatic Interferometric Radar for Bridge Monitoring
Abstract
:1. Introduction
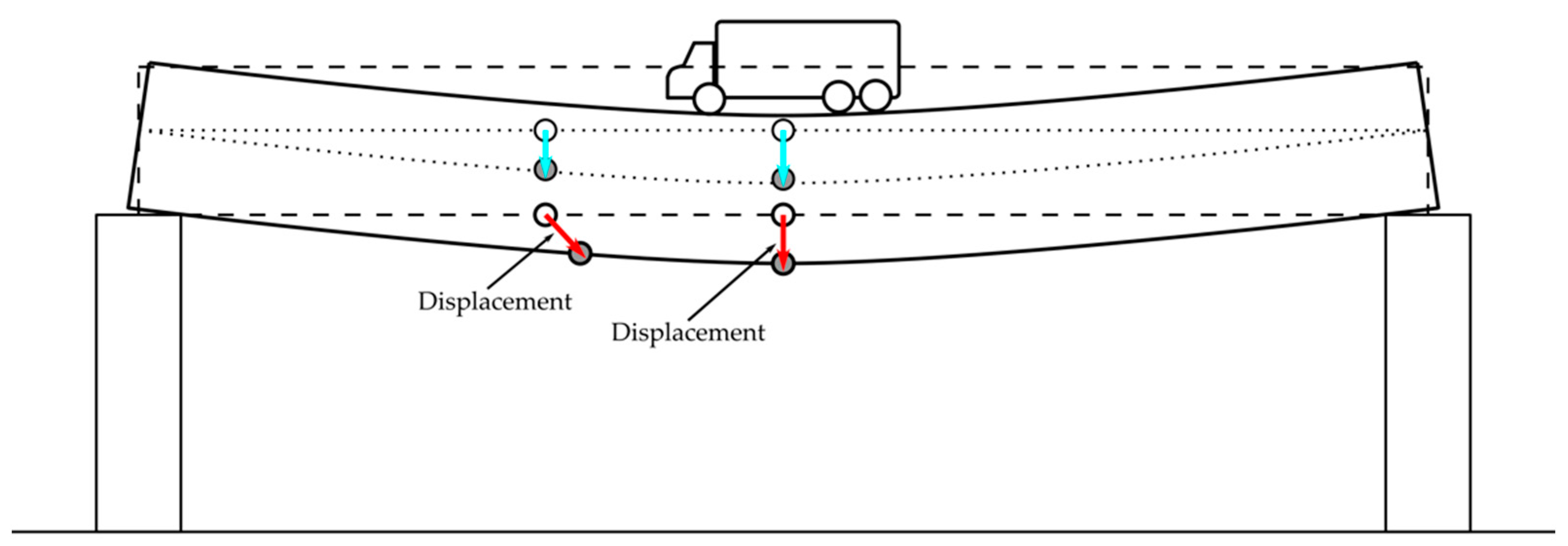
2. Materials and Methods
2.1. Methods
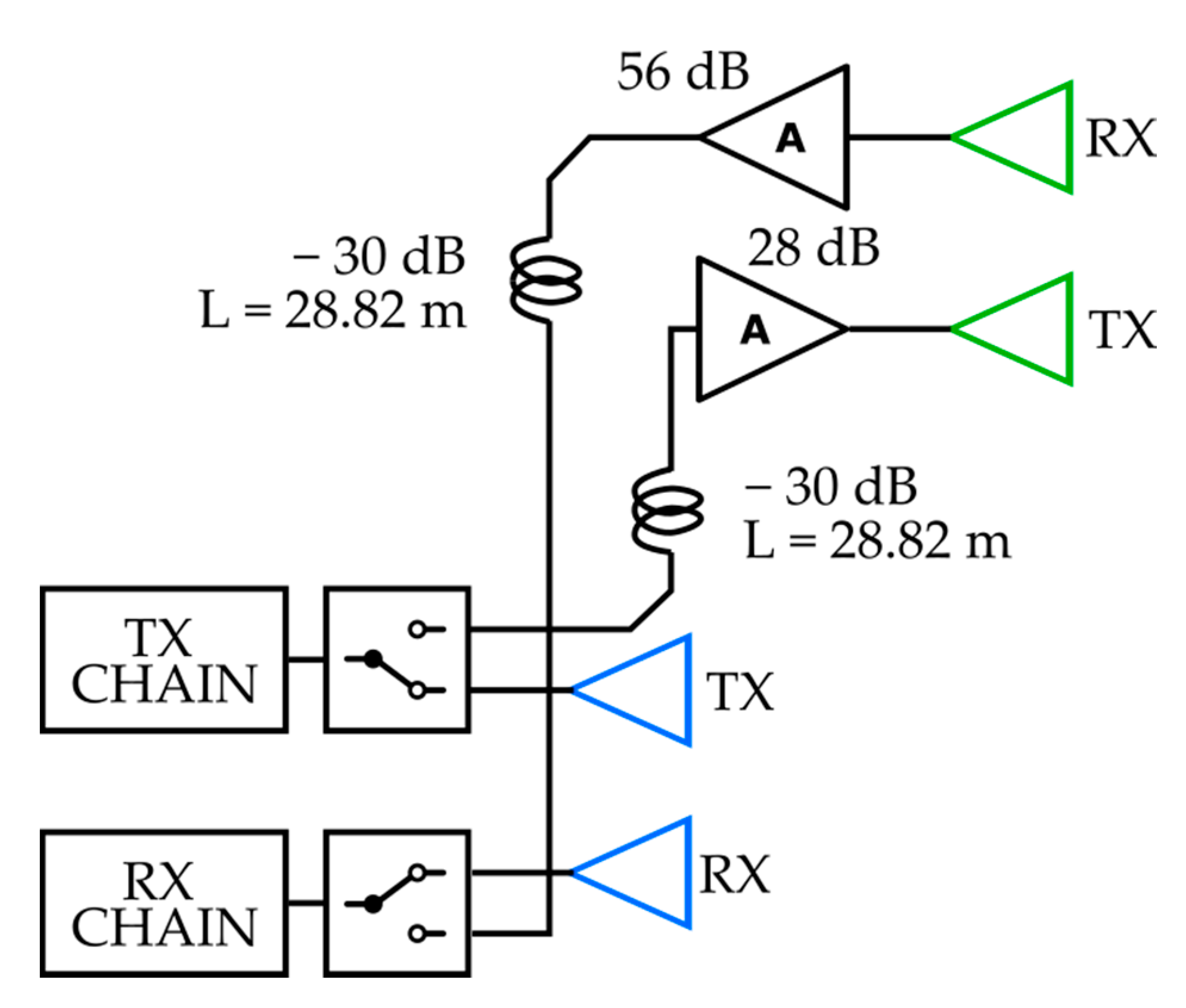
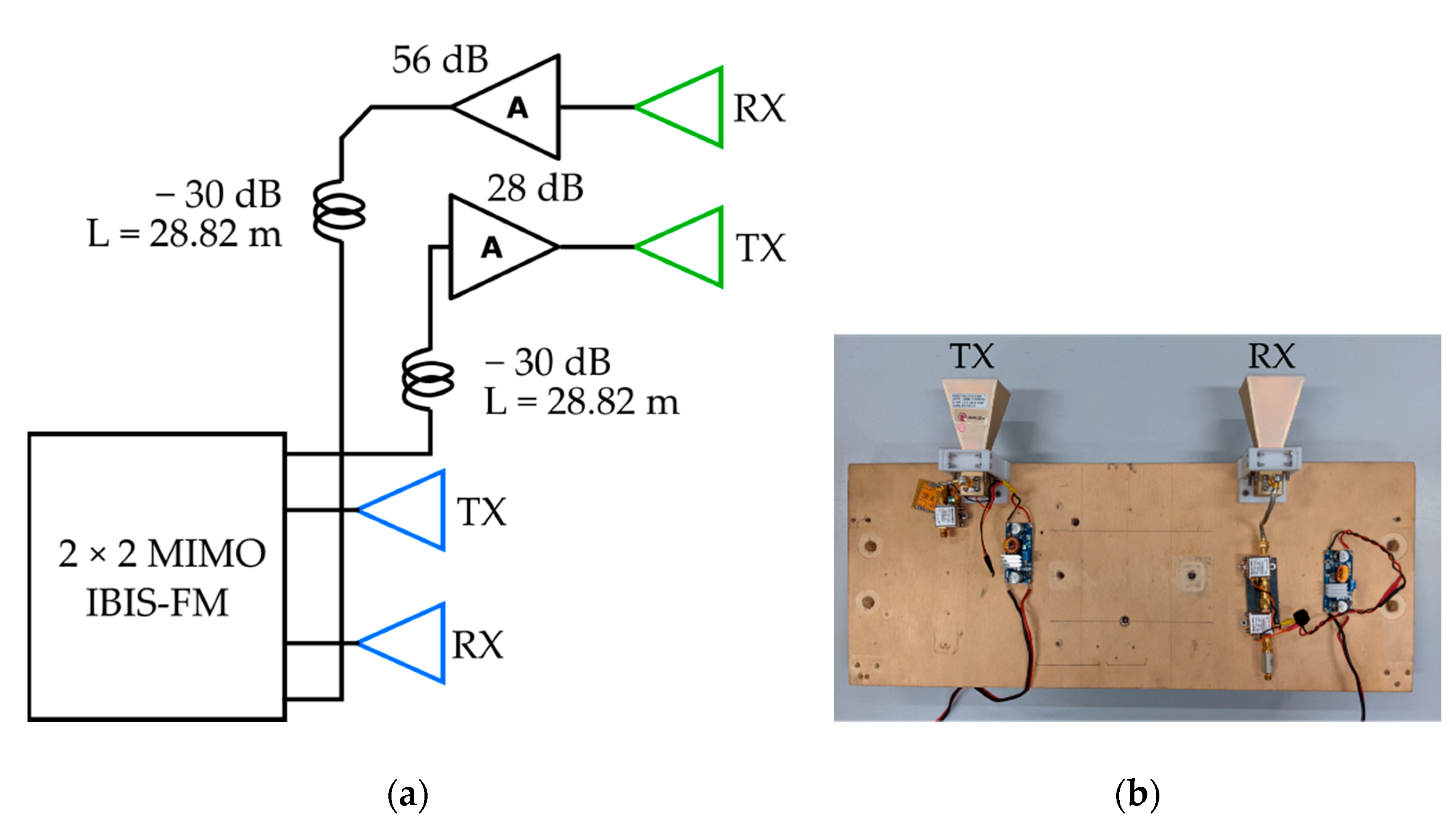
2.2. Radar Equipment
3. Results
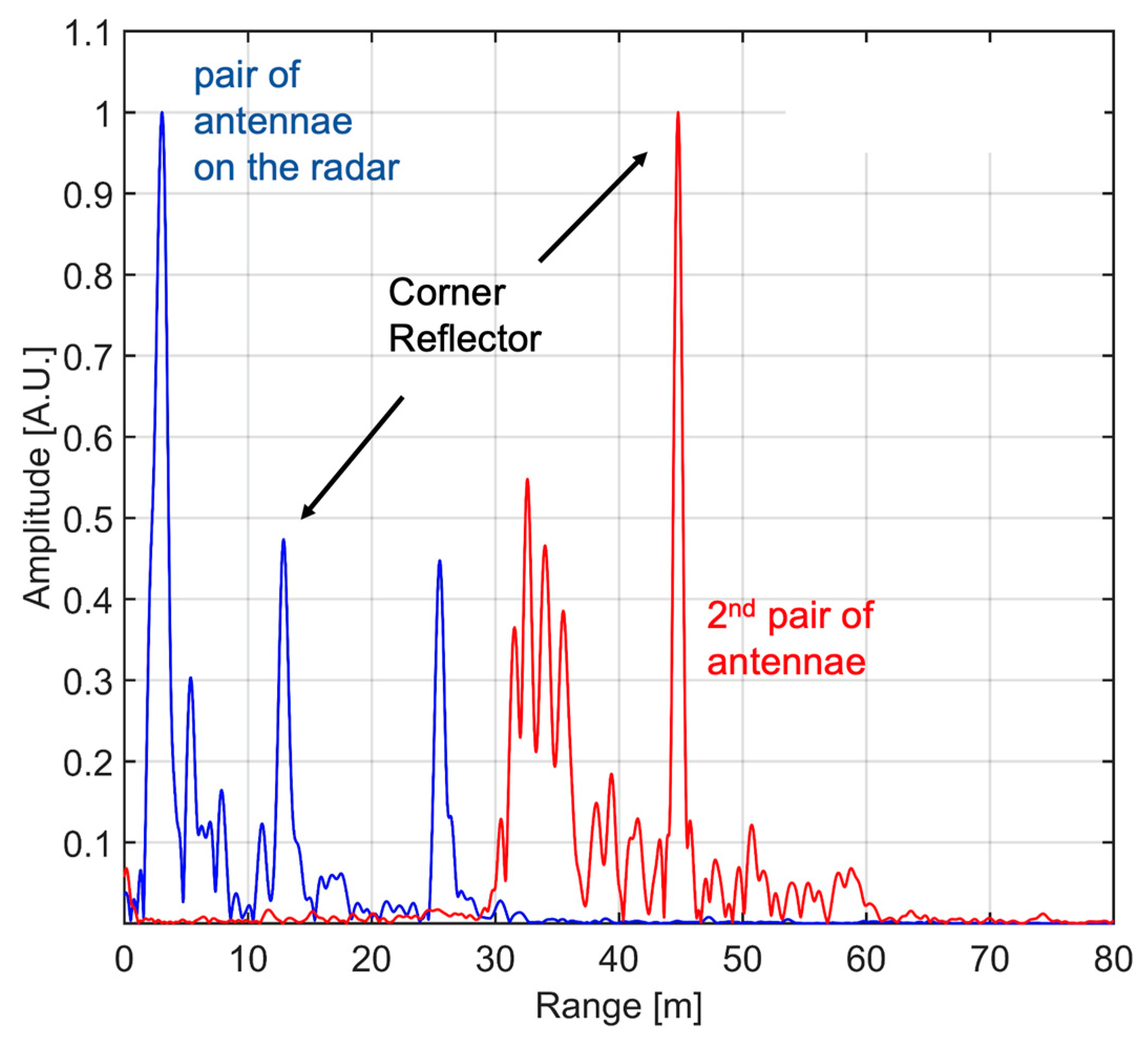
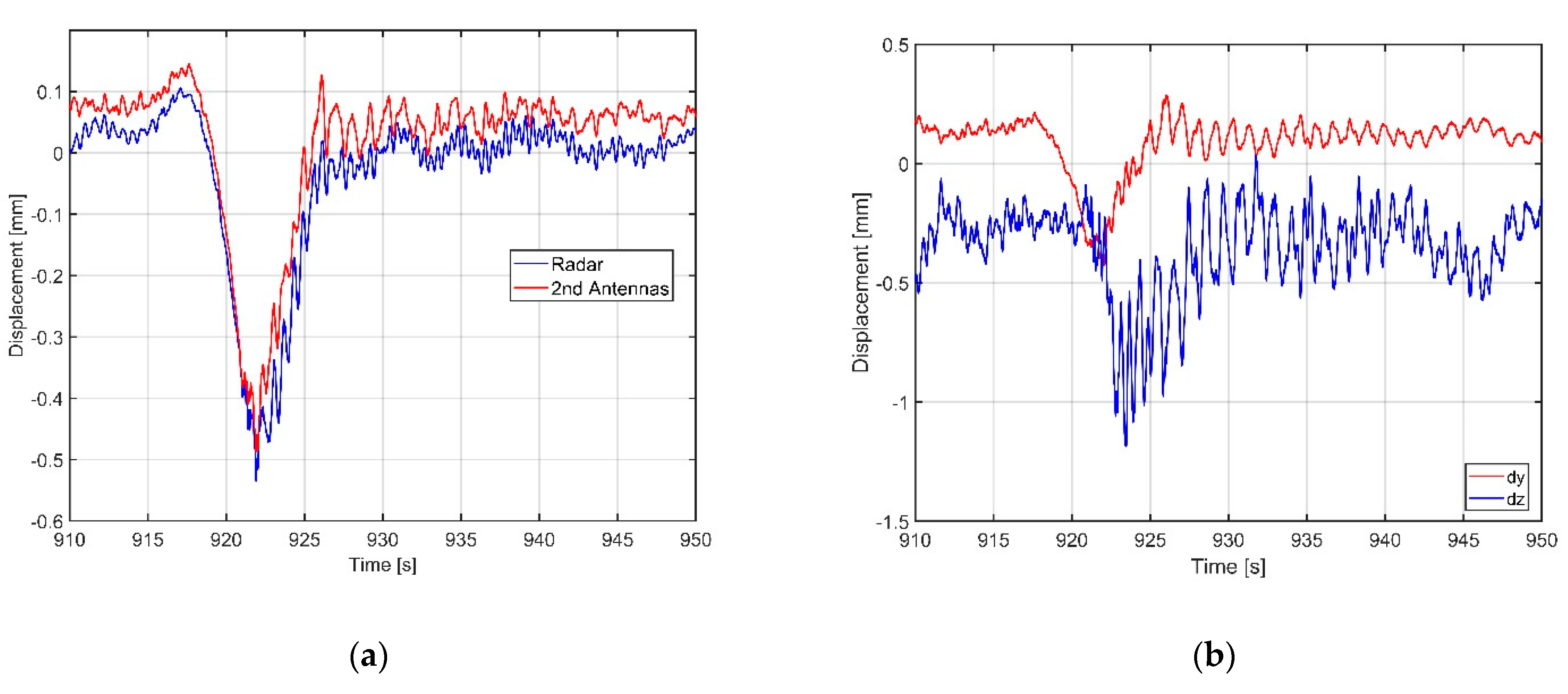
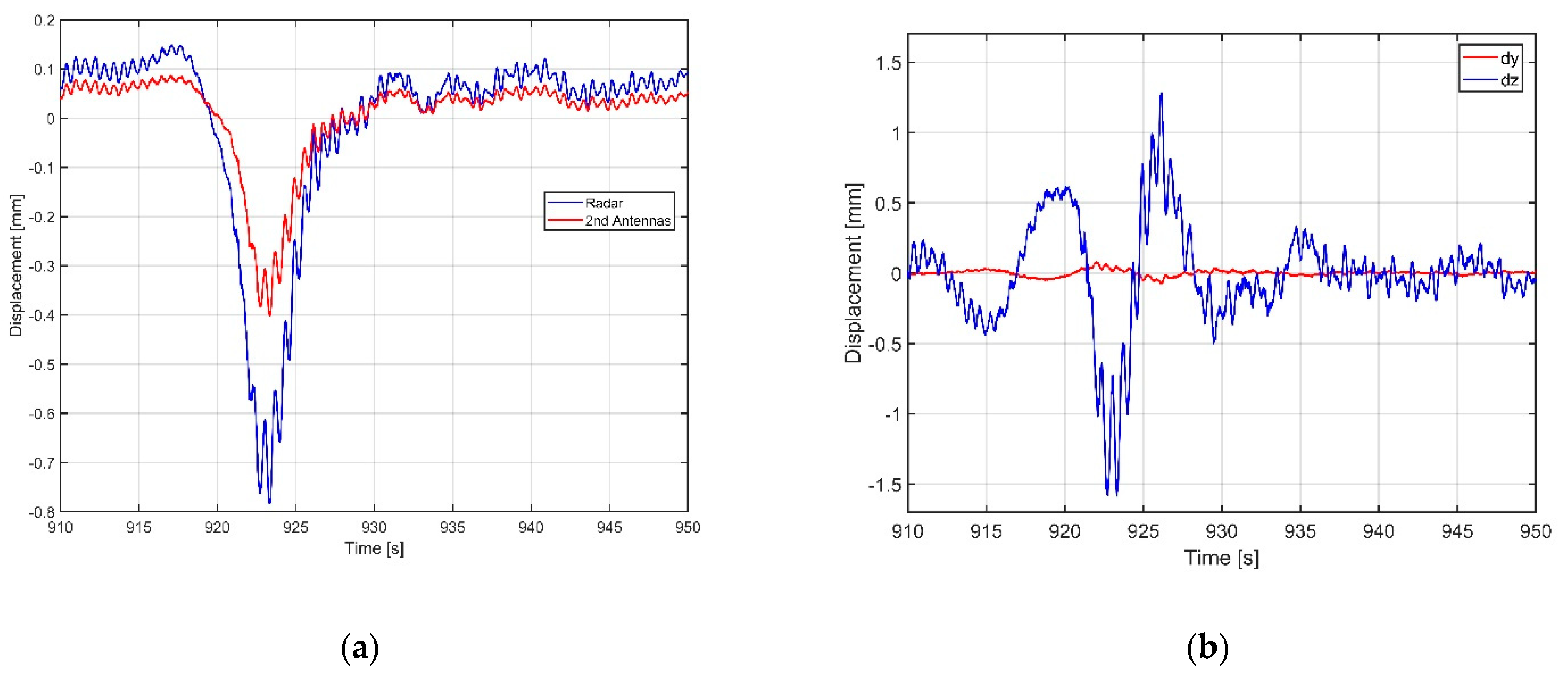
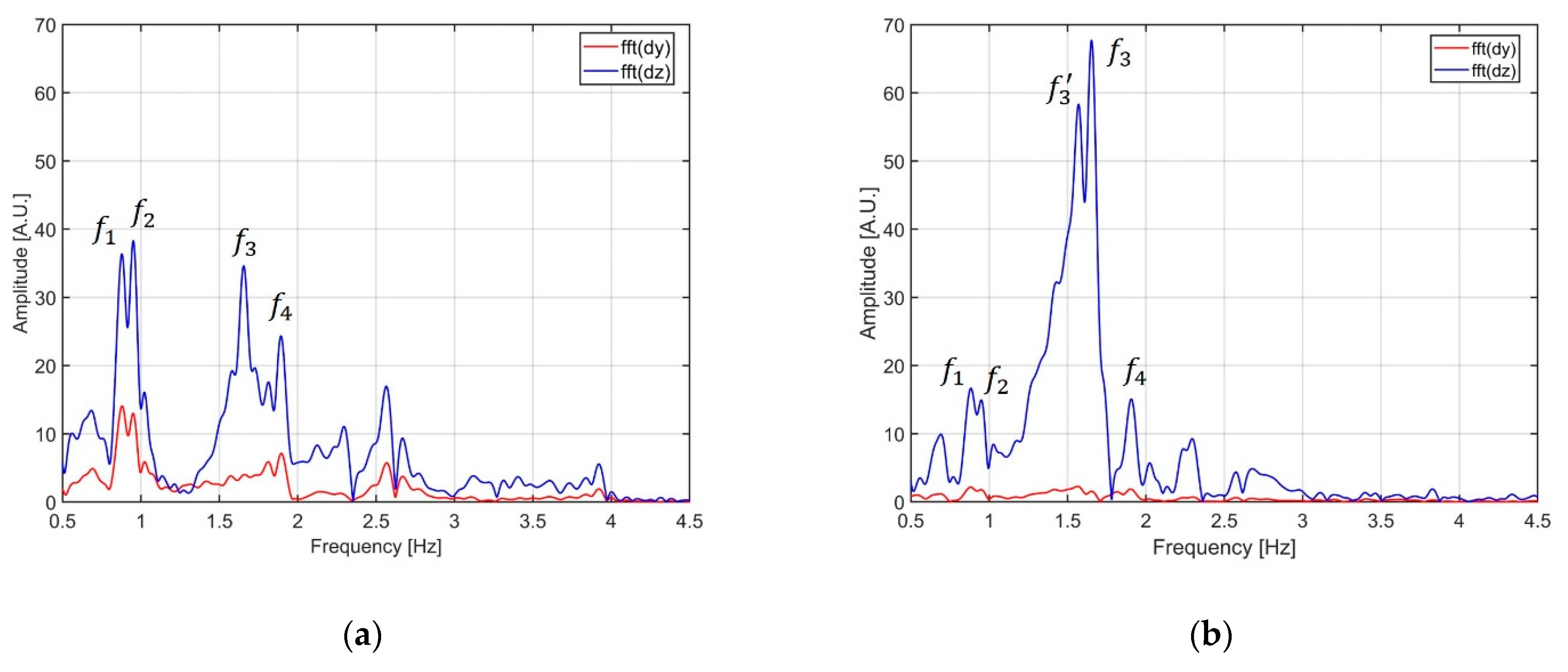
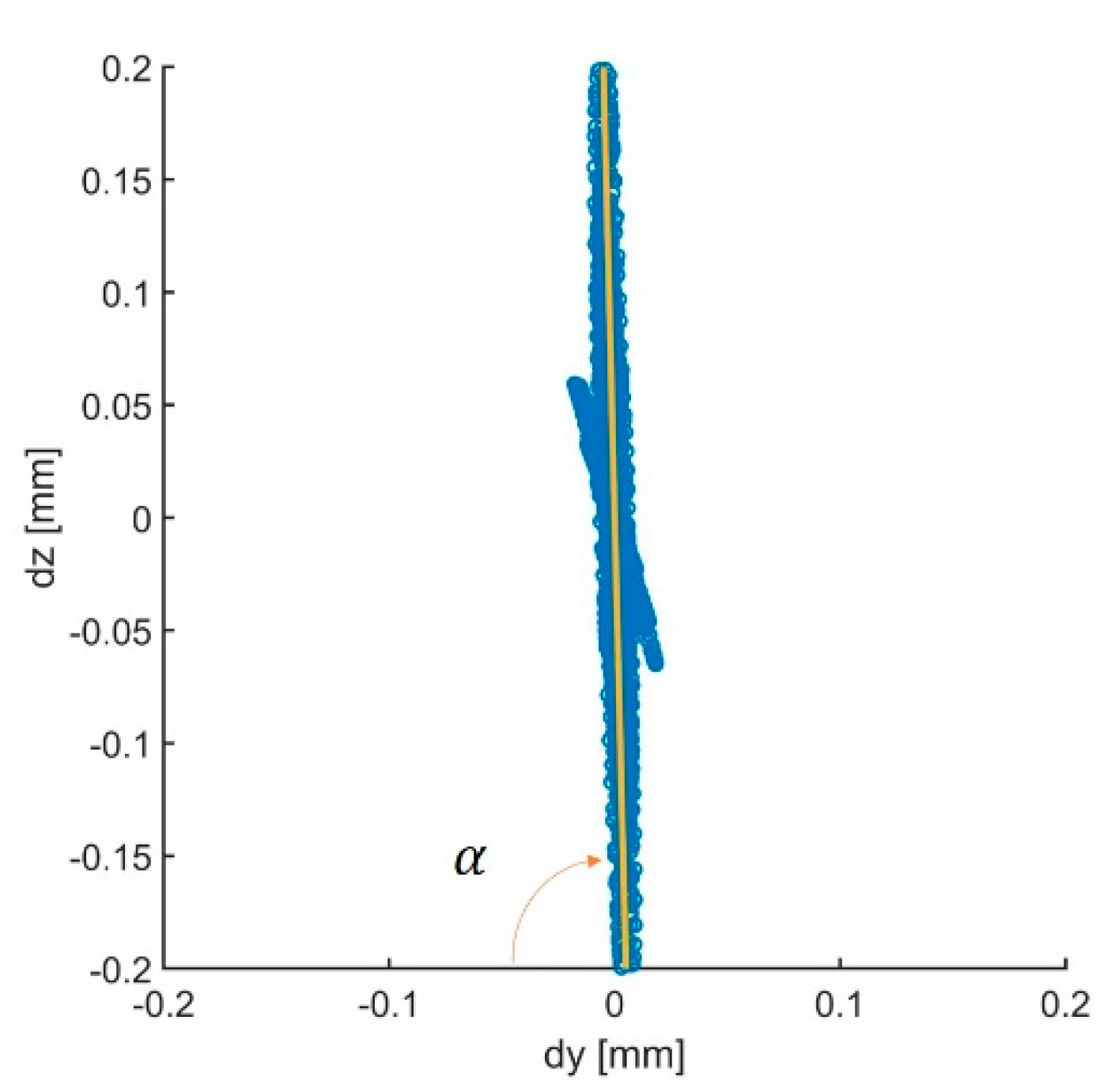
3.1. Experimental Results in Controlled Environment
3.2. Experimental Results of a Bridge
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pieraccini, M.; Parrini, F.; Fratini, M.; Atzeni, C.; Spinelli, P.; Micheloni, M. Static and dynamic testing of bridges through microwave interferometry. NDT E Int. 2007, 40, 208–214. [Google Scholar] [CrossRef]
- Stabile, T.A.; Perrone, A.; Gallipoli, M.R.; DiTommaso, R.; Ponzo, F.C. Dynamic Survey of the Musmeci Bridge by Joint Application of Ground-Based Microwave Radar Interferometry and Ambient Noise Standard Spectral Ratio Techniques. IEEE Geosci. Remote Sens. Lett. 2013, 10, 870–874. [Google Scholar] [CrossRef]
- Placidi, S.; Meta, A.; Testa, L.; Rodelsperger, S. Monitoring structures with FastGBSAR. In Proceedings of the 2015 IEEE Radar Conference, Johannesburg, South Africa, 27–30 October 2015; pp. 435–439. [Google Scholar]
- Luzi, G.; Crosetto, M.; Fernández, E. Radar Interferometry for Monitoring the Vibration Characteristics of Buildings and Civil Structures: Recent Case Studies in Spain. Sensors 2017, 17, 669. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, B.; Ding, X.; Werner, C.; Tan, K.; Zhang, B.; Jiang, M.; Zhao, J.; Xu, Y. Dynamic displacement monitoring of long-span bridges with a microwave radar interferometer. ISPRS J. Photogramm. Remote Sens. 2018, 138, 252–264. [Google Scholar] [CrossRef]
- Cardillo, E.; Caddemi, A. Radar Range-Breathing Separation for the Automatic Detection of Humans in Cluttered Environments. IEEE Sens. J. 2020, 1. [Google Scholar] [CrossRef]
- Rodriguez, D.; Li, C. Sensitivity and Distortion Analysis of a 125-GHz Interferometry Radar for Submicrometer Motion Sensing Applications. IEEE Trans. Microw. Theory Tech. 2019, 67, 5384–5395. [Google Scholar] [CrossRef]
- Dei, D.; Mecatti, D.; Pieraccini, M. Static Testing of a Bridge Using an Interferometric Radar: The Case Study of “Ponte degli Alpini,” Belluno, Italy. Sci. World J. 2013, 2013, 504958. [Google Scholar] [CrossRef] [PubMed]
- Guarnieri, A.M.; Falcone, P.; D’Aria, D.; Giunta, G. 3D Vibration Estimation from Ground-Based Radar. Remote Sens. 2018, 10, 1670. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Chen, L.; Liang, X.; Ding, C.-B.; Li, K. Implementation of the OFDM Chirp Waveform on MIMO SAR Systems. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5218–5228. [Google Scholar] [CrossRef]
- Tarchi, D.; Oliveri, F.; Sammartino, P.F. MIMO Radar and Ground-Based SAR Imaging Systems: Equivalent Approaches for Remote Sensing. IEEE Trans. Geosci. Remote Sens. 2013, 51, 425–435. [Google Scholar] [CrossRef]
- Michelini, A.; Coppi, F.; Bicci, A.; Alli, G. SPARX, a MIMO Array for Ground-Based Radar Interferometry. Sensors 2019, 19, 252. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hu, C.; Wang, J.; Tian, W.; Zeng, T.; Wang, R. Design and Imaging of Ground-Based Multiple-Input Multiple-Output Synthetic Aperture Radar (MIMO SAR) with Non-Collinear Arrays. Sensors 2017, 17, 598. [Google Scholar] [CrossRef] [PubMed]
- Cardillo, E.; Caddemi, A. A Review on Biomedical MIMO Radars for Vital Sign Detection and Human Localization. Electronics 2020, 9, 1497. [Google Scholar] [CrossRef]
- Deng, Y.; Hu, C.; Tian, W.; Zhao, Z. 3-D Deformation Measurement Based on Three GB-MIMO Radar Systems: Experimental Verification and Accuracy Analysis. IEEE Geosci. Remote Sens. Lett. 2020, 1–5. [Google Scholar] [CrossRef]
- Pieraccini, M.; Miccinesi, L.; Rojhani, N. A GBSAR Operating in Monostatic and Bistatic Modalities for Retrieving the Displacement Vector. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1–5. [Google Scholar] [CrossRef]
- Miccinesi, L.; Pieraccini, M. Monostatic/Bistatic Interferometric Radar for Monitoring Slander Structures. In Proceedings of the 2019 IEEE Conference on Antenna Measurements & Applications (CAMA), Kuta, Bali, Indonesia, 23–25 October 2019. [Google Scholar]
- Miccinesi, L.; Pieraccini, M. Bridge Monitoring by a Monostatic/Bistatic Interferometric Radar Able to Retrieve the Dynamic 3D Displacement Vector. IEEE Access 2020, 8, 210339–210346. [Google Scholar] [CrossRef]
- Pieraccini, M.; Fratini, M.; Parrini, F.; Atzeni, C.; Bartoli, G. Interferometric radar vs. accelerometer for dynamic monitoring of large structures: An experimental comparison. NDT E Int. 2008, 41, 258–264. [Google Scholar] [CrossRef]








| Position (x, y, z) [m] | |
|---|---|
| Radar | (0, 0, 0) |
| Second pair of antennae | (−7.33, 0, 0) |
| Target | (0, 12.88, 0) |
| Measurement 1 | Measurement 2 | Measurement 1 | Measurement 2 | |
|---|---|---|---|---|
| Radar component x | 1.737 | 1.734 | 3.490 | 3.517 |
| Radar component y | 1.755 | 1.764 | 3.486 | 3.518 |
| Accelerometer along y | 1.766 | – | N.D. | – |
| Accelerometer along x | – | N.D. 1 | – | 3.556 |
| Position (x, y, z) [m] | |
|---|---|
| Radar | (0, 0, 0) |
| Second group of antennae | (0, −2.86, 2.88) |
| Target A | (0, 23.27, 8.20) |
| Target B | (0, 33.16, 8.20) |
| Target A | Target B | |
|---|---|---|
| 0.883 | ||
| 0.950 | ||
| N.D. | 1.570 | |
| 1.906 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miccinesi, L.; Beni, A.; Pieraccini, M. Multi-Monostatic Interferometric Radar for Bridge Monitoring. Electronics 2021, 10, 247. https://doi.org/10.3390/electronics10030247
Miccinesi L, Beni A, Pieraccini M. Multi-Monostatic Interferometric Radar for Bridge Monitoring. Electronics. 2021; 10(3):247. https://doi.org/10.3390/electronics10030247
Chicago/Turabian StyleMiccinesi, Lapo, Alessandra Beni, and Massimiliano Pieraccini. 2021. "Multi-Monostatic Interferometric Radar for Bridge Monitoring" Electronics 10, no. 3: 247. https://doi.org/10.3390/electronics10030247
APA StyleMiccinesi, L., Beni, A., & Pieraccini, M. (2021). Multi-Monostatic Interferometric Radar for Bridge Monitoring. Electronics, 10(3), 247. https://doi.org/10.3390/electronics10030247







