A Single-Terminal Fault Location Method for HVDC Transmission Lines Based on a Hybrid Deep Network
Abstract
:1. Introduction
- (1)
- CNN-LSTM was used to solve many shortcomings of the single-ended traveling wave method, including high sampling frequency, difficulty to determine wave velocity and identify wave heads when an HIF occurs. It provides high precision and strong robustness to fault types, noise, sampling frequency, and different HVDC topologies in fault location.
- (2)
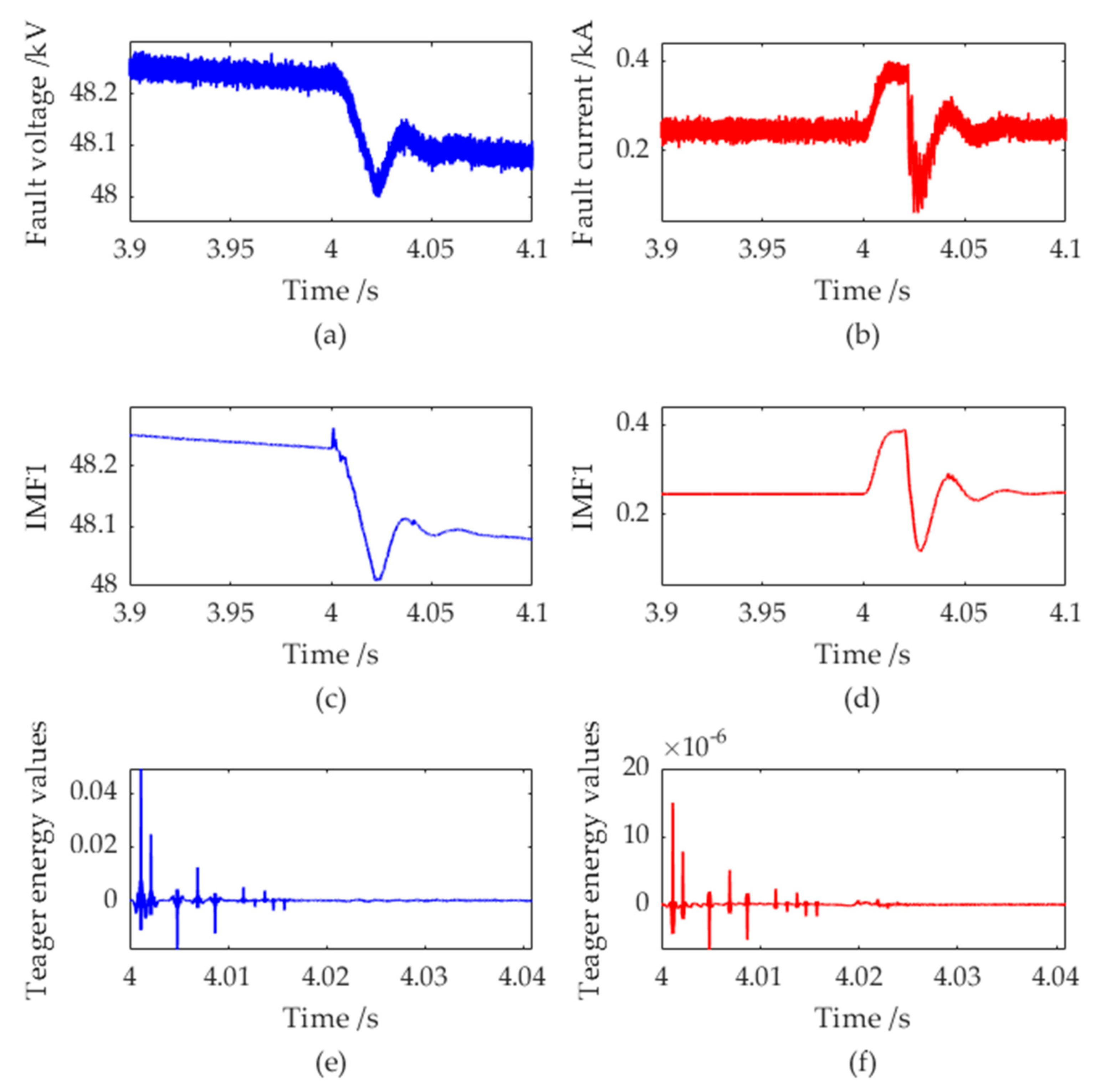
- VMD-TEO was used for feature engineering, which made the characteristics of the fault signals obvious. It reduced the dependence of deep learning on the number of samples to a certain extent, thereby improving the learning efficiency and accuracy of CNN-LSTM.
- (3)
- A comparison experiment of 1D-CNN and recurrent networks including LSTM, GRU and Bi-GRU as a regressor in the hybrid model explained the reason for choosing LSTM. Compared with feature engineering methods such as WT and HHT, VMD-TEO showed a better performance on the accuracy of fault location through CNN-LSTM.
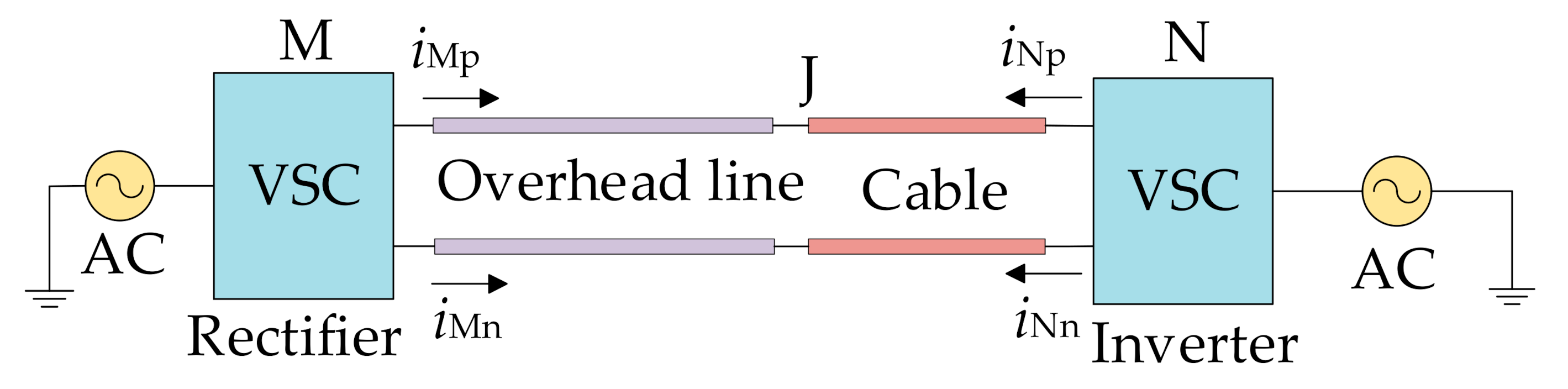
2. Fault Location Based on Traveling Wave Theory
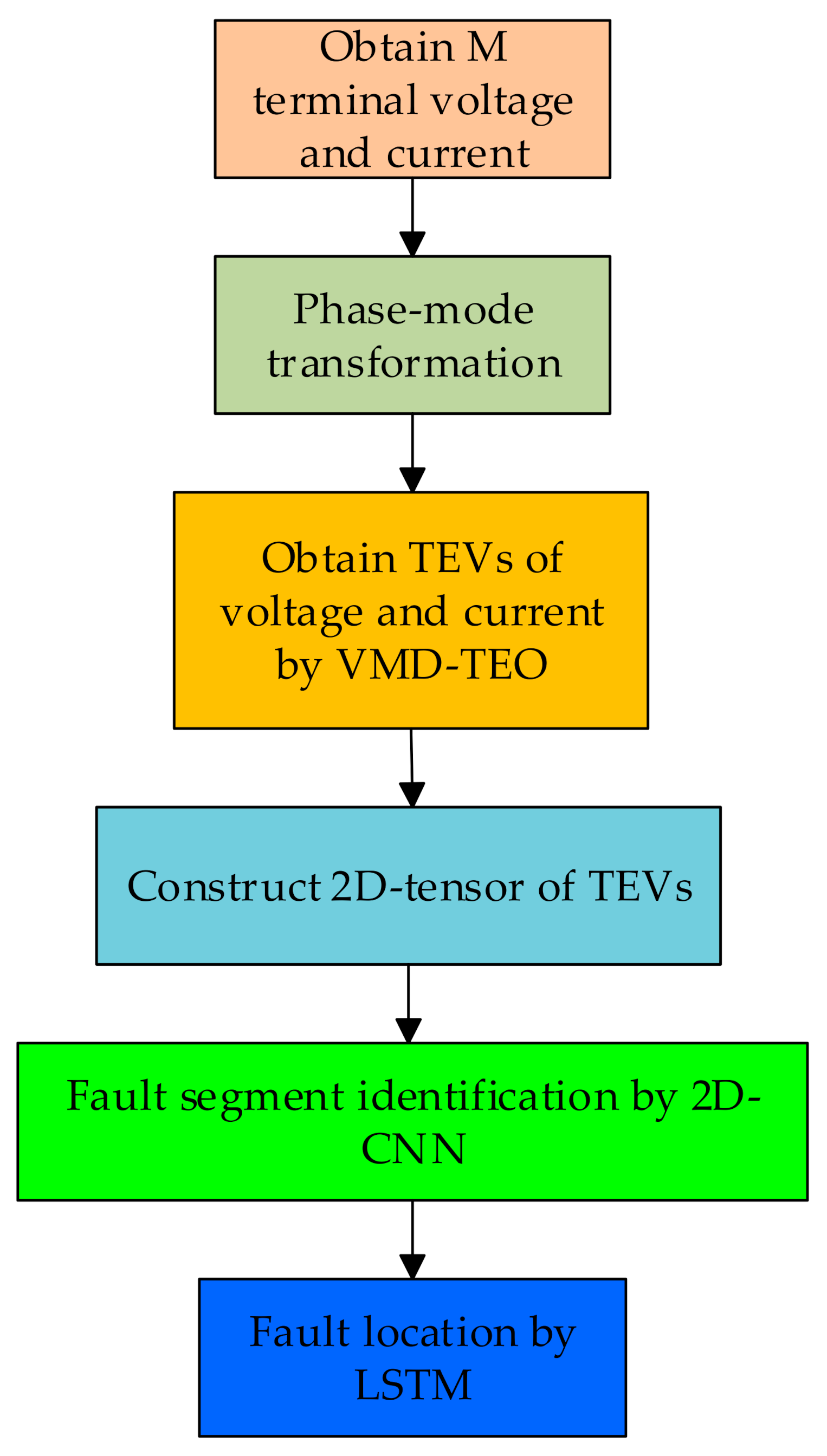
2.1. Feature Engineering and Acquisition of Samples
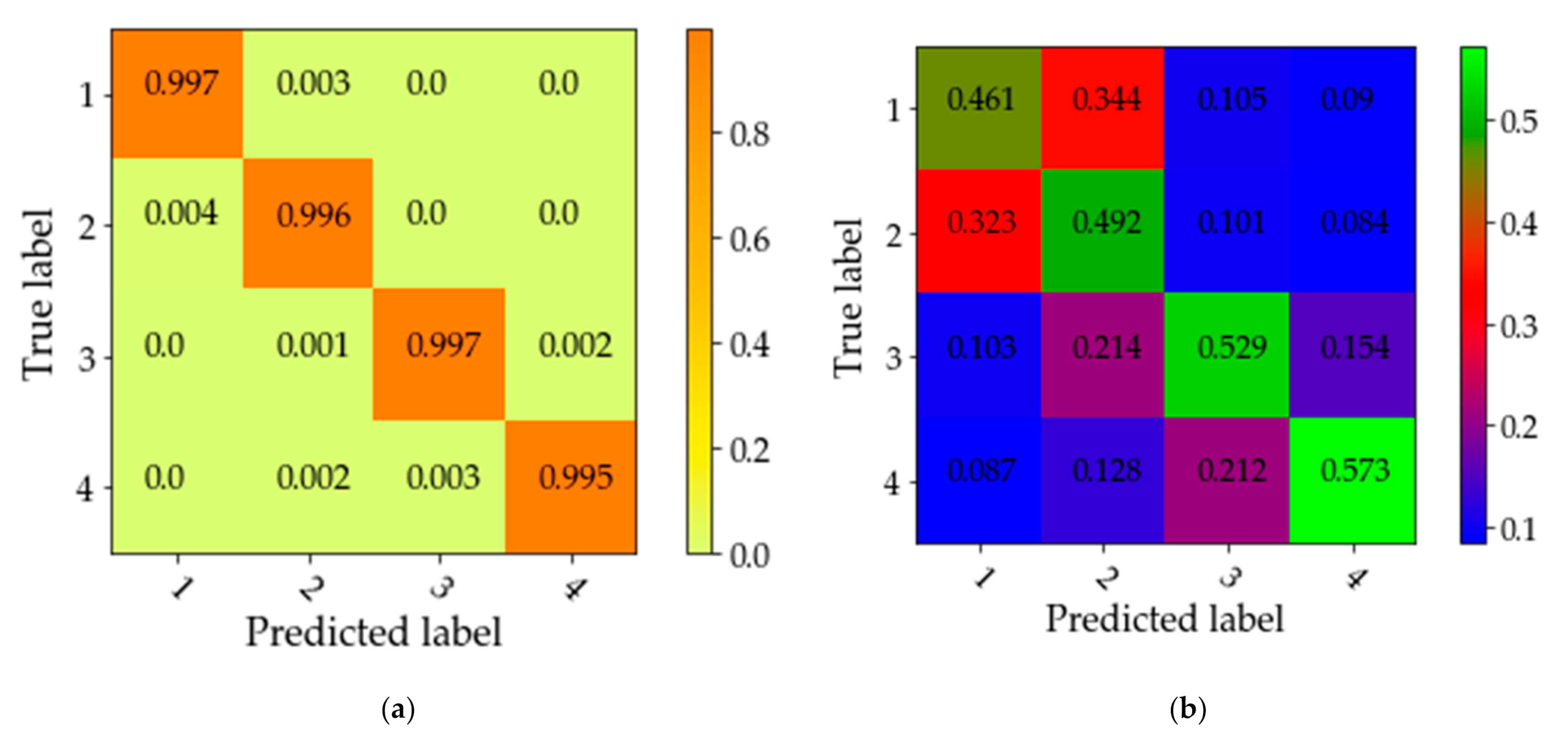
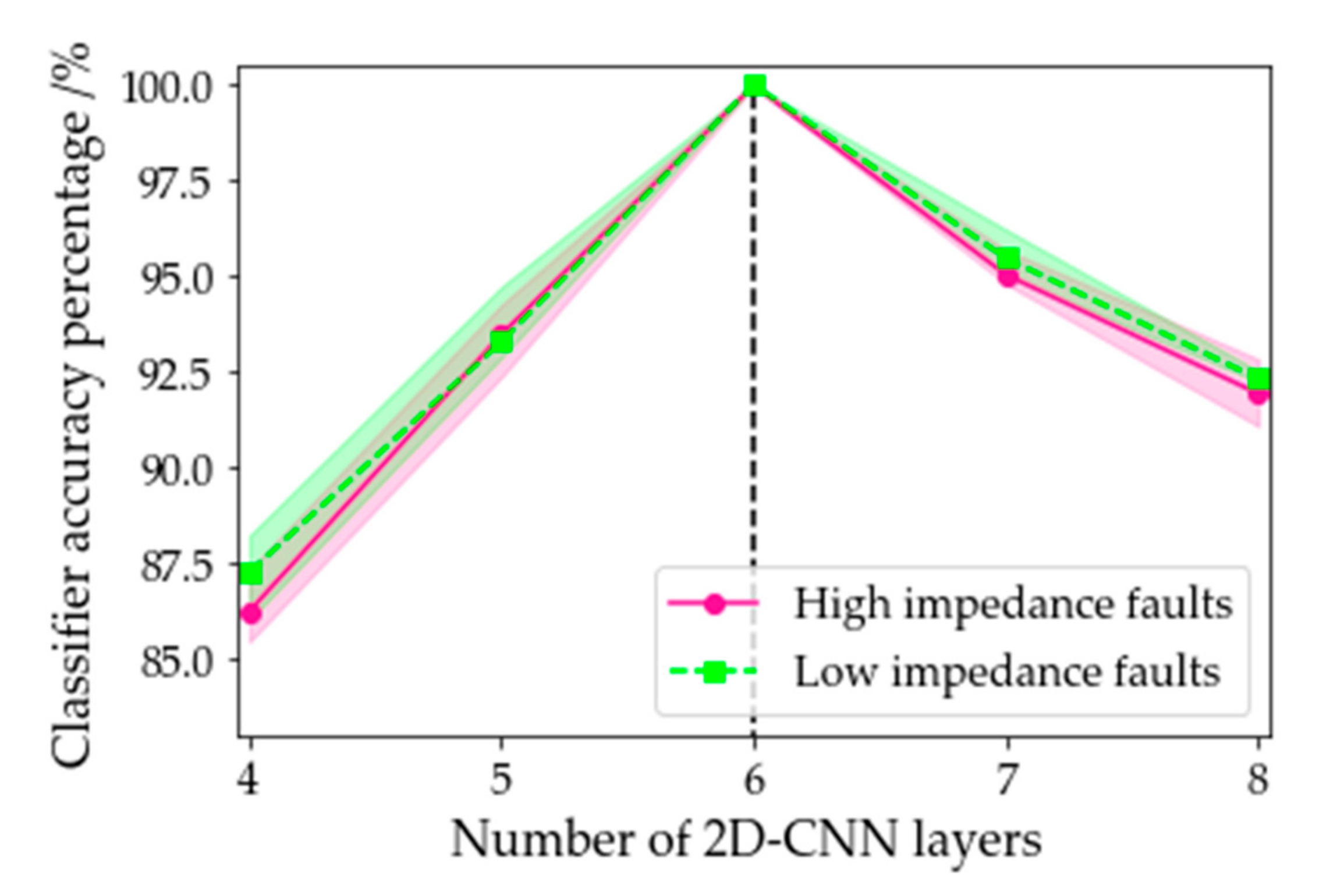
2.2. Fault Segment Identification Based on 2D-CNN
2.3. Single-Ended Traveling Wave Method for Fault Location
3. Fault Location Based on CNN-LSTM
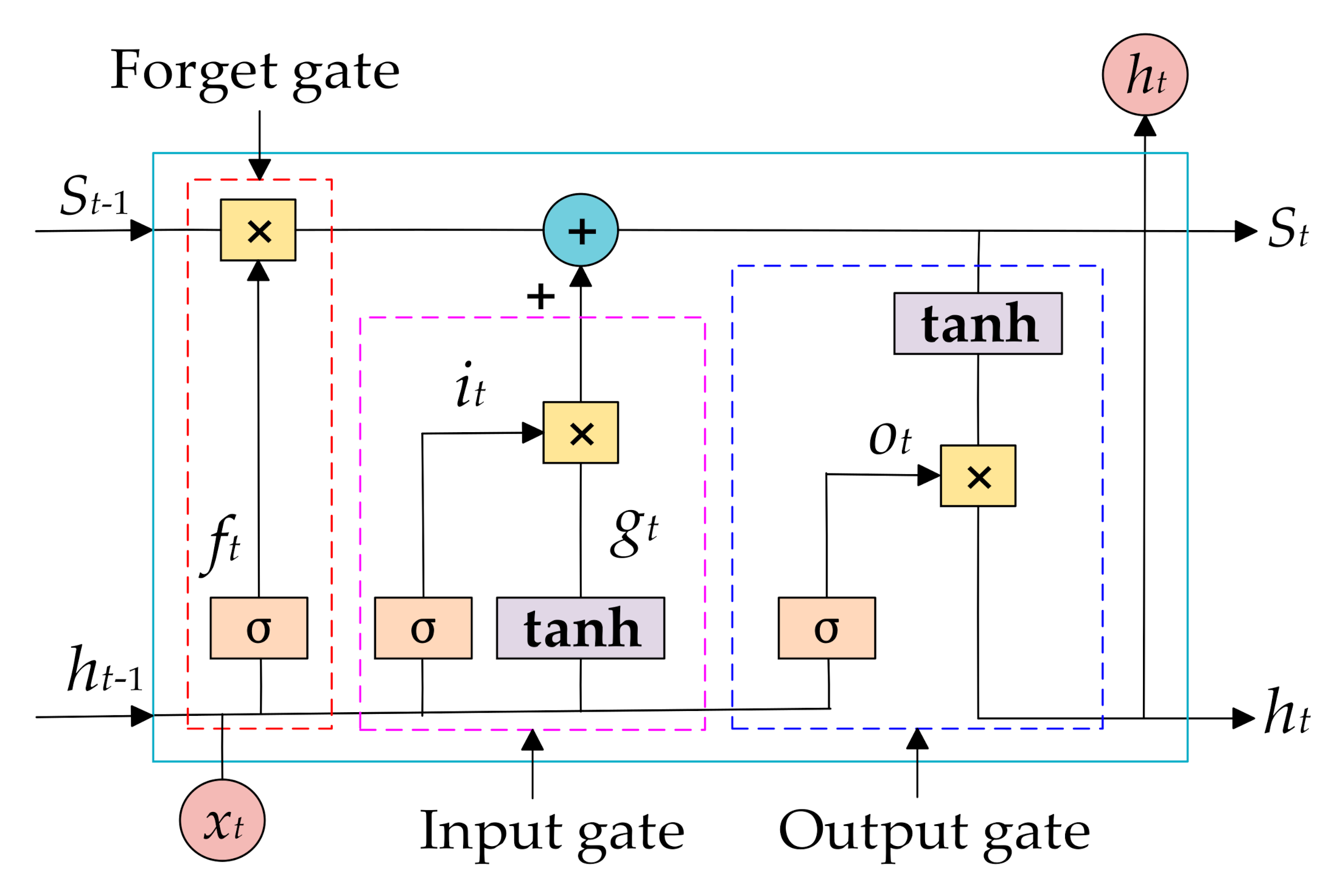
3.1. Theoretical Background of LSTM
3.2. CNN-LSTM Hybrid Model for Fault Location
4. Simulation Results and Analysis
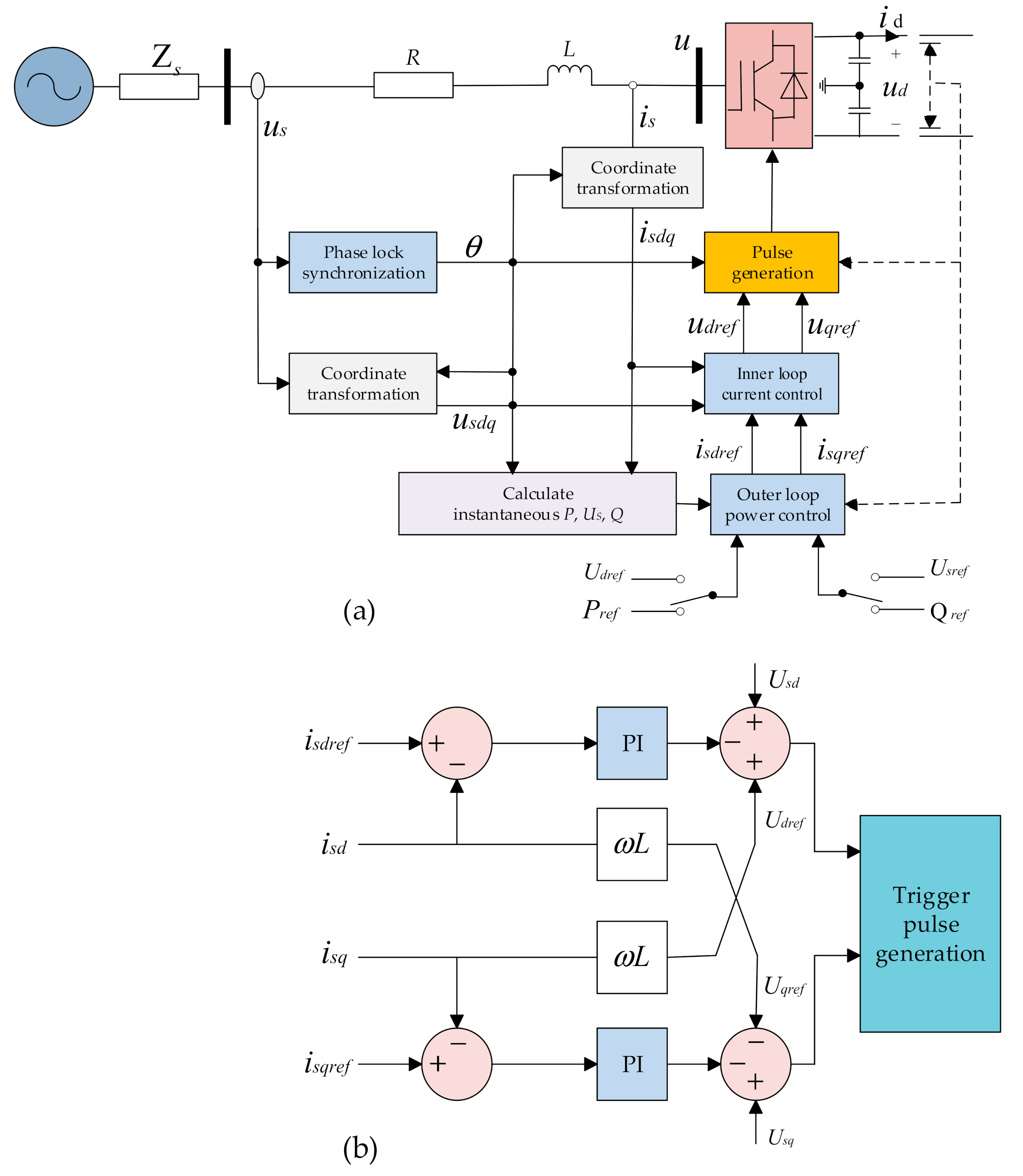
4.1. Simulation Model and Related Parameters
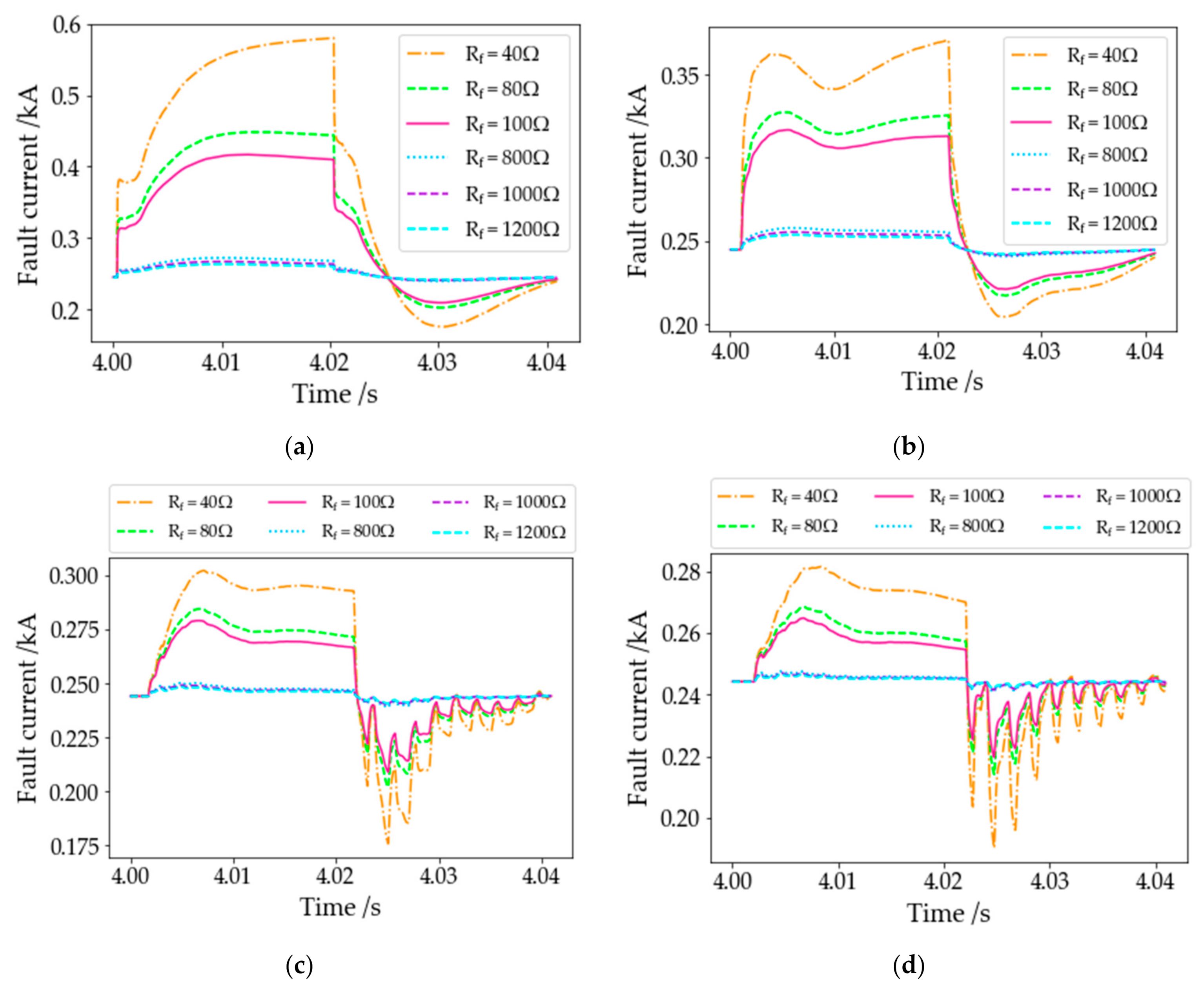
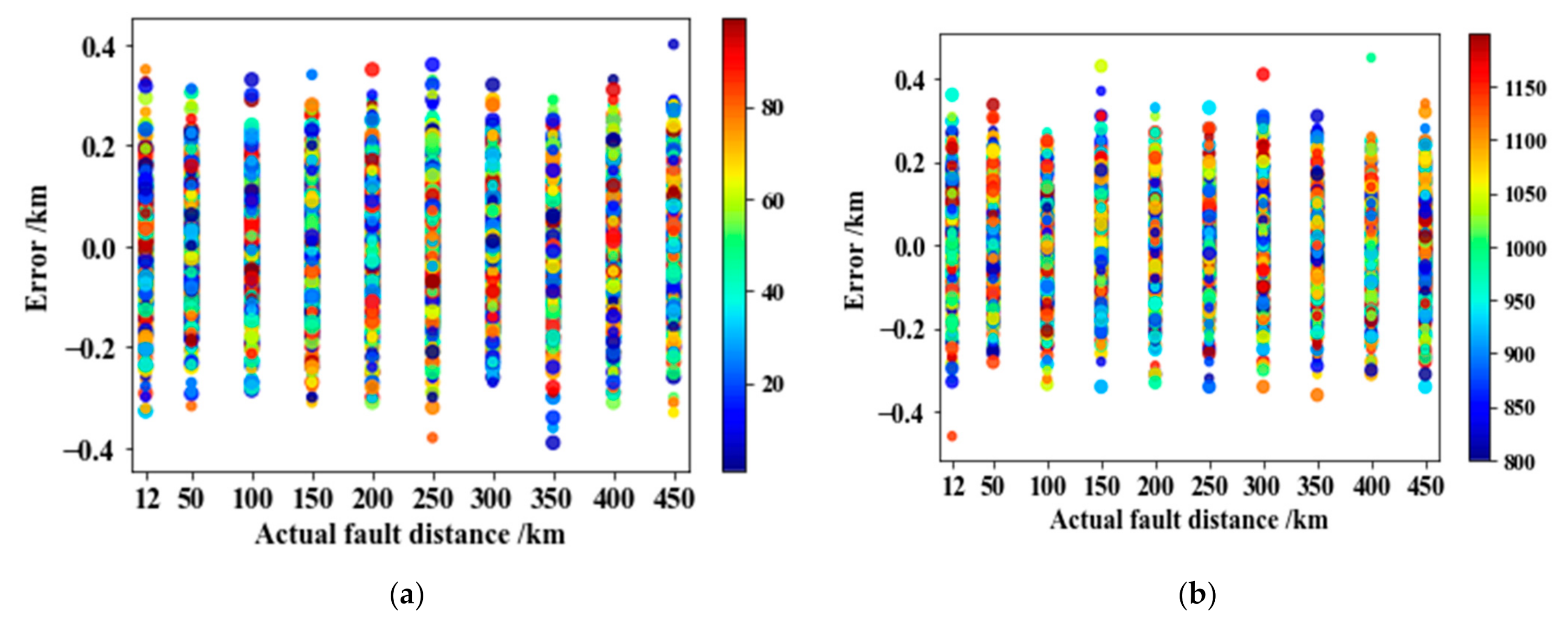
4.2. Experimental Result of Traveling Wave Method
- (1)
- The change step size of the fault distance is taken as 1 km.
- (2)
- Transition resistance Rf = 0.0001%, 1%, 2%, 3% … 100% of the maximum transition resistance.
- (3)
- Fault types include PG, NG, and PN.
4.3. Experimental Result of CNN-LSTM
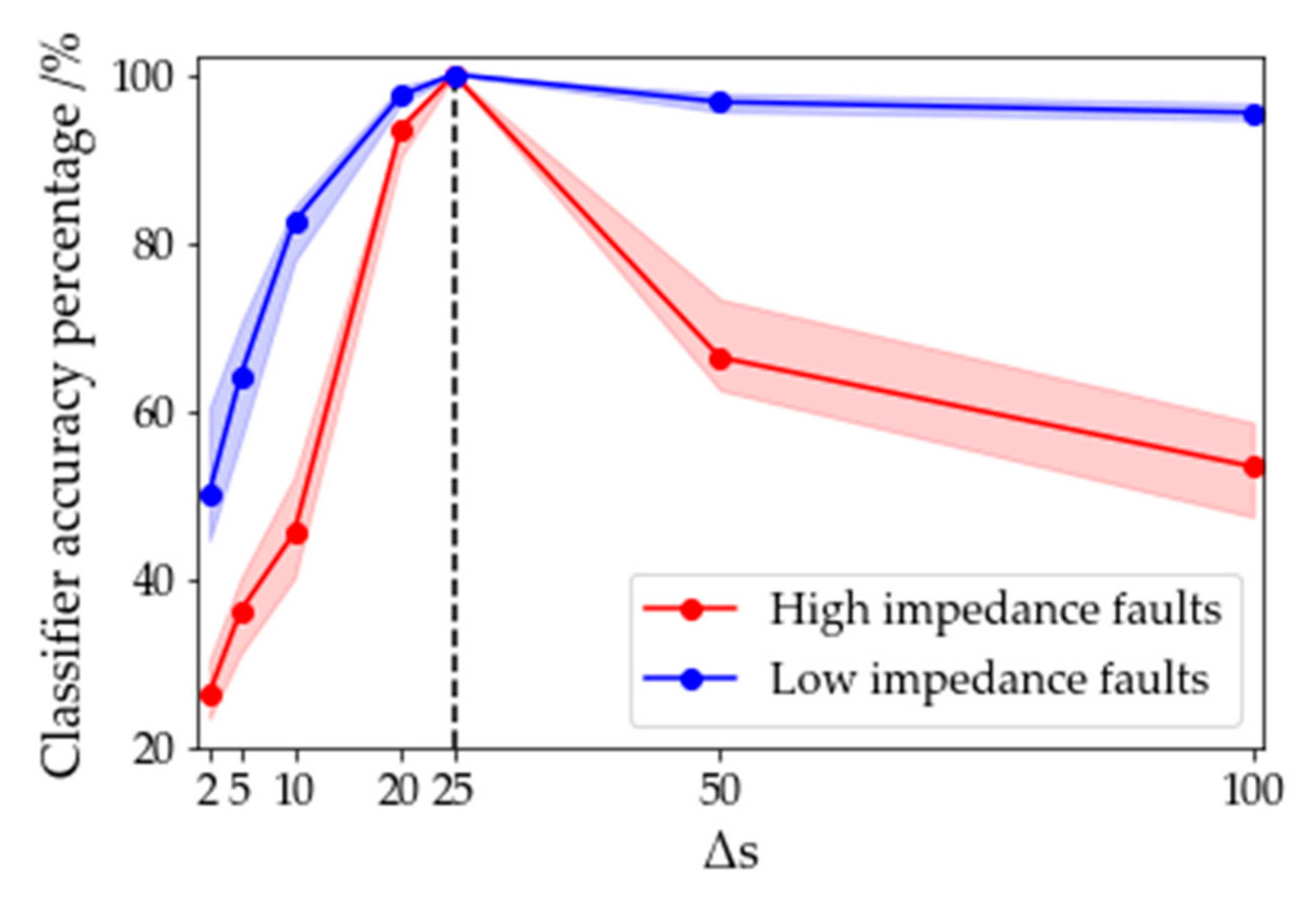
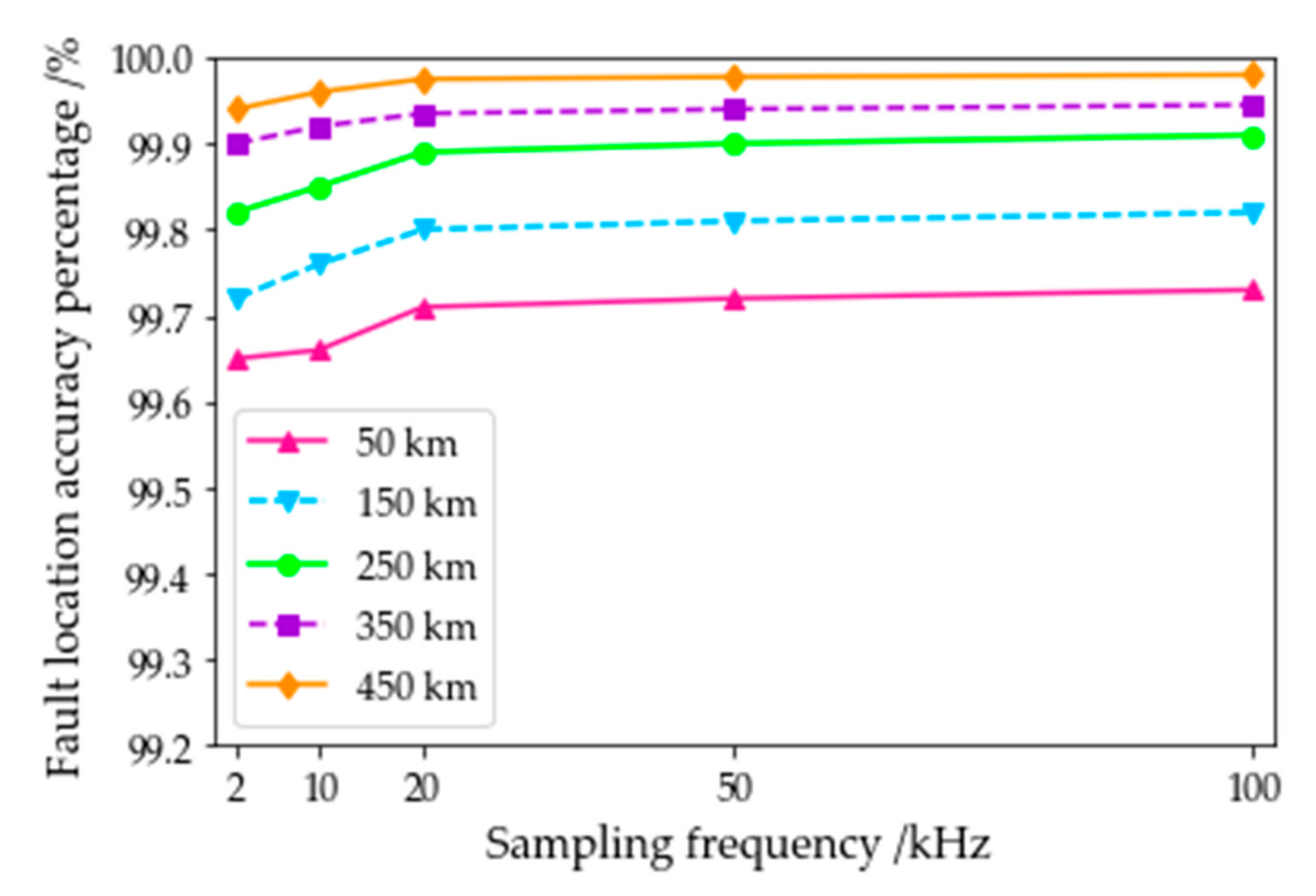
4.4. Influence of Sampling Frequency
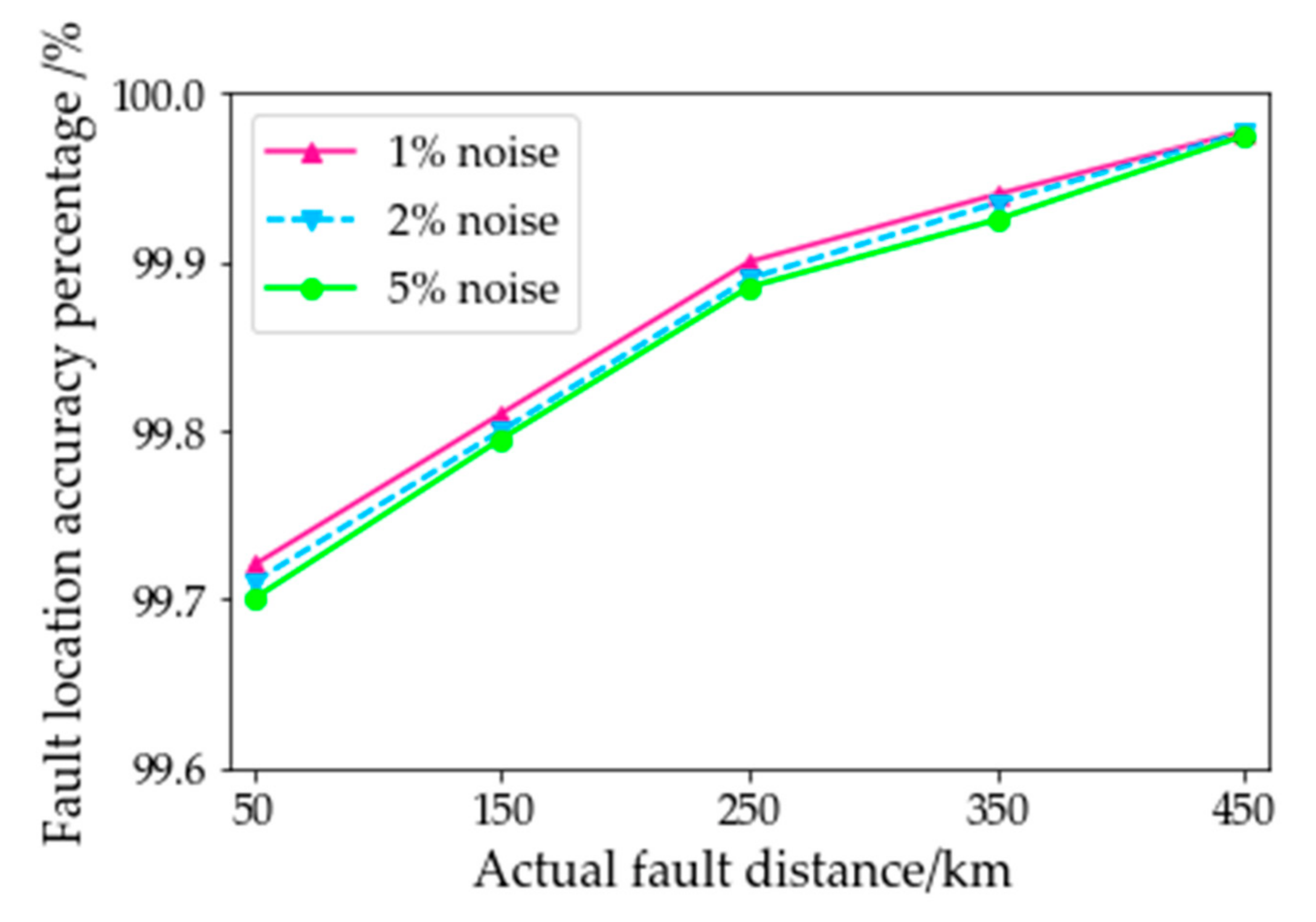
4.5. Influence of Noise
4.6. Comparison of Other Methods
4.7. Other HVDC Model
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| HVDC | High voltage direct current |
| CNN | Convolutional neural network |
| LSTM | Long short-term memory |
| VMD | Variational mode decomposition |
| TEO | Teager energy operator |
| WT | Wavelet transform |
| HHT | Hilbert–Huang transform |
| VMD-TEO | Variational mode decomposition–Teager energy operator |
| EMD | Empirical mode decomposition |
| LIF | Low impedance fault |
| HIF | High impedance fault |
| RNN | Recurrent neural network |
| GRU | Gated recurrent unit |
| Bi-GRU | Bidirectional gated recurrent unit |
| IMF | Intrinsic mode function |
| IMF1 | The first intrinsic mode function component |
| TEV | Teager energy value |
| VSC | Voltage source converter |
| NG | Negative ground |
| ELU | Exponential linear unit |
| PG | Positive ground |
| PN | Positive and negative |
References
- Nanayakkara, O.M.K.K.; Rajapakse, A.D.; Wachal, R. Location of DC line faults in conventional HVDC systems with segments of cables and overhead lines using terminal measurements. IEEE Trans. Power Deliv. 2012, 27, 279–288. [Google Scholar] [CrossRef]
- Chen, K.; Hu, J.; Zhang, Y.; Yu, Z.; He, J. Fault location in power distribution systems via deep graph convolutional networks. IEEE J. Sel. Areas Commun. 2020, 38, 119–131. [Google Scholar] [CrossRef] [Green Version]
- Bains, T.P.S.; Sidhu, T.S.; Xu, Z.H.; Voloh, I.; Zadeh, M.R.D. Impedance-based fault location algorithm for ground faults in series-capacitor-compensated transmission lines. IEEE Trans. Power Deliv. 2018, 33, 189–199. [Google Scholar] [CrossRef]
- Kezunovic, M. Smart Fault Location for Smart Grids. IEEE Trans. Smart Grid 2011, 2, 11–22. [Google Scholar] [CrossRef]
- Shu, H.C.; Han, Y.M.; Huang, R.; Tang, Y.T.; Cao, P.L.; Yang, B.; Zhang, Y. Fault Model and Travelling Wave Matching Based Single Terminal Fault Location Algorithm for T-Connection Transmission Line: A Yunnan Power Grid Study. Energies 2020, 13, 1506. [Google Scholar] [CrossRef] [Green Version]
- Lin, S.; He, Z.; Li, X. Travelling wave time-frequency characteristic-based fault location method for transmission lines. IET Gener. Transm. Distrib. 2012, 6, 764–772. [Google Scholar] [CrossRef]
- Livani, H.; Evrenosoglu, C.Y. A single-ended fault location method for segmented HVDC transmission line. Electr. Power Syst. Res. 2014, 107, 190–198. [Google Scholar] [CrossRef]
- Spoor, D.; Zhu, H.G. Improved single-ended traveling-wave fault-location algorithm based on experience with conventional substation transducers. IEEE Trans. Power Deliv. 2006, 21, 1714–1720. [Google Scholar] [CrossRef] [Green Version]
- He, Z.Y.; Liao, K.; Li, X.P.; Lin, S.; Yang, J.W.; Mai, R.K. Natural Frequency-based line fault location in HVDC lines. IEEE Trans. Power Deliv. 2014, 29, 851–859. [Google Scholar] [CrossRef]
- Zhang, C.; Song, G.; Wang, T.; Yang, L. Single-ended traveling wave fault location method in DC transmission line based on wave front information. IEEE Trans. Power Deliv. 2019, 34, 2028–2038. [Google Scholar] [CrossRef]
- Borghetti, A.; Bosetti, M.; Di Silvestro, M.; Nucci, C.A.; Paolone, M. Continuous-wavelet transform for fault location in distribution power networks: Definition of mother wavelets inferred from fault originated transients. IEEE Trans. Power Syst. 2008, 23, 380–388. [Google Scholar] [CrossRef]
- Bernadic, A.; Leonowicz, Z. Fault location in power networks with mixed feeders using the complex space-phasor and Hilbert–Huang transform. Int. J. Electr. Power Energy Syst. 2012, 42, 208–219. [Google Scholar] [CrossRef] [Green Version]
- Xie, L.; Luo, L.; Li, Y.; Zhang, Y.; Cao, Y. A traveling wave-based fault location method employing VMD-TEO for distribution network. IEEE Trans. Power Deliv. 2020, 35, 1987–1998. [Google Scholar] [CrossRef]
- Wang, L.; Liu, H.; Le Van, D.; Liu, Y. Novel method for identifying fault location of mixed lines. Energies 2018, 11, 1529. [Google Scholar] [CrossRef] [Green Version]
- Lan, S.; Chen, M.-J.; Chen, D.-Y. A novel HVDC double-terminal non-synchronous fault location method based on convolutional neural network. IEEE Trans. Power Deliv. 2019, 34, 848–857. [Google Scholar] [CrossRef]
- Duan, J.; Liu, J.; Lu, H.; Zhao, Z. Fault location method based on traveling-wave instantaneous frequency for HVDC transmission lines. Proc. CSEE. 2016, 36, 1842–1848. [Google Scholar]
- Zhang, X.; Tai, N.; Wang, Y.; Liu, J. EMTR-based fault location for DC line in VSC-MTDC system using high-frequency currents. IET Gener. Transm. Distrib. 2017, 11, 2499–2507. [Google Scholar] [CrossRef]
- Moradzadeh, A.; Zakeri, S.; Shoaran, M.; Mohammadi-Ivatloo, B.; Mohammadi, F. Short-term load forecasting of microgrid via hybrid support vector regression and long short-term memory algorithms. Sustainability 2020, 12, 7076. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Pham, L.H.; Mohammadi, F.; Kien, L.C. Optimal scheduling of large-scale wind-hydro-thermal systems with fixed-head short-term model. Appl. Sci. 2020, 10, 2964. [Google Scholar] [CrossRef]
- Dash, P.K.; Samantaray, S.R.; Panda, G. Fault classification and section identification of an advanced series-compensated transmission line using support vector machine. IEEE Trans. Power Deliv. 2007, 22, 67–73. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, Q.; Liu, Y. Novel fault location method for power systems based on attention mechanism and double structure GRU neural network. IEEE Access 2020, 8, 75237–75248. [Google Scholar] [CrossRef]
- Alves da Silva, A.P.; Lima, A.C.S.; Souza, S.M. Fault location on transmission lines using complex-domain neural networks. Int. J. Electr. Power Energy Syst. 2012, 43, 720–727. [Google Scholar] [CrossRef]
- Livani, H.; Evrenosoglu, C.Y. A machine learning and wavelet-based fault location method for hybrid transmission lines. IEEE Trans. Smart Grid 2014, 5, 51–59. [Google Scholar] [CrossRef]
- Shi, Z.; Liang, H.; Dinavahi, V. Direct interval forecast of uncertain wind power based on recurrent neural networks. IEEE Trans. Sustain. Energy 2018, 9, 1177–1187. [Google Scholar] [CrossRef]
- Ergen, T.; Kozat, S.S. Online training of LSTM networks in distributed systems for variable length data sequences. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 5159–5165. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ding, M.; Zhou, H.; Xie, H.; Wu, M.; Nakanishi, Y.; Yokoyama, R. A gated recurrent unit neural networks based wind speed error correction model for short-term wind power forecasting. Neurocomputing 2019, 365, 54–61. [Google Scholar] [CrossRef]
- Zhao, R.; Wang, D.; Yan, R. Machine health monitoring using local feature-based gated recurrent unit networks. IEEE Trans. Ind. Electron. 2018, 65, 1539–1548. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Du, Y.; Li, F.; Li, J.; Zheng, T. Achieving 100x acceleration for N-1 contingency screening with uncertain scenarios using deep convolutional neural network. IEEE Trans. Power Syst. 2019, 34, 3303–3305. [Google Scholar] [CrossRef]
- Passalis, N.; Tefas, A. Training lightweight deep convolutional neural networks using bag-of-features pooling. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 1705–1715. [Google Scholar] [CrossRef]
- Al Hassan, H.A.; Grainger, B.M.; McDermott, T.E.; Reed, G.F. Fault location identification of a hybrid HVDC-VSC system containing cable and overhead line segments using transient data. In Proceedings of the IEEE PES T&D 2016, Dallas, TX, USA, 3–5 May 2016. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A 1998, 454, 903–998. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Li, Y.; Fan, C.; Li, Y.; Wu, Q.; Ming, Y. Improving deep neural network with multiple parametric exponential linear units. Neurocomputing 2018, 301, 11–24. [Google Scholar] [CrossRef] [Green Version]
- Mohammadi, F.; Nazri, G.-A.; Saif, M. A new topology of a fast proactive hybrid DC circuit breaker for MT-HVDC Grids. Sustainability 2019, 11, 4493. [Google Scholar] [CrossRef] [Green Version]



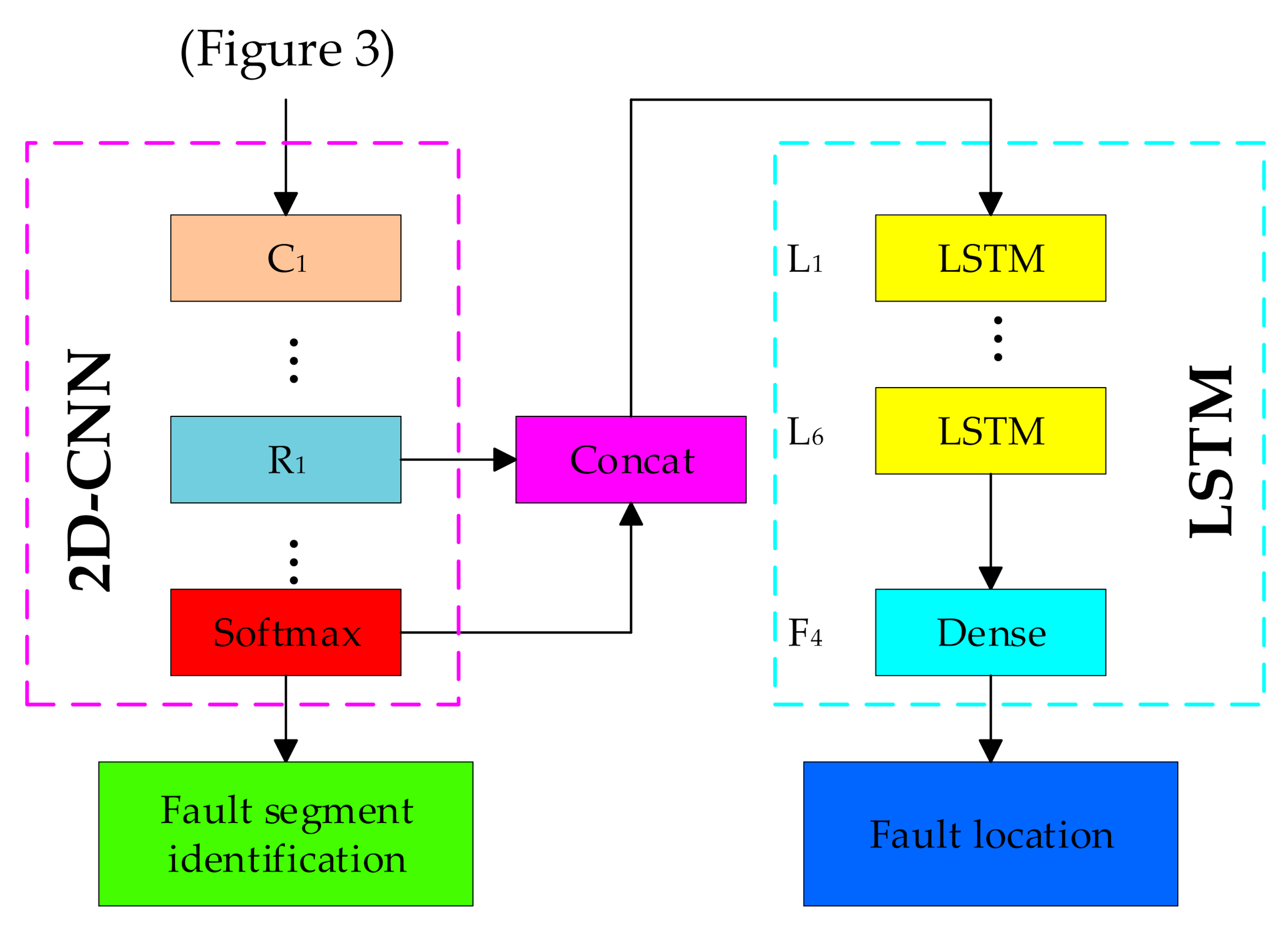





| Layer Types | Kernel/Pool Size | Sub- Sampling Layer | Stride | Number of Kernels | Number of Neurons | Activation Function | Outputs |
|---|---|---|---|---|---|---|---|
| Input layer | - | - | - | - | - | - | 2 × 4096 × 1 |
| C1 | 2 × 2 | - | 1 | 16 | - | ELU | 2 × 4096 × 16 |
| S1 | 2 × 2 | Maximum | 2 | - | - | - | 1 × 2048 × 16 |
| C2 | 2 × 2 | - | 1 | 16 | - | ELU | 1 × 2048 × 16 |
| S2 | 1 × 2 | Maximum | 2 | - | - | - | 1 × 1024 × 16 |
| C3 | 2 × 2 | - | 1 | 32 | - | ELU | 1 × 1024 × 32 |
| S3 | 1 × 2 | Maximum | 2 | - | - | - | 1 × 512 × 32 |
| C4 | 2 × 2 | - | 1 | 32 | - | ELU | 1× 512 × 32 |
| S4 | 1 × 2 | Maximum | 2 | - | - | - | 1 × 256 × 32 |
| C5 | 2 × 2 | - | 1 | 64 | - | ELU | 1 × 256 × 64 |
| S5 | 1 × 2 | Average | 2 | - | - | - | 1 × 128 × 64 |
| C6 | 2 × 2 | - | 1 | 64 | - | ELU | 1 × 128 × 64 |
| S6 | 1 × 2 | Average | 2 | - | - | - | 1 × 64 × 64 |
| R1 | - | - | - | - | - | - | 4096 |
| F1 | - | - | - | - | 200 | ELU | 200 |
| D1 | - | - | - | - | - | - | 200 |
| F2 | - | - | - | - | 64 | ELU | 64 |
| D2 | - | - | - | - | - | - | 64 |
| F3 | - | - | - | - | N | Softmax | N |
| Fault Distance | WT | HHT | VMD-TEO | |||
|---|---|---|---|---|---|---|
| Distance | Error | Distance | Error | Distance | Error | |
| (km) | (km) | (km) | (km) | (km) | (km) | (km) |
| 50 | 53.797 | 3.797 | 53.386 | 2.386 | 50.137 | 0.137 |
| 100 | 103.827 | 3.827 | 95.564 | 4.436 | 99.773 | 0.227 |
| 150 | 153.624 | 3.624 | 153.518 | 3.518 | 150.265 | 0.265 |
| 200 | 196.671 | 3.329 | 204.447 | 4.447 | 200.272 | 0.272 |
| 250 | 254.227 | 4.227 | 244.596 | 5.404 | 250.257 | 0.257 |
| 300 | 305.106 | 5.106 | 304.234 | 4.234 | 300.251 | 0.251 |
| 400 | 404.534 | 4.534 | 396.522 | 3.478 | 400.197 | 0.197 |
| 450 | 446.575 | 3.425 | 455.416 | 5.416 | 450.234 | 0.234 |
| Fault Distance | 1D-CNN | GRU | Bi-GRU | LSTM | ||||
|---|---|---|---|---|---|---|---|---|
| Distance | Error | Distance | Error | Distance | Error | Distance | Error | |
| (km) | (km) | (km) | (km) | (km) | (km) | (km) | (km) | (km) |
| 50 | 54.186 | 4.186 | 51.186 | 1.186 | 51.919 | 1.919 | 50.137 | 0.137 |
| 100 | 104.333 | 4.333 | 101.333 | 1.333 | 98.179 | 1.821 | 99.773 | 0.227 |
| 150 | 154.221 | 4.221 | 151.221 | 1.221 | 151.978 | 1.978 | 150.265 | 0.265 |
| 200 | 195.896 | 4.104 | 198.896 | 1.104 | 202.149 | 2.149 | 200.272 | 0.272 |
| 250 | 254.131 | 4.131 | 251.131 | 1.131 | 252.721 | 2.721 | 250.257 | 0.257 |
| 300 | 305.213 | 5.213 | 301.213 | 1.213 | 302.497 | 2.497 | 300.251 | 0.251 |
| 400 | 404.238 | 4.238 | 401.238 | 1.238 | 397.768 | 2.232 | 400.197 | 0.197 |
| 450 | 445.879 | 4.121 | 448.879 | 1.121 | 452.011 | 2.011 | 450.234 | 0.234 |
| Fault Location | Fault Type | Fault Resistance | Distance | Error |
|---|---|---|---|---|
| (km) | (Ω) | (km) | (km) | |
| 40 | PG | 900 | 39.739 | 0.261 |
| 80 | NG | 75 | 80.379 | 0.379 |
| 120 | PN | 1100 | 119.668 | 0.332 |
| 150 | PN | 65 | 149.618 | 0.382 |
| 180 | NG | 29 | 180.317 | 0.317 |
| 250 | PG | 840 | 249.749 | 0.251 |
| 310 | NG | 920 | 310.346 | 0.346 |
| 375 | PN | 1020 | 374.688 | 0.312 |
| 400 | PG | 1120 | 399.627 | 0.373 |
| 440 | NG | 54 | 440.249 | 0.249 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; He, Y.; Li, L. A Single-Terminal Fault Location Method for HVDC Transmission Lines Based on a Hybrid Deep Network. Electronics 2021, 10, 255. https://doi.org/10.3390/electronics10030255
Wang L, He Y, Li L. A Single-Terminal Fault Location Method for HVDC Transmission Lines Based on a Hybrid Deep Network. Electronics. 2021; 10(3):255. https://doi.org/10.3390/electronics10030255
Chicago/Turabian StyleWang, Lei, Yigang He, and Lie Li. 2021. "A Single-Terminal Fault Location Method for HVDC Transmission Lines Based on a Hybrid Deep Network" Electronics 10, no. 3: 255. https://doi.org/10.3390/electronics10030255
APA StyleWang, L., He, Y., & Li, L. (2021). A Single-Terminal Fault Location Method for HVDC Transmission Lines Based on a Hybrid Deep Network. Electronics, 10(3), 255. https://doi.org/10.3390/electronics10030255





