Highly Robust Observer Sliding Mode Based Frequency Control for Multi Area Power Systems with Renewable Power Plants

Abstract

This paper centers on the design of highly robust observer sliding mode (HROSM)-based load frequency and tie-power control to compensate for primary frequency control of multi-area interconnected power systems integrated with renewable power generation. At first, the power system with external disturbance is model in the state space form. Then the state observer is used to estimate the system states which are difficult or expensive to measure. Secondly, the sliding mode control (SMC) is designed with a new single phase sliding surface (SPSS). In addition, the whole system asymptotic stability is proven with Lyapunov stability theory based on the linear matrix inequality (LMI) technique. The new SPSS without reaching time guarantees rapid convergence of high transient frequency, tie-power change as well as reduces chattering without loss of accuracies. Therefore, the superiority of modern state-of-the-art SMC-based frequency controllers relies on good practical application. The experimental simulation results on large interconnected power systems show good performance and high robustness against external disturbances when compared with some modern state of art controllers in terms of overshoots and settling time.

1. Introduction

High level penetration of renewable generation systems into interconnected multi-area generation systems will make power sectors more economical and reliable to deliver power to end users. Since each area consists of increase numbers of generating sets, renewable power sets can be used as reservation for peak load demand. However, external disturbances such as intermittent generation associated with renewable sources and continuous load demand on one area can cause a high spike of frequency and tie-power flow in the multi-area [1]. Thus, frequency spike can damage power system equipment; can cause wear and tear of steam actuator valve, affects primary frequency control, etc. To solve this issue, load frequency control (LFC) is applied. LFC is one vital aspect of automatic generation control. Its duty is to compensate for primary control to ensure frequency and tie line flow at scheduled value [1]. Its design application in power systems follows two approaches, i.e., centralized and decentralized. The decentralized approach is commonly used since each local area is controlled on its own without interfering with neighboring areas. Furthermore, different techniques have been designed for LFC studies in various power systems. In the literature, early existing LFC methods were proportional-integral (PI) and proportional-integral-derivative (PID). These traditional schemes benefit in simple structures and performed well under parameters’ nominal operating points. However, they are degraded at variable points [2,3,4]. The degradation of PI and PID were solved with the development of intelligent control such as artificial neural network (ANN) and fuzzy logic given in [5,6,7,8]. Moreover, with the use of fuzzy logic, determining the accurate fuzzy set for tuning traditional control method is challenging. Optimal control techniques were applied with fuzzy logic to improve fuzzy set decision [9]. So far, both PI and intelligent control were combined to improve traditional LFC method [10,11,12,13,14,15]. Meanwhile, PI tuning has further improved with new algorithms given in [16,17,18]. Nevertheless, the major problem with interconnected power systems integrated with renewable power sets is that they result in a higher increase of the system order, the number of tuning control parameters, uncertainties in the system states and large external disturbances. When the power system is modeled, the external disturbance most especially cannot be avoided. Therefore, the requirement of the LFC must be robust against external disturbance in reality. Thus, sliding mode control (SMC) is used nowadays due to it robust against disturbance [19]. However, SMC based LFC is not new to control engineers. Various SMC-based LFC for power systems are briefly discussed. SMC was designed to control frequency, tie-power and area control errors for three area power system consisting of non-reheat, reheat and hydro-plant distributed in the areas [19]. Discrete-time SMC based LFC was constructed for controlling areas in power system with full state feedback [20]. A nonlinear SMC was proposed for mismatch power system with wind farms [21]. Furthermore, optimal LFC based SMC was designed for nonlinear power system [22]. Adaptive SMC based LFC for power systems are discussed in [23,24,25,26]. However, the SMC controllers discussed in the literature were designed with all power system states assumed to be measured. In practical power system, it is difficult to measure all system states [27]. To solve this problem, the SMC based observer technique is employed [28,29]. It estimates system states and filters higher frequency harmonics [30]. In addition, it provides cost effective design of LFC for power systems. SMC combined with an observer has been applied for LFC studies in power systems [31,32]. A robust higher observer SMC via nonlinear super twisting LFC was recently designed for multi-area power system with good performance and robustness of SMC which lies on the control switching law and sliding surface [31]. The switching laws ensure all system states deviations are driven to the sliding surface and remain therein. In studies, the robustness of an integral sliding surface combined with an observer was designed for the LFC of a power system which guarantees frequency deviation in the nominal value. However, these above SMCs combined with observer need time for the trajectories to reach the sliding surface, which may decrease the system performance [33]. In addition, a more robust controller without reaching time ensures system state trajectories starts from its surface at the initial time moment [33]. Therefore, the single phase sliding surface (SPSS) choice emerges to design sliding mode control. Thus, this motivates my interest to design an SMC via SPSS based on an observer for LFCs of a large power network. The novelties of this article are stated below:

❖

The new SMC via SPSS does not need reaching time as compared to [31,32] which can guarantee better system performance.

❖

The new SPSS and controller are designed to depend only on the observer which is useful for real power application where the system states variables are difficult or expensive to measure.

❖

The whole system stabilization is theoretically proven using Lyapunov stability theory based new linear matrix inequality (LMI) technique.

❖

Experimental simulation results depict the better performance in terms settling time and overshoot in comparison with recently results.

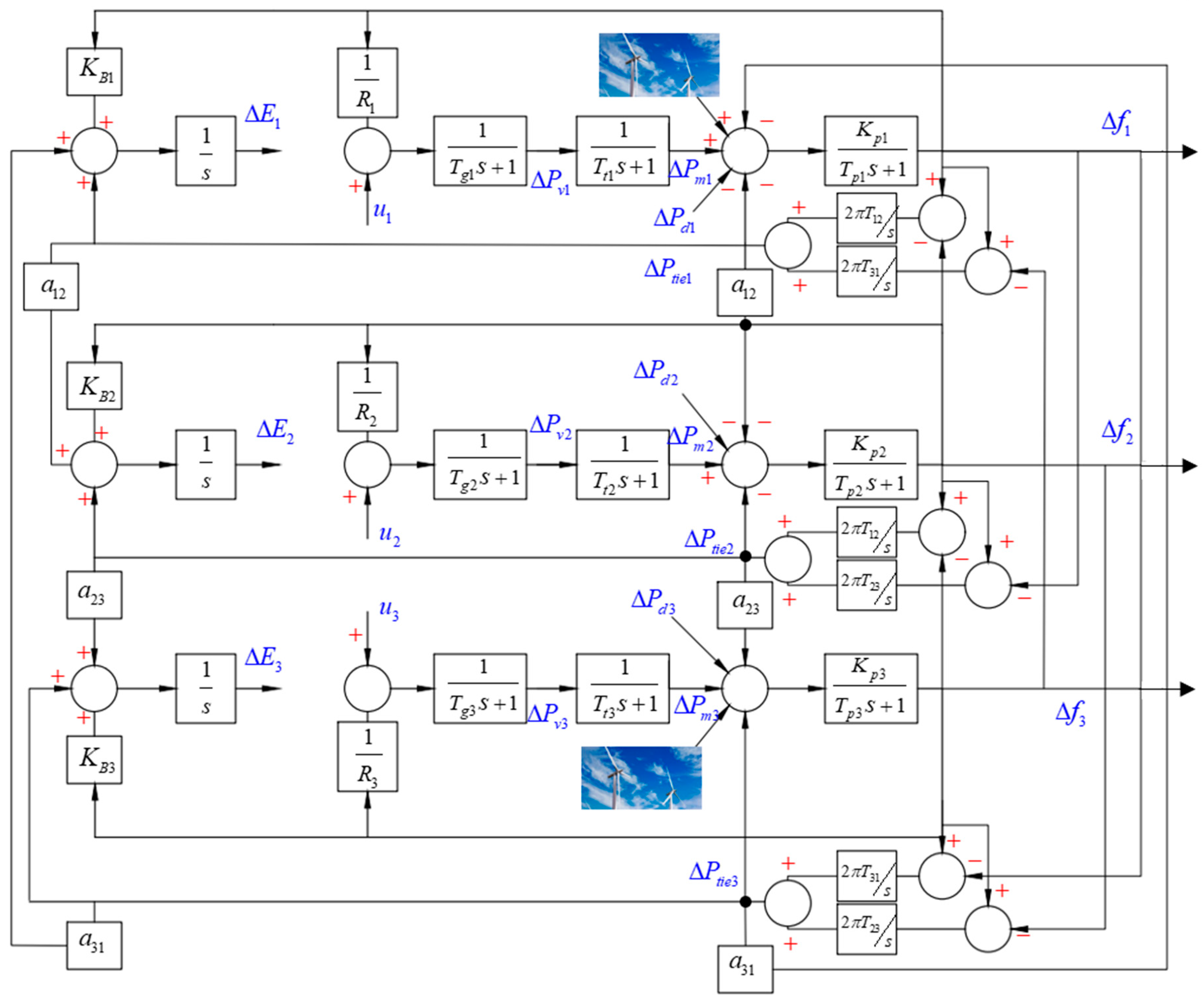
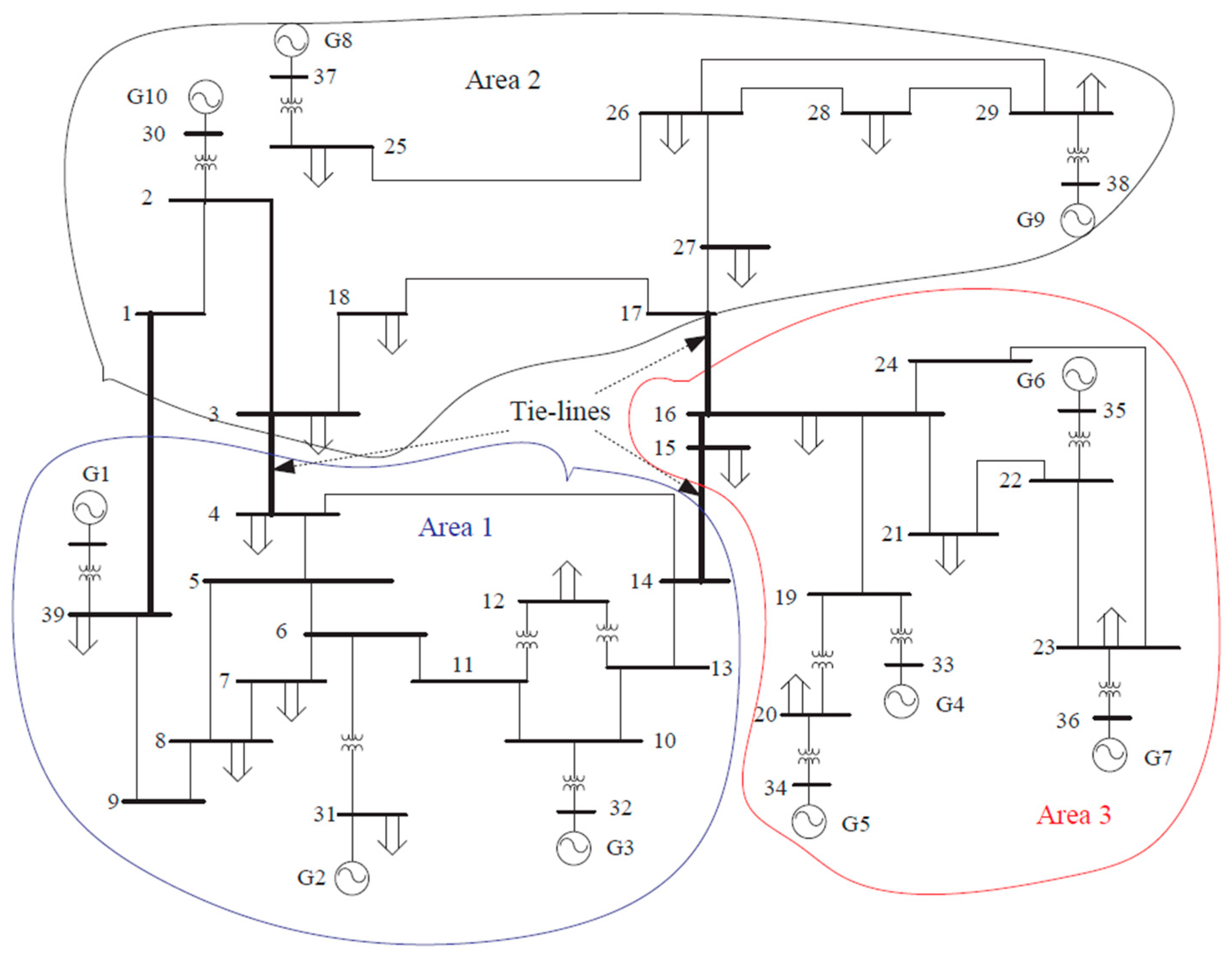
2. State Space Power System Model

In this part, we model the considered large interconnected power system and also the wind farms. Before proceeding, we briefly describe the power system which consists of three area interconnected electricity systems with non-reheat turbines shown in Figure 1. Areas 1 and 3 are integrated with wind power. Each block represents power generation components with their dynamics and subsystem parameters.

To derive the system states model, we begin from Area 1 to Area 3 in the following equation.

The frequency deviation of Areas 1, 2 and 3 is

$$\Delta {\dot{f}}_1(t)=-\frac{1}{T_{p1}}\Delta f_1(t)+\frac{K_{p1}}{T_{p1}}\Delta P_{m1}(t)-\frac{K_{p1}}{T_{p1}}\Delta P_{tie1}(t)-a_{31}\frac{K_{p1}}{T_{p1}}\Delta P_{tie3}(t)-\frac{K_{p1}}{T_{p1}}\Delta P_{d_1}-\frac{K_{p1}}{T_{p1}}\Delta P_{{\mathrm{W}}_1}$$

(1)

$$\Delta {\dot{f}}_2(t)=-\frac{1}{T_{p2}}\Delta f_2(t)+\frac{K_{p2}}{T_{p2}}\Delta P_{m2}(t)-a_{12}\frac{K_{p2}}{T_{p2}}\Delta P_{tie1}(t)-\frac{K_{p2}}{T_{p2}}\Delta P_{tie2}(t)-\frac{K_{p2}}{T_{p2}}\Delta P_{d_2}$$

(2)

$$\Delta {\dot{f}}_3(t)=-\frac{1}{T_{p3}}\Delta f_3(t)+\frac{K_{p3}}{T_{p3}}\Delta P_{m3}(t)-a_{23}\frac{K_{p3}}{T_{p3}}\Delta P_{tie2}(t)-\frac{K_{p3}}{T_{p3}}\Delta P_{tie3}(t)-\frac{K_{p3}}{T_{p3}}\Delta P_{d_3}-\frac{K_{p3}}{T_{p3}}\Delta P_{{\mathrm{W}}_3}$$

(3)

The mechanics power deviation of the 3-area power system are

$$\Delta {\dot{P}}_{m1}(t)=-\frac{1}{T_{t1}}\Delta P_{m1}(t)+\frac{1}{T_{t1}}\Delta P_{v1}(t)$$

(4)

$$\Delta {\dot{P}}_{m2}(t)=-\frac{1}{T_{t2}}\Delta P_{m2}(t)+\frac{1}{T_{t2}}\Delta P_{v2}(t)$$

(5)

$$\Delta {\dot{P}}_{m3}(t)=-\frac{1}{T_{t3}}\Delta P_{m3}(t)+\frac{1}{T_{t3}}\Delta P_{v3}(t)$$

(6)

The valve position deviation of the 3-area power system are given as

$$\Delta {\dot{P}}_{v1}(t)=-\frac{1}{R_1{T}_{g1}}\Delta f_1(t)-\frac{1}{T_{g1}}\Delta P_{v1}(t)+\frac{1}{T_{g1}}{u}_1$$

(7)

$$\Delta {\dot{P}}_{v2}(t)=-\frac{1}{R_2{T}_{g2}}\Delta f_2(t)-\frac{1}{T_{g2}}\Delta P_{v2}(t)+\frac{1}{T_{g2}}{u}_2$$

(8)

$$\Delta {\dot{P}}_{v3}(t)=-\frac{1}{R_3{T}_{g3}}\Delta f_3(t)-\frac{1}{T_{g3}}\Delta P_{v3}(t)+\frac{1}{T_{g3}}{u}_3$$

(9)

The area control error of Areas 1, 2 and 3 are as follows

$$\Delta {\dot{E}}_1(t)=K_{B1}\Delta f_1(t)+\Delta P_{tie1}(t)+a_{31}\Delta P_{tie3}(t)$$

(10)

$$\Delta {\dot{E}}_2(t)=K_{B2}\Delta f_2(t)+a_{12}\Delta P_{tie1}(t)+\Delta P_{tie2}(t)$$

(11)

$$\Delta {\dot{E}}_3(t)=K_{B3}\Delta f_3(t)+a_{23}\Delta P_{tie2}(t)+\Delta P_{tie3}(t)$$

(12)

The tie-line power deviation between the second area of Areas 1, 2 and 3 are presented as

$$\Delta {\dot{P}}_{tie1}(t)=2\pi (T_{12}+T_{31})\Delta f_1(t)-2\pi T_{12}\Delta f_2(t)-2\pi T_{31}\Delta f_3(t)$$

(13)

$$\Delta {\dot{P}}_{tie2}(t)=2\pi (T_{12}+T_{23})\Delta f_2(t)-2\pi T_{12}\Delta f_1(t)-2\pi T_{23}\Delta f_3(t)$$

(14)

$$\Delta {\dot{P}}_{tie3}(t)=2\pi (T_{31}+T_{23})\Delta f_3(t)-2\pi T_{31}\Delta f_1(t)-2\pi T_{23}\Delta f_2(t)$$

(15)

where $\Delta f_1$, $\Delta f_2(t)$ and $\Delta f_3(t)$ are frequency errors in area 1, 2 and 3, $\Delta E_1(t)$, $\Delta E_2(t)$ and $\Delta E_3(t)$ are the control area errors, and $\Delta P_{tie1}(t)$, $\Delta P_{tie2}(t)$ and $\Delta P_{tie3}(t)$ are total changes in tie-power. Equations (1)–(15) represent the dynamic characteristics of the power system with wind turbines. Therefore, the power system model is written in the state space form below

$$\begin{array}{l}\dot{x}\left(t\right)=Ax\left(t\right)+Bu\left(t\right)+F\Delta P\left(t\right)\\ y(t)=Cx(t)\end{array}$$

(16)

where $x\left(t\right)$ is the system states variable $x(t)\in R^n$, $u\left(t\right)$ is the control vector matrix $u(t)\in R^m$ and $\Delta P\left(t\right)$ is the disturbance vector matrix. The detail of the above variables are as follows: $x(t)={\left[\begin{array}{ccc}{x}_1(t)& x_2(t)& x_3(t)\end{array}\right]}^T$ in which $x_1(t)=\left[\begin{array}{ccccc}\Delta f_1(t)& \Delta P_{m1}(t)& \Delta P_{v1}(t)& \Delta E_1(t)& \Delta P_{tie1}(t)\end{array}\right]$; $x_2(t)=\left[\begin{array}{ccccc}\Delta f_2(t)& \Delta P_{m2}(t)& \Delta P_{v2}(t)& \Delta E_2(t)& \Delta P_{tie2}(t)\end{array}\right]$; $x_3(t)=\left[\begin{array}{ccccc}\Delta f_3(t)& \Delta P_{m3}(t)& \Delta P_{v3}(t)& \Delta E_3(t)& \Delta P_{tie3}(t)\end{array}\right]$; $u\left(t\right)={[\begin{array}{ccc}{u}_1& u_2& u_3\end{array}]}^T$; $\Delta P\left(t\right)={\left[\begin{array}{ccccc}\Delta P_{d1}& \Delta P_{d2}& \Delta P_{d3}& \Delta P_{W1}& \Delta P_{\mathrm{W}3}\end{array}\right]}^T$ and $y(t)$ is denoted the system output vector and A, B, F are the system matrices with $A\in R^{n\times n}$, $B\in R^{n\times m}$, $F\in R^{n\times k}$

$$\begin{gathered} \begin{array}{l}A=\\ \left[\begin{array}{ccccccccccccccc}-\frac{1}{T_{p1}}& \frac{K_{p1}}{T_{p1}}& 0& 0& -\frac{K_{p1}}{T_{p1}}& 0& 0& 0& 0& 0& 0& 0& 0& 0& -a_{31}\frac{K_{p1}}{T_{p1}}\\ 0& -\frac{1}{T_{t1}}& \frac{1}{T_{t1}}& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ -\frac{1}{R_1{T}_{g1}}& 0& -\frac{1}{T_{g1}}& \frac{1}{T_{g1}}& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ K_{B1}& 0& 0& 0& 1& 0& 0& 0& 0& 0& 0& 0& 0& 0& a_{31}\\ 2\pi (T_{12}+T_{31})& 0& 0& 0& 0& -2\pi T_{12}& 0& 0& 0& 0& -2\pi T_{31}& 0& 0& 0& 0\\ 0& 0& 0& 0& -a_{12}\frac{K_{p2}}{T_{p2}}& -\frac{1}{T_{p2}}& \frac{K_{p2}}{T_{p2}}& 0& 0& -\frac{K_{p2}}{T_{p2}}& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& -\frac{1}{T_{t2}}& \frac{1}{T_{t2}}& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& -\frac{1}{R_2{T}_{g2}}& 0& -\frac{1}{T_{g2}}& \frac{1}{T_{g2}}& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& a_{12}& K_{B2}& 0& 0& 0& 1& 0& 0& 0& 0& 0\\ -2\pi T_{12}& 0& 0& 0& 0& 2\pi (T_{12}+T_{23})& 0& 0& 0& 0& -2\pi T_{23}& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& -a_{23}\frac{K_{p3}}{T_{p3}}& -\frac{1}{T_{p3}}& \frac{K_{p3}}{T_{p3}}& 0& 0& -\frac{K_{p3}}{T_{p3}}\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& -\frac{1}{T_{t3}}& \frac{1}{T_{t3}}& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& -\frac{1}{R_3{T}_{g3}}& 0& -\frac{1}{T_{g3}}& \frac{1}{T_{g3}}& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& a_{23}& K_{B3}& 0& 0& 0& 1\\ -2\pi T_{31}& 0& 0& 0& 0& -2\pi T_{23}& 0& 0& 0& 0& 2\pi (T_{31}+T_{23})& 0& 0& 0& 0\end{array}\right];\end{array} \\ B={\left[\begin{array}{ccccccccccccccc}0& 0& \frac{1}{T_{g1}}& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& \frac{1}{T_{g2}}& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& \frac{1}{T_{g3}}& 0& 0\end{array}\right]}^T; \\ F={\left[\begin{array}{ccccccccccccccc}-\frac{K_{p1}}{T_{P1}}& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& -\frac{K_{P2}}{T_{P2}}& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& -\frac{K_{P3}}{T_{P3}}& 0& 0& 0\\ \frac{K_{p1}}{T_{P1}}& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& \frac{K_{P3}}{T_{P3}}& 0& 0& 0\end{array}\right]}^T. \end{gathered}$$

$T_{gi}$, $T_{ti}$ and $T_{pi}$ are governor, turbine and subsystem time constant in seconds. $K_{pi}$, $R_i$, and $K_{Bi}$ are power system gain (Hz/p.u. MW), speed regulation coefficient (Hz/p.u. MW), and frequency bias factor (p.u. MW/Hz), respectively. $T_{ij}$ is the synchronized coefficient. If there is no power exchange between each area $T_{ij}=0$. Furthermore, the wind output power is expressed below

$$P_{\omega }=\frac{1}{2}\rho \alpha V_{\omega }{}^3{C}_P(\lambda ,\beta )$$

(17)

where $\rho$ is the air density, $\alpha$ is the cross section of rotor, $\lambda$ is the tip speed ratio, $\beta$ is the pitch angle, and $C_P(\lambda ,\beta )$ is the power coefficient and $V_{\omega }{}^{}$ is the wind speed. Variation of wind speed can cause external disturbance to the interconnected power system. To proceed, we make some assumptions that will be beneficial in this work. The assumptions are as follows.

Assumption 1.

If the A, B pair are controllable by $u\left(t\right)$then A, C are observable [21].

Assumption 2.

The load disturbance$\Delta P\left(t\right)$is unknown and bounded, i.e., there exists a known scalar $\kappa$such that$\Vert \Delta P\left(t\right)\Vert \le \kappa$, where$\Vert .\Vert$is the norm.

3. Observer Design

To achieve a better LFC in power systems, all parameters values related to LFC are assumed to be measured probably by sensors. This will create a high cost. Therefore, to design a cost effective controller, an observer approach is introduced. The observer estimates system state variables to overcome the use of sensors. By applying the state observer, the estimator of the system state in Equation (16) is written as follows

$$\begin{array}{l}\dot{\widehat{x}}\left(t\right)=A\widehat{x}\left(t\right)+Bu\left(t\right)+L\left(y-\widehat{y}\right)\\ \widehat{y}(t)=C\widehat{x}(t)\end{array}$$

(18)

where $\widehat{x}(t)\in {\mathfrak{R}}^n$ is the estimate of $x(t)$, $\widehat{y}(t)\in {\mathfrak{R}}^p$ is the output of the observer, $L\in {\mathfrak{R}}^{nxp}$ is the gain of the observer. The observer takes a discontinuous signal in $u(t)$ and $y(t)$ as the input and $\widehat{y}(t)$ as output signal. The observer gain $\Gamma$ is chosen such that the eigenvalue of $A^T-C^T\Gamma$ lie in the desire location in the hyper plane. The observer gains matrix L for the original system, therefore, can be determined by using the relation L and ${\Gamma }^T$ give as

$$L={\Gamma }^T$$

(19)

4. SMC via Single Phase Surface Design

In this section, we design the SMC based single phase switching surface for large power systems and prove the system dynamics stabilization. To begin, a single phase switching surface is first designed and discussed below.

4.1. New Single Phase Sliding Surface

To design an SM controller, the choice for switching techniques and sliding surface are very important. The switching scheme is used to move the system states and maintain convergence at a designated sliding surface [21]. Hence, a new single phase sliding surface is constructed. The robustness at reaching stage without reaching time is guaranteed by the single phase switching surface given below.

$$\sigma [\widehat{x}(t)]=S\widehat{x}\left(t\right)-\underset{0}{\overset{t}{{\displaystyle \int }}}S\left(A-BK\right)\widehat{x}\left(\tau \right)d\tau -S\widehat{x}\left(0\right)e^{-\beta t}$$

(20)

where $\sigma \left[\widehat{x}\left(t\right)\right]$ denotes the single phase sliding surface. We take into account the SMC law that variables must reach the surface and remain therein that is, $\sigma [\widehat{x}(t)]\dot{\sigma }[\widehat{x}(t)]<0$ which denotes reachability of the system states trajectories, $\dot{\sigma }[\widehat{x}(t)]=\sigma [\widehat{x}(t)]=0$. At the beginning time t = 0, the SPSS in Equation (20) is equal zero $\sigma [\widehat{x}(t)]=0$ which shows the system remain on the single phase sliding surface for all time. In Equation (20), K is the design matrix gain. The matrix S is chosen carefully to ensure SB is invertible. Therefore, if we take the time derivative of Equation (20), we have

$$\dot{\sigma }[\widehat{x}(t)]=S\dot{\widehat{x}}\left(t\right)-S\left(A-BK\right)\widehat{x}\left(t\right)S\beta \widehat{x}\left(0\right)e^{-\beta t}$$

(21)

Substituting $\dot{\widehat{x}}\left(t\right)$ into Equation (21) gives us

$$\begin{array}{ll}\dot{\sigma }\left[\widehat{x}\left(t\right)\right]& =S\left[A\widehat{x}\left(t\right)+Bu\left(t\right)+L\left(y-\widehat{y}\right)\right]-S\left(A-BK\right)\widehat{x}\left(t\right)+S\beta \widehat{x}\left(0\right)e^{-\beta t}\\ & =SA\widehat{x}\left(t\right)+SBu\left(t\right)+SL\left(y-\widehat{y}\right)-S\left(A-BK\right)\widehat{x}\left(t\right)+S\beta \widehat{x}\left(0\right)e^{-\beta t}\\ & =SA\widehat{x}\left(t\right)+SBu\left(t\right)+SL\left(y-\widehat{y}\right)-SA\widehat{x}\left(t\right)+SBK\widehat{x}\left(t\right)+S\beta \widehat{x}\left(0\right)e^{-\beta t}\\ & =SBu\left(t\right)+SL\left(y-\widehat{y}\right)+SBK\widehat{x}\left(t\right)+S\beta \widehat{x}\left(0\right)e^{-\beta t}\end{array}$$

(22)

Therefore, if $\dot{\sigma }\left[\widehat{x}\left(t\right)\right]=0$ then, the corresponding equivalent controller $u_{eq}\left(t\right)$ can be determine as

$$u_{eq}\left(t\right)= -{(SB)}^{-1}\left[SBK\widehat{x}\left(t\right)+SL\left(y-\widehat{y}\right)+S\beta \widehat{x}\left(0\right)e^{-\beta t}\right]$$

(23)

However, to satisfy the reaching condition of system state trajectories, the design controller becomes

$$u\left(t\right)= u_{eq}\left(t\right)-{(SB)}^{-1}\delta sgn\left(\sigma \left[\widehat{x}\left(t\right)\right]\right)$$

(24)

where $u\left(t\right)$ is the designed controller for the power system. In practice, this new controller maintains nominal frequency at agreed value, i.e., 50 Hz/60 Hz and tie-power exchange between the multi-areas. The new controller is designed to depend only on the state observer written as

$$u\left(t\right)=-{(SB)}^{-1}\{SBK\widehat{x}\left(t\right)+SL\left(y-\widehat{y}\right)+S\beta \widehat{x}\left(0\right)e^{-\beta t}+\delta sgn\left( \sigma \left[\widehat{x}\left(t\right)\right]\right)\}$$

(25)

Next, we determine the system dynamic equation in the single phase sliding surface, we start by making $u(t)=u_{eq}(t)$ and substitute into (16) in the following

$$\dot{x}\left(t\right)=Ax\left(t\right)-BK\widehat{x}\left(t\right)-B{(SB)}^{-1}SL\left(y-\widehat{y}\right)-B{(SB)}^{-1}S\beta \widehat{x}\left(0\right)e^{-\beta t}+F\Delta P\left(t\right)$$

(26)

where $y(t)$ is the real output which is given as $y(t)=Cx(t)$ and $\widehat{y}(t)$ is the estimated output from the observer given as $\widehat{y}(t)=C\widehat{x}(t)$. Therefore, the Equation (26) can be achieved.

$$\begin{array}{ll}\dot{x}\left(t\right)=& Ax\left(t\right)-BKx\left(t\right)+BKx\left(t\right)-BK\widehat{x}\left(t\right)-B{(SB)}^{-1}SLC[x\left(t\right)-\widehat{x}\left(t\right)]\\ & -B{(SB)}^{-1}S\beta \widehat{x}\left(0\right)e^{-\beta t}+F\Delta P\left(t\right)\end{array}$$

(27)

By simplifying (27), the equation is written in the following

$$\dot{x}\left(t\right)=\left(A-BK\right)x\left(t\right)+\left[BK-B{\left(SB\right)}^{-1}SLC\right]\mathfrak{A}\left(t\right)+F\Delta P\left(t\right) -B{(SB)}^{-1}S\beta \widehat{x}\left(0\right)e^{-\beta t}$$

(28)

where $\mathfrak{A}\left(t\right)$ represents the error between the real system state and observer state given below

$$\mathfrak{A}\left(t\right)=x(t)-\widehat{x}(t)$$

(29)

If we take the time derivative of Equation (29) and using Equations (16) and (18), we have

$$\dot{\mathfrak{A}}\left(t\right)=\left(A-LC\right)\mathfrak{A}\left(t\right)+F\Delta \mathrm{P}\left(t\right)$$

(30)

Combining (28) and (30), therefore, the dynamic equation in the SPSS becomes

$$\left[\begin{array}{c}\dot{x}\left(t\right)\\ \dot{\mathfrak{A}}\left(t\right)\end{array}\right]=\left[\begin{array}{c}(A-BK) \left[BK-B{\left(SB\right)}^{-1}SLC\right]\\ 0 (A-LC)\end{array}\right]\left[\begin{array}{c}x\left(t\right)\\ \mathfrak{A}\left(t\right)\end{array}\right]+\left[\begin{array}{cc}I& \mathsf{\Pi }\\ I& 0\end{array}\right]\left[\begin{array}{c}F\Delta P\left(t\right)\\ e^{-\beta t}\end{array}\right].$$

(31)

where

$$\mathsf{\Pi }= -B{(SB)}^{-1}S\beta \widehat{x}\left(0\right)$$

Equation (31) represents the dynamic equation in the SPSS. It is designed in such a way that both $x\left(t\right)$ and $\mathfrak{A}\left(t\right)$ deviation begins at the surface at initial time moment. Meanwhile, $(BK-B{(SB)}^{-1}SLC)$ reflects the fact that system is constrained to remain on the defined single phase sliding surface at $\sigma \left[\widehat{x}\left(t\right)\right]=0$.

4.2. Theoretical Prove of System Dynamic Stabilization

It is very important to prove the stabilization of the whole system. In studies, Lyapunov stability theory is used theoretically to investigate differential systems. Some lemmas are also adopted and LMI theorem stated to support the stabilization proves which are given.

Lemma 1

([34]).If X and Y are real matrix of suitable dimension then, for any scalar$\mu >0$, the following matrix inequality holds

$$X^{T}Y+Y^{T}X\le \mu X^{T}X+{\mu }^{-1}{Y}^{T}Y$$

Lemma 2

([34]).For a given inequality

$$\left[\begin{array}{cc}Q\left(x\right)& S\left(x\right)\\ S{\left(x\right)}^T& R\left(x\right)\end{array}\right]<0$$

(32)

where$Q(x)=Q{(x)}^T$and$R(x)=R{(x)}^T$such that$S(x)$depend affinity on$x$, therefore,$R(x)<0$and$Q(x)-S(x)R{(x)}^{-1}S{(x)}^T<0$.

Theorem 1.

The system (31) is asymptotically stable, if there exist symmetric positive definite matrices$R>0$ and $P>0$ and positive scalars $\mu , \gamma$ and $\pi$ such that the below LMI holds

$$\left[\begin{array}{ccccc}R(A-BK) +{(A-BK)}^{T}R& R\left[BK-B{\left(SB\right)}^{-1}SLC\right]& 0& RIF& R\mathsf{\Pi }\\ {\left[BK-B{\left(SB\right)}^{-1}SLC\right]}^{T}R& P(A-LC)+{(A-LC)}^{T}P& PIF& 0& 0\\ 0& F^T{I}^{T}P& -{\pi }^{-1}I& 0& 0\\ F^T{I}^{T}R& 0& 0& {\mu }^{-1}& 0\\ {\mathsf{\Pi }}^{T}R& 0& 0& 0& {\gamma }^{-1}\end{array}\right]<0$$

(33)

To prove the stability of the system (31), the Lyapunov function $V\left(x\left(t\right),\mathfrak{A}\left(t\right)\right)$ is selected as

$$V\left(x\left(t\right),\mathfrak{A}\left(t\right)\right)={\left[\begin{array}{c}x\left(t\right)\\ \mathfrak{A}\left(t\right)\end{array}\right]}^T\left[\begin{array}{cc}R& 0\\ 0& P\end{array}\right]\left[\begin{array}{c}x\left(t\right)\\ \mathfrak{A}\left(t\right)\end{array}\right]$$

(34)

When we take the time derivative of (34), we have

$$\dot{V}\left(x\left(t\right),\mathfrak{A}\left(t\right)\right)={\left[\begin{array}{c}x\left(t\right)\\ \mathfrak{A}\left(t\right)\end{array}\right]}^T\left[\begin{array}{cc}R& 0\\ 0& P\end{array}\right]\left[\begin{array}{c}\dot{x}\left(t\right)\\ \dot{\mathfrak{A}}\left(t\right)\end{array}\right]+{\left[\begin{array}{c}\dot{x}\left(t\right)\\ \dot{\mathfrak{A}}\left(t\right)\end{array}\right]}^T\left[\begin{array}{cc}R& 0\\ 0& P\end{array}\right]\left[\begin{array}{c}x\left(t\right)\\ \mathfrak{A}\left(t\right)\end{array}\right]$$

(35)

Substitute $\dot{x}\left(t\right)$ and $\dot{\mathfrak{A}}\left(t\right)$ into (35), $\dot{V}\left(x\left(t\right),\mathfrak{A}\left(t\right)\right)$ becomes

$$\begin{array}{l}\dot{V}\left(x\left(t\right),\mathfrak{A}\left(t\right)\right)={\left[\begin{array}{c}x\left(t\right)\\ \mathfrak{A}\left(t\right)\end{array}\right]}^T\left[\begin{array}{cc}R& 0\\ 0& P\end{array}\right]\left[\left[\begin{array}{c}(A-BK) \left[BK-B{\left(SB\right)}^{-1}SLC\right]\\ 0 (A-LC)\end{array}\right]\left[\begin{array}{c}x\left(t\right)\\ \mathfrak{A}\left(t\right)\end{array}\right]+\left[\begin{array}{cc}I& \mathsf{\Pi }\\ I& 0\end{array}\right]\left[\begin{array}{c}F\Delta P(t)\\ e^{-\beta t}\end{array}\right]\right]\\ +{\left[\left[\begin{array}{c}(A-BK) \left[BK-B{\left(SB\right)}^{-1}SLC\right]\\ 0 (A-LC)\end{array}\right]\left[\begin{array}{c}x\left(t\right)\\ \mathfrak{A}\left(t\right)\end{array}\right]+\left[\begin{array}{cc}I& \mathsf{\Pi }\\ I& 0\end{array}\right]\left[\begin{array}{c}F\Delta P(t)\\ e^{-\beta t}\end{array}\right]\right]}^T\left[\begin{array}{cc}R& 0\\ 0& P\end{array}\right]\left[\begin{array}{c}x\left(t\right)\\ \mathfrak{A}\left(t\right)\end{array}\right]\end{array}$$

(36)

By simplifying (36) further, we have

$$\begin{array}{l}\dot{V}\left(x\left(t\right),\mathfrak{A}\left(t\right)\right)={\left[\begin{array}{c}x\left(t\right)\\ \mathfrak{A}( t) \end{array}\right]}^{ T } \left[ \begin{array}{c} R(A-BK) R\left[ BK-B{ ( SB ) }^{ -1 } SLC\right] \\ 0 P(A-LC) \end{array}\right]\left[ \begin{array}{c} x( t ) \\ \mathfrak{A}( t ) \end{array}\right]+{ \left[ \begin{array}{c} x( t ) \\ \mathfrak{A}( t ) \end{array}\right] }^{T } \left[ \begin{array}{cc} RI & R\mathsf{\Pi } \\ PI & 0 \end{array}\right]\left[ \begin{array}{c} F\Delta P(t) \\ { e }^{ -\beta t} \end{array}\right] \\ +{\left[ \begin{array}{c} x( t ) \\ \mathfrak{A}( t ) \end{array}\right]}^T \left[ \begin{array}{cc} { (A-BK) }^{T } R & 0 \\ { \left[ BK-B{ ( SB ) }^{ -1 } SLC\right]}^T R & { (A-LC) }^{T } P \end{array}\right]\left[ \begin{array}{c} x( t ) \\ \mathfrak{A}( t ) \end{array}\right]+{ \left[ \begin{array}{c} F\Delta P(t) \\ e^{ -\beta t} \end{array}\right]}^{ T } \left[ \begin{array}{cc} I^T R & I^T P \\ {\mathsf{\Pi }}^T R & 0 \end{array}\right]\left[ \begin{array}{c} x( t ) \\ \mathfrak{A}( t ) \end{array}\right] \\ ={ \left[ \begin{array}{c} x( t ) \\ \mathfrak{A}( t ) \end{array}\right] }^{T } \left[ \begin{array}{c} R(A-BK) +{ (A-BK) }^{T } R R\left[ BK-B{ ( SB ) }^{ -1} SLC\right] \\ \left[ BK-B{ ( SB ) }^{ -1} SLC\right]{ }^T R P(A-LC)+{ (A-LC)}^{ T } P \end{array}\right]\left[ \begin{array}{c} x( t ) \\ \mathfrak{A}( t ) \end{array}\right]+ \\ x{ (t) }^{T } RIF\Delta P(t) + x{ (t) }^{T } R\mathsf{\Pi }{ e }^{ -\beta t} +\Delta P{ (t) }^{T } F^T I^T Rx(t)+\Delta P{ (t) }^{T } F^T I^T P\mathfrak{A}(t)+\mathfrak{A}{ (t) }^{T } PIF\Delta P(t) + { (e^{ -\beta t} ) }^{T } {\mathsf{\Pi }}^T Rx(t) \end{array}$$

(37)

By applying Lemma 1 into (37), we therefore re-write Equation (37) in the following form

$$\begin{array}{c}\dot{V}\left(x\left(t\right),\mathfrak{A}\left(t\right)\right)\le {\left[\begin{array}{c}x\left(t\right)\\ \mathfrak{A}\left(t\right)\end{array}\right]}^T\left[\begin{array}{c}R(A-BK) +{(A-BK)}^{T}R R\left[BK-B{\left(SB\right)}^{-1}SLC\right]\\ {\left[BK-B{\left(SB\right)}^{-1}SLC\right]}^{T}R \mathrm{P}(A-LC)+{(A-LC)}^{T}P\end{array}\right]\left[\begin{array}{c}x\left(t\right)\\ \mathfrak{A}\left(t\right)\end{array}\right]\\ +\mu x{(t)}^{T}RIF{F}^T{I}^{T}Rx(t)+({\mu }^{-1}+{\pi }^{-1})\Delta P{(t)}^T\Delta P(t) +\gamma x{(t)}^{T}R\mathsf{\Pi }{\mathsf{\Pi }}^{T}Rx(t)\\ +{\gamma }^{-1} {(e^{-\beta t})}^T{e}^{-\beta t}+\pi \mathfrak{A}{(t)}^{T}PIF{F}^T{I}^{T}P\mathfrak{A}(t)\end{array}$$

(38)

Equation (38) is further simplified to give

$$\begin{array}{cc}\dot{V}\left(x\left(t\right),\mathfrak{A}\left(t\right)\right)\le & {\left[\begin{array}{c}x\left(t\right)\\ \mathfrak{A}\left(t\right)\end{array}\right]}^T\left[\begin{array}{c}R(A-BK) +{(A-BK)}^{T}R +\mu RIF{F}^T{I}^{T}R+\gamma R\mathsf{\Pi }{\mathsf{\Pi }}^{T}R R\left[BK-B{\left(SB\right)}^{-1}SLC\right]\\ {\left[BK-B{\left(SB\right)}^{-1}SLC\right]}^{T}R P(A-LC)+{(A-LC)}^{T}P+\pi PIF{F}^T{I}^{T}P\end{array}\right]\left[\begin{array}{c}x\left(t\right)\\ \mathfrak{A}\left(t\right)\end{array}\right]\\ & +\phi \Delta P{(t)}^T\Delta P(t)+{\gamma }^{-1}{(e^{-\beta t})}^T{e}^{-\beta t}\\ ={\left[\begin{array}{c}x\left(t\right)\\ \mathfrak{A}\left(t\right)\end{array}\right]}^T& \left[\begin{array}{c}R(A-BK) +{(A-BK)}^{T}R +\mu RIF{F}^T{I}^{T}R+\gamma R\mathsf{\Pi }{\mathsf{\Pi }}^{T}R R\left[BK-B{\left(SB\right)}^{-1}SLC\right]\\ {\left[BK-B{\left(SB\right)}^{-1}SLC\right]}^{T}R P(A-LC)+{(A-LC)}^{T}P+\pi PIF{F}^T{I}^{T}P\end{array}\right]\left[\begin{array}{c}x\left(t\right)\\ \mathfrak{A}\left(t\right)\end{array}\right]\\ & +\phi {\Vert \Delta P(t)\Vert }^2+{\gamma }^{-1}{(e^{-\beta t})}^T{e}^{-\beta t}\\ \le {\left[\begin{array}{c}x\left(t\right)\\ \mathfrak{A}\left(t\right)\end{array}\right]}^T& \left[\begin{array}{c}R(A-BK) +{(A-BK)}^{T}R +\mu RIF{F}^T{I}^{T}R+\gamma R\mathsf{\Pi }{\mathsf{\Pi }}^{T}R R\left[BK-B{\left(SB\right)}^{-1}SLC\right]\\ {\left[BK-B{\left(SB\right)}^{-1}SLC\right]}^{T}R P(A-LC)+{(A-LC)}^{T}P+\pi PIF{F}^T{I}^{T}P\end{array}\right]\left[\begin{array}{c}x\left(t\right)\\ \mathfrak{A}\left(t\right)\end{array}\right]\\ & +\phi {\kappa }^2+{\gamma }^{-1}{(e^{-\beta t})}^T{e}^{-\beta t}\end{array}$$

(39)

where $\phi ={\mu }^{-1}+{\pi }^{-1}$. By applying Lemma 2, the LMI (33) can be rewritten as

$$\left[\begin{array}{c}R(A-BK) +{(A-BK)}^{T}R +\mu RIF{F}^T{I}^{T}R+\gamma R\mathsf{\Pi }{\mathsf{\Pi }}^{T}R R\left[BK-B{\left(SB\right)}^{-1}SLC\right]\\ {\left[BK-B{\left(SB\right)}^{-1}SLC\right]}^{T}R P(A-LC)+{(A-LC)}^{T}P+\pi PIF{F}^T{I}^{T}P\end{array}\right]<0$$

(40)

The term ${\gamma }^{-1}{(e^{-\beta t})}^T{e}^{-\beta t}$ in Equation (39) will approach zero when the time approaches infinity. Therefore $\dot{V}\left(x\left(t\right),\mathfrak{A}\left(t\right)\right)\le 0$ is achieved by using Equations (39) and (40). If $\dot{V}\left(x\left(t\right),\mathfrak{A}\left(t\right)\right)\le 0$ shows that the LMI given in (33) holds, therefore, it further explains that the system (16) is asymptotically stable.

Furthermore, we theoretically prove the reachability of the system states to the SPSS. We assumed that $\widehat{x}\left(t\right)>0$ little above the equilibrium part at the surface, then the Lyapunov function is selected

$$V[\widehat{x}\left(t\right)]=\frac{1}{2} \sigma {[\widehat{x}\left(t\right)]}^T\sigma [\widehat{x}\left(t\right)]$$

(41)

If we take the time derivative of (41), we have

$$\dot{V}[\widehat{x}\left(t\right)]=\sigma {[\widehat{x}\left(t\right)]}^T\dot{\sigma }[\widehat{x}\left(t\right)]$$

(42)

Substituting Equation (22) into Equation (42) then it becomes

$$\dot{V}[\widehat{x}\left(t\right)]=\sigma {[\widehat{x}\left(t\right)]}^T\{S[A\widehat{x}\left(t\right)+Bu\left(t\right)+L\left(y-\widehat{y}\right)]-S\left(A-BK\right)\widehat{x}\left(t\right)+S\beta \widehat{x}\left(0\right)e^{-\beta t}\}$$

(43)

Using the controller (24), then

$$\dot{V}[\widehat{x}\left(t\right)]=-\delta \Vert \sigma \left[\widehat{x}\left(t\right)\right]\Vert$$

(44)

Therefore, Equation (44) indicates that $\dot{V}[\widehat{x}\left(t\right)]<0$ which proves the reachability of the system states to the SPSS. Next, the flowchart of the proposed control algorithm of highly robust observer sliding mode can be implemented as Figure 2.

Remark 1.

The stability of the LFC in power system using LMI technique can be seen in [35]. However, the above approach needs to find four positive matrices in the LMI equations. Thus, the proposed approach only needs to find two positive matrices in LMI equations making it easier to find a feasible solution.

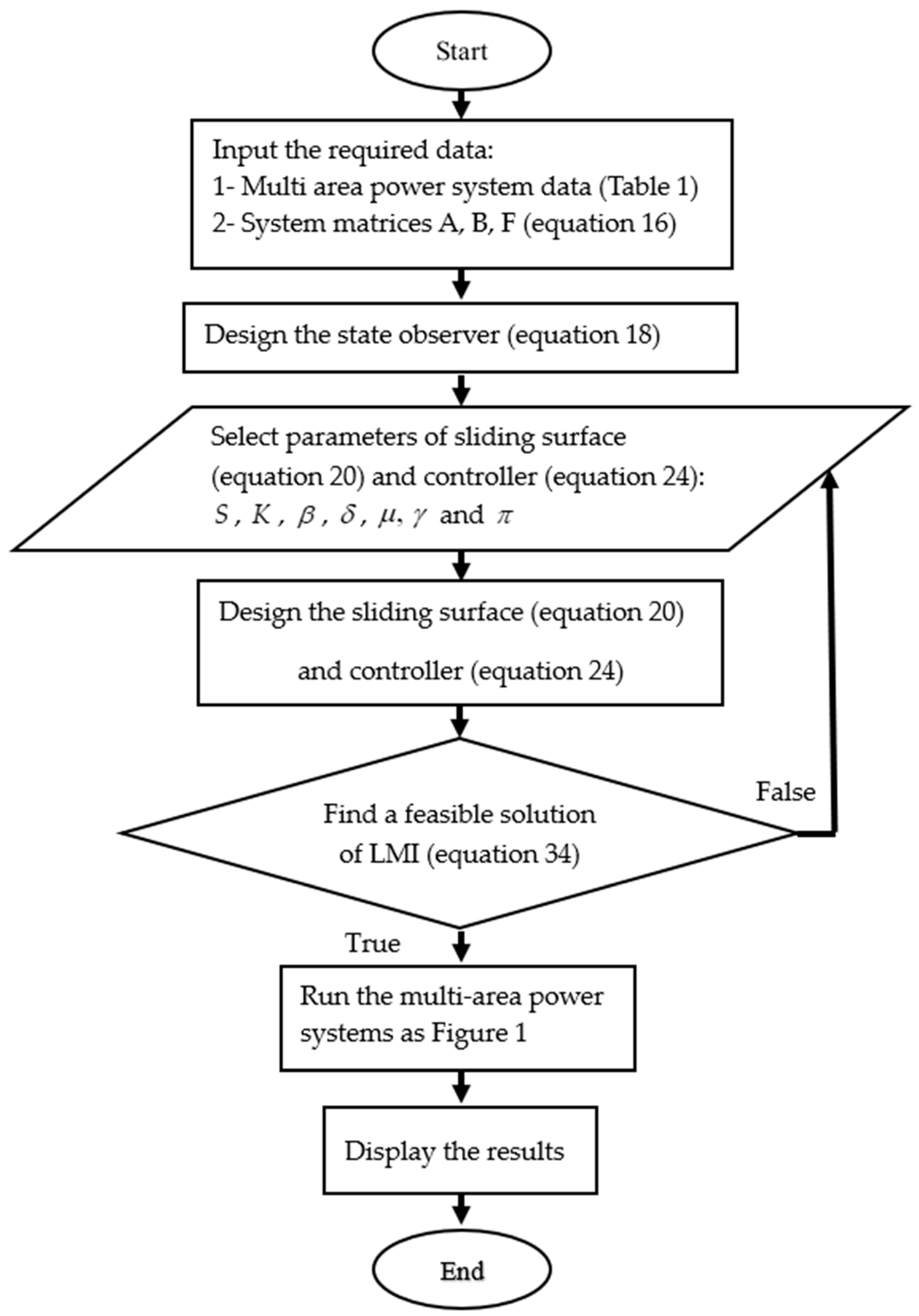
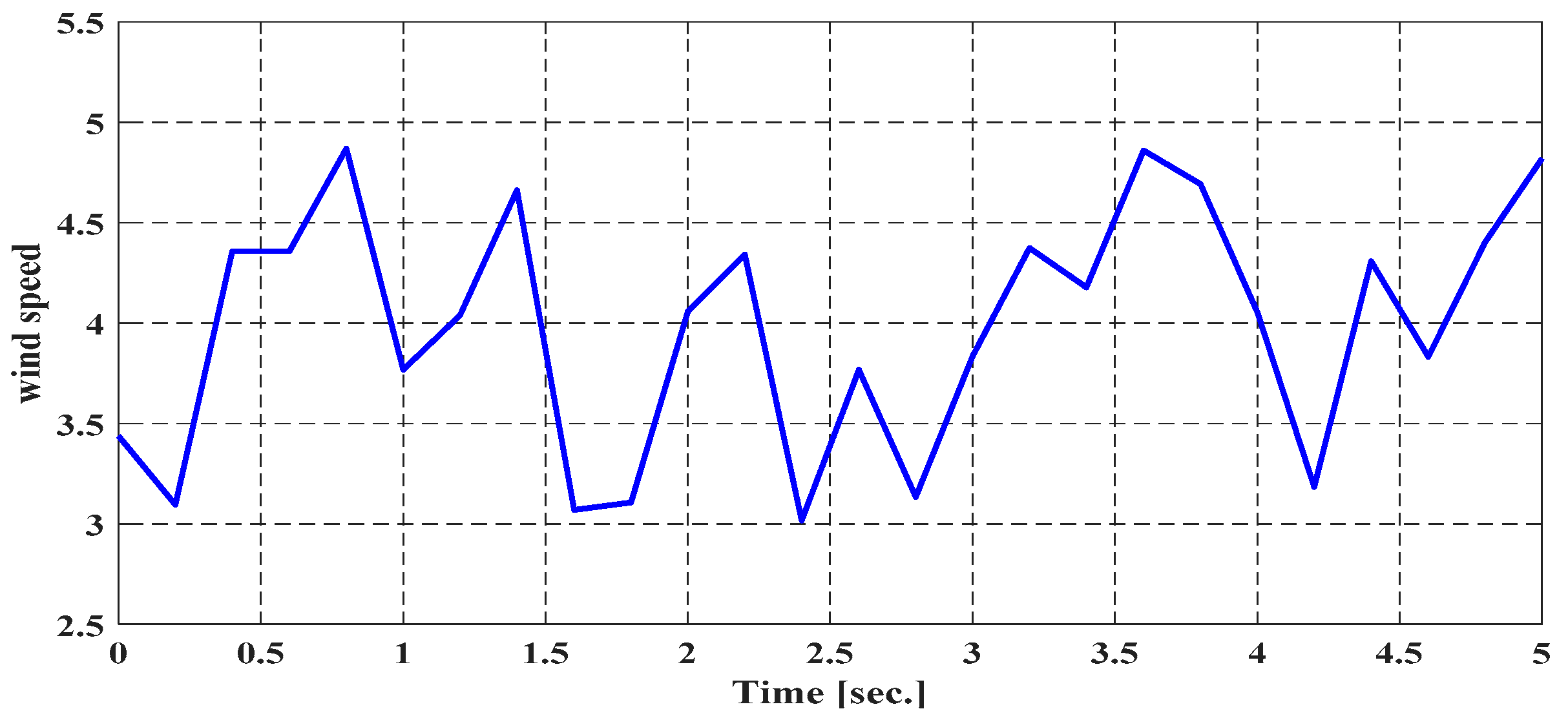
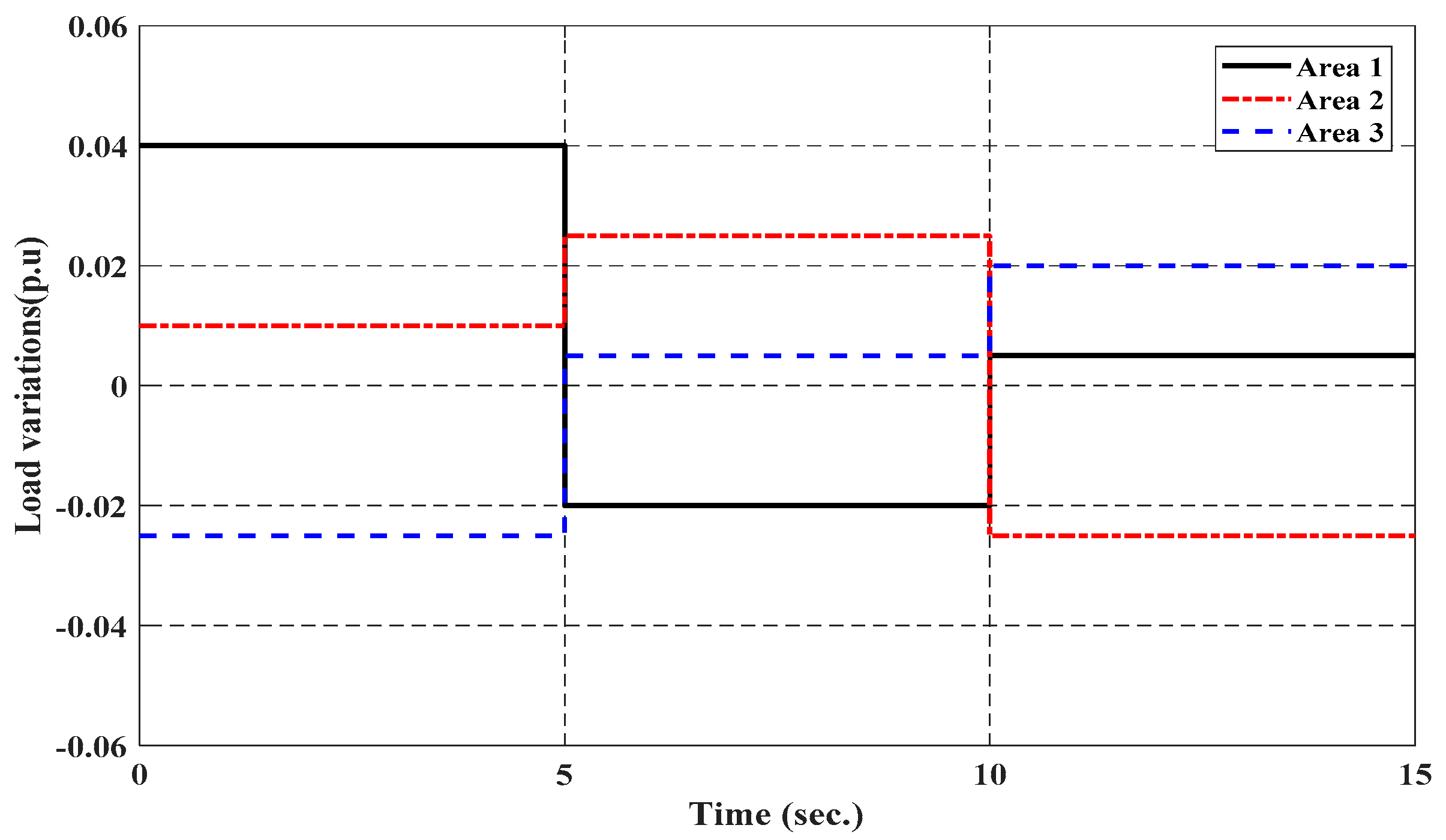
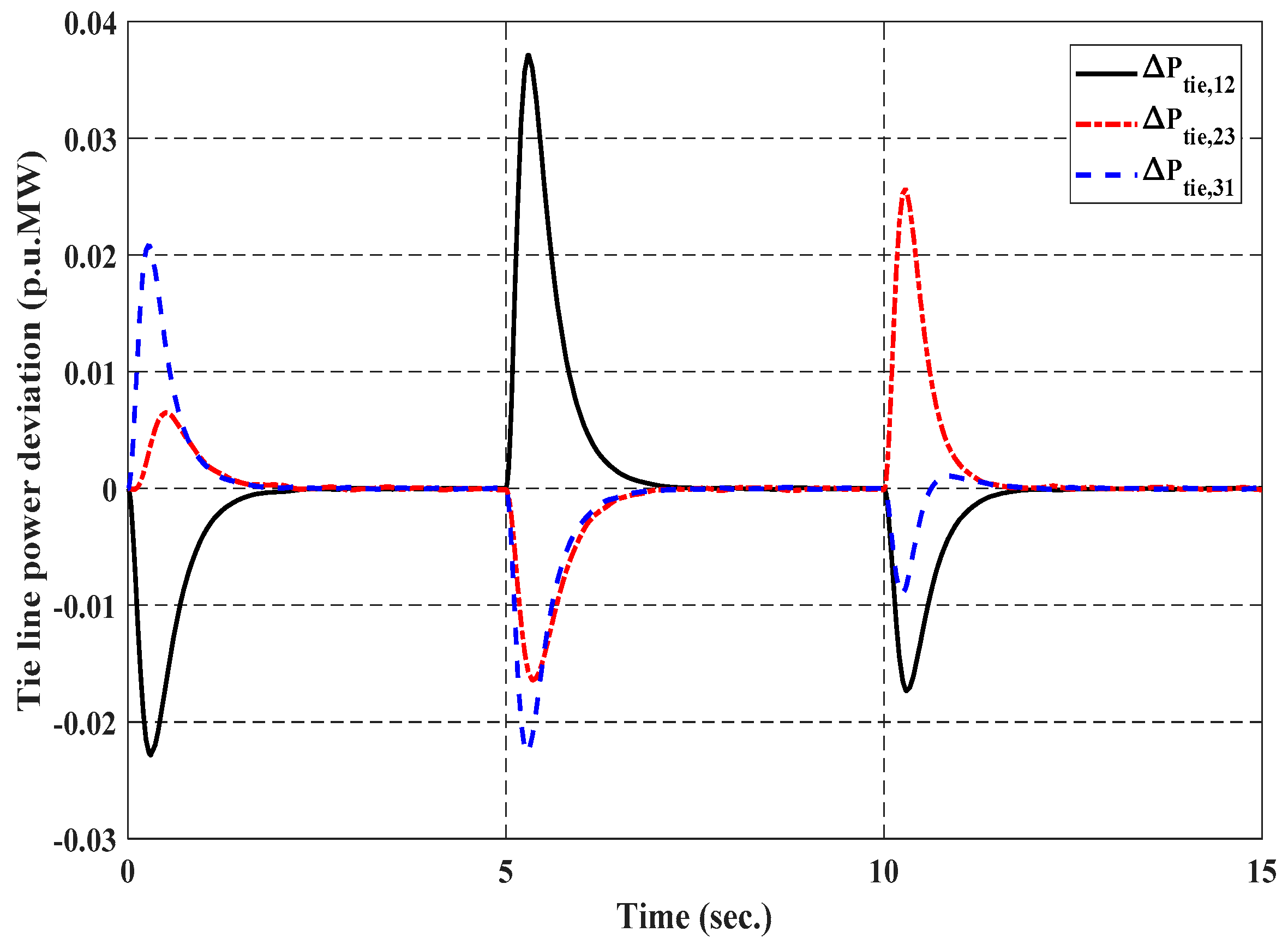
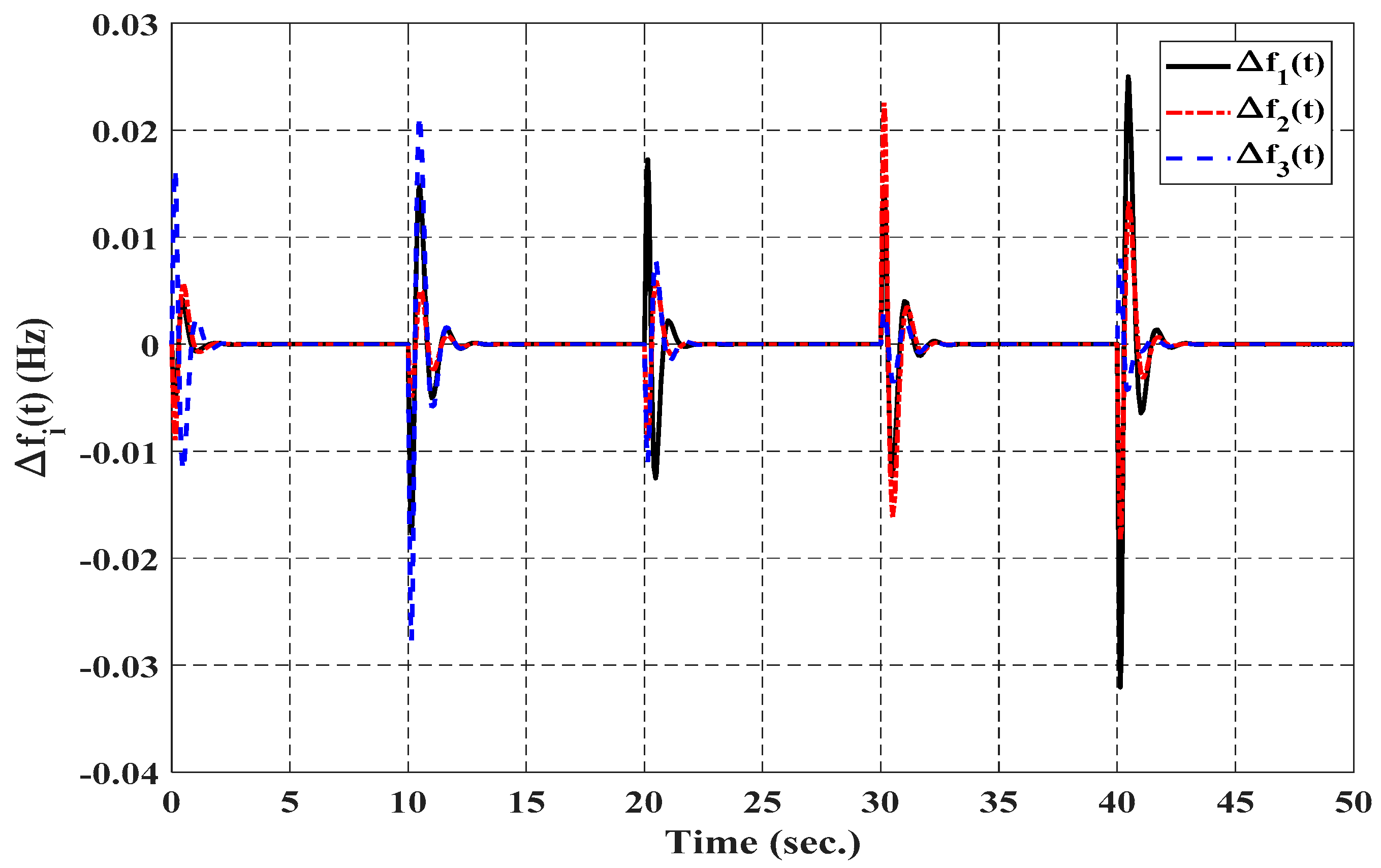
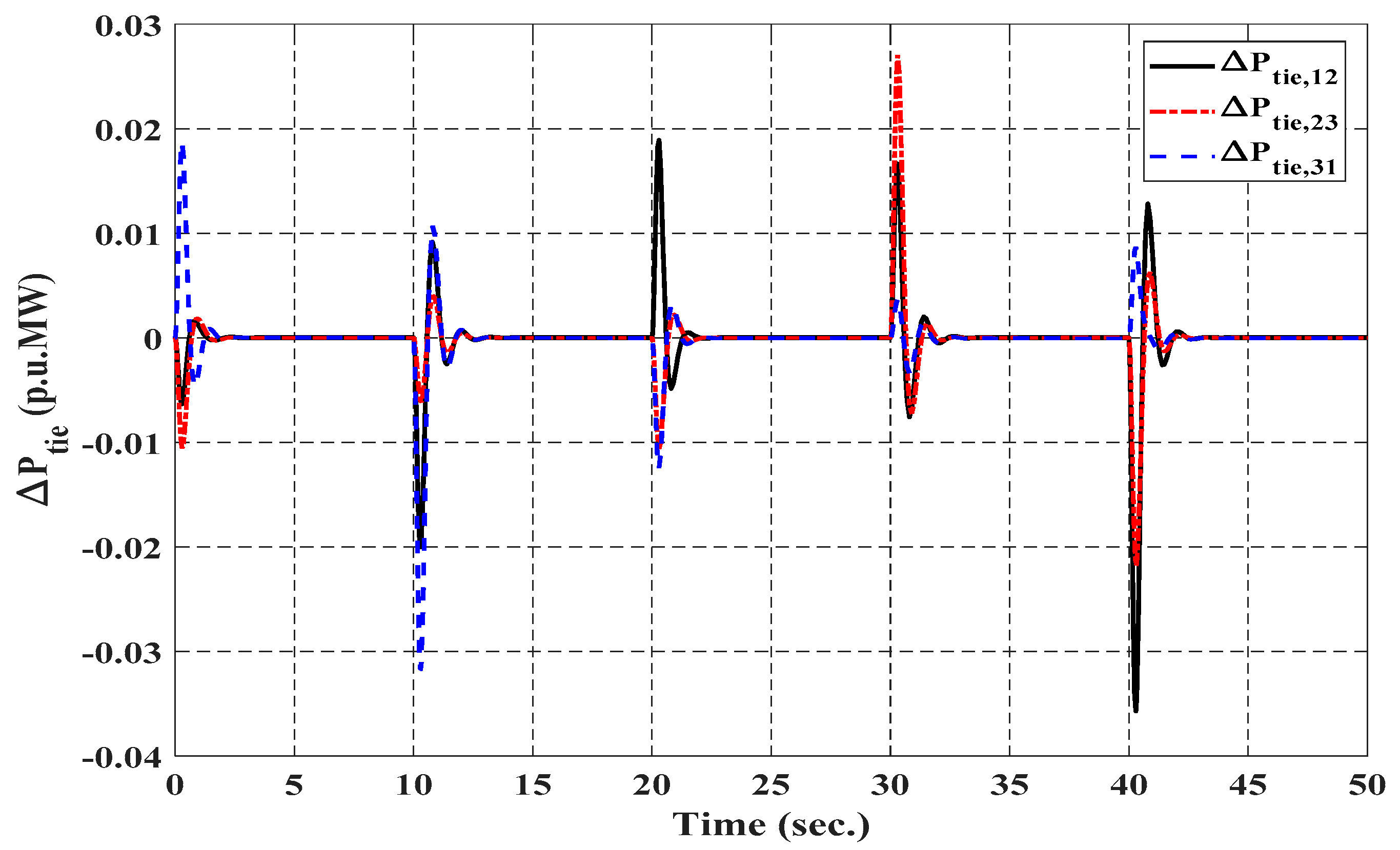
5. Simulation Results and Discussions

In this part, two simulations are done and the results are discussed and compared with other recent results.

5.1. Simulation 1

Parameters of the subsystem are obtained for simulation as given in [31] shown in

Table 1. Power system parameters.

Parameters	${\mathit{T}}_{\mathit{P}\mathit{i}}$	${\mathit{K}}_{\mathit{P}\mathit{i}}$	${\mathit{T}}_{\mathit{T}\mathit{i}}$	${\mathit{T}}_{\mathit{G}\mathit{i}}$	${\mathit{R}}_{\mathit{i}}$
Area 1	20	120	0.3	0.08	2.4
Area 2	25	112.5	0.33	0.072	2.7
Area 3	20	115	0.35	0.07	2.5

.

The system matrices are calculated as

$$A=\left[\begin{array}{ccccccccccccccc}-0.05& 6& 0& 0& -6& 0& 0& 0& 0& 0& 0& 0& 0& 0& -6\\ 0& -3.3& 3.3& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ -5.2& 0& -12.5& 12.5& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0.42& 0& 0& 0& 1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 1\\ 6.28& 0& 0& 0& 0& -3.45& 0& 0& 0& 0& -3.42& 0& 0& 0& 0\\ 0& 0& 0& 0& 4.5& -0.04& 4.5& 0& 0& -4.5& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& -3.03& 3.03& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& -5.14& 0& -13.8& 13.8& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0.42& 0& 0& 0& 1& 0& 0& 0& 0& 0& 0\\ -3.4& 0& 0& 0& 0& 6.28& 0& 0& 0& 0& -4.08& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& -5.75& -0.05& 5.75& 0& 0& 5.75\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& -2.85& 2.85& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& -5.71& 0& -14.28& 14.28& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 1& 0.42& 0& 0& 0& 1\\ -3.42& 0& 0& 0& 0& -4.08& 0& 0& 0& 0& 6.28& 0& 0& 0& 0\end{array}\right]$$

The design parameters in the propose control are chosen to be $\beta =0.015,$ $\mu =1.3,$

$$\begin{gathered} \gamma =2.2,\vartheta =2.2, \\ S=\left[\begin{array}{ccccccccccccccc}0& 0& 12.5& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 13.89& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 14.28& 0& 0\end{array}\right] \end{gathered}$$

and

$$\begin{array}{l}K=\\ \left[\begin{array}{ccccccccccccccc}172.5& 58.8& 5.3& -401.9& -592.8& 5.7& -0.8& -0.07& -427.6& -731.7& -10.4& -1.4& -0.04& -1028& -768\\ 15.9& 0.6& -0.04& -1498.8& -1093.1& 222.1& 59.1& 4.7& -922.2& -1125.2& 13.1& 2.6& 0.11& -979& -1229\\ -9.6& -2.46& -0.1& -839& -942.06& 12.1& 4.7& 0.3& -1127.5& -1015.7& 196.7& 59.6& 4.45& -740& -790\end{array}\right]\end{array}$$

By solving LMI (33), we have

$$R=\left[\begin{array}{cccccccc}0.001& 0& 0& 0.009& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0.009& 0& 0& 8.612& 3.4& -0.21& -0.01& 0\\ 0& 0& 0& 3.40& 2.12& -0.1& -0.02& 0\\ -0.001& 0& 0& -0.21& -0.1& 0.03& 0.002& 0\\ 0& 0& 0& -0.014& -0.02& 0& 0.001& 0\\ 0& 0& 0& -0.001& 0& 0& 0& 0\\ 0.002& 0& 0& 6.53& 2.87& -0.13& -0.008& 0\\ 0& 0& 0& 3.61& 2.14& -0.1& -0.015& 0\\ 0& 0& 0& -0.078& -0.06& 0& 0& 0\\ 0& 0& 0& -0.007& -0.01& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ -0.003& 0& 0& 5.91& 2.5& -0.13& -0.008& 0\\ 0& 0& 0& 3.68& 2.18& -0.11& -0.018& 0\end{array}\begin{array}{ccccccc}0.002& 0& 0& 0& 0& -0.004& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ -6.53& 3.6& -0.078& -0.008& 0& 5.9& 3.68\\ 2.87& 2.14& -0.06& -0.013& 0& 2.5& 2.18\\ -0.13& -0.1& 0& 0& 0& -0.13& -0.11\\ 0& -0.02& 0& 0& 0& -0.008& -0.02\\ 0& 0& 0& 0& 0& 0& 0\\ 6.07& 3.04& -0.11& -0.01& 0& 5.029& 3.04\\ 3.04& 2.19& -0.06& -0.01& 0& 2.655& 2.2\\ -0.11& -0.07& 0.016& 0.001& 0& -0.08& -0.05\\ -0.01& -0.01& 0.001& 0.001& 0& -0.007& -0.01\\ 0& 0& 0& 0& 0& 0& 0\\ 5.03& 2.65& -0.08& -0.007& 0& 4.49& 2.6\\ 3.05& 2.2& -0.06& -0.01& 0& 2.67& 2.2\end{array}\right]>0$$

and

$$\begin{array}{l}P=\\ \left[\begin{array}{ccccccccccccccc}0& 0& 0& 0& -0.01& 0& 0& 0& 0& 0& 0& 0& 0& -0.01& 0\\ 0& 15864& 0& 0.01& 0& 0& 0& 0& -0.01& 0& 0& 0.001& 0& 0& 0\\ 0& 0& 13564& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0.01& 0& 11847& -0.03& -0.35& 0.3& 0& 0.12& -0.02& -0.1& -0.02& 0& -0.05& -0.11\\ -0.01& 0& 0& -0.03& 10516& -0.22& 0& 0& -0.36& -0.3& -0.1& 0.02& 0& -0.21& -0.2\\ 0& 0& 0& -0.35& -0.22& 0.06& 0.01& 0& -0.13& -0.16& 0& 0& 0& -0.1& -0.13\\ 0& 0& 0& 0.028& 0& 0.011& 8586& 0& -0.03& -0.01& 0& 0.002& 0& 0& 0\\ 0& 0& 0& 0.002& 0& 0& 0& 7865& 0& 0& 0& 0& 0& 0& 0\\ 0& -0.01& 0& 0.12& -0.36& -0.13& -0.02& 0& 7255& -0.41& -0.14& 0.04& 0& -0.26& -0.2\\ 0& 0& 0& -0.02& -0.3& -0.15& -0.01& 0& -0.4& 6733& -0.12& 0.02& 0& -0.2& -0.18\\ 0& 0& 0& -0.12& -0.14& 0& 0& 0& -0.14& -0.12& 0.03& 0.006& 0& -0.07& -0.07\\ 0& 0& 0& -0.02& 0.02& 0& 0& 0& 0.03& 0.02& 0& 5886& 0& 0.01& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 5538& 0& 0\\ -0.01& 0& 0& -0.05& -0.21& -0.11& 0& 0& -0.26& -0.2& -0.07& 0.01& 0& 5228& -0.13\\ 0& 0& 0& -0.11& -0.19& -0.13& 0& 0& -0.2& -0.18& -0.07& 0.009& 0& -0.13& 4952\end{array}\right]>0\end{array}$$

Therefore, the LMI (33) is feasible.

5.1.1. Case 1

To examine the power system under the new algorithm, we apply step load changes with values of 0.01 p.u, 0.015 p.u and 0.02 p.u for Area 1, 2, and 3 together with wind speed variation in Figure 3. The respective results for incremental change in frequency and tie-flow distortion for the three areas are displayed in Figure 4 and Figure 5.

Both frequencies and tie-power flows spike at the initial point. At 2 s, the spikes are restored to zero point with lesser overshoots as compared to [31].

Table 2. Setting time $T_s$ and Maximum Overshoot (M.O.S).

	Proposed HROSM via Single Phase Sliding Surface		The Approach Given in [31]
Frequency Errors	Settling Time ${\mathit{T}}_{\mathit{s}}$ [s]	Max.O. S [pu]	Settling Time ${\mathit{T}}_{\mathit{s}}$ [s]	Max.O. S [pu]
$\Delta f_1$	1.5	0.003	2	0.005
$\Delta f_2$	1.5	0.0019	2	0.003
$\Delta f_3$	1.5	0.0019	2	0.003

HROSM: highly robust observer sliding mode.

gives a comparison result of both controllers. The single phase sliding surface without reaching time is used to cut-off the smaller overshoots.

Remark 2.

The power system response is seen better in terms of overshoots and settling time when compared with [31].

5.1.2. Case 2

In reality, there is always continuous load demand from industries, households, etc., therefore, we assumed random load variations at every 5 s intervals as shown in Figure 6. We simulate again and the incremental frequency and tie-flow fluctuation for the three areas are shown in Figure 7 and Figure 8, accordingly. At this time, the new controller proves to be robust and converge the errors to zero at every interval without loss of control accuracies. The power system response is seen to be much better. This is to say the new controller provides good correction signal to adjust the reference load in the speed changer motor (non-reheat systems).

Remark 3.

The new controller robustness is validated against random load change and variable wind speed. It also proves to be applicable in real power system in terms of the smaller overshoots seen which do not have any significant effect as to cause wear and tear of the actuator valve.

5.2. Simulation 2

In this section, we simulate the performance of HROSM control design in a New England (IEEE 39 bus system) with parameters and the performance indices calculation shown in

Table 3. Parameters of the New England IEEE 39 bus power system.

Generations (bus No.)	M (Moment of Inertia of the Generator)	D (Generator’s Damping Rations)	${\mathit{T}}_{\mathit{g}}$ (Governor Time Constant)	${\mathit{T}}_{\mathit{T}}$ (Turbine-Generator Time Constant)	Linearization Parameter of the Governor Characteristic
					${\mathit{K}}_{\mathit{t}}$	${\mathit{e}}_{\mathit{T}}$	r
G1 (39)	3.0	4.0	0.25	0.2	250	39.4	19
G2 (31)	2.5	4.0	0.25	0.2	250	39.4	19
G3 (32)	4.0	6.0	0.25	0.2	250	39.4	19
G4 (33)	2.0	3.5	0.25	0.2	250	39.4	19
G5 (34)	3.5	3.0	0.25	0.2	250	39.4	19
G6 (35)	3.0	7.5	0.25	0.2	250	39.4	19
G7 (36)	2.5	4.0	0.25	0.2	250	39.4	19
G8 (37)	2.0	6.5	0.25	0.2	250	39.4	19
G9 (38)	6.0	5.0	0.25	0.2	250	39.4	19
G10 (30)	4.0	5.0	0.25	0.2	250	39.4	19

as given in [36]. This system consists of 10 machines. The one-line diagram of the test system with its tie-line is displayed in Figure 9. Areas 1 and 2 have three generators, and there are four generators in Area 3; all generators are synchronized and operating in parallel running in a non-deregulated environment. The generators are equipped with governors. The total generated power and loads connected in Areas 1, 2 and 3 are 265.5, 233, 125 and 842 MW, respectively [36].

The New England system is simulated with the designed HROSM against variable load changes as shown in Figure 3. Figure 10 displayed the results of the frequency error of Area 3, while Figure 11 shows the tie-power exchange error results. In the results, it is seen that the new controller performance is good by damping the frequency and tie-power flow changes without loss of control and chattering free. The New England system response is better in terms of lesser settling time and overshoots which also cannot have any significant effect (i.e., wear and tear) on the governor steam actuator valve.

Remark 4.

It is seen that the new SPSS and the controller without reaching time keep frequency and tie-power flow at desired values in the New England 39 bus system with better response in overshoots and settling time. Therefore, this is the evidence that the new SPSS and controller without reaching time is good application for LFC of large power system.

6. Conclusions

In this paper, LFC problems in multi-area power integrated with renewable power plants is solved with proposed design of highly robust observer sliding mode via single phase switching. The proposed controller is designed to act only on the observer information and a single phase sliding is selected for SMC such that all estimated states trajectories begin at the surface at an initial time moment which makes it highly robust for applications. System stability is proved via the Lyapunov theory based on a new LMI scheme. Experimental simulation results show the new controller performed better when compared with recent SMC in terms of the rapid control of frequency and tie-flow spikes, and achieved chattering free without any weak control accuracies against external disturbances acting on the large multi-area power system. In addition, the proposed sliding surface and new controller, which depend on only the observer state estimation, are useful in applications for real power systems where all system state variables are difficult or expensive to measure.