FPGA Accelerator for Gradient Boosting Decision Trees

Abstract

A decision tree is a well-known machine learning technique. Recently their popularity has increased due to the powerful Gradient Boosting ensemble method that allows to gradually increasing accuracy at the cost of executing a large number of decision trees. In this paper we present an accelerator designed to optimize the execution of these trees while reducing the energy consumption. We have implemented it in an FPGA for embedded systems, and we have tested it with a relevant case-study: pixel classification of hyperspectral images. In our experiments with different images our accelerator can process the hyperspectral images at the same speed at which they are generated by the hyperspectral sensors. Compared to a high-performance processor running optimized software, on average our design is twice as fast and consumes 72 times less energy. Compared to an embedded processor, it is 30 times faster and consumes 23 times less energy.

1. Introduction

Decision trees are a light and efficient machine learning technique that have proved their effectiveness in several classification problems. In the context of embedded systems, energy efficiency is as much important as accuracy, so it is necessary to search for efficient algorithms liable to be accelerated. This makes the decision trees a perfect target to develop an FPGA accelerator.

A single decision tree is frequently not very accurate for complicated tasks but, thanks to ensemble methods, it is possible to combine several trees in order to deal with complex problems. Gradient Boosting Decision Trees (GBDT) [1] is an ensemble method that allows to improve the accuracy gradually adding new trees in each iteration that improve the result of the previous ones. Conventional implementations of GBDT suffer from poor scaling for large datasets or a large number of features, but recently some efficient implementations have overcome this drawback such as XCGBoost [2], CatBoost [3], or LightGBM [4]. For instance, LightGBM is a highly efficient open-source GBDT-based framework that offers up to 20 times higher performance over conventional GBDT. With the support of LightGBM, GBDTs are currently considered one of the most powerful machine learning models due to its efficiency and accuracy. For example, recently they have been used for many winning solutions in several machine learning competitions [5]. They can be used for very different problems. For instance, they have been successfully used to produce accurate forecasts for the COVID-19 evolution, and to identify factors that influence its transmission rate [6]; to detect fraud from customer transactions [7]; to estimate major air pollutants risks to human health [8] using satellite-based aerosol optical depth; or to classify the GPS signal reception in order to improve its accuracy [9]. Moreover, a recent publication [10] analyzed different machine learning methods for image processing in remote systems, focusing on on-board processing, which requires both performance and low-power. In this work the authors identified that GBDTs present a very interesting trade-off between the use of computational and hardware resources and the obtained accuracy. Their accuracy results were close to those obtained with convolutional neural networks, which currently is the most accurate method, while carrying out one order of magnitude less computational operations. Moreover, most of their operations during inference are integer comparisons, which can be efficiently calculated even by very simple low-power processors, and can be easily accelerated by FPGAs. For that reason they represent a good option for embedded system.

In this paper we present an accelerator for Gradient Boosting Decision Trees (GBDT) that can execute the GBDT trained with LightGBM. We have created a repository in which we include the GBDT models used, and our source codes [11]. Our accelerator has been designed for embedded systems, where hardware resources and power budget are very limited. Hence, our primary goal is efficiency. The register-transfer level (RTL) design of our accelerator has been written in VHDL, and, to demonstrate its potential, we have implemented it in a low-cost FPGA evaluation board (ZedBoard) [12], which includes an FPGA for embedded systems, and we have used our implementation for the relevant case study analyzed in [10]: pixel classification of hyperspectral images with the objective of processing the data at run-time. We have measured the execution time and power consumption of our accelerator and we have identified that our design can be used to process complex GBDT models even when using a small FPGA. In our case study, our accelerator can process the hyperspectral information at the same speed at which the hyperspectral sensors generate it, and the dynamic energy consumption due to the execution is an order of magnitude less in both cases, compared to a high performance CPU and compared to an embedded system CPU. Hence it could be used for on-board processing in remote sensing devices.

2. Related Work

Several previous works have targeted FPGA acceleration of Decision Trees. Reference [13] focuses on the training processes. In our case we assume that training is carried out offline and we want to focus on inference, which will be computed online. Reference [14] presented a custom pipeline architecture which demonstrated the potential of an accelerator for decision trees. However they do not support GBDT and they apply their techniques only to simple case studies. Reference [15] proposes to use a high-level synthesis approach to design an FPGA accelerator. They focus on Random Forest, which is an ensemble technique that calculates the average value of several trees trained with different input data to generate a more accurate and robust final output. We have decided to focus on GBDT instead of Random Forest since recently GBDT have demonstrated an enormous potential [5]. Moreover, [10] compared the results of Random Forest and GBDT and the results show that GBDT provided better accuracy while using smaller models, hence we believe that it is a better approach for embedded systems. Another difference is that we have designed a custom register-transfer level (RTL) architecture instead of using a high-level synthesis that will automatically generate the RTL design from a C-code. High-level synthesis is very interesting for portability, and to reduce the design cycle, but with our RTL design we can fully design the final architecture and explore several advanced optimization options. Reference [16] is another work that analyzes the benefits of implementing Random Forest on FPGAs. They compare the effectiveness of FPGAs, GP-GPUs, and multi-core CPUs for random forest classifiers. They conclude that FPGAs provide the highest performance solution, but they do not scale due to the size of the forest. In this sense, as explained before, GBDT models require fewer trees to obtain the same accuracy, so it is a more suitable model for FPGAs. Reference [17] proposes to use FPGAs to accelerate the execution of decision trees used in the Microsoft Kinect vision pipeline to recognize human body parts and gestures. They use a high performance FPGA, and obtain very good results for decision tress organized as random forest. However, they identify that their design cannot be used in low-power FPGAs due to its memory requirements. Reference [18] is a very recent work that presents an algorithm that produces compact and almost equivalent representations of the original input decision trees by threshold compaction. The main idea is to merge similar thresholds to reduce the number of different thresholds needed, and store those values as hard-wired logic. With this approach the size of the trees can be reduced. This technique is orthogonal to our approach and can be beneficial to our design since it reduces the size of the trees, which simplifies its storage in embedded systems. Reference [19] is another recent work that analyzes the benefits of FPGA acceleration for Gradient-boosted decision trees. In this case they evaluate the services provided by Amazon cloud, which include the access to high-performance FPGAs that can be used through high-level interfaces. Therefore, this work is complementary to ours, as it focuses on high-performance cloud servers while we focus on embedded systems.

In summary, the previous works indicate the potential of FPGAs for the execution of decision trees. Most of these works focus on Random Forest, and they either only implement small systems, or they need to use high performance FPGAs. Therefore, it is necessary to improve the scalability of these solutions in order to use them in embedded systems. In this paper we present a GBDT-based accelerator capable of solving very complex models even in a relatively small FPGA. GBDTs have achieved excellent results in various machine learning problems, and their characteristics are very interesting for embedded systems. Therefore, we have designed a hardware accelerator for FPGAs with the objective of running complex models based on GBDT in low-cost and low-energy consumption systems. To demonstrate the potential of our design we have implemented an equivalent solution to the most complex GBDT model proposed in [10], which used GPUs to execute the models, on a Xilinx Zedboard FPGA which is a small model oriented to embedded systems.

3. Gradient Boosting Decision Trees

A Decision Tree is a decision algorithm that uses a tree-like model to generate its output. It can be seen as a way to display an algorithm that only contains conditional control statements. In each tree the decision is based on a series of comparisons connected between them as in a binary tree structure. Each internal node represents a comparison used to decide the following node, and each leaf node contains the result of the prediction [20]. When decision trees are used for classification problems each leaf of the tree is labeled with the predicted class or with a probability for a given class or a probability distribution over all the classes. 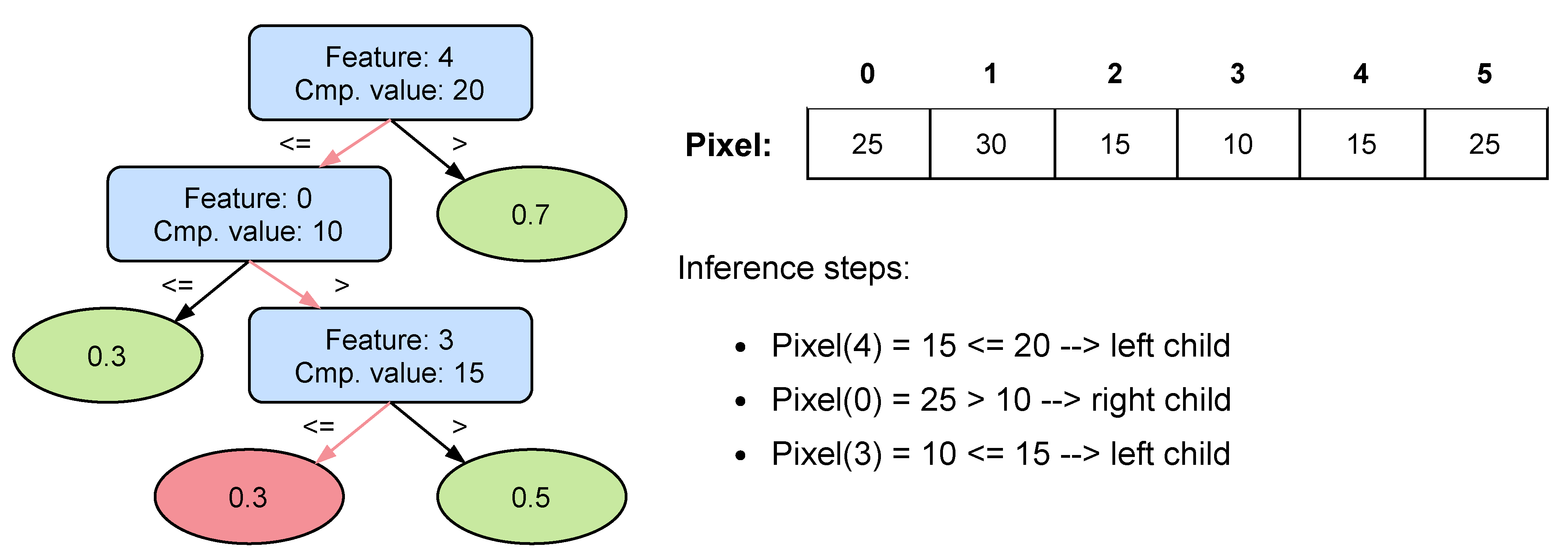Figure 1 shows the operation of a Decision Tree on a series of feature inputs with a toy example. In the first place, this tree takes feature 4 of the input and compares its value with 20; as the input value is lower it continues on the left child, and keeps with the same procedure until it reaches the leaf with $0.3$ as output value.

One of the benefits of using Decision Trees over other techniques is that they do not need any input preprocessing such as data normalization, scaling or centering. They work with the input data as it is [20]. The reason is that features are never mixed. As can be seen in Figure 1, in each comparison the trees compare the value of an input feature with another value of the same feature. Hence, several features can have different scales. In other Machine Learning models, features are mixed to generate a single value, therefore, if their values belong to different orders of magnitude, some features will initially dominate the result. This can be compensated during the training process, but in general normalization will be needed to speed up training and improve the results. Avoiding normalization reduces the run-time computations needed, hence it is a very interesting feature for embedded systems.

Besides, the size of the input data does not directly affect the size of the model, or its computations. Hence, dimensionality reduction techniques such as Principal Component Analysis are not needed to reduce the model size. Again, this is very interesting for embedded systems since it substantially reduces the amount of calculation needed at inference. During training the most meaningful features are selected and used for the comparisons in the tree. Hence the features that contain more information will be used more frequently for the comparison, whether those that do not provide useful information for the classification problem will simply be ignored. This is an interesting property of this algorithm since, based on the same decisions made during training to choose features, we can easily determine the feature importance. This means that Decision Trees can be used to find out which features provide more meaningful information, and this can be used to train even smaller models keeping most of the information with less memory impact.

Nevertheless, a single Decision Tree does not provide accurate results for complex classification tasks. The solution is to use an ensemble method that combines the results of several trees in order to improve the accuracy levels. Gradient Boosting is an ensemble method that combines the results of different predictors in such a way that each tree attempts to improve the results of the previous ones. Specifically, the gradient boosting method consists in training predictors sequentially so each new iteration try to correct the residual error generated in the previous one. That is, each predictor is trained to correct the residual error of its predecessor. Once the trees are trained, they can be used for prediction by simply adding the results of all the trees [20].

The GBDT model also allows designers to trade off accuracy for computation and model size. For example, if a GBDT is trained for 100 iterations, it will generate 100 trees for each class. Afterwards, the designer can decide whether to use all of them, or to discard the final ones. It is possible to find similar trade-offs with other ML models, for instance reducing the number of convolutional layers in a convolutional neural network (CNN). However, in that case, each possible design must be trained again, whereas in GBDT only one train is needed, and afterwards the designer can simply evaluate the results using different number of trees and generate a Pareto curve with the different trade-offs. Again, this is very suitable for embedded systems, as we can adjust the model size according to the available memory resources, or the execution time and power consumption restrictions.

In terms of computation, most of the machine learning algorithms need a significant amount of floating point operations for the inference process. For instance, CNNs and multilayer perceptrons (MLPs) are based on floating-point multiply-accumulate operations. By contrast, calculating the output of a tree only involves carrying out some comparisons. If the input data are integers, as is the case with the pixels in an image, all these comparisons will only use integers, which greatly reduces the computational load. The only floating point operation will be the accumulation of the outputs of each tree, in those cases where the final output is a probability represented in floating point. Hence, there will be a single floating point-addition for each tree. In embedded systems these additions can be replaced by operations in fixed precision and the whole model can be executed even in systems that do not have floating point units.

4. Design Architecture

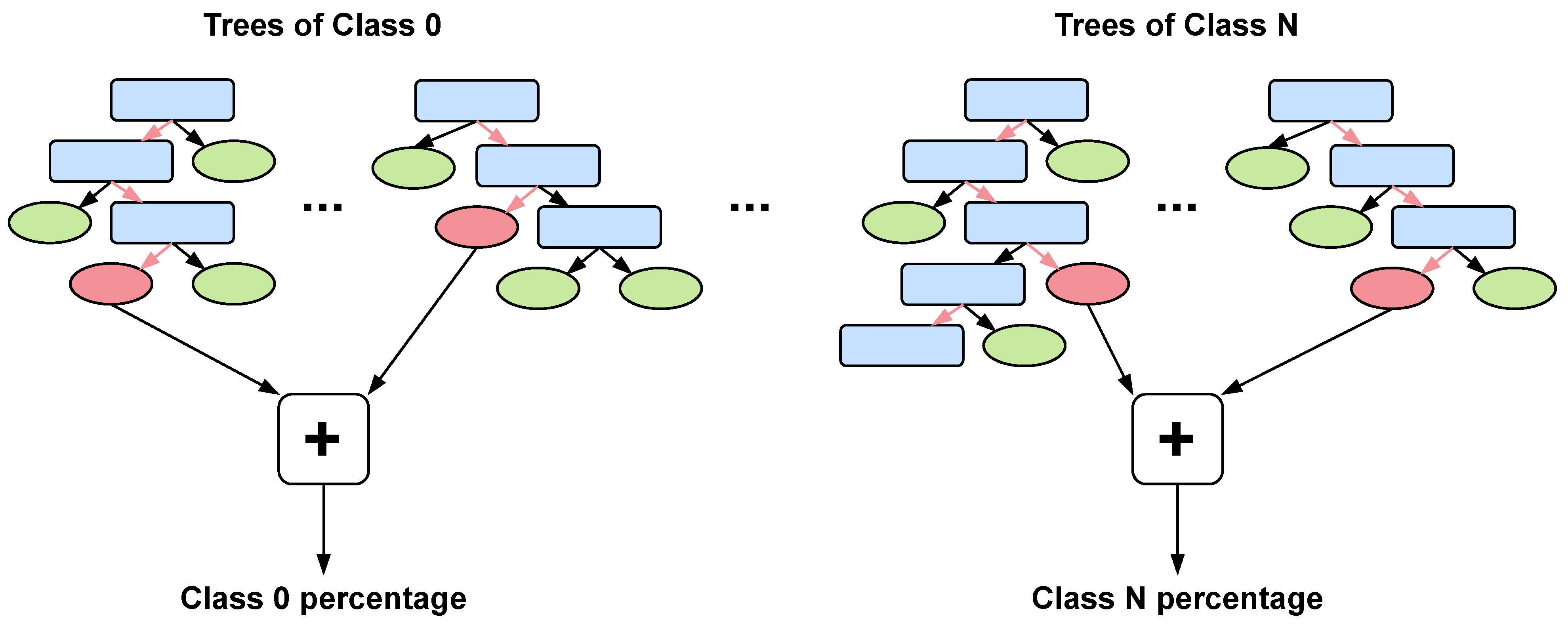
LightGBM follows a one-vs-all strategy for classification problems that consists in training a different estimator (i.e., a set of trees) for each class, so each one of them predicts the probability of belonging to that class. With this approach each class has their own private trees, and the probability of belonging to a given class is obtained by adding the results of its trees, as shown in Figure 2.

Hence, during inference, each class is independent from the others, and the trees of each class can be analyzed in parallel. Our accelerator takes advantage of this parallelism by including one specific module for each class.

To design an efficient accelerator, it is essential to optimize memory resources. Our goal is to store the trees in the on-chip memory resources of the FPGA to minimize data transfers with the external memory. However those resources are very limited, so a key point of the design is to optimize the format used to store the trees in order to reduce their memory requirements.

All the trees of a class are mapped into its trees_nodes RAM memory, which is local to the class module. Figure 3 present the representation that we have selected to store the tree structure on this memory. Our objective is to include all the information of each node in a 32-bit word. Since we use generic parameters in our code, this word size can be enlarged or reduced as needed. But in our experiments we have observed that 32 bits provides a good trade-off between the accuracy to represent the trees and the storage requirements. These 32 bits follow two different formats taking into account whether they are leaf nodes or not.

The format for non-leaf includes four fields. The first and the second field store the information needed to carry out the comparison, that is, which input will be used (8 bit), and with which value it will be compared (16 bit). Then we need to store the addresses of the child nodes. As we only have 8 bits remaining, it is not possible to store its absolute addresses. In fact, with the size of the memories that we are using, we would need almost all of the 32-bits to store that information. We have solved this issue with two solutions. First, in the trees_nodes memory, nodes are stored using the pre-order traversal method, that is, the left child of a non-leaf node is always allocated in the following memory position. With this approach the address of the left child does not need to be stored, since it can be obtained adding one to the current address. Hence, we only have to store the address of the right child. Second, instead of storing the absolute address of the right child, we store a relative address that indicates its distance with the current address. This relative distance is stored in a 7-bit field. With this approach the maximum depth of a tree is 128. This is more than enough for all the trees that we have analyzed, since GBDT does not rely on very large trees, but in using many of them. Finally, we have included a flag in the less significant bit of each node: This flag determines whether it is a leaf node or not.

In the case of the leaf nodes, the 32-bits memory word includes four fields. A 16-bits field stores the output of the three. The next 14-bits are used to store the address of the next tree. In our experiments 14 bits were enough for the absolute addresses. The original output of the LightGBM GBDTs is a 32-bit floating point. However, using a 16-bits fixed-point representation we obtain similar accuracy in our experiments. In any case, if needed, it is possible to use more bits for the output without increasing the size of the memory word by using relative addresses for the @next_tree field instead of absolute addresses. The last two bits are two flags that identify whether this is the last tree in the class, and whether the node is a leaf or not.

Figure 4 presents a simple example in which two trees of a class are stored. As can be seen in the figure, the root node of the first tree is stored in address 0. Then, the entire tree structure corresponding to its left child is stored, following these same rules recursively, and finally the right child is stored in the last place. The bits corresponding to rel@_right_child field store the relative jump to its right child. All the leaf nodes of the first tree indicate that the next tree begins in address 5. Finally, the leaf nodes of the second tree indicate that there are no more trees to process. This simple example includes 8 nodes. If we execute it in our architecture we will visit four or five of these nodes, it depends on the result of the first comparison, and we will need approximately one clock cycle to process each node. In larger trees, the number of visited nodes will be much lower than the number of total nodes, and the execution time will remain approximately one cycle per visited node.

Figure 5 depicts the internal design of one of the modules that execute the trees of a class. The design includes the previously described trees_nodes RAM memory, a register, @_last_node, that is used to store the address of the last visited node, and the logic that carries out the comparisons, compute the next node to visit, and accumulate the results of the trees.

In this design the @_ feature field of non-leaf nodes is used to select one feature among all the input features of the system. The selected feature is compared with the cmp_value field. If the value of the feature is less or equal than the cmp_value, the left child of the non-leaf node is selected. To this end, we add 1 to the @_last_node. Otherwise, we add the rel@_right_child to select the right child. This will generate the @_node that will be used to address the trees_nodes RAM memory in case that the current node is a non-leaf (is_leaf value is 0). If the current node is a leaf (is_leaf value is 1), and this is not the last tree (is_last_tree value is 0), the selected value to address the trees_nodes RAM memory will be the @_next_tree field of the leaf node. On every leaf node, the result register will accumulate the leaf_value field to the previous result value.

According to the selected memory representation of the nodes, the maximum size of the trees_nodes RAM will be $2^{14}$ words, as we dedicate 14 bits to the @_next_tree, and the theoretical maximum number of nodes of the same tree will be $2^6$ due to the size of the relative jump rel@_right_child. Regarding the size of the RAM, we could address any number of trees just making the @_next_tree a relative address from the current node by adding it to @_last_node, nevertheless the current size is even bigger than our needs. In our design we dedicate 8 BRAMs of 32 Kb to the trees of each class, which is 8192 words of 32 bits, so we are actually using the 13 less significant of the 14 bits available to address the trees_nodes RAM. Regarding the number of nodes of each tree, this is only a theoretical limit due to the relative jump, which actually affects only the left side of each node, that is, the left side of each node of the tree can only have 63 nodes, so we could reach the right child in a pre-order traversal. In any case, the maximum number of nodes of our trees is 61 and the average is between 7 and 22 depending on the dataset, so this is not a problem either.

Once we receive the features of one pixel, we only need to wait until every class module has finished and then check the output of the argmax module, which selects the number of the class with the higher result. Figure 6 depicts a simplified design of the accelerator showing this behavior, where we omitted the control lines and the management of the communications.

This design can process a node per class in each clock cycle. However, in our experiments, if we implement a system that uses most of the on-chip memory resources, the place&routing process becomes complex and the clock frequency is just 55 MHz. This can be solved by using a more modern FPGA, with more capacity, and better integration technology, but it can also be improved by applying some computer architecture optimizations similar to those that have been used to optimize the execution of general purpose processors. We will illustrate this with the following figures. In Figure 7a we present the execution of the previously described version (single-cycle implementation). The figure depicts the execution of the nodes in one of the classes. If we have N classes all of them will be executed in parallel. In the figure three nodes are executed in three clock cycles. However, as explained before, the clock period is long and the system runs slow.

Our goal is to improve the speed, while trying to keep processing one node per cycle. To reduce the clock cycle we have designed a multi-cycle implementation. We have explored three different options: two, three and four clock cycles. In these versions, additional registers have been added to the architecture in order to split the longest combinational paths. From that analysis we selected the option that executes the nodes in three cycles, because it achieves an important clock-period reduction and at the same time provides a clear architecture, in which it is easy to identify the actions that are carried out in each cycle. With four cycles, the benefits were very small, and the resulting execution scheme was not intuitive. Figure 7b presents the results after this step. AS can be seen in the figure, the clock frequency has been improved, but the system is slower than before, since we need three clock cycles for each node. However, since we have partitioned the design following a clear scheme, we could try to use a pipeline approach. As presented in Figure 8a we have three different pipeline stages, and each one of them uses different hardware resources. Hence, we can start executing a second node, as soon as the first one has finished the first stage. In our design the first step is used to read the node (fetch), the second step is used to identify the type of the node and read the needed feature (decode), and the last step is used to compare it with the comparison value, and identify the next node to execute (execution). The problem of this scheme is that we do not know the next node until the previous node has finished its execution stage. Hence we cannot fetch it in advance. Hence, a simple pipeline will not provide any benefit. This is the same problem that conventional processors have when dealing with instructions that include conditional branches. High-performance processors alleviate this problem by including complex support for speculative execution, but it is not an efficient solution for embedded systems, since it introduces important energy overheads, and it will not achieve good results, unless it is possible to identify clear patterns for branch predictions. Hence, there is no straightforward way to take advantage of the pipeline architecture.

However, this problem can be solved by combining the pipeline with a multi-threading approach. The idea is to include support to interleave the execution of three different trees. This can be done by including three @_last_node registers (that is the same as having three program counters in a processor). The trees in a class are divided in three sets, and each counter manages the execution of one of these sets. Figure 8b depicts how the executions of the three trees are interleaved. In this example three different trees (n, m and l) are executed. With this approach we have the same period that in the multi-cycle approach, and we can execute one node per cycle, as in the single-cycle implementation.

Figure 9 shows the final structure of the multi-threaded class module. As can be seen in the figure, the hardware overhead is small. We only need to include a few registers to store the information needed for each stage, the additional @_last_node counters, two additional registers which indicate the starting address of the first tree in each set, three 1-bit registers which store a flag indicating whether the processing of each set has been completed, and finally modify the control unit. Moreover, the memory resources, which are the most critical in our design, are the same in both versions.

The VHDL source codes of both versions are available in [11].

5. Datasets and Models

Hyperspectral images consist of hundreds of spectral bands, where each band captures the responses of ground objects at a particular wavelength. Therefore, each pixel of the image can be considered as a spectral signature, as in Figure 10. As analyzed in [10], machine learning techniques can achieve very good accuracy classifying the pixels of hyperspectral images. The best results were obtained using convolutional neural networks. However, the size of hyperspectral images makes it a very computationally intensive task, so in on-board systems with very limited resources it is not possible to use this solution. This study identified that GBDTs present a very interesting trade-off between the use of computational and hardware resources and the obtained accuracy because it achieved good accuracy rates, while carrying out few computational operations at run-time. For that reason GDBTs are a good candidate for an embedded on-board system, and we have selected it as a case study. Our objective is to achieve the same accuracy results reported in [10] while executing the trees in our accelerator implemented in a small FPGA. As a second objective, we want to process the pixels at the same speed at which they are generated by the hyperspectral sensors.

In hyperspectral images pixel classification, the input is a single pixel composed of a series of features, where each feature is a 16-bit integer. The number of features depends on the sensor used to obtain the image, in our case we used datasets from 103 to 224 features. Each node of the tree selects one of these features, and compares it with the value stored in the node to make their decision; that is, whether to select the left or the right child.

Our design has been written in VHDL using generic parameters to be very customizable. Hence, it can be used for different images with different number of classes, of input features, of trees per class...

Table 1. Datasets and model configuration.

	Image		Model			Top1 Accuracy
	ft.	cl.	Trees	m	d	Accelerator	LightGBM
IP	200	16	2533	20	20	$0.802$	$0.805$
KSC	176	13	2600	30	5	$0.894$	$0.894$
PU	103	9	1206	30	30	$0.922$	$0.924$
SV	224	16	2146	80	25	$0.926$	$0.928$

summarizes the main characteristics of the hyperspectral images analyzed, Indian Pines (IP), Kennedy Space Center (KSC), Pavia University (PU) and Salinas Valley (SV), and the selected configuration of the GBDT models, based on those presented in [10], which analyzed the different GBDT parameters and selected the optimal ones in each case. The table shows the number of features (ft.) and classes (cl.) of each image, the total number of trees used (trees), and some key model parameters used to train the models such as the minimum number of data to split a node (m) and maximum depth (d). Finally, it presents the accuracy obtained executing the models in [10] with the LightGBM library, and the achieved accuracy with the equivalent models adapted for our accelerator. As can be seen in the table, the changes in the original decision trees almost have no effect on the final accuracy.

The models codified according to the described node representation format are available in [11].

6. Experimental Results

The accelerator has been designed to fit in the FPGA of the Zedboard Xilinx Zynq-7000 (Digilent, Hong Kong, China) evaluation board [12]. This is a very small FPGA with an old technology, so the needs of the design are very restrictive. The main goal of using this device is to try to reproduce the characteristics of the rad-hard and rad-tolerant FPGAs approved for embedded on-board devices. These devices do not use the latest integration technologies, hence it will not be realistic to use the latest generation of FPGAs.

Table 2. Single-cycle vs. multi-threading resources.

		Single-Cycle	Multi-Threading	incr.
IP	LUTs	15,800 (29.70%)	17,027 (32.01%)	1.08
	Flip-Flops	4470 (4.20%)	6250 (5.87%)	1.40
	F7 Muxes	6657 (25.03%)	6657 (25.03%)	1
	F8 Muxes	3328 (25.02%)	3328 (25.02%)	1
	BRAMs (36Kb)	128 (91.43%)	128 (91.43%)	1
KSC	LUTs	11,749 (22.08%)	12,641 (23.76%)	1.08
	Flip-Flops	3909 (3.67%)	5351 (5.03%)	1.37
	F7 Muxes	4578 (17.21%)	4577 (17.21%)	1
	F8 Muxes	2288 (17.20%)	2288 (17.20%)	1
	BRAMs (36Kb)	104 (74.29%)	104 (74.29%)	1
PU	LUTs	5228 (9.83%)	5714 (10.74%)	1.09
	Flip-Flops	2455 (2.31%)	3436 (3.23%)	1.40
	F7 Muxes	2016 (7.58%)	2016 (7.58%)	1
	F8 Muxes	864 (6.50%)	864 (6.50%)	1
	BRAMs (36Kb)	72 (51.43%)	72 (51.43%)	1
SV	LUTs	17,462 (32.82%)	18,628 (35.02%)	1.07
	Flip-Flops	4862 (4.57%)	6638 (6.24%)	1.37
	F7 Muxes	7681 (28.88%)	7681 (28.88%)	1
	F8 Muxes	3584 (26.95%)	3584 (26.95%)	1
	BRAMs (36Kb)	128 (91.43%)	128 (91.43%)	1

shows the hardware resources of single-cycle and multi-threading designs in this FPGA.

The only perceptible increment is the number of LUTs and Flip-Flops, the rest are null or negligible. These increments are not important for the design, since it uses a small percentage of these resources. As can be seen in the table, the bottleneck of the system are the on-chip memory resources. In fact, some images use almost all memory resources. For that reason it was very important to optimize the memory format used to store the trees.

Table 3. Single-cycle vs. multi-threading throughput.

		Single-Cycle	Multi-Threading	Gain
IP	Freq. (MHz)	$60.61$	$105.263$	$1.69$
	Avg. Cycles/px.	$1658.15$	$1700.9$
	Avg. $\mathsf{\mu }$s/px.	$27.36$	$16.16$
	Avg. px/s.	$\mathrm{36,552.78}$	$\mathrm{61,886.65}$
	Avg. Cycles/Node	1	$1.026$
KSC	Freq. (MHz)	62.5	105.263	1.67
	Avg. Cycles/px.	2542.76	2564.55
	Avg. $\mathsf{\mu }$s/px.	40.69	24.36
	Avg. px/s.	24,579.60	41,045.41
	Avg. Cycles/Node	1	1.009
PU	Freq. (MHz)	66.67	125	1.80
	Avg. Cycles/px.	1857.34	1938.70
	Avg. $\mathsf{\mu }$s/px.	27.86	15.51
	Avg. px/s.	35,895.42	64,476.20
	Avg. Cycles/Node	1	1.044
SV	Freq. (MHz)	55.56	105.263	1.85
	Avg. Cycles/px.	1447.13	1479.37
	Avg. $\mathsf{\mu }$s/px.	26.05	14.05
	Avg. px/s.	38,393.23	71,153.94
	Avg. Cycles/Node	1	1.022

presents the performance results. In this case, the multi-threaded design provides a performance improvement of 67–85%. Hence, in this accelerator the computer architecture optimizations provide a major performance improvement with minimal area cost.

The Multi-threaded design has a small penalty, between 1% and 4%, in terms of the number of cycles needed to process each node (Avg. Cycles/Node), which leads to a higher number of cycles per pixel (Avg. Cycles/px.). The reason is that the trees are divided into three sets, which will not always be perfectly balanced. When one of the sets ends, only two of the three threads have useful work to do. To reduce this problem we grouped the trees taking into account their average depth, trying to make the workload similar in all groups. Since the depth of the trees depends on the path chosen, and will be different for each input, we can not guarantee a perfect balance, and these small penalties appear. Nevertheless, we achieved a very small penalty and the frequency increase is enough to reach better throughput.

Regarding the communications, in our design we have included a DMA to read the input data from the external off-chip memory. With this approach the latency of sending the input data of one pixel is smaller than the computation itself, so it can be entirely overlapped with the processing time of the previous input data, and does not affect the throughput.

In order to evaluate the performance of our multi-threading design, we have executed the inference of the models described in [10] in a high performance (HP) CPU, an Intel(R) Core(TM) i5-8400 CPU @ 2.80GHz (Intel Corporation, Santa Clara, CA, USA), and also in an embedded system (ES) CPU, the Dual-core ARM Cortex-A9 @ 667 MHz (Arm Ltd., Cambridge, England) that is part of the same system-on-a-chip as the FPGA in the Zedboard evaluation board [12]. Regarding the software, for the Intel i5-8400 we measured the execution of the LightGBM library inference, while for the Cortex-A9, we designed an equivalent C version that uses the same data format as the FPGA design, hence, it has the same computational and memory requirements. This code has been compiled with gcc 7.3.1 with -O3 optimization level.

Table 4. Energy and performance comparisons.

		Energy (J)			Performance (Pixels/s)
	Test Pixels	FPGA	HP CPU	ES CPU	FPGA	HP CPU	ES CPU
IP	8721	0.280	27.750	9.858	62,293	23,568	1327
KSC	4435	0.136	6.150	3.024	65,221	53,860	2200
PU	38503	1.194	58.500	15.960	64,494	49,336	3619
SV	48726	1.370	171.000	36.863	71,133	21,332	1983
Average		0.500	36.147	11.508	65,706	22,422	2139

shows the total energy required for the execution of the entire test set for each image and also the performance in pixels per second. These measurements have been performed with a Yokogawa WT210 digital power meter, a device accepted by standard performance evaluation corporation (SPEC) for power efficiency benchmarks [21]. In the table we only include the dynamic energy consumption, that is, the consumption due to the execution of the trees. To this end, we measured the power consumption of the FPGA, the Cortex-A9 and the i5-8400 during five minutes both in idle mode, and during the execution of the models, and from that measures we computed the average increase in the power consumption due to the execution of the trees in each case. The Power consumption measurements used to calculate the energy are 75 W for the HP CPU, 1.5 W for the ES CPU and 2 W for the FPGA.

According to these results, the HP CPU execution consumes in average 72 times more energy than the FPGA design to perform the inference of the test benches, while the FPGA design is twice faster. In the case of the ES CPU, it consumes 23 times more energy while the FPGA design is 30 times faster. The last comparison is interesting, because this processor is on the same chip as the FPGA, using the same main memory and a clock almost seven times faster. This demonstrates the benefits of a custom accelerator both for performance, and for energy efficiency.

Finally, one of our objectives was to process the pixels at the same speed at which they are generated by the hyperspectral sensors. According to [22] the AVIRIS sensor that was used to obtain most of our datasets must process $62,873.6$ pixels per second to fully achieve real-time performance. Our multi-threading design achieves this speed in three of the four images (KSC, PU and SV), and achieves 98.4% of that speed in a third one (IP). Hence, we can conclude that this design is capable of achieving real-time performance in many scenarios even using a small FPGA.

7. Conclusions

GDBT are a very powerful machine learning model. Its characteristics make it specially indicated to be accelerated in FPGAs, since its basic operations are simple comparisons. A key factor in the design of the accelerator has been the memory restrictions. Optimizing the format used to store the trees has been the key to allow complex models to be implemented in small FPGAs. Moreover, after analyzing the execution of our accelerator, we have managed to find a pipeline and multi-threading execution scheme that maximizes the utilization of the FPGA resources and achieves 67–85% performance improvement compared to the single-cycle execution. We have tested our accelerator with complex models for a relevant case-study, and we have demonstrated that it can be used to process data at run-time with a very small power-consumption overhead. Moreover, compared to the execution of LightGBM in a high performance CPU our model is capable of achieving 2x performance while consuming 72x less energy. In the case of an embedded system CPU, our design reaches a 30x performance improvement while maintaining 23x less energy consumption during the execution. Hence, this design is suitable to provide high-performance for embedded systems, that was our original target.