Image Distortion and Rectification Calibration Algorithms and Validation Technique for a Stereo Camera
Abstract
1. Introduction
2. Related Work and Basic Theory
3. Problems in the Existing Algorithms
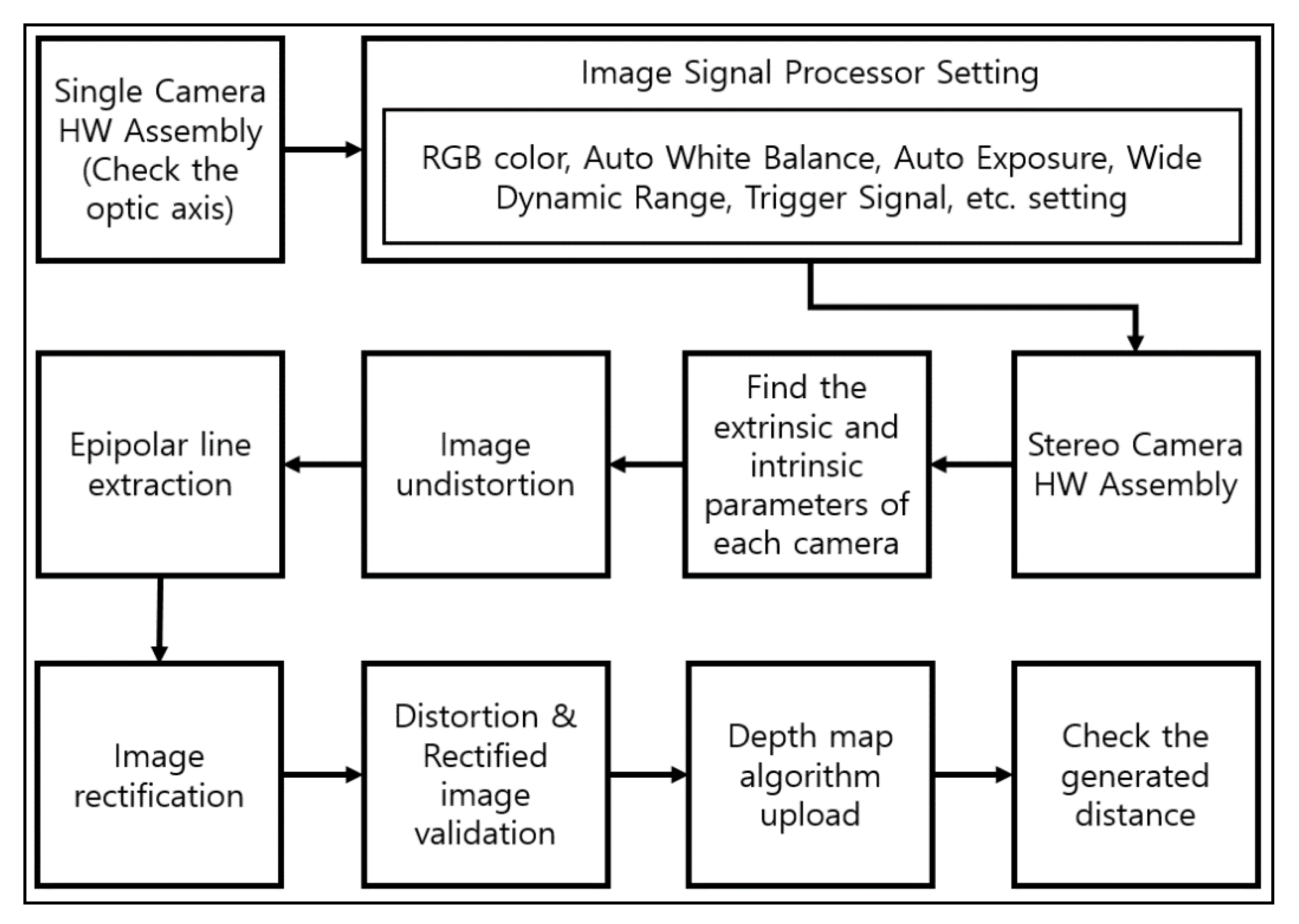
4. Solving Camera Calibration Techniques
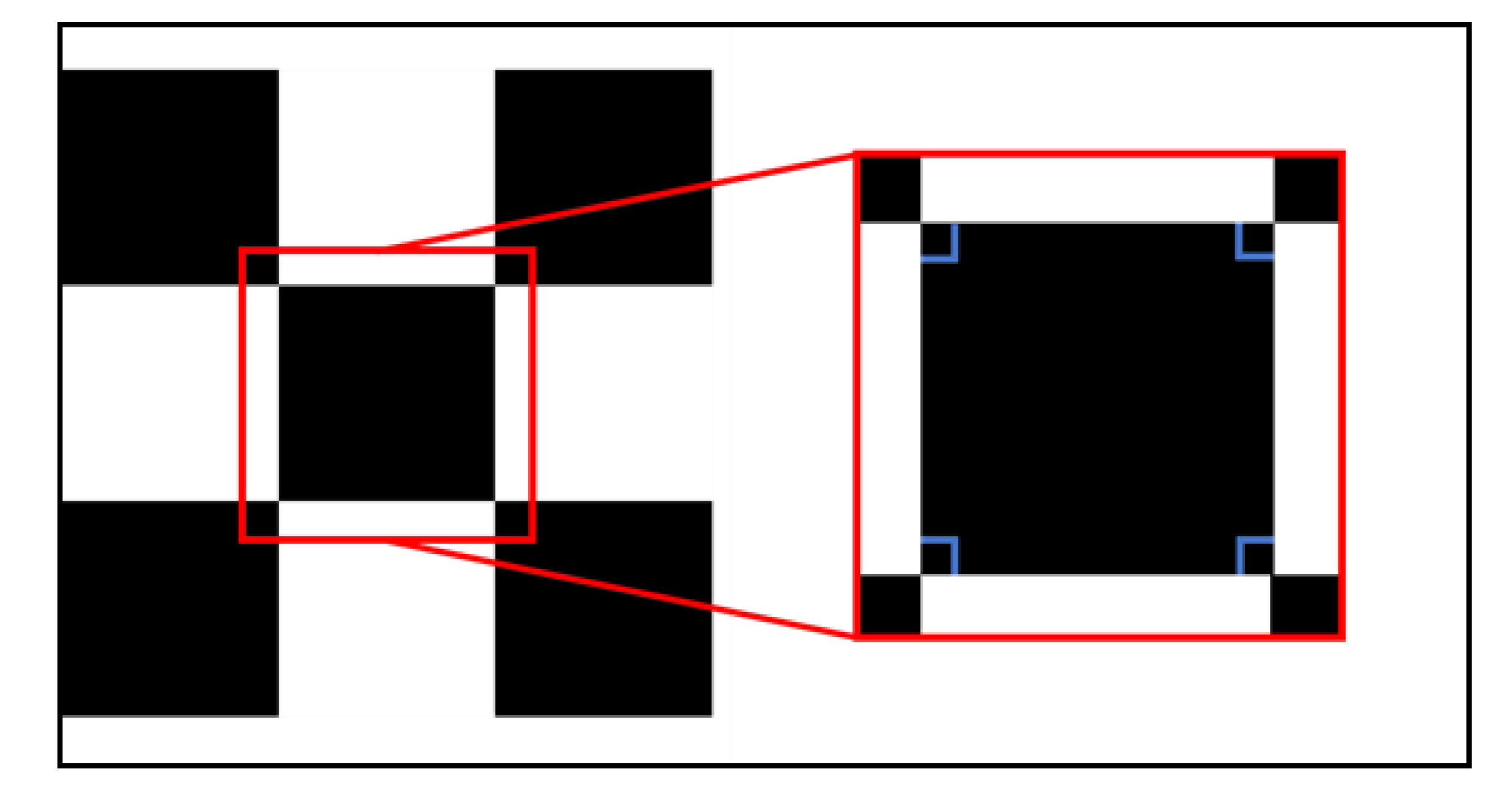
4.1. Method of Detecting Squares and Diamonds in the Proposed Calibration Board
4.2. Method of Verifying Distortion Calibration on the Proposed Calibration Board
5. Experiment
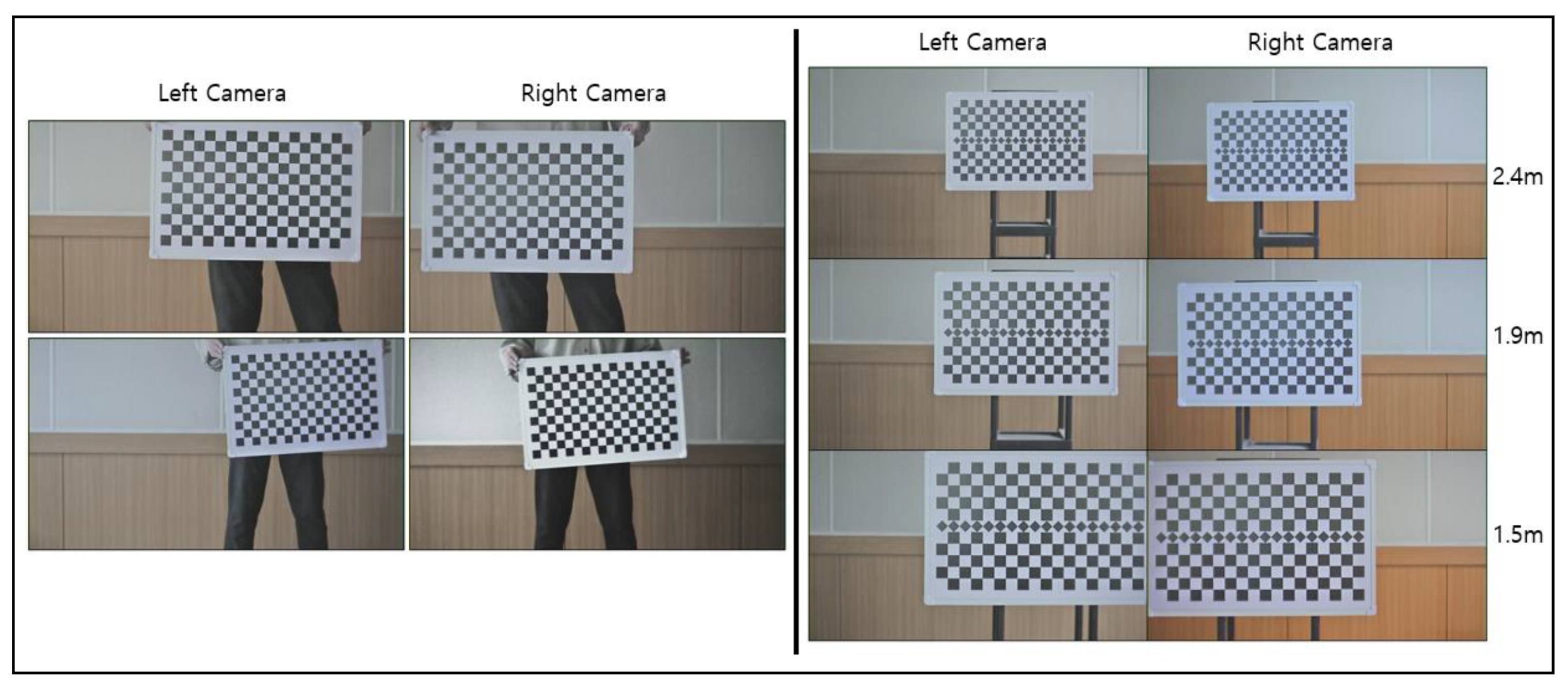
5.1. Experiment Environment
5.2. Detection of Vertex of Squares and Diamonds
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mercedes-Benz S-Class Stability System Uses Sensors, Stereo Camera. Available online: https://phys.org/news/2013-09-mercedes-benz-s-class-stability-sensors-stereo.html (accessed on 28 January 2020).
- Stereo Video Camera in Bosch Mobility Solutions. Available online: https://www.bosch-mobility-solutions.com/en/products-and-services/passenger-cars-and-light-commercial-vehicles/driver-assistance-systems/lane-departure-warning/stereo-video-camera/ (accessed on 28 January 2020).
- Subaru EyeSight. Available online: https://www.subaru.com/engineering/eyesight.html (accessed on 28 January 2020).
- Loop, C.; Zhang, Z. Computing rectifying homographies for stereo vision. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Fort Collins, CO, USA, 23–25 June 1999; Volume 1, pp. 125–131. [Google Scholar]
- Guan, B.; Shang, Y.; Yu, Q. Planar self-calibration for stereo cameras with radial distortion. Appl. Opt. 2017, 56, 9257. [Google Scholar] [CrossRef] [PubMed]
- Sturm, P.F.; Maybank, S.J. On Plane-Based Camera Calibration: A General Algorithm, Singularities, Applications. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition CVPR, Fort Collins, CO, USA, 23–25 June 1999; pp. 432–437. [Google Scholar]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Heikkila, J.; Silven, O. A four-step camera calibration procedure with implicit image correction. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Juan, PR, USA, 17–19 June 1997; pp. 1106–1112. [Google Scholar]
- Li, H.; Wang, K.; Yang, K.; Cheng, R.; Wang, C.; Fei, L. Unconstrained self-calibration of stereo camera on visually impaired assistance devices. Appl. Opt. 2019, 58, 6377–6387. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Zhang, Q.; Su, Y.; Wu, S. Accuracy evaluation of optical distortion calibration by digital image correlation. Opt. Lasers Eng. 2017, 98, 143–152. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Dinh, V.Q.; Nguyen, T.P.; Jeon, J.W. Rectification Using Different Types of Cameras Attached to a Vehicle. IEEE Trans. Image Process. 2018, 28, 815–826. [Google Scholar] [CrossRef]
- Scharstein, D.; Szeliski, R. A Taxonomy and Evaluation of Dense Two-Frame Stereo Correspondence Algorithms. Int. J. Comput. Vis. 2002, 47, 7–42. [Google Scholar] [CrossRef]
- Oleksandr, S. Analysis of camera calibration with respect to measurement accuracy. In Proceedings of the 48th CIRP International Conference on Manufacturing Systems, Ischia, Italy, 17–19 June 2015; pp. 765–770. [Google Scholar]
- Kukelova, Z.; Bujnak, M.; Pajdla, T. Real-time solution to the absolute pose problem with unknown radial distortion and focal length. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013. [Google Scholar]
- Carrera, G.; Angeli, A.; Davison, A.J. Slam-based automatic extrinsic calibration of a multi-camera rig. In Proceedings of the International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011. [Google Scholar]
- Zheng, Y.; Sugimoto, S.; Sato, I.; Okutomi, M. A general and simple method for camera pose and focal length determination. In Proceedings of the Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 21–12 June 2014. [Google Scholar]
- Camposeco, F.; Sattler, T.; Pollefeys, M. Non-parametric structure-based calibration of radially symmetric cameras. In Proceedings of the International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Dang, T.; Hoffmann, C.; Stiller, C. Continuous stereo self-calibration by camera parameter tracking. IEEE Trans. Image Process. 2009, 18, 1536–1550. [Google Scholar] [CrossRef] [PubMed]
- Rehder, E.; Kinzig, C.; Bender, P.; Lauer, M. Online stereo camera calibration from scratch. In Proceedings of the 2017 IEEEIntelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; pp. 1694–1699. [Google Scholar]
- Olson, E. Apriltag: A robust and flexible visual fiducial system. In Proceedings of the International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011. [Google Scholar]
- Chuang, J.-H.; Ho, C.-H.; Umam, A.; Chen, H.-Y.; Hwang, J.-N.; Chen, T.-A. Geometry-based Camera Calibration Using Closed-form Solution of Principal Line. IEEE Trans. Image Process. 2021. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhu, J.; Deng, H.; Chai, Z.; Ma, M.; Zhong, X. Multi-camera calibration method based on a multi-plane stereo target. Appl. Opt. 2019, 58, 9353–9359. [Google Scholar] [CrossRef] [PubMed]
- Dhall, A.; Chelani, K.; Radhakrishnan, V.; Krishna, K.M. LiDAR-camera calibration using 3D-3D point correspondences. arXiv 2017, arXiv:1705.09785. [Google Scholar]
- Strger, C.; UIrich, M.; Wiedemann, C. Machine Vision Algorithms and Applications, 2nd ed.; Wiley-VCH: Weinheim, Germany, 2018; p. 219. ISBN 9783527413652. [Google Scholar]
- Bradski, G.; Kaehler, A. Learning OpenCV: Computer Vision with the OpenCV Library, 1st ed.; O’Reilly Media, Inc.: Newton, MA, USA, 2008; ISBN 0596516134. [Google Scholar]
- Sels, S.; Ribbens, B.; Vanlanduit, S.; Penne, R. Camera calibration using gray code. Sensors 2019, 19, 246. [Google Scholar] [CrossRef] [PubMed]






















| Camera Parameters Using Normal Calibration Board | Values | Camera Parameters Using Proposed Calibration Board | Values |
|---|---|---|---|
| Camera 1 Focal Length | 2412.7, 2396.8 | Camera 1 Focal Length | 2073.3, 2067.9 |
| Camera 1 Principal Point | 597.43, 386.15 | Camera 1 Principal Point | 592.529, 390.279 |
| Camera 1 Radial Distortion | −0.2534, 0.9139 | Camera 1 Radial Distortion | −0.3626, 1.5353 |
| Camera 1 Tangential Distortion | −0.008, 0.00006 | Camera 1 Tangential Distortion | −0.0076, 0.00221 |
| Camera 2 Focal Length | 2448.6, 2435.1 | Camera 2 Focal Length | 2762.4, 2755.3 |
| Camera 2 Principal Point | 607.87, 454.44 | Camera 2 Principal Point | 555.73, 400.17 |
| Camera 2 Radial Distortion | −0.1971, 0.2698 | Camera 2 Radial Distortion | −0.4103, 3.9991 |
| Camera 2 Tangential Distortion | −0.0026, −0.003 | Camera 2 Tangential Distortion | −0.0096, −0.0533 |
| Line | Average Error |
|---|---|
| Line 1 | 3 |
| Line 2 | 4 |
| Line 3 | 4 |
| Line | Average Error | Line | Average Error | Line | Average Error |
|---|---|---|---|---|---|
| Line 1 | 3 | Line 7 | 3 | Line 13 | 3 |
| Line 2 | 4 | Line 8 | 4 | Line 14 | 3 |
| Line 3 | 3 | Line 9 | 4 | Line 15 | 3 |
| Line 4 | 3 | Line 10 | 4 | Line 16 | 2 |
| Line 5 | 3 | Line 11 | 3 | Line 17 | 3 |
| Line 6 | 2 | Line 12 | 3 | Line 18 | 3 |
| Original Image-Line | Average Error | Undistorted Image-Line | Average Error |
|---|---|---|---|
| Line 1 | 8 | Line 1 | 3 |
| Line 2 | 10 | Line 2 | 4 |
| Line 3 | 8 | Line 3 | 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.; Bae, H.; Lee, S.G. Image Distortion and Rectification Calibration Algorithms and Validation Technique for a Stereo Camera. Electronics 2021, 10, 339. https://doi.org/10.3390/electronics10030339
Kim J, Bae H, Lee SG. Image Distortion and Rectification Calibration Algorithms and Validation Technique for a Stereo Camera. Electronics. 2021; 10(3):339. https://doi.org/10.3390/electronics10030339
Chicago/Turabian StyleKim, Jonguk, Hyansu Bae, and Suk Gyu Lee. 2021. "Image Distortion and Rectification Calibration Algorithms and Validation Technique for a Stereo Camera" Electronics 10, no. 3: 339. https://doi.org/10.3390/electronics10030339
APA StyleKim, J., Bae, H., & Lee, S. G. (2021). Image Distortion and Rectification Calibration Algorithms and Validation Technique for a Stereo Camera. Electronics, 10(3), 339. https://doi.org/10.3390/electronics10030339






