A Neural Network Classifier with Multi-Valued Neurons for Analog Circuit Fault Diagnosis
Abstract
:1. Introduction
2. The Tools
2.1. Multilayer Neural Network with Multi-Valued Neurons (MLMVN) for Solving Classification and Regression Problems
2.2. SapWin Simulator
3. The Fault Diagnosis Procedure
3.1. Testability Analysis
- Canonic ambiguity group (CAG): an ambiguity group without any other ambiguity group (it is “minimum”);
- Global ambiguity group (GAG): an ambiguity group deriving from the union of two or more canonical ambiguity groups with at least one common element.
3.2. Fault Classes and Fault Classification
- If there is null intersection between CAGs of order 2, then each of them is assumed to be a FC.
- If there is a non-null intersection between the CAGs of order 2, then each GAG given by the intersection of the CAGs of order 2 with non-null intersection is assumed as a FC.
3.3. Fault Parameter Identification
4. Applications
4.1. Sallen-Key Bandpass Filter
- Testability T = 3 (in relative percent 42.85%);
- Number of CAGs = 2 (1 CAG of order 2).
- Multi-parameter: starting from the nominal value, the component parameter is randomly varied in the tolerance range. As specified above, in this example the tolerance values are taken equal to 10% for all the components. A larger tolerance range makes the classification task more challenging.
- In each simulation, just a single component is randomly varied in the range (0.01 pn–100 pn), where pn is the nominal value of the component.
- A set of simulations is generated with no fault element, in order to include also the class “0”, that is the circuit under nominal operating conditions.
- False negative: number of cases in which there was a fault, but the system classified it as a no-fault case.
- False positive: number of cases in which there was no fault, but the classifier returned a fault in the circuit.
- Precision: the percent of cases that were actually faulty, among all the cases that actually were detected to be faulty.
- Fault diagnosability: the percent of cases which were correctly detected to have a fault, among all the fault cases.
- Accuracy: ratio of correctly classified test cases to all the test cases.
- The number of neurons is varied from to (typically 10–300, but it can be increased if the result is not clear, that is if there is not a maximum in the range), using an incremental step 10.
- The number of hidden layer neurons is refined in a neighborhood of the best number obtained at point 1 and ±20, using a step 2 at this time.
4.2. Lowpass Biquadratic Filter
- Testability T = 5 (in relative percent 38.46%)
- Number of CAGs = 55 (among these, 7 CAGs have order 2)
- GAG1 = (R6, R7, R8, C2)
- GAG2 = (R9, R11)
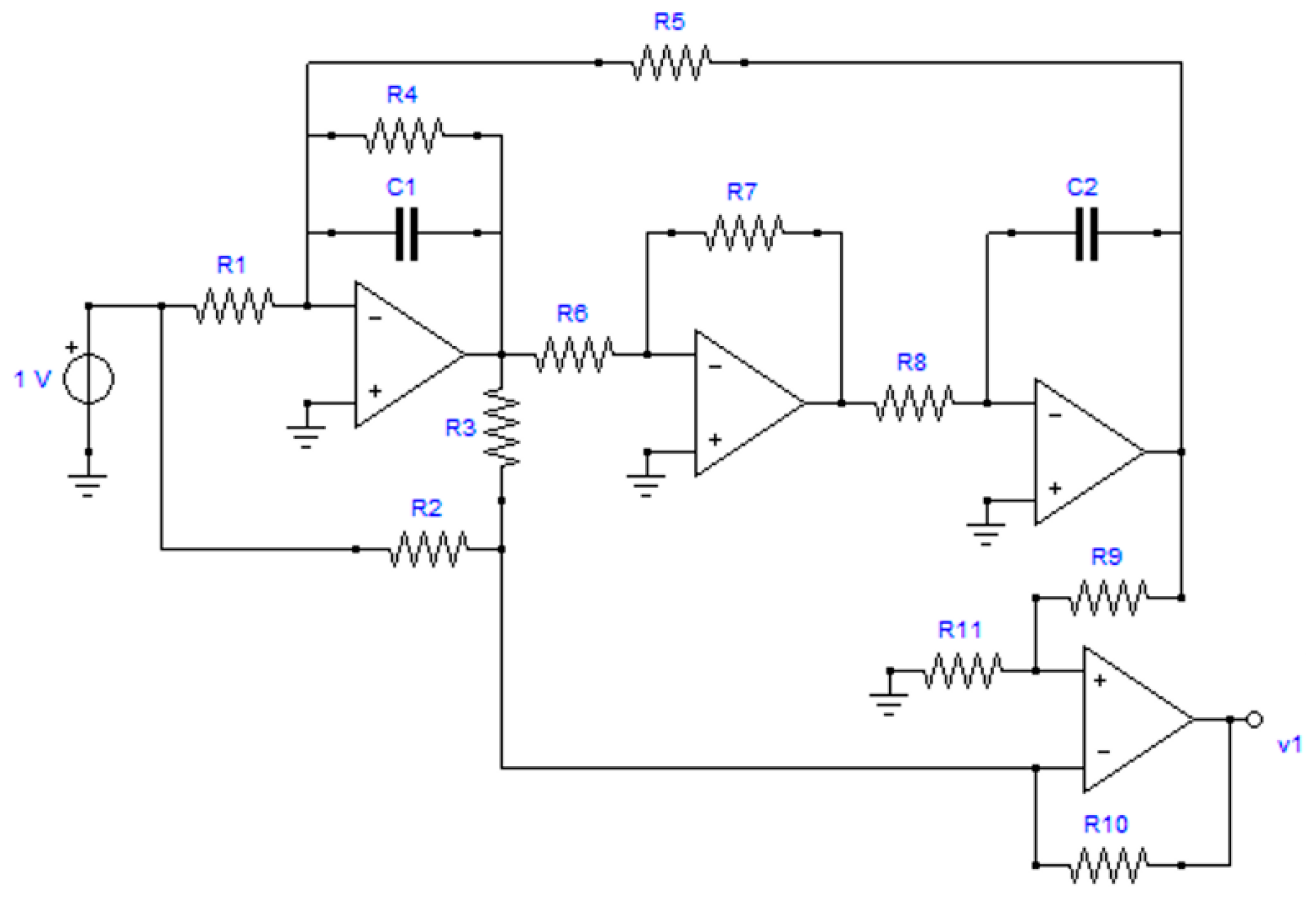
4.3. A Network Filter
- R3rd = 0.2 Ω; C3rd = 100 μF; L3rd = 11.258 mH;
- R5th = 0.5 Ω; C5th = 100 μF; L5th = 4.053 mH;
- R7th = 0.1 Ω; C7th = 5 mF; L7th = 10 mH.
- For each simulation, 7 frequencies are chosen, wherein magnitude and phase are measured; in this case, the used frequencies are those of 1st, 3rd, 5th, and 7th harmonics (in the range 50–350 Hz), increased by interposed samples.
- In this case, the tolerances are chosen following the typical specifications for this kind of filter, which is equal to 2% for capacitors and inductors and 5% for resistances.
- In each simulation, a single component value is randomly variated in the range (0.01 pn–100 pn), where pn is the nominal value of the component.
- The total number of simulations is 4000; 2500 are used for training and 1500 for failure classification.
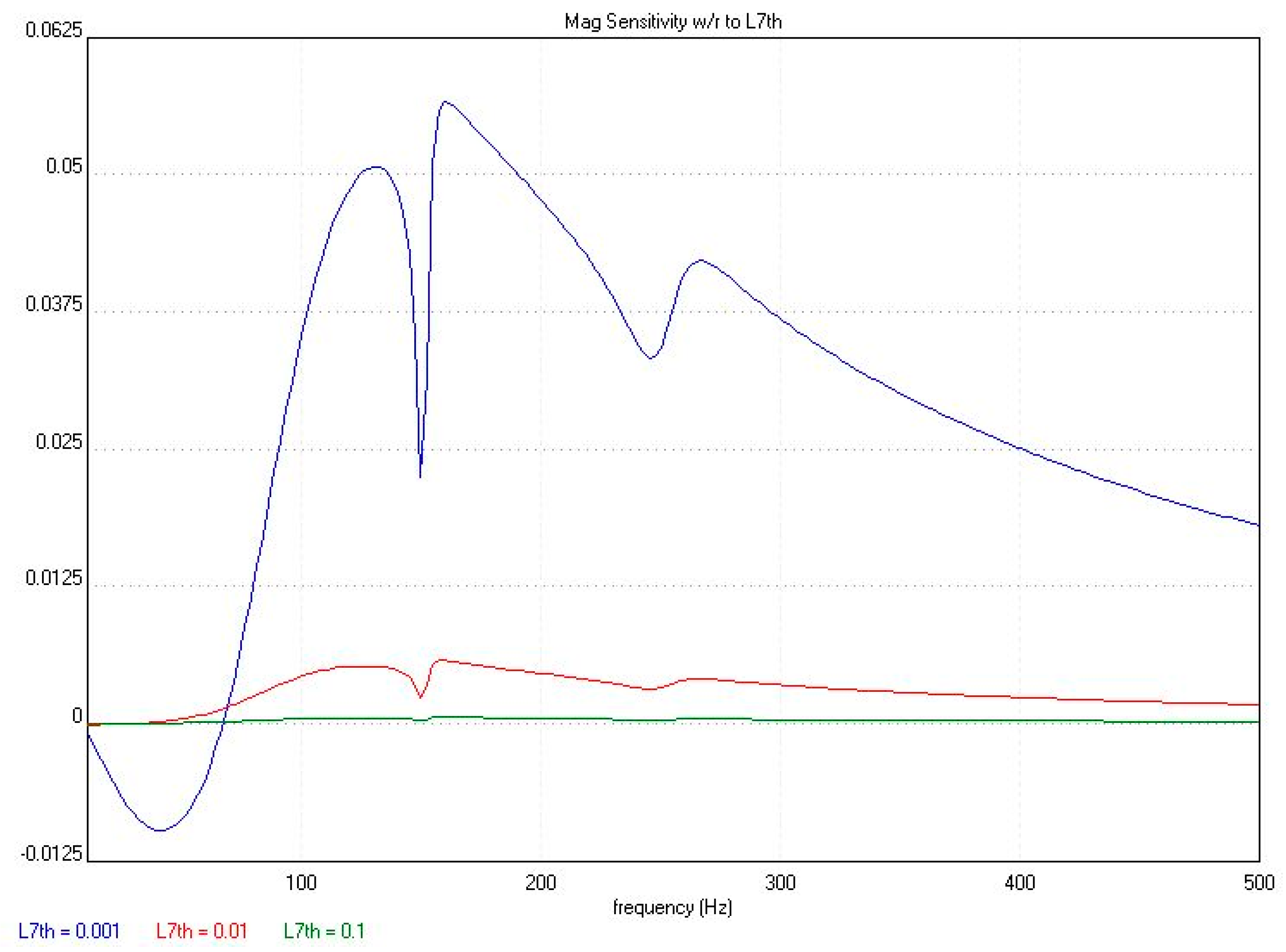
- There was a low sensitivity of some parameters of the system and then a small variation in the space of the solutions. In Figure 5, for instance, the parametric magnitude sensitivities of L7th is shown, which were associated to the FCs with the worst result.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cui, Y.; Shi, J.; Wang, Z. Analog circuit fault diagnosis based on Quantum Clustering based Multi-valued Quantum Fuzzification Decision Tree (QC-MQFDT). Measurement 2016, 93, 421–434. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Y.; Yu, Z.; Zeng, M. Incremental supervised locally linear embedding for machinery fault diagnosis. Eng. Appl. Artif. Intell. 2016, 50, 60–70. [Google Scholar] [CrossRef]
- Luo, H.; Lu, W.; Wang, Y.; Wang, L.; Zhao, X. A novel approach for analog fault diagnosis based on stochastic signal analysis and improved GHMM. Measurement 2016, 81, 26–35. [Google Scholar] [CrossRef]
- Rayudu, R.K. A knowledge-based architecture for distributed fault analysis in power networks. Eng. Appl. Artif. Intell. 2010, 23, 514–525. [Google Scholar] [CrossRef]
- Tadeusiewicz, M.; Hałgas, S. A Method for Local Parametric Fault Diagnosis of a Broad Class of Analog Integrated Circuits. IEEE Trans. Instrum. Meas. 2018, 67, 328–337. [Google Scholar] [CrossRef]
- Tan, S.C.; Lim, C.; Rao, M. A hybrid neural network model for rule generation and its application to process fault detection and diagnosis. Eng. Appl. Artif. Intell. 2007, 20, 203–213. [Google Scholar] [CrossRef]
- Tang, X.; Xu, A.; Niu, S. KKCV-GA-Based Method for Optimal Analog Test Point Selection. IEEE Trans. Instrum. Meas. 2016, 66, 24–32. [Google Scholar] [CrossRef]
- Tian, S.; Yang, C.; Chen, F.; Liu, Z. Circle Equation-Based Fault Modeling Method for Linear Analog Circuits. IEEE Trans. Instrum. Meas. 2014, 63, 2145–2159. [Google Scholar] [CrossRef]
- Yang, C.; Yang, J.; Liu, Z.; Tian, S. Complex Field Fault Modeling-Based Optimal Frequency Selection in Linear Analog Circuit Fault Diagnosis. IEEE Trans. Instrum. Meas. 2013, 63, 813–825. [Google Scholar] [CrossRef]
- Zhao, G.; Liu, X.; Zhang, B.; Liu, Y.; Niu, G.; Hu, C. A novel approach for analog circuit fault diagnosis based on Deep Belief Network. Measurement 2018, 121, 170–178. [Google Scholar] [CrossRef]
- Bindi, M.; Grasso, F.; Luchetta, A.; Manetti, S.; Piccirilli, M. Modeling and Diagnosis of Joints in High Voltage Electrical Transmission Lines. J. Physics: Conf. Ser. 2019, 1304. [Google Scholar] [CrossRef]
- Deng, Y.; Zhou, Y. Fault Diagnosis of an Analog Circuit Based on Hierarchical DVS. Symmetry 2020, 12, 1901. [Google Scholar] [CrossRef]
- Binu, D.; Kariyappa, B. A survey on fault diagnosis of analog circuits: Taxonomy and state of the art. AEU Int. J. Electron. Commun. 2017, 73, 68–83. [Google Scholar] [CrossRef]
- Spina, R.; Upadhyaya, S. Linear circuit fault diagnosis using neuromorphic analyzers. IEEE Trans. Circuits Syst. II Express Briefs 1997, 44, 188–196. [Google Scholar] [CrossRef]
- Aminian, F.; Collins, H. Analog fault diagnosis of actual circuits using neural networks. IEEE Trans. Instrum. Meas. 2002, 51, 544–550. [Google Scholar] [CrossRef]
- Aminian, M.; Aminian, F. A Modular Fault-Diagnostic System for Analog Electronic Circuits Using Neural Networks with Wavelet Transform as a Preprocessor. IEEE Trans. Instrum. Meas. 2007, 56, 1546–1554. [Google Scholar] [CrossRef]
- Aminian, M. Neural-network based analog-circuit fault diagnosis using wavelet transform as preprocessor. IEEE Trans. Circuits Syst. II Express Briefs 2000, 47, 151–156. [Google Scholar] [CrossRef]
- Fontana, G.; Luchetta, A.; Manetti, S.; Piccirilli, M.C. A Fast Algorithm for Testability Analysis of Large Linear Time-Invariant Networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2017, 64, 1564–1575. [Google Scholar] [CrossRef]
- Fontana, G.; Luchetta, A.; Manetti, S.; Piccirilli, M.C. An unconditionally sound algorithm for testability analysis in linear time-invariant electrical networks. Int. J. Circuit Theory Appl. 2015, 44, 1308–1340. [Google Scholar] [CrossRef]
- Fontana, G.; Luchetta, A.; Manetti, S.; Piccirilli, M.C. A Testability Measure for DC-Excited Periodically Switched Networks with Applications to DC-DC Converters. IEEE Trans. Instrum. Meas. 2016, 65, 2321–2341. [Google Scholar] [CrossRef]
- Fedi, G.; Manetti, S.; Piccirilli, M.C.; Starzyk, J. Determination of an optimum set of testable components in the fault diagnosis of analog linear circuits. IEEE Trans. Circuits Syst. I Regul. Pap. 1999, 46, 779–787. [Google Scholar] [CrossRef]
- Cannas, B.; Fanni, A.; Manetti, S.; Montisci, A.; Piccirilli, M.C. Neural network-based analog fault diagnosis using testability analysis. Neural Comput. Appl. 2004, 13, 288–298. [Google Scholar] [CrossRef]
- Fontana, G.; Grasso, F.; Luchetta, A.; Manetti, S.; Piccirilli, M.C.; Reatti, A. Testability Analysis Based on Complex-Field Fault Modeling. In Proceedings of the SMACD 2018—15th International Conference on Synthesis, Modeling, Analysis and Simulation Methods and Applications to Circuit Design, Prague, Czech Republic, 2–5 July 2018; pp. 33–36. [Google Scholar]
- Cui, J.; Wang, Y. A novel approach of analog circuit fault diagnosis using support vector machines classifier. Measurement 2011, 44, 281–289. [Google Scholar] [CrossRef]
- Grasso, F.; Luchetta, A.; Manetti, S.; Piccirilli, M.C.; Reatti, A. Single fault diagnosis in analog circuits: A multi-step approach. In Proceedings of the 5th IEEE Workshop on Advances in Information, Electronic and Electrical Engineering (AIEEE), Riga, Latvia, 24–25 November 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Vasan, A.S.S.; Long, B.; Pecht, M. Diagnostics and Prognostics Method for Analog Electronic Circuits. IEEE Trans. Ind. Electron. 2013, 60, 5277–5291. [Google Scholar] [CrossRef]
- Du, B.; He, Y.; Zhang, Y. Open-Circuit Fault Diagnosis of Three-Phase PWM Rectifier Using Beetle Antennae Search Algorithm Optimized Deep Belief Network. Electronics 2020, 9, 1570. [Google Scholar] [CrossRef]
- Aizenberg, I. MLMVN with Soft Margins Learning. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 1632–1644. [Google Scholar] [CrossRef]
- Aizenberg, I. Why We Need Complex-Valued Neural Networks? Geom. Uncertain. 2011, 353, 1–53. [Google Scholar] [CrossRef]
- Aizenberg, I.; Luchetta, A.; Manetti, S. A modified learning algorithm for the multilayer neural network with multi-valued neurons based on the complex QR decomposition. Soft Comput. 2011, 16, 563–575. [Google Scholar] [CrossRef]
- Aizenberg, I.; Moraga, C. Multilayer Feedforward Neural Network Based on Multi-valued Neurons (MLMVN) and a Backpropagation Learning Algorithm. Soft Comput. 2006, 11, 169–183. [Google Scholar] [CrossRef]
- Grasso, F.; Luchetta, A.; Manetti, S.; Piccirilli, M.C. A Method for the Automatic Selection of Test Frequencies in Analog Fault Diagnosis. IEEE Trans. Instrum. Meas. 2007, 56, 2322–2329. [Google Scholar] [CrossRef]
- Grasso, F.; Manetti, S.; Piccirilli, M.C. An approach to analog fault diagnosis using genetic algorithms. In Proceedings of the 12th IEEE Mediterranean Electrotechnical Conference (IEEE Cat. No.04CH37521), Dubrovnik, Croatia, 12–15 May 2004. [Google Scholar]
- Aizenberg, E.; Aizenberg, I. Batch linear least squares-based learning algorithm for MLMVN with soft margins. In Proceedings of the 2014 IEEE Symposium on Computational Intelligence and Data Mining (CIDM 2014), Orlando, FL, USA, 9–12 December 2014; pp. 48–55. [Google Scholar]
- Aizenberg, I. Hebbian and error-correction learning for complex-valued neurons. Soft Comput. 2012, 17, 265–273. [Google Scholar] [CrossRef]
- Grasso, F.; Luchetta, A.; Manetti, S.; Piccirilli, M.C.; Reatti, A. SapWin 4.0-a new simulation program for electrical engineering education using symbolic analysis. Comput. Appl. Eng. Educ. 2015, 24, 44–57. [Google Scholar] [CrossRef]
- Manetti, S.; Luchetta, A.; Piccirilli, M.C.; Reatti, A.; Grasso, F. Sapwin 4.0. Available online: www.sapwin.info (accessed on 29 January 2021).
- Sen, N.; Saeks, R. Fault diagnosis for linear systems via multifrequency measurements. IEEE Trans. Circuits Syst. 1979, 26, 457–465. [Google Scholar] [CrossRef]
- Grasso, F.; Luchetta, A.; Manetti, S.; Piccirilli, M.C. Symbolic techniques in neural network based fault diagnosis of analog circuits. In Proceedings of the XIth International Workshop on Symbolic and Numerical Methods, Modeling and Applications to Circuit Design (SM2ACD), Gammarth, Tunisia, 4–6 October 2010; pp. 1–4. [Google Scholar]
- Luchetta, A. Analog Circuits. Available online: https://data.mendeley.com/datasets/64psx4vkh7/1 (accessed on 29 January 2021).
- Chang, C.-C.; Lin, C.-J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Akagi, H.; Watanabe, E.H.; Aredes, M. Instantaneous Power Theory and Applications to Power Conditioning; Wiley: Hoboken, NJ, USA, 2017. [Google Scholar]



| Training Set | Test Set | |||
| MLMVN | SVM | MLMVN | SVM | |
| False negative | (23/700) 3.29% | (24/700) 3.43% | (11/300) 3.67% | (12/300) 4.00% |
| False positive | (0/700) 0.00% | (3/700) 0.43% | (0/300) 0.00% | (3/300) 1.00% |
| Precision | 100.00% | 99.33% | 100.00% | 98.29% |
| Fault diagnosability | 95.20% | 94.87% | 94.52% | 93.48% |
| Accuracy % | ||||
| MLMVN | SVM | MLMVN | SVM | |
| Overall | 92.86 | 93.86 | 91.67 | 90.00 |
| 0 (healthy) | 100.00 | 98.71 | 100.00 | 97.41 |
| 1 (C1) | 87.38 | 71.05 | 92.11 | 68.75 |
| 2 (C2) | 96.51 | 98.65 | 90.91 | 97.30 |
| 3 (R1) | 87.88 | 98.77 | 89.29 | 87.10 |
| 4 (R2) | 96.00 | 95.52 | 89.66 | 86.67 |
| 5 (R3) | 74.29 | 92.94 | 70.59 | 81.82 |
| 6 (GAG) | 93.67 | 91.76 | 92.31 | 88.89 |
| FC | Nominal Value | FCerr% (MLMVNN) |
|---|---|---|
| 1 (C1) | 5 × 10−9 F | 17.12 |
| 2 (C2) | 5 × 10−9 F | 11.4 |
| 3 (R1) | 5.18 kΩ | 26.2 |
| 4 (R2) | 1000 Ω | 14.9 |
| 5 (R3) | 2 kΩ | 17.7 |
| 6 (GAG) | 4 kΩ (R4–R5) | 31.2 |
| Training Set | Test Set | |||
| MLMVN | SVM | MLMVN | SVM | |
| False negative | (16/1500) 1.07% | (13/1500) 0.87% | (3/500) 0.60% | (8/500) 1.60% |
| False positive | (7/1500) 0.47% | (1/1500) 0.07% | (1/500) 0.20% | (1/500) 0.20% |
| Precision | 99.21% | 99.89% | 99.66% | 99.66% |
| Fault diagnosability | 98.26% | 98.61% | 99.01% | 97.38% |
| Accuracy % | ||||
| MLMVN | SVM | MLMVN | SVM | |
| Overall | 98.40 | 98.93 | 98.80 | 95.60 |
| 0 (healthy) | 98.79 | 99.82 | 99.49 | 99.49 |
| 1 (C1) | 100.00 | 100.00 | 100.00 | 100.00 |
| 2 (GAG1) | 100.00 | 100.00 | 100.00 | 97.37 |
| 3 (R1) | 100.00 | 100.00 | 100.00 | 96.30 |
| 4 (R10) | 100.00 | 91.95 | 97.56 | 84.62 |
| 5 (GAG2) | 88.28 | 92.47 | 84.21 | 76.47 |
| 6 (R2) | 100.00 | 100.00 | 100.00 | 100.00 |
| 7 (R3) | 97.96 | 99.12 | 96.77 | 91.89 |
| 8 (R4) | 100.00 | 100.00 | 100.00 | 97.14 |
| 9 (R5) | 100.00 | 100.00 | 100.00 | 97.30 |
| FC | Nominal Value | FCerr% (MLMVNN) |
|---|---|---|
| 1 (C1) | 1 × 10−7 F | 8.2 |
| 2 (GAG1) | 1 × 10−7 F (C2) | 9.6 |
| 3 (R1) | 1000 Ω | 62.6 |
| 4 (R10) | 1000 Ω | 51.0 |
| 5 (GAG2) | 1000 Ω (R11) | 47.1 |
| 6 (R2) | 1000 Ω | 2.3 |
| 7 (R3) | 1000 Ω | 38.5 |
| 8 (R4) | 500 Ω | 2.8 |
| 9 (R5) | 1000 Ω | 46.2 |
| Training Set | Test Set | |||
| MLMVN | SVM | MLMVN | SVM | |
| False negative | (131/2500) 5.24% | (185/2500) 7.40% | (98/1500) 6.53% | (120/1500) 8.00% |
| False positive | (0/2500) 0.00% | (0/2500) 0.00% | (0/1500) 0.00% | (0/1500) 0.00% |
| Precision | 100.00% | 100.00% | 100.00% | 100.00% |
| Fault diagnosability | 92.02% | 88.73% | 89.55% | 87.21% |
| Accuracy | ||||
| MLMVN | SVM | MLMVN | SVM | |
| Overall | 93.68 | 88.28 | 89.80 | 87.33 |
| 0 (healthy) | 100.00 | 100.00 | 100.00 | 100.00 |
| 1 (C3rd) | 98.40 | 98.40 | 94.69 | 98.23 |
| 2 (C5th) | 96.81 | 79.79 | 93.58 | 77.06 |
| 3 (C7th) | 100.00 | 100.00 | 87.76 | 100.00 |
| 4 (L3rd) | 90.51 | 87.34 | 84.00 | 78.00 |
| 5 (L5th) | 98.56 | 86.54 | 94.90 | 85.71 |
| 6 (L7th) | 44.28 | 40.80 | 29.41 | 28.43 |
| 7 (R3rd) | 91.12 | 55.03 | 85.42 | 56.25 |
| 8 (R5th) | 97.75 | 94.94 | 84.76 | 88.57 |
| 9 (R7th) | 100.00 | 100.00 | 95.73 | 100.00 |
| Training Set | Test Set | |||
| MLMVN | SVM | MLMVN | SVM | |
| False negative | (1/2500) 0.04% | (0/2500) 0.00% | (2/824) 0.24% | (3/824) 0.36% |
| False positive | (0/2500) 0.00% | (0/2500) 0.00% | (0/824) 0.00% | (0/824) 0.00% |
| Precision | 100.00% | 100.00% | 100.00% | 100.00% |
| Fault diagnosability | 99.94% | 100.00% | 99.63% | 99.44% |
| Accuracy | ||||
| MLMVN | SVM | MLMVN | SVM | |
| Overall | 99.04 | 95.88 | 97.09 | 95.39 |
| 0 (healthy) | 100.00 | 100.00 | 100.00 | 100.00 |
| 1 (C3rd) | 97.55 | 94.12 | 95.08 | 93.44 |
| 2 (C5th) | 100.00 | 84.51 | 98.48 | 89.39 |
| 3 (C7th) | 100.00 | 100.00 | 98.88 | 100.0 |
| 4 (L3rd) | 91.89 | 91.89 | 87.50 | 86.11 |
| 5 (L5th) | 100.00 | 84.62 | 100.00 | 84.85 |
| 6 (L7th) | 97.73 | 100.00 | 87.50 | 100.00 |
| 7 (R3rd) | 100.00 | 100.00 | 98.25 | 98.25 |
| 8 (R5th) | 100.00 | 100.00 | 90.70 | 88.37 |
| 9 (R7th) | 100.00 | 100.00 | 95.38 | 98.46 |
| FC | Nominal Value | Mean Error % (MLMVNN) |
|---|---|---|
| 1 (C3rd) | 1 × 10−4 F | 7.9 |
| 2 (C5th) | 1 × 10−4 F | 25.1 |
| 3 (C7th) | 5 × 10−4 F | 7.7 |
| 4 (L3rd) | 11.258 mH | 48.1 |
| 5 (L5th) | 4.053 mH | 15.5 |
| 6 (L7th) | 10 mH | 36.2 |
| 7 (R3rd) | 0.2 Ω | 33.7 |
| 8 (R5th) | 0.5 Ω | 12.1 |
| 9 (R7th) | 0.1 Ω | 3.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aizenberg, I.; Belardi, R.; Bindi, M.; Grasso, F.; Manetti, S.; Luchetta, A.; Piccirilli, M.C. A Neural Network Classifier with Multi-Valued Neurons for Analog Circuit Fault Diagnosis. Electronics 2021, 10, 349. https://doi.org/10.3390/electronics10030349
Aizenberg I, Belardi R, Bindi M, Grasso F, Manetti S, Luchetta A, Piccirilli MC. A Neural Network Classifier with Multi-Valued Neurons for Analog Circuit Fault Diagnosis. Electronics. 2021; 10(3):349. https://doi.org/10.3390/electronics10030349
Chicago/Turabian StyleAizenberg, Igor, Riccardo Belardi, Marco Bindi, Francesco Grasso, Stefano Manetti, Antonio Luchetta, and Maria Cristina Piccirilli. 2021. "A Neural Network Classifier with Multi-Valued Neurons for Analog Circuit Fault Diagnosis" Electronics 10, no. 3: 349. https://doi.org/10.3390/electronics10030349
APA StyleAizenberg, I., Belardi, R., Bindi, M., Grasso, F., Manetti, S., Luchetta, A., & Piccirilli, M. C. (2021). A Neural Network Classifier with Multi-Valued Neurons for Analog Circuit Fault Diagnosis. Electronics, 10(3), 349. https://doi.org/10.3390/electronics10030349












