Abstract
This paper proposes Hermes, a container-based preemptive GPU scheduling framework for accelerating hyper-parameter optimization in deep learning (DL) clusters. Hermes accelerates hyper-parameter optimization by time-sharing between DL jobs and prioritizing jobs with more promising hyper-parameter combinations. Hermes’s scheduling policy is grounded on the observation that good hyper-parameter combinations converge quickly in the early phases of training. By giving higher priority to fast-converging containers, Hermes’s GPU preemption mechanism can accelerate training. This enables users to find optimal hyper-parameters faster without losing the progress of a container. We have implemented Hermes over Kubernetes and compared its performance against existing scheduling frameworks. Experiments show that Hermes reduces the time for hyper-parameter optimization up to 4.04 times against previously proposed scheduling policies such as FIFO, round-robin (RR), and SLAQ, with minimal time-sharing overhead.
1. Introduction
Deep learning (DL) has recently seen immense success in various fields, such as computer vision and natural language processing. When developing DL applications, users construct a DL model and train it using learning algorithms such as stochastic gradient descent. While the success of DL has been driven by the ability to train millions of parameters purely from data, a handful of parameters are often needed to be prespecified and fixed by the user. These so-called hyper-parameters include learning rates in learning algorithms and the strength of regularizers.
Unfortunately, the accuracy of a DL model is greatly affected by these hyper-parameters. Therefore, it is common for DL users to spend an excessive amount of time for finding an optimal combination of hyper-parameters. This process, called hyper-parameter optimization, is often performed by training a DL model with various hyper-parameter combinations and determining which combination is optimal. Determining which hyper-parameter is the most promising is done by receiving convergence feedback from the training process. Since the optimality of a particular combination (based on a certain performance metric) is only given at the end of training, hyper-parameter optimization is time-consuming. Nonetheless, it is an essential process to obtain a good quality DL model.
With the advance of high performance computing (HPC) environments such as GPU clusters and clouds, it is natural that DL users utilize these environments for hyper-parameter optimization [1,2]. In these cases, hyper-parameter optimization jobs are often packed into containers (for example, docker containers) and submitted to a cluster manager for execution. Since DL training jobs extensively use GPUs, the scheduling policy of a cluster manager directly affects the efficiency of hyper-parameter optimization. A widely adopted ad-hoc scheduling strategy is to use kill-based preemption [3].
In kill-based preemption, users continuously monitor the convergence of DL training jobs and manually kill the containers not making progress. This manual process is not only tedious and error-prone, but it is unscalable when a large number of containers are used. Moreover, a decision to terminate a container cannot be reversed once done. Instead of relying on manual strategies such as kill-based preemption, we focus on the development of a cluster manager-level solution.
Traditional cluster managers such as YARN [4], Mesos [5], and Kubernetes [6] exclusively allocate a single GPU to each container. Because of this, if a hyper-parameter optimization job is not granted GPU resources, convergence feedback will be significantly delayed. Since the decision of choosing a hyper-parameter combination can only be made once all the necessary feedback is collected, the overall process will slow down unreasonably. Moreover, training unpromising hyper-parameter combinations sequentially intensifies the head-of-line-blocking (HOL-blocking) problem [7].
Currently, most cloud manager solutions do not exploit the specific setting of hyper-parameter optimization. For example, Sherpa [2], a recently introduced framework specifically designed for hyper-parameter optimization, does not include a scheduling strategy that considers convergence feedback. Other DL oriented cluster managers such as Tiresias [1], Optimus [8], Cynthia [9], and Flowcon [10] only focus on reducing the average waiting time. Meanwhile, Themis [11] considers shortening work time and fairness. However, this method is not suitable for hyper-parameter optimization since convergence feedback is not received early. Gandiva [7] on the other hand, proposes parallelizing DL training jobs so that early feedback can be received quickly. While hyper-parameter optimization definitely benefit from parallelization, Gandiva’s focus on improving fairness is harmful since unpromising hyper-parameter combinations receive equal amount of service. Lastly, SLAQ [12] prioritizes low-performing DL jobs by receiving convergence feedback.
Ironically, this can harm the performance of hyper-parameter optimization by executing unpromising hyper-parameter combinations first. Overall, hyper-parameter optimization has seen limited benefit (if not harmed) from the recent advances in DL focused cluster managers. To accelerate hyper-parameter optimization of DL, this paper proposes Hermes, a container-based GPU scheduling framework.
In summary, this paper makes the following specific contributions.
- Parallelization of hyper-parameter optimization process: Hermes parallelizes hyper-parameter optimization by time-sharing between containers running DL jobs. The container preemption is implemented using the model checkpointing feature supported by TensorFlow [13].
- Convergence-aware scheduling policy: Hermes accelerates hyper-parameter optimization by prioritizing jobs based on the convergence speed. This sharply contrasts to the Gandiva’s approach [7] since not all tasks are trained equally, but important tasks are selected and accelerated.
- No prior knowledge and modification of user code: In contrast to previous works, Hermes does not need prior knowledge about the jobs such as job completion time (JCT) distribution. Moreover, it does not try to predict the JCT of the jobs. Moreover, Hermes does not require modification to the user code and all modifications are transparent to the users.
- Real implementation: We have implemented Hermes over Kubernetes [6], one of the most popular open-source platforms for container orchestration.
We evaluate the performance of Hermes using the convolutional neural network (CNN) benchmark [14] from TensorFlow. Performance results show that Hermes shortens the hyper-parameter optimization process up to 4.04 times with minimal time-sharing overhead when compared against scheduling policies supported by other cluster managers such as FIFO, round-robin (RR), and SLAQ.
2. Background and Motivation
2.1. Training of Deep Learning Models
DL is a family of machine learning (ML) methods for learning and predicting complex nonlinear relationship from data. It has recently seen huge success in numerous fields including image recognition, speech recognition, and recently, natural language processing. The process of inferring patterns from data is often called deep learning training (DLT). Compared to other machine learning methods, inference of DL models is notoriously difficult. This is because DL models often include a huge number of parameters, and the problems to which DL is applied often involve large datasets. For this reason, efficient management of computational resources during DL training is becoming increasingly important.
2.1.1. Overview of Deep Learning Training
The general process of DLT involves minimizing a loss function by solving an optimization problem. Before starting the optimization procedure, multiple parameters have to be manually predetermined and fixed throughout the training process. These parameters are called hyper-parameters and we will provide some concrete examples below.
Formally, the optimization problem is formulated as
where is the concatenation of the trainable parameters of the DL model, is the loss function or empirical risk of a data point, is the training dataset, and is the concatenation of the hyper-parameters. The goal of DLT is to minimize the loss over the dataset (hence the expectation over ). As a result, DL users can obtain a set of DL model parameters () that hopefully achieve good predictive performance.
DLT is most often solved using variants of the stochastic gradient descent (SGD, [15]) algorithm. A popular choice is the Adam optimizer [16] and has three internal hyper-parameters that need to be determined. At each iteration of SGD, a noisy estimator of the gradient of the training objective in Equation (1) is obtained by sampling a subset of the train data. The size of this subset, or mini-batch, is an important hyper-parameter and is known to highly affect the performance of SGD [17].
Despite the fact that hyper-parameters, including some examples mentioned above, cannot be learned from data, they strongly affect the final performance of the trained model. This fact has led to the development of various hyper-parameter optimization strategies (see Section 2.1.2).
2.1.2. Hyper-Parameter Optimization
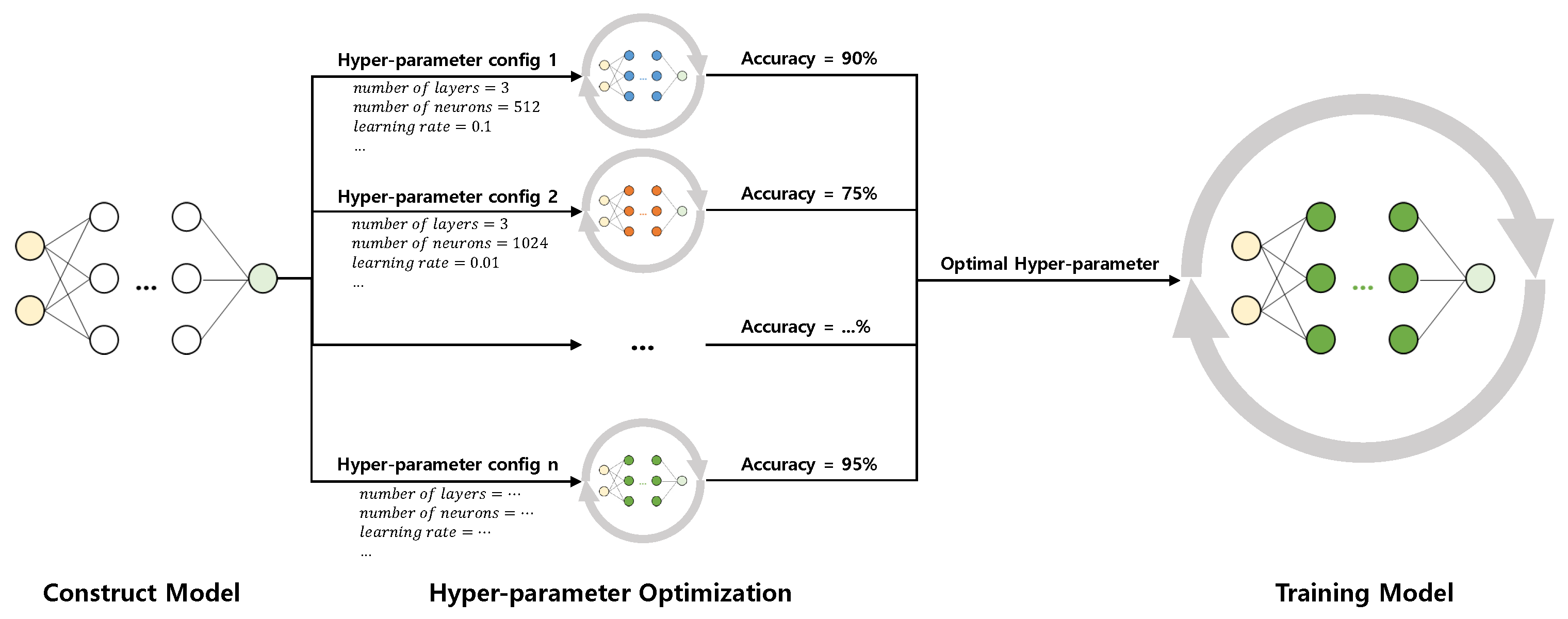
Hyper-parameters used for DLT often significantly affect the resulting performance of a DL model. For this reason, DLT in practice can be divided into two parts: hyper-parameter optimization and the actual DLT. During hyper-parameter search, users search for the most promising hyper-parameter configuration. Since the performance of a hyper-parameter setting is often unveiled until the end of a training process, hyper-parameter optimization involves repeating multiple (possibly short) preliminary DLT runs. Unfortunately, the cost of this process can easily out-weight the cost of the “final” DLT run that is performed with the optimal hyper-parameter setting. The overall process of DLT is illustrated in Figure 1.
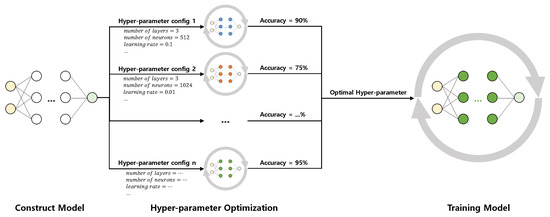
Figure 1.
Deep learning training process.
Apart from relying on heuristics [18], various methods for accelerating hyper-parameter optimization have been proposed including grid search [19], random search [20], and Bayesian optimization (BO, [21,22,23]).
2.1.3. Grid Search
Grid search is a method of optimization by setting a bounded search space and partitioning it into grids. Since all the grid points must be investigated, the cost of hyper-parameter optimization grows exponentially with the resolution of the grid. However, grid search is arguably one of the most employed method for hyper-parameter optimization because of its simplicity.
2.1.4. Random Search
While similar to grid search, random search chooses a non-deterministic approach. Instead of evaluating the performance of all the grid points in the search space, hyper-parameter configurations are randomly selected. Conceptually, the resolution of the optimization process is not restricted. For this reason, it is possible to discover more promising hyper-parameter settings compared to grid search. However, random search does not utilize information about the search space acquired during the optimization process.
2.1.5. Bayesian Optimization
In contrast to grid search or random search, BO adaptively utilizes the information acquired during the optimization process. It fits a surrogate model of the performance of the hyper-parameters, and utilizes it for deciding on which point to try out next. Despite being more systematic, BO comes with its own set of hyper-parameters complicating its use. Moreover, its performance is limited when the dimension of the search space increases. Meanwhile, all of the aforementioned methods focus on reducing the number of DLT runs. Still, a lot of preliminary DLT runs must be performed in order to uncover promising hyper-parameter configurations. For this reason, hyper-parameter optimization is still one of the most costly process in DL.
2.2. Motivation
The main challenge of hyper-parameter optimization is how to find an optimal hyper-parameter combination fast that maximizes the accuracy of a DL model. To accelerate hyper-parameter optimization, Hermes determines which hyper-parameter combination is likely to be optimal by receiving early-feedback from training. Mainly, we exploit the fact that only a small fraction of hyper-parameter combinations actually converge to an acceptable level and they can be identifiable at early stages of training. More concretely, “The promising combinations converge quickly in the beginning” [12].
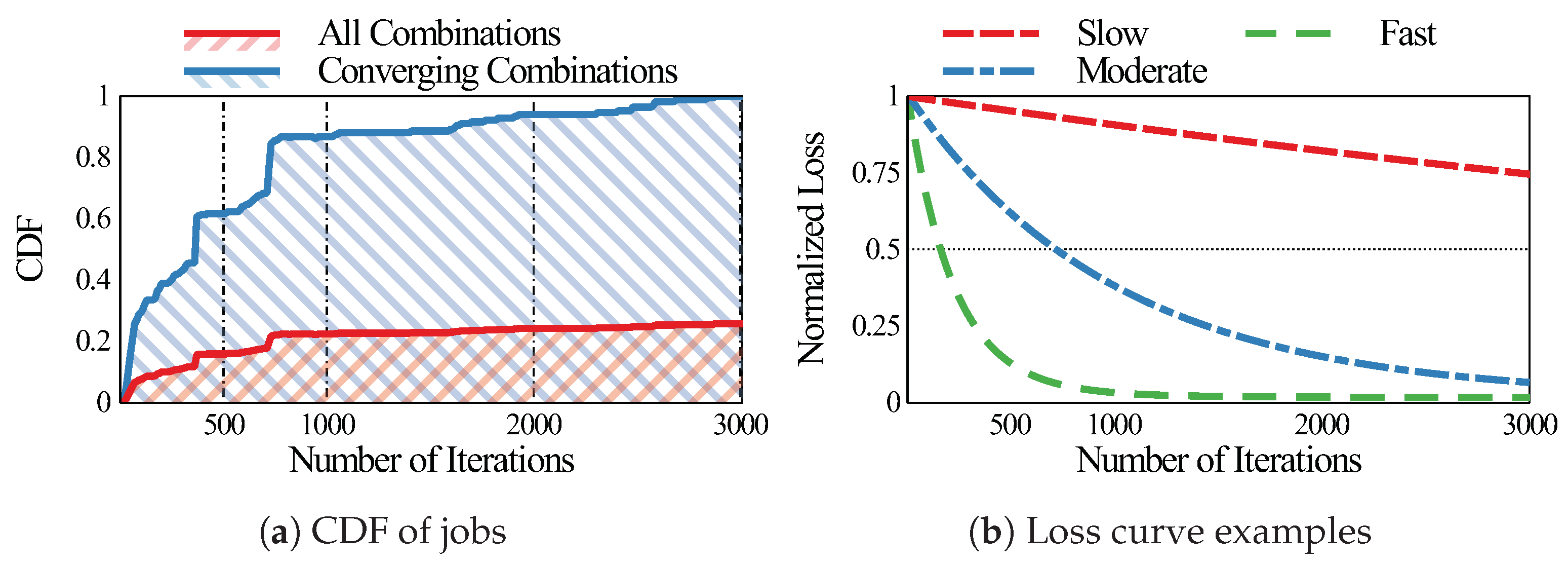
To confirm this, we trained 4 CNN models up to 3000 iterations with 192 hyper-parameter configurations, and investigated their convergence patterns. We measured the number of iterations required to achieve at least 50% of the loss of the most promising combination. The considered hyper-parameter combinations are summarized in Table 1.

Table 1.
Considered hyper-parameter configurations. 192 random combinations () are used for each model.
The cumulative distribution functions (CDF) of the number of training iterations spent are shown in Figure 2a. As shown in the figure, only 25% of all the combinations (red CDF) achieve the 50% goal after 3000 iterations. This shows the fact that only a handful of hyper-parameter combinations are “promising” and achieve good convergence. It is thus crucial to quickly identify and concentrate computational resources to these combinations.
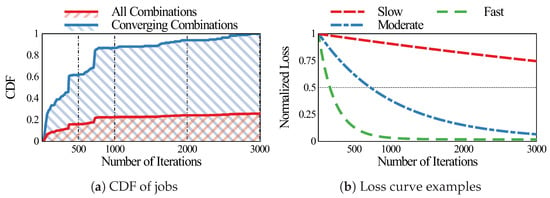
Figure 2.
(a) Cumulative distribution functions (CDF) of all the combinations are in blue and the combinations achieving at least 50% of the loss of the optimal combination are in red. Note that the red CDF stagnates around 0.2 because only about 20% of the combinations converged. (b) Example loss curves from our experiment.
The blue CDF is the CDF of the “promising” jobs. Among the converging combinations, about 85% converge to the goal within 1000 iterations, while about 60% converge within 500 iterations. This confirms the fact that promising jobs exhibit fast convergence, and can be identified by their convergence speed. We categorized the convergence rate of the former as moderate (converge within 1000 iterations), the later as fast (converge within 500 iterations), and the rest as slow. Example loss curves from each of the three categories are shown in Figure 2b. It is visually clear that the fast and moderate converging cases achieve the 50% goal very early on.
Based on these observations, Hermes employs a convergence-aware scheduling strategy which enables acceleration of hyper-parameter optimization. Briefly, Hermes identifies and prioritizes jobs that quickly converge in the beginning.
3. Design and Implementation
3.1. Overall Architecture of Hermes
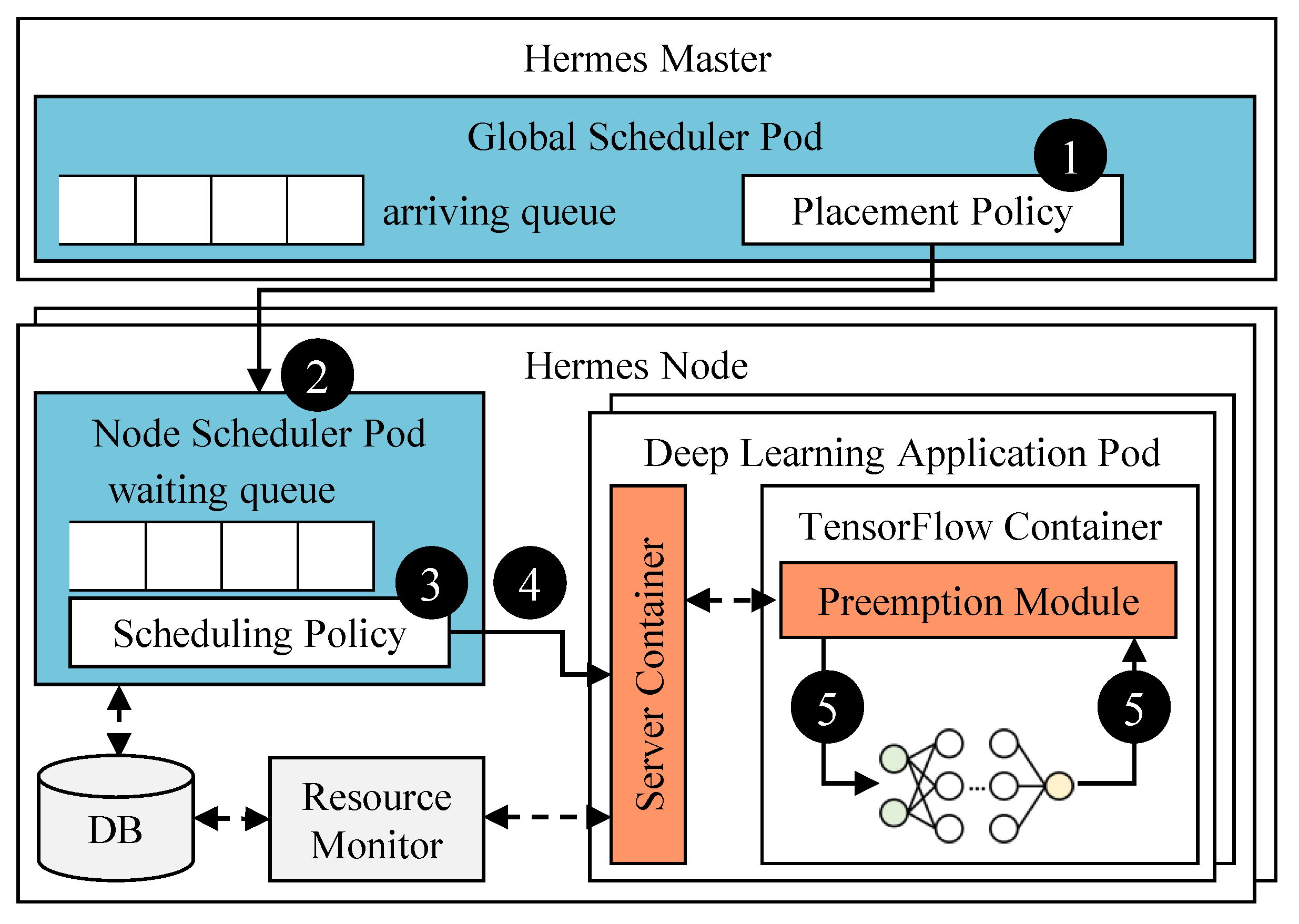
Hermes is composed of two schedulers (blue plates), the time-sharing supporter (orange plates), and the resource monitor as shown in Figure 3. The schedulers are structured in two-levels: the global scheduler and the node scheduler. The global scheduler in the Hermes master is responsible for distributing DL containers to a worker node based on its placement policy. The node scheduler residing on the Hermes node schedules the containers with its convergence-aware scheduling policy. It is also responsible for making the preemption decisions. This two-level structure increases portability while minimizing communication overhead caused by preemption.
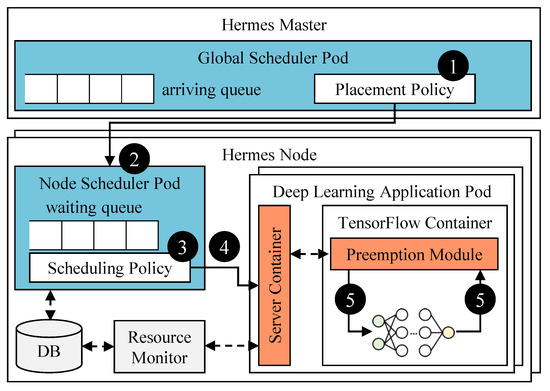
Figure 3.
Overall architecture of Hermes.
The time-sharing supporter in the DL applications consists of a server container for communicating with other components, and a preemption module for performing the suspend-resume-based preemption. For enabling time-sharing between DL containers, it is required to release the GPU memory occupied by a container. To efficiently implement this, the preemption module offloads part of the DL container utilizing the GPU memory to a sub-process. The GPU memory can now be managed by killing (freeing) or spawning (reclaiming) this accompanying sub-process.
The resource monitor periodically checks the loss of DL containers and their GPU usage. This information is maintained in the database. The communications between containers as well as between pods happen through REST API.
The overall scheduling flow is also illustrated in Figure 3. First, the global scheduler selects a DL container from the arriving queue and assigns it to an appropriate Hermes node ➁ according to its placement policy ➀. Currently, the global scheduler uses a load-balancing placement policy such that the number of containers in Hermes nodes is evenly distributed. Then, the node scheduler executes a container from the waiting queue according to the scheduling policy at every time quantum (currently set to 10 s) ➂. If a preemption request is made from the node scheduler, it is delivered to the preemption module in the target DL container via server container ➃. The preemption module in turn releases the GPU after the current training iteration is finished ➄. Once the node scheduler confirms that the GPU is finally released, it runs the selected (pending) DL container.
3.2. Global Scheduler
User jobs are primarily submitted to the global scheduler residing in the master node of Kubernetes. Then, according to the placement policy, the global scheduler determines which node will execute the job. The placement algorithm shown in Algorithm 1 is based on the information in the node table that maintains information about each node. The execution configuration of the placed job is sent to the scheduler of the selected node in the form of a REST API.
The current placement policy shown in Algorithm 2 focuses on balancing the load of the main resource: the GPUs. The submitted jobs are evenly distributed across Hermes nodes with the available GPUs and share the GPU resources via time-sharing. Thus, as the number of jobs increases, the GPU holding time in each node decreases. Consequently, the overall preemption overhead increases as well. To mitigate this problem, we heuristically set the maximum number of jobs per GPU (). This effectively bounds the preemption overhead with the minimal expense of load balancing. Once all nodes have reached their maximum job capacity, the remaining jobs remain in the global scheduler queue. We set the threshold as throughout this work.
| Algorithm 1 Placement Algorithm |
| Input: GPUs , Job |
| 1: for job do |
| 2: |
| 3: if then |
| 4: Initialize J |
| 5: Enqueue J to |
| 6: end if |
| 7: end for |
| Algorithm 2 Find_Available_GPU |
| Input: GPUs |
| Output: |
| 1: // : job count threshold in each GPU |
| 2: |
| 3: for GPU do |
| 4: if # of job in G is fewer than then |
| 5: if is null or # of job in G is fewer than then |
| 6: |
| 7: end if |
| 8: end if |
| 9: end for |
| 10: return |
3.3. Node Scheduler
Each worker node in Hermes has a dedicated node scheduler and dedicated GPU resources. Since there is a dedicated node scheduler on each node, different scheduling policies can be used simultaneously. The node schedulers are responsible for scheduling the jobs received from the global scheduler. Through kube-apiserver, the container information of the node and the DL job information (such as the ip) are obtained, and used to manage the jobs allocated to the node.
The node scheduler currently runs a single DLT job over a single GPU at the same time. That is, temporal GPU sharing is only permitted while spatial sharing is not possible. At each scheduling period, the node scheduler receives information about the DLT jobs running in the worker node from the Resource Monitor and schedules them according to the convergence rate of each job. If preemption is required in order to execute a selected job, a suspend command is requested to the preempted job. The job then completes its current iteration and the current training progress is saved into a Tensorflow checkpoint. Finally, the GPU is released and the selected job is executed soon after. If the selected job is a job that has never been executed, a request is sent to kube-apiserver to create a new job. If the selected job has been suspended (or preempted) before, a resume command is requested to the job. The job is now reallocated to the GPU, resuming training.
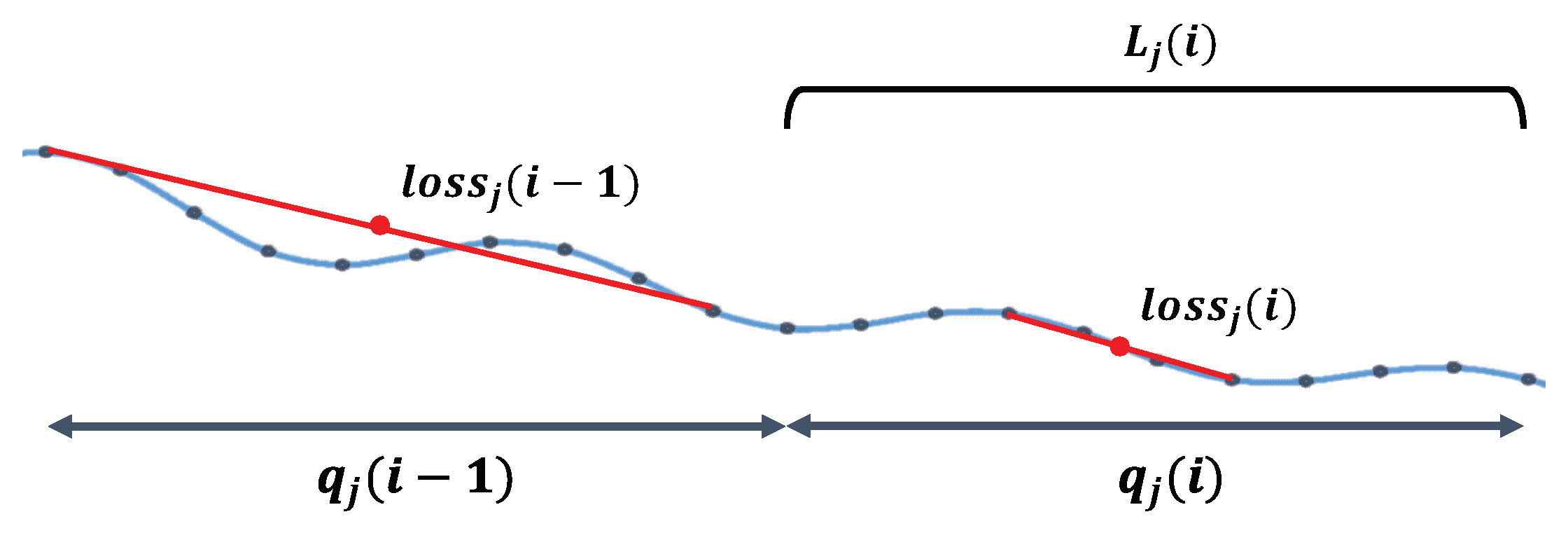
Hermes calculates the convergence of job j as shown in Figure 4, where is the i-th time quantum of job j, and is a set of losses obtained from the job j during . The loss of DL models can fluctuate as shown in Figure 4. Therefore, to circumvent the fluctuation effect, Hermes uses
as the representative loss of the -th cycle. The convergence of is now defined as
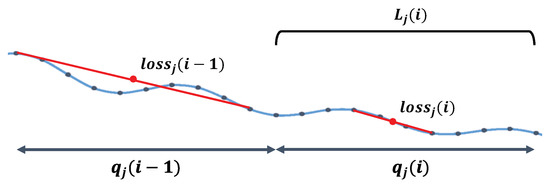
Figure 4.
Example of . The blue line shows a “noisy” example loss curve. The red line shows the estimated loss curve, which is less affected by noise.
If the task i has been executed only once, the loss of previous cycles are unavailable. Thus, we instead define C such that
At each time quantum, the node scheduler compares the recent of each task. By executing tasks with a large , hyper-parameter optimization is accelerated. The convergence-aware scheduling policy is shown in Algorithm 3.
Another important consideration is that the slope of loss curves decreases exponentially. As a result, the slope difference between different loss curves also becomes smaller, complicating Hermes’ decision based on priority. To mitigate this, we gradually increase the length of a job’s quantum once it achieves a certain milestone. This ensures that the slope difference between loss curves is maintained at a certain level. The milestones are set by the user as the percentage decrease of the loss.
| Algorithm 3 Convergence-aware Scheduling Algorithm |
| Input: Iteration i, Convergences , GPUs |
| 1: for do |
| 2: |
| 3: |
| 4: |
| 5: if then |
| 6: continue |
| 7: end if |
| 8: for do |
| 9: if J is WAITING then |
| 10: Enqueue J to |
| 11: end if |
| 12: end for |
| 13: |
| 14: if needs preemption then |
| 15: if is PREEMPTIBLE then |
| 16: Preempt |
| 17: end if |
| 18: end if |
| 19: Schedule |
| 20: end for |
3.4. Preemption Module
The preemption module executes the suspend and resume requests issued by the node scheduler. Both are implemented using TensorFlow hooks (supported from TensorFlow version r0.12), which is a feature for executing a predetermined function before and after each iteration of DLT is performed. Using TensorFlow hooks, Hermes supports preemption of TensorFlow jobs without modifying existing users’ code. Currently, the preemption module checks whether the running job must be suspended or resumed.
Before the imminent DLT iteration starts, the preemption module checks whether a request has been received from the node scheduler. If a suspend request has been issued, the current state is saved into a TensorFlow checkpoint. The GPU is then released and the job is suspended soon after. In the midst of a DLT iteration, suspend requests are not handled until it is finished. Once a resume request is received, the preemption module reallocates the GPU, restores the previously stored checkpoint, and resumes training.
A major implementation issue in the preemption module is that Tensorflow does not free GPU memory even if session.close() is executed unless the process has been terminated. Moreover, if the GPU is completely turned off (i.e., using cuda.close() of the python Numba library), the GPU cannot be used even if a session is regenerated. To solve this without modifying existing users’ code, Hermes creates a sub-process where the actual DLT iterations are executed. By doing this, the GPU can be easily released by terminating the corresponding sub-process during a suspend operation with low overhead (session.close() takes about and cuda.close() takes about ). Likewise, for a resume operation, a new sub-process is created and allocated a GPU. At the same time, all the DLT related data used by TensorFlow such as the computation graph are transferred to the sub-process.
4. Performance Evaluation
From now on, we will demonstrate that Hermes can reduce the time for finding optimal performing hyper-parameter combinations on authentic DL workloads.
4.1. Experiment Setup
4.1.1. Testbed
We evaluated Hermes over a testbed with one Hermes master and four Hermes nodes. Each Hermes node is comprised of two Intel Xeon Silver 4210@2.20 GHz processors (10 physical cores, Intel, Santa Clara, CA, USA) with 128 GB RAM, and one NVIDIA RTX 2080 Ti GPU (Nvidia, Santa Clara, CA, USA). Moreover, each node runs on Ubuntu 18.04, Kubernetes 1.15.3, and Docker 18.09. Since Hermes does not target at multi-GPU training, distributed DL and job migration, we only used the local file system (Ext4) for saving and restoring checkpoints.
Although our testbed only consists of NVIDIA RTX 2080 Ti GPUs (Nvidia, Santa Clara, CA, USA), our method does not assume anything about the underlying hardware. Thus, our empirical results should naturally apply to other types of GPUs from different vendors.
4.1.2. Workloads
We constructed workloads using the TensorFlow v1.13.2 framework. We fixed the random seed and randomized the order of the jobs entering the queue. We trained four CNN models using ImageNet dataset and hyper-parameters provided by TensorFlow CNN benchmark suite [14] as shown in Table 1. We used manual search in hyper-parameter optimization and several meaningful range learning rate with some difference to result because the experiment takes long time. The final loss of each hyper-parameter combination was obtained by training for 1000 iterations on a TITAN V GPU. The amount of good hyper-parameter combinations versus bad hyper-parameter combinations affects the performance of different scheduling strategies. To evaluate this effect, we constructed two different types of job bins. Bin type 1 has 4 good combinations while having 16 jobs in total. Bin type 2 has 12 good combinations while also having 16 jobs. For Hermes’ time-quantum, we used a length of 10 s. Then, during execution, we gradually increased the quantum as the number of preemptions adds up. For Gandiva and SLAQ, we set the time quantum to be 30 s. For the comparison, we measured the normalized execution times of four algorithms using four CNN models. The presented values are the averages of five iterations.
4.1.3. Baselines
We chose three baseline scheduling policies: FIFO, round-robin (RR), and SLAQ [12]. For FIFO, which is the default scheduler of Kubernetes, we do not use preemption and do not perform additional tuning. We included RR with GPU time-sharing because previous works such as Gandiva [7], Tiresias [1], and Themis [11] adopt this policy. Lastly, SLAQ, is an algorithm for improving the DL quality by prioritizing jobs with high loss.
4.2. Hyper-Parameter Optimization Speed
To evaluate the performance of Hermes, we measured the normalized average execution time for the good performing hyper-parameter combinations to achieve at least 90% of the optimal loss (time until ).
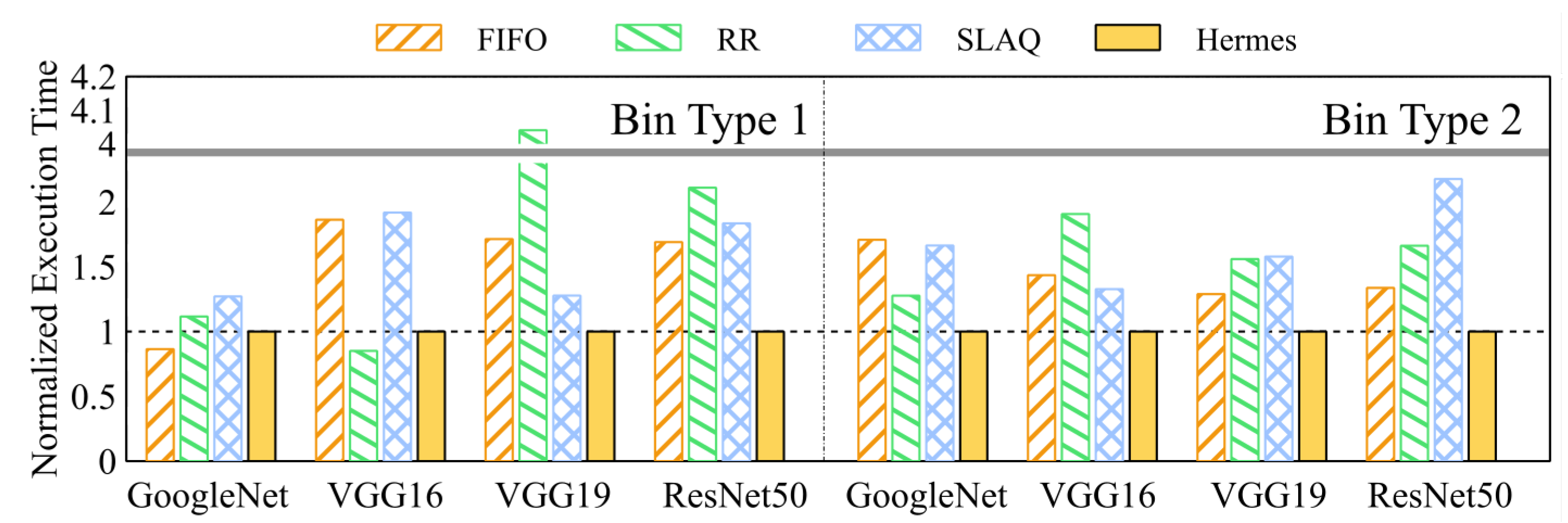
The results for Bin type 1 and Bin type 2 are shown in Figure 5. Except for the case of GoogleNet in Bin type 1, Hermes achieves the lower average hyper-parameter optimization time in most cases.
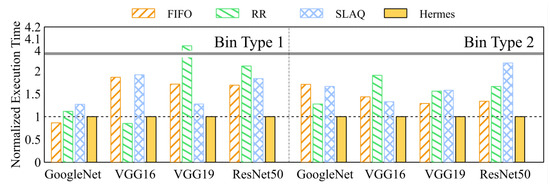
Figure 5.
Average execution time that all jobs in Bin types 1 and 2 reach 90%.
We first focus on the case where only a small amount of hyper-parameter combinations are good (represented by Bin type 1). SLAQ shows poor performance. This is caused by SLAQ’s prioritization of poorly performing jobs. Potentially good performing hyper-parameter combinations are only explored at later phases. Gandiva also appears to be heavily affected by the amount of poor hyper-parameter combinations. Since all the jobs are treated equally, poorly performing jobs consistently cause preemption overhead. On the other hand, Hermes, is much less affected by the number of poorly performing combinations.
In the cases where Hermes did not perform the best, two reasons can be found. In GoogleNet, the duration of training is relatively short. As a result, the time-sharing overhead of Hermes becomes relatively dominant, which can be mitigated by increasing its time-quantum. Since the training times of VGG16, VGG19, and ResNet50 are longer, the preemption overhead of Hermes is less dominant, resulting in better performance.
Moreover, the performance of FIFO is highly dependent on the job submission order. If by pure luck the promising jobs happen to be submitted earlier, FIFO ends up performing very well, which is what happened with GoogleNet. On the other hand, RR is the least affected by the job submission order compared to other algorithms. Thus, if the promising jobs are submitted later, RR can uncover them quickly despite the preemption overhead. Hermes in contrast can be seen as a compromise of the two. While it is not unaffected by the job submission order as RR, it is much less affected than FIFO. This can be confirmed from the consistent performance of Hermes. Even when it did not perform the best, it performed very closely to the best performing algorithm.
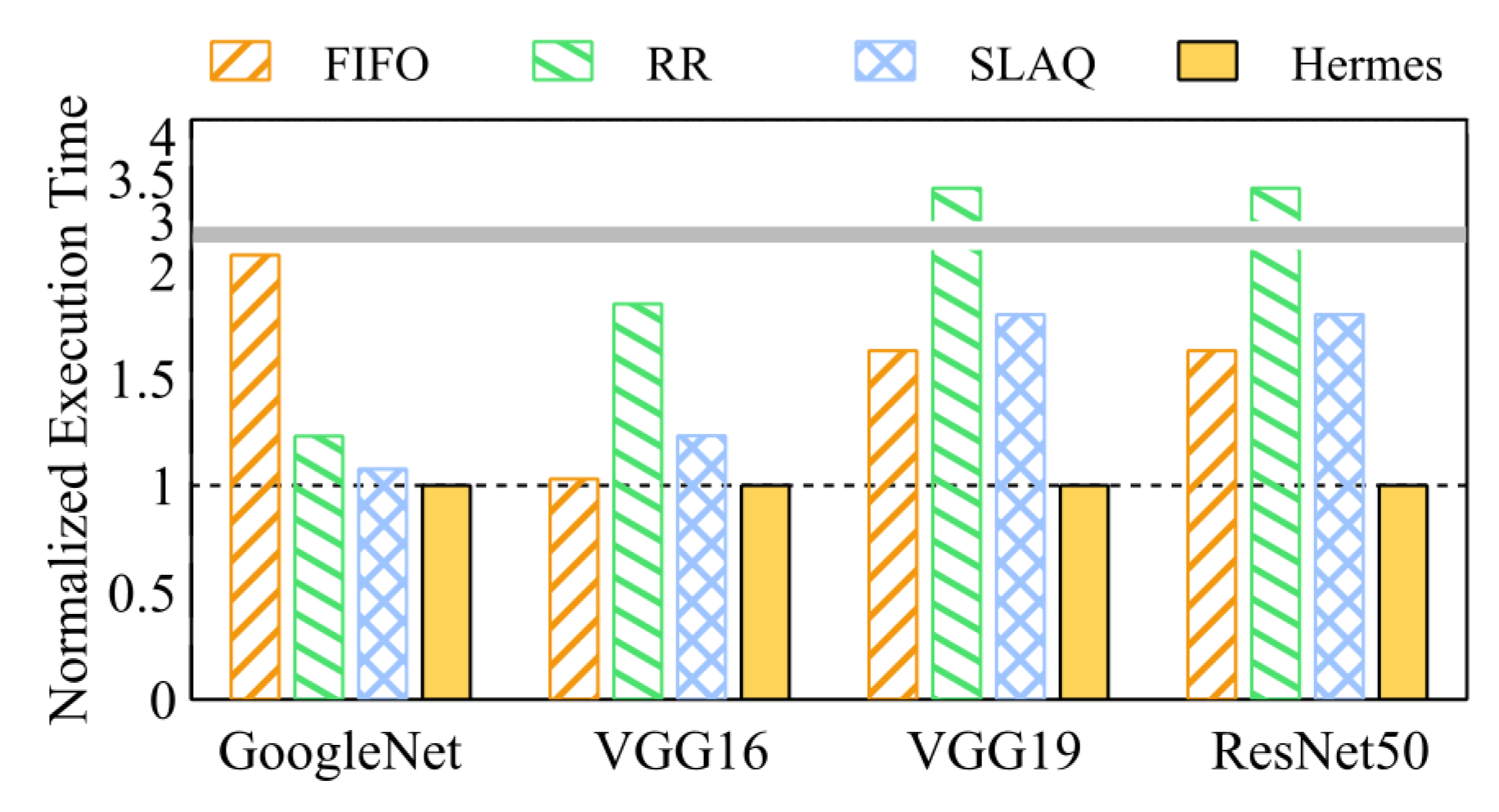
Now, we evaluated how effectively Hermes can uncover the best performing combinations among multiple good performing ones (This scenario is represented by Bin type 2). The results for the normalized average execution time are shown in Figure 6. Hermes is able to quickly find optimal hyper-parameter combinations among a vast set of potentially optimal combinations. For example, the resulting average speedup is 2.68. On the other hand, Gandiva suffers severely from the time-sharing overhead. Moreover, since most hyper-parameter combinations achieve good performance, SLAQ achieves less poor performance compared to the case in Bin type 1.
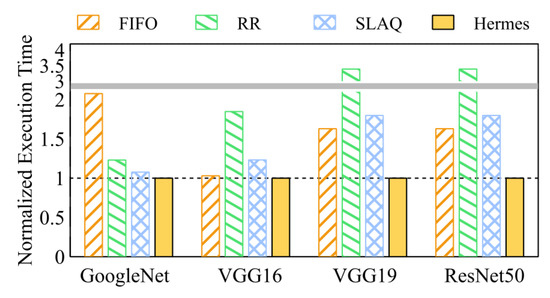
Figure 6.
Comparison of top-4 jobs reaching 90% (Bin type 2).
In summary, the average speedups of hyper-parameter optimization for GoogleNet, VGG16, VGG19 and ResNet50 are 2.08, 1.92, 4.04, and 3.39, respectively. Specifically, it outperformed all other methods except in two cases in Bin type 1. In these two cases, it performed closely to the best performing method. Other DL oriented schedulers on the other hand, generally achieve poor performance except for FIFO, which does not suffer from time-sharing overhead. However, experimental results show that Hermes accelerates hyper-parameter optimization in most cases.
4.3. Overhead Analysis
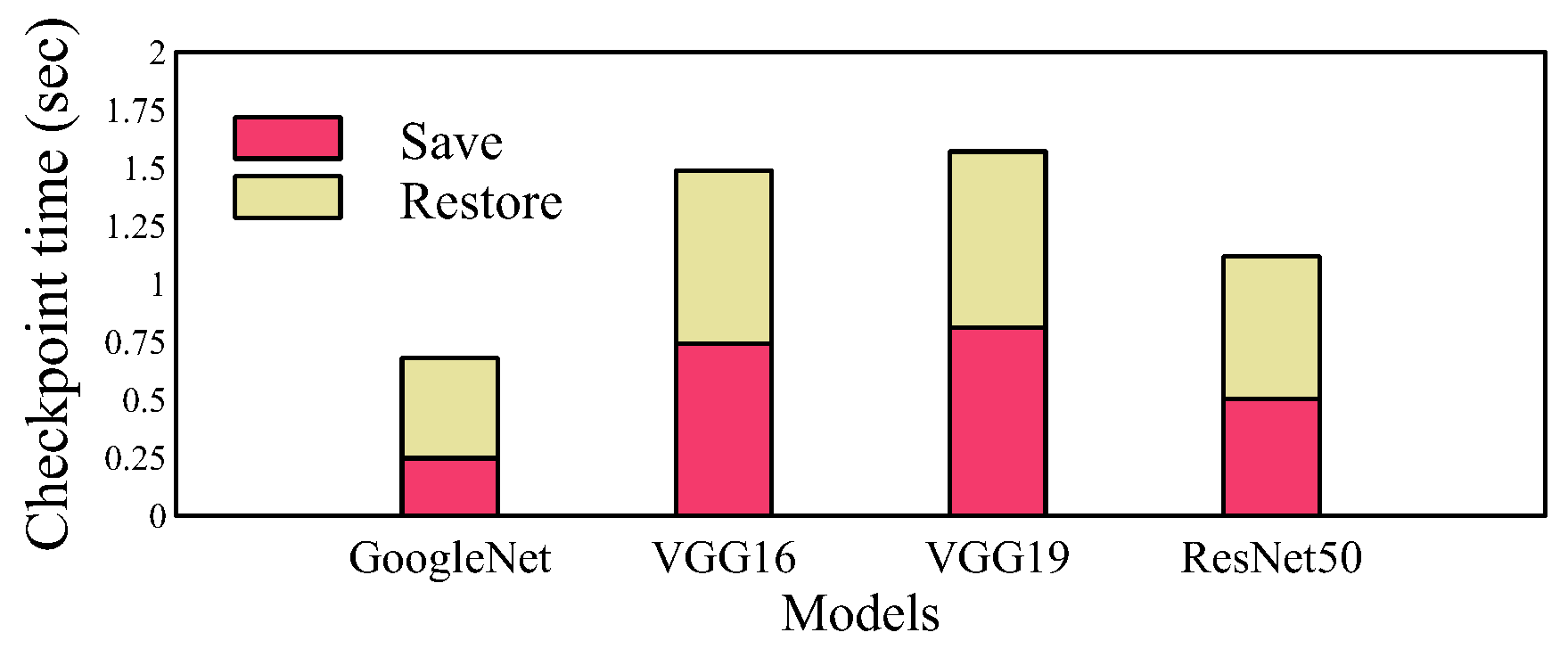
We also evaluated the time-sharing overhead of Hermes. The preemption process mainly consists of saving and restoring the current job as a TensorFlow checkpoint. The overhead of saving and restoring a job is shown in Figure 7. In the case of GoogleNet, which is the smallest model we consider, the time for saving and restoring a job only takes 0.67 s (0.24 s for save and 0.43 s for restore). On the other hand, VGG19 which is the largest model we consider takes 1.57 s for preemption. Considering that Hermes’ time quantum is 10 s and we also increase the quantum once a job achieves a certain milestone, the overhead incurred by time-sharing is minimal.
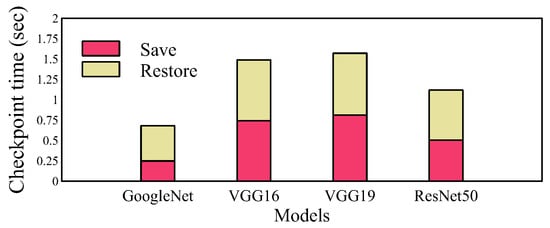
Figure 7.
Preemption overhead of each model.
Lastly, we analyzed the overhead of using sub-processes for managing GPU resources. We compared the execution time of Hermes against directly training a model using TensorFlow. We run SGD for 1000 iterations with a fixed batch size of 16. The results are shown in Table 2. In the case of GoogleNet, which takes the shortest time to train, it takes 2.5 s per 1000 iterations as overhead. However, in the case of VGG19 with a long training time, there is only a slight overhead of less than 2.1%.

Table 2.
Execution time comparison.
5. Related Work
Hermes is a deep learning scheduling framework that mainly aims to accelerate the feedback speed of hyper-parameter optimization by GPU preemption and convergence-rate-aware scheduling algorithm. Therefore, existing studies related with deep learning scheduling and hyper-parameter optimization frameworks are presented in this section. Table 3 summarizes the deep learning scheduling frameworks and their comparison with Hermes.

Table 3.
Summary of deep learning scheduling frameworks.
5.1. Deep Learning Scheduling Frameworks
Gandiva [7] aims to provide early feedback and fairness among jobs through round robin (RR) scheduling and migration. Gandiva reduces preemption overhead by modifying user codes written by the DL frameworks such as TensorFlow [13] and PyTorch [24]. The average JCT is also reduced by packing and migration. However, providing early feedback is limited especially when the distribution of convergence speeds among job varies. This is because Gandiva does not consider DL quality.
Tiresias [1] propose a gittin index scheduling policy that considers execution time and resources simultaneously. The placement policy is based on profiling Tensor of DL model for minimizing communication overhead. In order to get a gittin index, JCT distribution is required to calculate the probability of job completion within the next service quantum. Moreover, accelerating feedback is not a main concern because Tiresias gives higher priority to jobs that are likely to be finished earlier in the next service quantum.
Themis [11] propose a two-level scheduling architecture with semi-optimistic auction for finish-time fairness. In Themes, each application bids for a set of GPUs and a centralized arbiter allocates GPUs appropriately by setting a winning bid. By considering placement sensitivity in auction, Themis can ensure finish-time fairness in the long term, while achieving efficiency for fairness in the short term. However, like Gandiva, Themis does not consider the DLT quality and feedback speed, thus it is not suitable for early feedback.
Optimus [8] and Cynthia [9] are also deep learning scheduling frameworks that dynamically allocate resources to jobs by considering distributed deep learning (DDL) related factors such as optimizer and communication overhead. One of the problems in these studies is that they need prior knowledge of optimizer models. In addition, the performance model is not accurate especially when interference happens in the network, PCI, and storage. As these studies mainly target at minimizing average JCT with remaining-time-driven scheduling, they are not suitable for early feedback.
FlowCon [10] is another resource management framework that dynamically adjusts the amount of resources based on the growth efficiency which is a measure of convergence speed of a DL job. The goal of FlowCon is to minimize average JCT rather than early feedback. FlowCon does not support preemptive scheduling, which makes it hard to accelerate feedback speed. It also does not consider hyper-parameter optimization in scheduling.
SLAQ [12] proposes a quality driven scheduling for machine learning jobs to maximize system-wide quality improvement in CPU-based cluster. Because SLAQ consider ML quality (i.e., loss) and resource allocation in hyper-parameter exploration without time, it is hard to measure changes within equal time. Thus, this policy could give higher priority to quantitatively reduced job not over efficiency in time.
Most of these previous methods, however, are not suited for hyper-parameter optimization, as they do not prioritize jobs with promising hyper-parameter combinations. In contrast, Hermes utilizes the information available during DLT, and operates a convergence-aware policy for prioritizing promising jobs. As the results in Section 4 imply, Hermes is able to efficiently utilize GPU resources and accelerate hyper-parameter optimization.
Lastly, Sherpa [2] is a recently introduced framework with the specific goal of hyper-parameter optimization. However, the scheduling strategies provided by Sherpa do not consider convergence feedback. For this reason, the user need to monitor the progress of the jobs and manually manage the GPU resources. Since Sherpa provides an extendable interface for its internal scheduler, it would be possible to implement Hermes’s scheduling strategy on Sherpa and enjoy the benefits of both frameworks.
5.2. Hyper-Parameter Optimization Frameworks
HyperSched [25] proposes a scheduling policy to maximize system-wide accuracy within a fixed deadline. Therefore, it is difficult to accelerate feedback speed because the goal is to maximize accuracy rather than early feedback. Meanwhile, HyperOpt [26] proposes a parallelization framework for hyper-parameter optimization based on Bayesian optimization. As the main objective of this research is to provide an efficient hyper-parameter optimization method for model selection rather than early feedback, it is hard to accelerate multiple hyper-parameter optimization jobs. Other similar research efforts related to hyper-parameter optimization such as HyperDrive [27] and HyperBand [28] are proposed. However, these are also not suitable for early feedback because of the same reasons mentioned above.
6. Conclusions
Hyper-parameter optimization is an essential process in DLT to improve the quality of DL models. Due to the large number of hyper-parameters and the size of DL models used nowadays, accelerating this process is vital. This paper presented Hermes, a GPU scheduling framework to accelerate hyper-parameter optimization in DL clusters. Hermes enables parallel optimization of hyper-parameters by time-sharing between DL jobs. Moreover, it utilizes the feedback about the convergence rate at the early stages of training for adaptively setting the priority of DL jobs. By combining time-sharing and our scheduling strategy, Hermes accelerates hyper-parameter optimization by up to 4.04 times with minimal time-sharing overhead compared to previous studies.
Author Contributions
J.S. and Y.Y. made substantial contributions to the original ideas, designed the experiments and wrote the initial manuscript. K.-r.K. improved the original ideas and helped experimental setup. Y.K. and K.L. gave ideas for the experiments and discussed the results. S.P. also made contributions to the original ideas, rewrote the whole manuscript and confirmed the results. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Institute of Information and Communications Technology Planning and Evaluation (IITP), Korea government (MSIT) (Development of low-latency storage module for I/O intensive edge data processing) under Grant 2020–0–00104, and in part by the MSIT (Ministry of Science, ICT), Korea, under the ITRC (Information Technology Research Center) support program (IITP–2020–2016–0–00465) supervised by the IITP (Institute for Information & communications Technology Planning & Evaluation).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Gu, J.; Chowdhury, M.; Shin, K.G.; Zhu, Y.; Jeon, M.; Qian, J.; Liu, H.; Guo, C. Tiresias: A GPU Cluster Manager for Distributed Deep Learning. In Proceedings of the 16th USENIX Symposium on Networked Systems Design and Implementation (NSDI 19); USENIX Association: Boston, MA, USA, 2019; pp. 485–500. [Google Scholar]
- Hertel, L.; Collado, J.; Sadowski, P.; Ott, J.; Baldi, P. Sherpa: Robust hyperparameter optimization for machine learning. SoftwareX 2020, 12, 100591. [Google Scholar] [CrossRef]
- Domhan, T.; Springenberg, J.T.; Hutter, F. Speeding up Automatic Hyperparameter Optimization of Deep Neural Networks by Extrapolation of Learning Curves. In Proceedings of the 24th International Conference on Artificial Intelligence; AAAI Press: Palo Alto, CA, USA, 2015; pp. 3460–3468. [Google Scholar]
- Vavilapalli, V.K.; Seth, S.; Saha, B.; Curino, C.; O’Malley, O.; Radia, S.; Reed, B.; Baldeschwieler, E.; Murthy, A.C.; Douglas, C.; et al. Apache Hadoop YARN: Yet another resource negotiator. In Proceedings of the 4th annual Symposium on Cloud Computing-SOCC ’13; ACM Press: Santa Clara, CA, USA, 2013; pp. 1–16. [Google Scholar] [CrossRef]
- Hindman, B.; Konwinski, A.; Zaharia, M.; Ghodsi, A.; Joseph, A.D.; Katz, R.; Shenker, S.; Stoica, I. Mesos: A Platform for Fine-Grained Resource Sharing in the Data Center. In Proceedings of the 8th USENIX Conference on Networked Systems Design and Implementation; USENIX Association: Berkeley, CA, USA, 2011; pp. 295–308. [Google Scholar]
- Foundation, C.N.C. Kubernetes. Available online: https://kubernetes.io (accessed on 1 December 2020).
- Xiao, W.; Bhardwaj, R.; Ramjee, R.; Sivathanu, M.; Kwatra, N.; Han, Z.; Patel, P.; Peng, X.; Zhao, H.; Zhang, Q.; et al. Gandiva: Introspective Cluster Scheduling for Deep Learning. In Proceedings of the 13th USENIX Symposium on Operating Systems Design and Implementation (OSDI 18); USENIX Association: Carlsbad, CA, USA, 2018; pp. 595–610. [Google Scholar]
- Peng, Y.; Bao, Y.; Chen, Y.; Wu, C.; Guo, C. Optimus: An efficient dynamic resource scheduler for deep learning clusters. In Proceedings of the Thirteenth EuroSys Conference on-EuroSys ’18; ACM Press: Porto, Portugal, 2018; pp. 1–14. [Google Scholar] [CrossRef]
- Zheng, H.; Xu, F.; Chen, L.; Zhou, Z.; Liu, F. Cynthia: Cost-Efficient Cloud Resource Provisioning for Predictable Distributed Deep Neural Network Training. In Proceedings of the 48th International Conference on Parallel Processing-ICPP 2019; ACM Press: Kyoto, Japan, 2019; pp. 1–11. [Google Scholar] [CrossRef]
- Zheng, W.; Tynes, M.; Gorelick, H.; Mao, Y.; Cheng, L.; Hou, Y. FlowCon: Elastic Flow Configuration for Containerized Deep Learning Applications. In Proceedings of the 48th International Conference on Parallel Processing-ICPP 2019; ACM Press: Kyoto, Japan, 2019; pp. 1–10. [Google Scholar] [CrossRef]
- Mahajan, K.; Balasubramanian, A.; Singhvi, A.; Venkataraman, S.; Akella, A.; Phanishayee, A.; Chawla, S. Themis: Fair and Efficient GPU Cluster Scheduling. In Proceedings of the 17th USENIX Symposium on Networked Systems Design and Implementation (NSDI 20); USENIX Association: Santa Clara, CA, USA, 2020; pp. 289–304. [Google Scholar]
- Zhang, H.; Stafman, L.; Or, A.; Freedman, M.J. SLAQ: Quality-driven scheduling for distributed machine learning. In Proceedings of the 2017 Symposium on Cloud Computing-SoCC ’17; ACM Press: Santa Clara, CA, USA, 2017; pp. 390–404. [Google Scholar] [CrossRef]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: tensorflow.org (accessed on 29 January 2021).
- Tensorflow. TensorFlow Benchmark. Available online: https://github.com/tensorflow/benchmarks (accessed on 1 December 2020).
- Robbins, H.; Monro, S. A Stochastic Approximation Method. Ann. Math. Statist. 1951, 22, 400–407. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. Available online: https://openreview.net/forum?id=8gmWwjFyLj (accessed on 29 January 2021).
- Shallue, C.J.; Lee, J.; Antognini, J.; Sohl-Dickstein, J.; Frostig, R.; Dahl, G.E. Measuring the Effects of Data Parallelism on Neural Network Training. J. Mach. Learn. Res. 2019, 20, 1–49. [Google Scholar]
- Hinton, G.E. A Practical Guide to Training Restricted Boltzmann Machines. In Neural Networks: Tricks of the Trade, 2nd ed.; Montavon, G., Orr, G.B., Müller, K.R., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 599–619. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Müller, A.; Nothman, J.; Louppe, G.; et al. Scikit-learn: Machine Learning in Python. arXiv 2018, arXiv:1201.0490. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random Search for Hyper-Parameter Optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Sequential Model-Based Optimization for General Algorithm Configuration. In Learning and Intelligent Optimization; Coello, C.A.C., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 507–523. [Google Scholar]
- Bergstra, J.S.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for Hyper-Parameter Optimization. In Advances in Neural Information Processing Systems 24; Shawe-Taylor, J., Zemel, R.S., Bartlett, P.L., Pereira, F., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, US, 2011; pp. 2546–2554. [Google Scholar]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. arXiV 2012, arXiv:1206.2944. Available online: https://arxiv.org/abs/1206.2944 (accessed on 29 January 2021).
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32; Wallach, H., Larochelle, H., Beygelzimer, A., Alché-Buc, F.d., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, US, 2019; pp. 8024–8035. [Google Scholar]
- Liaw, R.; Bhardwaj, R.; Dunlap, L.; Zou, Y.; Gonzalez, J.E.; Stoica, I.; Tumanov, A. HyperSched: Dynamic Resource Reallocation for Model Development on a Deadline. In Proceedings of the ACM Symposium on Cloud Computing-SoCC ’19; ACM Press: Santa Cruz, CA, USA, 2019; pp. 61–73. [Google Scholar] [CrossRef]
- Bergstra, J.; Yamins, D.; Cox, D.D. Hyperopt: A python library for optimizing the hyperparameters of machine learning algorithms. In Proceedings of the 12th Python in Science Conference, Austin, TX, USA, 24–29 June 2013; pp. 13–20. [Google Scholar]
- Rasley, J.; He, Y.; Yan, F.; Ruwase, O.; Fonseca, R. HyperDrive: Exploring hyperparameters with POP scheduling. In Proceedings of the 18th ACM/IFIP/USENIX Middleware Conference on-Middleware ’17; ACM Press: Las Vegas, NV, USA, 2017; pp. 1–13. [Google Scholar] [CrossRef]
- Li, L.; Jamieson, K.; DeSalvo, G.; Rostamizadeh, A.; Talwalkar, A. Hyperband: A Novel Bandit-Based Approach to Hyperparameter Optimization. J. Mach. Learn. Res. 2017, 18, 6765–6816. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).