Parameters Evaluation in 3D Spare Parts Printing
Abstract
:1. Introduction
2. Methods and Experimental Settings
- a satisfactory precision of the print layout,
- a dual extrusion for the filament (two would be better),
- a auto-leveling heated bed (no need for additional heaters),
- a supported standard STL (Standard Tessellation Language) files, and
- a communication to the computer by a USB port, which is standard nowadays.
3. Results
3.1. Relationships between Infill Density, Printing Time, and Material’s Length
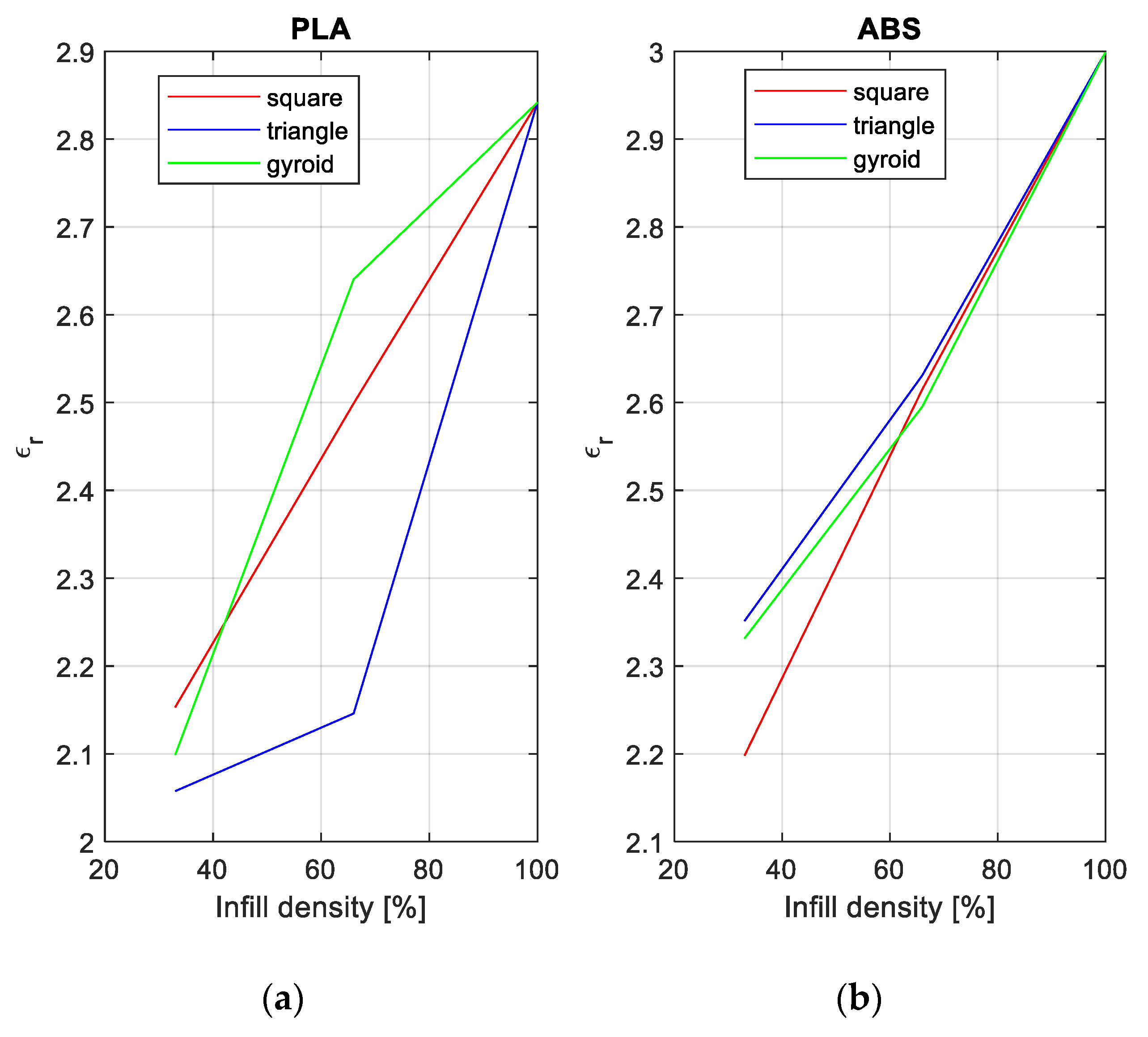
3.2. Dielectric Property Measurements
4. Statistical Analysis and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ramanayaka, K.H.; Chen, X.; Shi, B. UNSCALE: A fuzzy-based multi-criteria usability evaluation framework for measuring and evaluating library websites. IETE Tech. Rev. 2018, 36, 412–431. [Google Scholar] [CrossRef]
- Singh, M.; Pati, D. Countermeasures to replay attacks: A review. IETE Tech. Rev. 2019. [Google Scholar] [CrossRef]
- Kostidi, E.; Nikitakos, N. Is it time for the maritime industry to embrace 3d printed spare parts? TransNav 2018, 12, 557–564. [Google Scholar] [CrossRef]
- Felski, A.; Zwolak, K. The ocean-going autonomous ship—Challenges and threats. J. Mar. Sci. Eng. 2020, 8, 41. [Google Scholar] [CrossRef] [Green Version]
- 3D Print in the Maritime Industry. 2016. Available online: https://greenship.org/project/3d-print-in-the-maritime-industry-ii/ (accessed on 22 August 2019).
- Altan, B.D.; Kovan, V.; Altan, G. Numerical and experimental analysis of a 3D printed Savonius rotor with built-in extension plate. Wind Struct. 2018, 27, 1–9. [Google Scholar] [CrossRef]
- Bergsma, J.M.; van der Zalm, M.; Pruyn, J.F.J. 3D-printing and the maritime construction sector. In Proceedings of the 10th Symp High-Performance Marine Vehicles HIPER′16, Cortina, Italy, 17–19 October 2016; pp. 428–442. [Google Scholar]
- Boat and Ship Industry Ideal for 3D Printer R & D Tax Credits. 2017. Available online: https://3dprint.com/177513/boatand-ship-3d-printing/ (accessed on 22 August 2019).
- 3D Printing in the Port of Rotterdam. 2016. Available online: https://www.portofrotterdam.com/en/business-opportunities/innovation-smartest-port/cases/3d-printing-in-the-port-of-rotterdam (accessed on 22 August 2019).
- Pilot Project: 3D Printing Marine Spares. 2016. Final Report, Rotterdam. Available online: https://www.portofrotterdam.com/sites/default/files/report-3d-printing-marine-spares.pdf?token=sexODksY (accessed on 22 August 2019).
- Li, S.; Ning, J.; Zhang, G.-F.; Zhang, L.-J.; Wu, J.; Zhang, L.-X. Microstructural and mechanical properties of wire-arc additively manufactured Al–Zn–Mg aluminum alloy: The comparison of as-deposited and heat-treated samples. Vacuum 2021, 108, 109860. [Google Scholar] [CrossRef]
- Wang, Y.; Chena, X.; Konovalov, S.; Su, C.; Siddiquee, A.N.; Gangild, N. In-situ wire-feed additive manufacturing of Cu-Al alloy by addition of silicon. Appl. Surf. Sci. 2019, 487, 1366–1375. [Google Scholar] [CrossRef]
- Marine Sector Embraces New Initiatives in 3D Printing. 2016. Available online: https://tech-labs.com/blog/marine-sector-embraces-new-initiatives-3d-printing (accessed on 22 August 2019).
- Cilia, T.; Bertetta, D.; Gualeni, P.; Tani, G. Additive manufacturing application to a ship propeller model for experimental activity in the cavitational tunnel. J. Ship Prod. Des. 2019, 35, 364–373. [Google Scholar] [CrossRef]
- Goh, G.D.; Dikshit, V.; An, J.; Yeong, W.Y. Process-structure-property of additively manufactured continuous carbon fiber reinforced thermoplastic: An investigation of mode I interlaminar fracture toughness. Mech. Adv. Mater. Struct. 2020. [Google Scholar] [CrossRef]
- Tanikella, N.; Wittbrodt, B.; Pearce, J. Tensile strength of commercial polymer materials for fused filament fabrication 3D printing. Addit. Manuf. 2017, 15, 40–47. [Google Scholar] [CrossRef] [Green Version]
- Luis, E.; Pan, H.M.; Sing, S.L.; Bastola, A.K.; Goh, G.D.; Goh, G.L.; Tan, H.K.J.; Bajpai, R.; Song, J.; Yeong, W.Y. Silicone 3D Printing: Process Optimization, Product Biocompatibility, and Reliability of Silicone Meniscus Implants. 3D Print Addit. Manuf. 2019, 6, 319–332. [Google Scholar] [CrossRef]
- Kostidi, E.; Nikitakos, N. Disrupting the spare parts supply chain in the shipping industry with the introduction of 3D printing. In Proceedings of the International Scientific Conference eRA-11, Piraeus, Greece, 23 September 2016. [Google Scholar]
- Knulst, R. 3D Printing of Marine Spares: A Case Study on the Acceptance in the Maritime Industry. Master’s Thesis, Open Universiteit, Heerlen, The Nederland, 2016. [Google Scholar]
- Vujović, I.; Šoda, J.; Kuzmanić, I. Utjecaj tehnologije 3D tiskanja na raspoloživost brodskih sustava. Naše More 2015, 62, 93–96. [Google Scholar] [CrossRef]
- Top 10 3D Printing Applications in Maritime. 2017. Available online: https://www.3dnatives.com/en/3d-printing-maritime-applications230820174 (accessed on 22 August 2019).
- Nickels, L.; Fowler, L. Researches Tackle 3D Printing for Maritime Duties. Met. Powder Rep. 2017, 72, 363–364. [Google Scholar] [CrossRef]
- Mohammed, J.S. Applications of 3D printing technologies in oceanography. Method Oceanogr. 2016, 17, 97–117. [Google Scholar] [CrossRef]
- Pour, M.A.; Zanoni, S. Impact of merging components by additive manufacturing in spare parts management. Procedia Manuf. 2017, 11, 610–618. [Google Scholar] [CrossRef]
- Jiang, R.; Kleer, R.; Piller, F.T. Predicting the future of additive manufacturing: A Delphi study on economic and societal implications of 3D printing for 2030. Technol. Forecast. Soc. 2017, 117, 84–97. [Google Scholar] [CrossRef]
- Abbas, M.A.; Lichti, D.D.; Chong, A.K.; Setan, H.; Majid, Z.; Lau, C.L.; Idris, K.M.; Ari, M.F.M. Improvements to the accuracy of prototype ship models measurement method using terrestrial laser scanner. Measurement 2017, 100, 301–310. [Google Scholar] [CrossRef]
- Audette, M.A.; Jovanovic, V.; Bilgen, O.; Arcaute, K.; Dean, A.W. Creating the fleet maker: A 3D printing-centered STEM learning environment for the stimulation of innovative thinking and empowerment of sailors. In Proceedings of the ASNE Day 2017-Technology, Systems & Ships, Arlington, VA, USA, 14–16 February 2017. [Google Scholar]
- Calle, M.A.G.; Salmi, M.; Mazzariol, L.M.; Alves, M.; Kujala, P. Additive manufacturing of miniature marine structures for crashworthiness verification: Scaling technique and experimental tests. Mar. Struct. 2020, 72, 102764. [Google Scholar] [CrossRef]
- Zolfagharian, A.; Kaynak, A.; Khoo, S.Y.; Zhang, J.; Nahavandi, S.; Kouzani, A. Control-oriented modelling of a 3D-printed soft actuator. Materials 2019, 12, 71. [Google Scholar] [CrossRef] [Green Version]
- Stano, G.; Arleo, L.; Percoco, G. Additive manufacturing for soft robotics: Design and fabrication of airtight, monolithic bending PneuNets with embedded air connectors. Micromachines 2020, 11, 485. [Google Scholar] [CrossRef]
- Terzić, V. Implementation Possibilities for 3D Printing of Spare Parts. Master’s Thesis, University of Split, Faculty of Maritime Studies, Split, Croatia, 2019. [Google Scholar]
- Billah, K.M.; Coronel, J.L.; Halbig, M.C.; Wicker, R.B.; Espalin, D. Electrical and thermal characterization of 3D printed thermoplastic parts with embedded wires for high current-carrying applications. IEEE Access 2019, 7, 18799–18810. [Google Scholar] [CrossRef] [PubMed]
- Aloyaydi, B.A.; Sivasankaran, S.; Ammar, H.R. Influence of infill density on microstructure and flexural behavior of 3D printed PLA thermoplastic parts processed by fusion deposition modelling. AIMS Mater. Sci. 2019, 6, 1033–1048. [Google Scholar] [CrossRef]
- Saniman, M.N.F.; Hashim, M.M.; Mohammad, K.A.; Abd Wahid, K.A.; Muhamad, W.W.; Mohamed, N.N. Tensile Characteristics of Low Density Infill Patterns for Mass Reduction of 3D Printed Polylactic Parts. Int. J. Automot. Mech. Eng. 2020, 17, 7927–7934. [Google Scholar] [CrossRef]
- 123Design. Available online: https://autodesk-123d-design.en.lo4d.com/windows (accessed on 12 December 2020).
- van de Geer, S. Least squares estimation. In Encyclopedia of Statistics in Behavioural Science; Everitt, B.S., Howell, D.C., Eds.; John Wiley & Sons: Chichester, UK, 2005; Volume 2, pp. 1041–1045. [Google Scholar]
- Veselý, P.; Tichý, T.; Šefl, O.; Horynová, E. Evaluation of dielectric properties of 3D printed objects based on printing resolution. In Proceedings of the IOP 5th International Conference Recent Trends in Structural Materials, Pilsen, Czech Republic, 14–18 November 2018; Volume 461, p. 012091. [Google Scholar]


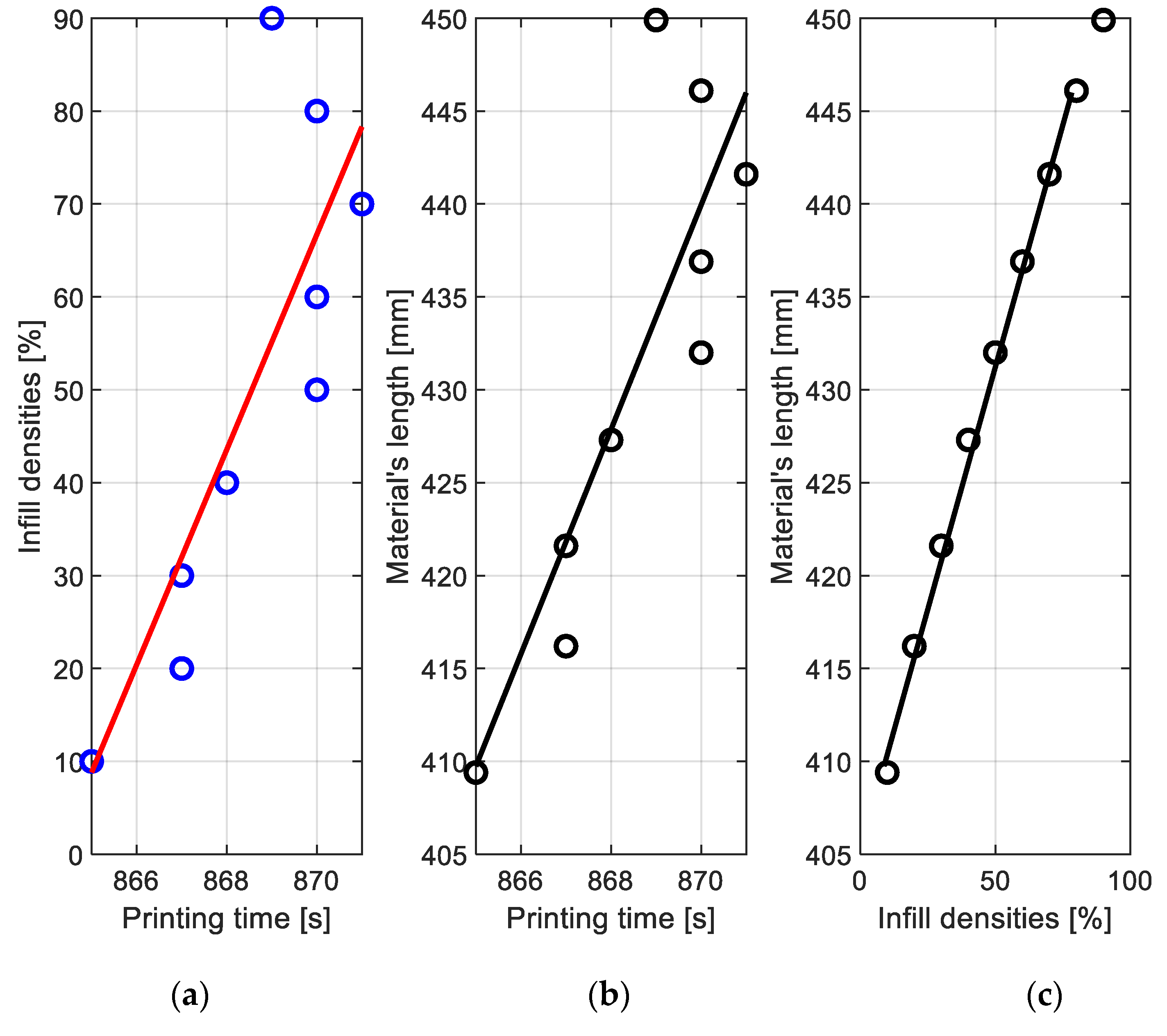
| Printing Time | Infill Density | Material’s Length | |
|---|---|---|---|
| Printing time | 1 | ||
| Infill density | 0.8219 | 1 | |
| The Material’s length | 0.8517 | 0.9975 | 1 |
| Source of Variation | F | p-Value | Fcrit |
|---|---|---|---|
| Between Groups | 26228.2 | 3.402826 |
| Regression Type | T | F | P | r2 | adj r2 |
|---|---|---|---|---|---|
| tp = f(ID) | 3.817 | 14.575 | 0.0065 | 0.6755 | 0.6292 |
| tp = f(Lm) | 4.3 | 18.496 | 0.003 | 0.7254 | 0.6862 |
| tp = f(ID, Lm) | N/A * | 21.907 ** | 0.00174 | 0.8795 | 0.8394 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vujović, I.; Šoda, J.; Kuzmanić, I.; Petković, M. Parameters Evaluation in 3D Spare Parts Printing. Electronics 2021, 10, 365. https://doi.org/10.3390/electronics10040365
Vujović I, Šoda J, Kuzmanić I, Petković M. Parameters Evaluation in 3D Spare Parts Printing. Electronics. 2021; 10(4):365. https://doi.org/10.3390/electronics10040365
Chicago/Turabian StyleVujović, Igor, Joško Šoda, Ivica Kuzmanić, and Miro Petković. 2021. "Parameters Evaluation in 3D Spare Parts Printing" Electronics 10, no. 4: 365. https://doi.org/10.3390/electronics10040365
APA StyleVujović, I., Šoda, J., Kuzmanić, I., & Petković, M. (2021). Parameters Evaluation in 3D Spare Parts Printing. Electronics, 10(4), 365. https://doi.org/10.3390/electronics10040365







