Modeling and Electrical Characterization of a Bilayer Pt/AlN/Sapphire One Port Resonator for Sensor Applications

Abstract

This paper presents a two-dimensional FEM (Finite Element Method) modeling and simulation of a surface acoustic wave (SAW) resonator based on a layered Pt/AlN/Sapphire structure. Such structure that exploits the electromechanical coupling of piezoelectric film is of high interest for harsh environments. By harsh environment we mean any environment that could hinder the operation of the device. Hardness can come from a variety of sources, and examples include the following: High pressure, High temperature, Shock/high vibration, Radiation, Harsh chemicals, etc. As part of this work, we are looking for high temperature sensor applications and only operating drifts due to temperature will be studied. SAW resonator is made from piezoelectric thin film Aluminum Nitride (AlN) layer on Sapphire substrate. Modal analysis is used to determine the eigen mode and the eigenfrequency of the system and the study of the frequency domain is used to determine the response of the model under influence of a harmonic excitation for one or more frequencies. In the FEM modeling, various parameters of the surface waves in the films, such as the surface velocity, the displacement of the piezoelectric thin film, the electrical potential, the electromechanical coefficient (k²), and the quality factor (Q) were studied. A comparative study between modeled and experimental curves showed a good agreement and allowed to validate our simulation method. Finally, a FEM study of the influence of normalized thickness of AlN thin film on resonator performances was carried out and compared with theorical results of literature.

1. Introduction

SAW (Surface Acoustic Wave) devices play a very important role in modern telecommunications [1]. Different types of SAW devices have been studied by researchers and are used in electronic equipment [2,3,4]. SAWs are widely used in the electronics industry, for the production of filters, delay lines and resonators operating at frequencies ranging from a few tens of Megahertz to a few Gigahertz [5,6,7]. SAW devices consist primarily of interdigital electroacoustic transducers (IDTs) fabricated on a piezoelectric substrate [7,8]. By using layered structures such as piezoelectric on insulator (POI), incredible high performance SAW devices are achievable leading to keep this technology as key components for new generations of cellular-phone such as 5G and future 6G. Furthermore, the sensitivity of SAW devices to physically end chemical properties of the environments make them very attractive for sensing applications.

The ZnO film structure is used to improve the sensitivity of bio-sensors [9] and AlN thin film is used for the high temperature sensor [10]. Further studies have shown that it is possible to produce SAW temperature sensors [11,12] and SAW magnetic sensors [2,13]. Besides being used in SAW devices associated with good piezoelectric coupling, AlN has high acoustic velocity and good thermal and chemical stability. It was also demonstrated that SAW-based AlN/Sapphire structure can operate under irradiation inside a nuclear reactor [14]. This AlN epitaxial layer is deposited by MOCVD technique on a c-axis sapphire substrate. The performance of AlN films for piezoelectric application in SAW electroacoustic devices is closely related to the microstructure and composition of thin films. Although AlN monocrystalline films are the ideal option for this application, it has been shown that preferentially oriented polycrystalline films can achieve adequate performance as well. Hence, AlN/Sapphire is a promising solution as a piezoelectric structure for high temperature SAW applications [10,11,12,13,14,15].

Modeling is of primary interest in many fields. It allows appropriate optimization of components or structures before the manufacturing steps. An effective device design process is a balanced combination of simulation and experimental work. SAW components can be modeled by different techniques [16,17,18,19,20]. However, these methods require considerable experience and strong background in the field, which makes them impractical for non-specialists. The Finite Element Method (FEM), which can be implemented through commercial software such as COMSOL Multiphysics, has proven to be excellent for the design, modeling, analysis, and optimization of SAW devices.

In recent work, there have been increased efforts to identify materials that are better able to propagate SAWs quickly and efficiently, with the goal of achieving higher frequencies and full compatibility with microelectromechanical systems (MEMS). Therefore, new applications for SAW sensors based on AlN piezoelectric thin film are being developed rapidly [21,22]. Assessments of SAW propagation properties, such as wave modes or the resonant frequency of the piezoelectric resonator, are needed to improve the design of SAW sensors [23,24].

In this work, we discuss the finite element method [24] modeling and simulation of a one-port Pt/AlN/Sapphire surface acoustic wave resonator. This modeling is carried out in two dimensions using COMSOL Multiphysics [25]. The geometry of structure, the mathematical model, and the properties of the materials are presented. Modal analysis is used to determine the Rayleigh waves velocity, the first mode of wave propagation, the amplitude of mechanical displacements, and the electric potential generated by the structure. In addition, the frequency analysis allowed us to plot the parameter S₁₁ to determine the resonance and antiresonance frequencies as well as the k² coefficient. The good agreement between the modeled and experimental curves allowed us to validate our modeling method. Additionally, using modeling we analyze the impact of AlN layer thickness on the performance of resonator. To this end, the electrical properties of SAW Pt/AlN/Sapphire resonators operating in the 2.42 GHz band are investigated as a function of the AlN thin film thickness in the range between 0.5 µm and 2 µm. The evolutions of the acoustic velocity, the quality factor, and the electromechanical coupling coefficient of SAW devices are presented and discussed as a function of the thickness of AlN thin film.

2. Mathematical Model, Device Geometry, and Materials Properties

2.1. Mathematical Model

The mathematical model that governs the propagation of SAWs is based on differential equations. These equations which must be solved taking into account geometric complexity of device, properties of materials, and boundary conditions. The details of this mathematical resolution method are given in our previous paper [26].

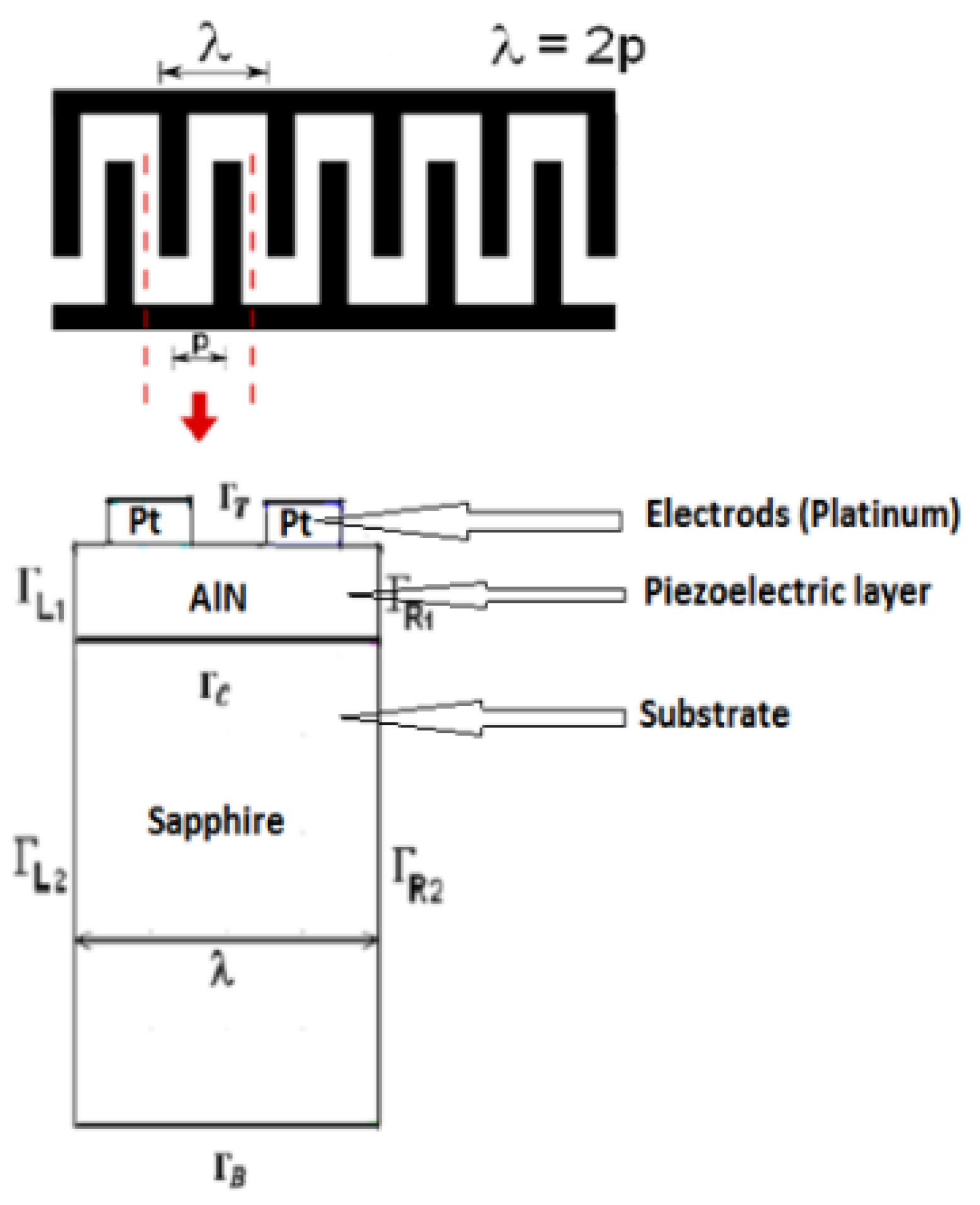
2.2. Device Geometry

In Theory, SAW resonators often consist of hundreds of electrodes. These electrodes can be 100-times longer than wide, which makes it possible to consider the resonator as an infinitely long periodic structure [27,28] and to neglect the edge effects. In this work, the SAW resonator considered in the experimental part consists of one synchronous one-port resonator consisting of one interdigital transducer (IDT) and two reflective gratings located on both sides at some distance (Bragg mirror configuration). The IDT contained 100 equal-interval-finger electrodes, and each reflector contained 400 short-circuited fingers. For modeling, the model geometry was simplified and reduced to one single cell, as shown in Figure 1. The periodicity of structure is advantageous for the numeric model because it makes it possible to reduce the calculation time of simulation. In addition, from a basic periodic cell, we can get all the essential information about the central frequency and the surface acoustic modes of resonator.

Surface acoustic waves propagate with most of the energy concentrated near the surface. Platinum IDTs (interdigitated transducers) are electrodes made on the thin film of the AlN piezoelectric substrate. As shown in Figure 1, elastic wavelength λ is fixed by the period of the interdigital transducer (IDT) λ = 2p, where p is the distance between successive electrodes. The associated frequency, f, of waves propagating with a speed v, is given by the relation f = v/λ. The symmetrical nature of our structure allows us to model the SAW resonator as a whole using a single period of the electrode. The SAW resonator may have hundreds of electrodes, and each electrode’s length can be far larger than its width. As the resonator can be considered as an infinitely long periodic structure [27,28], edge effects can be ignored and the model geometry can be reduced to one cell [29].

The main geometric characteristics of our device are as follows: Wavelength λ = 1.7 µm, platinum electrode thickness 90 nm, width of the platinum electrode, width of AlN c-axis layer 1 µm, tantalum adhesion layer of 10 nm and width of sapphire substrate c-axis 50 µm. As we do not include a wave absorber in the model, the waves can reflect off the underside. On the right and on the left, the structure is considered to be infinite due to the periodicity of the resonator.

2.3. Materials Properties

In total, three categories of material properties must be taken into account in the modeling of the SAW resonator: Mechanical, electrical, and piezoelectric properties. The mechanical properties must be defined for all the materials constituting the resonator (Platinum, AlN and Sapphire). The piezoelectric properties are defined only for the aluminum nitride layer. These properties are inserted in the simulator in form of matrix coefficients. Other properties must be taken, such as: density, Young’s modulus, Poisson’s ratio as well as mechanical, dielectric, and piezoelectric loss factors. The tables grouping all these parameters are given in our previous article [26]. Boundary conditions are also discussed in this article. COMSOL Multiphysics offers the possibility of creating a personalized mesh for each user. A preliminary mesh optimization study is necessary to find the best compromise between computation time and precision. Our model takes into account the existence of propagation losses in the resonator studied. For sapphire substrate and AlN thin film, we used a pre-validated set of physical constants [26].

3. Experimental Aspects

In order to carry out a comparative study between experimental measurements and simulation, we fabricated and experimentally measured our SAW Pt/AlN/Sapphire resonator [11]. The substrate consists of a 1 μm thick of AlN epitaxial layer deposited by MOCVD technique on a c-axis sapphire substrate. Above this AlN layer is deposited 10 nm thick of tantalum as an adhesion layer by the RF magnetron sputtering technique and again above 90 nm of platinum IDT. IDTs were fabricated with electron beam lithography and ion beam etching. To fabricate SAW resonator operating in 2.45 GHz ISM band, the spatial period of the IDTs was fixed to 1.7 μm. Electrical characterization of the resonator was performed by measuring S parameter using a vector network analyzer (Agilent PNA 5230A, Santa Clara, CA, USA) and an RF probe station (PM5 Suss Microtech, Garching, Germany) [26].

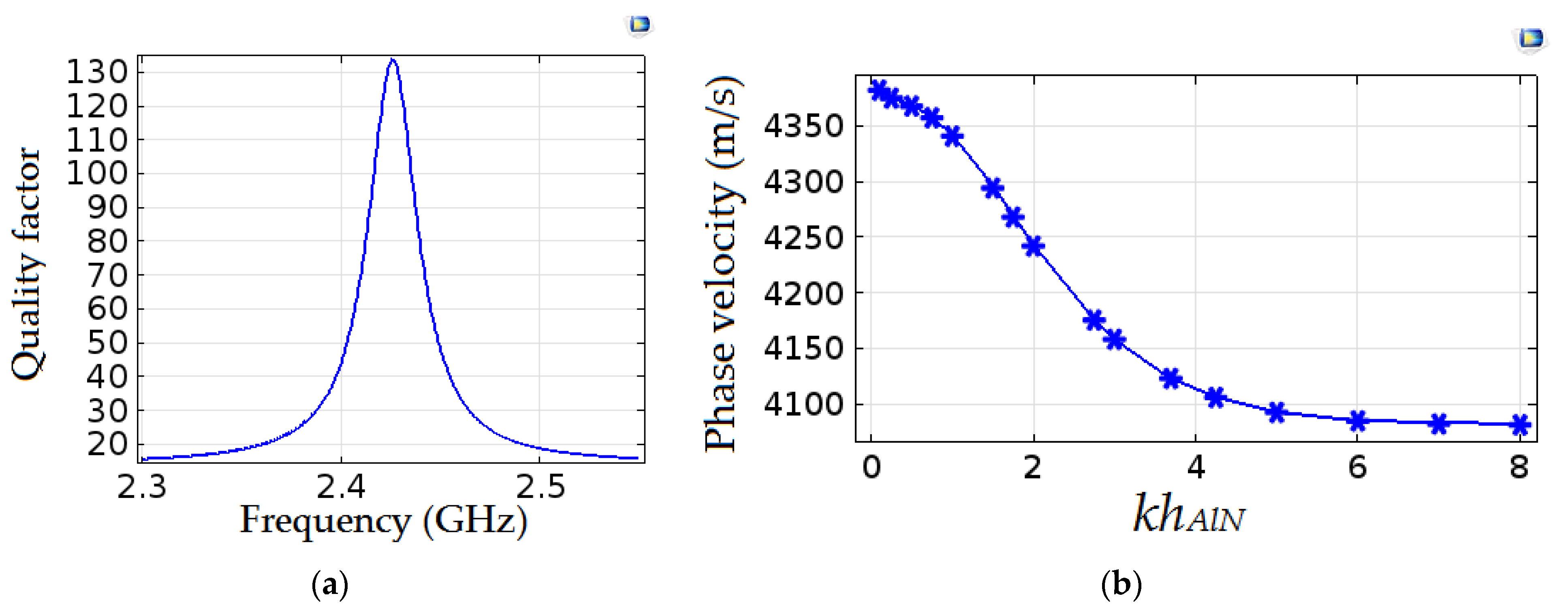
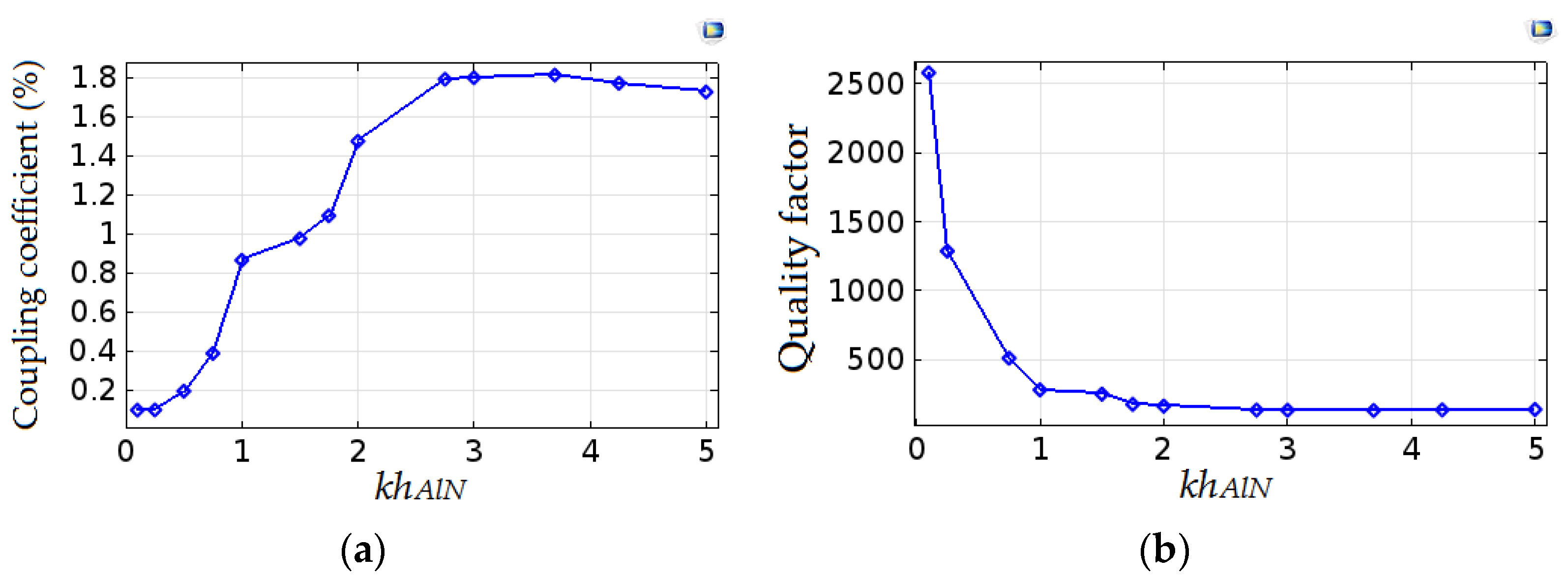
4. Results and Discussion

We have modeled in two dimensions a cell with a wavelength equal to λ [30] of our Pt/AlN/Sapphire one port resonator. This cell corresponding to a period of the infinite periodic structure. The modal analysis can be used to determine the natural frequency of the SAW resonator, this natural frequency being used subsequently in the frequency analysis. The boundary conditions must allow a periodic deformation of the model. These conditions are satisfied by coupling the individual degree of freedom on the left and right sides of the model. The bottom of the model is fixed and the top is free [25].

We limit our study on the propagation of Rayleigh waves in the sagittal plane (x1, x2) or (x; y). The study of frequencies is used to determine the eigen modes propagating in the structure, the eigenfrequencies of vibrations, and the electrical potential [25]. The surface wave is generated by the piezoelectric AlN thin film, and therefore, the thickness of the sapphire does not affect the Rayleigh wave characteristics. Figure 2a shows the field of mechanical deformations of the structure at 2.42568 GHz. We observe that the mechanical deformations are localized on the surface, inside the AlN layer with an amplitude of 1.363 nm. In addition, we note the asymmetry due to the difference in sign of alternative current.

The Rayleigh wave phase velocity is obtained by $v=\lambda f$. Phase velocity resulting from the simulation is 4122.84 m/s and experimentally is 4122.67 m/s. These two values are relatively equal, but are much lower than that of the literature (5700 m/s) [29] obtained for the same structure but for lower frequencies (i.e., acoustic wave propagation is more located in sapphire substrate). Furthermore, the waves undergo a slowdown due to the mass loading effect between AlN layer and the platinum IDTs [30,31]. Figure 2b shows the measured frequency responses of fabricated one-port SAW resonators. We can observe a clear resonance peak of SAW device. The resonance frequency is around 2.43 GHz. We note a good agreement between modeled and measured S₁₁ parameters.

The electric impedance Z is one of the parameters used to assess electrical response of SAWs. The evolution of its module versus frequency makes it possible to determine electrical resonance frequencies (minimum of curve) and antiresonance (maximum of curve). It can be defined as follows [30,31]: $Z=\frac{V}{jwq}$. Where V is electric potential, w angular frequency and $q$ electric charge. The values of resonance frequency (f_r) and antiresonance one (f_a) are 2.415 GHz and 2.4329 GHz, respectively.

Electromechanical coupling coefficient is determined from the following equation [17]:

$$k^2=\frac{\pi }{2}\left(\frac{f_r}{f_a}\right)tan\left[\frac{\pi }{2}\left(\frac{f_a-f_r}{f_a}\right)\right]$$

(1)

The value of electromechanical coupling coefficient of our modeled SAW resonator is approximately 1.80%. This result is in agreement with the measured value 1.85%.

Frequency spectrum of quality factor is determined from the following equation [32]:

$$Q=\left|\frac{Im\left(if\right)}{2Re\left(if\right)}\right|$$

(2)

Frequency spectrum of quality factor of Pt/AlN/Sapphire resonator is shown in Figure 3a. This figure represents evolution of the quality factor as a function of the frequency. The quality factor curve obtained shows a damped resonator. We obtain a quality factor at resonance frequency equal to 133.6 corresponding to the peak of the frequency spectrum of quality factor. This value is close to that of experimental measurement which is 132. Our model integrates various losses: mechanical, electrical, and dielectric. In practice, these losses are taken into account through the imaginary part of the materials matrix’s coefficients.

Due to specific properties of AlN layer, some parameters like phase velocity or electromechanical coupling are very sensitives to relative thickness of AlN. In order to study influence of AlN layer thickness on phase velocity, electromechanical coupling coefficient, and quality factor of Pt/AlN/Sapphire SAW resonator, we used FEM modeling. We can determine, from COMSOL, the variation of the propagation velocity v, k² coefficient and quality factor Q as a function of the normalized thickness kh (kh = 2πh/λ). Where h is the thickness of AlN layer and λ acoustic wavelength.

Simulation of Rayleigh wave velocity variation as a function of AlN layer thickness is shown in Figure 3b. We note that Rayleigh wave velocity decreases suddenly for layers of normalized thickness of AlN less than six which corresponds to an approximate thickness of 1.64 µm. This velocity becomes almost constant for thicknesses of AlN greater than six. Indeed, the acoustic wave propagation being fully in the AlN film.

The dispersion phenomenon which occurs for kh_AlN < 6 is specific to multilayer structures [33]: the aluminum nitride layer and sapphire substrate contribute to wave propagation. On the other hand, invariance of velocity when layer thickness is greater than 1.64 µm reflects that the wave remains confined in the AlN layer. These two phenomena are illustrated in Figure 4 for the cases kh = 3 and kh = 8, respectively.

The prepared SAW resonator is characterized in terms of the Q-factor and electromechanical coupling coefficients k² to evaluate the performance of the SAW device. The k² of resonator can be deducted from the Equation (2). Figure 5a shows evolution of electromechanical coupling coefficient as a function of normalized aluminum nitride thickness. We observe that this response as a similar than theory and experimental results [11].

Quality factor dispersion curve is shown in the Figure 5b. We can observe a quick reduction for quality factor when thickness of AlN layer increases up to kh_AlN = 2; then stabilizes for the values of kh between 2 and 5. The losses in our structure increase in the first region of thickness, stabilize in the second region, and decrease slightly in the last region.

The factor of merit that could be approximated by the product of Q and k² is plotted in Figure 6. This factor, which gives a precise indication of the re-radiated energy, makes it possible to evaluate the potential of using the resonator as a wireless sensor. A value greater than two is very promising [34,35]. In order to evaluate the potential of using the Pt/AlN/Sapphire structure as a wireless temperature sensor in a harsh environment, we have plotted the figure of merit versus the normalized thickness. One can observe that the lowest value of the figure of merit is obtained for kh_AlN = 3.7, which corresponds to a 1µm thick of AlN, i.e., the resonator manufactured and characterized experimentally. Thus, it is possible to improve the performance of the resonator. If we exclude the point corresponding to kh_AlN = 0.1, or (i.e., h_AlN = 27 nm) which is a low value to have a layer with good homogeneity and good piezoelectric characteristics, we notice that the optimum (Q.k²) is obtained for khAlN between 1 and 1.5. This corresponds to an AlN thickness between 270 nm and 400 nm. However, we can also observe that the factor of merit is almost constant and its value range from 2.42 and 2.47, which shows that this structure is not very dispersive and allows good tolerance on the thickness of the piezoelectric layer. New devices will therefore be produced to check this point experimentally.

5. Conclusions

SAW resonator Pt/AlN/Sapphire-based layered structure was investigated in this work by comparison between modeled and experimental results. The acoustic wave propagation in AlN/Sapphire structure was modeled and simulated by finite element method. In the modelling, FEM code COMSOL was used, where modal and transient analysis are performed. Modal analysis is used to determined eigenfrequency of the system and the frequency is used as input in transient analysis as frequency of excitation. First, we validated our simulation method by a comparative study between experimental and simulated results. In particular, we obtained a good agreement (modeled and measured) for S₁₁ and of the impedance Z modules curves. After which, we analyzed influence of AlN layer thickness on device performance through characteristic parameters: Rayleigh waves phase velocity, electromechanical coupling coefficient, and quality factor. The phase velocity of our device decreases from the initial value 4360 m/s to the final value 4085 m/s. The electromechanical coupling coefficient evolves according to theory and reaches the maximum value 1.55% for the normalized AlN thickness of 2.6. Quality factor rapidly decreases to the value 200 for normalized AlN thickeners inferior to 2.6. This work may assist us to optimize design, to fabricate future SAW resonators with high factor of merit Q.k² leading to enhance interrogation distance in the case of wireless SAW sensors.