Development and Realization of an Experimental Bench Test for Synchronized Small Angle Light Scattering and Biaxial Traction Analysis of Tissues

Abstract

Insights into the mechanical and microstructural status of biological soft tissues are fundamental in analyzing diseases. Biaxial traction is the gold standard approach for mechanical characterization. The state of the art methods for microstructural assessment have different advantages and drawbacks. Small angle light scattering (SALS) represents a valuable low energy technique for soft tissue assessment. The objective of the current work was to develop a bench test integrating mechanical and microstructural characterization capabilities for tissue specimens. The setup’s principle is based on the integration of biaxial traction and SALS analysis. A dedicated control application was developed with the objective of managing the test procedure. The different components of the setup are described and discussed, both in terms of hardware and software. The realization of the system and the corresponding performances are then presented.

1. Introduction

For biological tissues, biomechanics and microstructural analysis constitute a high interest research field. Their analysis provides meaningful information concerning the tissue status, including pathological conditions. Relevant examples of this principle are given by different tissue categories. The importance of microstructural features was, in fact, reported for arteries [1,2], heart valves [3], tendon filaments [4] and others. Tissue diseases are driven by the biological activity in response to both biomechanical and biochemical stimuli. The biomechanical degradation of the tissue is highly correlated with the microstructural components’ status: aneurysms are an example of pathologies caused by these alterations. The main components of biological tissues are given by fibers and extracellular matrix [5,6], which are the principal factors responsible for their macroscopic behavior. The strict connection between microstructural components and macrostructural mechanics holds for a wide number of biological actors [7]. To understand the mechanical effects in the pathological tissue, several mechanical characterization studies have been reported in the literature. The most used mechanical tests are based on bulge inflation [8] and on uniaxial traction tests [9,10,11]. Despite their diffusion, these tests present limitations and drawbacks because of the anisotropic behavior of soft biological tissue. Testing the tissue along a single direction provides a too narrow an analysis for the assessment of the tissue status [12,13]. Biaxial traction bench tests provide a more complete approach [14] via the analysis of different stress configurations of the tissue [15,16]. The corresponding experimental data allow the fitting of a model through anisotropic constitutive equations. The current state of the art biomechanical models [17,18] account for material anisotropy and require biaxial data for a correct fitting. Another advantage is the possibility to model the incompressible behavior of soft tissue [19,20].

Different experimental setups were developed in the state of the art for microstructural analysis as well. Examples of these techniques are given by second harmonic generation (SHG) [21], the small angle X-ray scattering (SAXS) [22,23] and other microscopy approaches [24,25]. All these methods produce quantitative data in a layer-by-layer fashion. That represents a great advantage in this context. Nevertheless, microscopy approaches, such as SHG, often require highly specific and dedicated hardware. In cases like SAXS, the energies involved for the characterization of the tissue are high and potentially harmful to handle. An interesting alternative is given by the small angle light scattering (SALS). SALS is an established optical and non-destructive technique providing semi-quantitative microstructural information about fiber-based structures, including biological tissues [26]. The principle behind the SALS setup is light irradiation of tissues at low energy and acquisition of the corresponding scattered light patterns. The resulting light spot contains information concerning the presence and orientation of embedded fibrous structures. The scattering occurs according to the physical principle of multiple scattering through a dense connective matrix [27,28]. The advantage of the SALS setup is the low energy involved and the requirement for relatively compact hardware to be realized. These features solve the drawbacks of the SHG and SAXS techniques.

The aim of this work is to provide a new contribution in the landscape of tissue characterization. The objective was to realize a novel bench test (OptiMech2) through the integration of a biaxial traction and a SALS setup with a dedicated application to test biological specimens. In the first section of the manuscript we recall the necessary theoretical background about the mechanical testing of soft tissues. We then describe the electronic and mechanical components and the developed software. A preliminary biaxial traction test case is presented. At last, the setup’s realization and relative performances are discussed.

2. Mechanical Theory Background

Soft biological tissues present a strongly anisotropic nature [29]. The collagen fiber distributions, orientations and interconnections are at the basis of anisotropy. This microstructural behavior produces a mechanical response dependent on the direction of the test. Beyond anisotropy, another important feature to be reported is the nonlinear mechanical behavior (hyperelasticity). The constraint of mechanical incompressibility is usually imposed as well, given the high water content of soft tissues [30]. The internal constitution of a material defines the material’s response to applied loads. Consequently, the definition of the strain energy density function W is sufficient to obtain a complete description of the material’s stress state [31]. Starting from the theory of continuum, the basic relationship is the following:

$$\sigma =\frac{1}{J}\mathbf{F}·\left(2\frac{\delta W\left(\mathbf{C}\right)}{\delta \mathbf{C}}-p{\mathbf{C}}^{-\mathbf{1}}\right)·{\mathbf{F}}^{\mathbf{T}}$$

(1)

where $\sigma$ is the Cauchy stress tensor, J is the volumetric Jacobian, F is the deformation gradient, C is the right Cauchy–Green deformation tensor and p is a Lagrangian constant accounting for incompressibility. The $\sigma$ is a second-order tensor completely defining the tension state of the material [32]. State of the art formulations for the strain-energy density function consider both the hyperelasticity and anisotropy of the soft tissue [33]. The expression for W depends on both the deformation state of and the mechanical parameters of the tissue, usually linked with directional stiffness. A state of the art model is given by the fiber-based strain energy function expressed by [17], in which two main fiber families with dispersion are assumed:

$$W=\frac{c}{2}({\mathbf{I}}_{\mathbf{1}}-3)+\frac{k_1}{2k_2}\sum _{i=4,6}[e^{\left(k_2^i{({\mathbf{I}}_{\mathbf{i}}^{*}(\varphi ,k_{ip},k_{op})-1)}^2\right)}-1]$$

(2)

where c, $k_1$ and $k_2$ are the model mechanical parameters representing the cellular matrix stiffness, the fiber stiffness and the stiffening factor, respectively. The I₁ is the first right Cauchy–Green strain tensor invariant and I${}_i^{*}$ is the pseudo-invariant of the i-th fiber family, depending on the fiber angle $\varphi$ and dispersion parameters $k_{ip}$ and $k_{op}$.

Since a uniaxial test procedure could carry stiffness estimation errors, the biaxial procedure is the preferred tool for testing anisotropic and hyperelastic materials [34,35]. The planar biaxial tension state of an incompressible square flat specimen can be assumed as a satisfactory approximation of in vivo loading conditions [19]. As a consequence, the only non-zero components of the stress tensor are given by ${\sigma }_{xx}$ and ${\sigma }_{yy}$, where x and y are the biaxial testing directions. The Cauchy stress values can be evaluated as:

$${\sigma }_{ii}=(F_{ii}/A_0){\lambda }_{ii}$$

(3)

where i represents one of the two testing directions ($x,y$), $F_{ii}$ represents the tensioning force, $A_0$ represents the unloaded specimen cross-section and ${\lambda }_{ii}$ represents the corresponding stretch. According to Equation (3), under the assumption of planar biaxial status of the tissue it is hence sufficient to record the tensioning forces and stretches to obtain the Cauchy stresses.

3. Design and Materials

In this section, the components of the setup will be presented, including the technical specifications to be achieved, the selected hardware and the implemented applications. At last, the test case procedure is described.

3.1. Technical Specifications

The technical specifications for the experimental OptiMech2 setup design were determined first. The main features required for the system are the following:

• A hardware setup allowing for soft tissue biaxial tensioning, with a software algorithm to control the tension status of the specimen. The possibility to impose different tension ratios has to be included, with a mechanical force accuracy of at least 0.1 N.
• A contactless system for the deformation recording allowing for biaxial stretches registration, with an accuracy of 0.1%.
• A laser system allowing for SALS irradiation of soft tissues and a corresponding actuation system for local evaluation of fiber distribution along a prescribed pattern.
• An optical system to record the SALS spots and an algorithm to extract significant SALS parameters has to be included.

The performances of the OptiMech2 system were compared with an actual biaxial commercial system (Instron-Sacks biaxial testing system—Instron®, Inc., Canton, MA, USA). The commercial system’s specifications were taken from literature [36].

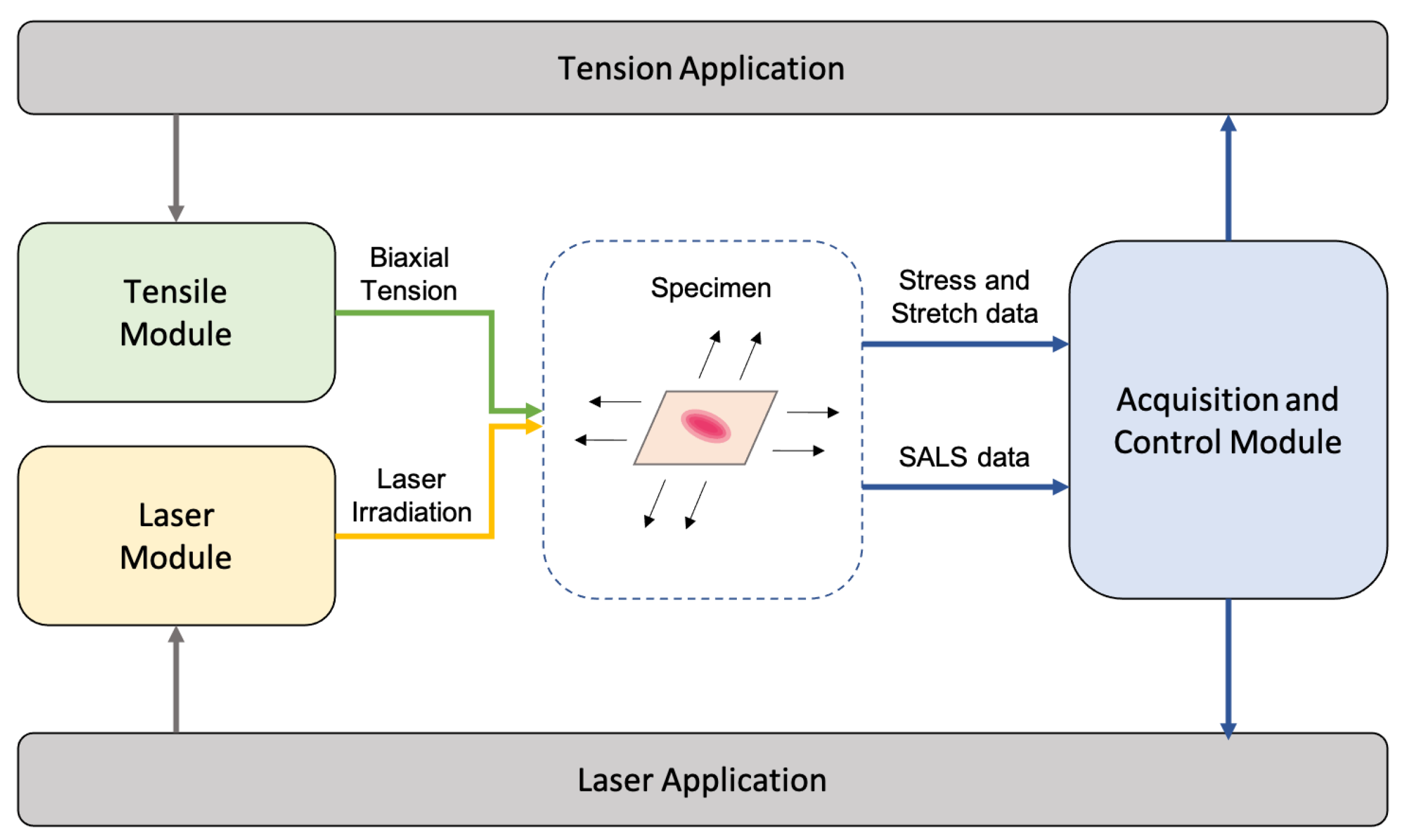
3.2. Modules and Applications

After assessing the specifications, the different OptiMech2 hardware modules were identified. A dedicated module for each role was designed.

• Tensile module (TM)—for the mechanical actuation and tensioning of the specimen.
• Laser module (LM)—for the irradiation of the specimen during the tensioning.
• Acquisition/control module (ACM)—for signal registration and hardware control during the test procedure.

Additionally, two dedicated software applications were provided for the test bench control. The applications’ main functions are the tensioning control, the irradiation control and the graphical user interfaces (GUIs).

• Tension application (TA)—for the control of TM hardware, tension/deformation signal acquisition and mechanical results’ visualization;
• Laser application (LA)—for the control of LM hardware, laser pattern acquisition/ processing and fiber distribution results visualization.

In Figure 1, the OptiMech2 system and the corresponding modules and applications are summarized.

First, the hardware components for the TM, LM and ACM are described. A subsection is then dedicated to the description of the control applications.

3.3. Tensile Module

The TM was designed to impose a planar mechanical static stimulus on the tissue specimen along two main perpendicular directions. Its main functions are (i) specimen holding, (ii) tensioning and (iii) force recording. A schematic of the TM with its hardware components and its connections with the other modules and applications are reported in Figure 2.

The specimen holding was granted by two pneumatic grippers (Schunk®) for each axis. Compressed air was supplied to the grippers to permit their opening/closure with three-way manual valves (Festo®). The pressure from the air supply was provided by a controlled compressor. A dedicated proportional valve allowed for gripping force regulation. The regulation was required to avoid tissue damage caused by the gripping. Specific arms and gripper fingers were designed and realized through additive manufacturing to permit the correct positioning and holding of the specimen. The fingers were customized to allow the traction of square tissue specimens with a minimum size of 25 mm. The usage of these custom fingers allowed the avoidance of hooks to prevent tissue damaging. Sand paper was fixed on the finger surface to improve the holding of the specimens.

The specimen actuation was granted by four brushless servomotors (Kollmorgen®). Each motor was coupled with a linear recirculating ball bearing guide (Festo®). Each couple of actuators is responsible for the movement along a single direction axis. For each motor, an electronic servo-drive (Kollmorgen®) was adopted for correct current supply and control. To grant movement safety, two electromagnetic limit switches were included on each mechanical drive. The switches were mounted to provide both forward and backward movement thresholds on each axis. The servo-drives were connected in daisy-chain and the communication was granted by the EtherCAT industrial protocol. The EtherCAT master was given by a real-time processor on the ACM side (Figure 2a). The actuation system was designed in order to permit a movement accuracy of 0.1 mm.

A strain-gauge load cell (HBM®) with a 50 N full scale was included on each axis for force recording. Each cell was directly connected as input to the ACM hardware for signal acquisition (Figure 2a). The force measurement accuracy was granted to be below 0.02 N.

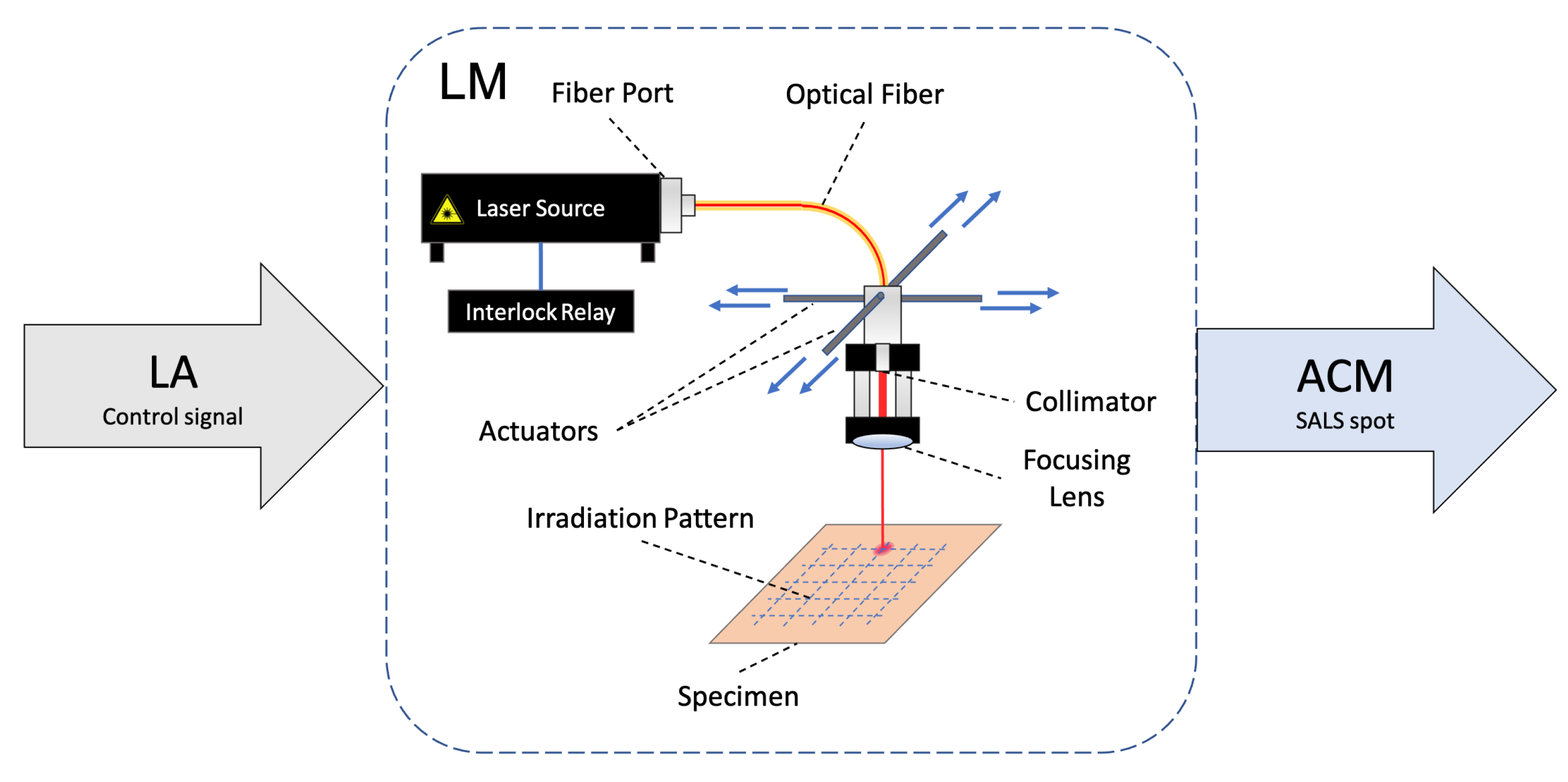
3.4. Laser Module

The LM was designed to permit the laser operation safety and the correct irradiation of the specimen. Its main functions are (i) the light transmission from the source and (ii) the SALS irradiation pattern imposition. A schematic of the LM with its hardware components and its connections with the other modules and applications are reported in Figure 3.

The energy source was provided by a low-power He–Ne laser (Thorlabs®) with a wavelength of 680 nm. The wavelength grants the detection of collagen fiber within biological tissues [37]. The laser source safety was controlled with a relay circuit for light safety locking. The lock signal was provided by an analog output hardware from the LA software side. The light was transmitted with a multi-modal optical fiber with an embedded collimator (Thorlabs®). An adjustable port device was used to connect the optical fiber to the laser source output. The fiber was chosen to grant the system compactness. The beam exiting from the collimator was then focalized by adding a double-focal lens (Thorlabs®) with a focusing depth of 150 mm. For the sake of compactness, collimator and focusing lens were kept coaxial through a cage structure. The lens was positioned to project a spot with an size of about 100 μm on the specimen plane. The SALS spot resulting from the specimen irradiation procedure was recorded by the ACM hardware.

A system for spatial irradiation control was then provided. Hardware components were included to control the irradiation of the specimen according to a predefined grid pattern. To achieve this, two actuators were added to move the collimator–lens assembly. Two servomotor linear actuators with high spatial resolution (minimum spatial increment of 0.05 μm) and with dedicated servo-controllers (Thorlabs®) were provided. The adoption of two axes permitted us to cover all the possible positions on the specimen plane. A grid pattern of 5 × 5 irradiation points was considered. The initial pattern was characterized by a size of 10 mm, and its shape was updated according to the recorded deformation of the specimen, as described in the LA section. The communication for the servomotor’s control was obtained through a USB 3.0 protocol.

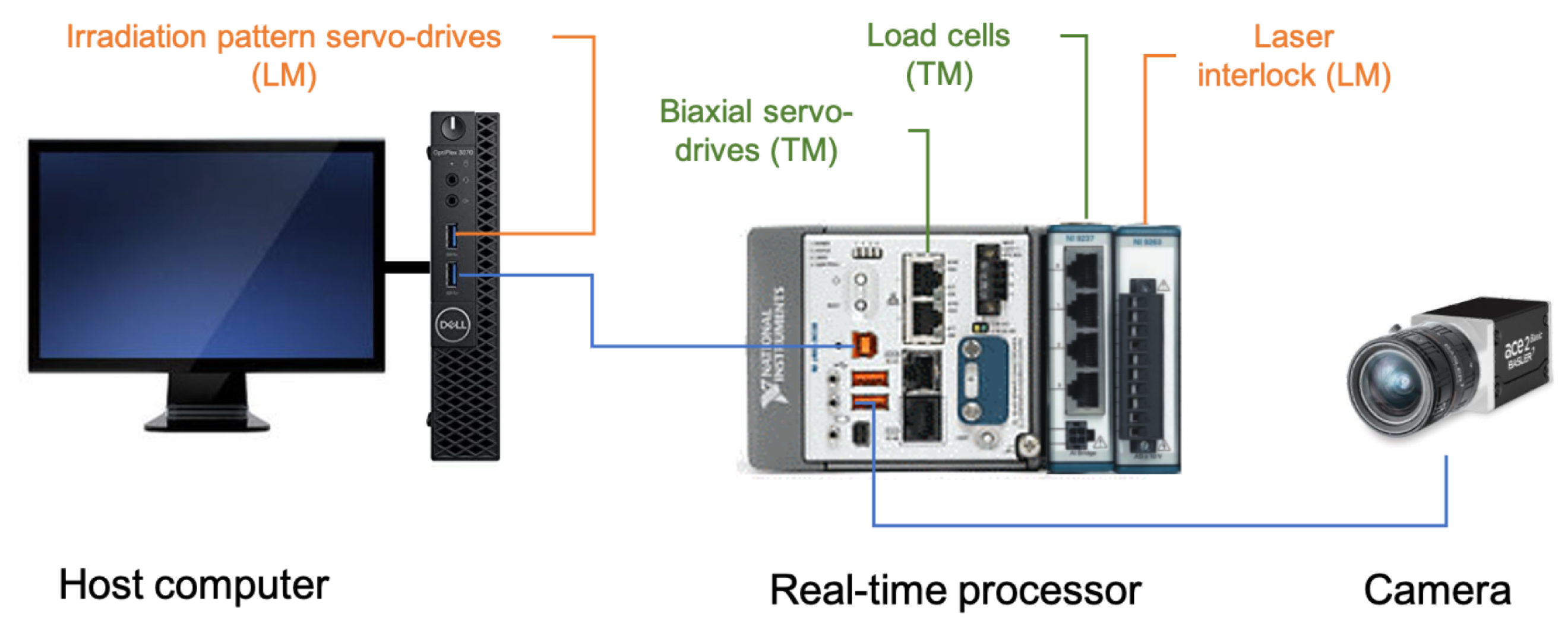
3.5. Acquisition/Control Module

The ACM section was designed to manage the signals resulting from the specimen testing and to impose the correct optical/mechanical stimuli according to the software applications. Its main components are (i) a camera, (ii) a real-time processor and (iii) a host computer. A schematic of the ACM setup is summarized in Figure 4.

The camera (Basler®) is characterized by a resolution of 9 MP and a frame rate of 10 fps. The camera was included in the test bench to allow for the SALS spot collection and deformation registration. A macro optic with a focal length of 35 mm (Ricoh®) was adopted to permit focusing on the specimen’s surface. An annular light was included to grant the specimen illumination during the test. A set of four calibrated markers with a diameter of 1 mm was placed directly on the specimen according to a square pattern of 10 mm side for deformation registration through the camera.

The real-time processor (National Instruments®) was included to control the operations on both TM and LM sides. The processor was characterized by a quad core CPU @ 1.6 GHz and by eight flexible slots for signal input/output modules. A strain-gauge input module (NI 9237) for the registration of the TM load cells and an analog output module (NI 9263) for the LM interlock control were included. The processor communicated with the camera according to a GigE protocol and served as the EtherCAT master for the TM servomotors control.

The host computer (Dell®) was included for user interfacing and data post-processing. The host GUI was designed to post-process the different data from the bench test, and to control the laser irradiation pattern and the tension set-points. The computer hardware communicates with the real-time processor and the servo-drives for LM irradiation pattern via USB 3.0 protocol.

3.6. Tension Application

The TA software was implemented to be deployed on both the real-time processor and the host computer. The biaxial tensioning control was managed within the real-time processor, while user data input and the presentation/post-processing of mechanical were managed within the host computer. The communication between the computer and the processor was imposed with a system of network-shared variables. Axis position control was allowed before proceeding with the biaxial tension test. For that purpose, a jog interface to move the four mechanical guides independently was programmed. The jog control was implemented to permit the positioning of the specimen prior to testing. The tension control protocol for a single axis of the biaxial system is summarized in Figure 5a. An array of set-points from the host is passed to the real-time section at the beginning of the test. The algorithm was designed to impose different tension ratios between the two axis by imposing an editable weighting of the set-points. The load cell reading is first low-pass filtered according to an averaging process of 20 samples. The data are then compared with the reference value given by the current set-point to compute the error. The error is then fed to a PID controller to adjust the corresponding axis position. The proportional and integral constants of the PID are assigned according to specimen’s estimated stiffness. The set-point conditions are assumed to be met as long as the error is contained within the force measurement accuracy. Once the set-point is reached, the stress and stretches are registered as output. The tension is maintained until the subsequent irradiation procedure executed by the LA is completed. At this point, the tension protocol proceeds with a new set-point from the user defined array.

The deformation registration algorithm was implemented as well. The image signal from the camera is transmitted from the real-time processor to the host for post-processing. The image processing is summarized in Figure 5b. Four ROIs are defined on the basis of marker initial positions. During the tensioning, the positions are updated according to the detected marker centroid. The marker detection is obtained by implementing a local ROI segmentation and a size/shape filtering based on the expected area/circularity. The positions of the markers are then used to evaluate the biaxial stretches as:

$$\begin{array}{c}\hfill {\lambda }_{xx}=\frac{1}{2}\left(\frac{(x_1-x_2)}{L_x^0}+\frac{(x_3-x_4)}{L_x^0}\right)\end{array}$$

(4)

$$\begin{array}{c}\hfill {\lambda }_{yy}=\frac{1}{2}\left(\frac{(y_1-y_2)}{L_y^0}+\frac{(y_3-y_4)}{L_y^0}\right)\end{array}$$

(5)

where $i=1,2,3,4$ are the marker indexes (Figure 5b), $x_i$/$y_i$ are the marker centroid coordinates, $L_x^0$/$L_y^0$ are the initial distances between markers along the two directions and ${\lambda }_{xx}$/${\lambda }_{yy}$ are the resulting stretches.

3.7. Laser Application

The LA software was designed to be deployed on both the real-time processor and the host computer. The main function implemented for the processor is the control for the safety interlock relay. The movement control for the irradiation pattern definition and for the laser locking/unlocking were implemented for the host. The application was designed to pilot the lock/unlock status of the laser with a switch in the host side interface. The switch lock command is passed to the real-time target and the corresponding analog signal is transmitted to the relay. The laser locking is also granted during the execution of the tensioning.

The protocol implemented for the servo-drive piloting is summarized in Figure 5c. Like the TA, a jog interface was provided to manually set the position on the axes. Before the test, the laser head is homed automatically according to the position of the optical markers on the unloaded specimen. The LA process is started by reaching the tension set-point. Subsequently, the pattern is defined by imposing a spatial transformation of the initial 10 mm side pattern, according to the ${\lambda }_{xx}$/${\lambda }_{yy}$ stretches from the TA algorithm. The laser head is then moved according to the updated pattern. The pattern is covered according to a “snake-like” approach (Figure 5c). For each point, the camera acquires a single shot image of the corresponding SALS spot. The image is then associated with the given position on the specimen surface and post-processed. The image processing algorithm extracts the tissue preferential fiber direction according to the SALS theory, based on the spot elliptical shape [26]. To achieve this, a custom ROI is automatically defined on the basis of the SALS spot size. The spot is segmented and the corresponding contour is extracted and under sampled. The point samples of the contour are used to fit an elliptical model, according to the Least Square minimization of the following score:

$${\displaystyle J(A,B,C,D)=\sum _{i=1}^N{(A{x}_i^2+B{x}_i{y}_i+C{y}_i^2+D)}^2}$$

(6)

where $A,B,C$ and D are the ellipse Cartesian coefficients and $(x_i,y_i)$ are the N samples from the segmented contour. For each ellipses, the eccentricity (E) and inclination angle of the main axis ($\varphi$) are calculated according to:

$$\begin{array}{}\mathrm{(7)}& E=\sqrt{1-{(b/a)}^2}\mathrm{(8)}& \varphi =atan\left(\frac{1}{B}(C-A-\sqrt{{(A-C)}^2+B^2)}\right)\end{array}$$

where b and a are the ellipses minor and major axes. For each point, the E and $\varphi$ parameters are stored as SALS outputs. Both the local fiber distribution on the specimen under tension and the average trend are reported in the user interface. The process is repeated for each point in the pattern gird. At the end of the procedure, the laser head is homed, the tension set-point is updated and the process restarts from the TA algorithm.

3.8. Test Case

To validate the setup design, a test case procedure was imposed. A porcine aortic tissue specimen was tested with the OptiMech2 setup for a complete biaxial tensioning. The specimen under analysis was retrieved from a local slaughterhouse. A square shape of about 30 × 30 mm was cut in the outer curvature of the ascending aortic section. Before testing, the tissue was maintained at room temperature in saline solution. We avoided freezing the sample in order to prevent microstructural disruptions. The OptiMech2 testing procedure was carried out about 3 h after the harvesting to prevent any tissue degradation.

A total of five biaxial tension ratios were imposed on the specimen: 1:1, 0.5:1, 0.75:1, 1:0.5, 1:0.75. The maximum tension imposed was set to 147 N/m with a tension set-point increase of 3.3 N/m. For each test, the resulting stress and stretches were reported along the two tension directions identified as circumferential ($\theta \theta$) and longitudinal ($zz$). Additionally, the eccentricity variation and fiber preferential angle average trend were reported.

4. Results

4.1. Realization

The OptiMech2 setup complete assembly is reported in Figure 6. The realized GUIs for TA and LA are represented in Figure 7 and Figure 8.

In Figure 7 the implementation of the jog interface for the biaxial axis positioning, the automatic marker segmentation for deformation recording, the tension control algorithm and data registration are shown. An example of mechanical data registration in terms of stress–stretch curves is reported in Figure 7c. Figure 8 displays the different components of the LA side interface. The implementation of the jog for the laser head movement, the interface for the SALS pattern monitoring and the output visualization are reported. Figure 8b reveals the implementation of SALS spot elliptical fitting, with highlights on the major and minor axes. In Figure 8c, an example of the distribution of fiber orientation at a given tension set-point and the E and $\varphi$ average trend are shown.

The comparison of performances between the OptiMech2 and the commercial system from literature is reported in

Table 1. Table for the comparison of OptiMech2 system specifics with a commercial device [36].

Specifics	OptiMech2 System	Biaxial Commercial System
Maximum displacement	100 mm	110 mm
Maximum load	50 N	±5 N
Force accuracy measurement	0.2%	0.5%
Specimen gripping approach	Clamps with tunable pressure	Clamps
Displacement recording approach	Optical markers	Optical markers

.

4.2. Test Case

The test case was carried out with success. The feasibility of the microstructural characterization with our OptiMech2 setup was confirmed. The test case procedure results are reported in Figure 9 and Figure 10. The data are presented both in terms of mechanical and microstructural data. The material anisotropy was confirmed by the experimental data. Moreover the data show a strong correlation between the tensional state and the microstructural parameters.

5. Discussion

This study proposed a novel test bench to simultaneously characterize mechanical and microstructural properties of soft biological tissue. The preliminary tests performed on a biological specimen confirmed the material anisotropy (Figure 9) and stress with eccentricity and angle variations as functions of the different tensioning (Figure 10).

The consequences of microstructural modifications on the material mechanics are often times underlined in different works [38,39]. For example, Robitaille et al. adopted the SALS technique for microstructural characterization of cornea tissues under mechanical strain [40]. In their work the eccentricity of the spot was correlated with induced strain, nevertheless the interest was limited to uniaxial traction. Another recent example is provided by the work of Whelan et al. [41]. In this study, heart valve specimens were tensioned and inspected with SALS irradiation. The local fiber distribution was evaluated by developing an irradiation grid pattern revealing a high dispersion arrangement. The approach presented the uniaxial approach limitation as well. The OptiMech2 approach overcomes this drawback by introducing a biaxial controlled tension protocol. The interest in this combined approach is demonstrated by additional recent studies. Shiwarski and colleagues [42] proposed a 3D printed biaxial setup compatible with fluorescence microscopy. Nevertheless, pure displacement control was imposed and the full biaxial tensioning on the specimen was not controlled. OptiMech2 works under force control with different set-points, allowing different biaxial ratios. According to literature, in fact, this approach represents an established gold standard for biomechanical characterization of tissues [43,44,45]. The adoption of optical markers for the deformation registration is a contact-less approach, and it is fundamental to avoid the effect of any potential tissue slippage. It is well know that the clamping methods plays a significant role on the final testing results [46,47]. For this reason, custom gripper fingers design were used to control and adjust the compressive force in a non-destructive manner. As reported in Table 1, the performances of the OptiMech2 were demonstrated to be comparable to the ones taken from an actual commercial system [36] in terms of maximum displacement and load and force accuracy measurements. In addition, the reported system presents the advantage of high customizability and of integration with a SALS system.

Even if the presented technique was designed for mechano-biological analysis for soft biological tissues, its customizability allows the usage in other biomedical fields, such as vascular grafts and cardiovascular valves prostheses [48,49]. The results derived from this approach will permit to quantify and interpret the effect of fiber distribution for mechanical constitutive modeling [43]. According to the publication of the ASME V&V 40-2018 technical standard “Assessing Credibility of Computational Modeling through Verification and Validation: Application to Medical Devices” (www.asme.org/codes-standards/find-codes-standards/v-v-40-assessing-credibility-computational-modeling-verification-validation-application-medical-devices), the conjunction of uncertainties with experimental results provides insights concerning the adjustments in the model to potentially improve agreement between simulation and experiment [50]. With this in mind, the uncertainty metric will be essential to assessing the credibility of higher risk models [51,52].

Further work may include integration of deformation control protocols using marker positions. Such features will be particularly important for correlations of fiber orientation in the soft tissue during the tests. Digital image correlation algorithms represent potential add-ons for the OptiMech2 setup to improve deformation investigations. An additional point of interest would be to modify the gripping approach and the load cell system to allow smaller specimen testing. In the current state, the minimum specimen side is limited to 25 mm and the minimum load to 0.1 N. The current features do not allow cellular scale testing, which represents a well established research field [53,54]. By adopting load cells with lower scale and modified gripper fingers, it would be possible to reach smaller scales of specimen testing.

6. Conclusions

The importance of the microstructure and mechanics of soft tissues is a research topic of great interest nowadays. Their correlation plays a key role within this context, and new investigation methods are currently under development. An experimental setup design for this purpose was proposed within this paper. The OptiMech2 system provides a test bench for simultaneous microstructural and mechanical investigations of soft tissues. In particular, the biaxial tensioning process is synchronized with SALS local irradiation. The different hardware components and software applications involved for the system realization were discussed and the resulting specifications were satisfactory. The OptiMech2 design provides a new setup for mechanical and microstructural characterization.