1. Introduction
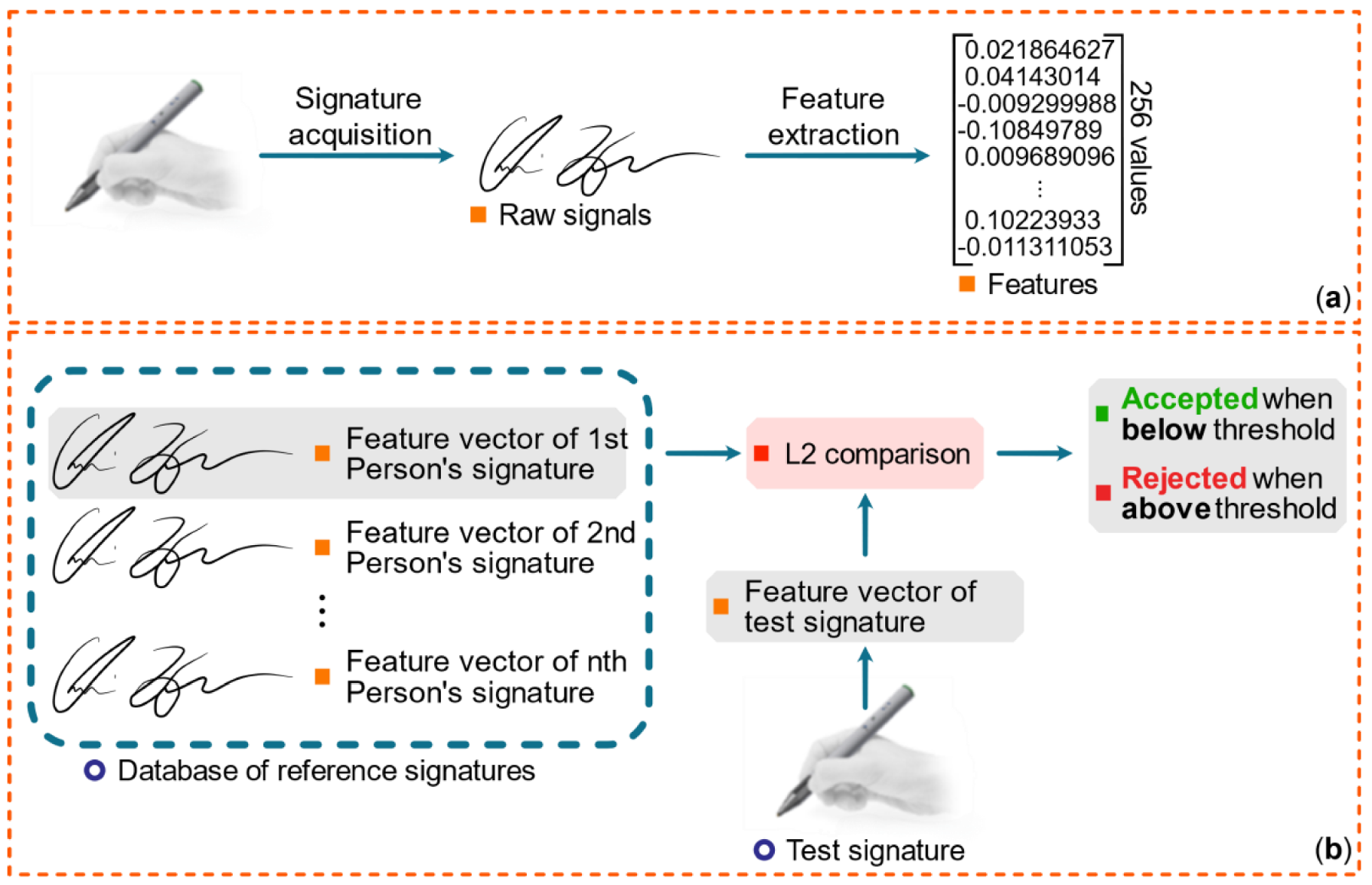
The development of biometric verification methods is one of the significant trends in current scientific research. Meanwhile, currently used methods of biometry are known for many problems that limit the scope of their application. Consequently, numerous research teams around the world are looking for new or improved approaches to the acquisition, processing, interpretation, and protection of biometrical data. Similar projects are also carried out at the Gdansk University of Technology in cooperation with the largest Polish bank, particularly those that assume a multimodal approach to biometric authentication. A simplified flowchart of the system visible in
Figure 1 shows how each signature is converted from raw signals to a high-dimensional feature representation and how the verification process is organized.
As opposed to the static ones, the handwritten signature’s dynamic parameters describe the process of creating the signature, which enables its fuller and more stable representation. The group of dynamic parameters includes the duration of creating a signature, the pen pressure on the surface, the tilt of the pen, and others. These parameters are variable during the signature creation, making it possible to extract the individual features. Thanks to the continuous recording of the signature’s parameters, it is much less likely to impersonate another person than using the static (graphical) signature representation. The dynamic signature can serve as a biometric modality that uses the writer for recognition purposes—their individual anatomical and behavioral characteristics. Dynamic signature devices should not be confused with electronic signature capture systems used to capture the signature’s graphic image, which is common in locations where merchants are capturing signatures for transaction authorizations.
The primary task is to develop efficient algorithms and identity verification methods based on dynamic analysis of electronically handwritten signatures. In the course of the work, methods of acquiring individual characteristics of signatures were developed and tested for their suitability in the verification process. First, the signatures were obtained using the device designed at the Gdańsk University of Technology (GUT), namely the experimental electronic pen. A large-scale biometric experiment was organized in a major Polish bank using an earlier pen prototype [
1,
2]. Still, so far, no neural networks have been researched in this context (the scope of hitherto experiments conducted by GUT was limited to overall signature verification using the Dynamic Time Warping algorithm [
3,
4]). Meanwhile, as it has been known for a long time, neural network methods can help in the detection of many unique characteristics of the signature author, which in turn, is an additional confirmation of identity [
5,
6,
7].
It is worth adding that forensic science experts commonly use the grapho-analytic analysis (different from “graphological”). Still, its principles have not yet been reflected adequately in the algorithmic analysis of signatures created with digital styluses or machine learning methods. The handwritten signature still remains a legally required confirmation of many types of contracts and transactions. Meanwhile, dynamic signature recognition research does not focus on static or geometric characteristics (i.e., how the signature looks like), but the interest is in dynamic features (how the signature was created). Dynamic signatures use multiple attributes in the analysis of an individual’s handwriting. Most of them are active rather than static or geometric, although the latter representations can also be included in the study. Principles of analysis of handwritten signatures by human investigators are standardized in the field of grapho-analytics and forensics. They depend on handwritten text features as slant, commencement and terminating strokes, size or style of words, spacing, pressure, frequency of words, letter proportions, and many others [
8]. It is also important to note that in the field of forensics, what separates an untrained person from a skilled investigator is the rate of false positives and the number of cases for which only an inconclusive opinion about the authors’ identity may be expressed [
9]. Many systems help to analyze a handwritten text [
10,
11,
12,
13,
14], which utilizes such experts’ features. There are also methods, based on signature analysis, that help diagnose a variety of illnesses, such as Parkinson’s and Alzheimer’s disease [
15,
16,
17,
18]. However, the last-mentioned topics are beyond the scope of this paper.
Meanwhile, common dynamic characteristics include velocity, acceleration, timing, pressure, and direction of the signature strokes. Some dynamic signature recognition algorithms incorporate learning functions to account for natural changes or drifts that occur in an individual’s signature over time [
19]. The characteristics used for dynamic signature recognition are almost impossible to replicate. Unlike a graphical image of the signature, which can be reproduced by a trained human forger, a computer manipulation, or a photocopy, dynamic characteristics are complicated, so they are unique to the individual’s handwriting style.
There are many approaches to the classification of a handwritten text, i.e., signature-based person authentication [
11]. Examples of such methods are dynamic time warping, Gaussian mixture models, fuzzy modeling, and many others. Meanwhile, deep learning is one of the more promising techniques employed for signature-based verification, which allows for obtaining satisfactory high true-positive and low false-positive rates of detection. Applications of deep learning are mainly based on convolutional, recurrent, and generative adversarial neural networks.
We developed an algorithm based on a convolutional neural network trained with the triplet loss method. This network is then utilized to analyze dynamic features obtained from the biometric pen’s sensors, as well as static features (i.e., the shape of the signature), and output a fixed-length representation that could be used to compare and group together signatures. In comparison to analyzing only the shape of a signature, this method has an advantage. It is no longer sufficient to provide a signature with a convincingly similar shape as the way a particular user handles the device while signing contributes substantially to the network’s final output.
Many other methods, some of which we discuss briefly, also rely on the computation of signatures’ representations using a deep neural network and involve performing the comparison using an additional neural network [
20,
21]. They are usually composed of multiple feed-forward layers. The approach we used has been previously used to perform verification for face images [
22]. We show that it can also be successfully used for the modality of dynamic signatures.
An overview for the rest of the article is as follows: In
Section 2, we describe the biometric pen, a novel device designed specifically for biometric verification, and the data acquired by its many sensors.
Section 3 details the method we use to extract features from signatures to determine their similarity.
Section 3.1 contains information about the dataset we gathered and used for training a deep convolutional neural network to extract signatures’ features.
Section 3.2 contains the implementation details of our neural network architecture, and
Section 3.3 concerns the training process. Finally, in
Section 4, we present quantitative results of our work and discuss them in
Section 5, comparing them to other authors’ methods.
2. Biometric Pen
The dynamic biometric signature is well embedded in law at the international level; there are two corresponding documents: ISO/IEC FCD 19794-7: Information technology—biometric data interchange formats, Part 7: Signature; and ISO/IEC WD 19794-11: Information technology—biometric data interchange formats, Part 11: Signature Processed Dynamic Data. In this document, one can find that a valid biometric signature is a data series—a collection of points comprising of timestamp, 2D position, velocity, acceleration, pen pressure, and pen angle. However, the abovementioned general requirements do not define signal analysis methods that should be used to perform the signature verification (recognition). Meanwhile, proper recording and signature verification require the use of compatible devices, allowing for the registration of biometric data with a sufficient time resolution and with enough pressure levels. These requirements are described in ISO/IEC FDIS 19794-7 standards for a biometric signature.
An electronic pen was developed at the Gdańsk University of Technology to satisfy the above demands. Components of the device and its interaction with a tablet can be seen in
Figure 2.
The pen has the following resources and properties:
works with a variety of computer and mobile phone screens
has a pressure sensor
6-axis gyroscope-accelerometer
3-axis inclinometer
2 MEMS (Microelectromechanical systems) microphones
miniature speaker
BLE (Bluetooth Low Energy) radio interface
specialized module with built-in Bluetooth antenna
built-in rechargeable battery
wireless charging
over-the-air software update
passive NFC (Near-Field Communication) tag for pen authorization in the system (pairing)
active mode and status detected by an accelerometer (no external buttons)
signaling lights illuminated through the casing (no holes in the casing)
USB-2.0 (Universal Serial Bus) interface for system communication and power supply
cordless pen charger
NFC transceiver to communicate with the pen (authorization data in BLE)
Each signature collected via the biometric pen is represented as a data structure containing samples sent from the device’s sensors and recorded screen coordinates of the pen tip. Data from sensors are acquired with a constant sampling rate of 50 S/s. Pen tip coordinates are recorded as Windows cursor coordinates with a mean sampling rate of 80 S/s. The exact amount of coordinate samples may vary even among signatures that have the same duration because samples are not collected if the pen tip is not touching the tablet surface or not changing position.
Table 1 shows the biometric pen’s data to the receiving computer and recorded by the computer.
A typical signature created in around 6.6 s could contain 230 samples received from the biometric device and 388 samples recorded as screen coordinates. Depending on a person and circumstances, a signature might take a varying amount of time to complete, thus producing a different number of samples for both data streams each time.
Figure 3 demonstrates example data acquired for a single signature.
3. Methods
The algorithm presented in this section utilizes a convolutional neural network to extract meaningful features from signatures supplied for biometric authentication. In a typical usage scenario, one would keep a database of users with one or more signatures assigned to each of them. Whenever a need for authentication arises, the system would ask a person claiming to be a registered user to provide their signature (a test signature). The neural network would then process this signature to obtain a fixed-length 256-dimensional embedding. Afterward, the system sends it to the authentication server. The server would fetch the signature assigned for that user (already in embedding form) from the database. Having both the test embedding and the reference embedding, one can calculate the Euclidean distance between them. As the network is designed to constrain an embedding onto a unit hypersphere, such a distance is bound to lie anywhere in a interval. The server would authenticate the user successfully, should the calculated distance be lower than a predefined threshold. It should be noted that the method we describe in this work assumes each registered user has just one signature associated with them in the database, and a single test signature is used for comparison. Our method, however, may also be extended to make use of an additional number of signatures stored in the database, which can contribute to higher recognition (authentication) rates.
As the method we develop is designed for user authentication, not for classification, we are only concerned with finding a function mapping signature samples to a new embedding space. Points corresponding to the same person should lie close together, and different people’s points should be far apart. This way, it is easy to determine if two arbitrarily chosen signatures are similar, i.e., correspond to the same person.
In the triplet loss algorithm, a neural network is optimized using triplets. Each triplet consists of two similar samples (and therefore should lie together in the embedding space) plus one sample that is not (should be pushed away). The network is trained to ensure that every triplet does not violate the triplet loss condition. The triplet loss formula is defined as follows:
where
(anchor) and
(positive) represent signatures that should be close in the embedding space, and
(negative) stands for a signature that is different from both
and
. It should be noted that
,
and
are feature vectors extracted by the neural network, not raw signatures. The loss function is designed to ensure that for every triplet, the distance between
and
is greater than the distance between
and
by at least the margin
.
Figure 4 demonstrates the relationship between triplet elements and shows various triplet types.
Several other deep metric learning methods have been proposed that depend on similar principles. The Contrastive Loss [
23] algorithm uses pairs, instead of triplets, to group together similar samples and push away samples belonging to other classes. There are also methods utilizing not pairs or triplets but a greater number of points per training example, such as Quadruple Loss [
24] and N-Pair Loss [
25]. Magnet Loss [
26], on the other hand, penalizes the degree of overlap between clusters.
3.1. Dataset Structure and Acquisition
To train and evaluate the proposed algorithm’s quality, we gathered multiple signature samples, using an early version of the biometric pen, from 2264 participants. Each person provided, on average, five signatures during a single session. In total, 10,622 signatures were obtained. Biometric system safety needs to accept the natural variability occurring in one’s handwriting style while also rejecting uncharacteristic deviations that might indicate an attack attempt.
We required that each person provide successive signatures in a single style characteristic for that participant’s signature-making style. Consequently, we found multiple recurring types of mistakes across the dataset. Examples of such errors are shown in detail in
Figure 5.
The presence of such mistakes throughout the dataset necessitated the need to perform a manual cleanup to guarantee that each person’s signatures are consistent and can be treated as multiple occurrences of one’s signature style. Despite most of such cases being successfully eliminated, a small margin of them persisted in the dataset. In spite of that, the neural network training managed to converge. We mention this issue as we think it is essential to keep in mind that dataset acquisition is just as crucial as a thoughtful design of the network architecture or training algorithm.
For evaluation purposes, we gathered an additional smaller set of 244 signatures collected from 10 people. Each time we gathered signatures, we asked a pair of participants to sign on average 10 times. While the first participant was signing, the other one studied the first one’s way of signing and practiced forging their signature. After the first participant had finished, the second one tried to forge the first participant’s signatures on average 10 times. After that, they switched roles. In this way, we generated, on average, 40 signatures per pair of participants—10 reference signatures and 10 forgery attempts of each person.
Figure 6 shows an example of skilled forgery cases acquired in the additional dataset.
For both datasets, the signatures were acquired on a capacitive touch screen with a biometric pen. Each participant was sitting with the screen lying flat in front of them.
3.2. Selection of Neural Network Architecture
Even though fully convolutional neural networks do not restrict input data to a fixed size, to generate embeddings of the same size, we adjust collected data so that the number of samples used is constant at all times. To do this, we resample each data series to 512 samples via linear interpolation. After this step, a single signature contains 512 samples, each having 9 values, which adds up to 4608 values per signature.
After resampling and before the signature can be used as an input for the neural network, it undergoes further preprocessing, consisting of coordinate system conversion and the normalization of samples gathered from the biometric pen and screen.
Screen coordinate samples conversion—we calculate the mean position from the screen coordinates so that the center of the coordinate system lies in the middle of the signature. Afterward, each sample is converted to polar coordinates . The normalization step divides radius r by the maximum value for the signature so that it remains in the range . We also normalize azimuth angle θ from range to .
Biometric pen samples conversion—We convert accelerometer and gyroscope vectors from cartesian vectors to spherical coordinates. We divide the radius by the maximal possible acceleration/angular velocity, which was defined to be ±2 g and ±2000°/s, respectively, in order to keep its value in the range of . The azimuth angle θ is normalized from the range of to , while the polar angle φ is from the range of to . Pen pressure is also constrained to range .
After this procedure, each data series contains a fixed amount of normalized samples in the shape of 512 features per 9 channels. The signature in this form can then be fed into the neural network to produce a 256-dimensional embedding. We tried many other architectures with different amounts of layers and with different hyperparameters. The one that yielded the best results can be seen in
Figure 7.
As training the network with the triplet loss algorithm takes a long time to finish, we modified the network’s structure mostly by trial and error instead of using automatic methods, such as random search or grid search.
In place of regular convolutional layers, we use depthwise separable convolutional layers, which allow for substantial speedup without sacrificing quality, as explained in [
27]. Except for the one directly before the L2 normalization layer, every such layer utilizes the PReLU (Parametric Rectified Linear Unit) [
28] activation function. This way, the activation function’s slope can be optimized and set for each neuron independently, unlike in Leaky ReLU (Rectified Linear Unit), for instance.
The last layer, called L2 normalization, flattens the output of its preceding layer to a 256-dimensional vector and projects it onto the surface of a unit hypersphere. It is done by calculating the length of this vector, using the Euclidean metric, and dividing all its components.
3.3. Network Training Algorithm
To train the network, we used the triplet loss algorithm. It is a well-established method that finds its uses in many areas, including image retrieval, object recognition, and biometric verification [
22,
29,
30]. This approach especially lends itself to the problem of biometric verification, as there exist a considerable amount of classes (each person could be considered a separate class), and their total number is not known at the training time. When using the network in a production environment, new people will be registered, therefore introducing new classes. The crucial thing to consider is that the algorithm is expected to work without the need to retrain it after registering new people.
We divide the dataset into 2 subsets—a training set consisting of 2064 clients and a validation set having 200 clients. The training set is randomly sampled with a uniform distribution to generate a batch containing 256 triplets during the training phase. We employ semi-hard negative mining [
30] to ensure that every triplet contributes to the gradient update and maintains training stability. Due to this, we also noticed that the training procedure slows down dramatically in the later stages, as it becomes increasingly challenging to find semi-hard triplets.
We used a fixed margin of 0.25 to define the triplet loss formula [
30] and Adam optimizer [
31] with a learning rate set to 0.01. Neural network accuracy and loss values during training can be seen in
Figure 8 and
Figure 9, respectively. We define 1 epoch as 5 network’s weights updates, as it is infeasible to iterate over the set of all possible triplets.
The total time to train the network was 26 h and 17 min using a PC with an Nvidia Geforce RTX 1080 Ti GPU.
4. Results
This section describes a trained neural network’s evaluation results using a validation set to measure its quality, considering signatures that were not taking part in the training. This set contains 200 clients and 1043 signatures in total. We carried out an experiment in which we compare pairs of signatures for every client. If one picks two signatures belonging to the same person, it is expected that the Euclidean distance between them should be below a certain small threshold. In addition to that, pairs of signatures belonging to two different clients were also compared, yielding a distance above that threshold.
In a single test, we make 2306 comparisons of signature pairs of a single person and 539,721 comparisons of signature pairs where signatures belong to different clients. We repeat this test for 200 thresholds uniformly distributed over the range
, as distances between two random embeddings are constrained to this range. Our network scored 5.94% EER (equal error rate) for threshold 1.055.
Figure 10 depicts the ROC (receiver operating characteristic) curve where each point corresponds to a single test for a certain threshold.
To further ensure that our evaluation method is not dependent on validation set composition (i.e., which samples are used for evaluation) and would generalize well on new data, we carried a test akin to cross-validation. As it is very time-consuming to train a neural network model from scratch, we do it only once. Still, we perform tests described earlier in this section multiple times for randomly sampled subsets of the validation set.
We randomly divide the validation set into 5 subsets of 40 clients. For each subset, we calculate the EER. This procedure is then repeated 20 times to obtain 100 EER values. This way, we obtained a mean EER value of 5.77% and a confidence interval of with a standard 95% confidence level. The standard deviation for the EER was 1.265 with minimum and maximum values of 2.69% and 9.508%, respectively.
To present the results graphically, we used the t-SNE (t-Distributed Stochastic Neighbor Embedding) algorithm [
32], which can be seen in
Figure 11. We used a subset of the validation set containing 100 clients to generate the visualization. Each signature manifests as a color dot. Signatures of a single person are connected with a line. It can be observed that the same person’s signatures lie close together and clump into tight groups, separating from other groups, as is expected. Whenever signatures of the different color group together is a sign of incorrect neural network prediction or a consequence of the presence of mistakes, as was described earlier in
Section 3.1. Dataset structure and acquisition.
Some signatures’ representations are distant in the graph because they are mislabeled samples in the dataset. Such samples would be incorrectly shown with the wrong person’s color and connected by a line to the wrong sample group. It is one of the reasons why we mention errors in the dataset in
Section 3.1. Due to the big size of the dataset, it is difficult to perform a complete cleanup of mistakes present. In the case of mislabeled signatures, one would have to manually compare pairs of signatures, which is infeasible due to the number of comparisons that would have to be performed. On the other hand, heuristic methods by definition do not guarantee that a cleanup performed with such techniques is correct. Some feature vectors could also be outliers and thus be distant in the graph.
To emphasize the separation of distances obtained for pairs of similar signatures (of the same person) and dissimilar ones (from different clients), we calculated histograms for a single test using the whole validation set, which can be seen in
Figure 12. A “Genuine” histogram was created using 2306 comparisons and an “Impostor” with 539,721.
The “Genuine” histogram has a mean distance of 0.6653 with a confidence interval and a standard deviation of 0.2173. “Impostor” has a mean distance of 1.3601 with a confidence interval and a standard deviation of 0.178.
Lastly, we show the separation using a boxplot in
Figure 13. The solid line inside each box is the mean value, and the dotted line shows the median. Box bottom and top boundaries are defined by the 1st and 3rd quartile, and the whiskers are 1.5*IQR (interquartile range) apart from the boundaries.
We also evaluated our method on the smaller set we described at the end of
Section 3.1. to check the neural network’s ability to differentiate between genuine signatures of a particular person and forgery attempts of an attacker trying to mimic that person’s shape and dynamic features. We calculated distances between each participant’s pairs of signatures. Additionally, distances between genuine and skilled forgery signatures have been calculated. Afterward, all calculated distances were compared with the threshold. Our neural network achieved 11.114% EER in this test. The ROC curve can be seen in
Figure 14.
The distribution of distances for pairs of genuine signatures and pairs consisting of one genuine and one forged signature can be seen in
Figure 15.
A boxplot showing the separation between “Genuine” and “Impostor” scenarios is additionally shown in
Figure 16.
5. Discussion
We demonstrated that it is feasible to construct an algorithm to perform user authentication employing a neural network to extract meaningful features from handwritten signatures. We used a device designed specifically for biometric verification; however, this method is general enough to be used in other areas, where different hardware is employed to acquire samples. In the following subsections, we compare our results with other authors’ findings. Lastly, we indicate areas we would like to focus on in future work.
5.1. Performance Concerning the State of the Art
In this subsection, we explore other approaches to online signature verification compared to the method presented in this article.
Tolosana et al. [
20] employ a Siamese architecture based on bidirectional LSTM (Long Short-Term Memory) and GRU (Gated Recurrent Unit) neural networks. The authors used a BiosecurID database [
33] of comparable size to ours, consisting of 11,200 signatures. The recurrent network extracts meaningful features from both tested and registered signatures, and after that, a separate multilayer perceptron network calculates the similarity between features of both signatures. In our method, a single neural network is used to extract features, which can then be directly compared using the L2 norm. This distance comparison is a counterpart to the multilayer perceptron used. The authors achieve a comparable 5.28% EER using the BLSTM (Bidirectional Long Short-Term Memory) network trained on random forgery cases while comparing one test signature to one registered signature. However, our experiments report EER values as low as 2.69%. To perform a fair comparison, both methods ought to be implemented on the same dataset to determine which method is more applicable.
Ahrabian and BabaAli [
21] propose a method where an LSTM autoencoder transforms signatures into a fixed-length latent space representation and uses a Siamese network to determine how similar the tested signatures are. The authors achieve 8.65% EER on the SigWiComp2013 Japanese dataset.
Schroff et al. [
22] use the triplet loss algorithm to directly teach a neural network how to encode face images to a fixed-length 128-dimensional representation. The authors use an approach similar to the one presented in this article, even though it concerns a different modality.
A comparison of the approach presented in this article with the state-of-the-art methods can be found in
Table 2.
5.2. Future Work
An interesting problem is comparing a “wet” signature (written on paper) with a signature placed on an electronic screen’s surface. In order to perform research on this subject, an extensive set of data should be collected, including wet signatures generated with a regular pen on paper and so-called in vitro signatures created with an electronic stylus. Hence, the task is to determine the relationship between these two types of signatures to determine whether the signatures made with styluses have enough standard parameters for recognition and the nature of those parameters. Such signatures can be compared because each literate person has preconceived graphology parameters of their signature. These parameters may not be valid for electronic signatures. However, we presume that there exists a relation between wet and in vitro signatures. Based on the collected samples of different signatures from many individuals, we will investigate the correlation and relationships between signatures.
We want to investigate our method’s performance on skilled forgery attempts using a neural network trained using random forgery and skilled forgery training examples. Due to our dataset not having skilled forgery cases, we could not perform this kind of analysis so far.
So far, we only considered how our method behaves when only a single reference signature is assigned to each user. We believe one could achieve better results if more signatures are used and would like to emphasize how to do this in the future.
Another area we would like to focus on is signature aging. As pointed out by Galbally et al. [
13], aging in the signature trait is a specifically user-dependent effect. Moreover, it does not seem to depend on the signature’s complexity, as it affects both simple and complex ones. The main conclusion is that, in general, a user affected by signature aging will perform poorly regardless of the method used. The simplest solution could be to give a user a way to register again, perhaps after successful authentication with an additional biometric modality.
We would like to explore how other deep metric learning methods could be used further to improve the quality of such a biometric verification system. One of the significant flaws of the triplet loss algorithm used in our method is that it becomes progressively slower as the training procedure continues. Lastly, we want to investigate how one could integrate this approach to dynamic signature verification as a part of a comprehensive multimodal biometric system.