Algorithm for Automated Foot Detection in Thermal and Optical Images for Temperature Asymmetry Analysis

Abstract

Infrared thermography has been proven to be an effective non-invasive method in diabetic foot ulcer prevention, yet current image processing algorithms are inaccurate and impractical for clinical work. The aim of this study was to investigate the accuracy of our automated algorithm for feet outline detection and localization of potential inflammation regions in thermal images. Optical and thermal images were captured by a Flir OnePro camera connected with an Apple iPad Air tablet. Both thermal and optical images were merged into an edge image and used for the estimation of foot template transformations during the localization process. According to the feet template transformations, temperature maps were calculated and compared with each other to detect a set of regions exceeding the defined temperature threshold. Finally, a set of potential inflammation regions were filtered according to the blobs features to obtain the final list of inflammation regions. In this study, 168 thermal images were analyzed. The developed algorithm yielded 95.83% accuracy for foot outline detection and 94.28% accuracy for detection of the inflammation regions. The presented automated algorithm with enhanced detection accuracy can be used for developing a mobile thermal imaging system. Further studies with patients who have diabetes and are at risk of foot ulceration are needed to test the significance of our developed algorithm.

1. Introduction

Diabetes mellitus is one of the most prevalent chronic diseases. While diabetes itself is like the tip of an iceberg, diabetes-related complications, especially diabetic foot ulcers (DFUs), are the biggest concern. The DFUs are difficult to diagnose early and even more challenging to treat. Delayed diagnosis increases the need for surgical interventions and the risk of amputations [1]. Thus, a new diagnostic tool for early diagnosis of DFUs is fundamental to reduce adverse outcomes and economic cost [2,3].

Since Armstrong and colleagues determined that temperature changes in the foot can be an early indication of a DFU [4], researchers have been searching for a convenient and accurate way to identify these changes. It was discovered that temperatures of corresponding areas between feet do not usually differ by more than 1 °C, and a temperature difference of more than 2.2 °C is considered abnormal [4,5]. More importantly, the increased temperature may be presented even a week before a DFU appears [6], and frequent temperature assessment and treatment for these patients can prevent diabetic foot complications [7,8].

Infrared thermography (IRT) is a non-invasive and non-contact method for screening of human skin temperature that allows spatial temperature distributions to be visualized based on the emitted heat (thermal radiation). While previous research focused on early diagnosis and screening purposes, recent data shows that IRT could also be useful in follow-up as it can predict the healing status of the DFU [2]. Even more, according to J. Cwajda-Białasik et al., a prolonged temperature increase of at least 1.11 °C at the wound site, could indicate the existence of infections [9]. These findings suggest that the application of IRT could be expanded from screening to follow-up of patients with current ulcers and even suspected early infections.

IRT has been successfully used in many other medical fields. An extensive literature review, published by Lahiri, et al. covers other possible medical applications of IRT, including diagnosis of breast cancer and peripheral vascular disorders, detecting problems related to gynecology, kidney transplantation, dermatology, heart, neonatal physiology, fever screening and brain imaging [10]. A more recent review by John et al. covers IRT application of IRT in plastic surgery [11]. A new ongoing study of a systematic literature review and meta-analysis of IRT use for musculoskeletal injuries diagnosis is essential as current diagnosis techniques are often associated with radiation exposure [12].

Despite rising research interest, efforts and progress to use IRT for diabetic foot disease [13], a user-friendly device for DFU monitoring is yet to be established. The absence of an automated algorithm that is accurate and can effectively analyze thermal images of diabetic foot is one of the reasons. Recently proposed image processing algorithms have significant limitations in the segmentation of the feet from the background or being semi-automated [14]. In order to solve the segmentation problem, in several studies, some type of cloth or plastic panels were used to cover the background around feet to reduce the influence of thermal radiation from other objects around [15,16]. In some studies, an even more complicated thermally insulated boxes were designed for this purpose [6,17]. A novel concept of reconstructed 3D models of the diabetic foot and thermal images was introduced by Van Doremalen et al. [18]. However, such a system is quite complicated and not portable. In addition, Van Doremalen et al. represented the results of 32 participants with peripheral neuropathy and showed reliable validity of mobile phone or tablet-based thermal camera to be applied for assessment of the diabetic foot. Also, it requires segmentation of foot contour in the thermal images [15]. Manual segmentation of foot contours was also widely used in other studies [19,20].

The objective of our study was to develop a real-time screening technology that is able to analyze foot images and detect signs of inflammation that might be indicative of a DFU onset. In this article, we demonstrate how our automated algorithm with enhanced detection accuracy detects the outline of the feet from the background noise during processing optical images and localizes the inflammation regions after processing thermal images of both feet. This technology could be used for an AI-based (tele) medicine system and serve as a self-monitoring tool.

2. Materials and Methods

2.1. Study Design

With this experiment, we wanted to verify our algorithm’s accuracy to detect feet outline and localize the potential inflammation regions. Two data sets of images with and without phantom feet were used for this purpose, named accordingly: Phantom Feet and No Feet (Figure 1).

Silicone phantom feet were used to produce similar-looking images with ideally shaped feet and an irregular feet position inside the frame. Simulated inflammation zones were created manually by heating up randomly selected regions of the phantom soles with a heated metal spoon, in a way that is similar to previous research [21]. The edges of the soles were not heated in order not to compromise the automatic detection of the feet outline. Several images from the simulated inflammation regions are shown in Figure 2.

The surrounding items such as walls, furniture, electrical equipment, heating devices, and human body parts (excluding feet) were captured in images used in No Feet data set to replicate accidentally captured images. Such images were necessary to test the functionality of algorithm’s automatic function to exclusively detect the feet outline. All photos in Phantom Feet dataset had an uneven background without thermal artifacts. The experimental set-up is shown schematically in Figure 3.

2.2. Image Acquisition

The experiment took place in a controlled environment with a mean temperature of 22 ± 0.5 °C and relative humidity of 45 ± 5%. It was ensured that no direct lighting was pointing towards the lens of the camera.

Thermal and color optical images were captured by a Flir OnePro camera (FLIR Systems, Wilsonville, OR, USA) connected with an Apple iPad Air tablet (Apple, Cupertino, CA, USA). Images were taken by holding the tablet with the Flir OnePro camera (number of pixels for thermal image 160 × 120 and optical 1440 × 1080) in hands from a distance of 0.3 ± 0.05 m. Focus and exposure were estimated automatically by the embedded logic of the thermal imaging camera. The resolution of the temperature sensing was 0.1 °C.

Silicone phantom feet were heated in a special low-temperature oven to reach the natural feet temperature of +29 °C. This temperature was concluded from our early experiments and supported by other trials [22]. A digital temperature controlled thermostat connected to the oven heating control system was used to ensure the accuracy of the phantom’s temperature without deviations above ±0.1 °C. Both the thermal and visual images were stored in the tablet’s memory in a binary format. The thermogram was acquired in a raw format and stored as a 2D matrix consisting of 16 bit values per pixel. The visual image was acquired in an RGB format and stored as a 2D matrix of 24 bit values per pixel.

2.3. Study Methods

We started testing our algorithm from the detection of the feet outline in optical images. First of all, the estimation of Dense Edge Points (DEP) was added to the baseline algorithm, which was performed by doubling the key points of foot outline to increase the foot shape recognition. Then, Extended Foot Shape (EFS) was performed by using standard foot outlines to improve the quality of detection of the base foot location. Therefore, three algorithms, namely: (1) baseline algorithm; (2) baseline algorithm with DEP; and (3) baseline algorithm with DEP and EFS, were tested during the experiment. Later, we tested the ability of our algorithm to detect and evaluate the potential inflammation regions in thermal images. This work was performed with the Phantom Feet data set using pictures with and without simulated potential inflammation regions.

2.4. Overview of the Proposed Methodology

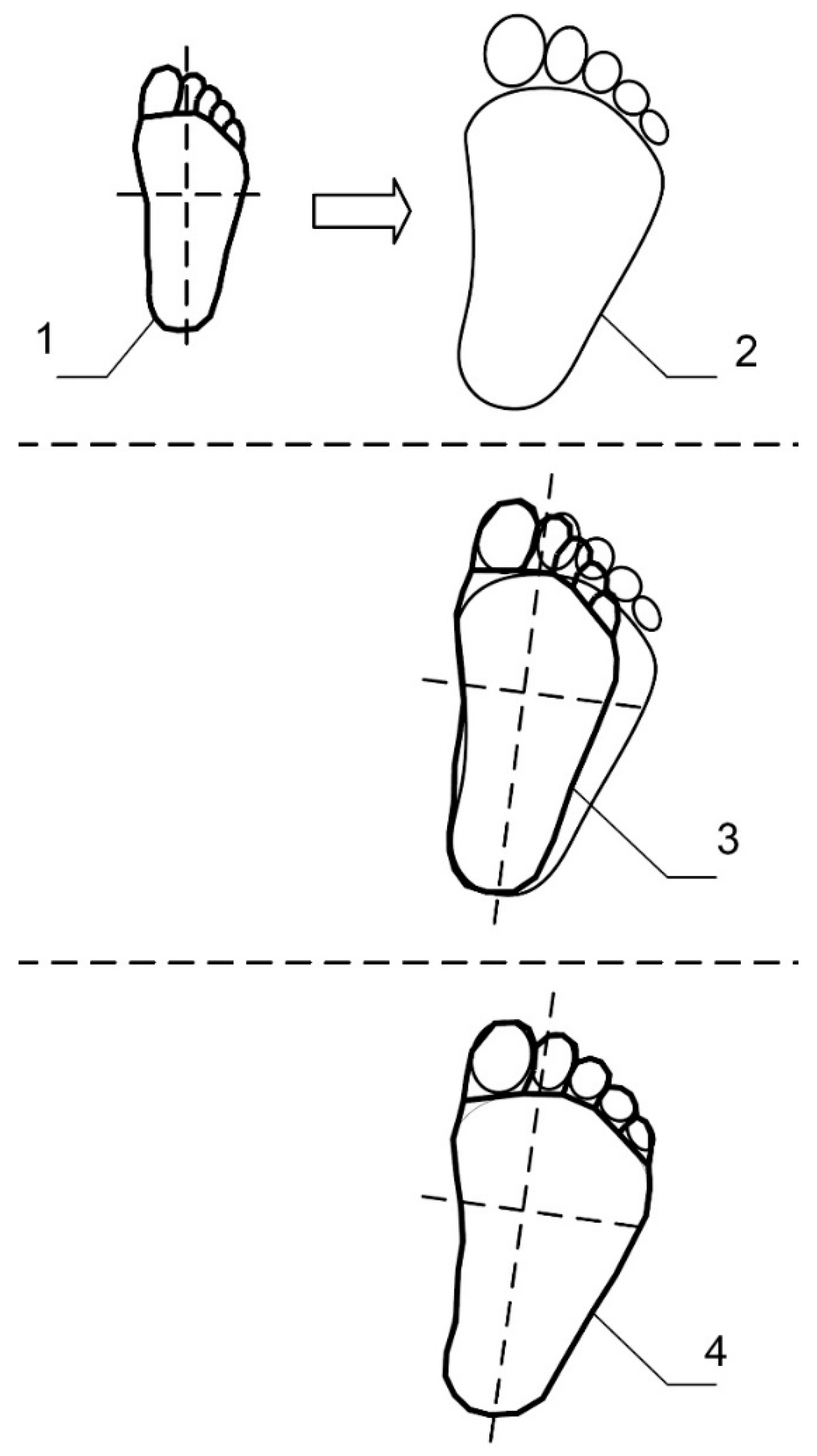
The proposed methodology for the analysis of thermal and optical images in order to perform an automatic detection of potential inflammation regions is presented in the block diagram in Figure 4 and schematically in Figure 5. The inspected foot is marked as (1), while the contralateral foot is marked as (2). After fine-tuning the inspected foot template, the inspected foot with a fitted template is created (3). The same procedure of fine-tuning of the foot template is performed on a contralateral foot, so the contralateral foot with a fitted template is created (4). The initial template with a grid (6) is applied for both the inspected and the contralateral feet. As a result, the inspected foot template with a grid (7) and the contralateral foot template with a grid (8) are obtained. Then, the temperature maps for both feet are estimated according to the appropriate set of points-of-interest. Temperature maps of the inspected and contralateral feet are shown in (9) and (10), respectively. The estimation of the temperature disparity map is performed by subtracting the temperature values in the reference foot temperature map from the appropriate temperature values in the inspected foot temperature map, creating the temperature difference map (11). The temperature difference map (11) shows the temperature differences between the inspected and the contralateral feet. The threshold for these temperature differences could be set for different values. If the temperature differences surpass the medically-based threshold value, this temperature asymmetry indicates a possible inflammation region.

2.5. Image Processing

Our image processing algorithm consists of several steps described in the following subsections. Special software for optical and thermal image processing was designed to be used with a tablet or a smartphone. The entire application was implemented in Java programming language while the image processing algorithm was completed in C++ programming language.

2.5.1. Estimation of Displacement in the Thermal and the Optical Images

Thermal image $I_T$ and optical image $I_O$ were captured simultaneously. Both cameras, thermal and optical, are placed on the board as close to each other as the device design allows; nevertheless, the remaining difference produces a notable displacement in both images caused by an offset of camera focus centers. Therefore, the optical image was shifted according to the thermal image’s position to align the outlines of the feet in both images. For this purpose, edge images $E_T$ and $E_O$ were estimated for $I_T$ and $I_O$ respectively. Sobel operator [23] was used for edges’ estimation. Thus, the pixels in edge images represent a magnitude of the edge slope in range 0–255. The higher value corresponds to the steeper slope.

The edge detecting functions are defined as:

$$E_x=\left[\begin{array}{ccc}+1& 0& -1\\ +2& 0& -2\\ +1& 0& -1\end{array}\right]\ast I$$

(1)

$$E_y=\left[\begin{array}{ccc}+1& +2& +1\\ 0& 0& 0\\ -1& -2& -1\end{array}\right]\ast I$$

(2)

$$E=\sqrt{E_x^2+E_y^2}$$

(3)

where $\ast$ denotes the 2-dimensional image convolution.

Optimal offset was achieved by solving the optimization problem with Descent Gradient method [24]. Zero-normalized cross-correlation (ZNCC) [25] was used as a cost function:

$$ZNCC\left(n,m\right)=\frac{1}{n}{\displaystyle \sum _{(x,y)}\frac{\left(E_T\left(x+n,y+m\right)-{\mu }_T\right)\left(E_O\left(x,y\right)-{\mu }_O\right)}{{\sigma }_T{\sigma }_O}}$$

(4)

where $n$ is the number of pixels in images $E_T$ and $E_O$, ${\mu }_T$ and ${\mu }_O$ are the mean values, and ${\mathsf{\sigma }}_T$ and ${\mathsf{\sigma }}_O$ are the variations of the covering part of images $E_T$ and $E_O$ respectively.

Finally, edge images $E_T$ and $E_O$ were combined into the one edge image $E$. The point values in this image were estimated as this:

$$E\left(x,y\right)=max\left(E_T\left(x,y\right),E_O\left(x,y\right)\right)$$

(5)

2.5.2. Localization of Inspected Foot Template

Foot outline was localized by applying the appropriate transformation to the base foot template $T_B$. The base foot template represents a polyline composed of finite number of points $T_B\left(i\right)=\left\{x_i,y_i\right\}$. It was obtained by averaging manually marked foot outlines in sample images. Foot template localization to the foot outline was performed by estimating rigid transformation $R^R$ capable to transform the base foot template $T_B$ to the inspected foot template $T_I$ which best fits the foot outline in the edge image $E$. Rigid transformation parameters (scale, rotation, translation, and mirror) were estimated by solving the optimization problem descent gradient method. Foot template compliancy was estimated as a line correspondence to the foot edge represented in image. Rigid transformation $R^R$ obtained during this step was defined as $4\times 4$ transformation matrix.

2.5.3. Fine-Tuning of Inspected Foot Template

The inspected foot template $T_I$ obtained during the localization, corresponds to the foot outline inaccurately, because the rigid transformation is unable to fit the base foot template to a specific foot outline. In order to achieve pixel-wise accuracy, the connection points of the inspected foot template were additionally matched with the edges of the foot outline in edge image $E$ during the fine-tuning process. Pixel-wise shifting of foot template connection points was performed by shifting them across the bisectors. Working in narrow bounds (usually 5–10 pixels), allowed us to adjust the foot template flexibly, while remaining shape distorted within tolerance. We used a simple maximum value function for accurate foot outline edge detection. This method is presented in Figure 6.

The transformation capable of transforming the foot template connection points coordinated to the fine-tuned positions may be represented as a matrix of the Thin Plate Spline transformation coefficients. Coefficients are estimated by relating the base foot template points and the inspected foot template points according to the following equation:

$$f\left(x,y\right)=a_1+a_{2}x+a_{3}y+{\displaystyle \sum _{i=1}^n{w}_{i}U\left(\left|T_B\left(i\right)-\left(x,y\right)\right|\right)}$$

(6)

where $U$ is defined as $U\left(r\right)=r^{2}log\left(r\right)$ and $\left|T_B\left(i\right)-\left(x,y\right)\right|$ is the distance between the control point $T_B\left(i\right)$ and modified point $\left(x,y\right)$. Unknowns $a_1$, $a_2$, $a_3$ and ${\omega }_i$ forms the coefficients vector ${\left(\begin{array}{ccccc}w& |& a_1& a_2& a_3\end{array}\right)}^T$. Coefficients vector is estimated according to the equation:

$${\left(\begin{array}{ccccc}w& |& a_1& a_2& a_3\end{array}\right)}^T=L^{-1}v$$

(7)

where values vector $v$ and computation matrix $L$ are defined as follows:

$$v^T=\left[\begin{array}{ccccccc}{v}_1& v_2& \cdots & v_n& 0& 0& 0\end{array}\right]$$

(8)

$$L=\left[\begin{array}{cc}K& P\\ P^T& 0\end{array}\right]$$

(9)

$$K=\left[\begin{array}{ccc}U\left(r_{11}\right)& U\left(r_{12}\right)& \cdots \\ U\left(r_{21}\right)& U\left(r_{22}\right)& \cdots \\ \cdots & \cdots & U\left(r_{nn}\right)\end{array}\right]$$

(10)

$$P=\left[\begin{array}{l}\begin{array}{ccc}1& x_1& y_1\end{array}\\ \begin{array}{ccc}1& x_2& y_2\end{array}\\ \begin{array}{ccc}\cdots & & \end{array}\\ \begin{array}{ccc}1& x_n& y_n\end{array}\end{array}\right]$$

(11)

This equation may be solved by finding the inverse $L^{-1}$. Two separate equations were used for $x$ and $y$ coordinates estimation for inspected foot template $T_I^{\prime }$. Thus, two coefficients vectors ${\left(\begin{array}{ccccc}w& |& a_1& a_2& a_3\end{array}\right)}_x^T$ and ${\left(\begin{array}{ccccc}w& |& a_1& a_2& a_3\end{array}\right)}_y^T$ are used to represent the non-rigid transformation $R^N$. Detailed fine-tuning process of a foot template and estimation of optimal points is demonstrated in Figure 6 and Figure 7.

2.5.4. Localization and Fine-Tuning of Contralateral Foot Template

Localization and fine-tuning of the contralateral foot template $T_c^{\prime }$ was performed in the same manner as the tuning of the inspected foot template $T_I^{\prime }$. The only difference is that the initial template for contralateral foot $T_B^m$ was obtained by applying a vertical reflection transformation (negating $x$ axis) to the points of base foot template $T_B$:

$$T_B^m\left(i\right)=R^m\left(T_B\left(i\right)\right)$$

(12)

where $T_B\left(i\right)$ represents the base template point in homogeneous coordinates as $T_B\left(i\right)={\left(\begin{array}{ccc}{x}_i& y_i& 1\end{array}\right)}^T$, and reflection transformation $R^m$ is defined as:

$$R^m=\left[\begin{array}{ccc}-1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$$

(13)

2.5.5. Estimation of Sets of Points-of-Interest

Fine-tuning of both the inspected foot template $T_I^{\prime }$ and the contralateral foot template $T_C^{\prime }$ to the appropriate feet outlines in thermal and optical images, allowed to estimate sets of points-of-interest. The base set of points-of-interest $P_B$ was represented as a grid of points over the base foot template $T_B$. Modified positions of points-of-interest were estimated by applying the rigid transformation $R^R$, followed by a non-rigid transformation $R^N$ in succession to the base set of points-of-interest $P_B$. Those two sets of points-of-interest $P_I^{\prime }$ and $P_C^{\prime }$ were obtained for both inspected and contralateral feet by applying corresponding transformations:

$$P_I^{\prime }\left(i,j\right)=R_I^N\left(R_I^R\left(P_B\left(i,j\right)\right)\right)$$

(14)

$$P_C^{\prime }\left(i,j\right)=R_C^N\left(R_C^R\left(P_B\left(i,j\right)\right)\right)$$

(15)

Points inside of the inspected foot shape matched the paired points inside of the contralateral foot shape. This method ensures that even different shaped and sized feet can be evaluated by comparing temperature values in paired points of both feet templates.

2.5.6. Estimation of Temperature Maps

According to the values indicated by the sets of points-of-interest $P_I^{\prime }$ and $P_C^{\prime }$, temperature maps $M_I$ and $M_C$ were estimated for both the inspected and contralateral feet respectively. Each value of temperature maps $M\left(i,j\right)$ was estimated by generalizing temperature values situated near by the position of point–of-interest $P_{i,j}$ in the thermal image $I_T$ of the appropriate foot. We used the weighted mean method for temperature values estimation:

$$M\left(i,j\right)=\frac{1}{n}{\displaystyle \sum _{(x,y)\in Q_{p_{i,j}}}{I}_T\left(x,y\right)}$$

(16)

$Q_{p_{i,j}}$ represents the set of points in thermal image $I_T$ laying inside the foot template $T^{\prime }$ and closer to $P_{i,j}$ than to the any other point from the set of points–of-interest $P^{\prime }$:

$$Q_{p_{i,j}}=F\cap \left\{q:dist\left(q,p_{i,j}\right)<dist\left(q,p\in P^{\prime }\right)\right\}$$

(17)

where $dist\left(q,p\right)$ defines the Euclidian distance between the points $q$ and $p$. $F$ defines the set of points inside the foot outline defined by template $T^{\prime }$.

Assessment of temperature disparity map $D$ was done by subtracting the temperature values of the temperature map of contralateral foot $M_C$ from the appropriate temperature values of inspected foot $M_I$. Subtraction of temperature values was done one by one in a two-dimensional array:

$$D\left(i,j\right)=M_I\left(i,j\right)-M_C\left(i,j\right)$$

(18)

2.5.7. Composition of a Set of Inflammation

The composition of set of inflammation $W$ was performed by analyzing the temperature disparity map $D$ to find the local areas containing temperature disparity values higher than the medically based threshold. Potential inflammation regions $\omega$ consist of the nearby points of temperature disparity map exceeding the medically-based threshold. Those binary images $B$ were obtained by setting their points as:

$$B\left(i,j\right)=\{\begin{array}{cc}1,& D\left(i,j\right)\ge t\\ 0,& otherwise\end{array}$$

(19)

where $t$ is a medically approved threshold. We used t = 2.2 °C in all our experiments. Thus, the binary image $B$ was obtained by containing 1 at points exceeding threshold and 0 elsewhere. Two-pass connected components labeling [26] was used to collect inflammation regions into the list of blobs $H$ while analyzing the binary image $B$. A descriptive feature vector was created for each candidate inflammation region $h$, that consisted of generalized values of points interposition and temperatures or a combination of both.

2.5.8. Analysis of Inflammation Regions

Analysis of inflammation regions was performed by examining the feature vectors. During this process, non-confident inflammation regions were rejected in order to clear the list against accidentally marked non-inflammable regions (e.g., the area deemed too small, or having considerably small temperature excess, etc.). We used the Support Vector Machine (SVM) classifier [27] to perform this task. The positive sign of the disparity value was used for attribution of a particular foot possessing the inflammation region.

The final list of inflammation $H^{\prime }$ contains the potential pathologies. An empty list indicates no inflammation was found and no action is needed, while the non-empty list indicates that the algorithm has found an inflammation region and suggests consulting with a healthcare specialist.

3. Results

The algorithm analyzed 168 thermal images in total: 70 in Phantom Feet and 98 in No Feet data sets. The results are demonstrated in

Table 1. Baseline algorithm with DEP and EFS experiment results for feet outline detection.

Dataset	Number of Images	Detected	Ratio
Phantom Feet
Baseline algorithm	70	49	70.00%
Baseline algorithm + DEP	70	63	90.00%
Baseline algorithm + DEP + EFS	70	65	92.86%
No Feet
Baseline algorithm	98	2	2.04%
Baseline algorithm + DEP	98	2	2.04%
Baseline algorithm + DEP + EFS	98	2	2.04%

and

Table 2. Testing of inflammation detection algorithm with phantoms

Dataset	Number of Images	Detected	Ratio
Phantom with simulated regions of inflammation	40	36	90.00%
Phantom without simulated regions of inflammation	30	0	100%

. Modifications of a baseline algorithm improved the true-positive results by 22.86% and achieved 95.83% accuracy with 92.86% sensitivity and 98% specificity in detection of the feet outlines. During the phantom investigation, the inflammation localization algorithm achieved 94.28% accuracy, 90.00% sensitivity, and 100.00% specificity.

4. Discussion

The principal task for our developed automated algorithm was to determine foot outlines precisely, as this directly affects the accuracy of the final results. We found that blurred foot contour segments in one image can be compensated from another image (thermal or optical); therefore, merging the edges of both thermal and optical images enabled a better detection of the foot outline. Our results showed that background artifacts were the main reason for poor detection of the outline of the feet in the baseline algorithm. DEP and EFS modifications improved the baseline algorithm and achieved a notable 95.83% accuracy and 92.86% sensitivity. False-positive cases were mainly caused by the relatively hot objects in the background in No feet data set. The detection of possible inflammation zones achieved 94.28% accuracy and 90.00% sensitivity. Several reasons impaired the possible inflammation zone detection. The main reason for false-negative results was an uneven temperature over the soles of the feet, i.e. the feet were not symmetrical across the temperature map. Furthermore, false-negative results were related to the marginal temperature differences value, i.e. the temperature difference did not exceed the threshold value across the inflammation area. There were several limitations to this study. First of all, we used phantom feet instead of actual patients with diabetes because of the coronavirus SARS-Cov-2 (disease COVID-19) outbreak worldwide and in our country. However, we believe that the phantom feet image data is sufficient enough for the feet outline detection purposes, which was the main object in this study. Secondly, phantom feet are ideally shaped, and that may lead to better outline detection results. Certainly, future studies with people who have diabetes are needed to verify our results.

For possible inflammation zone detection, we used an asymmetric temperature analysis when the plantar temperature is compared between both feet. If the same inflammations exist in both feet, or if partial or entire foot amputation was performed, this method is unable to determine the possible inflammation areas over the soles of the foot.

5. Conclusions

The automated algorithm with an enhanced detection accuracy that is able to analyze the optical and thermal images of the foot and to detect feet outline from the background noise and localize inflammation regions was developed. Merging the edges of both thermal and optical images into an edge image and using it to estimate the foot template transformations during the localization process, instead of the widely used segmentation process by other algorithms developers, allowed us to achieve pixel-wise accuracy. Different from other publications, our algorithm is entirely automated and does not require the interference of an operator. Another superiority of our algorithm is that it is reliably suitable to perceive the shape of the foot instead of distinguishing the foot area from the background area.

We are currently testing our automated algorithm with healthy volunteers to validate these results. We are also preparing a study with patients with diabetes, and planning to verify other possible applications of our proposed method. This includes following up on the patients with current ulcers in order to evaluate of the healing process and suspected infections.

We believe that our algorithm could be used for the development of a new screening tool to enable patients to perform monitoring of the feet from the comfort of their home. Furthermore, such a device could be used in clinics to assist the physicians with decision support. The proposed portable screening system will be implemented using a specialized mobile application where the optical and thermal images will be acquired, processed, and analyzed for detection of signs of inflammation over the soles of the feet.

6. Patents

A patent application for the described system, method, and apparatus for temperature asymmetry measurement of body parts was filed with the International Bureau of the World Intellectual Property Organization (RO/IB) on 6 March 2020 with international application number: PCT/IB2020/051950.