Efficient Design Strategy for Optimizing the Settling Time in Three-Stage Amplifiers Including Small- and Large-Signal Behavior
Abstract
:1. Introduction
2. Settling-Time Modeling in Three-Stage Amplifiers
2.1. Modeling of a Pure Three-Pole Amplifier
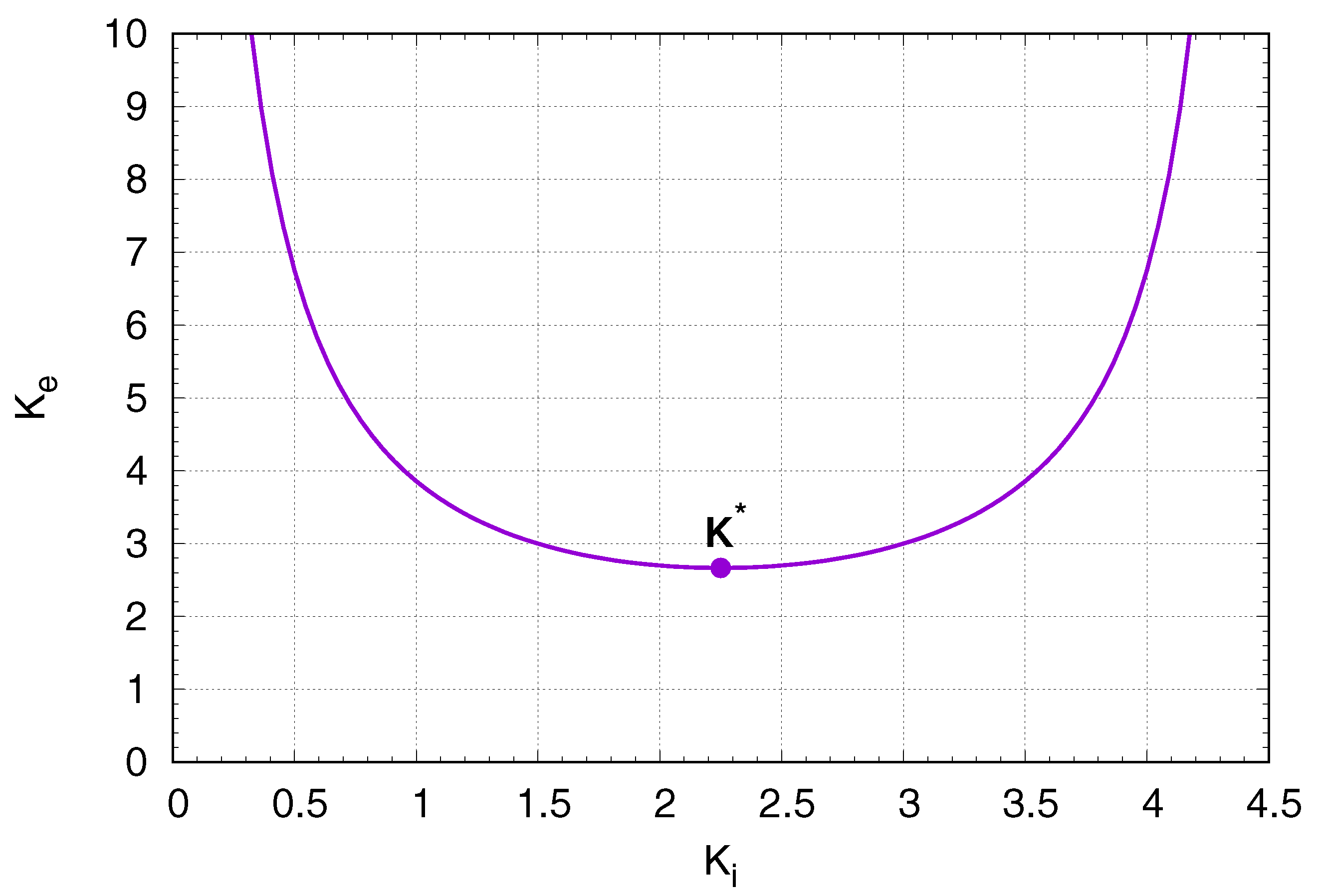
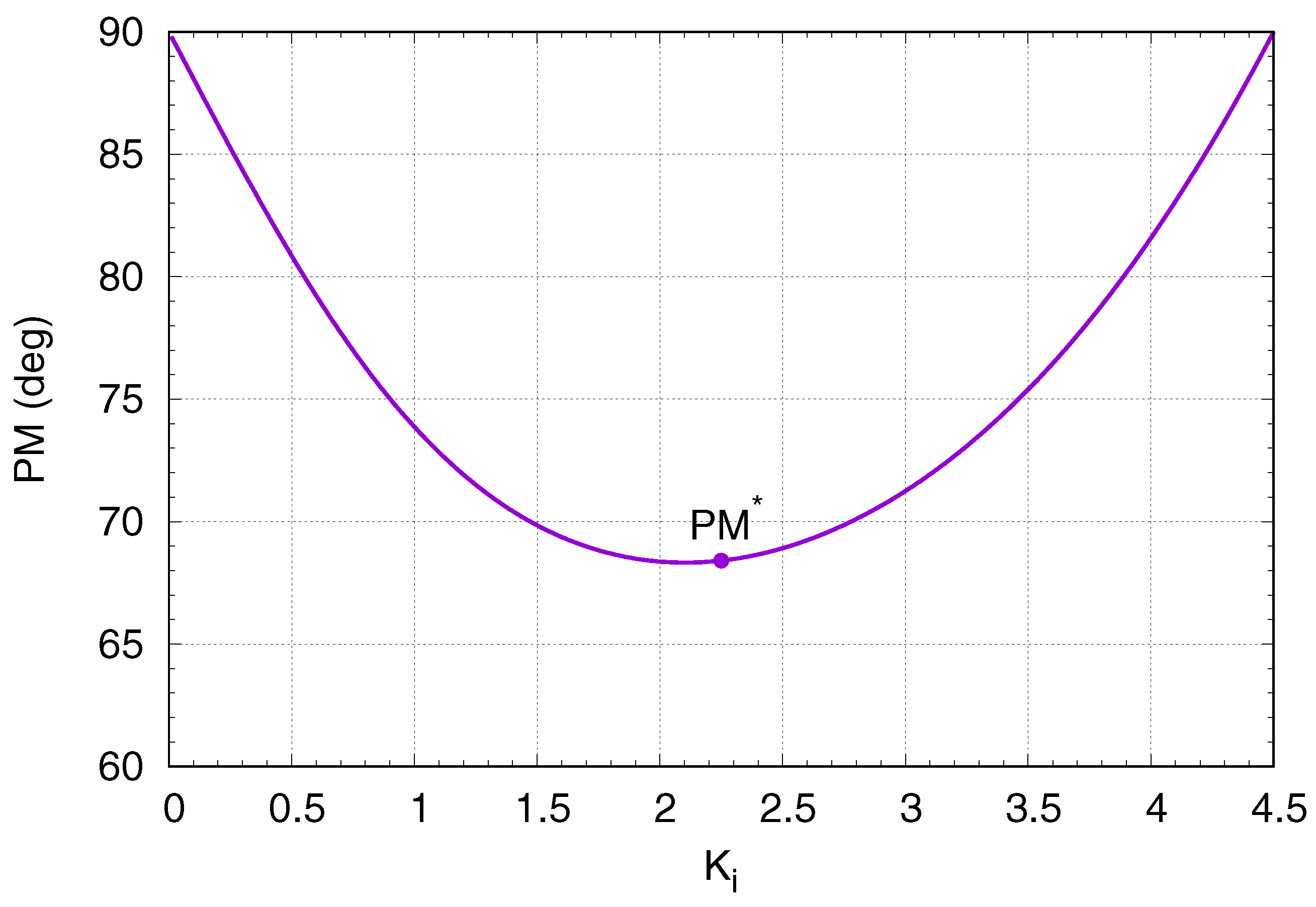
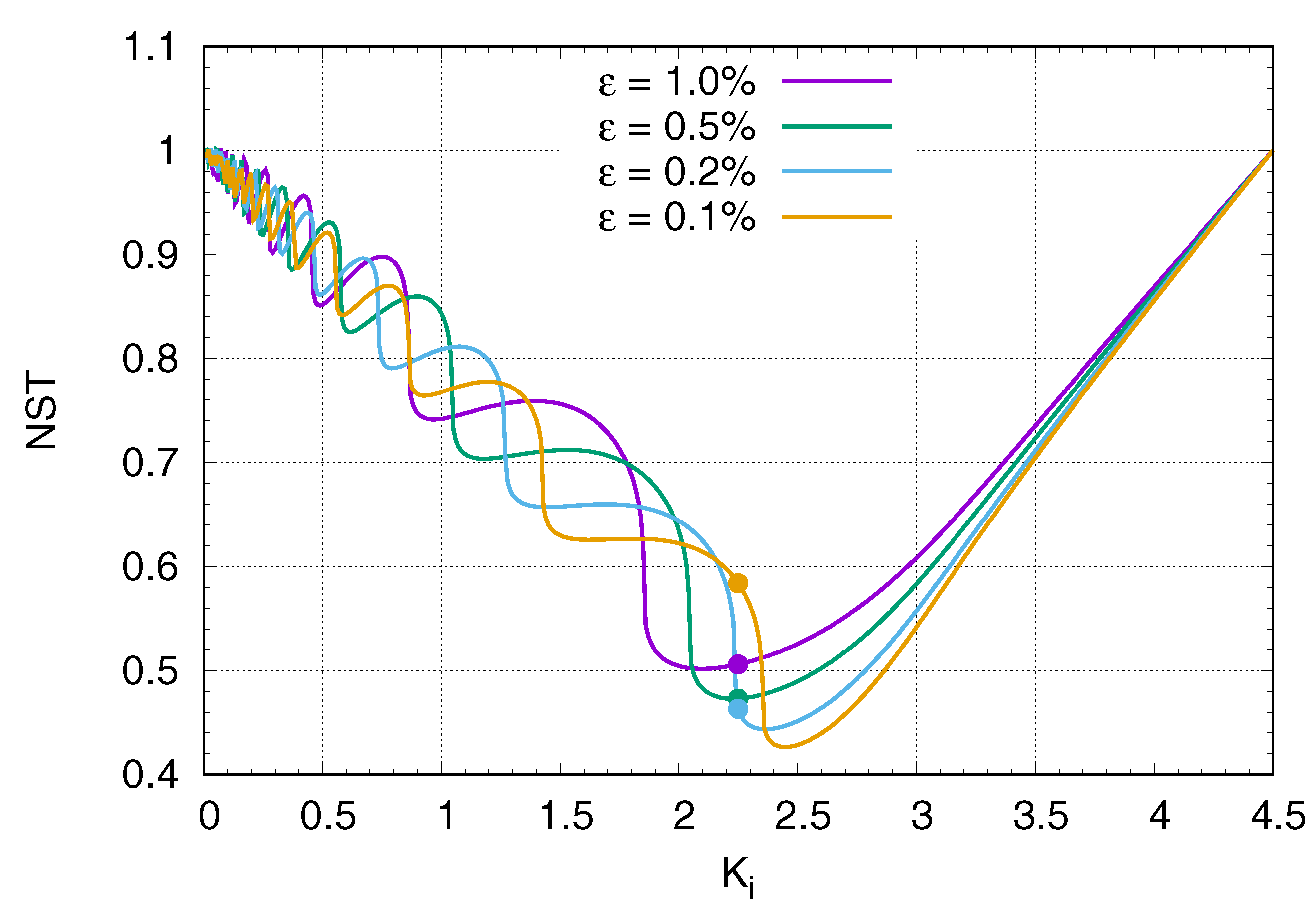
2.2. Optimization of the Dimensionless Settling Time
2.3. Extension to Generic Three-Pole Amplifiers
2.4. Extension to Slew-Rate Modeling
3. The Design Strategy with Settling-Time Constraints
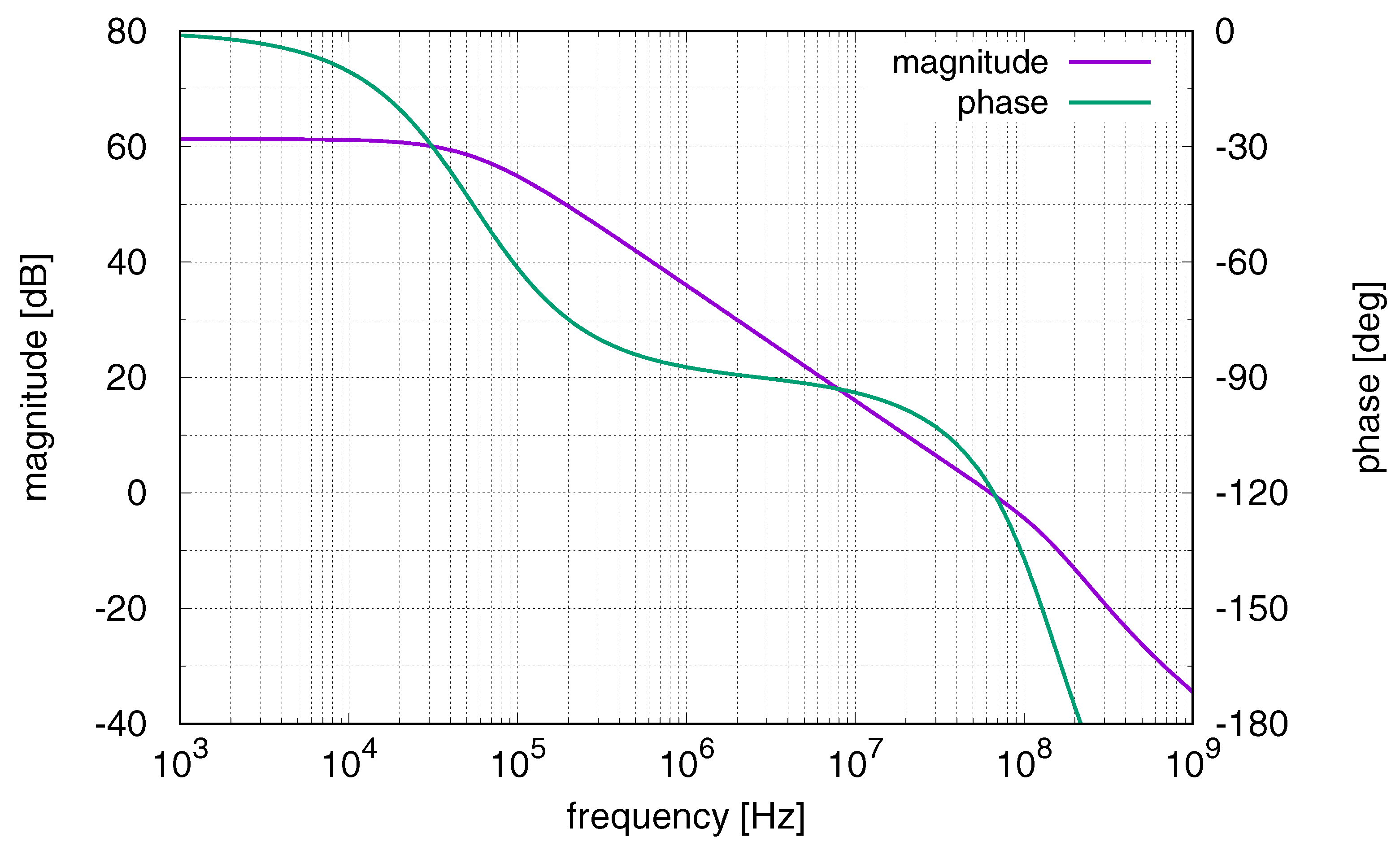
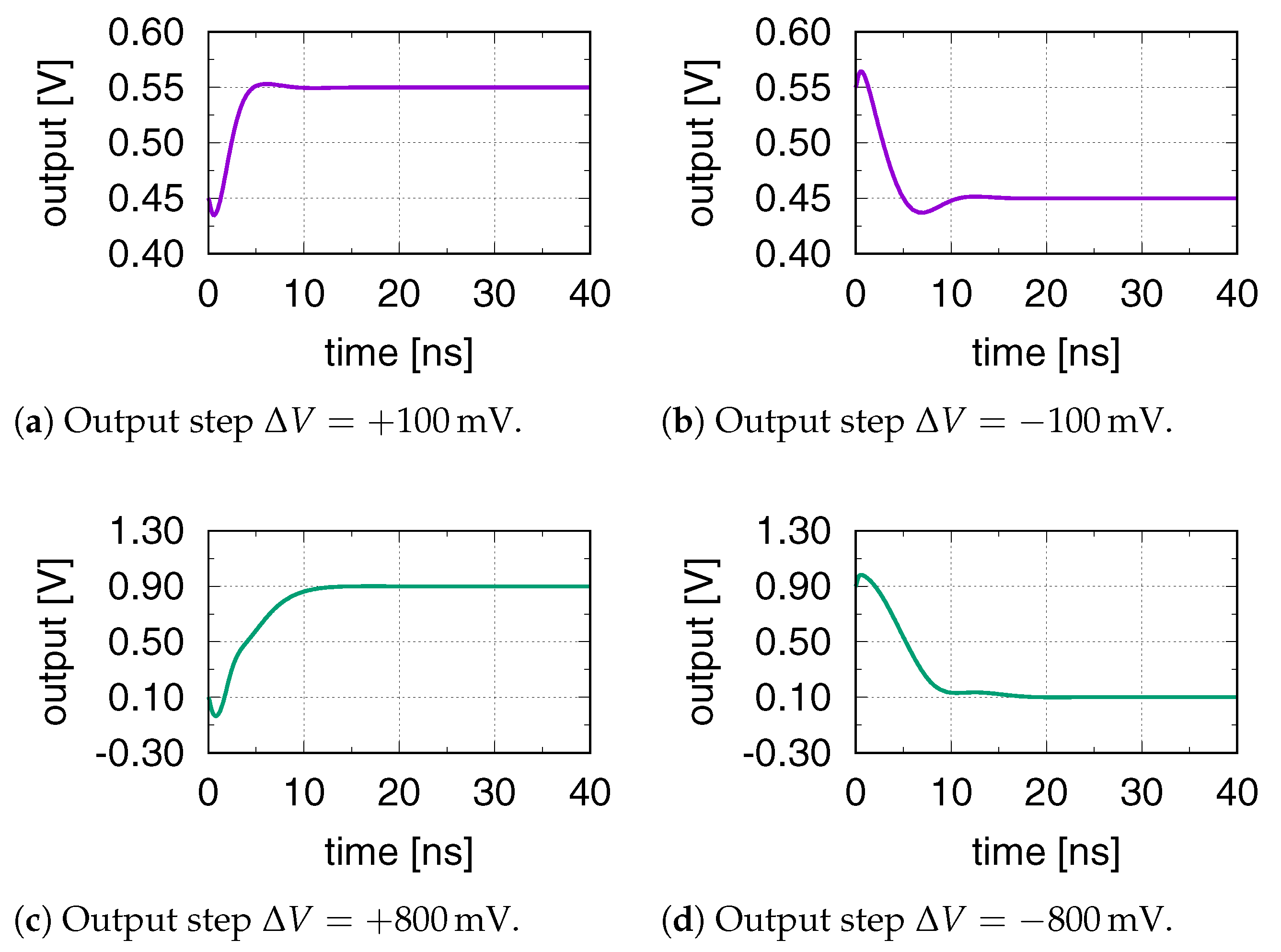
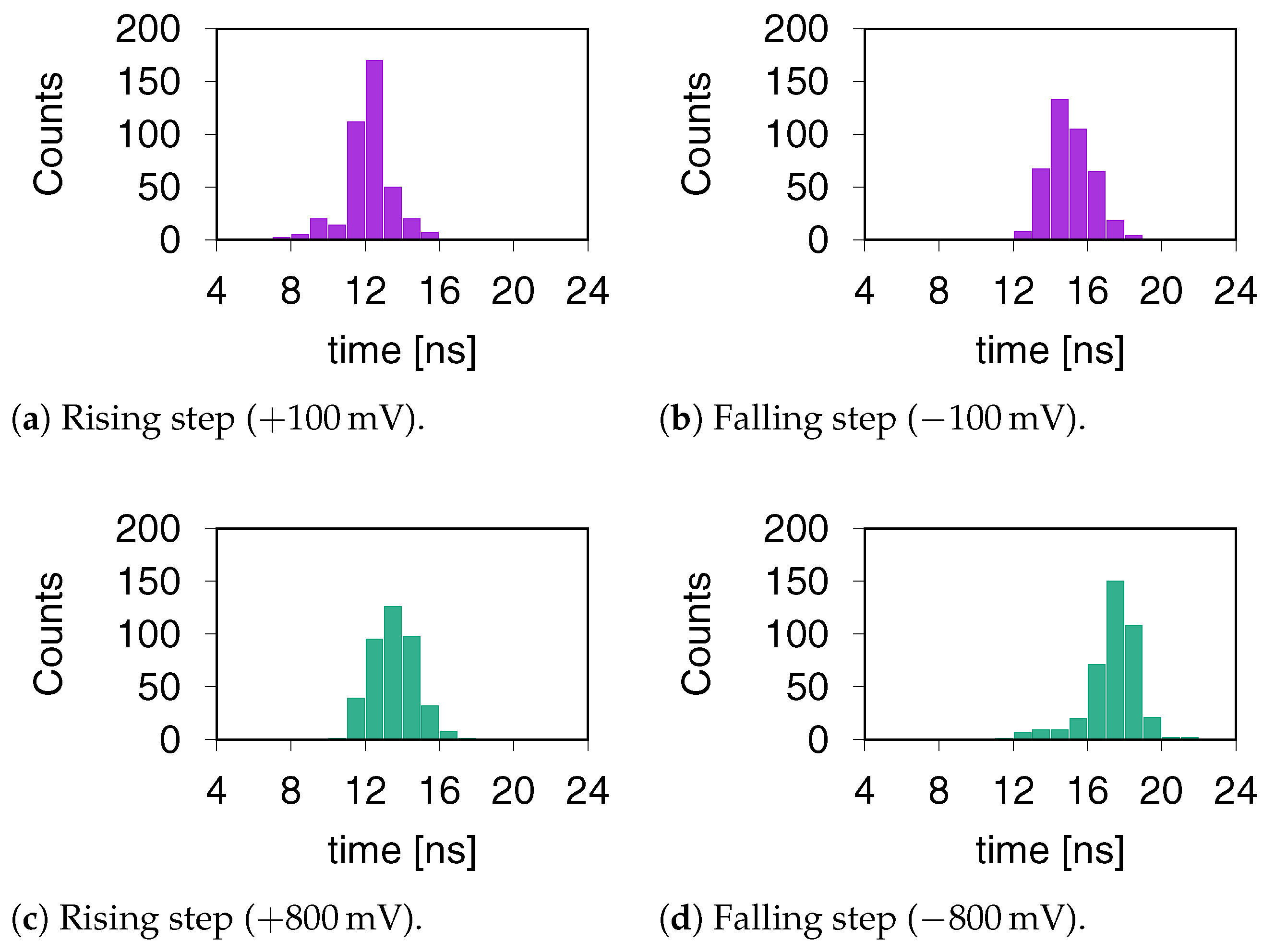
4. Design Example and Validation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Global Separation Factors
References
- Arnaud, A.; Fiorelli, R.; Galup-Montoro, C. Nanowatt, Sub-nS OTAs, With Sub-10-mV Input Offset, Using Series-Parallel Current Mirrors. IEEE J. Solid-State Circuits 2006, 41, 2009–2018. [Google Scholar] [CrossRef]
- Giustolisi, G.; Palumbo, G. Dynamic-biased capacitor-free NMOS LDO. IET Electron. Lett. 2009, 45, 1140–1141. [Google Scholar] [CrossRef]
- Giustolisi, G.; Palumbo, G.; Spitale, E. A 50-mA 1-nF Low-Voltage Low-Dropout Voltage Regulator for SoC Applications. ETRI J. 2010, 32, 520–529. [Google Scholar] [CrossRef]
- Taherzadeh-Sani, M.; Hamoui, A.A. A 1-V Process-Insensitive Current-Scalable Two-Stage Opamp With Enhanced DC Gain and Settling Behavior in 65-nm Digital CMOS. IEEE J. Solid-State Circuits 2011, 46, 660–668. [Google Scholar] [CrossRef]
- Giustolisi, G.; Palumbo, G. Compensation strategy for high-speed three-stage switched-capacitor amplifiers. IET Electron. Lett. 2016, 52, 1202–1204. [Google Scholar] [CrossRef]
- Centurelli, F.; Monsurrò, P.; Parisi, G.; Tommasino, P.; Trifiletti, A. A Topology of Fully Differential Class-AB Symmetrical OTA With Improved CMRR. IEEE Trans. Circuits Syst. II 2018, 65, 1504–1508. [Google Scholar] [CrossRef]
- Centurelli, F.; Monsurrò, P.; Parisi, G.; Tommasino, P.; Trifiletti, A. A 0.6 V class-AB rail-to-rail CMOS OTA VDD exploiting threshold lowering. IET Electron. Lett. 2018, 54, 930–932. [Google Scholar] [CrossRef]
- Cellucci, D.; Centurelli, F.; Di Stefano, V.; Monsurrò, P.; Pennisi, S.; Scotti, G.; Trifiletti, A. 0.6-V CMOS cascode OTA with complementary gate-driven gain-boosting and forward body bias. Int. J. Circ. Theor. Appl. 2020, 48, 15–27. [Google Scholar] [CrossRef]
- Prasopsin, P.; Wattanapanitch, W. A Sub-Microwatt Class-AB Super Buffer: Frequency Compensation for Settling-Time Improvement. IEEE Trans. Circuits Syst. II 2018, 65, 26–30. [Google Scholar] [CrossRef]
- Lavalle-Aviles, F.; Torres, J.; Sánchez-Sinencio, E. A High Power Supply Rejection and Fast Settling Time Capacitor-Less LDO. IEEE Trans. Power Electron. 2019, 34, 474–484. [Google Scholar] [CrossRef]
- Mandal, D.; Desai, C.; Bakkaloglu, B.; Kiaei, S. Adaptively Biased Output Cap-Less NMOS LDO With 19 ns Settling Time. IEEE Trans. Circuits Syst. II 2019, 66, 167–171. [Google Scholar] [CrossRef]
- Pugliese, A.; Amoroso, F.A.; Cappuccino, G.; Cocorullo, G. Settling time optimisation for two-stage CMOS amplifiers with current-buffer Miller compensation. IET Electron. Lett. 2007, 43, 1257–1258. [Google Scholar] [CrossRef]
- Pugliese, A.; Cappuccino, G.; Cocorullo, G. Nested Miller compensation capacitor sizing rules for fast-settling amplifier design. IET Electron. Lett. 2005, 41, 573–575. [Google Scholar] [CrossRef]
- Nguyen, R.; Murmann, B. The Design of Fast-Settling Three-Stage Amplifiers Using the Open-Loop Damping Factor as a Design Parameter. IEEE Trans. Circuits Syst. I 2010, 57, 1244–1254. [Google Scholar] [CrossRef]
- Pugliese, A.; Cappuccino, G.; Cocorullo, G. Design Procedure for Settling Time Minimization in Three-Stage Nested-Miller Amplifiers. IEEE Trans. Circuits Syst. II 2008, 55, 1–5. [Google Scholar] [CrossRef]
- Pugliese, A.; Amoroso, F.A.; Cappuccino, G.; Cocorullo, G. Settling Time Optimization for Three-Stage CMOS Amplifier Topologies. IEEE Trans. Circuits Syst. I 2009, 56, 2569–2582. [Google Scholar] [CrossRef]
- Seth, S.; Murmann, B. Settling Time and Noise Optimization of a Three-Stage Operational Transconductance Amplifier. IEEE Trans. Circuits Syst. I 2013, 60, 1168–1174. [Google Scholar] [CrossRef]
- Giustolisi, G.; Palumbo, G. Bessel-like compensation of three-stage operational transconductance amplifiers. Int. J. Circ. Theor. Appl. 2018, 46, 729–747. [Google Scholar] [CrossRef]
- Giustolisi, G.; Palumbo, G. Design of CMOS three-stage amplifiers for near-to-minimum settling-time. Microelectron. J. 2021, 107. [Google Scholar] [CrossRef]
- Gray, P.; Meyer, R. Recent Advances in Monolithic Operational Amplifier Design. IEEE Trans. Circuits Syst. 1974, CAS-21, 317–327. [Google Scholar] [CrossRef]
- Kamath, B.Y.; Meyer, R.G.; Gray, P.R. Relationship Between Frequency Response and Settling Time of Operational Amplifiers. IEEE J. Solid-State Circuits 1974, SC-9, 347–352. [Google Scholar] [CrossRef]
- Chuang, C.T. Analysis of the Settling Behavior of an Operational Amplifier. IEEE J. Solid-State Circuits 1982, SC-17, 74–80. [Google Scholar] [CrossRef]
- Lin, J.-C.; Nevin, J.H. A Modified Time-Domain Model for Nonlinear Analysis of an Operational Amplifier. IEEE J. Solid-State Circuits 1986, SC-21, 478–483. [Google Scholar] [CrossRef]
- Wang, F.; Harjani, R. An Improved Model for the Slewing Behavior of Opamps. IEEE Trans. Circuits Syst. II 1995, 42, 679–681. [Google Scholar] [CrossRef]
- Yavari, M.; Maghari, N.; Shoaei, O. An Accurate Analysis of Slew Rate for Two-Stage CMOS Opamps. IEEE Trans. Circuits Syst. II 2005, 52, 164–167. [Google Scholar] [CrossRef]
- Rezaee-Dehsorkh, H.; Ravanshad, N.; Lotfi, R.; Mafinezhad, K. Modified Model for Settling Behavior of Operational Amplifiers in Nanoscale CMOS. IEEE Trans. Circuits Syst. II 2009, 56, 348–388. [Google Scholar] [CrossRef]
- Ruiz-Amaya, J.; Delgado-Restituto, M.; Rodríguez-Vázquez, Á. Accurate Settling-Time Modeling and Design Procedures for Two-Stage Miller-Compensated Amplifiers for Switched-Capacitor Circuits. IEEE Trans. Circuits Syst. I 2009, 56, 1077–1087. [Google Scholar] [CrossRef]
- Giustolisi, G.; Palumbo, G. Design of Three-Stage OTA Based on Settling-Time Requirements Including Large and Small Signal Behavior. IEEE Trans. Circuits Syst. I 2021, 68, 998–1011. [Google Scholar] [CrossRef]
- Giustolisi, G.; Palumbo, G. Robust design of CMOS amplifiers oriented to settling-time specification. Int. J. Circ. Theor. Appl. 2017, 45, 1329–1348. [Google Scholar] [CrossRef]
- Giustolisi, G.; Palumbo, G. Three-Stage Dynamic-Biased CMOS Amplifier With a Robust Optimization of the Settling Time. IEEE Trans. Circuits Syst. I 2015, 62, 2641–2651. [Google Scholar] [CrossRef]
- Giustolisi, G.; Palumbo, G. In-depth Analysis of Pole-Zero Compensations in CMOS Operational Transconductance Amplifiers. IEEE Trans. Circuits Syst. I 2019, 66, 4557–4570. [Google Scholar] [CrossRef]
- Cabrera-Bernal, E.; Pennisi, S.; Grasso, A.D.; Torralba, A.; Gonzalez Carvajal, R. 0.7-V Three-Stage Class-AB CMOS Operational Transconductance Amplifier. IEEE Trans. Circuits Syst. I 2016, 63, 1807–1815. [Google Scholar] [CrossRef]
- Giustolisi, G.; Palumbo, G.; Pennisi, S. Class-AB CMOS output stages suitable for low-voltage amplifiers in nanometer technologies. Microelectron. J. 2019, 92. [Google Scholar] [CrossRef]
- Silveira, F.; Flandre, D.; Jespers, P.G.A. A gm/ID based methodology for the design of CMOS analog circuits and its application to the synthesis of a silicon-on-insulator micropower OTA. IEEE J. Solid-State Circuits 1996, 31, 1314–1319. [Google Scholar] [CrossRef]
- Kinget, P.R. Device Mismatch and Tradeoffs in the Design of Analog Circuits. IEEE J. Solid-State Circuits 2005, 40, 1212–1224. [Google Scholar] [CrossRef]


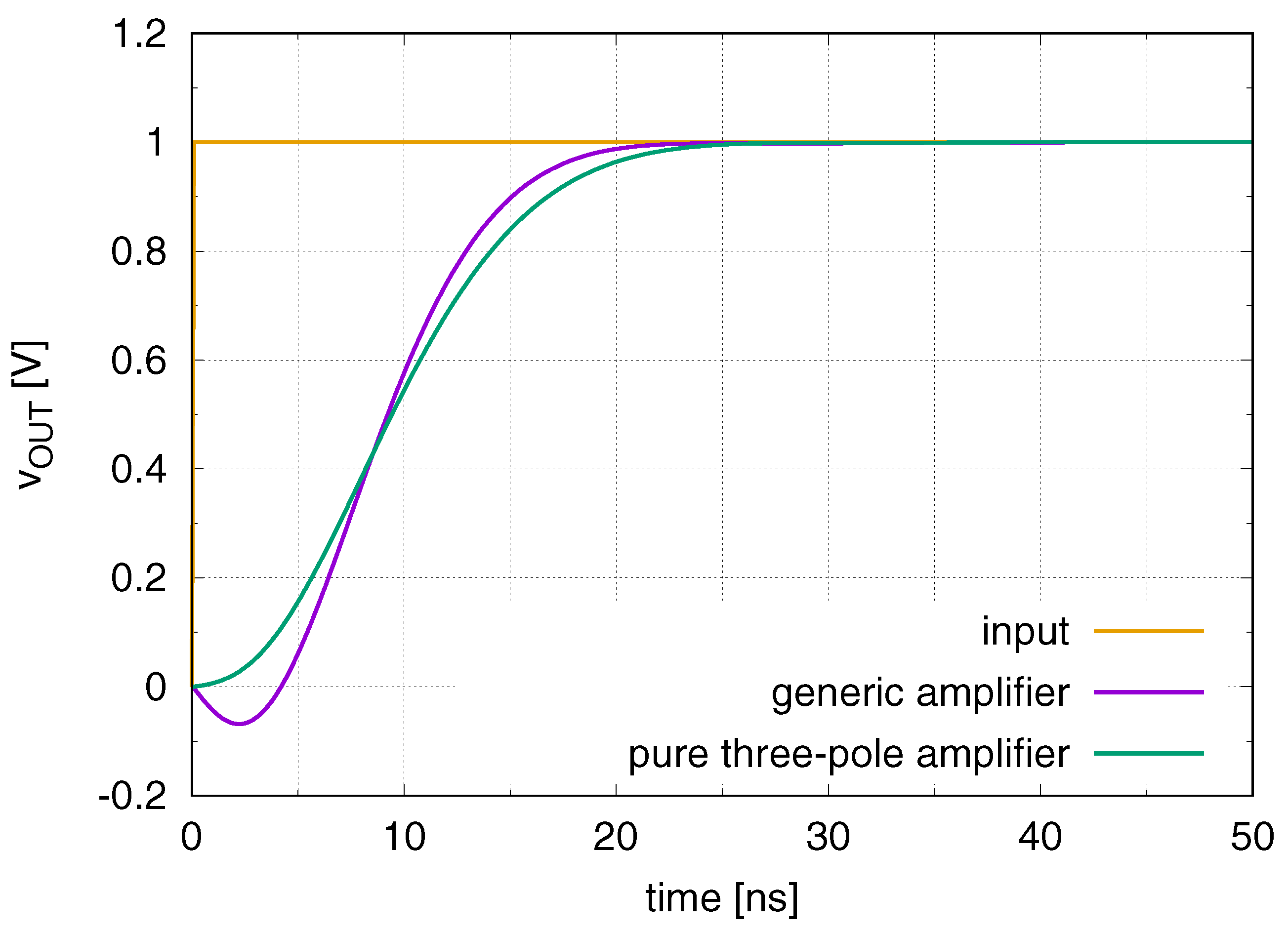
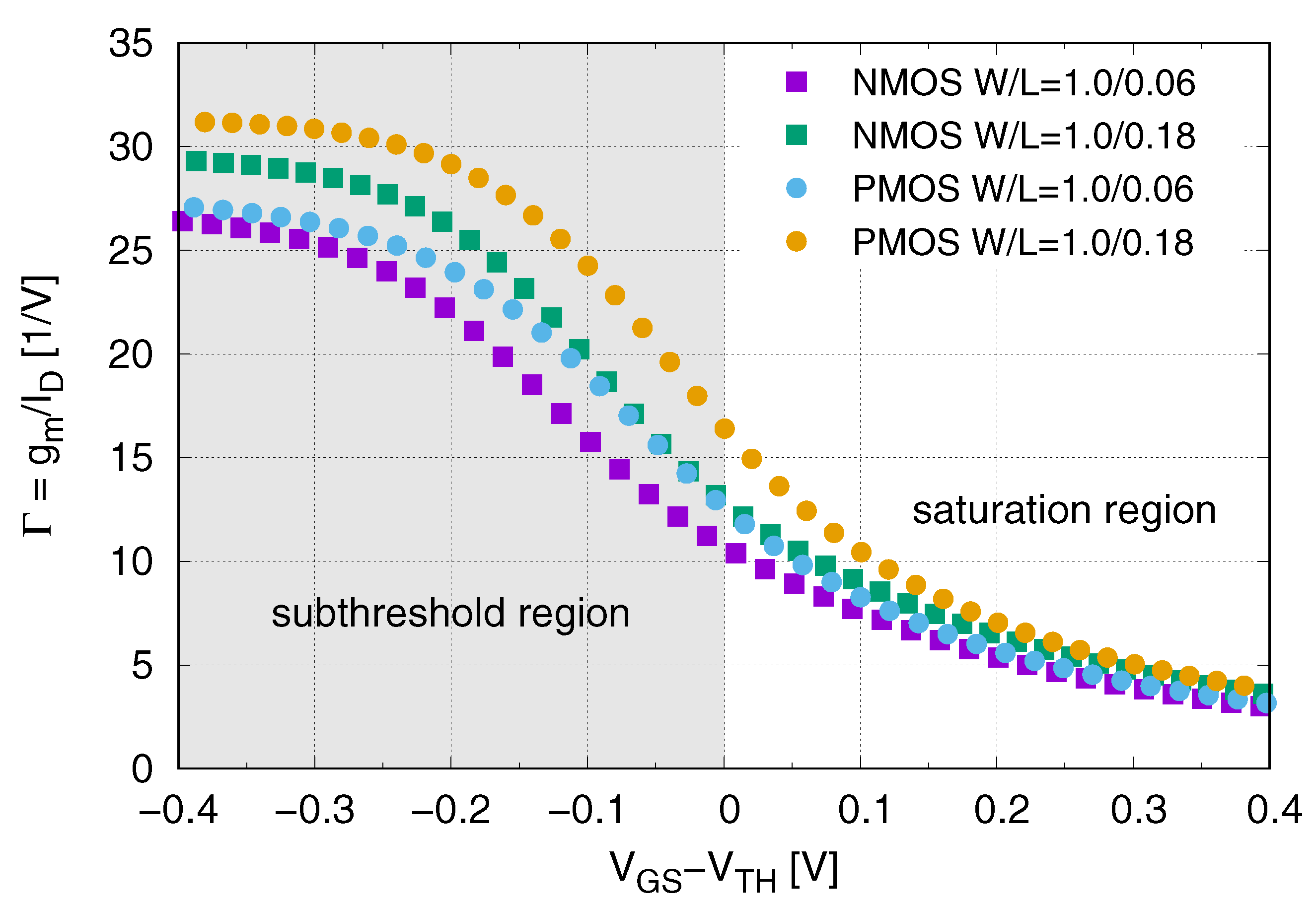
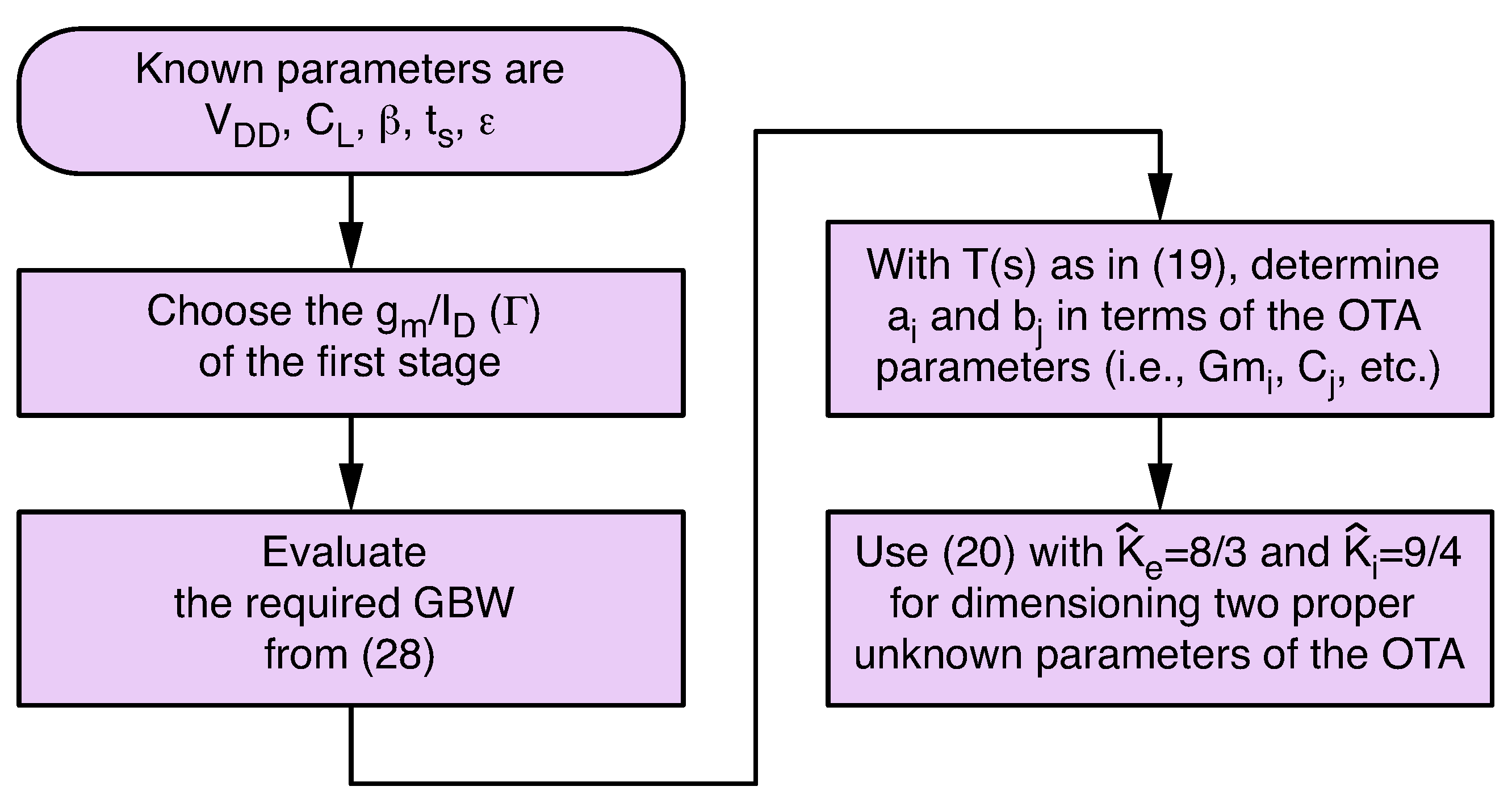
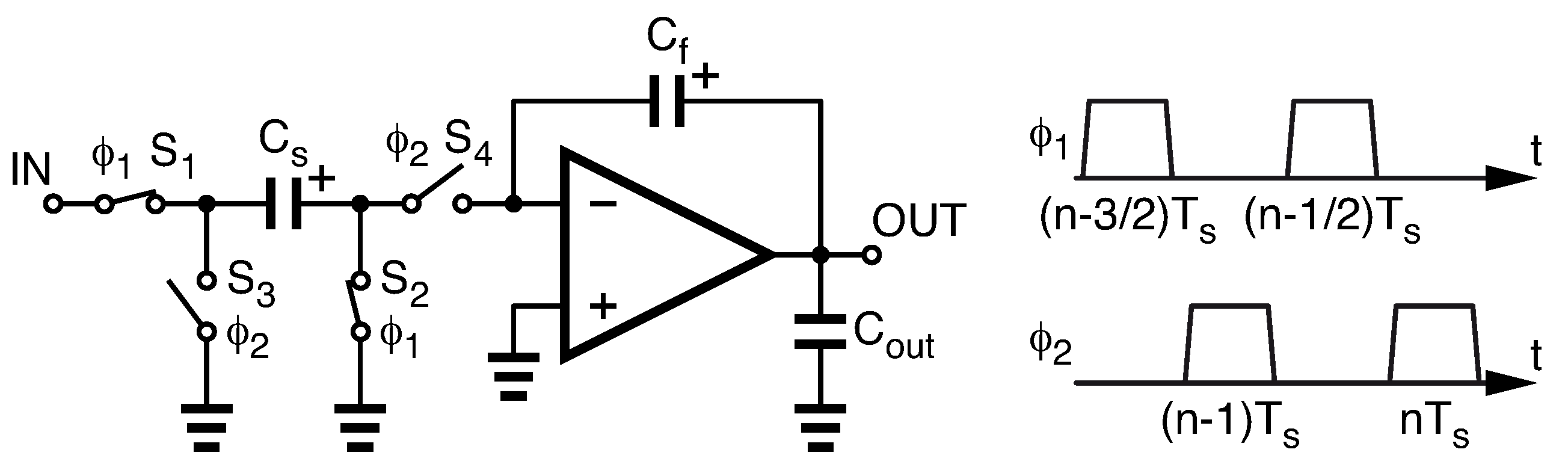

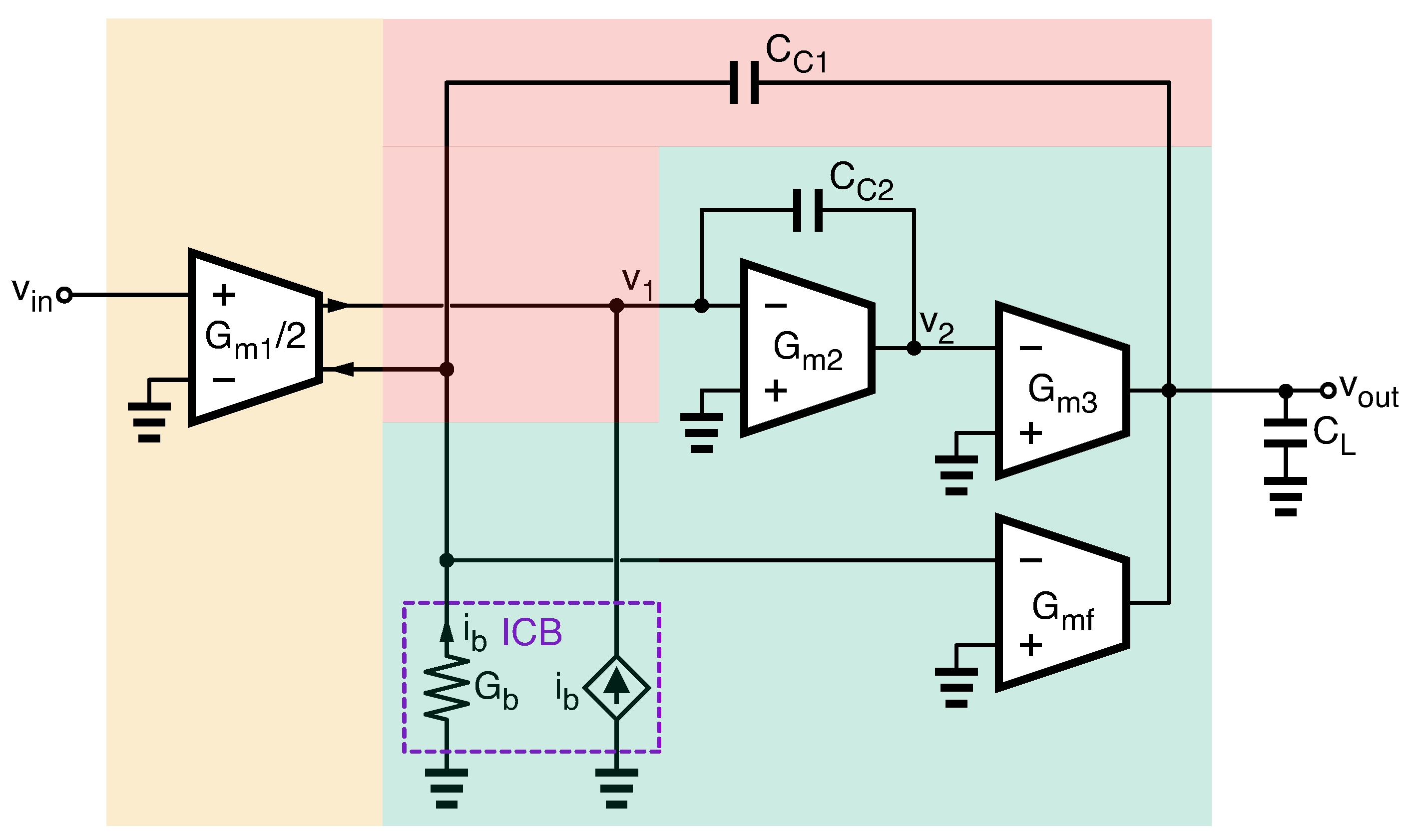

% | Generic Amplifier (ns) ( [–]) | Pure Three-Pole Amplifier (ns) ( [–]) |
|---|---|---|
| 1.0 | 20.4 (0.44) | 23.5 (0.51) |
| 0.5 | 21.8 (0.41) | 25.3 (0.48) |
| 0.2 | 30.4 (0.49) | 29.2 (0.47) |
| 0.1 | 35.8 (0.52) | 40.4 (0.58) |
| n – | m – | (μA/V) | (μA/V) | (μA/V) | (pF) | (pF) | (μA) | FOM (–) | Noise (nV/Hz) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2000 | 2000 | 2000 | 2.40 | 2.40 | 500 | 0.50 | 4.70 |
| 1 | 2 | 464 | 929 | 929 | 0.56 | 0.51 | 174 | 1.42 | 9.76 |
| 1 | 3 | 252 | 756 | 756 | 0.30 | 0.27 | 126 | 2.00 | 13.2 |
| 1 | 4 | 172 | 687 | 687 | 0.21 | 0.18 | 107 | 2.29 | 16.0 |
| 2 | 1 | 663 | 332 | 663 | 0.80 | 1.33 | 145 | 1.71 | 8.16 |
| 2 | 2 | 6611 | 6611 | 13221 | 7.97 | 17.7 | 2066 | 0.12 | 2.58 |
| 2 | 3 | 658 | 987 | 1975 | 0.79 | 1.14 | 267 | 0.93 | 8.19 |
| 2 | 4 | 309 | 619 | 1239 | 0.37 | 0.45 | 155 | 1.62 | 11.9 |
| Transistor | Aspect Ratio |
|---|---|
| M1 *, M2 * | |
| M3, M4 | |
| M5 | |
| M6, M9 | |
| M7 | |
| M8 | |
| M10 ** | |
| MB |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giustolisi, G.; Palumbo, G. Efficient Design Strategy for Optimizing the Settling Time in Three-Stage Amplifiers Including Small- and Large-Signal Behavior. Electronics 2021, 10, 612. https://doi.org/10.3390/electronics10050612
Giustolisi G, Palumbo G. Efficient Design Strategy for Optimizing the Settling Time in Three-Stage Amplifiers Including Small- and Large-Signal Behavior. Electronics. 2021; 10(5):612. https://doi.org/10.3390/electronics10050612
Chicago/Turabian StyleGiustolisi, Gianluca, and Gaetano Palumbo. 2021. "Efficient Design Strategy for Optimizing the Settling Time in Three-Stage Amplifiers Including Small- and Large-Signal Behavior" Electronics 10, no. 5: 612. https://doi.org/10.3390/electronics10050612
APA StyleGiustolisi, G., & Palumbo, G. (2021). Efficient Design Strategy for Optimizing the Settling Time in Three-Stage Amplifiers Including Small- and Large-Signal Behavior. Electronics, 10(5), 612. https://doi.org/10.3390/electronics10050612







