High Velocity Lane Keeping Control Method Based on the Non-Smooth Finite-Time Control for Electric Vehicle Driven by Four Wheels Independently
Abstract
:1. Introduction
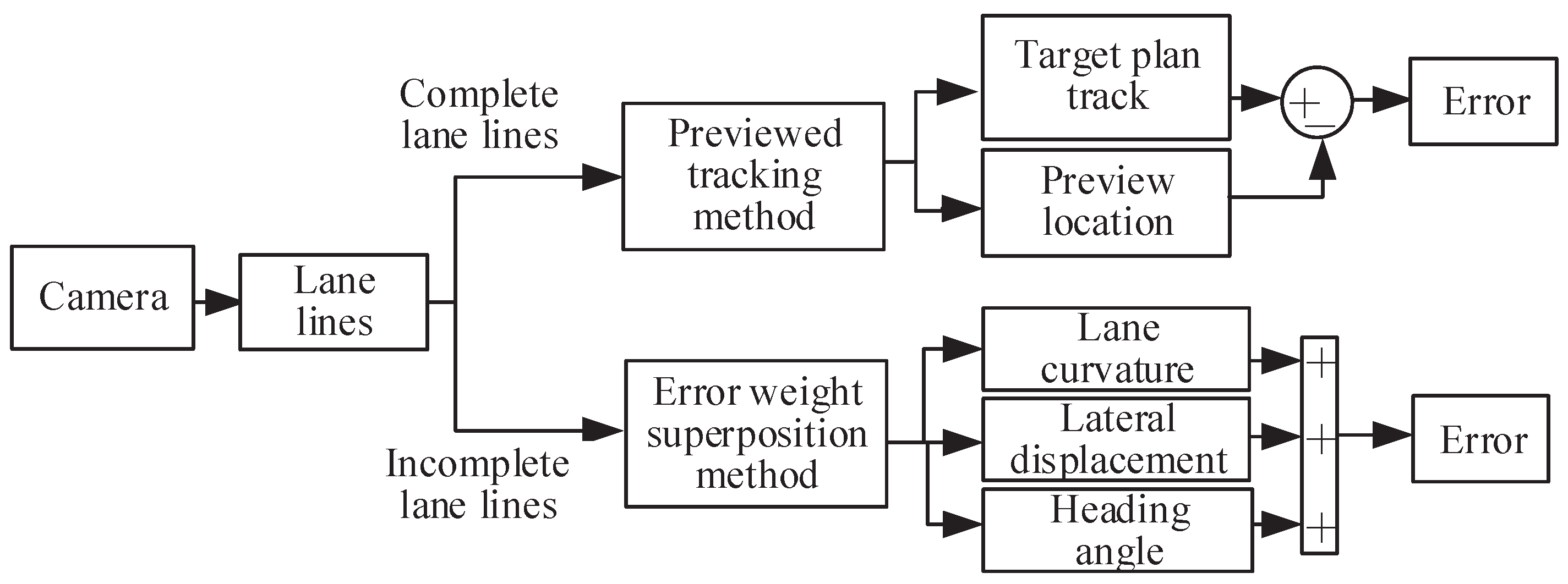
- Two kinds of tracking error computing methods of the lane keeping, previewed tracking and error weight superposition, are proposed to deal with different conditions for EV-DFWI.
- An NoS-FT lane keeping controller was designed, which can stabilize the vehicle to run in the desired lane when suffers external disturbance. The controller is proved by the Lyapunov method.
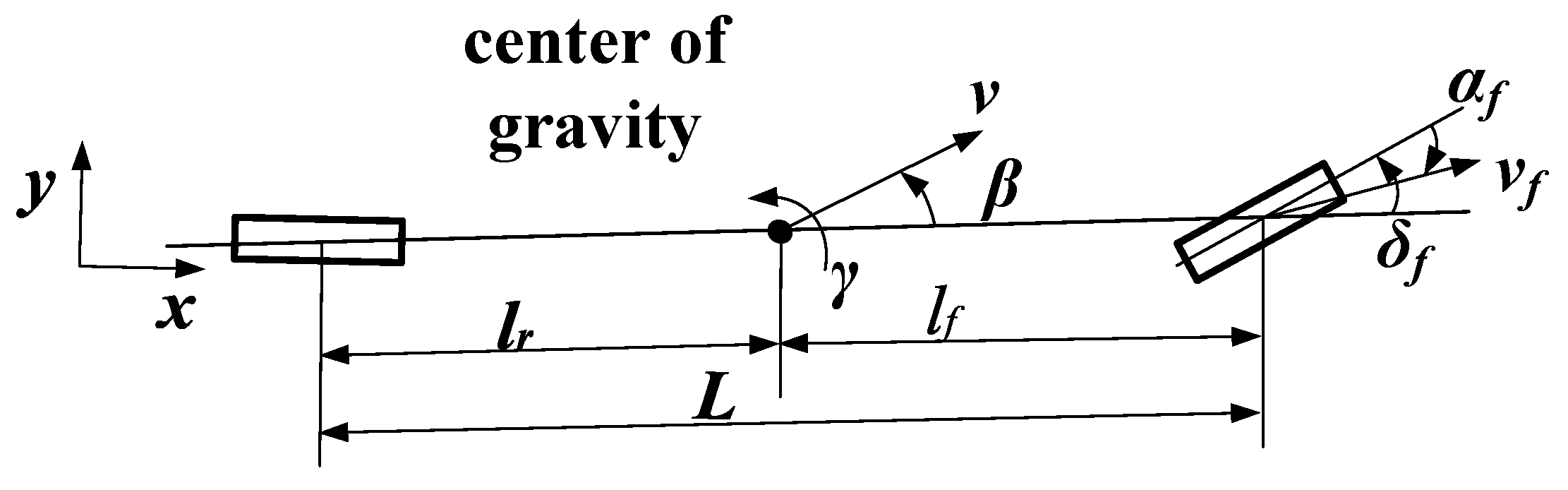
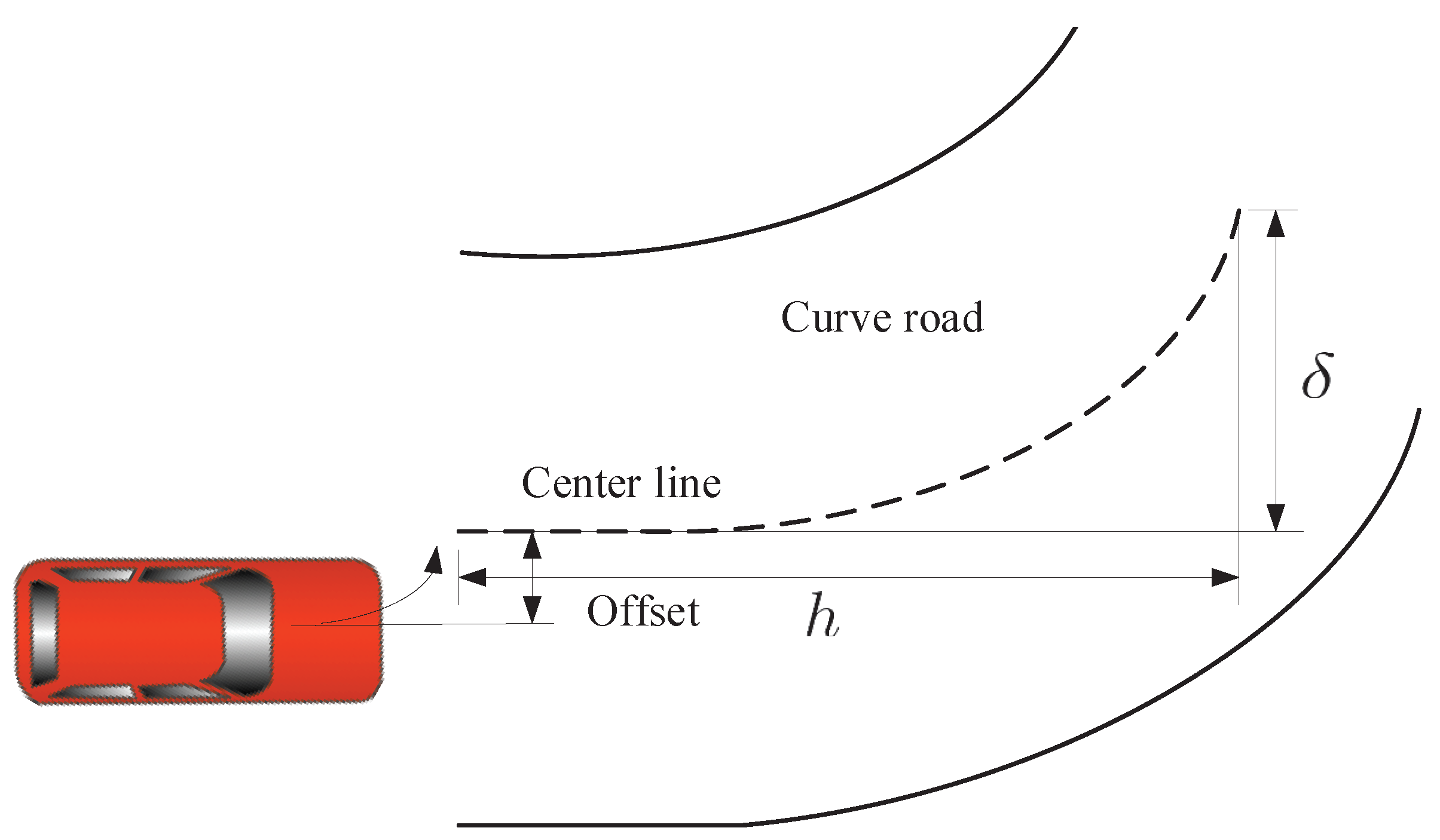
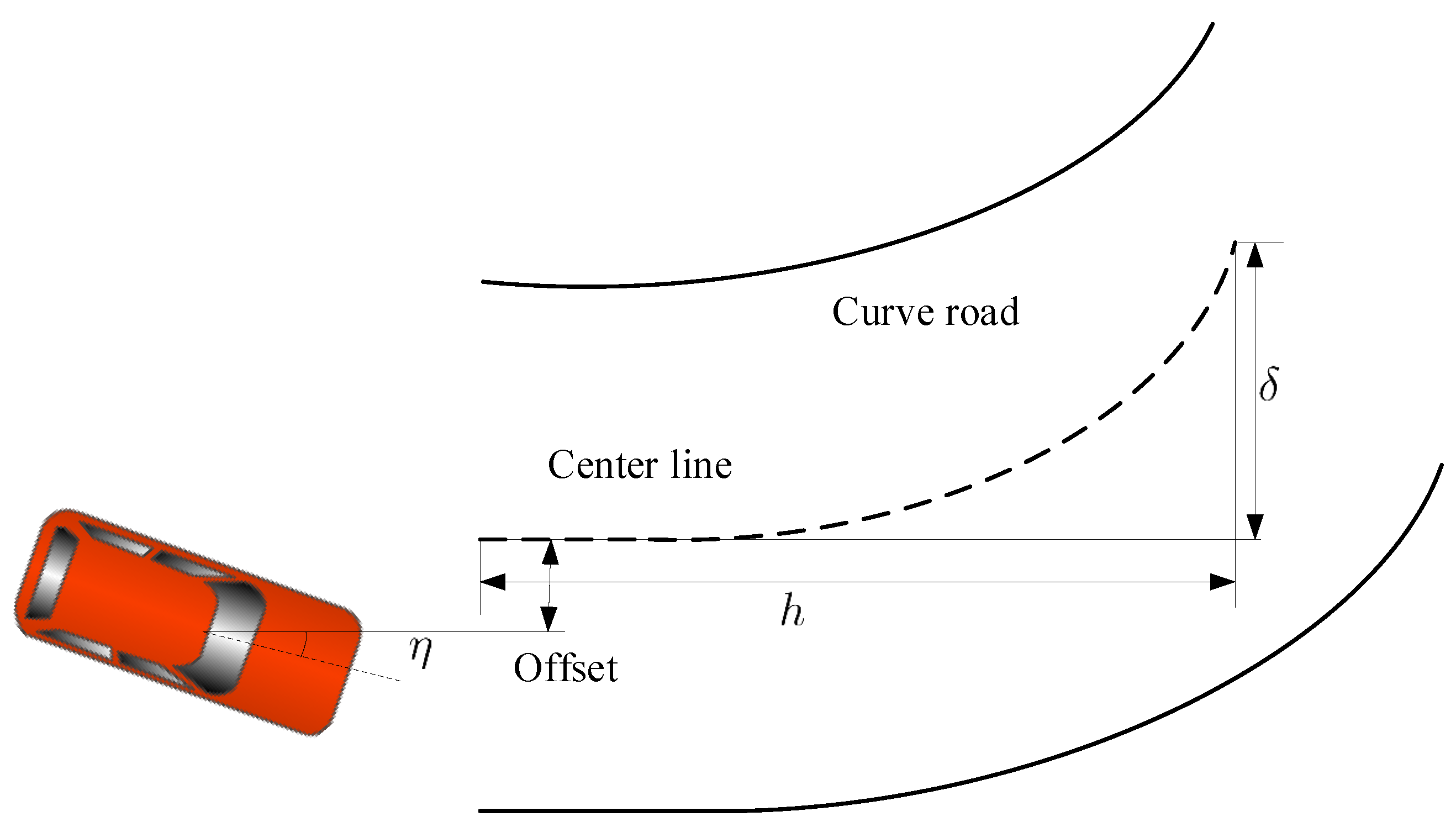
2. Modeling of the LKC for the EV-DFWI
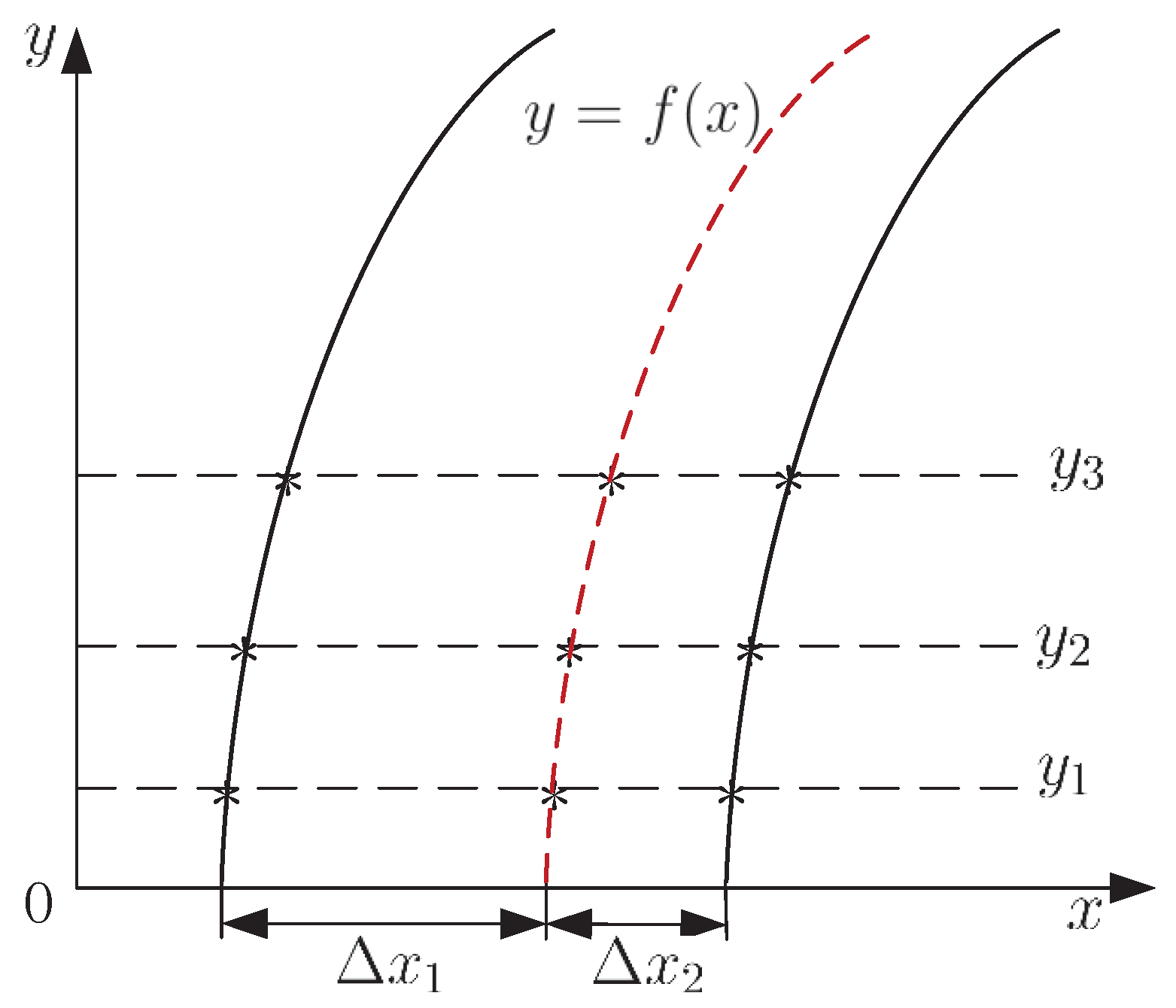
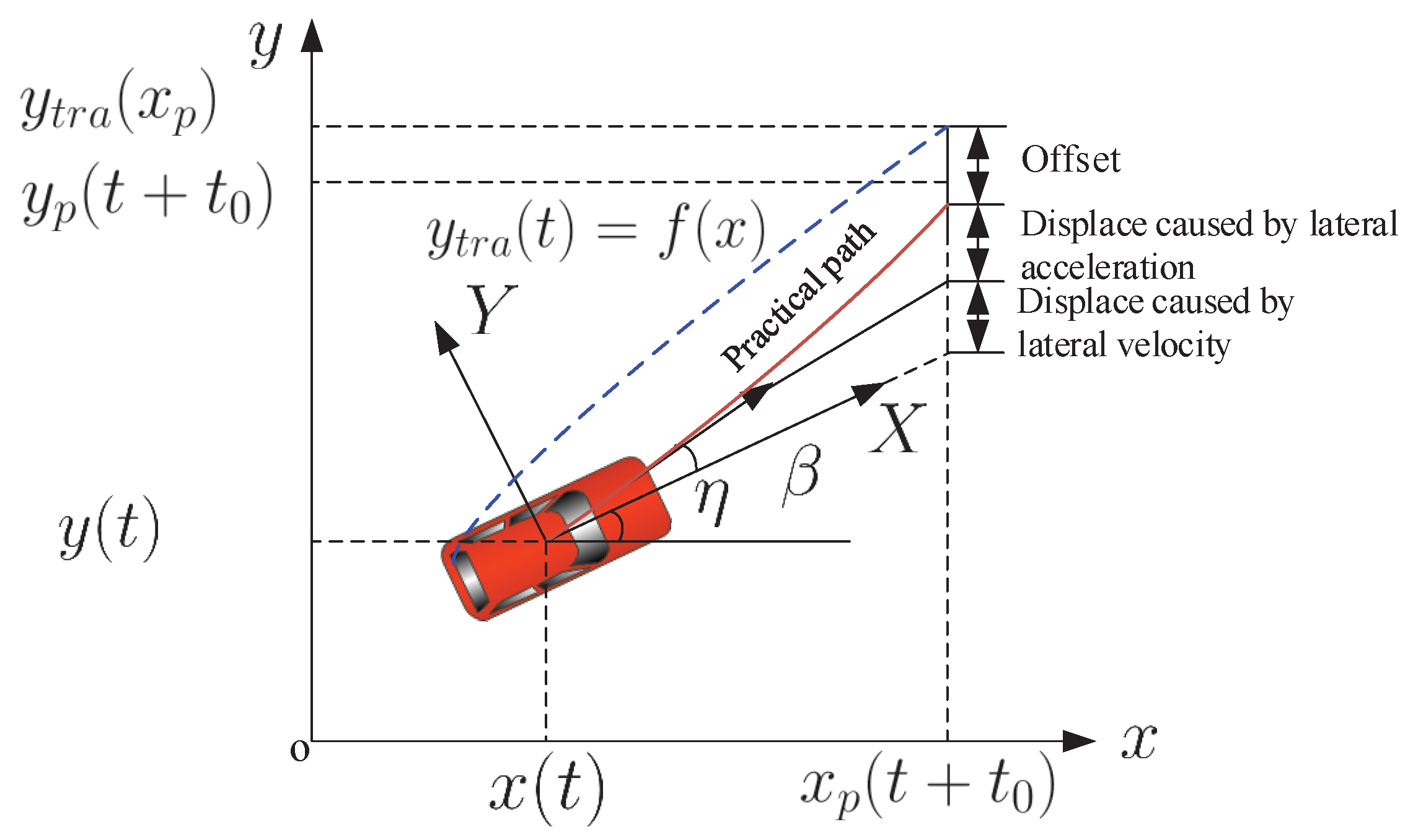
Tracking Error Computing of the LKC
3. Design of the Lane Keeping Controller Based on NoS-FT Control Method
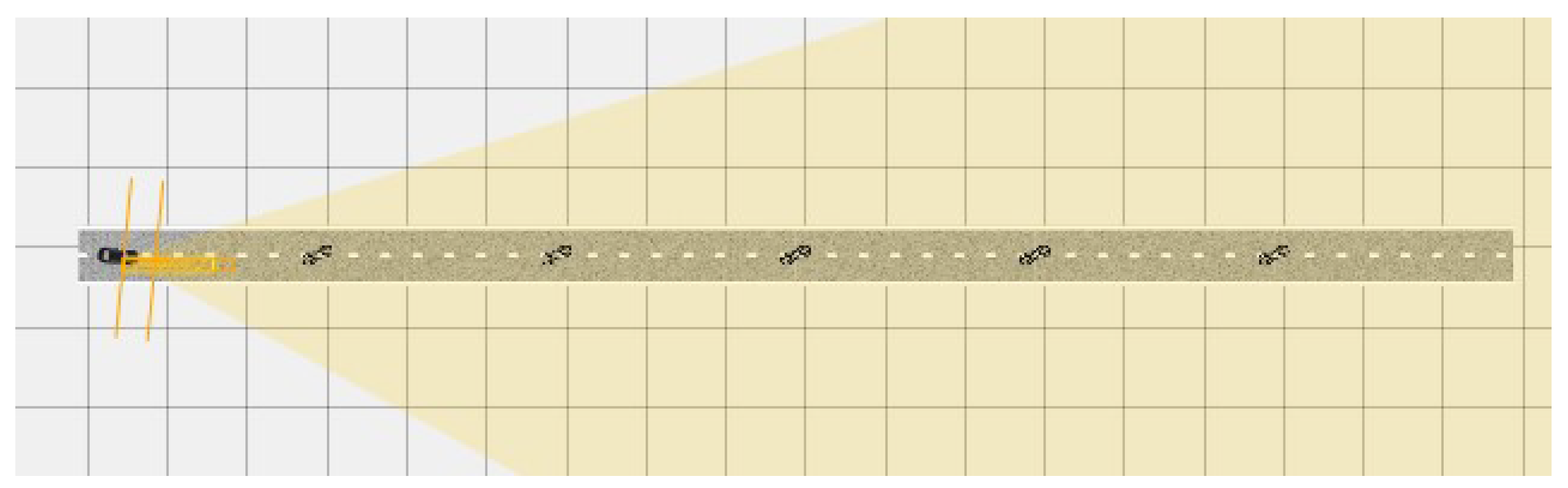
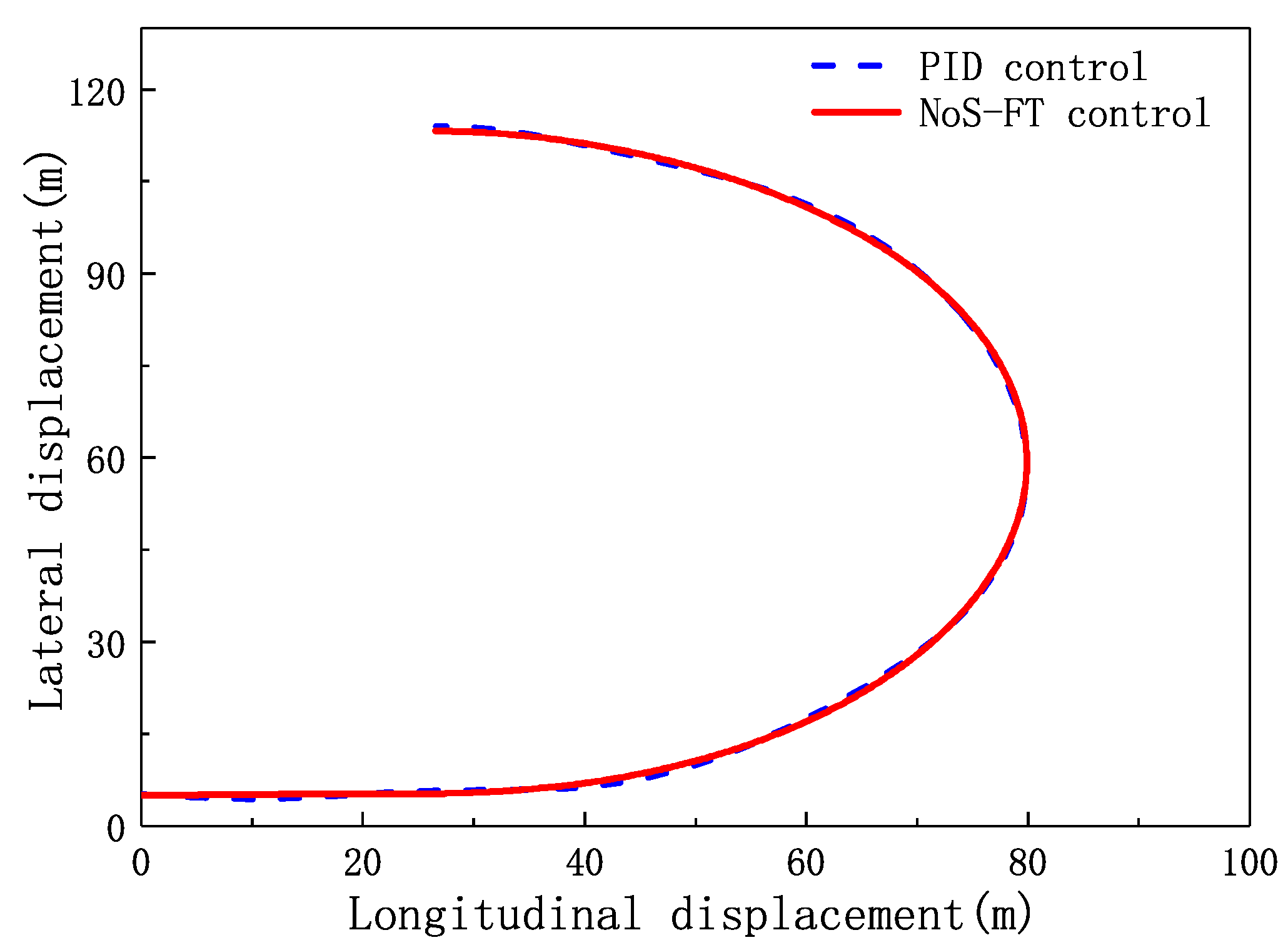
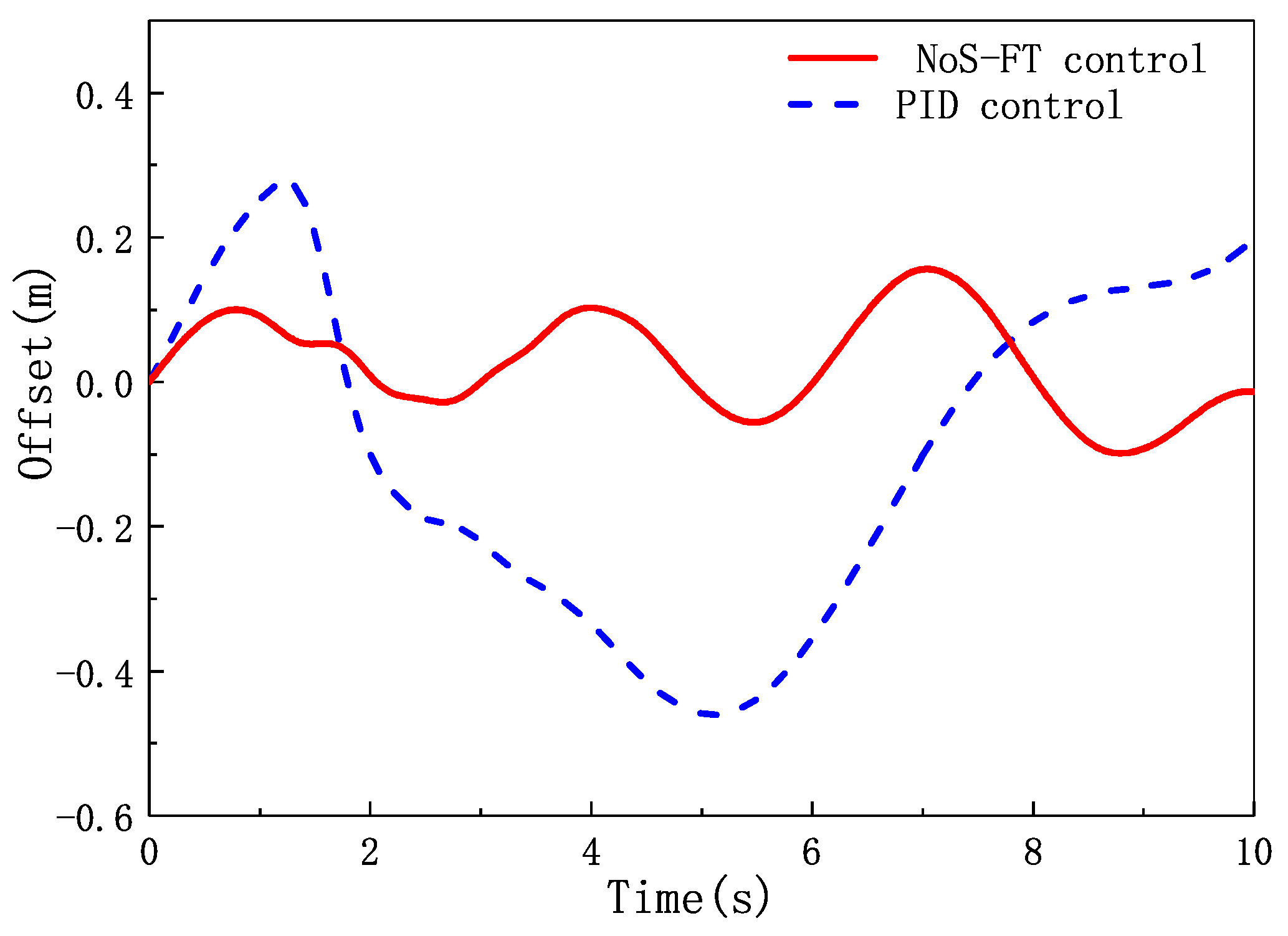
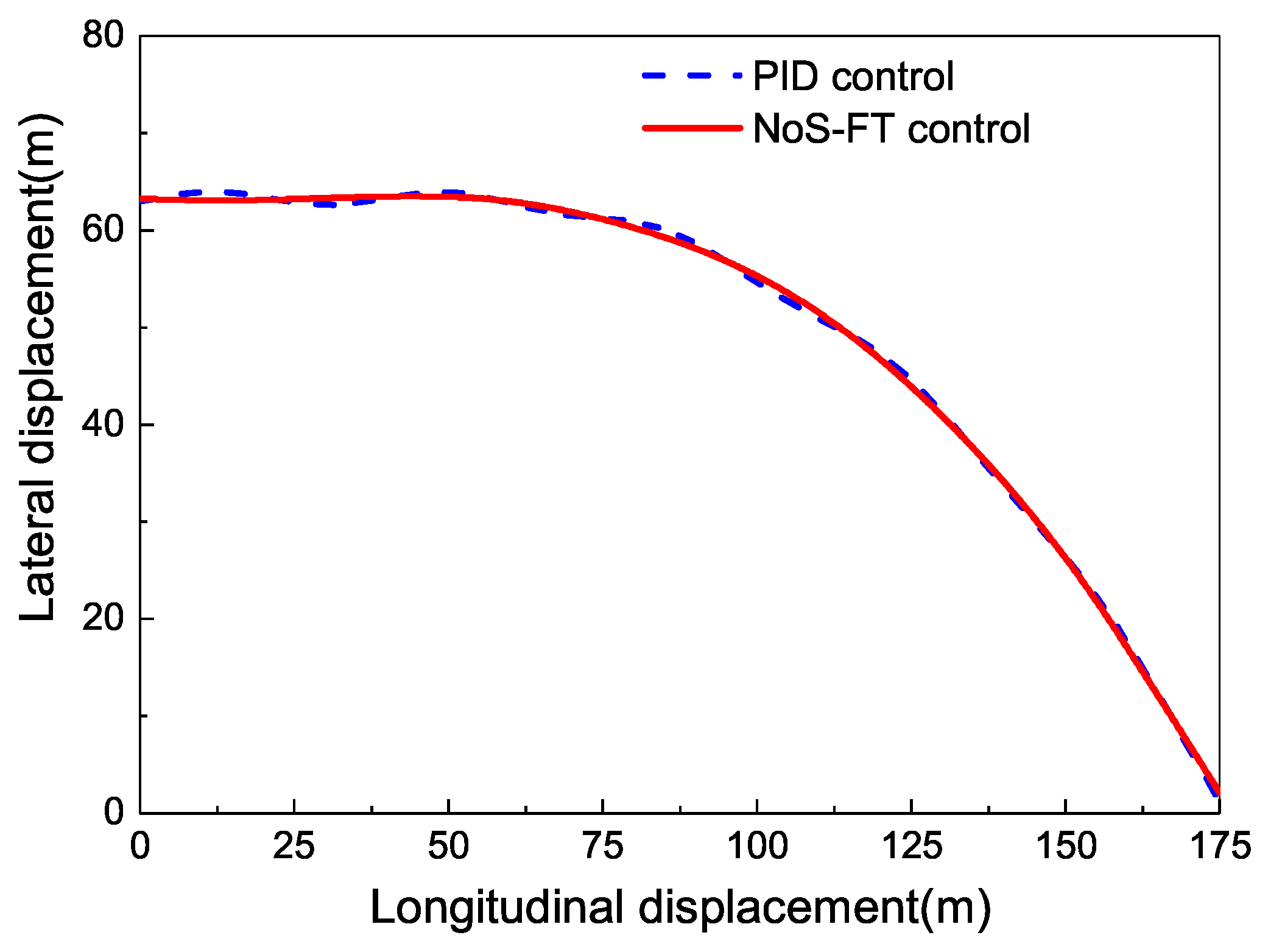
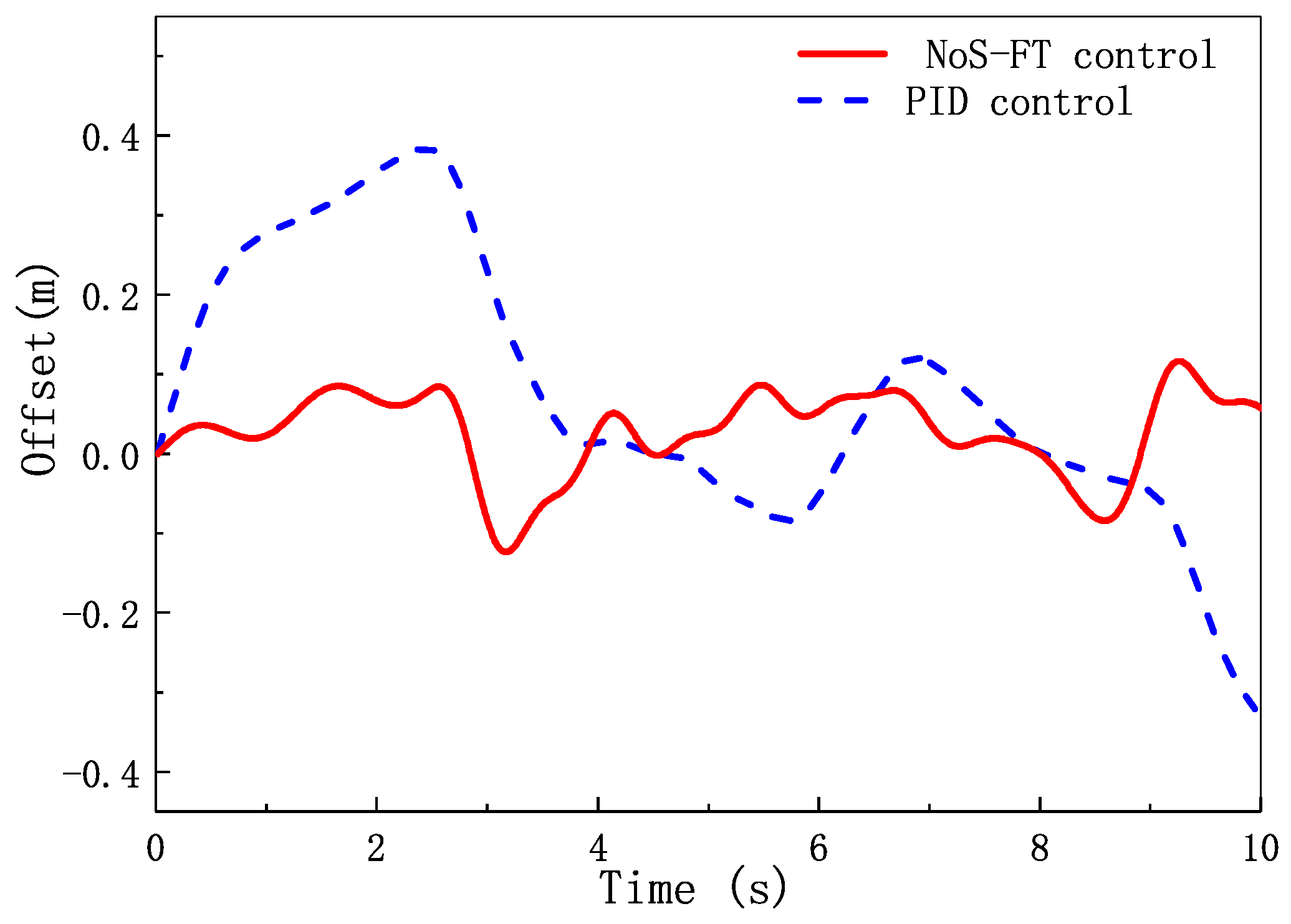
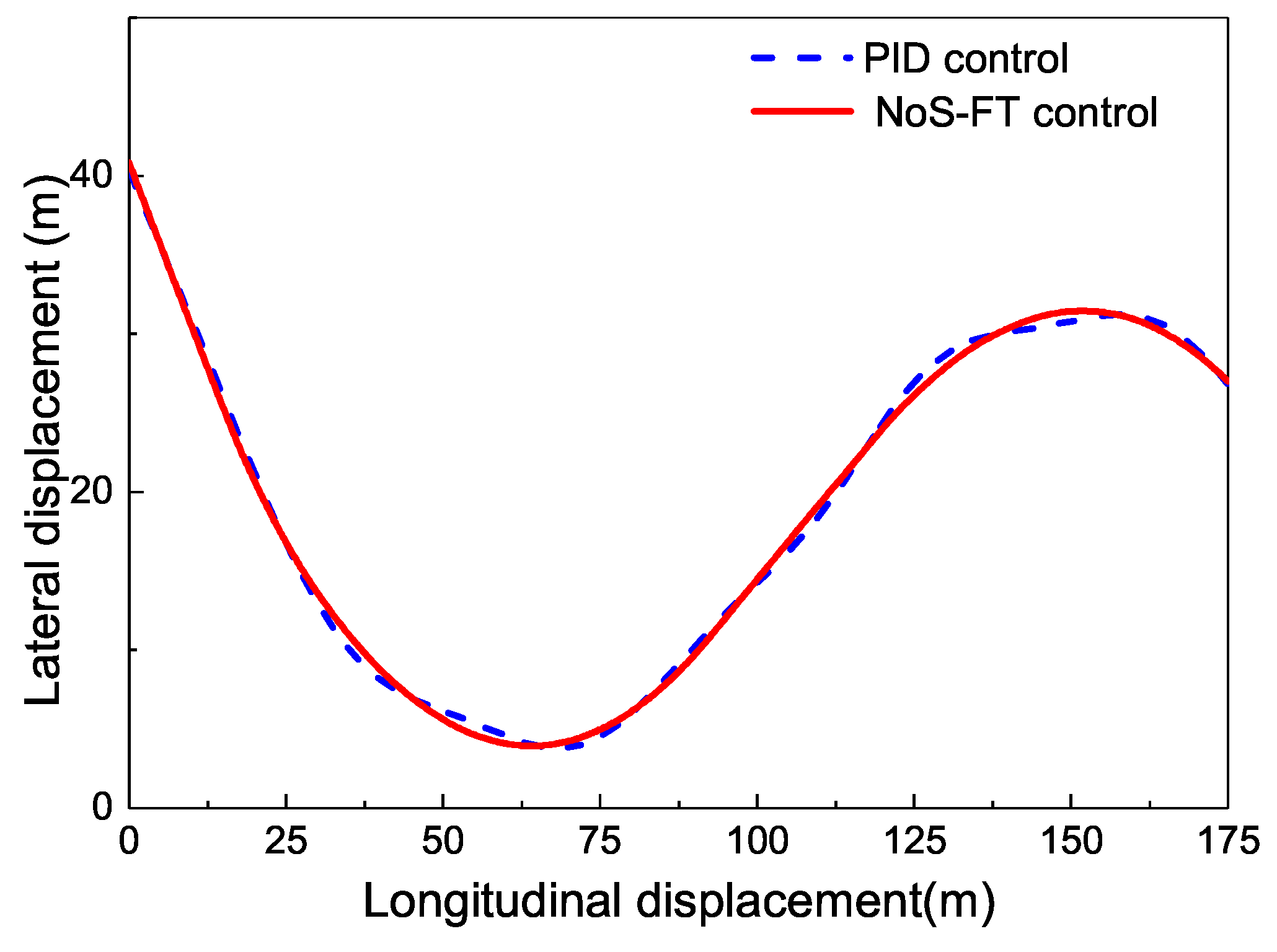
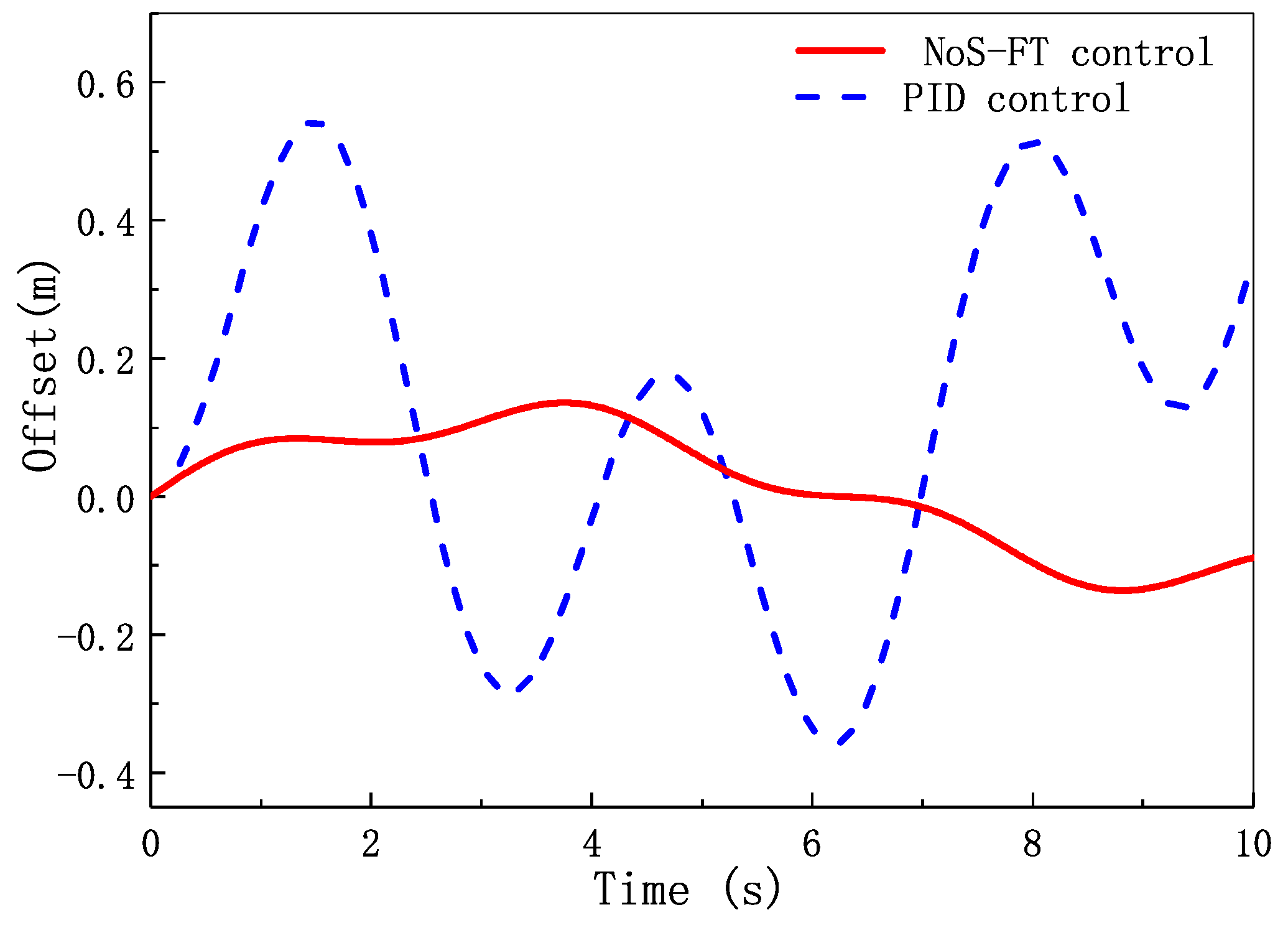
4. Simulation and Analysis
5. Conclusions
- The designed NoS-FT controller can stabilize the lateral displacement of the EV-DFWI to zero faster than the PID controller running along a straight road.
- The designed NoS-FT controller has a smaller offset and better effectiveness than the PID controller under other different conditions.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| EV-DFWI | Electric Vehicle Driven by Four Wheels Independently |
| EV | Electric Vehicle |
| NoS-FT | Non-Smooth Finite-Time |
| LKC | Lane Keeping Control |
References
- Zhang, J.; Sun, W.; Du, H. Integrated Motion Control Scheme for Four-Wheel-Independent Vehicles Considering Critical Conditions. IEEE Trans. Veh. Technol. 2019, 68, 7488–7497. [Google Scholar] [CrossRef]
- Merabet, A. Advanced Control for Electric Drives: Current Challenges and Future Perspectives. Electronics 2020, 9, 1762. [Google Scholar] [CrossRef]
- Lim, D.H.; Lee, M.Y.; Lee, H.S.; Kim, S.C. Performance Evaluation of an In-Wheel Motor Cooling System in an Electric Vehicle/Hybrid Electric Vehicle. Energies 2014, 7, 961–971. [Google Scholar] [CrossRef] [Green Version]
- Xu, Q.; Zhou, C.; Huang, H.; Zhang, X. Research on the Coordinated Control of Regenerative Braking System and ABS in Hybrid Electric Vehicle Based on Composite Structure Motor. Electronics 2021, 10, 223. [Google Scholar] [CrossRef]
- Yim, S. Vehicle Stability Control with Four-Wheel Independent Braking, Drive and Steering on In-Wheel Motor-Driven Electric Vehicles. Electronics 2020, 9, 1934. [Google Scholar]
- Han, K.; Choi, M.; Lee, B.; Choi, S.B. Development of a Traction Control System Using a Special Type of Sliding Mode Controller for Hybrid 4WD Vehicles. IEEE Trans. Veh. Technol. 2018, 67, 264–274. [Google Scholar] [CrossRef]
- Meng, Q.; Sun, Z.Y.; Shu, Y.; Liu, T. Lateral motion stability control of electric vehicle via sampled-data state feedback by almost disturbance decoupling. Int. J. Control 2019, 92, 734–744. [Google Scholar] [CrossRef]
- Li, Z.; Cui, G.; Li, S.; Zhang, N.; Tian, Y.; Shang, X. Lane Keeping Control Based on Model Predictive Control Under Region of Interest Prediction Considering Vehicle Motion States. Int. J. Automot. Technol. 2020, 21, 1001–1011. [Google Scholar] [CrossRef]
- Chen, W.; Zhao, L.; Wang, H.; Huang, Y. Parallel Distributed Compensation/H(infinity)Control of Lane-keeping System Based on the Takagi-Sugeno Fuzzy Model. Chin. J. Mech. Eng. 2020, 33, 1–13. [Google Scholar] [CrossRef]
- Salt Ducajú, J.M.; Salt Llobregat, J.J.; Cuenca, Á.; Tomizuka, M. Autonomous Ground Vehicle Lane-Keeping LPV Model-Based Control: Dual-Rate State Estimation and Comparison of Different Real-Time Control Strategies. Sensors 2021, 21, 1531. [Google Scholar] [CrossRef] [PubMed]
- Suryanarayanan, S.; Tomizuka, M. Appropriate Sensor Placement for Fault-Tolerant Lane-Keeping Control of Automated Vehicles. IEEE/ASME Trans. Mechatron. 2007, 12, 465–471. [Google Scholar] [CrossRef]
- Junyeon, H.; Kunsoo, H.; Hyukmin, N.; Hogi, J.; Hyungjin, K.; Paljoo, Y. Evaluation of lane keeping assistance controllers in HIL simulations. IFAC Proc. 2008, 41, 9491–9496. [Google Scholar]
- Katzourakis, D.I.; Lazic, N.; Olsson, C.; Lidberg, M.R. Driver Steering Override for Lane-Keeping Aid Using Computer-Aided Engineering. IEEE-ASME Trans. Mechatron. 2015, 20, 1543–1552. [Google Scholar] [CrossRef]
- Son, Y.S.; Kim, W.; Lee, S.H.; Chung, C.C. Robust Multirate Control Scheme With Predictive Virtual Lanes for Lane-Keeping System of Autonomous Highway Driving. IEEE Trans. Veh. Technol. 2015, 64, 3378–3391. [Google Scholar] [CrossRef]
- Merah, A.; Hartani, K.; Draou, A. A new shared control for lane keeping and road departure prevention. Veh. Syst. Dyn. 2016, 54, 86–101. [Google Scholar] [CrossRef]
- Shu, P.; Sagara, S.; Wang, Q.; Oya, M. Improved adaptive lane-keeping control for four-wheel steering vehicles without lateral velocity measurements. Int. J. Robust Nonlinear Control 2017, 27, 4154–4168. [Google Scholar] [CrossRef]
- Kang, C.M.; Lee, S.H.; Chung, C.C. Multirate Lane-Keeping System With Kinematic Vehicle Model. IEEE Trans. Veh. Technol. 2018, 67, 9211–9222. [Google Scholar] [CrossRef]
- Chu, Z.; Sun, Y.; Wu, C.; Sepehri, N. Active disturbance rejection control applied to automated steering for lane keeping in autonomous vehicles. Control Eng. Pract. 2018, 74, 13–21. [Google Scholar] [CrossRef]
- Kuo, C.Y.; Lu, Y.R.; Yang, S.M. On the Image Sensor Processing for Lane Detection and Control in Vehicle Lane Keeping Systems. Sensors 2019, 19, 1665. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Lin, H. Backstepping Fuzzy Sliding Mode Control for the Antiskid Braking System of Unmanned Aerial Vehicles. Electronics 2020, 9, 1731. [Google Scholar] [CrossRef]
- Ahn, T.; Lee, Y.; Park, K. Design of Integrated Autonomous Driving Control System that Incorporates Chassis Controllers for Improving Path Tracking Performance and Vehicle Stability. Electronics 2021, 10, 144. [Google Scholar] [CrossRef]
- Levant, A.; Yu, X. Sliding Mode Based Differentiation and Filtering. IEEE Trans. Autom. Control 2018, 63, 3061–3067. [Google Scholar] [CrossRef]
- Fridman, L. Technical Committee on Variable Structure and Sliding Mode Control. IEEE Control Syst. Mag. 2018, 38, 17–18. [Google Scholar]
- Zhang, C.; Yang, J.; Yan, Y.; Fridman, L.; Li, S. Semiglobal Finite-Time Trajectory Tracking Realization for Disturbed Nonlinear Systems via Higher-Order Sliding Modes. IEEE Trans. Autom. Control 2019, 65, 2185–2191. [Google Scholar] [CrossRef]
- Ding, S.; Mei, K.; Li, S. A new second-order sliding mode and its application to nonlinear constrained systems. IEEE Trans. Autom. Control 2018. [Google Scholar] [CrossRef]
- Ding, S.; Lu, L.; Wei, X.Z. Sliding Mode Direct Yaw-Moment Control Design for In-Wheel Electric Vehicles. IEEE Trans. Ind. Electron. 2017, 64, 6752–6762. [Google Scholar] [CrossRef]
- Ren, C.; Li, X.; Yang, X.; Ma, S. Extended State Observer-Based Sliding Mode Control of an Omnidirectional Mobile Robot With Friction Compensation. IEEE Trans. Ind. Electron. 2019, 66, 9480–9489. [Google Scholar] [CrossRef]
- Zhai, J.Y.; Song, Z.B. Adaptive sliding mode trajectory tracking control for wheeled mobile robots. Int. J. Control 2019, 92, 2255–2262. [Google Scholar] [CrossRef]
- Lei, J. Research on a kind of sliding mode lane keeping control for automated vehicles based on hybrid information of position and angular velocity. Optik 2016, 127, 9344–9360. [Google Scholar] [CrossRef]
- Mao, J.; Yang, J.; Li, S.; Yan, Y.; Li, Q. Output feedback-based sliding mode control for disturbed motion control systems via a higher-order ESO approach. IET Control Theory Appl. 2018, 12, 2118–2126. [Google Scholar] [CrossRef]
- Hu, C.; Qin, Y.; Cao, H.; Song, X.; Jiang, K.; Rath, J.J.; Wei, C. Lane keeping of autonomous vehicles based on differential steering with adaptive multivariable super-twisting control. Mech. Syst. Signal Process. 2019, 125, 330–346. [Google Scholar] [CrossRef]
- Hu, C.; Wang, Z.; Taghavifar, H.; Na, J.; Qin, Y.; Guo, J.; Wei, C. MME-EKF-based path-tracking control of autonomous vehicles considering input saturation. IEEE Trans. Veh. Technol. 2019, 68, 5246–5259. [Google Scholar] [CrossRef] [Green Version]
- Majumder, K.; Patre, B.M. Adaptive sliding mode control for asymptotic stabilization of underactuated mechanical systems via higher-order nonlinear disturbance observer. J. Vib. Control 2019, 25, 2340–2350. [Google Scholar] [CrossRef]
- Argha, A.; Su, S.W.; Zheng, W.X.; Celler, B.G. Sliding-mode fault-tolerant control using the control allocation scheme. Int. J. Robust Nonlinear Control 2019, 29, 6256–6273. [Google Scholar] [CrossRef]
- Sun, Z.Y.; Yun, M.M.; Li, T. A new approach to fast global finite-time stabilization of high-order nonlinear system. Automatica 2017, 81, 455–463. [Google Scholar] [CrossRef]
- Meng, Q.; Sun, Z.Y.; Li, Y. Finite-time Controller Design for Four-wheel-steering of Electric Vehicle Driven by Four In-wheel Motors. Int. J. Control Autom. Syst. 2018, 16, 1814–1823. [Google Scholar] [CrossRef]
- Meng, Q.; Qian, C.; Sun, Z.Y. Finite-time stability control of an electric vehicle under tyre blowout. Trans. Inst. Meas. Control 2019, 41, 1395–1404. [Google Scholar] [CrossRef]
- Lin, X.; Yang, Z.; Li, S. Finite-time boundedness and finite-time weighted L-2-gain analysis for a class of neutral type switched systems with time-varying delays. Int. J. Syst. Sci. 2019, 50, 1703–1717. [Google Scholar] [CrossRef]
- Ding, S.; Zhang, Z.; Chen, X. Guidance law design based on non-smooth control. Trans. Inst. Meas. Control 2013, 35, 1116–1128. [Google Scholar] [CrossRef]
- Meng, Q.; Zhao, T.; Qian, C.; Sun, Z.; Ge, P. Integrated stability control of AFS and DYC for electric vehicle based on non-smooth control. Int. J. Syst. Sci. 2018, 49, 1518–1528. [Google Scholar] [CrossRef]
- Xia, C.; Li, S.; Shi, Y.; Zhang, X.; Sun, Z.; Yin, W. A Non-Smooth Composite Control Approach for Direct Torque Control of Permanent Magnet Synchronous Machines. IEEE Access 2019, 7, 45313–45321. [Google Scholar] [CrossRef]




| Parameters | Value |
|---|---|
| Mass m/kg | 1800 |
| Rotary inertia | 3000 |
| Length between front axle and centroid | 1.2 |
| Length between rear axle and centroid | 1.8 |
| Lateral stiffness of front axle | –1500 |
| Lateral stiffness of rear axle | –1200 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, Q.; Zhao, X.; Hu, C.; Sun, Z.-Y. High Velocity Lane Keeping Control Method Based on the Non-Smooth Finite-Time Control for Electric Vehicle Driven by Four Wheels Independently. Electronics 2021, 10, 760. https://doi.org/10.3390/electronics10060760
Meng Q, Zhao X, Hu C, Sun Z-Y. High Velocity Lane Keeping Control Method Based on the Non-Smooth Finite-Time Control for Electric Vehicle Driven by Four Wheels Independently. Electronics. 2021; 10(6):760. https://doi.org/10.3390/electronics10060760
Chicago/Turabian StyleMeng, Qinghua, Xin Zhao, Chuan Hu, and Zong-Yao Sun. 2021. "High Velocity Lane Keeping Control Method Based on the Non-Smooth Finite-Time Control for Electric Vehicle Driven by Four Wheels Independently" Electronics 10, no. 6: 760. https://doi.org/10.3390/electronics10060760
APA StyleMeng, Q., Zhao, X., Hu, C., & Sun, Z.-Y. (2021). High Velocity Lane Keeping Control Method Based on the Non-Smooth Finite-Time Control for Electric Vehicle Driven by Four Wheels Independently. Electronics, 10(6), 760. https://doi.org/10.3390/electronics10060760







