A New Grid-Connected Constant Frequency Three-Phase Induction Generator System under Unbalanced-Voltage Conditions
Abstract
:1. Introduction
- to obtain constant active and reactive powers without a ripple;
- to obtain constant electromagnetic torque and reactive power without a ripple;
- to obtain a symmetrical and sinusoidal stator current.
2. Induction Generator System Model
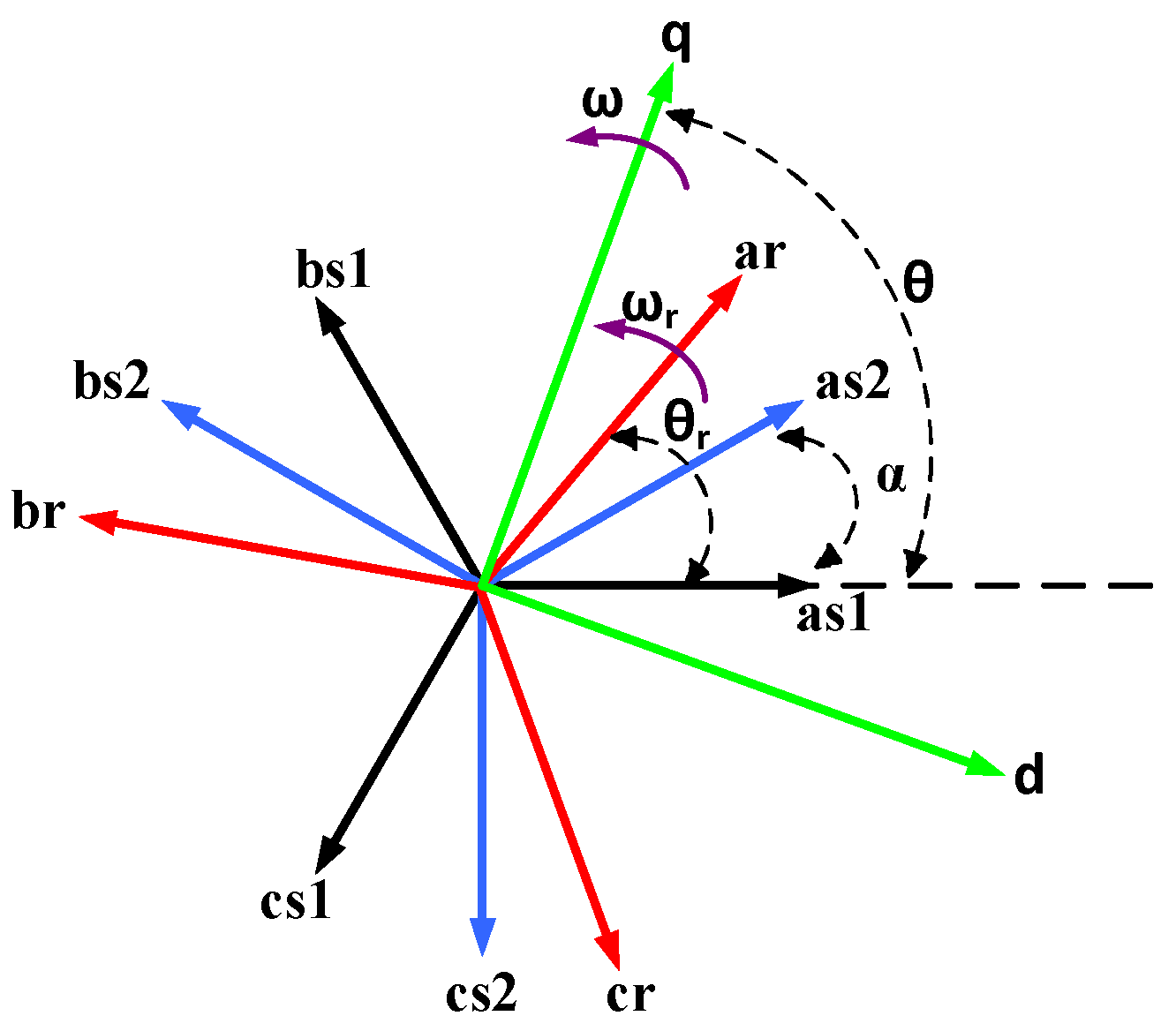
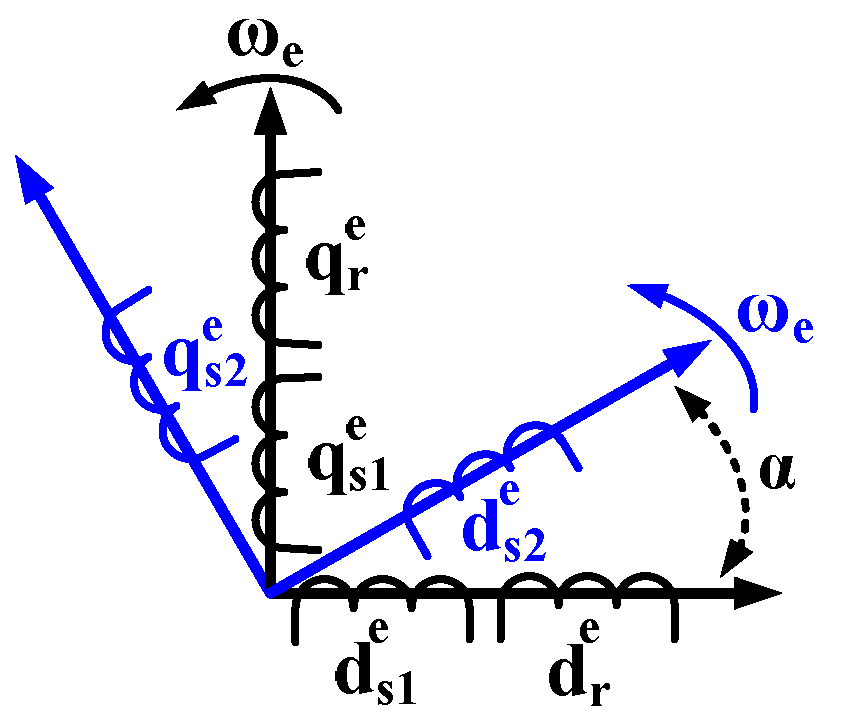
2.1. Machine Model
2.2. Generator State Space Model
2.3. Wind Turbine Model
3. Sliding Mode Controllers
3.1. Positive Sequence SMC
3.2. Negative Sequence SMC
4. Simulation and Results
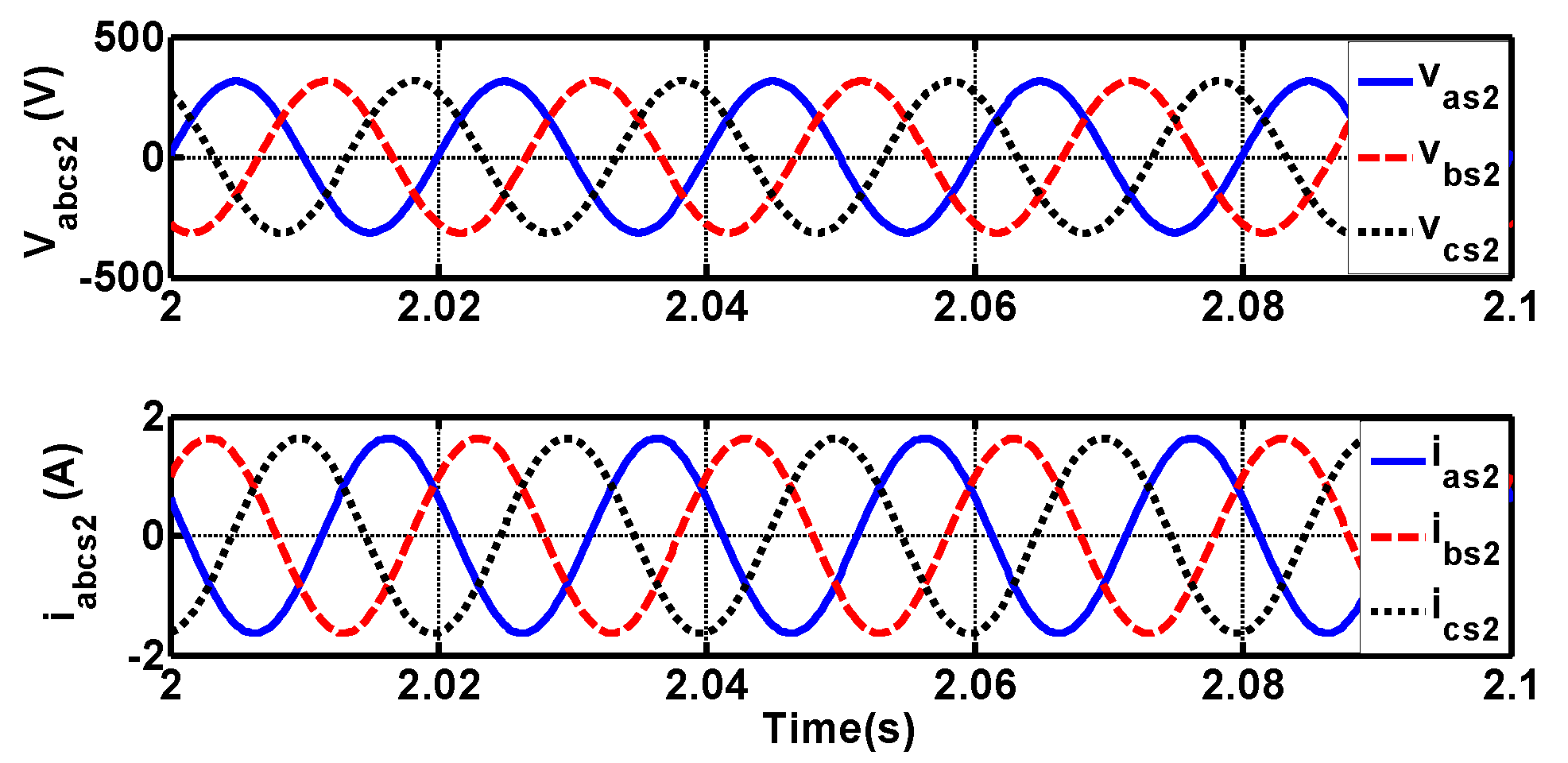
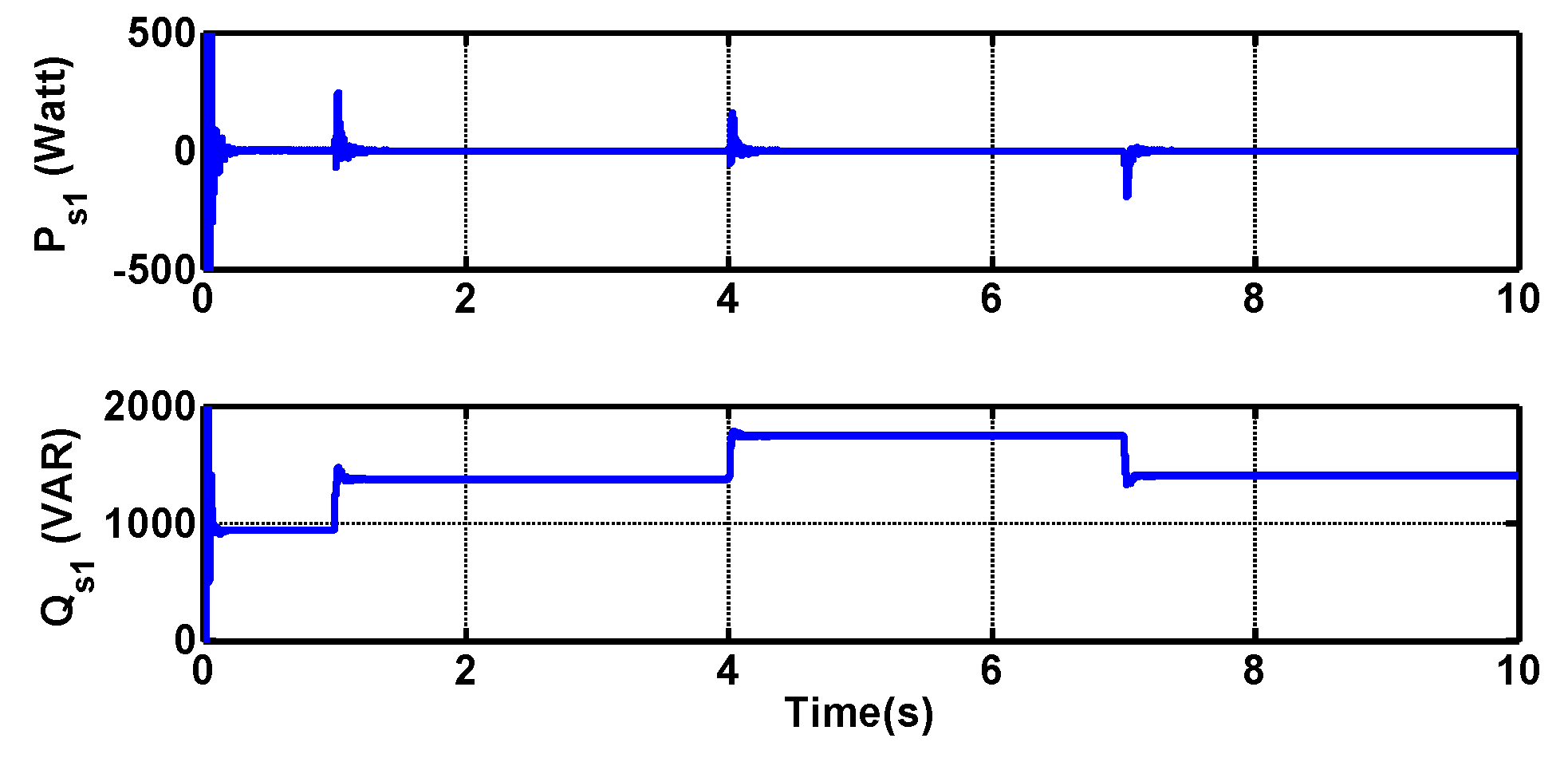
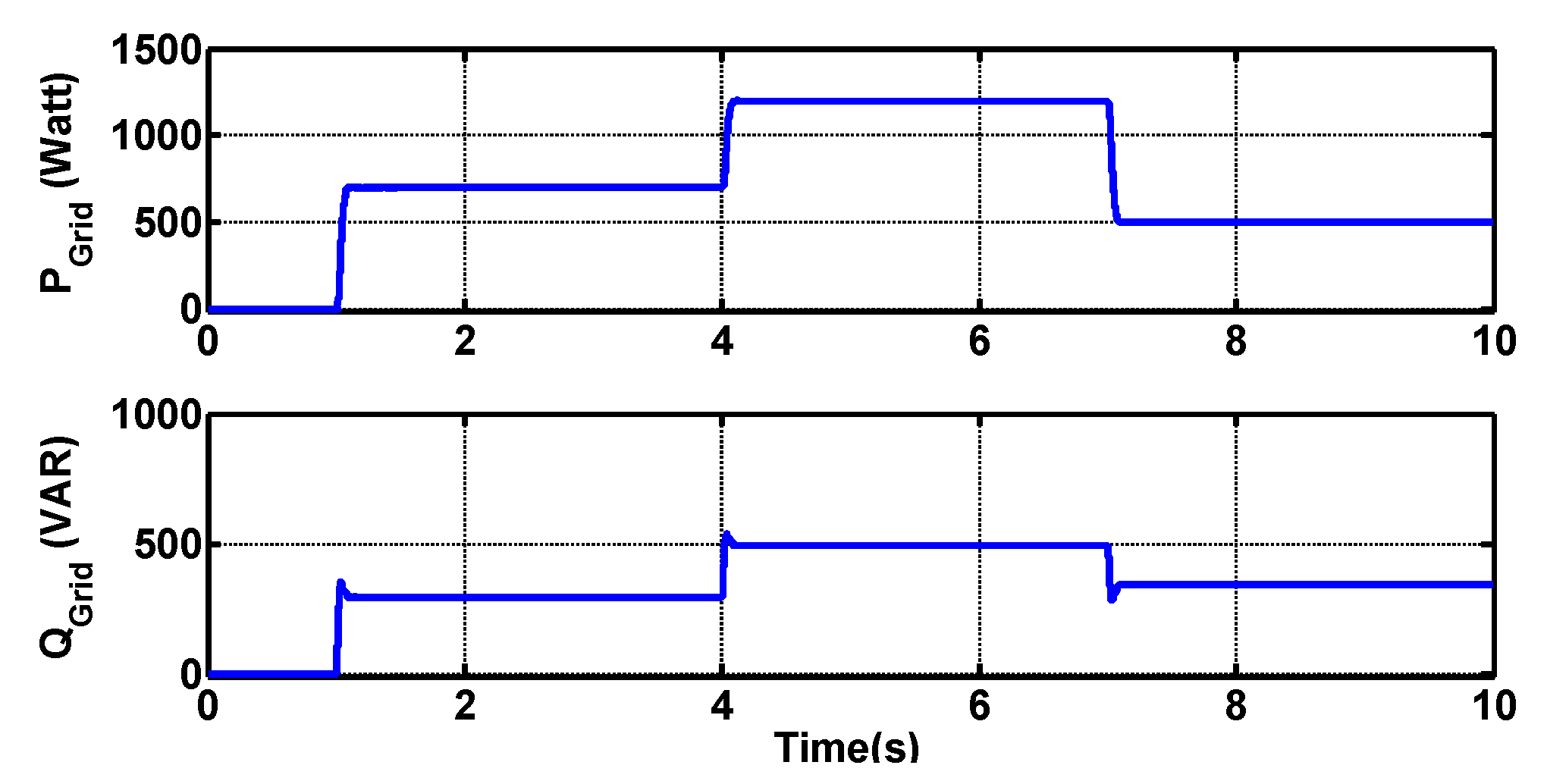
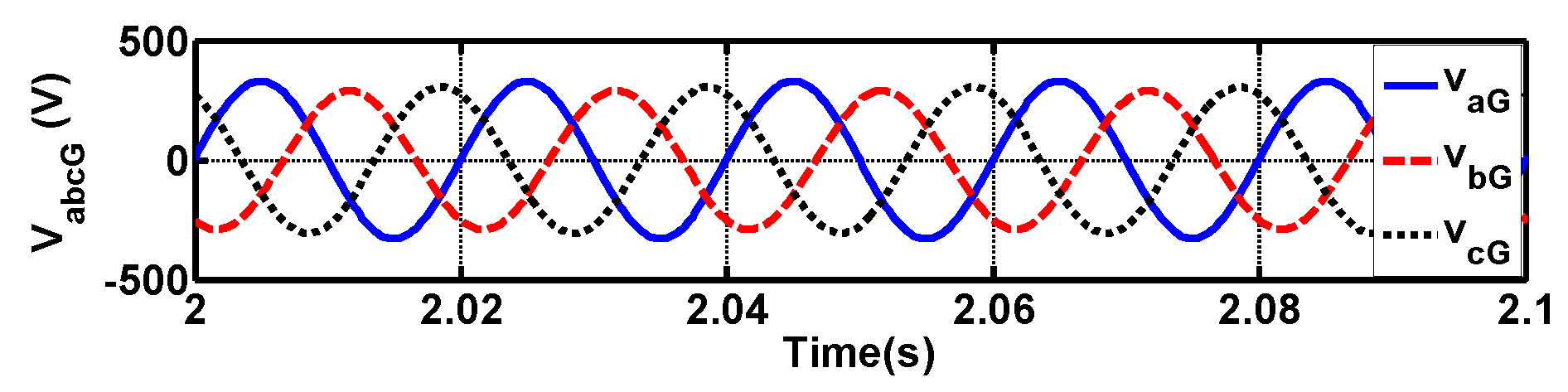
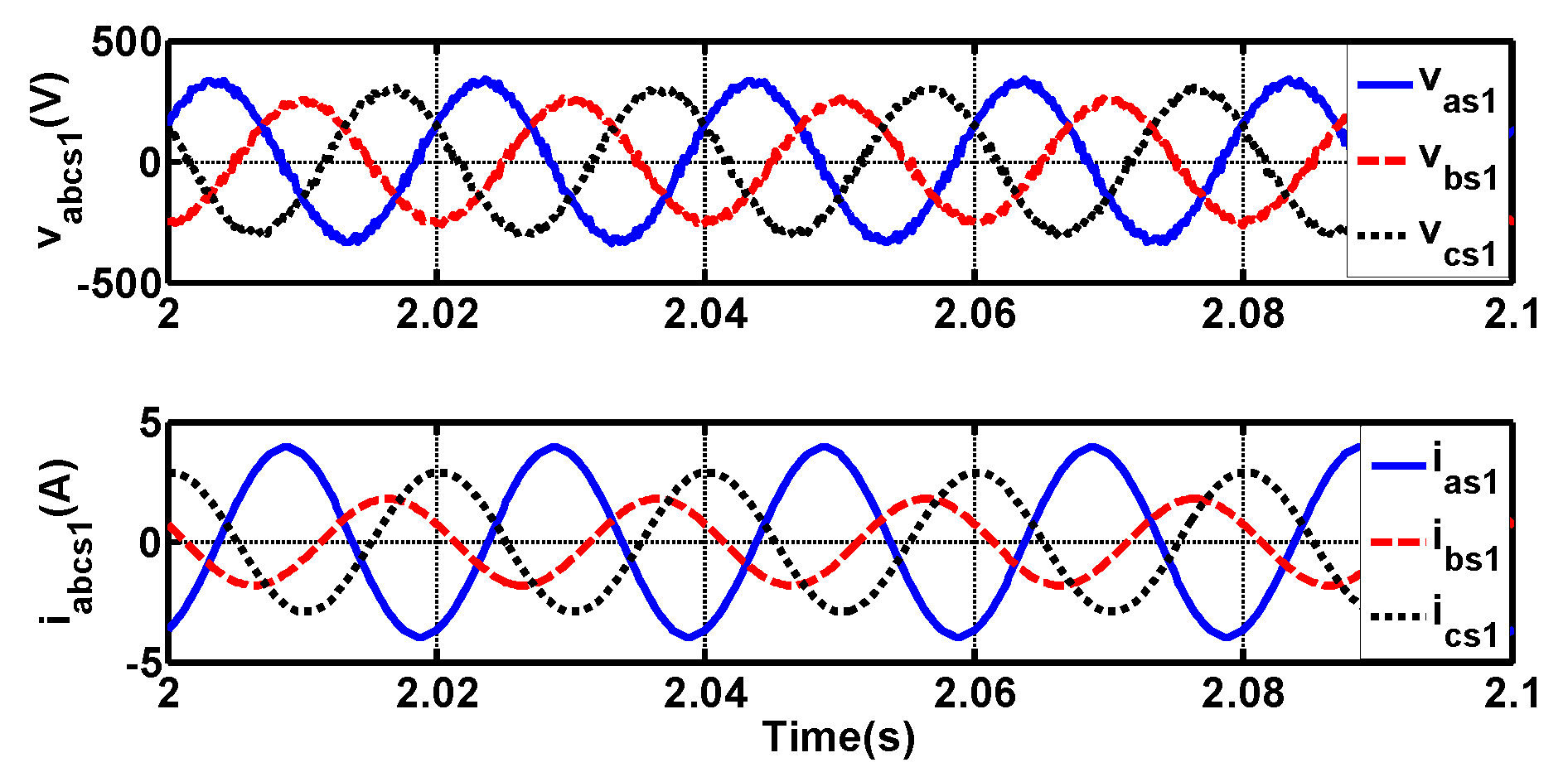
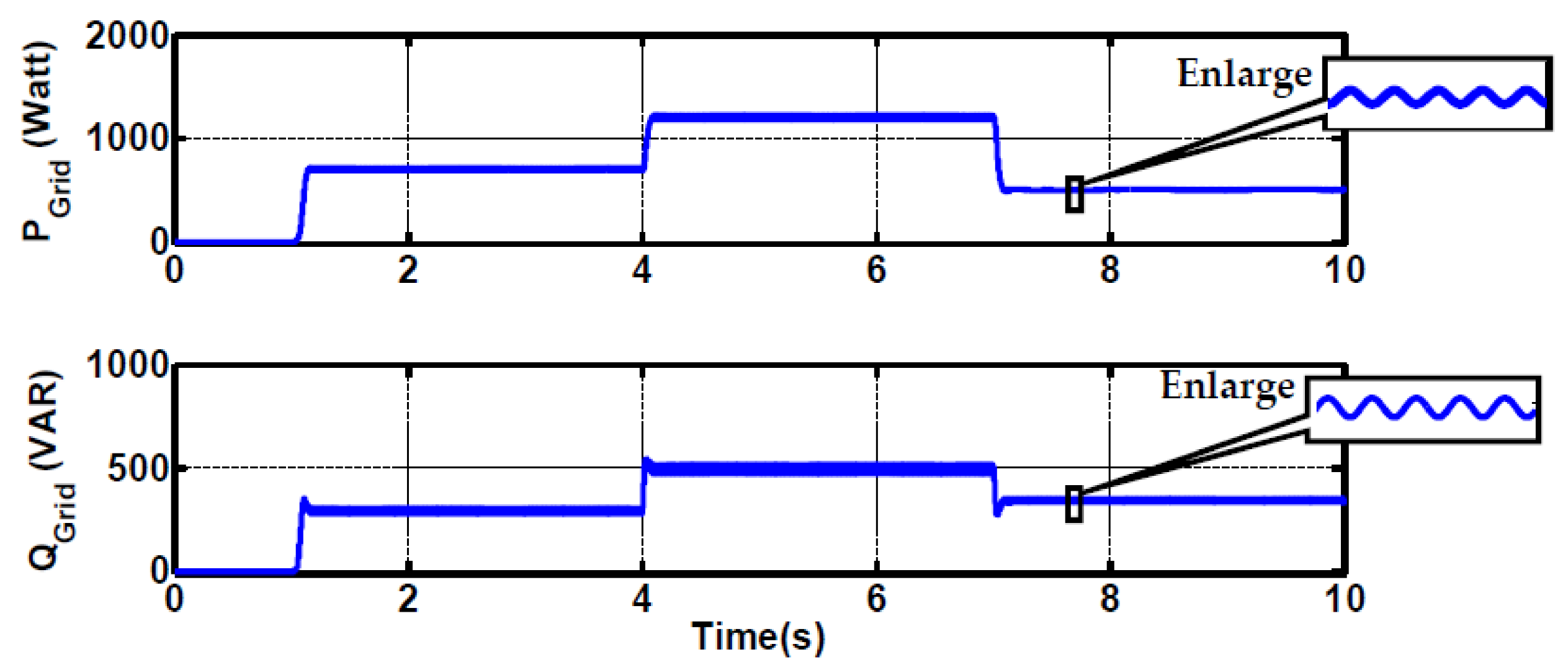
4.1. Balanced Grid Results
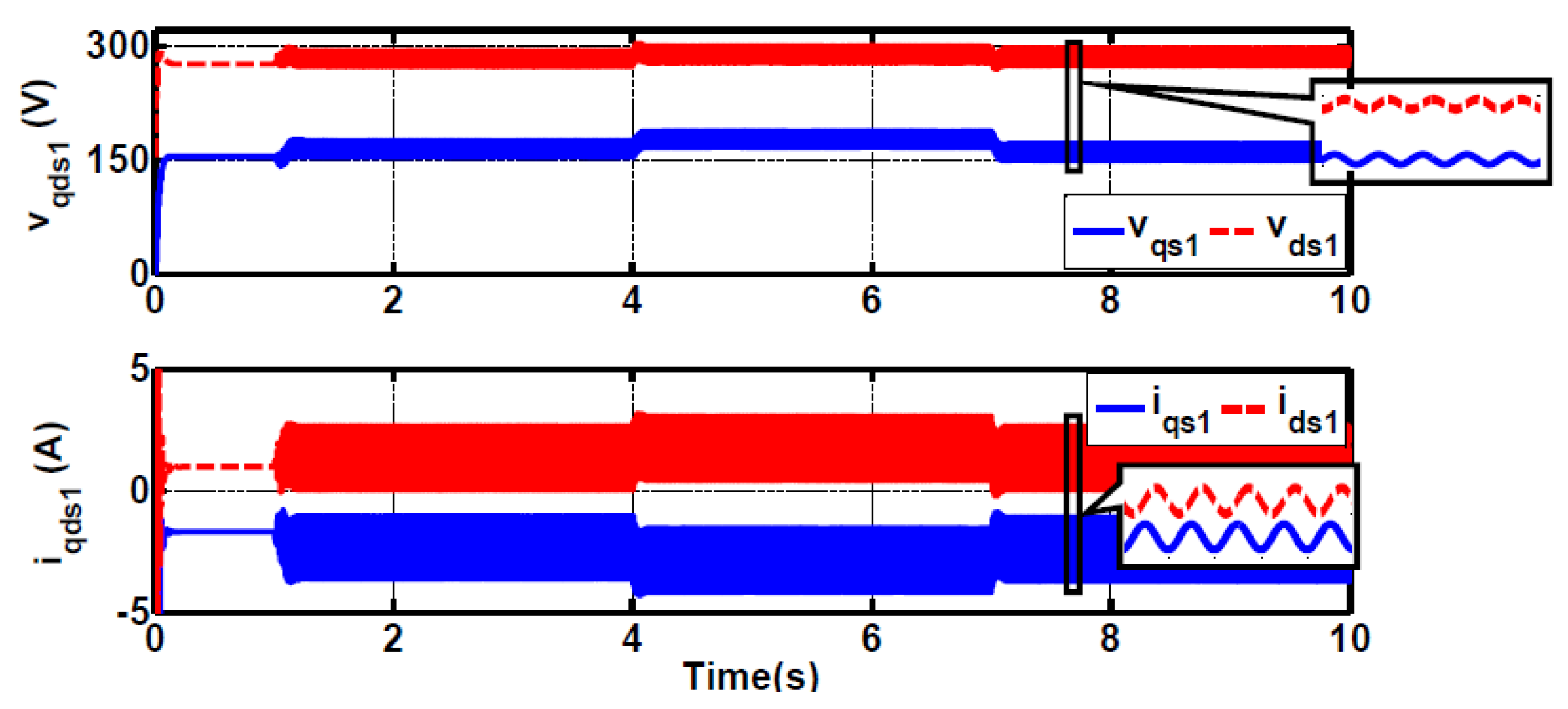
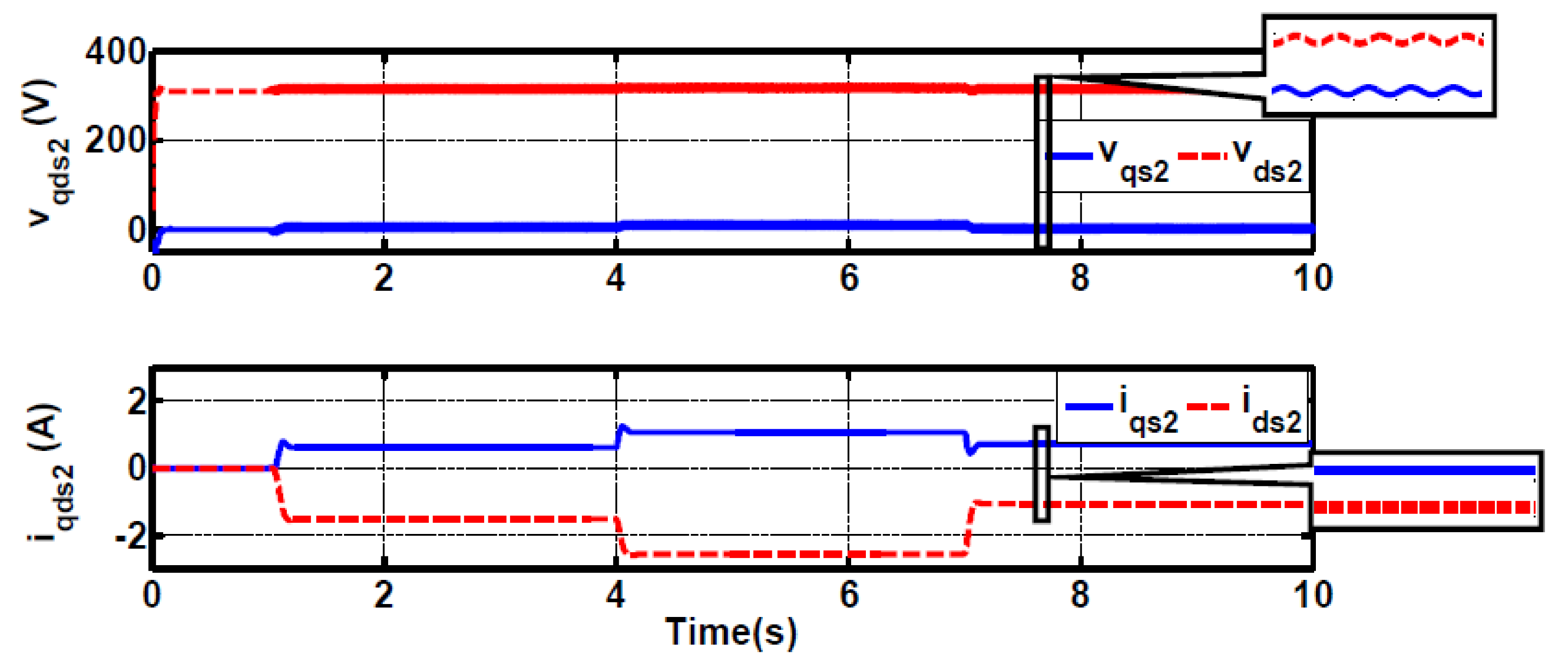
4.2. Unbalanced Grid Results
5. Conclusion
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Wafaa, M.B.; Dessaint, L.A. Approach to Dynamic Voltage Stability Analysis for DFIG Wind Parks Integration. IET Renew. Power Gener. 2017, 12, 190–197. [Google Scholar] [CrossRef]
- Carrasco, J.M.; Franquelo, L.G.; Bialasiewicz, J.T.; Galván, E.; PortilloGuisado, R.C.; Prats, M.M.; Moreno-Alfonso, N. Power-Electronic Systems for the Grid Integration of Renewable Energy Sources: A Survey. IEEE Trans. On Ind. Electron. 2006, 53, 1002–1016. [Google Scholar] [CrossRef]
- Wang, R.; Xie, Y.; Zhang, H.; Li, C.; Li, W.; Terzija, V. Dynamic Power Flow Algorithm Considering Frequency Regulation of Wind Power Generators. IET Renew. Power Gener. 2017, 11, 1218–1225. [Google Scholar] [CrossRef]
- Silva, E.O.; Vanço, W.E.; Guimarães, G.C. Capacitor Bank Sizing for Squirrel Cage Induction Generators Operating in Distributed Systems. IEEE Access 2020, 8, 27507–27515. [Google Scholar] [CrossRef]
- Chinmaya, K.A.; Singh, G.K. Modeling and Experimental Analysis of Grid-Connected Six-Phase Induction Generator for Variable Speed Wind Energy Conversion System. Electr. Power Syst. Res. 2019, 166, 151–162. [Google Scholar] [CrossRef]
- Zhang, F.; Yu, S.; Wang, Y.; Jin, S.; Jovanovic, M.G. Design and Performance Comparisons of Brushless Doubly Fed Generators with Different Rotor Structures. IEEE Trans. On Ind. Electron. 2018, 66, 631–640. [Google Scholar] [CrossRef] [Green Version]
- Kusiak, A.; Zhang, Z.; Li, M. Optimization of Wind Turbine Performance with Data-Driven Models. IEEE Trans. On Sustain. Energy 2010, 1, 66–76. [Google Scholar] [CrossRef]
- Singh, B.; Kasal, G.K. Independent Voltage and Frequency Controller for a Parallel Operated Isolated Three-Phase Asynchronous Generators. Eur. Trans. On Electr. Power 2009, 19, 839–853. [Google Scholar] [CrossRef]
- Leon, A.E.; Farias, M.F.; Battaiotto, P.E.; Solsona, J.A.; Valla, M.I. Control Strategy of a DVR to Improve Stability in Wind Farms Using Squirrel-Cage Induction Generators. IEEE Trans. on Power Syst. 2010, 26, 1609–1617. [Google Scholar] [CrossRef]
- Alharbi, M.; Alfaris, F.E.; Bhattacharya, S. A Novel Current Control Strategy for a Back-to-Back HVDC Applications Under Unbalanced Operation Conditions. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, Ohio, USA, 1–5 October 2017; pp. 1263–1269. [Google Scholar] [CrossRef]
- Arya, S.R.; Niwas, R.; Bhalla, K.K.; Singh, B.; Chandra, A.; Al-Haddad, K. Power Quality Improvement in Isolated Distributed Power Generating System Using DSTATCOM. IEEE Trans. On Ind. Appl. 2015, 51, 4766–4774. [Google Scholar] [CrossRef]
- Satpathy, A.S.; Kastha, D.; Kishore, K. Control of a STATCOM-Assisted Self-Excited Induction Generator-Based WECS Feeding Non-Linear Three-Phase and Single-Phase Loads. IET Power Electron. 2018, 12, 829–839. [Google Scholar] [CrossRef]
- Peng, Y.; Li, Y.; Lee, K.Y.; Tan, Y.; Cao, Y.; Wen, M.; Li, W. Coordinated Control Strategy of PMSG and Cascaded H-Bridge STATCOM in Dispersed Wind Farm for Suppressing Unbalanced Grid Voltage. IEEE Trans. on Sustain. Energy 2020, 12, 349–359. [Google Scholar] [CrossRef]
- Chaudhary, S.K.; Teodorescu, R.; Rodriguez, P.; Kjaer, P.C.; Gole, A.M. Negative Sequence Current Control in Wind Power Plants with VSC-HVDC Connection. IEEE Trans. Sustain. Energy 2012, 3, 535–544. [Google Scholar] [CrossRef]
- Koutiva, X.I.; Vrionis, T.D.; Vovos, N.A.; Giannakopoulos, G.B. Optimal Integration of an Offshore Wind Farm to a Weak AC Grid. IEEE Trans. on Power Deliv. 2006, 21, 987–994. [Google Scholar] [CrossRef]
- Hongbo, Q.; Yanqi, W.; Ran, Y. The Influence of Unbalance Load on the Electromagnetic and Temperature Field of High-Speed Permanent Magnet Generator. IEEE Trans. Magn. 2018, 55, 1–4. [Google Scholar] [CrossRef]
- Mishra, R.; Saha, T.K. Control of SCIG Based Distributed Power Generation Scheme Supplying Nonlinear and Unbalanced Load. In Proceedings of the 2018 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Chennai, India, 18–21 December 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Yao, J.; Li, H.; Chen, Z.; Xia, X.; Chen, X.; Li, Q.; Liao, Y. Enhanced Control of a DFIG-Based Wind-Power Generation System with Series Grid-Side Converter Under Unbalanced Grid Voltage Conditions. IEEE Trans. Power Electron. 2012, 28, 3167–3181. [Google Scholar] [CrossRef]
- Iqbal, A.; Singh, G.K. Modeling and Stability Analysis of Three-and Six-Phase Asymmetrical Grid-Connected Induction Generator. Electr. Eng. 2020, 1–13. [Google Scholar] [CrossRef]
- Li, Z.; Xie, Z.; Wang, Z.; Weng, H.; Wang, L. A New Protection Strategy Based on Negative Sequence Current Coordinated Control on the Generator Extremity. IEEE Access 2020, 8, 135329–135338. [Google Scholar] [CrossRef]
- Zeng, X.; Yao, J.; Chen, Z.; Hu, W.; Chen, Z.; Zhou, T. Co-Ordinated Control Strategy for Hybrid Wind Farms with PMSG and FSIG Under Unbalanced Grid Voltage Condition. IEEE Trans. Sustain. Energy 2016, 7, 1100–1110. [Google Scholar] [CrossRef] [Green Version]
- Xu, L.; Cheng, M.; Wei, X.; Yan, X.; Zeng, Y. Dual Synchronous Rotating Frame Current Control of Brushless DoublyFed Induction Generator under Unbalanced Network. IEEE Trans. Power Electron 2020. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Al-Saud, M.S.; Abo-Khalil, A.G. Dynamic Control of a DFIG Wind Power Generation System to Mitigate Unbalanced Grid Voltage. IEEE Access 2020, 8, 39091–39103. [Google Scholar] [CrossRef]
- Rezaei, E.; Ebrahimi, M.; Tabesh, A. Control of DFIG Wind Power Generators in Unbalanced Microgrids Based on Instantaneous Power Theory. IEEE Trans. Smart Grid 2016, 8, 2278–2286. [Google Scholar] [CrossRef]
- Gao, S.; Zhao, H.; Gui, Y.; Zhou, D.; Terzija, V.; Blaabjerg, F. A Novel Direct Power Control for DFIG with Parallel Compensator under Unbalanced Grid Condition. IEEE Trans. Ind. Electron. 2020. [Google Scholar] [CrossRef]
- Wang, X.; Sun, D.; Zhu, Z.Q. Resonant-Based Backstepping Direct Power Control Strategy for DFIG Under Both Balanced and Unbalanced Grid Conditions. IEEE Trans. Ind. Appl. 2017, 53, 4821–4830. [Google Scholar] [CrossRef]
- Rani, M.A.A.; Nagamani, C.; Ilango, G.S. Compensation of Magnetizing Current for Enhanced Operation of DFIG Under Grid Unbalance. IEEE Trans. Power Electron. 2016, 32, 5214–5226. [Google Scholar] [CrossRef]
- Iwanski, G.; Łuszczyk, T.; Pura, P.; Szypulski, M. Indirect Torque and Stator Reactive Power Control of Doubly Fed Induction Machine Connected to Unbalanced Power Network. IEEE Trans. Energy Convers. 2016, 31, 1202–1211. [Google Scholar] [CrossRef]
- Moradian, M.; Soltani, J. A Novel Control Method for an Isolated Three-Phase Induction Generator with Constant Frequency and Adjustable Output Voltage. Int. Trans. Electr. Energy Syst. 2016, 26, 2074–2086. [Google Scholar] [CrossRef]
- Moradian, M.; Soltani, J. Sliding Mode Control of a New Wind-Based Isolated Three-Phase Induction Generator System with Constant Frequency and Adjustable Output Voltage. J. Power Electron. 2016, 16, 675–684. [Google Scholar] [CrossRef] [Green Version]
- Moradian, M.; Soltani, J. An Isolated Three-Phase Induction Generator System with Dual Stator Winding Sets Under Unbalanced Load Condition. IEEE Trans. Energy Convers. 2016, 31, 531–539. [Google Scholar] [CrossRef]
- Vas, P. Electrical Machines and Drives: A Space-Vector Theory Approach; Clarendon Press: Oxford, UK, 1992; Volume 1. [Google Scholar]
- Barakati, S.M.; Kazerani, M.; Aplevich, J.D. Maximum Power Tracking Control for a Wind Turbine System Including a Matrix Converter. IEEE Trans. Energy Convers. 2009, 24, 705–713. [Google Scholar] [CrossRef]
- Slotine, J.J.E.; Li, W. Applied Nonlinear Control; Prentice Hall: Englewood Cliffs, NJ, USA, 1991; Volume 199. [Google Scholar]







| Number of Pole Pairs | Pole | 1 |
|---|---|---|
| Frequency | Fn | 50 Hz |
| Power | Pn | 1.8 kW |
| Both stator line voltages | VL | 380 V |
| Both stator line currents | IL | 3.5 A |
| Stator EW resistance | Rs1 | 2.4 Ω |
| Stator PW resistance | Rs2 | 2.4 Ω |
| Rotor resistance | Rr | 4.1 Ω |
| Stator EW leakage inductance | Lls1 | 11 mH |
| Stator PW leakage inductance | Lls2 | 11 mH |
| Rotor leakage inductance | Llr | 11 mH |
| Magnetization inductance | Lm | 374 mH |
| EW and PW spatial phase difference | α | 30°e |
| Inertia momentum | J | 0.038 Kgm2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moradian, M.; Soltani, J.; Arab Markadeh, G.R.; Shahinzadeh, H.; Amirat, Y. A New Grid-Connected Constant Frequency Three-Phase Induction Generator System under Unbalanced-Voltage Conditions. Electronics 2021, 10, 938. https://doi.org/10.3390/electronics10080938
Moradian M, Soltani J, Arab Markadeh GR, Shahinzadeh H, Amirat Y. A New Grid-Connected Constant Frequency Three-Phase Induction Generator System under Unbalanced-Voltage Conditions. Electronics. 2021; 10(8):938. https://doi.org/10.3390/electronics10080938
Chicago/Turabian StyleMoradian, Mohammadreza, Jafar Soltani, Gholam Reza Arab Markadeh, Hossein Shahinzadeh, and Yassine Amirat. 2021. "A New Grid-Connected Constant Frequency Three-Phase Induction Generator System under Unbalanced-Voltage Conditions" Electronics 10, no. 8: 938. https://doi.org/10.3390/electronics10080938
APA StyleMoradian, M., Soltani, J., Arab Markadeh, G. R., Shahinzadeh, H., & Amirat, Y. (2021). A New Grid-Connected Constant Frequency Three-Phase Induction Generator System under Unbalanced-Voltage Conditions. Electronics, 10(8), 938. https://doi.org/10.3390/electronics10080938








