Phase and Neutral Current Ripple Analysis in Three-Phase Four-Wire Split-Capacitor Grid Converter for EV Chargers

Abstract

The current switching ripple in a three-phase four-wire split-capacitor converter is analyzed in this paper for all the four ac output wires in relation to both balanced and unbalanced working conditions. Specifically, analytical formulations of the peak-to-peak and root mean square (RMS) current ripples are originally evaluated as a function of the modulation index, separately for the three phases and the neutral wire. Initially, the single-carrier sinusoidal pulse width modulation (PWM) technique is outlined, as it generally concerns a straightforward and effective modulation. With the aim of mitigating the current ripple in the neutral wire, the interleaved multiple-carrier PWM strategy is adopted, also avoiding any repercussion on the phase one. Numerical simulations and experimental tests were carried out to verify all the analytical developments.

1. Introduction

Three-phase four-wire voltage-source converters are applied to many power applications, including unbalanced AC loads and AC sources. Owing to their intrinsic capability of dealing with the zero-sequence rather than only the negative-sequence voltage and current components, they have been introduced in grid-forming inverters [1,2], shunt active filters [3,4], active rectifiers [5], electric drives [6], and renewable energy sources applications. Furthermore, the growing deployment of electric vehicles (EVs) has allowed the adoption of three-phase four-wire inverters as a front-end stage in on-board/off-board EV chargers, offering vehicle-to-grid (V2G), vehicle-for-grid (V4G), vehicle-to-home (V2H), vehicle-to-vehicle (V2V), and vehicle-to-load (V2L) services in both three-phase and single-phase modes [7,8]. Different neutral forming topologies have been proposed and discussed, such as three H-bridges [4,9], split capacitors [1,2,3,4,5,9,10], four-leg [3,4,9,11], and independently controlled neutral module [2,7,12].

Carrier-based pulse width modulation (PWM) schemes are broadly adopted in most AC–DC converters by virtue of their effectiveness and simplicity in digital and analog implementations, besides the renowned harmonic spectrum property [13]. Additionally, the fixed switching frequency leads to simple control of the switching losses and, hence, a more precise converter design, as well as a more accurate computation of the losses [14].

The AC current ripple is one of the most helpful parameters in designing a power switching converter. If correctly determined, it paves the way for a set of design optimization possibilities ranging from converter weight, volume, and cost to filtering stage complexity and power efficiency. Deep knowledge of the current spectral content results vital in EV charging applications, where grid harmonic pollution is regulated by international standards [8]. Moreover, optimizing converter performance might be especially effective in on-board chargers (OBCs), where strict design constraints are unavoidable.

In [8], the peak-to-peak and root mean square (RMS) values of the AC current ripple were exhaustively analyzed in a three-phase four-leg AC–DC converter, as well as analytically described as a function of the modulation index for both phase and neutral wires, under sinusoidal PWM (SPWM), and space vector PWM (SVPWM). The latter study has been extended in [15] to the three-phase four-leg SPWM converter with neutral line inductor proposing optimal phase to neutral inductor ratio for achieving performance optimization in grid-connected applications. Authors in [14] studied the close relationship between AC current ripple and switching losses under discontinuous PWM (DPWM) in three-phase four-leg inverters. In [16], the AC phase current ripple in three-phase split-capacitor inverters was preliminarily studied, but no experimental validation has been proposed. Three-phase split-capacitor inverter switching voltage ripple has been studied in [17] under single-phase, two-phase, and three-phase working conditions. Many papers have reported results of the output current ripple analysis in the three-phase three-wire VSIs as well. However, no similar studies other than [16] AC current ripple analysis in three-phase, four-wire, split-capacitor converters. No thorough investigation of the neutral current ripple has been delineated in the literature yet.

A possible way to reduce the current ripple in PWM converters is to interleave the leg carriers. For example, an interleaved control strategy that can guarantee ripple-free operation for any working condition has been introduced in [18] in the case of multi-leg DC–DC converters. A method that relies on carriers interleaving in three-phase, three-wire VSIs was proposed in [19] with a view to achieving a significant reduction of peak-to-peak and RMS values of common-mode voltage. This method has been successfully extended to multiphase inverters in [20]. Similarly, an original technique that suppresses zero-sequence circulating current in modular, interleaved, three-phase, three-wire VSIs has been proposed in [21]. Authors in [22] proposed an interleaved half-bridge submodule-based modular multilevel converter (MMC) capable of reducing current ripple and increasing the number of voltage levels.

This paper is aimed to render an analytical evaluation of the AC current ripple in three-phase, four-wire, split-capacitor converters in the case of balanced and unbalanced working conditions for phase and neutral wires. Outcomes on peak-to-peak and RMS values of phase current ripple only have been preliminarily introduced in [16] (without experimental validation), as functions of the modulation index, enabling a straightforward comparison with the corresponding characteristics of three-phase three-wire VSIs. The analysis is carried out with reference to the sinusoidal PWM since the degree of freedom of the common-mode injection in the modulating signals is missing for this topology. The single-carrier PWM, which has been employed for the three-phase, four-wire, split-capacitor topology, does not differ from the conventional PWM adopted for the three-phase, three-wire topology since no modulation is required for the neutral leg. On the other hand, the multiple-carrier PWM strategy proposed in [5] has been examined for the neutral current ripple mitigation. This neutral current ripple reduction method takes advantage of carriers interleaving (mentioned above), partially canceling phase current ripples, rather than summing them up. Original analytical developments to determine peak-to-peak and RMS of the neutral current ripple have also been performed in this paper considering interleaved carriers.

The discussion is arranged as follows. In Section 2, the basic assumptions and the PWM principle are introduced. Section 3 shows mathematical formulations of the phase current ripple related to peak-to-peak and RMS values for balanced and unbalanced operating conditions (i.e., three phases with different modulation indices). The neutral current ripple assessments in single- and multiple-carrier PWM cases are given in Section 4 and Section 5, respectively. Section 6 reports experimental results to verify the validity of the proposed analytical developments. Lastly, conclusions are drawn in Section 7.

2. Basic Assumptions and Modulation Principle

The considered circuit scheme is represented in Figure 1. It consists of a three-phase, four-wire, split-capacitor converter. In comparison with a three-phase, three-wire inverter, a 4th wire is inserted to directly connect the midpoint of the DC-link (split) capacitors to the neutral wire of the grid/load. In the case of a grid connection, as in EV applications, the converter can work as an active rectifier: with AC-to-DC power flow when operating in grid-to-vehicle (G2V) operations or DC-to-AC power flow in case of V2G ones (Figure 1). For this reason, words like converter, inverter, and active rectifier are considered interchangeable. The converter presents inherent flexibility that permits topology reconfigurations to enable single-phase, two-phase, and three-phase balanced/unbalanced operations that can be extensively used in innovative services like V2G, V4G, V2H, V2V, and V2L [17]. The three AC-link filter inductors L are here considered to be magnetically independent.

For carrier-based PWM inverters, the three modulating signals are given by the sinusoidal phase reference voltages (normalized by the dc-link voltage V_dc):

$$u_x\left(t\right)=m_x\cos \left(\mathsf{\omega }t+{\mathsf{\phi }}_x\right)=m_x\cos \left({\mathsf{\vartheta }}_x\right)$$

(1)

being x the phase index (a, b, c), ϑ_x and φ_x the phase angles, ω the fundamental (grid) angular frequency, and m the modulation index defined as:

$$m_x=\frac{\sqrt{2}{V}_x^{*}}{V_{dc}}$$

(2)

being $V_x^{*}$ the RMS value of the reference phase voltage.

The carrier range is ±0.5, and the corresponding linear modulation span is m = [0, 0.5]. The main PWM signals are summarized in Figure 2.

Thanks to the phase independence guaranteed by this topology, it is theoretically possible to drive this converter employing any grade of unbalance freely. For this reason, when possible, analytical derivations are kept general preserving subscript “x” for both modulation index m_x and phase angle ϑ_x. Considering balanced operating conditions, the parameters in Equations (1) and (2) become m_a = m_b = m_c = m and ϑ_a = ϑ = ωt, ϑ_b = ϑ − 2π/3, ϑ_c = ϑ + 2π/3. For simplicity reasons, the unbalanced working condition is depicted only by different modulation indices (e.g., m_a = 0.3, m_b = 0.4, and m_c = 0.5), assuming symmetric phase angles. In such a manner, although grid-connected applications are usually employed with almost symmetric modulation indices (m_a ≅ m_b ≅ m_c = m), three cases with different modulation indices are displayed and validated simultaneously. Since introducing phase angle unbalances would only lead to current ripple shifting in time without interferences between the phases, current ripple illustrations later provided in Section 3 do not lose generality.

3. Evaluation of the Phase Current Ripple

With reference to Figure 1, for each phase (inductive load/grid), the inverter phase voltage equation can be written as:

$$v_x\left(t\right)=R{i}_x\left(t\right)+L\frac{d{i}_x\left(t\right)}{dt}+e_x\left(t\right)$$

(3)

where $v_x$ depicts the inverter instantaneous phase voltage, $i_x$ is the instantaneous phase current, $e_x$ represents the grid phase voltage, and R is the equivalent series resistance. Both $v_x$ and $i_x$ can be written in terms of harmonic components as:

$$\{\begin{array}{c}{v}_x\left(t\right)={\overline{v}}_x\left(t\right)+{\widehat{v}}_x\left(t\right)\\ i_x\left(t\right)={\overline{i}}_x\left(t\right)+{\widehat{i}}_x\left(t\right) \end{array}$$

(4)

where ${\overline{v}}_x$ and ${\overline{i}}_x$ represent the fundamental (low-frequency) components (i.e., the instantaneous values averaged over the switching period T_sw), and ${\widehat{v}}_x$ and ${\widehat{i}}_x$ represent the switching ripple components (high-frequency). It must be noted that grid phase voltage $e_x$ is eventually almost sinusoidal, with negligible ripple components. Consequently, by rewriting Equation (3) and focusing solely on the ripple components, one may obtain:

$${\widehat{v}}_x\left(t\right)=R{\widehat{i}}_x\left(t\right)+L\frac{d{\widehat{i}}_x\left(t\right)}{dt}$$

(5)

Since the resistive voltage drop due to current ripple ${\widehat{i}}_x$ is negligible in comparison with the voltage ripple component ${\widehat{v}}_x$ (having an amplitude in the order of V_dc), Equation (5) is simplified as:

$${\widehat{v}}_x\left(t\right)\cong L\frac{d{\widehat{i}}_x\left(t\right)}{dt}$$

(6)

Finally, as commonly accepted, the instantaneous current ripple can be computed by replacing Equation (4) in Equation (6) and integrating over any abstract period (t), leading to:

$${\widehat{i}}_x\left(t\right)-{\widehat{i}}_x\left(0\right)\cong \frac{1}{L}{{\displaystyle \int }}_0^t{\widehat{v}}_x\left(t\right)dt=\frac{1}{L}{{\displaystyle \int }}_0^t\left[v_x\left(t\right)-{\overline{v}}_x\left(t\right)\right]dt$$

(7)

The peak-to-peak current ripple over the switching period T_sw (depicted in Figure 2) can be defined as:

$${\widehat{i}}_{x,pp}\left(m_x,{\mathsf{\vartheta }}_x\right)={{\widehat{i}}_x\left(t\right)|}_{T_{sw}}^{max}-{{\widehat{i}}_x\left(t\right)|}_{T_{sw}}^{min}$$

(8)

3.1. Peak-to-Peak of Phase Current Ripple

Basing on Figure 2, and considering the modulating signals introduced in Equation (1), the application time intervals t_x are expressed as follow:

$$t_x\left({\mathsf{\vartheta }}_x\right)=\left[\frac{1}{2}+m_x\cos \left({\mathsf{\vartheta }}_x\right)\right]\frac{T_{sw}}{2}$$

(9)

In the linear modulation range, the inverter phase voltage averaged over the switching period is given by:

$${\overline{v}}_x\left({\mathsf{\vartheta }}_x\right)=V_{dc}{m}_x\cos \left({\mathsf{\vartheta }}_x\right)$$

(10)

To determine the peak-to-peak current ripple, only the intervals t_x can be considered. By introducing Equation (10) in Equation (7) and bearing in mind that ${\widehat{i}}_x\left(0\right)=0$ (Figure 2), Equation (7) can be rewritten as follows:

$${\widehat{i}}_{x,pp}\left(m_x,{\mathsf{\vartheta }}_x\right)=\frac{2}{L}\left[\frac{V_{dc}}{2}-V_{dc}{m}_x\cos \left({\mathsf{\vartheta }}_x\right)\right]t_x\left({\mathsf{\vartheta }}_x\right)$$

(11)

By replacing Equation (9) in Equation (11) and simplifying, it becomes:

$${\widehat{i}}_{x,pp}\left(m_x,{\mathsf{\vartheta }}_{\mathrm{x}}\right)=\frac{V_{dc}}{ 2f_{sw}L}\left[\frac{1}{2}-2 m_x^2{\cos }^2\left({\mathsf{\vartheta }}_x\right)\right]$$

(12)

Equation (12) can be normalized by the factor of V_dc/(2Lf_sw), obtaining the normalized peak-to-peak current ripple:

$${\widehat{r}}_{x,pp}\left(m_x,{\mathsf{\vartheta }}_x\right)=\frac{1}{2}-2 m_x^2{\cos }^2\left({\mathsf{\vartheta }}_x\right)$$

(13)

Figure 3 displays the distribution of the normalized peak-to-peak current ripple magnitude, given by Equation (13), for a three-phase, four-wire, split-capacitor inverter with modulation range m_x = [0, 0.5] and phase angle ϑ_x diapason [−π/2, π/2].

To compare the conventional three-wire (3-leg) VSI with the considered four-wire split-capacitor configuration, the maximum peak-to-peak ripple currents for both topologies are depicted in Figure 3, as a function of m_x (2D traces on the left-hand side of the 3D axes box). About the three-wire topology, one can observe that the maximum peak-to-peak current ripple rises with the modulation index. Nevertheless, considering the four-wire split-capacitor inverter, the normalized maximum peak-to-peak value of the phase current ripple occurs at ϑ_x = π/2, and it is always constant (equal to 0.5) and independent from the modulation index.

To validate the theoretical developments presented in this and the following sections, some numerical simulations are carried out in MATLAB/Simulink environment. The inverter load consists of an RLC circuit with a unity power factor (at the fundamental frequency) to emulate a typical grid-connected application. In this way, the inverter modulation can be performed without grid current controllers, then an open-loop operation is allowed for the system. The circuit model has been set with the actual setup parameters later used in Section 6 (experimental results).

The simulation results of Figure 4 illustrate the three-phase currents along with the calculated envelopes (Equation (12)) in case of modulation amplitude unbalance m_a = 0.3, m_b = 0.4, and m_c = 0.5.

Figure 5 presents the detail of the normalized phase current ripples with the calculated envelopes. Each frame shows the same current profile of Figure 4 after filtering (removal of the fundamental current component) and normalization action. Note that the upper/lower envelopes correspond to half of the peak-to-peak values given in Equations (11) and (12). As expected, the simulation results show a very good match with the derived equations.

3.2. RMS of Phase Current Ripple

Basing on the previous analysis, the instantaneous current ripple always has a triangular wave shape with a peak-to-peak amplitude obtained by Equation (12), justifiable for both balanced and unbalanced conditions. Bearing in mind that the crest factor of a triangular waveform is $\sqrt{3}$, the current ripple RMS over the half of the fundamental period is determined as:

$${\widehat{I}}_x\left(m_x\right)=\sqrt{\frac{1}{\pi }{{\displaystyle \int }}_0^{\pi }{\left[{\widehat{i}}_x\left(m_x,{\mathsf{\vartheta }}_x\right)\right]}^{2}d{\mathsf{\vartheta }}_x}=\frac{1}{\sqrt{3}}\sqrt{\frac{1}{\pi }{{\displaystyle \int }}_0^{\pi }{\left[\frac{{\widehat{i}}_{x,pp}\left(m_x,{\mathsf{\vartheta }}_x\right)}{2}\right]}^{2}d{\mathsf{\vartheta }}_x}$$

(14)

By introducing Equation (12) in Equation (14), and integrating, leads to:

$${\widehat{I}}_x\left(m_x\right)=\frac{V_{dc}}{2L{f}_{sw}} \frac{1}{4\sqrt{3}}\sqrt{1-4m_x^2+6m_x^4}$$

(15)

Similar to Equation (12), the normalization of Equation (15) leads to the normalized RMS of the phase current ripple:

$${\widehat{R}}_x\left(m_x\right)=\frac{1}{4\sqrt{3}}\sqrt{1-4m_x^2+6m_x^4}\cong 0.14 \sqrt{1-4m_x^2+6m_x^4}$$

(16)

Equations (15) and (16) can be effortlessly used for computing harmonic pollution figures of merit like total harmonic distortion (THD), total demand distortion (TDD), and distortion index (DIN).

Figure 6 depicts the normalized phase current ripple RMS calculated by Equation (16) (blue line) and the corresponding values obtained by numerical simulations (red squares). A perfect agreement between analytical and numerical results can be observed.

By comparison, the normalized phase current ripple RMS for a three-phase three-wire inverter is also depicted in Figure 6 (black dashed line). In this case, the phase current ripple RMS is nearly a linear function of modulation index, starting from 0 (m = 0) up to 0.055 (m = 0.5), whereas a decreasing function of the modulation index in the case of the four-wire, split-capacitor inverter is observed, from 0.144 (m = 0) up to 0.085 (m = 0.5).

As a result, and in the effort to reduce the AC current ripple, it appears opportune to use this four-wire, split-capacitor topology only when there is a real need to handle unbalanced currents (through the neutral wire in either single-phase, two-phase, and three-phase conditions), whereas, in case of balanced currents, the conventional three-wire inverter would be a preferable choice (i.e., the neutral wire should be isolated).

Aiming to reduce harmonic pollution, novel techniques might benefit from the presented phase current ripple analysis for fine-tuning variable switching frequency PWM techniques capable of reducing maximum current ripple peak-to-peak at high values of modulation index. Thanks to the phase independence, particularly appreciable results are to be expected.

4. Evaluation of Neutral Current Ripple

Concerning Figure 1, the instantaneous neutral current i_n and “virtual” neutral voltage $v_n$ are defined as:

$$\{\begin{array}{c}{i}_n\left(t\right)=i_a\left(t\right)+i_b\left(t\right)+i_c\left(t\right) \\ v_n\left(t\right)=v_a\left(t\right)+v_b\left(t\right)+v_c\left(t\right)\end{array}$$

(17)

note that $v_n$ corresponds to three times the inverter common-mode voltage. Similar to phase quantities, neutral current, and voltage can be specified in terms of low- and high-frequency harmonic components by setting x = n in Equation (4).

To preserve a generic analysis of neutral current ripple, all the parameters m_x and ϑ_x that are describing the phase currents $i_x$ should be considered in Equation (17). However, for practical applicability purposes, the neutral current ripple has been analyzed considering nearly balanced modulating signals (m_a ≅ m_b ≅ m_c = m). In fact, due to the grid voltage symmetry and the small value of the AC-link reactance (usually in the order of 0.05–0.08 p.u.), most of the grid-connected applications (such as EV charging) concern with almost balanced modulating signals even in the presence of unbalanced currents. In this way, neutral current ripple analytical derivations are kept simple and straightforward. However, their validity results to be reduced in load-driving configurations, where strongly unsymmetric voltages would be beneficial for compensating unbalances/faults. As known, unbalanced phase currents introduce a fundamental component also in the neutral current.

Figure 7 shows the virtual neutral voltage $v_n$ (top) and neutral current ripple ${\widehat{i}}_n$ (bottom) in one switching period. Referring to Figure 2 and Figure 7, in case of balanced working conditions, the time intervals within the phase range 0 ≤ ϑ ≤ π/3 are given by:

$$\{\begin{array}{c}{t}_1=t_c=\left(\frac{1}{2}+m \cos \left(\mathsf{\vartheta }+\frac{2\pi }{3}\right)\right)\frac{T_{sw}}{2}\\ t_2=t_b-t_c=\sqrt{3}m \sin \left(\mathsf{\vartheta }\right)\frac{T_{sw}}{2} \\ t_3=t_a-t_b=\sqrt{3}m \cos \left(\mathsf{\vartheta }+\frac{\pi }{6}\right)\frac{T_{sw}}{2}\\ t_4=\frac{T_{sw}}{2}-t_a=\left(\frac{1}{2}-m \cos \left(\mathsf{\vartheta }\right)\right)\frac{T_{sw}}{2}\end{array}$$

(18)

4.1. Peak-to-Peak of Phase Current Ripple

The instantaneous neutral current ripple variation can be calculated similarly to Equation (7). By considering nearly balanced working conditions, ${\overline{v}}_n\approx 0$ (${\widehat{v}}_n\approx v_n$), it gives:

$${\widehat{i}}_n\left(t\right)-{\widehat{i}}_n\left(0\right)=\frac{1}{L}{{\displaystyle \int }}_0^t{\widehat{v}}_n\left(t\right) dt$$

(19)

In the case of single-carrier PWM, one may notice that the neutral current ripple has a periodicity of T/6. Consequently, the analysis can be restricted to a phase angle range of π/3. With reference to the phase angle range 0 ≤ ϑ ≤ π/3, the peak-to-peak neutral current ripple can be evaluated based on Equation (19). Taking into account the time intervals t₁ and t₂ (Figure 7) and bearing in mind that, due to the symmetry, ${\widehat{i}}_n\left(0\right)=0$, Equation (19) gives:

$${\widehat{i}}_{n,pp}\left(m,\mathsf{\vartheta }\right)=\frac{V_{dc}}{L}\left(3t_1+t_2\right)$$

(20)

By introducing Equation (18) in Equation (20), and simplifying, yields to:

$${\widehat{i}}_{n,pp}\left(m,\mathsf{\vartheta }\right)=\frac{V_{dc}}{ 2L{f}_{sw}}\left[\frac{3}{2}-\sqrt{3}m \cos \left(\mathsf{\vartheta }-\frac{\pi }{6}\right)\right]$$

(21)

A normalization factor V_dc/(2Lf_sw) can be considered for Equation (21), leading to the normalized peak-to-peak neutral current ripple:

$${\widehat{r}}_{n,pp}\left(m,\mathsf{\vartheta }\right)=\frac{3}{2}-\sqrt{3}m \cos \left(\mathsf{\vartheta }-\frac{\pi }{6}\right)$$

(22)

In the considered phase angle range 0 ≤ ϑ ≤ π/3, which is the period of the peak-to-peak neutral current ripple, the maximum occurs at the range borders, i.e., for ϑ = 0 and π/3, leading to:

$${\widehat{r}}_{n,pp}^{max}\left(m\right)=\frac{3}{2}\left(1-m\right)$$

(23)

In the next section is presented the normalized peak-to-peak of the neutral current, given by Equation (22), together with its maximum, given by Equation (23), as a function of m.

4.2. RMS of Neutral Current Ripple

As shown in Figure 7, the neutral current ripple does not have a triangular-like waveform. For this reason, the calculation of its RMS is not straightforward, unlike the phase current ripple one. The neutral current ripple has a linear piecewise waveform, made of four intervals in one-half of the switching period (here identified with k = 1, 2, …, 4). The neutral current ripple can be seen as the composition of DC and AC components over each time interval. The AC component has a sawtooth-like waveform. Given that DC and AC components are for the RMS orthogonal, the RMS value ${\widehat{I}}_{nk}$ over each interval can be written as:

$${\widehat{I}}_{nk}\left(m,\mathsf{\vartheta }\right)=\sqrt{{\left({\widehat{I}}_{nk}^{dc}\right)}^2+{\left({\widehat{I}}_{nk}^{ac}\right)}^2}$$

(24)

Considering that $\sqrt{3}$ is the sawtooth crest factor, and according to Figure 7, Equation (24) can be explicitly rewritten as:

$${\widehat{I}}_{nk}\left(m,\mathsf{\vartheta }\right)=\{\begin{array}{l}{\widehat{I}}_{n1}=\frac{V_{dc}}{2L}\sqrt{{\left(\frac{3t_1}{2}\right)}^2+{\left(\frac{3t_1}{2\sqrt{3}}\right)}^2}\\ {\widehat{I}}_{n2}=\frac{V_{dc}}{2L}\sqrt{{\left(3t_1+\frac{t_2}{2}\right)}^2+{\left(\frac{t_2}{2\sqrt{3}}\right)}^2}\\ {\widehat{I}}_{n3}=\frac{V_{dc}}{2L}\sqrt{{\left(3t_4+\frac{t_3}{2}\right)}^2+{\left(\frac{t_3}{2\sqrt{3}}\right)}^2}\\ {\widehat{I}}_{n4}=\frac{V_{dc}}{2L}\sqrt{{\left(\frac{3t_4}{2}\right)}^2+{\left(\frac{3t_4}{2\sqrt{3}}\right)}^2}\end{array}$$

(25)

For the odd symmetry of the neutral current ripple, its RMS over the whole switching period T_sw can be calculated by composing the individual RMS over each time interval k (25) as:

$${{\widehat{I}}_n\left(m,\mathsf{\vartheta }\right)|}_{T_{sw}}=\sqrt{\frac{2}{T_{sw}}{\displaystyle \sum }_k{t}_k{\left[{\widehat{I}}_{nk}\left(m,\mathsf{\vartheta }\right)\right]}^2}$$

(26)

Finally, the total neutral current ripple RMS is obtained by integrating Equation (26) over the phase angle period [0, π/3]:

$${\widehat{I}}_n\left(m\right)=\sqrt{\frac{3}{\pi }{{\displaystyle \int }}_0^{\frac{\pi }{3}}{\left[{{\widehat{I}}_n\left(m,\mathsf{\vartheta }\right)|}_{T_{sw}}\right]}^{2}d\mathsf{\vartheta }}=\frac{V_{dc}}{2L{f}_{sw}}\sqrt{\frac{3}{16}-\frac{9}{8}{m}^2+\frac{2\sqrt{3}}{\pi }{m}^3}$$

(27)

By normalizing Equation (27), as for Equations (21) and (22), it becomes:

$${\widehat{R}}_n\left(m\right)=\frac{\sqrt{3}}{4}\sqrt{1-6m^2+\frac{32}{\sqrt{3}\pi }{m}^3}$$

(28)

5. Mitigation of Neutral Current Ripple

In applying the conventional PWM strategy to the four-wire, split-capacitor configuration, a single triangular carrier is adopted for all three phases. As mentioned in the foregoing sections, the three phases of such inverter topology are entirely independent of each other, owing to the shared fourth wire connection. Consequently, an effective way to attenuate the neutral current ripple is to consider three interleaved carriers (cr_a, cr_b, cr_c) and comparing to the corresponding three modulating signals (u_a, u_b, u_c) to drive the three inverter legs [5]. Although the line-to-line voltage waveforms slightly degrade in this circumstance, it does not introduce any effects on the line-to-neutral voltages and the corresponding phase currents.

Differently from the single-carrier PWM, levels and pulse durations of ${\widehat{v}}_n$ within the linear range of m depend on both m, and ϑ. In this context, several subcases are possible. Based on the example of Figure 8, that is valid in the case of balanced sinusoidal modulation and with m < 1/3, the time intervals become:

$$\{\begin{array}{l}{t}_1=\left(\frac{1}{3}-m \cos \left(\mathsf{\vartheta }\right)\right)\frac{T_{sw}}{2}\\ t_2=\left(\frac{1}{3}+m \cos \left(\mathsf{\vartheta }+\frac{2\pi }{3}\right)\right)\frac{T_{sw}}{2}\\ t_3=\left(\frac{1}{3}-m \cos \left(\mathsf{\vartheta }-\frac{2\pi }{3}\right)\right)\frac{T_{sw}}{2}\\ t_4=\left(\frac{1}{3}+m \cos \left(\mathsf{\vartheta }\right)\right)\frac{T_{sw}}{2}\\ t_5=\left(\frac{1}{3}-m \cos \left(\mathsf{\vartheta }+\frac{2\pi }{3}\right)\right)\frac{T_{sw}}{2}\\ t_6=\left(\frac{1}{3}+m \cos \left(\mathsf{\vartheta }-\frac{2\pi }{3}\right)\right)\frac{T_{sw}}{2}\end{array}$$

(29)

5.1. Peak-to-Peak of Neutral Current Ripple (Interleaved)

Unlike in Figure 2 and Figure 7, the envelope of ${\widehat{i}}_n$ is not symmetric anymore and ${\widehat{i}}_n\left(0\right)\ne 0$. Given that the average of ${\widehat{i}}_n$ must be zero over a switching period, the neutral current ripple is determined from Equation (19) as:

$${\widehat{i}}_n\left(0\right)=\frac{1}{T_{sw}}{{\displaystyle \int }}_0^{T_{sw}}\frac{1}{L}{{\displaystyle \int }}_0^t{\widehat{v}}_n\left(t^{\prime }\right)d{t}^{\prime }dt$$

(30)

Considering the pulse pattern of Figure 8 and the timings introduced in Equation (29), Equation (30) can be formulated as follows:

$${\widehat{i}}_n\left(0\right)=\frac{V_{dc}}{2L}\overline{t}$$

(31)

where $\overline{t}$ is an equivalent time period depending on the phase pulses disposition at the initial time t = 0, resulting in:

$$\overline{t}=\frac{1}{ f_{sw}}\left[\frac{\sqrt{3}}{6}m \cos \left(\mathsf{\vartheta }+\frac{\pi }{6}\right)-\frac{1}{12}\right]$$

(32)

It has been noticed that the neutral current ripple has asymmetric positive (upper) and negative (lower) envelope profiles, both having the same shape and the same periodicity 2π/3 (T/3) but displaced by π/3 one from another. Thus, the analysis can be limited to the angle range π/3.

Concerning the phase angle range −π/6 ≤ ϑ ≤ π/6 and to the example shown in Figure 8, the positive (upper) envelope of the neutral current ripple can be evaluated by considering the time intervals t₁, t₂, t₃, leading to:

$${\widehat{i}}_{n,pk}^{+}\left(m,\mathsf{\vartheta }\right)=\frac{V_{dc}}{2L}\left(t_1-t_2+t_3\right)+{\widehat{i}}_n\left(0\right)=\frac{V_{dc}}{2L{f}_{sw}}\left[\frac{1}{12}+\frac{\sqrt{3}}{6}m\cos \left(\mathsf{\vartheta }+\frac{\pi }{6}\right)\right]$$

(33)

Similarly, the negative (lower) envelope is given by:

$${\widehat{i}}_{n,pk}^{-}\left(m,\mathsf{\vartheta }\right)=\frac{V_{dc}}{2L}\left(t_1-t_2+t_3-t_4\right)+{\widehat{i}}_n\left(0\right)=-\frac{V_{dc}}{ 2L{f}_{sw}}\left[\frac{1}{12}+\frac{\sqrt{3}}{6}m\cos \left(\mathsf{\vartheta }-\frac{\pi }{6}\right)\right]$$

(34)

By the definition given by Equation (8), the peak-to-peak neutral current ripple in case of interleaved carriers (here denoted by an asterisk, “*”) becomes:

$${\widehat{i}}_{n,pp}^{*}\left(m,\mathsf{\vartheta }\right)={\widehat{i}}_{n,pk}^{+}\left(m,\mathsf{\vartheta }\right)-{\widehat{i}}_{n,pk}^{-}\left(m,\mathsf{\vartheta }\right)=\frac{V_{dc}}{ 2L{f}_{sw}}\left[\frac{1}{6}+\frac{1}{2}m\cos \left(\mathsf{\vartheta }\right)\right]$$

(35)

Note that the same result can be obtained by considering the maximum time interval t_k to calculate the peak-to-peak ripple:

$${\widehat{i}}_{n,pp}^{*}\left(m,\mathsf{\vartheta }\right)=\frac{V_{dc}}{2L}\max \left(t_k\right)=\frac{V_{dc}}{ 2L{f}_{sw}}\left[\frac{1}{6}+\frac{1}{2} \max \left|u_x\left(\mathsf{\vartheta }\right)\right|\right]$$

(36)

The peak-to-peak neutral current ripple can also be defined over the whole fundamental period and by considering the double of the maximum positive (or minimum negative) ripple amplitude, i.e., by replacing ϑ = −π/6 in Equation (33):

$${{\widehat{i}}_{n,pp}^{*}|}_T\left(m\right)=2 {{\widehat{i}}_{n,pk}^{+}\left(m,\mathsf{\vartheta }\right)|}_T^{max}=\frac{V_{dc}}{ 2L{f}_{sw}}\left(\frac{1}{6}+\frac{\sqrt{3}}{3}m\right)$$

(37)

It has been numerically verified that practically the same results (33)–(37) can be obtained for higher values of m, i.e., 1/3 < m < 1/2, despite the increased complexity of the derivation process.

5.2. RMS of Neutral Current Ripple (Interleaved)

By following the same approach introduced in Section 4.2, it is possible to evaluate the neutral current ripple RMS in interleaved carriers PWM. Results can be distinguished from Section 4.2 ones because denoted with the “*” symbol. In this context, ${\widehat{i}}_n\left(0\right)$ should be considered in Equation (24). Thus, the ripple RMS ${\widehat{I}}_{nk}^{\ast }$ in the six intervals is:

$${\widehat{I}}_{nk}^{\ast }\left(m,\mathsf{\vartheta }\right)=\{\begin{array}{l}{\widehat{I}}_{n1}^{\ast }=\frac{V_{dc}}{2L}\sqrt{{\left(\overline{t}+\frac{t_1}{2}\right)}^2+{\left(\frac{t_1}{2\sqrt{3}}\right)}^2} \\ {\widehat{I}}_{n2}^{\ast }=\frac{V_{dc}}{2L}\sqrt{{\left(\overline{t}+t_1-\frac{t_2}{2}\right)}^2+{\left(\frac{t_2}{2\sqrt{3}}\right)}^2} \\ {\widehat{I}}_{n3}^{\ast }=\frac{V_{dc}}{2L}\sqrt{{\left(\overline{t}+t_1-t_2+\frac{t_3}{2}\right)}^2+{\left(\frac{t_3}{2\sqrt{3}}\right)}^2}\\ {\widehat{I}}_{n4}^{\ast }=\frac{V_{dc}}{2L}\sqrt{{\left(\overline{t}+t_6-t_5+\frac{t_4}{2}\right)}^2+{\left(\frac{t_4}{2\sqrt{3}}\right)}^2}\\ {\widehat{I}}_{n5}^{\ast }=\frac{V_{dc}}{2L}\sqrt{{\left(\overline{t}+t_6-\frac{t_5}{2}\right)}^2+{\left(\frac{t_5}{2\sqrt{3}}\right)}^2}\\ {\widehat{I}}_{n6}^{\ast }=\frac{V_{dc}}{2L}\sqrt{{\left(\overline{t}+\frac{t_6}{2}\right)}^2+{\left(\frac{t_6}{2\sqrt{3}}\right)}^2} \end{array}$$

(38)

By replacing Equation (38) in Equation (26), yields to:

$${{\widehat{I}}_n^{*}\left(m,\mathsf{\vartheta }\right)|}_{T_{sw}}=\frac{V_{dc}}{2L{f}_{sw}}\frac{1}{12\sqrt{3}}\sqrt{1+18m^2}={\widehat{I}}_n^{*}\left(m\right)$$

(39)

Unlike the single-carrier PWM, the RMS of the neutral current ripple over each switching period is invariant from phase angle ϑ. Consequently, Equation (39) also represents the RMS of the neutral current ripple over a fundamental period.

As stated before, voltage levels may change depending on m and ϑ. Thus, Equation (39) is valid for m ≤ 1/3. However, it has been numerically verified that Equation (39) gives an excellent approximation also in case of higher values of m, avoiding cumbersome calculations without additional insights.

Equation (39) can be normalized, leading to:

$${\widehat{R}}_n^{*}\left(m\right)=\frac{1}{12\sqrt{3}}\sqrt{1+18m^2}$$

(40)

As pointed out for the phase current ripple RMS, Equations (27), (28), (39) and (40) permit the simple computations of common metrics such as THD, TDD, and DIN.

5.3. Comparison of Neutral Current Ripple in Case of Single-Carrier and Three Interleaved Carries

By comparison, Figure 9 shows peak-to-peak neutral current ripple (normalized) in the case of single-carrier and three interleaved carriers, given by Equations (21) and (36), respectively, as a function of modulation index m and angle ϑ in a 3D plot.

The maximum peak-to-peak neutral current ripples over one fundamental period are shown in Figure 9 as a function of m (2D plot on the left-hand side of the 3D axes box) for both the modulation cases. The benefit of interleaving carriers is evident, resulting in a relevant decrease of the peak-to-peak neutral current ripple in the whole range of m and ϑ. In the worst case (high values of modulating index), the maximum peak-to-peak results are halved compared to the single carrier counterpart.

Figure 10 illustrates the instantaneous neutral current ripple and the calculated envelopes for the two considered cases in the normalized form. For the single-carrier PWM, the neutral current ripple envelopes ($\pm {\widehat{i}}_{n,pp}/2$) are defined by Equation (21), whereas, in the case of interleaved carriers PWM, upper and lower envelopes (${\widehat{i}}_{n,pk}^{+}$ and ${\widehat{i}}_{n,pk}^{-}$) are evaluated by Equations (33) and (34), respectively.

Figure 11 illustrates the comparison of the normalized neutral current ripple RMS as a function of m for both modulation techniques. The RMS is calculated by Equations (28) and (40) in single-carrier and interleaved-carriers PWMs, respectively. As shown, the matching between analytically derived values (continuous lines) and numerical simulation results (green squares/diamonds) is more than satisfactory. It worth noticing that the neutral current ripple mitigation technique here studied reduces by at least 50% the neutral current ripple RMS in comparison with the standard single-carrier PWM. Moreover, similarly to the phase current ripple RMS of Figure 6, normalized values range around 0.1 p.u. level. In this way, taking advantage of phase filter sizing, the neutral wire might not need a specific filter design to comply with international standards like IEC 61000-3-2 and IEEE Std 519.

A similar technique has been proposed in [19,20], aimed to mitigate the common-mode output voltage in three-phase, three-wire inverters. However, in the case of three wires, the modulation method with interleaved carriers degrades the harmonic spectrum of the output voltages/currents compared to standard single-carrier PWM methods [19].

6. Experimental Results

The theoretical developments introduced in the previous sections have been verified by the experimental tests carried out by the setup shown in Figure 12a. As visible in Figure 12b, the circuit scheme corresponds to a unity power-factor three-phase load connected to the four-wire split-capacitor inverter. In this way, it is possible to emulate power flow from the DC to AC side as it would happen in V2G applications without involving any closed-loop control. Test bench main parameters are given in

Table 1. Main system parameters.

Label	Description	Parameters
Vdc	dc voltage supply	100 V
C	DC-link split capacitance (2×)	2 mF
R, L	AC-link inductor (series RL)	0.727 Ω, 1.73 mH
Ro,Co	equivalent grid (parallel RC)	6.6 Ω, 45 µF
f	fundamental frequency	50 Hz
fsw	switching frequency	3.6 kHz

. The three-phase split-capacitor inverter is made out of one IGBT (insulated-gate bipolar transistor) from Mitsubishi Electric (PS22A76), and it is feed by a TDK-Lambda (GEN100-33) controllable power supply. The inverter is driven using a Texas Instruments (TMS320 F28379D) DSP controlled from MATLAB/Simulink (Mathworks) environment. Currents and voltages are sensed using LEM LA 55-P current sensors and Pico TA057 voltage probes, respectively. Data is acquired employing Rigol (DS1054Z) digital oscilloscopes using a sampling rate of 5MS/s.

Figure 13 shows measured phase currents with their calculated envelopes for the corresponding case study presented in Figure 4 (modulation index unbalance m_a = 0.3, m_b = 0.4, and m_c = 0.5). Moreover, having conducted experimental results employing the same switching frequency used in numerical validation of Figure 4, an at-glance comparison between the two pictures is enabled. The bounding envelopes (black lines) described by Equation (12) are exactly the same used in Figure 4.

Figure 14 shows the instantaneous neutral current ripples for single-carrier PWM (upper plot) and three interleaved carriers PWM (bottom plot), along with their theoretical envelopes. The experimental results presented in Figure 14 corresponds to the simulation results presented in Figure 10, considering balanced working conditions (m = 0.4) and switching frequency f_sw = 3.6 kHz. Also in this case, the neutral current ripple envelopes have been evaluated by Equation (21) for single-carrier PWM ($\pm {\widehat{i}}_{n,pp}/2$), and by Equations (33) and (34) for interleaved carriers PWM (${\widehat{i}}_{n,pk}^{+}$ and ${\widehat{i}}_{n,pk}^{-}$, respectively). Different from Figure 10, traces in Figure 14 are not normalized. A high-pass filter (1 kHz cut-off frequency) has been applied to eliminate the low-frequency noise, due to the small unbalance of the actual setup load. A reasonably good matching between experimental, numerical, and theoretical results can be observed.

The effect of interleaving the carriers is not visible in the phase-to-neutral voltages (and in phase currents), whereas it appears on the line-to-line voltages. In particular, Figure 15 shows the line-to-line voltages measured between phases b and c (v_bc) in the cases of single-carrier PWM (upper plot) and interleaved carriers PWM (bottom plot).

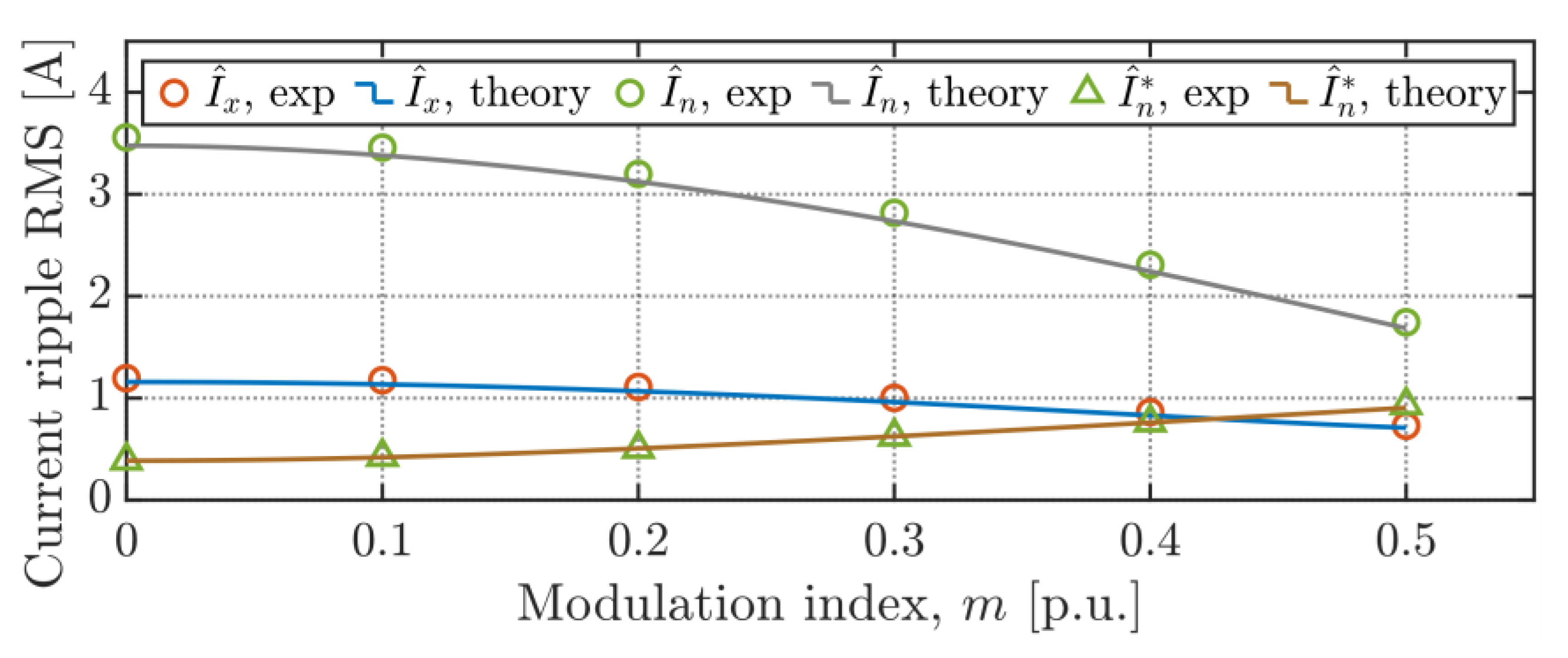
Finally, Figure 16 shows the RMS values of phase and neutral current ripples (in balanced modulation conditions) for single-carrier and interleaved carriers PWM. The theoretical results obtained by Equations (15), (27) and (39) are displayed by continuous lines, whereas circular and triangular markers identify the experimental measurements. Also in this case, a good agreement between experimental and theoretical results can be observed in the whole range of the modulation index m.

7. Conclusions

The characterization of instantaneous AC output current ripple for a three-phase, four-wire, split-capacitor PWM converter is provided in this paper. Specifically, the peak-to-peak current ripple has been analytically defined over the entire fundamental period as a function of the generic modulation index and phase angle for balanced and unbalanced operating conditions. In this way, presented mathematical tools can be utilized in theoretically any context where a converter capable of morphing into single-phase, two-phase, and three-phase is requested. The maximum boundary of the peak-to-peak current ripple has also been obtained, based on analytical functions. The current ripple RMS has been computed as well. It has been shown that the maximum peak-to-peak phase current ripple is constant in the whole modulation index range, and the lower is the modulation index, the higher is the phase current ripple RMS. The results have been compared with the corresponding ones in the case of a three-phase, three-wire PWM inverter.

The analysis of both peak-to-peak and RMS of the current ripple has also been considered for the neutral (4th) wire in case of quasi-balanced operating conditions. This permits to have straightforward and effective formulations useful in grid-connected applications. The study has also been extended to the case of interleaved carriers PWM, implemented to reduce the neutral current ripple without drawbacks on the phase current ripples. In particular, a reduction of at least 50% in the maximum neutral current ripple peak-to-peak and neutral current ripple RMS has been achieved. Moreover, this technique makes neutral ripple magnitude comparable (if not even smaller) to phase one for the benefits of the converter design. From these appreciable results, it is clear that, although a slight degradation of the line-to-line voltage is introduced, four-wire split-capacitor inverters should be driven using a multi-carrier approach.

Numerical and experimental tests have been performed to demonstrate the efficacy of the analytical developments for both peak-to-peak and RMS of both phase and neutral current ripples. A particularly good matching among analytical formulations, numerical simulations, and experimental tests validates the results’ efficacy and methodology validity in all the cases.

The presented equations and diagrams can be usefully embraced to determine the AC current ripple parameters with a view to design AC filters, calculate the AC losses, and ensure consistency with the grid/load quality benchmarks. In particular maximum current ripple peak-to-peak can be used for assessing IEC 61000-3-2 and IEEE Std 519 standards compliance. On the other hand, the current ripple RMS makes it particularly effortless to calculate harmonic pollution figures of merit like THD, TDD, and DIN. Future developments might take advantage of the detailed ripple characterization for proposing variable switching frequency PWM modulation techniques capable of optimizing converter harmonic performances. EV charging application appears to be the principal potential beneficiary of this characteristic which could be extensively used for carrying out V2G, V2H, and V2V implementations.