An Advanced Angular Velocity Error Prediction Horizon Self-Tuning Nonlinear Model Predictive Speed Control Strategy for PMSM System
Abstract
:1. Introduction
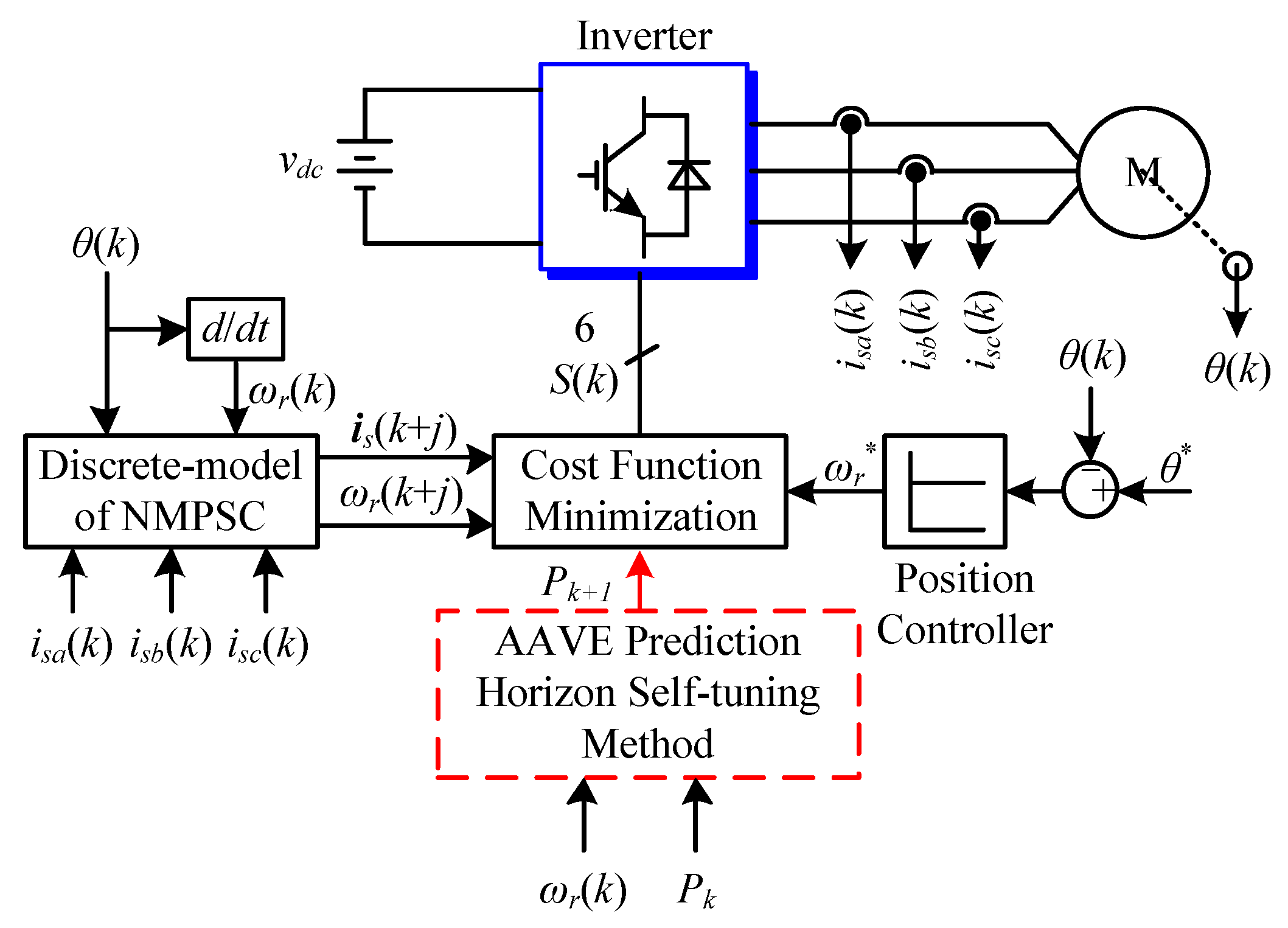
2. PMSM Model and NMPSC Strategy
2.1. Problem Description
2.2. Discrete-Time Model
2.3. NMPSC Strategy
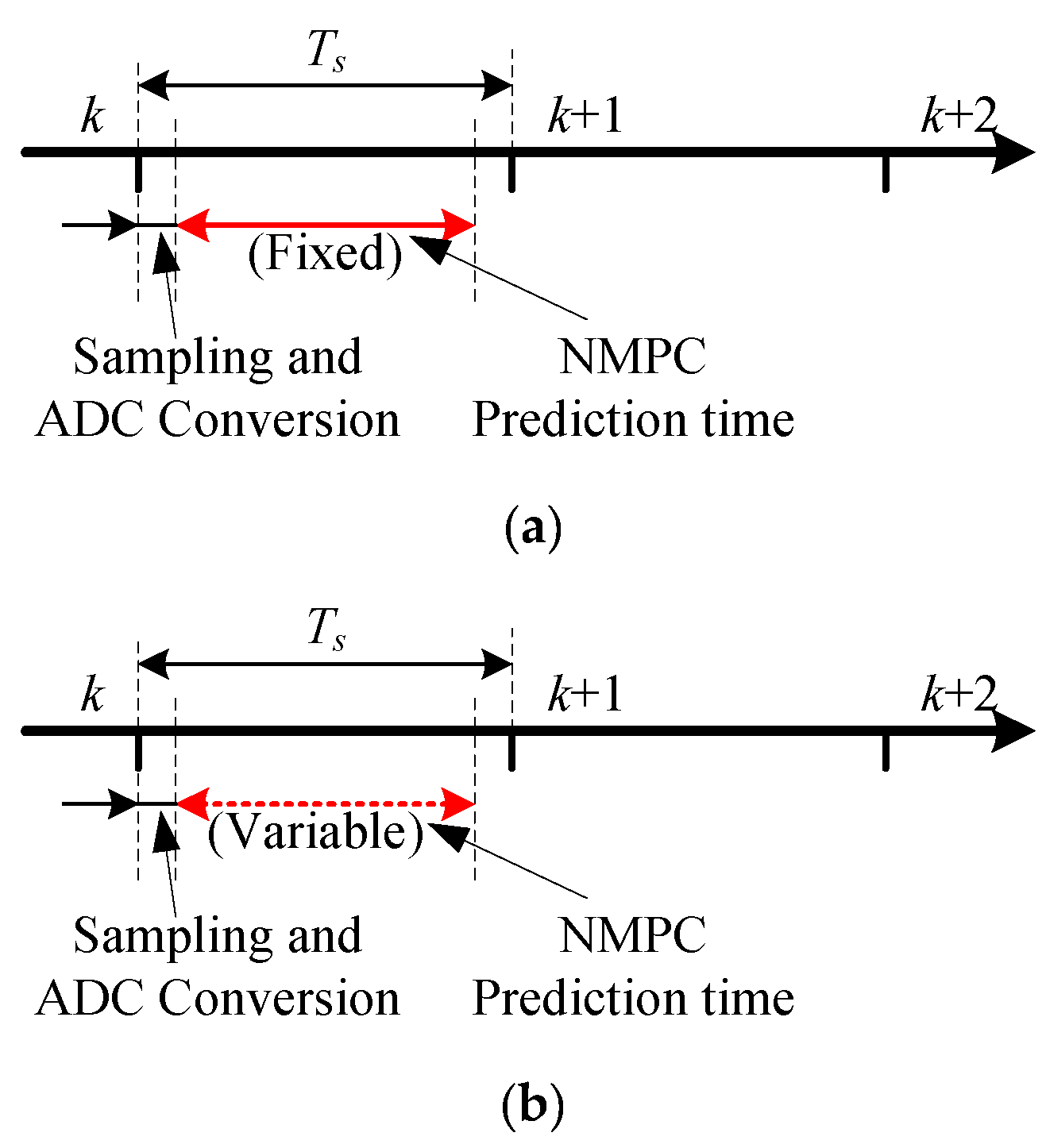
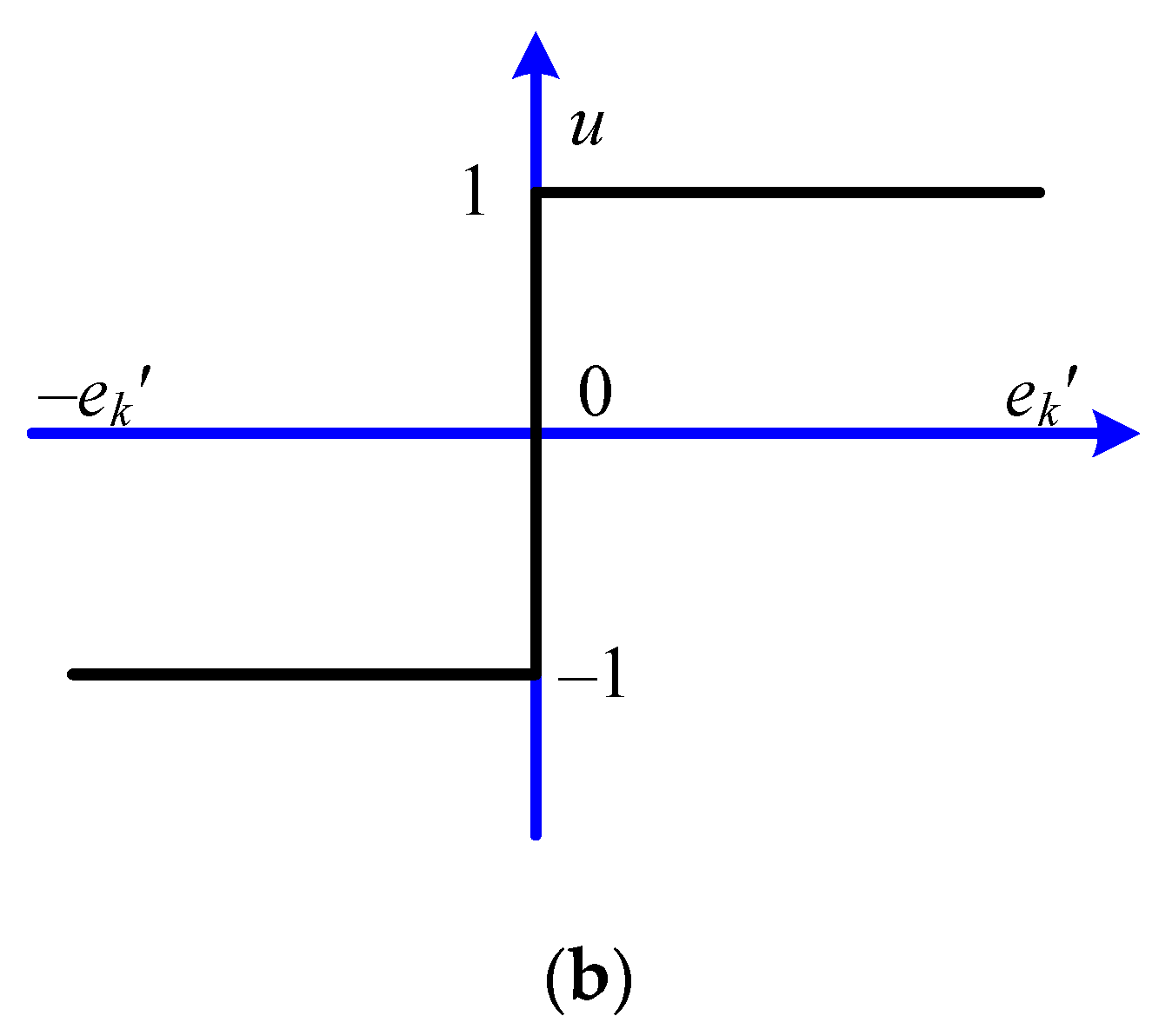
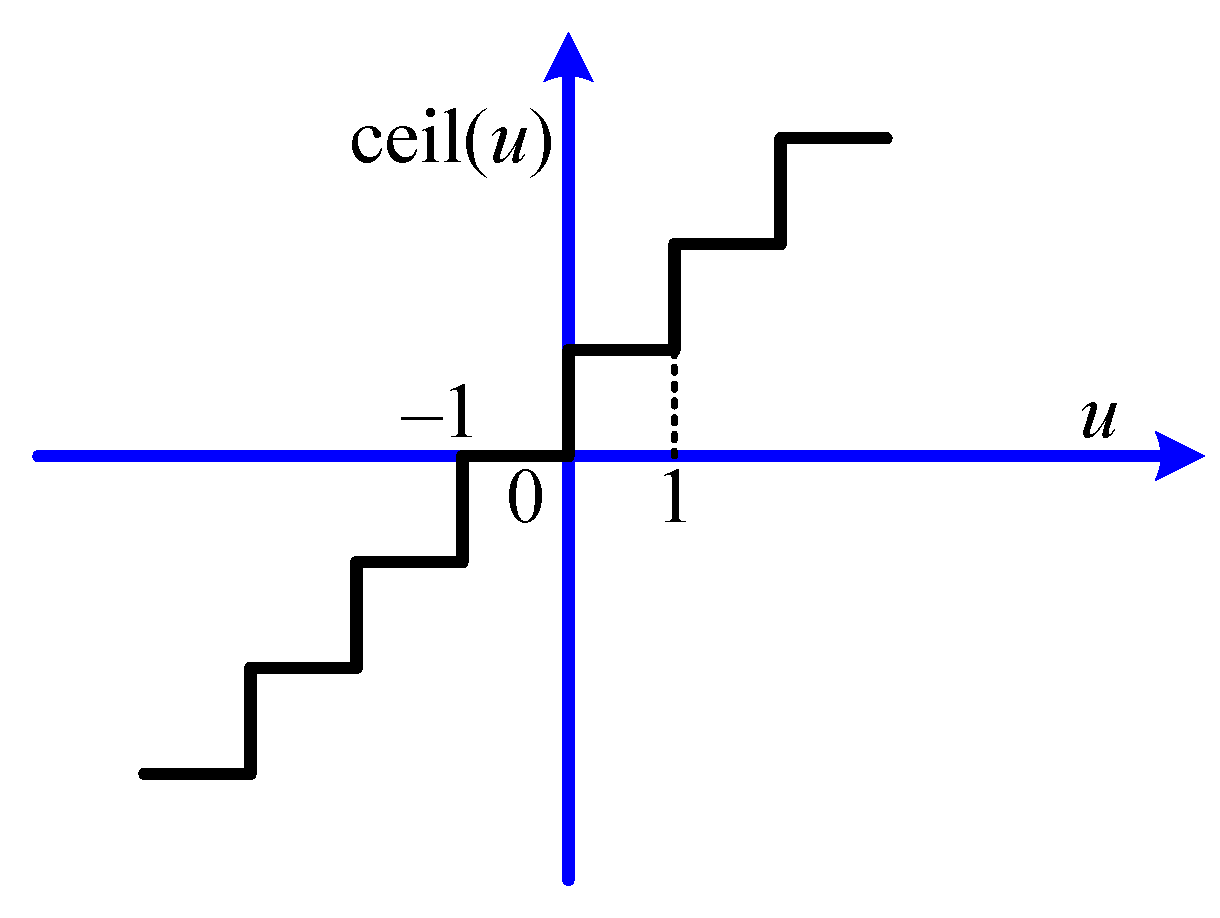
3. Proposed AAVE Method
- Measurement and detection;
- 2.
- Virtual reference and step generation;
- Prediction horizon calculation and range judgment.
4. Simulation Results and Analysis
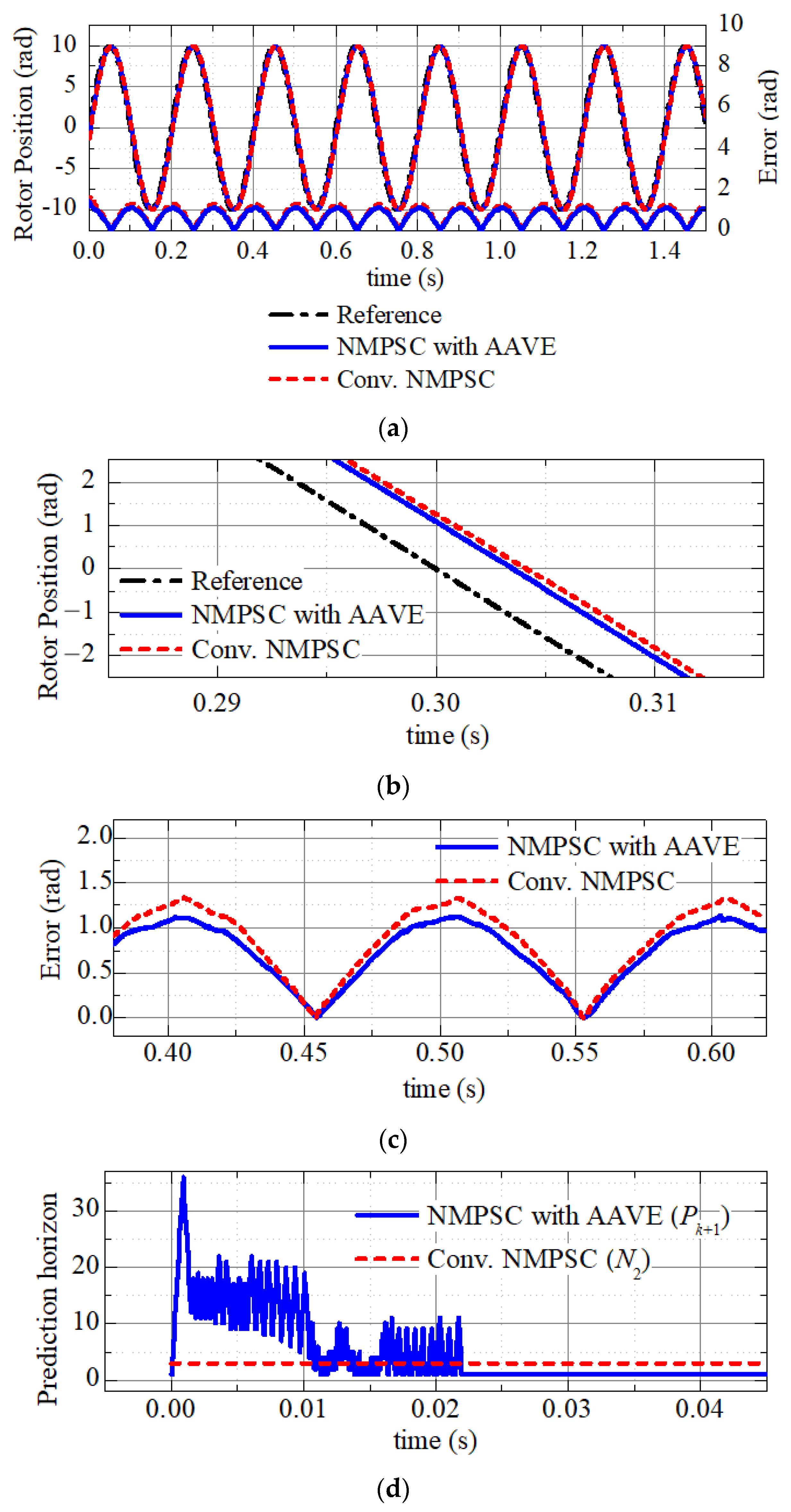
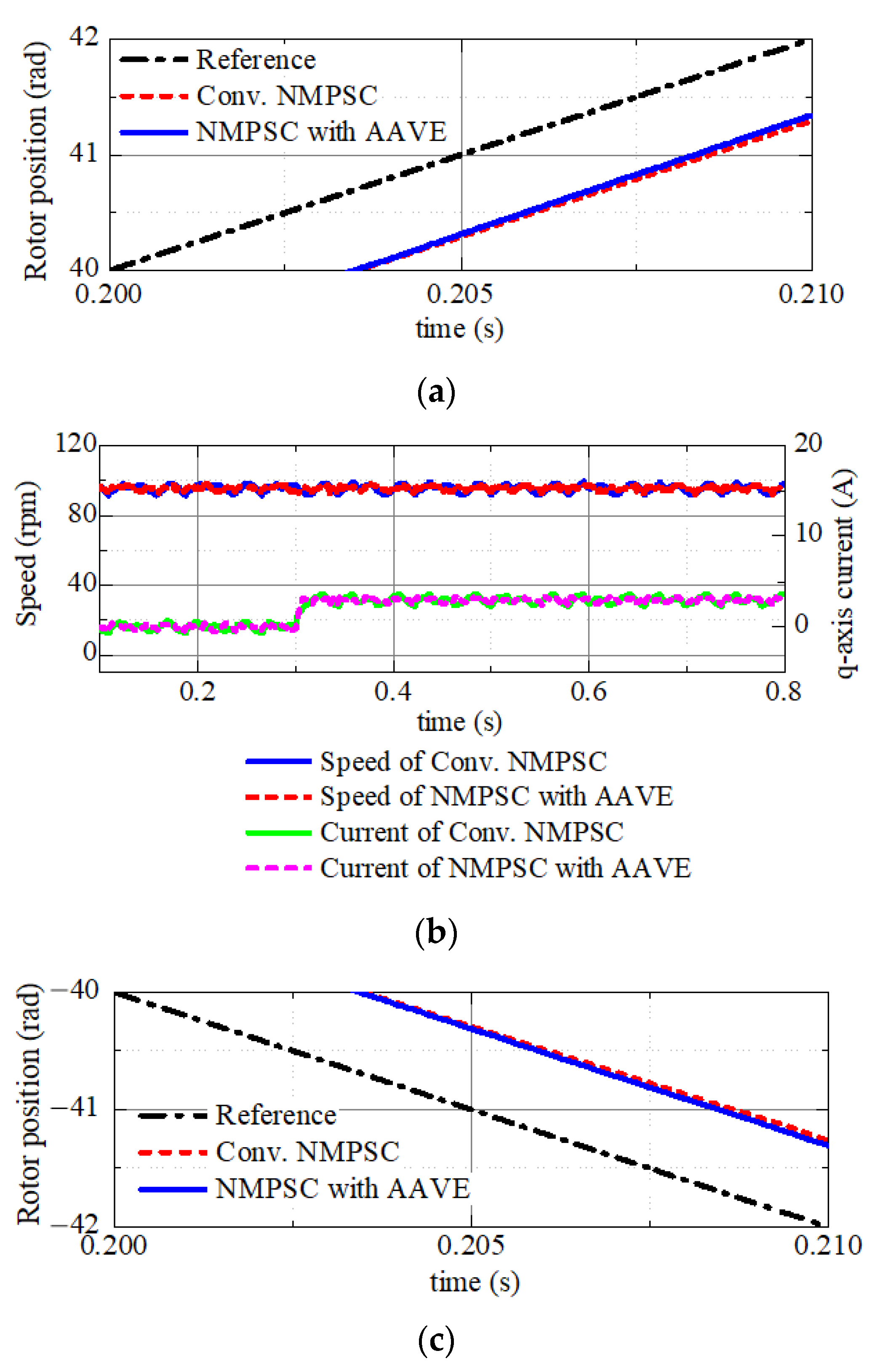
4.1. Tracking Performance Analysis
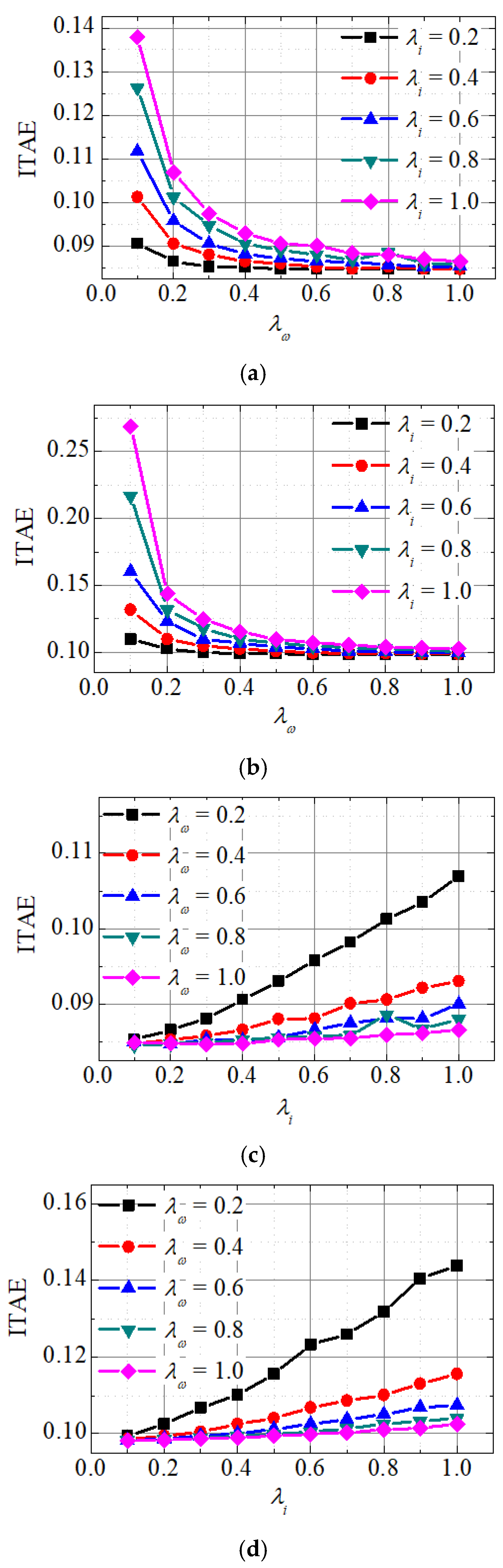
4.2. Weighting Factor Sensitivities
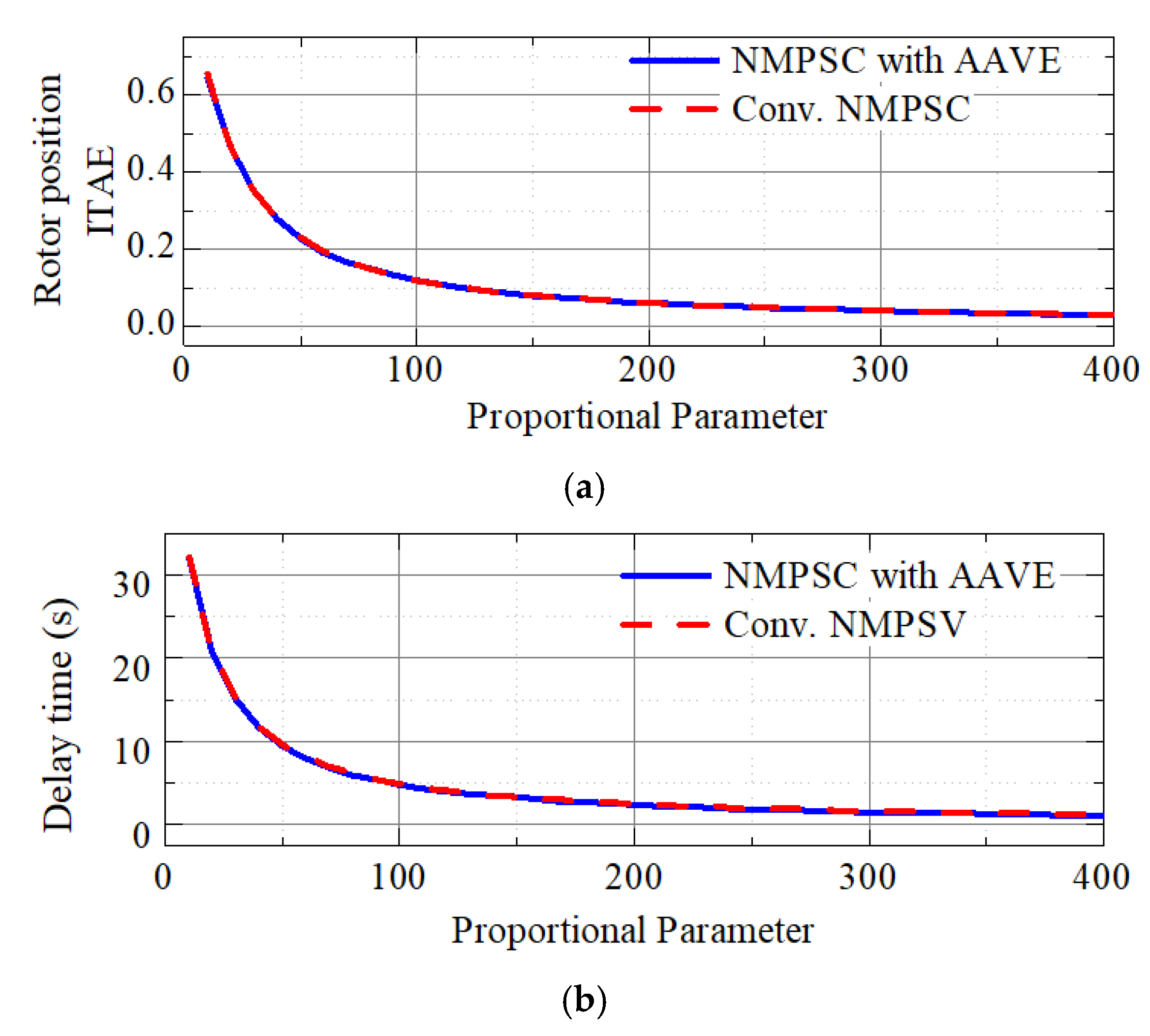
4.3. Propotional Parameter Selection
4.4. Proportional Parameter Selection
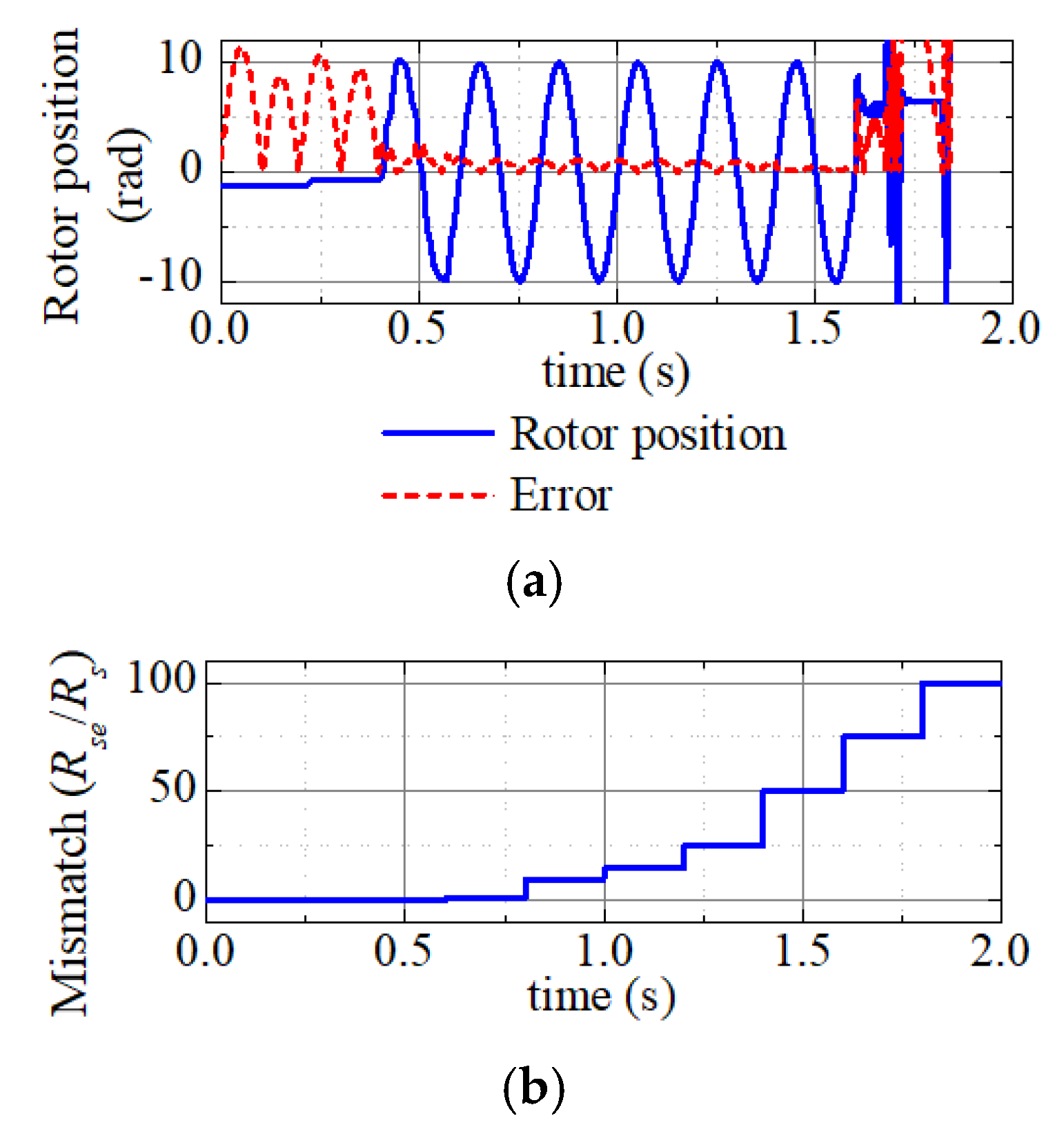
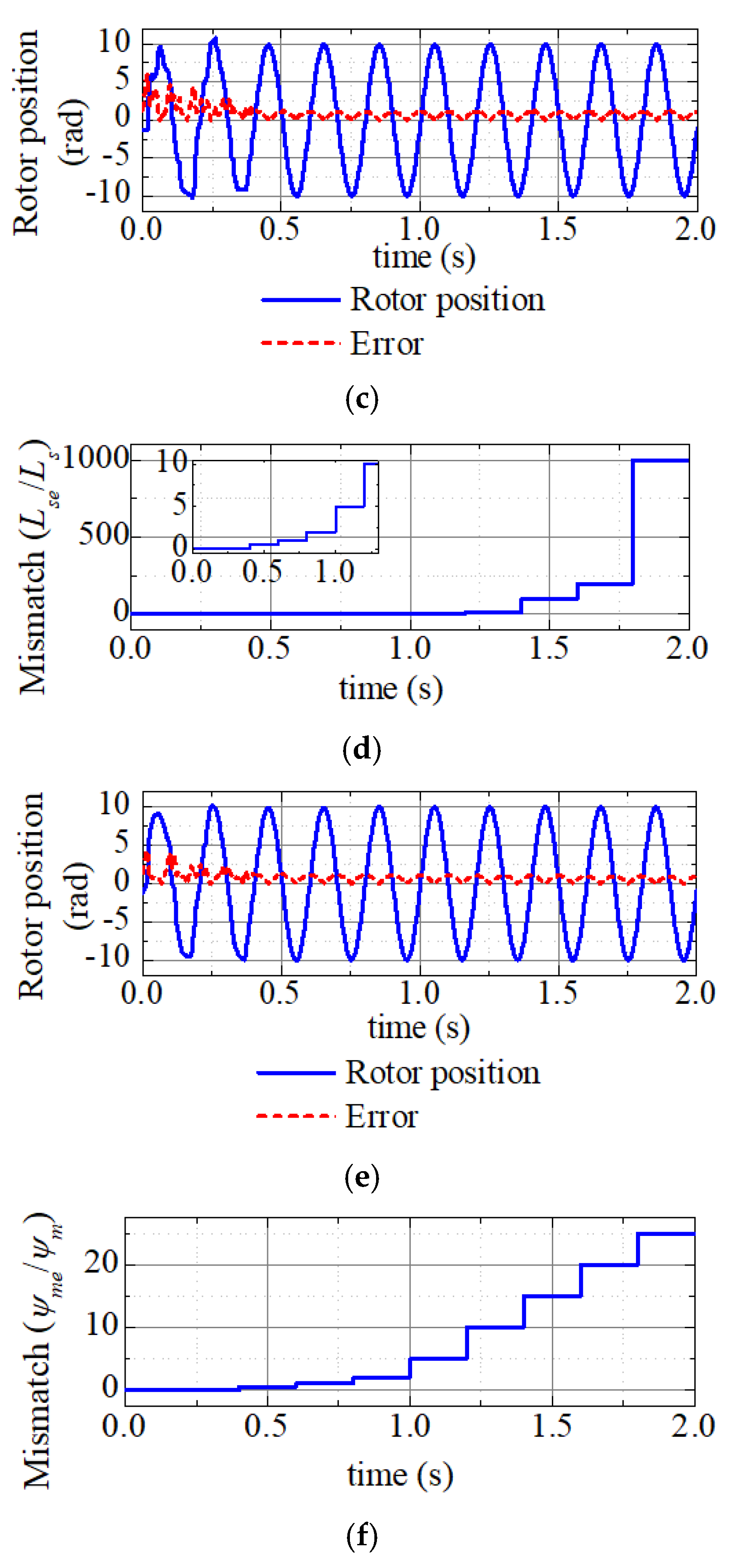
4.5. Servo Stiffness Analysis
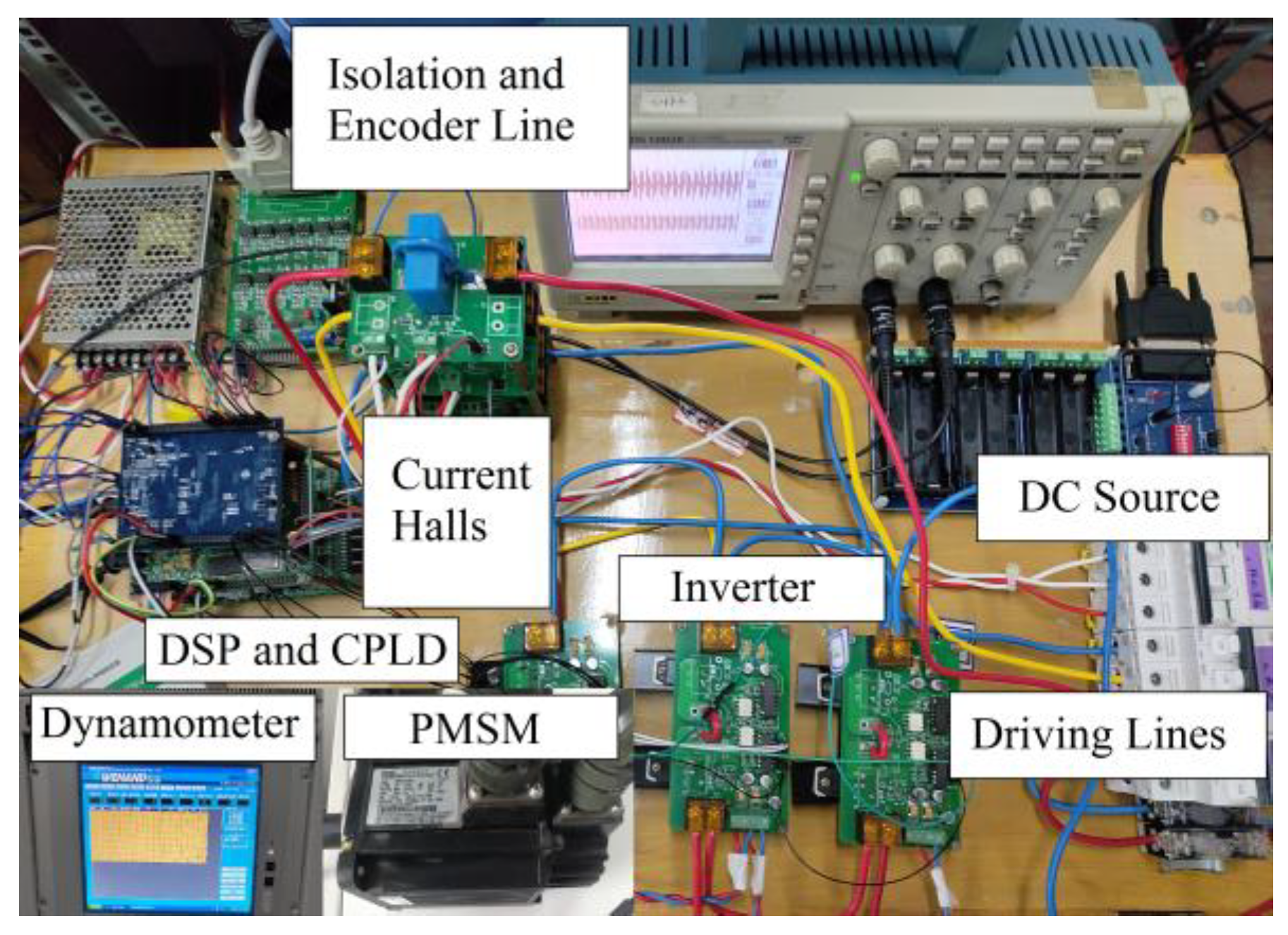
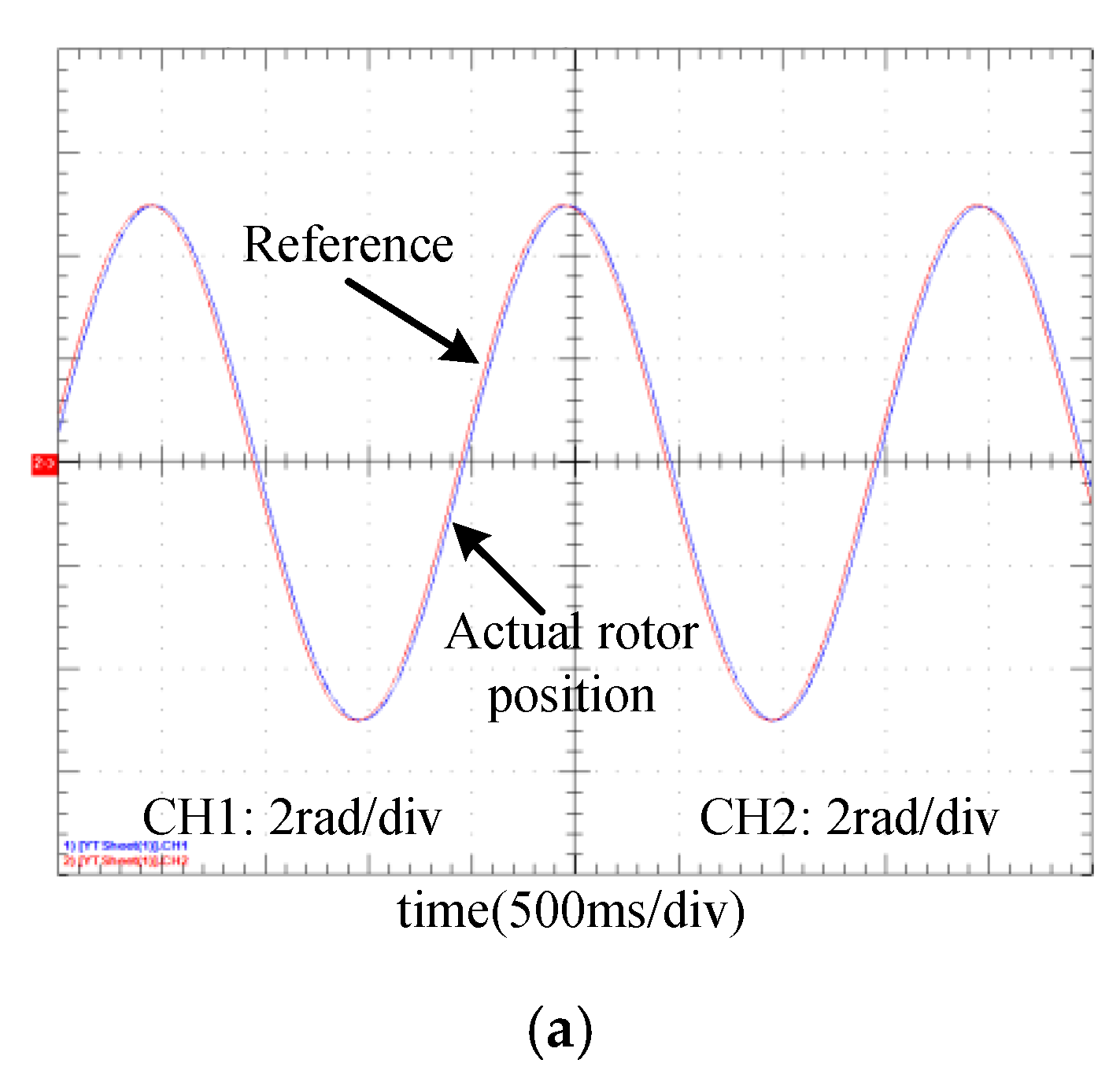
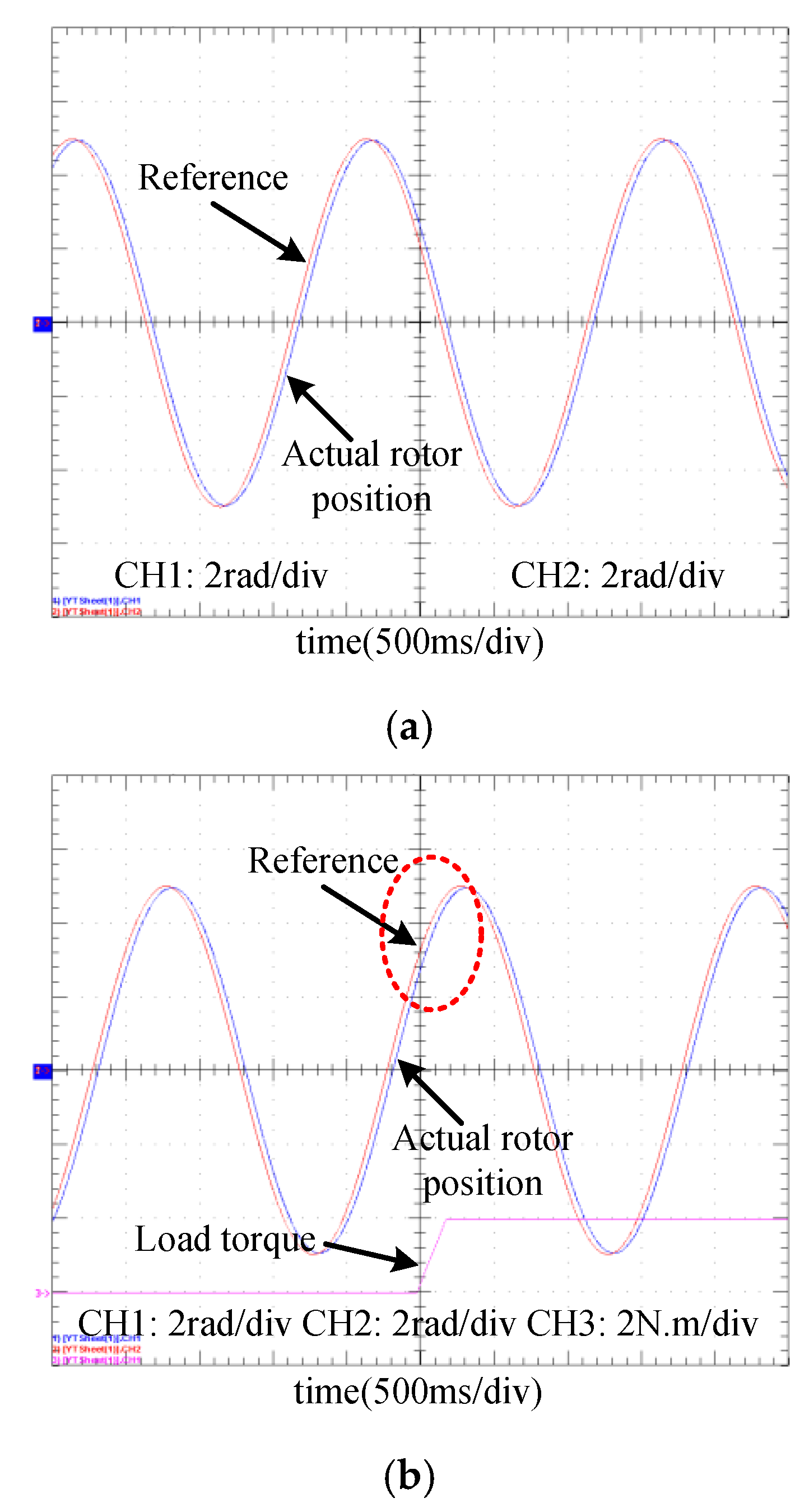
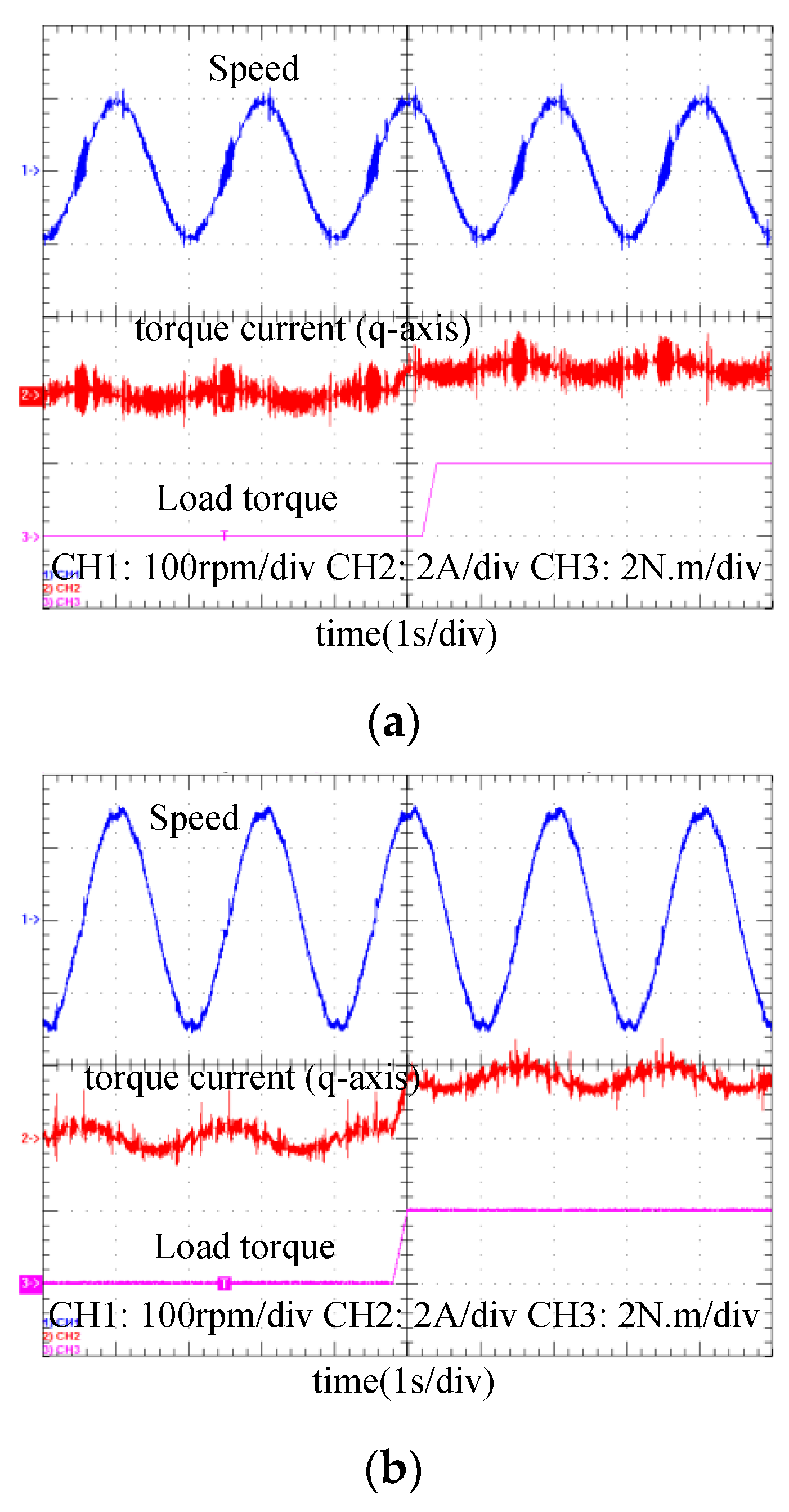
5. Experimental Results
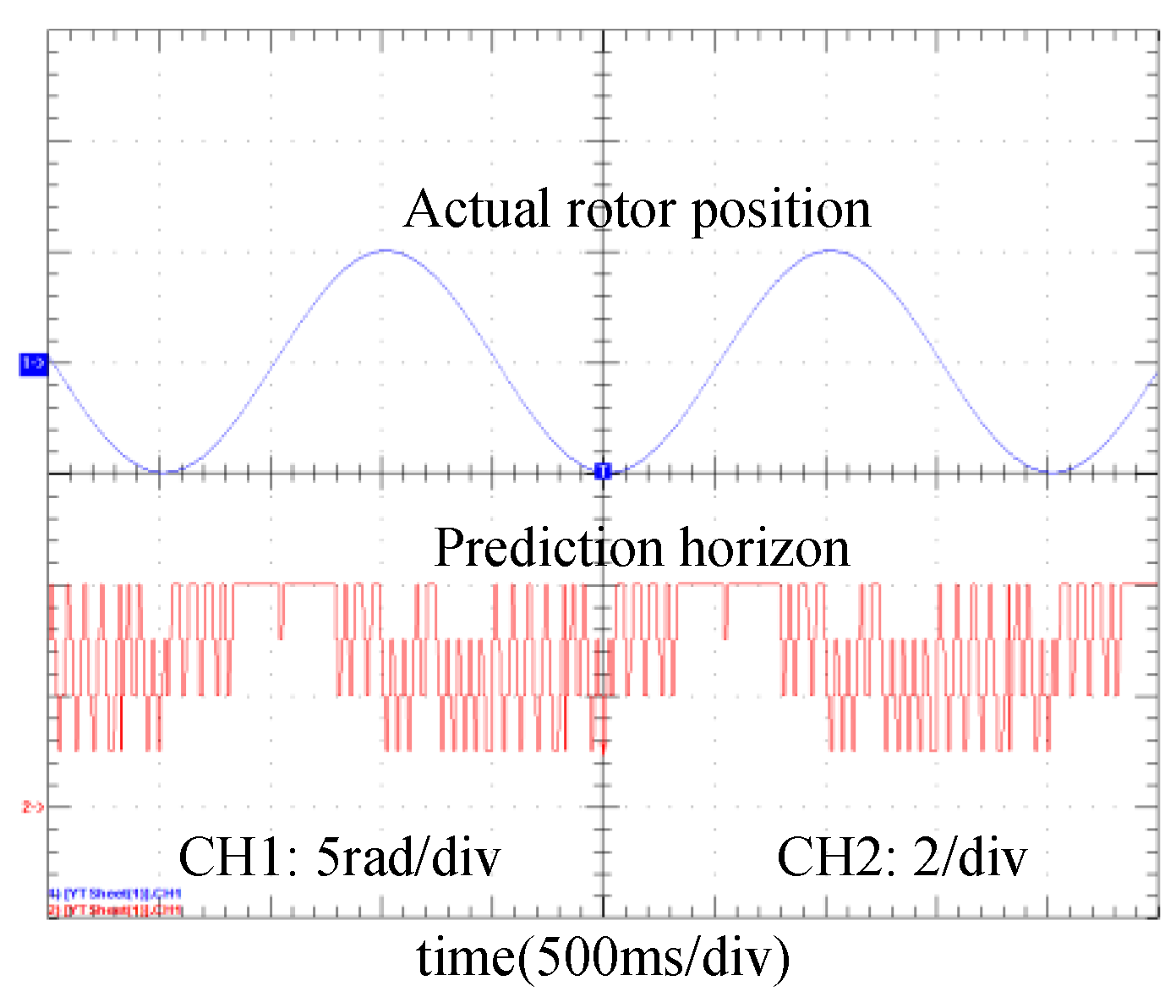
5.1. Tracking Comparison
5.2. Computation Burden
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tripathi, S.M.; Dutta, C. Enhanced efficiency in vector control of a Surface-mount PMSM drive. J. Frankl. Inst. 2018, 355, 2392–2423. [Google Scholar] [CrossRef]
- Mondal, R.; Dey, J. Performance Analysis and Implementation of Fractional Order 2-DOF Control on Cart–Inverted Pendulum System. IEEE Trans. Ind. Appl. 2020, 56, 7055–7066. [Google Scholar] [CrossRef]
- Li, P.; Zhu, G.; Zhang, M. Linear Active Disturbance Rejection Control for Servo Motor Systems with Input Delay via Internal Model Control Rules. IEEE Trans. Ind. Electron. 2021, 68, 1077–1086. [Google Scholar] [CrossRef]
- Yan, L.; Wang, F.; Dou, M.; Zhang, Z.; Kennel, R.; Rodríguez, J. Active Disturbance-Rejection-Based Speed Control in Model Predictive Control for Induction Machines. IEEE Trans. Ind. Electron. 2020, 67, 2574–2692. [Google Scholar] [CrossRef]
- Rodriguez, J.; Cortes, P. Predictive Control of Power Converters and Electrical Drives; IEEE Press-Wiley: Oxford, UK, 2012; pp. 133–176. [Google Scholar]
- Wang, F.; Ke, D.; Yu, X.; Huang, D. Enhanced Predictive Model Based Deadbeat Control for PMSM Drives Using Exponential Extended State Observer. IEEE Trans. Ind. Electron. 2021. [Google Scholar] [CrossRef]
- Wang, J.; Tang, Y.; Qi, Y.; Lin, P.; Zhang, Z. A Unified Startup Strategy for Modular Multilevel Converters with Deadbeat Predictive Current Control. IEEE Trans. Ind. Electron. 2021, 68, 6401–6411. [Google Scholar] [CrossRef]
- Pei, G.; Li, L.; Gao, X.; Liu, J.; Kennel, R. Predictive Current Trajectory Control for PMSM at Voltage Limit. IEEE Access 2019, 8, 1670–1679. [Google Scholar] [CrossRef]
- Novak, M.; Xie, H.; Dragicevic, T.; Wang, F.; Rodriguez, J.; Blaabjerg, F. Optimal Cost Function Parameter Design in Predictive Torque Control (PTC) Using Artificial Neural Networks (ANN). IEEE Trans. Ind. Electron. 2021, 68, 7309–7319. [Google Scholar] [CrossRef]
- Wang, F.; Zuo, K.; Tao, P.; Rodriguez, J. High Performance Model Predictive Control for PMSM by using Stator Current Mathematical Model Self-Regulation Technique. IEEE Trans. Power Electron. 2020, 35, 13652–13662. [Google Scholar] [CrossRef]
- Kawai, H.; Zhang, Z.; Kennel, R. Finite Control Set-Model Predictive Speed Control with a Voltage Smoother. In Proceedings of the 44th Annual Conference of the IEEE Industrial Electronics Society (IECON-2018), Washington, DC, USA, 21–23 October 2018. [Google Scholar]
- Wang, F.; He, L. FPGA-Based Predictive Speed Control for PMSM System Using Integral Sliding-Mode Disturbance Observer. IEEE Trans. Ind. Electron. 2021, 68, 972–981. [Google Scholar] [CrossRef]
- Wang, F. Control System Analysis and Design–Process Control System; Tsinghua University Press: Beijing, China, 2014; pp. 228–258. [Google Scholar]
- Geyer, T. Model Predictive Control of High Power Converters and Industrial Drives; Wiley: London, UK, 2016; pp. 153–194. [Google Scholar]
- Wei, Y.; Wei, Y.; Sun, Y.; Qi, H.; Guo, X. Prediction Horizons Optimized Nonlinear Predictive Control for PMSM Position System. IEEE Trans. Ind. Electron. 2020, 67, 9153–9163. [Google Scholar] [CrossRef]
- Errouissi, R.; Ouhrouche, M. Nonlinear predictive controller for a permanent magnet synchronous motor drive. Math. Comput. Simul. 2010, 81, 394–406. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, H. Two-Vector-based Model Predictive Torque Control without Weighting Factors for Induction Motor Drives. IEEE Trans. Power Electron. 2016, 31, 1381–1390. [Google Scholar] [CrossRef]
- Wang, F.; Xie, H.; Chen, Q.; Davari, S.A.; Rodriguez, J.; Kennel, R. Parallel Predictive Torque Control for Induction Machines without Weighting Factors. IEEE Trans. Power Electron. 2020, 35, 1779–1788. [Google Scholar] [CrossRef]
- Cortes, P.; Rodriguez, J.; Silva, C.; Flores, A. Delay Compensation in Model Predictive Current Control of a Three-Phase Inverter. IEEE Trans. Ind. Electron. 2012, 59, 1323–1325. [Google Scholar] [CrossRef]
- Wang, X.; Sun, D. Three-Vector-Based Low-Complexity Model Predictive Direct Power Control Strategy for Doubly Fed Induction Generators. IEEE Trans. Power Electron. 2017, 32, 773–782. [Google Scholar] [CrossRef]
- Wei, Y.; Li, M.; Wei, Y.; Qi, H. A Quadra-Layer Direct Speed SMPC Strategy for PMSM Rotor Position. In Proceedings of the 9th Frontier Academic Forum of Electrical Engineering (FAFEE 2020), Xi’an, China, 26–28 August 2020. [Google Scholar]
- Kong, F.; Keyser, R.D. Criteria for choosing the horizon in extended horizon predictive control. IEEE Trans. Autom. Control 1994, 39, 1467–1470. [Google Scholar] [CrossRef]
- Younesi, A.; Tohidi, S.; Feyzi, M.R.; Baradarannia, M. An improved nonlinear model predictive direct speed control of permanent magnet synchronous motors. Int. Trans. Elect. Energy Syst. 2018, 16, 2535–2550. [Google Scholar] [CrossRef]
- Younesi, A.; Tohidi, S.; Feyzi, M.R. Improved Optimization Process for Nonlinear Model Predictive Control of PMSM. Iran. J. Elect. Electron. Eng. 2018, 14, 278–288. [Google Scholar]
- Sun, Z.; Dai, L.; Liu, K.; Dimarogonas, D.V.; Xia, Y. Robust Self-Triggered MPC with Adaptive Prediction Horizon for Perturbed Nonlinear Systems. IEEE Trans. Autom. Control. 2019, 64, 4780–4787. [Google Scholar] [CrossRef]
- Dong, L.; Yan, J.; Yuan, X.; He, H.; Sun, C. Functional Nonlinear Model Predictive Control Based on Adaptive Dynamic Programming. IEEE Trans. Cybern. 2019, 49, 4206–4218. [Google Scholar] [CrossRef] [PubMed]
- Ionescu, C.M.; Copot, D.; Maxim, A.; Dulf, E.; Both, R.; Keyser, R.D. Robust Autotuning MPC for a Class of Process Control Applications. In Proceedings of the IEEE International Conference on Automation, Quality and Testing, Robotics (AQTR), Cluj-Napoca, Romania, 19–21 May 2016. [Google Scholar]
- Bonilla, J.; Keyser, R.D.; Plaza, D. Nonlinear Predictive Control of a DC-DC Converter: A NEPSAC approach. In Proceedings of the 2007 European Control Conference (ECC), Kos, Greece, 2–5 July 2007. [Google Scholar]
- Hernandez, A.; Keyser, R.D.; Dutta, A.; Nopens, I. Robust Nonlinear Extended Prediction Self-Adaptive Control (NEPSAC) of Continuous Bioreactors. In Proceedings of the Mediterranean Conference on Control & Automation (MED), Barcelona, Spain, 3–6 July 2012. [Google Scholar]
- Chen, H. Stability and Robustness Considerations in Nonlinear Model Predictive Control; VDI: Verlag, Germany, 1997; pp. 153–194. [Google Scholar]
- Kou, B.; Cheng, S. AC Servo Motor and Control Chap. 4; China Machine Press: Beijing, China, 2008; pp. 45–76. [Google Scholar]





| Symbol | Quantity | Value |
|---|---|---|
| Rs | Stator resistance | 2.875 Ω |
| Ls | Stator self-inductance | 0.835 mH |
| J | Rotor inertia | 0.0008 kg∙m2 |
| B | Friction coefficient | 0.0008 N∙m·s |
| p | The number of pole pairs | 4 |
| ψm | Flux magnitude due to rotor magnets | 0.175 Wb |
| nn | Rated speed | 3000 rpm |
| fn | Rated frequency | 200 Hz |
| Pn | Rated power | 1 kW |
| Vn | Rated voltage | 380 V |
| In | Rate current | 3.65 A |
| η | Shaft driving efficiency | 82.6% |
| Control Performances | NMPSC with the Proposed Method | Conventional NMPSC |
|---|---|---|
| Rotor position ITAE | 0.7771 | 0.9499 |
| Speed ITAE | 7.931 | 10.73 |
| Control Strategies | Speed Direction | NMPSC with the Proposed Method | Conventional NMPSC |
|---|---|---|---|
| NMPSC with the proposed method | Positive | 0.2241 | 1.982 |
| Negative | 0.2171 | 1.718 | |
| Conventional NMPSC | Positive | 0.232 | 2.15 |
| Negative | 0.213 | 1.504 |
| Control Strategies | Weighting Factors | Average Value of Servo Stiffness | Mean Square Error of Servo Stiffness | |
|---|---|---|---|---|
| λω | λi | |||
| NMPSC with the proposed method | 1 | 1 | 31.6162 | 16.3266 |
| 1 | 0.6 | 65.3566 | 52.0645 | |
| 1 | 0.2 | 105.8032 | 75.4438 | |
| 0.6 | 1 | 37.1100 | 26.0345 | |
| 0.6 | 0.6 | 31.6480 | 16.2684 | |
| 0.6 | 0.2 | 50.7884 | 26.2203 | |
| 0.2 | 1 | 6.5644 | 3.5587 | |
| 0.2 | 0.6 | 14.5511 | 7.8493 | |
| 0.2 | 0.2 | 31.6480 | 16.2684 | |
| Conventional NMPSC | 1 | 1 | 18.3050 | 10.0392 |
| Control Performances | NMPSC with the Proposed Method | Conventional NMPSC |
|---|---|---|
| Rotor position ITAE | 2.323 | 2.734 |
| Maximal speed | 117.937 rpm | 158.665 rpm |
| Maximal static error | 0.366 rad | 0.408 rad |
| Average prediction horizon | 2.973 | 3 (Constant) |
| Maximal delay time | 40 ms | 52 ms |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Y.; Wei, Y.; Sun, Y.; Qi, H.; Li, M. An Advanced Angular Velocity Error Prediction Horizon Self-Tuning Nonlinear Model Predictive Speed Control Strategy for PMSM System. Electronics 2021, 10, 1123. https://doi.org/10.3390/electronics10091123
Wei Y, Wei Y, Sun Y, Qi H, Li M. An Advanced Angular Velocity Error Prediction Horizon Self-Tuning Nonlinear Model Predictive Speed Control Strategy for PMSM System. Electronics. 2021; 10(9):1123. https://doi.org/10.3390/electronics10091123
Chicago/Turabian StyleWei, Yao, Yanjun Wei, Yening Sun, Hanhong Qi, and Mengyuan Li. 2021. "An Advanced Angular Velocity Error Prediction Horizon Self-Tuning Nonlinear Model Predictive Speed Control Strategy for PMSM System" Electronics 10, no. 9: 1123. https://doi.org/10.3390/electronics10091123
APA StyleWei, Y., Wei, Y., Sun, Y., Qi, H., & Li, M. (2021). An Advanced Angular Velocity Error Prediction Horizon Self-Tuning Nonlinear Model Predictive Speed Control Strategy for PMSM System. Electronics, 10(9), 1123. https://doi.org/10.3390/electronics10091123






