Power Quality Enhancement in Electric Arc Furnace Using Matrix Converter and Static VAR Compensator
Abstract
:1. Introduction
- To design the cutting-edge electric furnace model for a virtual demonstration.
- To adopt the advanced power converters for EAF.
- To integrate the compensating devices along with advanced power converters.
- To improve the overall performance of the power supply, such as arc voltage, arc current, THDI (Current THD), THDV (Voltage THD), power factor, and voltage flicker.
2. Proposed Methodologies
- function v = fcn(f,i)
- C = 23,000;
- D = 5000;
- m = 0.8;
- Vat0 = 200;
- vt = Vat0(1 + (mf));
- v = sign(i)(vt + (C/(D + abs(i))));
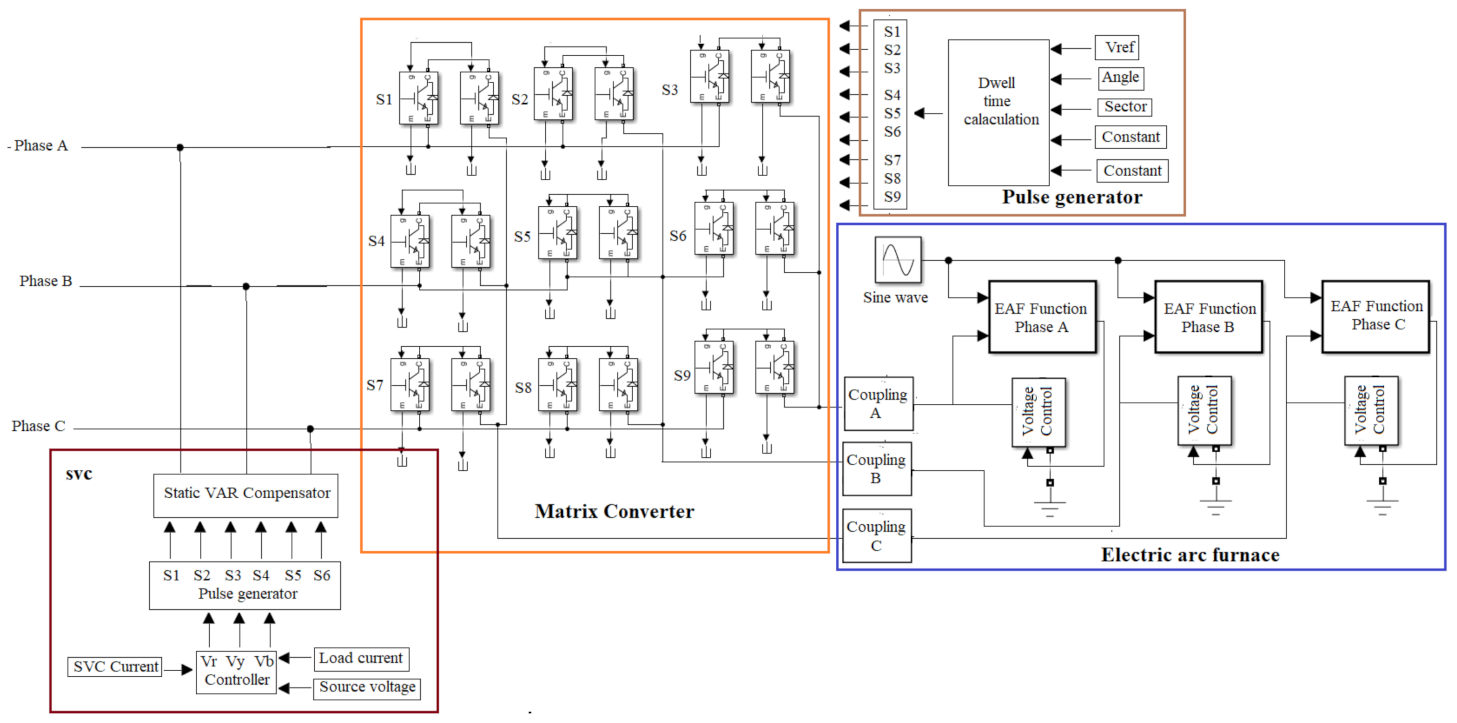
2.1. Matrix Converter (MC)
2.2. Furnace Transformer
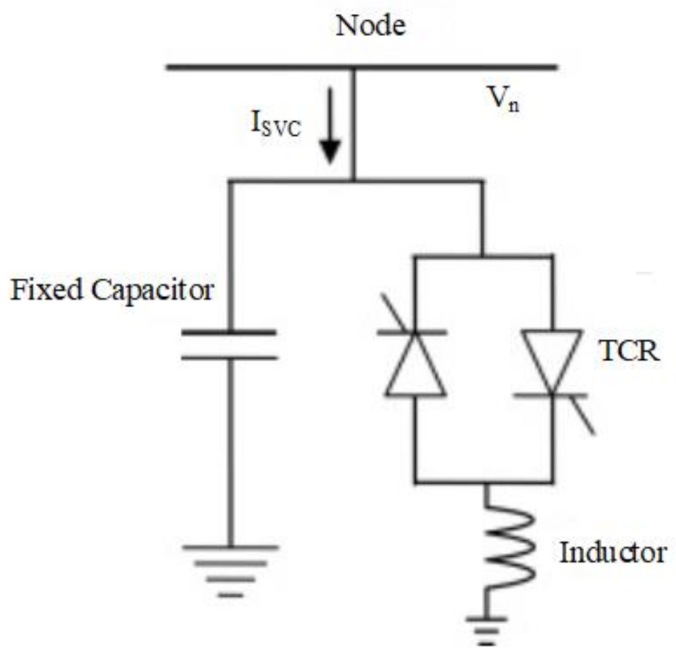
2.3. SVC
2.4. Electric Arc Furnace (EAF)
2.4.1. Approximation Model
2.4.2. Piecewise Model
2.4.3. Hybrid Model (Exponential-Hyperbolic)
3. Results and Discussions
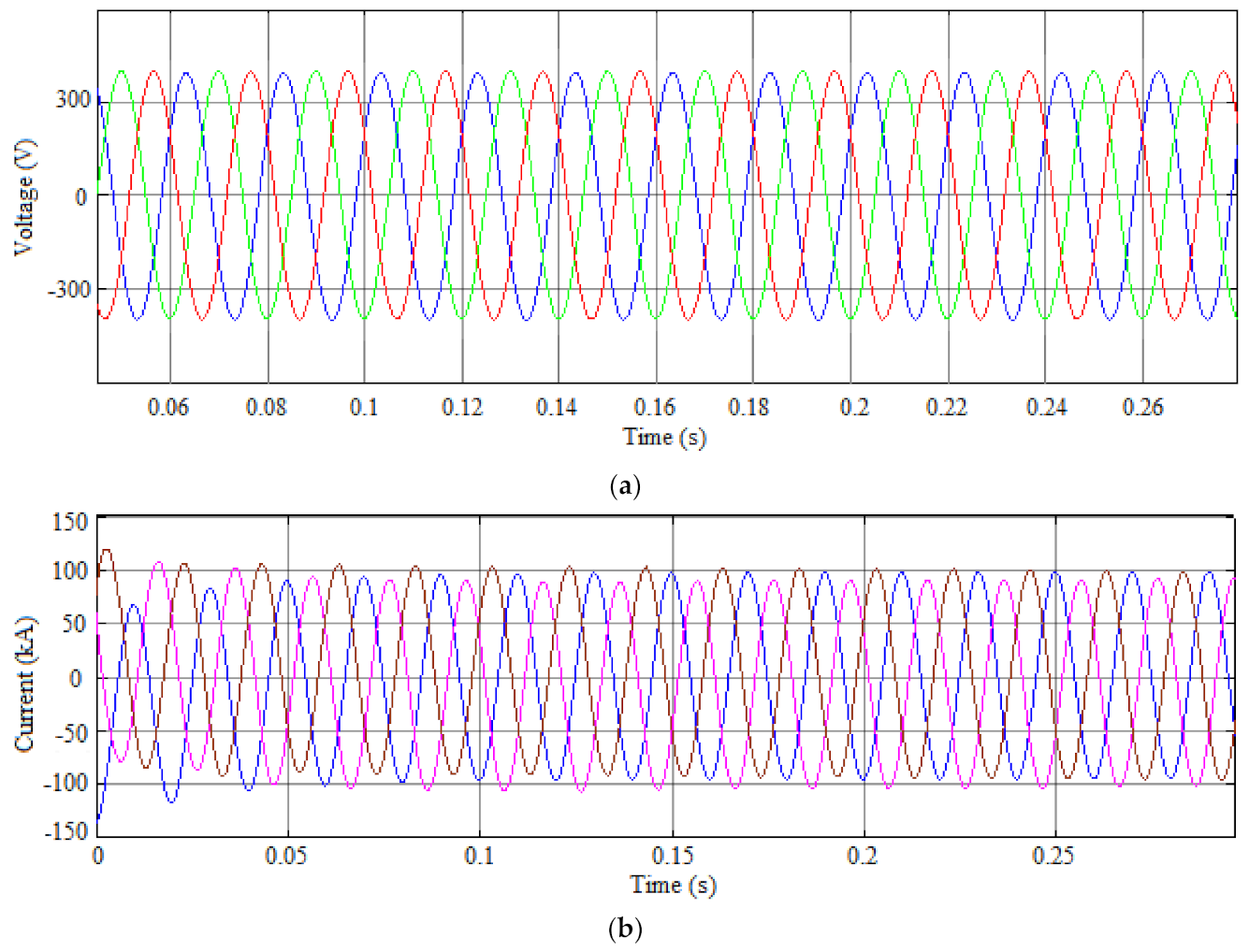
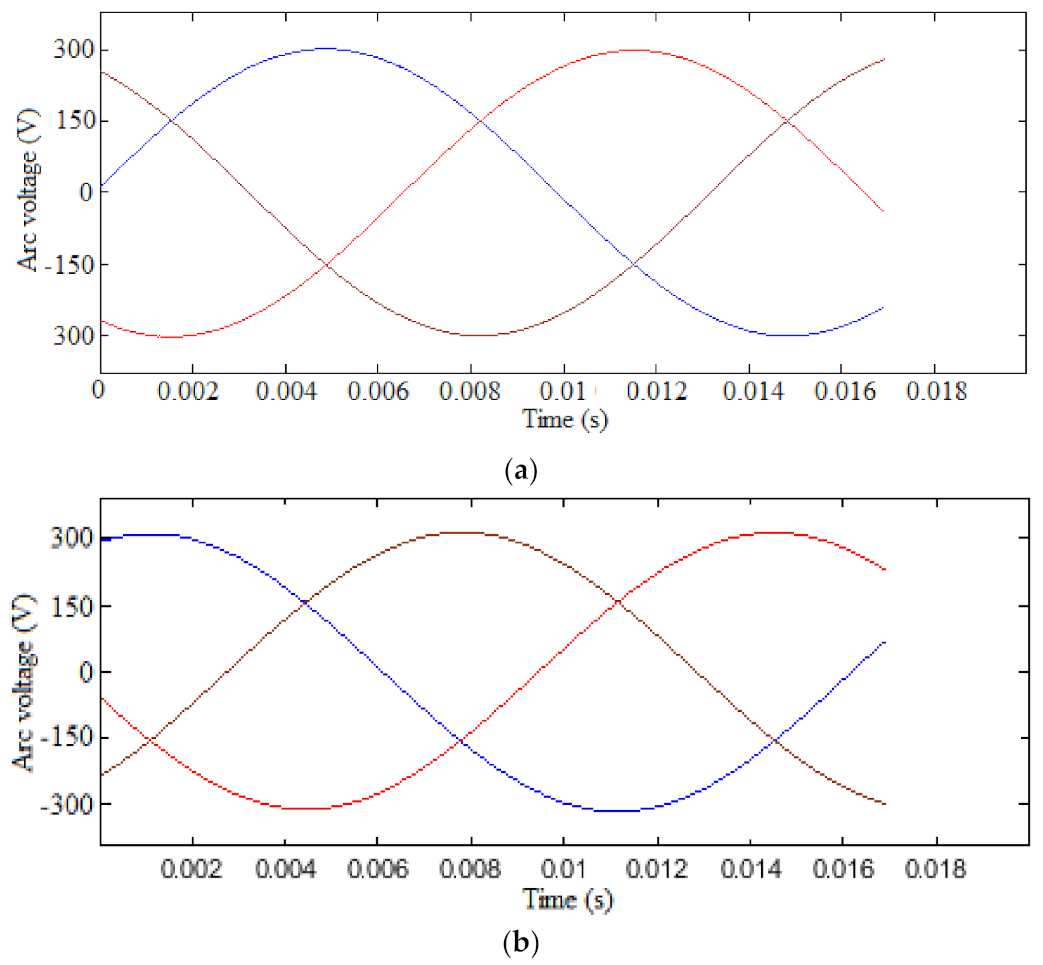
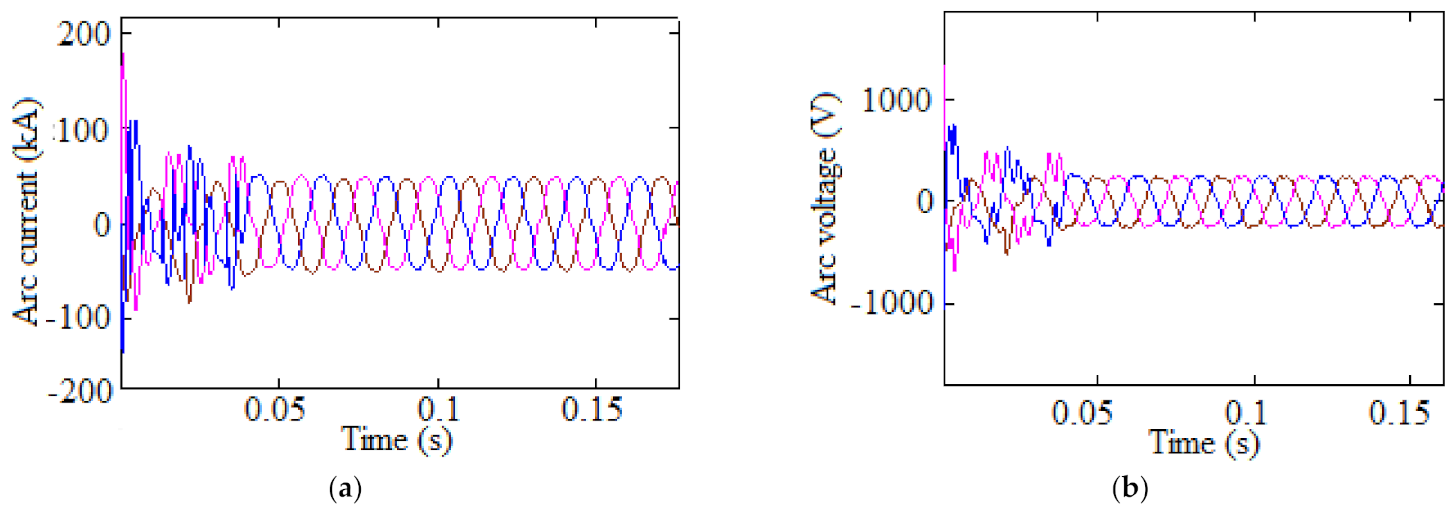
3.1. Current and Voltage Waveforms
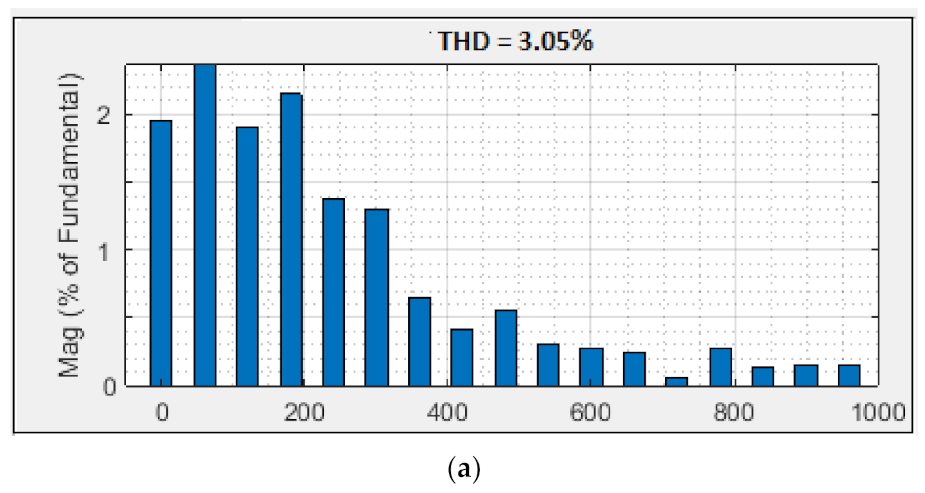
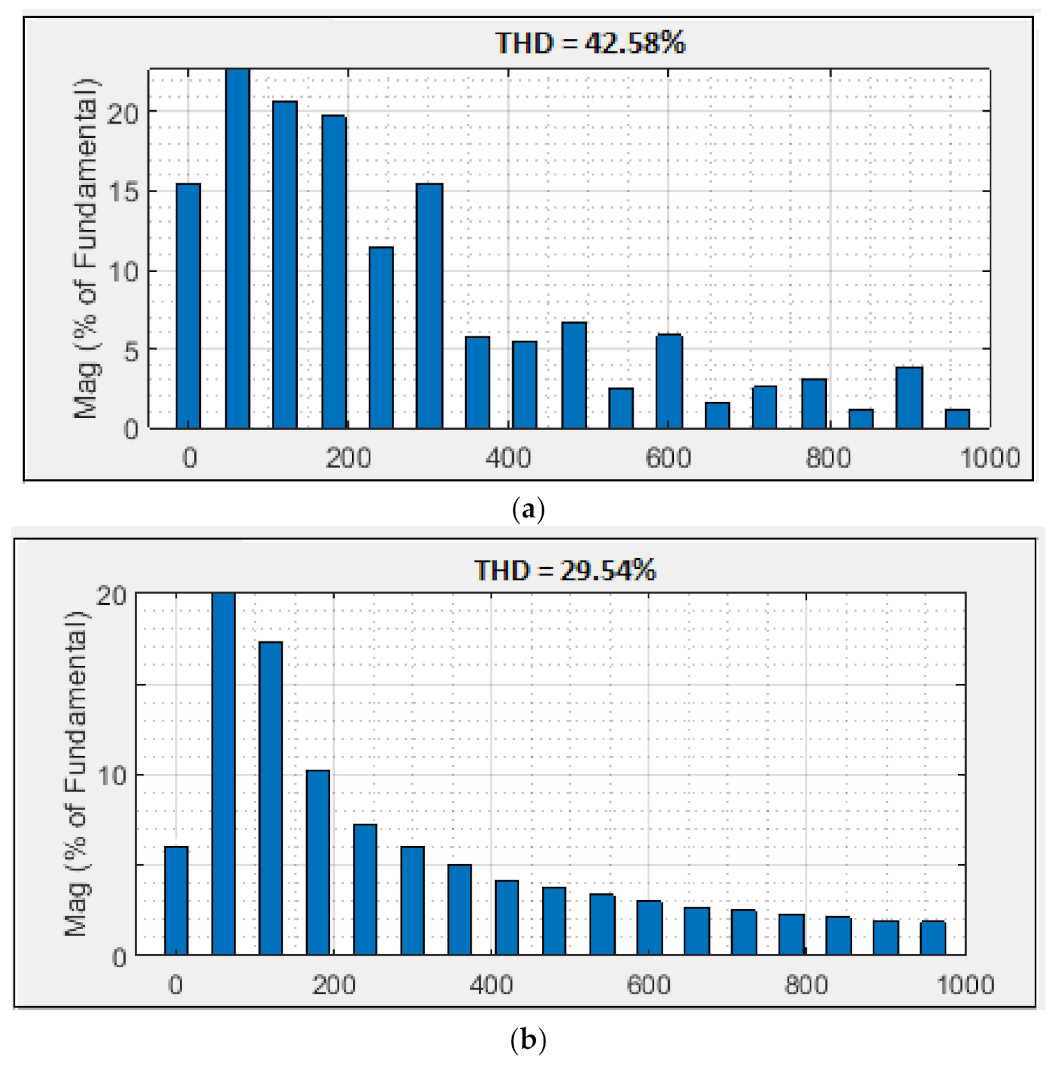
3.2. Harmonic Analysis
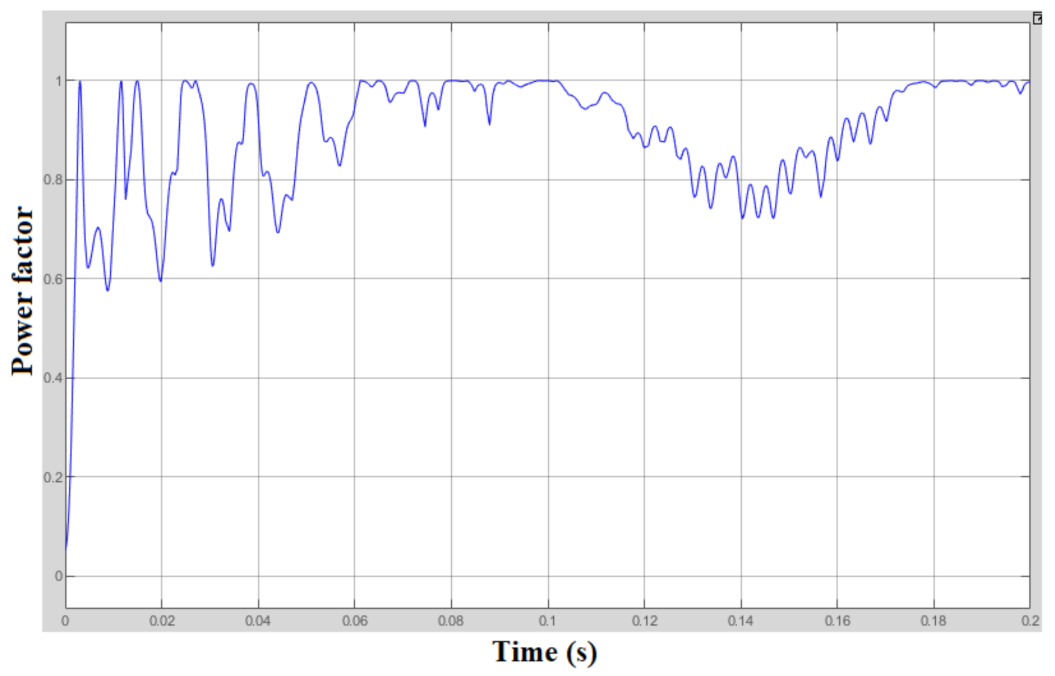
3.3. Power Factor
3.4. Voltage Flicker
4. Comparative Analysis
5. Conclusions
- The proposed model offers superior outcomes compared with existing EAF models.
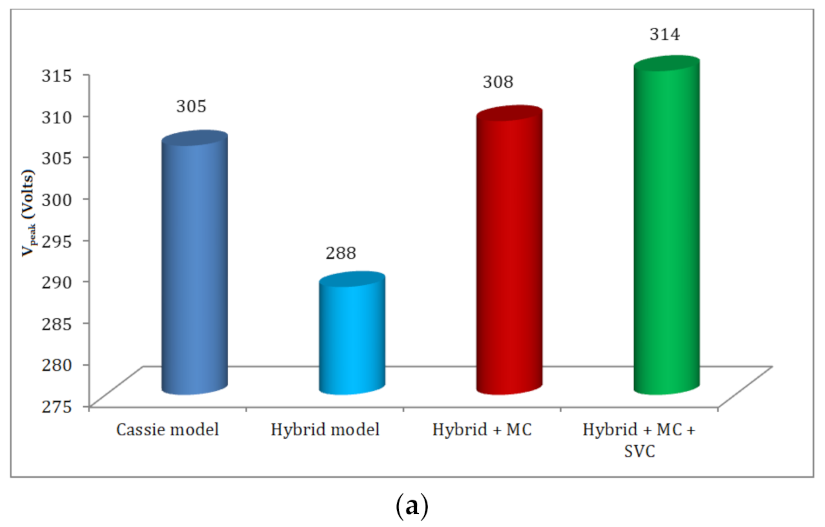
- Arc currents and voltages (peak value) show greater magnitudes of about 123.26 kA and 314 V, respectively.
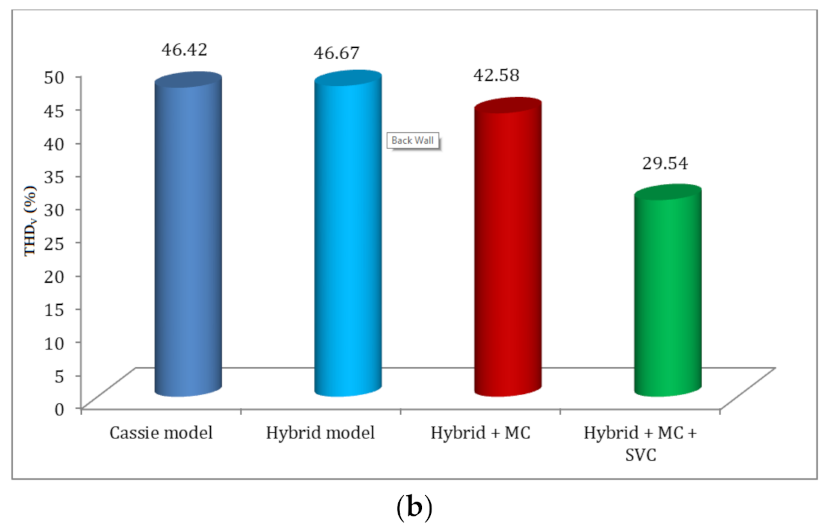
- The proposed scheme offers the slightest current and voltage THD values of about 2.85% and 29.54%.
- The voltage flickering of the proposed model shows minimum scale compared with other existing models, i.e., 1.26%.
- The power factor of the proposed scheme shows a superior rate of about 0.9975.
Author Contributions
Funding
Conflicts of Interest
References
- World Steel Association. World Steel in Figures. 2020. Available online: https://www.worldsteel.org/en/dam/jcr:f7982217-cfde-4fdc-8ba0-795ed807f513/World%2520Steel%2520in%2520Figures%25202020i.pdf (accessed on 1 May 2021).
- Garcia-Segura, R.; Castillo, J.V.; Martell-Chavez, F.; Longoria-Gandara, O.; Aguilar, J.O. Electric Arc Furnace Modeling with Artificial Neural Networks and Arc Length with Variable Voltage Gradient. Energies 2017, 10, 1424. [Google Scholar] [CrossRef]
- Teklić, A.T.; Filipović-Grčić, B.; Pavić, I. Modelling of three-phase electric arc furnace for estimation of voltage flicker in power transmission network. Electr. Power Syst. Res. 2017, 146, 218–227. [Google Scholar] [CrossRef]
- IEEE 1993. IEEE Recommended Practices and Requirements for Harmonic Control in Electrical Power Systems; IEEE: New York, NY, USA, 1993. [Google Scholar]
- Ozgun, O.; Abur, A. Development of an arc furnace model for power quality studies. In Proceedings of the IEEE Power Engineering Society Summer Meeting, Edmonton, AB, Canada, 18–22 July 1999; Volume 1, pp. 507–511. [Google Scholar]
- Rodriguez, J.R.; Rivera, M.; Kolar, J.W.; Wheeler, P.W. A Review of Control and Modulation Methods for Matrix Converters. IEEE Trans. Ind. Electron. 2012, 59, 58–70. [Google Scholar] [CrossRef]
- Khosravi, M.; Amirbande, M.; Khaburi, D.A.; Rivera, M.; Riveros, J.; Rodriguez, J.; Vahedi, A.; Wheeler, P. Review of model predictive control strategies for matrix converters. IET Power Electron. 2019, 12, 3021–3032. [Google Scholar] [CrossRef]
- Zhang, G.; Yang, J.; Sun, Y.; Su, M.; Zhu, Q.; Blaabjerg, F. A Predictive-Control-Based Over-Modulation Method for Conventional Matrix Converters. IEEE Trans. Power Electron. 2017, 33, 3631–3643. [Google Scholar] [CrossRef]
- Ashraf, N.; Izhar, T.; Abbas, G. A Single-Phase Buck-Boost Matrix Converter with Low Switching Stresses. Math. Probl. Eng. 2019, 2019, 1–19. [Google Scholar] [CrossRef]
- Vidhya, D.S.; Venkatesan, T.; Kanagaraj, N. Fuzzy Logic Controller for Variable Boost Function in Quasi Z Source Indirect Matrix Converter during Voltage Sag Condition. Int. J. Fuzzy Syst. 2016, 19, 1093–1103. [Google Scholar] [CrossRef]
- Basri, H.M.; Mekhilef, S. Experimental Evaluation of Model Predictive Current Control for a Modified Three-Level Four-Leg Indirect Matrix Converter. IET Electr. Power Appl. 2017, 12, 114–123. [Google Scholar] [CrossRef]
- Garcia, C.F.; Rivera, M.E.; Rodriguez, J.R.; Wheeler, P.W.; Pena, R.S. Predictive Current Control with Instantaneous Reactive Power Minimization for a Four-Leg Indirect Matrix Converter. IEEE Trans. Ind. Electron. 2017, 64, 922–929. [Google Scholar] [CrossRef]
- Mir, T.N.; Singh, B.; Bhat, A.H. New Modulation Techniques for Single Phase to Three Phase Matrix Converter. In Proceedings of the 2018 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Chennai, India, 18–21 December 2018; pp. 1–6. [Google Scholar]
- Sun, Y.; Xiong, W.; Su, M.; Li, X.; Dan, H.; Yang, J. Topology and Modulation for a New Multilevel Diode-Clamped Matrix Converter. IEEE Trans. Power Electron. 2014, 29, 6352–6360. [Google Scholar] [CrossRef]
- Casadei, D.; Clare, J.; Empringham, L.; Serra, G.; Tani, A.; Trentin, A.; Wheeler, P.; Zarri, L. Large-Signal Model for the Stability Analysis of Matrix Converters. IEEE Trans. Ind. Electron. 2007, 54, 939–950. [Google Scholar] [CrossRef]
- Chang, G.; Liu, Y.; Huang, H.; Chu, S. Harmonic analysis of the industrial power system with an AC electric arc furnace. In Proceedings of the 2006 IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006; p. 4. [Google Scholar]
- Barbouche, M.; Hajji, M.; Ezzaouia, H. Electric Arc Furnace Design and Construction for Metallurgical and Semiconductor Re-search. Inter. J. Adv. Manuf. Technol. 2016, 82, 997–1006. [Google Scholar] [CrossRef]
- Hooshmand, R.; Banejad, M.; Esfahani, M.T. A New Time Domain Model for Electric Arc Furnace. J. Electr. Eng. 2008, 59, 195–202. [Google Scholar]
- Ladoux, P.; Postiglione, G.; Foch, H.; Nuns, J. A Comparative Study of AC/DC Converters for High-Power DC Arc Furnace. IEEE Trans. Ind. Electron. 2005, 52, 747–757. [Google Scholar] [CrossRef]
- Hote, Y.V.; Jain, S. PID Controller Design for Load Frequency Control: Past, Present and Future Challenges. IFAC Pap. OnLine 2018, 51, 604–609. [Google Scholar] [CrossRef]
- Patel, J.; Sood, V.K. Review of Digital Controllers in Power Converters. In Proceedings of the 2018 IEEE Electrical Power and Energy Conference (EPEC), Toronto, ON, Canada, 10–11 October 2018; pp. 1–8. [Google Scholar]
- Liou, W.-R.; Lacorte, W.B.; Caberos, A.B.; Yeh, M.-L.; Lin, J.-C.; Lin, S.-C.; Sun, C.-S. A Programmable Controller IC for DC/DC Converter and Power Factor Correction Applications. IEEE Trans. Ind. Inform. 2012, 9, 2105–2113. [Google Scholar] [CrossRef]
- Ribeiro, R.L.D.A.; De Azevedo, C.C.; De Sousa, R.M. A Robust Adaptive Control Strategy of Active Power Filters for Power-Factor Correction, Harmonic Compensation, and Balancing of Nonlinear Loads. IEEE Trans. Power Electron. 2012, 27, 718–730. [Google Scholar] [CrossRef]
- Liu, Y.-W.; Rau, S.-H.; Wu, C.-J.; Lee, W.-J. Improvement of Power Quality by Using Advanced Reactive Power Compensation. IEEE Trans. Ind. Appl. 2017, 54, 18–24. [Google Scholar] [CrossRef]
- Naderipour, A.; Abdul-Malek, Z.; Gandoman, F.H.; Nowdeh, S.A.; Shiran, M.A.; Moghaddam, M.J.H.; Davoodkhani, I.F. Optimal Designing of Static Var Compensator to Improve Voltage Profile of Power System Using Fuzzy Logic Control. Energy 2020, 192, 116665. [Google Scholar] [CrossRef]
- Babaei, E.; Kangarlu, M.F.; Sabahi, M. Mitigation of Voltage Disturbances Using Dynamic Voltage Restorer Based on Direct Converters. IEEE Trans. Power Deliv. 2010, 25, 2676–2683. [Google Scholar] [CrossRef]
- Habib, A.; Rani, S.; Hasan, M.; Chowdhury, D. Mitigation of Power Quality Disturbances Using Dynamic Voltage Restorer with PI Controller, PLL and Super Capacitor Based Storage System. In Proceedings of the 2020 IEEE Region 10 Symposium (TENSYMP), Dhaka, Bangladesh, 5–7 June 2020; pp. 120–125. [Google Scholar]
- Kabir, A.; Mahbub, U. Synchronous detection and digital control of Shunt Active Power Filter in power quality improvement. In Proceedings of the 2011 IEEE Power and Energy Conference at Illinois, Urbana, IL, USA, 25–26 February 2011; pp. 1–5. [Google Scholar]
- Siami, M.; Khaburi, D.A.; Rodriguez, J. Simplified Finite Control Set-Model Predictive Control for Matrix Converter-Fed PMSM Drives. IEEE Trans. Power Electron. 2017, 33, 2438–2446. [Google Scholar] [CrossRef]
- Vijayagopal, M.; Zanchetta, P.; Empringham, L.; De Lillo, L.; Tarisciotti, L.; Wheeler, P. Control of a Direct Matrix Converter with Modulated Model-Predictive Control. IEEE Trans. Ind. Appl. 2017, 53, 2342–2349. [Google Scholar] [CrossRef]
- Siami, M.; Khaburi, D.A.; Rivera, M.; Rodriguez, J. A Computationally Efficient Lookup Table Based FCS-MPC for PMSM Drives Fed by Matrix Converters. IEEE Trans. Ind. Electron. 2017, 64, 7645–7654. [Google Scholar] [CrossRef]
- Zhang, J.; Li, L.; Dorrell, D.G. Control and Applications of Direct Matrix Converters: A Review. Chin. J. Electr. Eng. 2018, 4, 18–27. [Google Scholar]
- Samet, H.; Mojallal, A.; Ghanbari, T.; Farhadi, M.R. Enhancement of SVC performance in electric arc furnace for flicker suppression using a Gray-ANN based prediction method. Int. Trans. Electr. Energy Syst. 2019, 29, e2811. [Google Scholar] [CrossRef]
- Vardani, B. Optimum Location of SVC in an IEEE 33 Bus Radial Distribution System Using Power Sensitivity Index. In Proceedings of the 2019 International Conference on Electrical, Electronics and Computer Engineering (UPCON, Aligarh, India, 8–10 November 2019; pp. 1–5. [Google Scholar]
- Nasir, M.S.A.; Jumaat1, S.A. Impact of Static Var Compensator (SVC) Installation in Power System Stability. J. Electr. Volt. Appl. 2020, 1, 20–26. [Google Scholar]









| On States of Switches | ||||||
|---|---|---|---|---|---|---|
| 0 | ||||||
| 0 | ||||||
| 0 | ||||||
| 0 | ||||||
| 0 | ||||||
| 0 | ||||||
| 0 | - | 0 | - | |||
| 0 | - | 0 | - | |||
| 0 | - | 0 | - | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jebaraj, B.S.; Bennet, J.; Kannadasan, R.; Alsharif, M.H.; Kim, M.-K.; Aly, A.A.; Ahmed, M.H. Power Quality Enhancement in Electric Arc Furnace Using Matrix Converter and Static VAR Compensator. Electronics 2021, 10, 1125. https://doi.org/10.3390/electronics10091125
Jebaraj BS, Bennet J, Kannadasan R, Alsharif MH, Kim M-K, Aly AA, Ahmed MH. Power Quality Enhancement in Electric Arc Furnace Using Matrix Converter and Static VAR Compensator. Electronics. 2021; 10(9):1125. https://doi.org/10.3390/electronics10091125
Chicago/Turabian StyleJebaraj, Bharath Singh, Jaison Bennet, Raju Kannadasan, Mohammed H. Alsharif, Mun-Kyeom Kim, Ayman A. Aly, and Mohamed H. Ahmed. 2021. "Power Quality Enhancement in Electric Arc Furnace Using Matrix Converter and Static VAR Compensator" Electronics 10, no. 9: 1125. https://doi.org/10.3390/electronics10091125






