A Novel Hybrid Active Power Filter with Multi-Coupled Coils

Abstract

This paper proposes a hybrid active power filter (HAPF) with multi-coupled coils, applied to a medium- and high-voltage power grid. The passive filter of the proposed HAPF adopts the structure of multi-coupled coils to compress the traditional multiple LC branches into one branch which presents the same harmonic impedance characteristics as the former multiple LC branches. In the active power filter of the HAPF, a coupled inductor, instead of a transformer, is used to connect with the passive filter. The coupled inductor has mutual inductances with inductors of the passive filter. Through spatial magnetic coupling, the active power filter can inject compensation current into the power grid to eliminate the residual harmonics and absorb active power from the power grid to maintain the DC capacitor voltage. When the active power filter is open-circuited or short-circuited, the filtering effect of the passive filter can still be guaranteed, which improves the reliability of the filter. The benefits of the proposed HAPF with excellent harmonic filtering performance are that the inductors occupy only 1/3 space as compared with traditional three-tuned LC filter, and very small power of the active power filter. The feasibility of the proposed HAPF is verified through simulations and experiment.

1. Introduction

In the power grid, nonlinear loads result in harmonic problems: increasing the power loss in the power system, interfering with the communication network, affecting the performance of high-precision devices, etc. [1,2].

The power filter is usually used to deal with harmonic problems in the power system, which can be classified as passive filter (PF), active power filter (APF), and hybrid active power filter (HAPF). PF is widely used in the power grid because of its simple structure, low cost, and mature technology [3,4,5]. However, the filtering effect of PF depends on its own element parameters and the grid parameters. Besides, PF usually has large volume, large required space. Compared with PF, the filtering effect of APF is not affected by grid parameters and the control of APF is flexible [6,7,8]. However, standalone APF has limited capacity and high cost, which is not suitable for high-voltage and a large-capacity situation.

In order to combine the advantages of both PF (large capacity, high reliability) and APF (excellent control performance), HAPFs of various topologies were proposed, which can reduce the capacity of active power filter in the medium- and high-voltage power grid [9,10,11,12,13,14,15,16,17,18,19,20,21,22]. There are two types of HAPFs: series HAPFs and shunt HAPFs. In series HAPF, the active power filter is connected to the power grid in series using a transformer [9]. The series HAPF has good filtering performance, but the fundamental current flows through the transformer, limiting the feasibility of the practical application.

The common topologies of shunt HAPF can be divided into the following three types:

(1)

The active power filter that is in parallel with the passive filter [10,11]. In this type of topology, the active power filter is connected to the power grid through a transformer, whose volume is large. The topology is simple, but on the low-voltage side of the transformer, the current is relatively large. Besides, the output current of the active power filter may flow into the parallel PF.

(2)

The active power filter that is in series with the passive filter [12,13,14,15,16,17,18]. In this type of topology, the active power filter can be connected in series with the passive filter directly or through a transformer. The passive filter bears most of the fundamental voltage and the fundamental voltage of the active power filter is very small. Considering that the active power filter and the passive filter are in series, once the active power filter is open-circuited, the high fundamental voltage will be applied to the transformer winding.

(3)

The injection-type HAPF: the active power filter is shunted to a fundamental resonance circuit, through a matching transformer [19,20,21,22]. The injection-type HAPF can significantly reduce the fundamental voltage of the active power filter. However, the fundamental resonator has a large volume. In addition, an additional rectifier is needed to support the DC-side voltage.

The passive filter of HAPF is generally the LC filter, which is used to eliminate characteristic harmonics, such as 3rd, 5th, 7th, and 11th harmonics. Three inductors are needed for each phase to eliminate 5th, 7th, and 11th harmonics, so, for three phases, nine inductors are needed. These inductors are usually arranged separately (straight-line shape, triangle, etc.) to eliminate the effect of mutual inductances. Thus, these inductors would occupy a large area. The conventional dry-type air core reactor also has a stacking mode, but in order to eliminate mutual inductances and other reasons, the stacking mode will significantly raise the center of gravity of the reactor as a whole, increasing the requirements for the safety design of structural accessories.

Authors developed a new method for calculating the inductance of air-core circular coils with rectangular cross section and parallel axes [23,24]. Moreover, a compact multi-tuned filter with coupled inductors was proposed in [5], which can reduce the required space of inductors while eliminating characteristic harmonics. However, this structure still has other inherent problems of conventional passive filters (detuning, resonance, etc.).

Based on this, this paper proposes a novel hybrid active power filter (HAPF) with multi-coupled coils. The passive filter of the HAPF uses a multi-coupled coils structure, and the design method of the multi-coupled coils is the same as [5]. The active power filter of the HAPF includes an active converter and a coupled inductor. Mutual inductances exist between the coupled inductor and each coil of the passive filter. The active power filter is connected with the passive filter through the coupled inductor.

In hybrid compensation, the converter generates a current on the coupled inductor. Then, this output current will be injected into the passive filter branch through spatial magnetic coupling to eliminate the residual harmonics. At the same time, the active converter would absorb the active power from the grid to maintain the DC capacitor voltage. The coupled inductor of the active power filter is closest to the main coil of the passive filter, which can obtain a high coupling coefficient.

The proposed HAPF topology in this paper has two distinct innovations:

(1)

The multi-coupled coils used in the passive filter of the HAPF compress the traditional multiple LC branches into one branch which presents the same harmonic impedance characteristics as the former multiple LC branches. The inductors occupy only 1/3 of the space as compared with the traditional three-tuned LC filter.

(2)

A coupled inductor, instead of a transformer, is used in the active power filter of the HAPF to connect with the passive filter. When the active power filter is open-circuited or short-circuited (even if the protection does not work and not cut off from the active power filter), the filtering effect of the passive filter can still be guaranteed. The capacity of the active power filter in the proposed HAPF is small.

This paper is structured as follows: Firstly, the structure of the proposed HAPF is introduced. Secondly, the working principle of the HAPF is analyzed. Thirdly, the control strategy of hybrid compensation is proposed. Then, the effectiveness of the control strategy is verified through simulations. At last, an experimental platform is built and the feasibility of the HAPF is verified by experiments.

2. Main Circuit

2.1. Passive Filter with Multi-Coupled Coils

The passive filter of the proposed HAPF is shown in Figure 1. Figure 1a represents the schematic diagram of a three-tuned passive filter with multi-coupled coils. In Figure 1a, i_L is the load current, i_S is the supply current, and i_f is the filter branch current. C₃, C₄, and C₅ are the capacitors in passive filter. L₁, L₂, L₃, L₄, and L₅ are the inductors in the passive filter.

L₁, L₂, L₃, L₄, L₅ have mutual inductances among one another, which is the biggest difference between the passive filter in the proposed HAPF and the conventional multi-tuned LC filter. Conventional multi-tuned LC filters ignore the coupling effect between the inductors. To ensure this, the inductors in conventional multi-tuned LC filters need to be arranged separately, resulting in a large required space.

In this paper, a prototype of multi-coupled coils has been designed and manufactured, which is shown in Figure 1b, according to the design process in [5]. There are mutual inductances among the inductors. The multi-coupled coils are designed as a layered structure of multiple coaxial round wire discs, whose required space is reduced. For a set of the n-tuned filter, the required space of the multi-coupled coils is about 1/n of the required space of inductors in the traditional passive filter. At present, the capacity of actually manufactured multi-coupled coils ranges from dozens of kvar to several Mvar.

However, the requirements for assembly of the passive filter with multi-coupled coils in Figure 1b are higher than that of the traditional LC filter. In this structure, the number of coil turns determines the self-inductance. Moreover, the number of coil turns and the relative positions of the coils determine the mutual inductances together. Therefore, an accurate installation of this structure is crucial for obtaining the required parameters.

The passive filter with multi-coupled coils also has the inherent drawbacks of the conventional passive filter. The filtering effect of the passive filter can be affected by the grid parameters. In severe cases, the passive filter may resonate at a certain frequency. According to the design principle of the passive filter, considering the frequency offset in the power grid and the equipment manufacturing error, the tuned frequency of the passive filter should be set 3–15% lower than the characteristic frequency [25].

Therefore, on the basis of the passive filter with multi-coupled coils, this paper also connects an active filter to the passive filter via a coupled inductor, to eliminate the remaining harmonic current after passive compensation.

2.2. Deign of the Passive Filter with Multi-Coupled Coils

In the passive filter with multi-coupled coils, there are mutual inductances among the inductors. Therefore, in the design process, the self-inductances and mutual inductances need to be calculated and designed [5]. The basic design flow chart is shown in Figure 2.

According to Figure 2, the first step of the design process is to determine the parameters of the uncoupled passive filter considering the rated voltage, capacity. One type of uncoupled passive filter is shown in Figure 3a. In Figure 3a, the inductors L_a, L_b, L_c and the capacitors C₃, C₄, C₅ are determined in this step.

The second step is to establish the design equations for the multi-coupled coils structure. Figure 3b shows the passive filter with multi-coupled coils. In Figure 3a,b, the values of capacitor C₃, C₄, C₅ are the same. To make the network shown in Figure 3b equivalent to the network in Figure 3a, it is necessary to ensure that when the two networks have the same excitation, the voltages at point a, b, c, d and the current i₁, i₂, i₃, i₄, i₅ in the two figures are the same. Moreover, according to this relationship, formulas are as follows:

L₁ − 2M₁₄ +L₄ = L_a

(1)

−L₄ + M₁₂ − M₁₃ +M₁₄ − M₂₄ + M₃₄ = 0

(2)

M₁₃ + M₁₅ − M₃₄ − M₄₅ = 0

(3)

L₂ + L₃ + L₄ + 2 M₂₄ − 2 M₃₄ − 2 M₂₃ = L_b

(4)

−L₃ + M₂₃ + M₂₅ + M₃₄ − M₃₅ + M₄₅ = 0

(5)

L₃ + L₅ + 2 M₃₅ = L_c

(6)

in which, L₁, L₂, L₃, L₄, L₅ are the self-inductances of the inductors in the passive filter with multi-coupled coils; M_ij is the mutual inductance between L_i and L_j (i, j = 1, 2, 3, 4, 5 and i ≠ j); L_a, L_b, L_c are the self-inductances of the inductors in the Cauer I form three-tuned filter.

In (1)–(6), the self-inductances L₁, L₂, L₃, L₄, L₅ and the mutual inductances M₁₂, M₁₃, M₁₄, M₁₅, M₂₃, M₂₄, M₂₅, M₃₄, M₃₅, M₄₅ are unknown quantities. Since the multi-coupled coils are designed as a layered structure of multiple coaxial round wire discs, the number of turns of each coil (N₁, N₂, N₃, N₄, N₅) and the relative position between the coils (d₁, d₂, d₃, d₄, d₅) determine the self-inductances and mutual inductances of the coils. Thus, (1)–(6) can be converted into equations about the number of coil turns (N₁, N₂, N₃, N₄, N₅) and the relative positions of the coils (d₁, d₂, d₃, d₄, d₅). There are 6 equations and 10 unknowns. Therefore, initial conditions are needed. We can set the position d₁ of inductor L₁, and set the coil turn N₁ of L₁ according to the value of L_a. Two mutual inductance relationships (such as: M₁₂ = M₁₃, M₃₄ = M₃₅) can be added. In this way, there are 8 equations and 8 unknowns, and the design equation set of the multi-coupled coils structure can be obtained.

The third step is to solve the nonlinear equations. The unknowns in the aforementioned equations can be worked out using the inductance calculation formula in [23,24]. If the nonlinear equations cannot be solved, the initial conditions shall be changed. In this way, the number of coil turns and the relative positions of the coils can be obtained. The passive filter with multi-coupled coils can be designed.

2.3. Structure of the HAPF with Multi-Coupled Coils

The topology of the HAPF with multi-coupled coils is shown in Figure 4, in which an active power filter is added to the passive filter. The active power filter consists of an H-bridge converter and a LCL filter. The inductor L_g of the LCL filter is the coupled inductor of the active power filter.

There are mutual inductances between the coupled inductor L_g and the inductors in the passive filter. The coupled inductor L_g is closest to inductor L₁ and most closely coupled with L₁. When the active power filter works, the converter generates a controllable AC current i_g to the coupled inductor L_g. Since the spatial magnetic coupling exists among L_g and the inductors in the passive filter, a current can be injected into the passive filter branch, thereby changing the current of the passive filter branch i_f. Thus, the remaining characteristic harmonic currents after passive compensation can be eliminated.

Compared with the conventional shunt HAPF topology, the proposed HAPF has the similar current compensation principle. The passive filter of the proposed HAPF bears the fundamental voltage and eliminates most of the characteristic harmonic currents. The active power filter bears a very small fundamental voltage and eliminates the remaining harmonic currents.

In the proposed HAPF, the connection mode of the active power filter and the passive filter is different from the traditional HAPF. For the traditional HAPF topology in which the active power filter is in series with the passive filter through a transformer, the series connection of the transformer changes the filter loop of the passive filter. In Figure 4, the active power filter of the proposed HAPF connects with the passive filter through spatial magnetic coupling instead of a transformer. The coupled inductor L_g is designed as a round wire disc, which is placed very close to the multi-coupled coils in the passive filter. The coupled inductor L_g is not directly connected in series to the filter loop of the passive filter. So, the coupled inductor L_g does not change the filter loop of the passive filter. Compared to a transformer, the cost of the coupled inductor L_g in Figure 4 is relatively small in the entire HAPF. This connection mode ensures that whether the active converter is open-circuited or short-circuited, the filtering effect of the passive filter always exists and the safety of the power grid will not be at stake. Besides, the coaxial round wire discs inductor structure can enhance the coupling effect and increase the overall efficiency of the system.

3. Working Principle

The equivalent schematic of the hybrid compensation of the proposed HAPF is shown in Figure 5, where u₁ to u₅ are the induced voltages controlled by the output current i_g of the converter through spatial magnetic coupling and u_g is the voltage source controlled by all the currents of the passive filter.

Because the coupled inductor L_g is placed above the multi-coupled coils, it is closest to inductor L₁, which is at the top of the multi-coupled coils. So, the mutual inductance M_g1 between L_g and L₁ is relatively large, and the effect of the induced voltage source u₁ is relatively large. For an inductor that is relatively far from L_g in space, the mutual inductance between it and L_g will be much smaller than M_g1.

The self-inductance and mutual inductance of each coil in Figure 1b were measured. The measurement results show that the mutual inductance M_g1 (between L₁ and L_g) and M_g3 (between L₃ and L_g) are much larger than M_g2 (between L₂ and L_g), M_g4 (between L₄ and L_g), and M_g5 (between L₅ and L_g). Therefore, to simplify the theoretical analysis, the mutual inductance M_g2, M_g3, M_g4, M_g5 are combined to an equivalent inductance M_g’ in Figure 6, where u’ represents the equivalent induced voltage source generated in the filter branch by M_g’. For the characteristic harmonic, the impedance of the passive filter branch is very small. L_th and R_th represent the equivalent inductance and resistance of the passive filter branch at harmonic frequencies, respectively. L_s and R_s represent the supply-system inductance and resistance, respectively.

The current i_fh represents the harmonic component of the filter branch current i_f. The current i_fhw represents the passive current component of i_fh, which is the harmonic component when only the passive filter works; the current i_fhy represents the injected current component of i_fh by the active power filter. i_Lh is the harmonic component of the load current i_L. Figure 6 is only used to simplify the theoretical analysis.

According to Figure 6, the induced voltage u₁ and u’ caused by i_g can generate the injected current i_fhy on the passive filter branch. In the harmonic current loop, L_th, R_th, L_s, and R_s will affect the value of i_fhy.

At tuned frequencies, series resonance occurs in the passive filter branch and the values of L_th and R_th are very small. Therefore, at tuned frequencies, the current i_g can produce a relatively large i_fhy. By controlling the output current i_g of the active power filter, the injected current component i_fhy of i_fh can be adjusted, then so can the harmonic i_fh.

As long as the active power filter generates a current i_g of a certain frequency, the injected current i_fhy of corresponding frequency will be generated on the passive filter branch. Besides the tuned frequencies, the active power filter in the proposed HAPF can also filter harmonic currents at other frequencies. However, at these frequencies, the values of L_th and R_th are relatively large. Therefore, the current i_fhy generated on the passive filter branch with the same magnitude of current i_g will be relatively smaller than that generated at the tuned frequency.

When the amplitude of each characteristic harmonics of i_fh and i_Lh are the same, and the phases are opposite, the harmonics in the supply current i_S can be completely eliminated.

4. Control Strategy

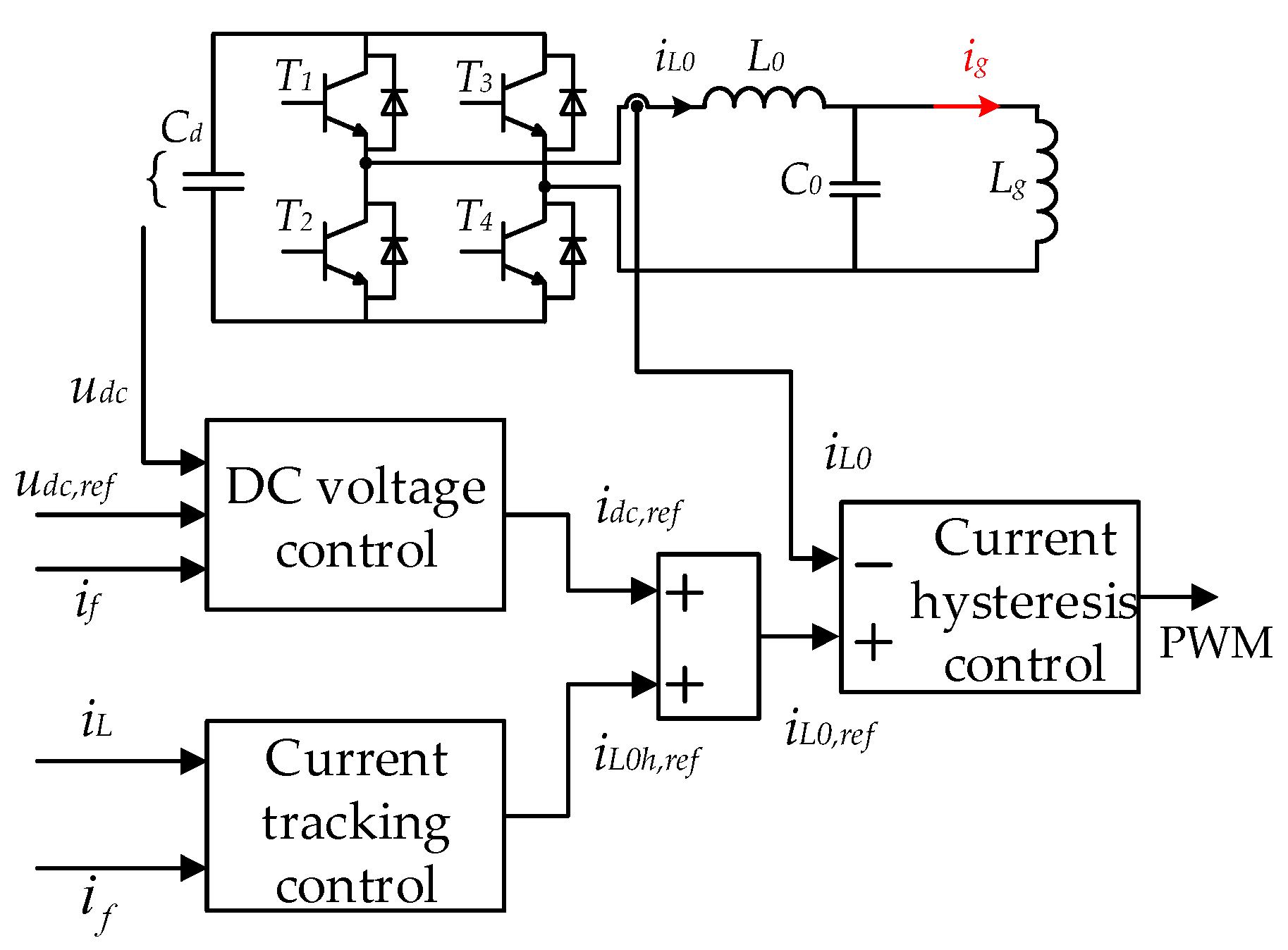
When the active power filter of the proposed HAPF works, the accurate harmonic current tracking control is needed, as well as the capacitor voltage control on the DC side of the active converter. Therefore, the control block diagram of hybrid compensation is shown in Figure 7, which consists of three parts: DC voltage control module, current tracking control module, and current hysteresis control module.

The DC voltage control module is used to stabilize the DC capacitor voltage. The output of the DC voltage control module is i_dc,ref, which represents the reference value of the active current exchanged between the converter and the grid.

The current tracking control module is used to make the filter branch current accurately track the load harmonic current. The output of the current tracking control module is i_L0h,ref.

The sum of i_dc,ref and i_L0h,ref is i_L0,ref, which is the input of the current hysteresis control module. The output of the current hysteresis control module is the PWM control signal of the active converter. The current hysteresis control can directly track the current at high speed, so the converter can be considered as a current source.

4.1. DC Capacitor Voltage Control

The stability of DC capacitor voltage is the prerequisite for the proposed HAPF to work stably. In order to maintain a stable DC capacitor voltage, it is necessary for the active converter to exchange active power with the induced voltage source u_g.

Current i_dc is the active current, which is the active component of i_L0. If the phase of i_dc is the same as the phase of u_g, the converter absorbs active power from u_g, to support the DC capacitor voltage. If the phase of i_dc is opposite to the phase of u_g, the converter exports active power to u_g. So, in Figure 8, it is critical to properly set the amplitude and phase of i_dc,ref, which is the reference value of i_dc.

To obtain the amplitude I_dc,ref of current i_dc,ref, in Figure 8, the DC capacitor voltage u_dc is compared with the reference value u_dc,ref, and the comparison result is sent to the PI controller. The output of the PI controller is I_dc,ref.

The induced voltage u_g cannot be measured directly, and it is controlled by all the currents in the passive filter. Since the coupled inductor L_g is closest to inductor L₁ and the most closely coupled with L₁, only the filter branch current i_f (the current on inductor L₁) is considered here. Then, u_g can be expressed as:

$$u_g=M_{g1}\frac{d{i}_f}{dt}$$

(7)

where, M_g1 is the mutual inductance between the coupled inductor L_g and inductor L₁.

So, according to (7), a unit signal i_dc0,ref, which has the same waveform with u_g, can be obtained by current derivation, LPF, and waveform normalization in Figure 8. By multiplying i_dc0,ref to I_dc,ref, the reference current i_dc,ref of the active current i_dc can be obtained.

Considering the 3rd, 5th, 7th, 11th harmonic components of i_dc, the active current i_dc can be expressed as:

$$i_{dc}=I_{dc,ref}{\displaystyle \sum _{n=1,3,5,7,11}{a}_n\sin (n\omega t+{\theta }_n)}$$

(8)

where, a_n is the amplitude of each harmonic component of the unit signal i_dc0,ref.

When the phase of i_dc is the same with u_g, u_g can be expressed as:

$$u_g=U_g{\displaystyle \sum _{n=1,3,5,7,11}{a}_n\sin (n\omega t+{\theta }_n)}$$

(9)

The instantaneous power that u_g exports is:

$$p=U_g{I}_{dc,ref}{\displaystyle \sum _{n=1,3,5,7,11}\frac{a_n^2}{2}+}{p}_{ac}$$

(10)

where, p_ac is the AC component, which represents the reactive power. Additionally, the DC component in (10) represents the active power, which is influenced by I_dc,ref. Therefore, in DC capacitor voltage control, by controlling I_dc,ref, the active power exchanged between the converter and u_g can be adjusted to support the DC capacitor voltage. In addition, from (10), it can be seen that the active power is provided by the fundamental and harmonic components in u_g together.

4.2. Harmonic Current Control

For harmonic current elimination, at the characteristic frequencies, the amplitude and phase of the output current i_g are controlled to track the harmonic current.

Taking n^th load harmonic as an example, current i_fhn, i_fhwn, i_fhyn, i_Lhn, and i_gn are the n^th component of current i_fh, i_fhw, i_fhy, i_Lh, and i_g, respectively. According to Figure 6, current i_fhn, i_fhwn, i_fhyn can be expressed with phasor method as:

$$I_{fhn}\angle {\theta }_{fhn}=I_{fhwn}\angle {\theta }_{fhwn}+I_{fhyn}\angle {\theta }_{fhyn}$$

(11)

$$I_{fhwn}\angle {\theta }_{fhwn}=\frac{-(R_s+jn\omega L_s)}{R_{th}+R_s+jn\omega (L_{th}+L_s)}·I_{Lhn}\angle {\theta }_{Lhn}$$

(12)

$$I_{fhyn}\angle {\theta }_{fhyn}=\frac{-jn\omega (M_{g1}+M_{g’})}{R_{th}+R_s+jn\omega (L_{th}+L_s)}·I_{gn}\angle {\theta }_{gn}$$

(13)

where, I_fhn, I_fhwn, I_fhyn, I_Lhn, I_gn are the amplitude of i_fhn, i_fhwn, i_fhyn, i_Lhn, and i_gn, respectively. θ_fhn, θ_fhwn, θ_fhyn, θ_Lhn, θ_gn are the phase angles of i_fhn, i_fhwn, i_fhyn, i_Lhn, and i_gn, respectively.

When the n^th load harmonic current i_Lhn is completely eliminated, we have the following relationship:

$$I_{fhn}\angle {\theta }_{fhn}+I_{Lhn}\angle {\theta }_{Lhn}=0$$

(14)

Substituting (11)–(13) into (14) results in:

$$Z_{thn}{I}_{Lhn}\angle ({\theta }_{Lhn}+{\theta }_{thn})=n\omega M{I}_{gn}\angle ({\theta }_{gn}+90°)$$

(15)

where, $Z_{thn}=\sqrt{R_{th}^2+{(n\omega L_{th})}^2}$, ${\theta }_{thn}=\arctan \frac{n\omega L_{th}}{R_{th}}$, $M=M_{g1}+M_{g^{\prime }}$.

In (15), the amplitude I_gn and phase angle θ_gn of current i_gn are adjustable. When the n^th load harmonic current i_Lhn is definite, there is a unique I_gn and a unique θ_gn that suit Equation (15).

From (15), I_gn and θ_gn should be:

$$I_{gn}=\frac{Z_{thn}{I}_{Lhn}}{n\omega (M_{g1}+M_{g^{\prime }})}$$

(16)

$${\theta }_{gn}={\theta }_{Lhn}+{\theta }_{thn}-90°$$

(17)

According to (16) and (17), I_gn and θ_gn are only related to n^th load harmonic current i_Lhn. Therefore, in theory, the n^th harmonic current i_Lhn can be completely eliminated by controlling the amplitude and phase angle of the output current i_gn of the active power filter.

Consequently, the active power filter is controlled as an adjustable current source. Each characteristic harmonic i_gn of output current i_g is controlled individually. Through joint control of the amplitude and phase of i_gn, each characteristic harmonic i_fhn of the filter branch current i_f can be adjusted, thereby eliminating the load harmonic current i_Lh.

As shown in Figure 9, the amplitude and phase of each characteristic harmonic component of the load current i_L and filter branch current i_f can be obtained by FFT. The amplitudes and phases obtained from i_L are reference values. The amplitudes and phases obtained from i_f are feedback signals.

These reference values and feedback signals are sent to their respective PI controllers, and then synthesized to obtain the reference signal for hysteresis control. Finally, the PWM control signal of the active converter is obtained. The hysteresis control can track the current i_L0 well and the active power filter can generate the desired current i_g. In this paper, the width of the hysteresis band is 0.2 A.

In order to improve response speed, the phase feedforward control is adopted, which is shown in Figure 9. In the phase feedforward control, p_dif3 is the phase response with the 3rd harmonic of i_L0 as the excitation and the 3rd harmonic of current i_f as the output. k is the coefficient of the phase feedforward control, whose value is slightly less than 1. The phase response can be obtained through simulation, and its value does not need to be precise.

5. Simulation Results

In order to verify the effectiveness of the proposed scheme, simulations of a single-phase 10 kV hybrid active power filter with multi-coupled coils, which is shown in Figure 4, are carried out in MATLAB/Simulink. The load harmonic source includes 5th, 7th, and 11th harmonic current. The inductance parameters and capacitance parameters of the multi-coupled coils are calculated according to the method in [5]. The main simulation parameters except for the inductance parameters of the multi-coupled coils are shown in

Table 1. Main simulation parameters.

Categories	Variables	Value
Supply-system parameters	voltage	10 kV
	frequency	50 Hz
	LS	1.2 mH
Load harmonic parameters	amplitude of 5th harmonic	40 A
	amplitude of 7th harmonic	30 A
	amplitude of 11th harmonic	20 A
Converter parameters	L0	0.8 mH
	C0	6 μF
	Cdc	4700 μF
	udc	800 V
Passive filter parameters	C3	25 μF
	C4	55 μF
	C5	21 μF

.

The inductance matrix of the multi-coupled coils is shown in

Table 2. Inductance matrix of 10 kV HAPF with multi-coupled coils.

Inductance/μH	Lg	L1	L2	L3	L4	L5
Lg	4088	1061	103	1578	116	109
L1	1061	813	61	1047	60	62
L2	103	61	800	721	330	662
L3	1578	1047	721	10793	557	695
L4	116	60	330	557	7364	547
L5	109	62	662	695	547	1168

.

According to the inductance and capacitance parameters in Table 1 and Table 2, the impedance–frequency characteristic of the passive filter is simulated as shown in Figure 10.

Figure 10 shows the tuned frequencies of the passive filter deviate from 250 Hz, 350 Hz, and 550 Hz (line frequency is 50 Hz in China). So, the passive filter is unable to completely eliminate the 5th, 7th, and 11th characteristic harmonics.

To improve the filtering effect of the passive filter, the active power filter generates current i_g to compensate the remaining harmonic currents. In the hybrid compensation simulations, the control strategy shown in Figure 7, Figure 8 and Figure 9 is used.

5.1. Current Compensation Effect

Figure 11 shows the waveforms of supply current i_S under different compensation strategies. The waveform of i_S without any compensation is shown in Figure 11a. The waveform of i_S with passive compensation is shown in Figure 11b. The waveform of i_S with hybrid compensation is shown in Figure 11c.

From Figure 11a, it can be seen that without any compensation, the total harmonic distortion (THD) of i_S is 26.33%. Further, the distortion of 5th, 7th, and 11th harmonics of i_S are 19.57%, 14.66%, and 9.74%, respectively. From Figure 11b, it can be seen that with passive compensation, the THD of i_S is reduced to 5.79%. Further, the distortion of 5th, 7th, and 11th harmonics are 4.55%, 3.36%, and 1.22%, respectively. From Figure 11c, it can be seen that the THD of i_S is reduced to 0.38%. The distortion of 5th, 7th, and 11th harmonics are 0.27%, 0.26%, and 0.09%, respectively.

In addition, it can be seen that in Figure 11a, the amplitude of the fundamental component of i_S is 204.1 A. While in Figure 11b,c, the amplitude of the fundamental component of i_S is 340 A, which is larger. The reason is that after the passive filter works, the capacitive fundamental current increases, which can compensate the inductive current in the grid.

5.2. Compensation Characteristic Simulation

In hybrid compensation, the stability of DC capacitor voltage is the prerequisite. The output current i_g will directly change the filter branch current i_f and affect the filtering effect.

In order to study the compensation characteristic, Figure 12a–c shows the waveform of the output current i_g of the active power filter, the waveform of the filter branch current i_f, and the waveform of the DC capacitor voltage u_dc in hybrid compensation, respectively.

In Figure 12a, the amplitude of the 5th, 7th, and 11th harmonics of i_g are 27.51 A, 51.34 A, and 4.90 A, respectively. These harmonic currents are injected into the filter branch through spatial magnetic coupling, to change the filter branch current i_f.

In Figure 12b, the amplitude of the 5th, 7th, and 11th harmonics of i_f are 39.92 A, 29.54 A, and 19.98 A, respectively. The harmonic components i_fh of i_f in hybrid compensation includes the passive current component i_fhw (the harmonic component when only the passive filter works) and the injected current component i_fhy (injected by the active power filter).

From Figure 12c, it can be seen that in hybrid compensation, the DC capacitor voltage u_dc can be stabilized at 800 V with only small voltage fluctuations. The cause of the fluctuation is the active power exchange between the converter and the induced voltage u_g.

The apparent power of the active power filter can be calculated using the following equation:

$$S_{APF}=\frac{V_d}{\sqrt{2}}{I}_{grms}$$

(18)

in which, S_APF represents the apparent power of the active power filter; V_d represents the DC voltage of the active power filter; I_grms represents the RMS value of the output current i_g.

In simulation, V_d is 800 V. I_grms is 41.33 A. So, the apparent power S_APF = 23.38 kVA, according to (18).

The apparent power of the proposed HAPF can be calculated using the following equation:

$$S_{HAPF}=U_{Frms}·I_{frms}$$

(19)

in which, S_HAPF represents the apparent power of the proposed HAPF; U_Frms represents the RMS value of the voltage of the proposed HAPF; I_frms represents the RMS value of the current i_f.

In simulation, I_frms is 194.35 A, and U_Frms is 5845 V. So, the apparent power S_HAPF = 1135.975 kVA, according to (19).

S_PF represents the apparent power of the passive filter. The ratio between S_APF and S_PF is:

$$K=\frac{S_{APF}}{S_{PF}}=\frac{S_{APF}}{S_{HAPF}-S_{APF}}=\frac{23.38}{1135.975-23.38}\approx 2.10\%$$

(20)

It can be found that the capacity ratio of the active power filter to the passive filter in the proposed HAPF is very small.

5.3. Fault Simulation of the Active Power Filter

The open-circuit and short-circuit fault diagram of the active power filter is shown in Figure 13. As is introduced before, the proposed HAPF has no additional coils in series connected to the passive filter branch, and the filtering effect of the passive filter will be guaranteed whether the active power filter is open or short-circuited. To verify this, simulations in two cases (open-circuit and short-circuit) are conducted.

According to Figure 13, under normal working condition, point a and point b are connected to each other, while point b and point c are not connected. When the connection between point a and point b is broken, the active power filter is open-circuited. At this time, the current i_g is zero and the influence of the active power filter on the passive filter no longer exists. The open-circuit fault simulation result is shown in Figure 14a. Compared with the waveform of i_S when only the passive filter works in Figure 11b, the waveform of i_S in Figure 14a is almost the same.

When point b and point c are connected, the active power filter is short-circuited. In this case, current i_g is completely generated by the induced voltage u_g. At this time, the influence of the current i_g on the passive filter is small. The short-circuit fault simulation result is shown in Figure 14b. Compared with the waveform in Figure 11b, the waveform of i_S in Figure 14b is very similar.

In summary, whether the active power filter is open-circuited or short-circuited, the filtering effect of the passive filter can be guaranteed.

5.4. Simulation of Three-Phase Hybrid Active Power Filter

To prove that the proposed HAPF topology is available for the three-phase system, a three-phase 10 kV hybrid active power filter simulation was carried out. In the three-phase system, three single-phase hybrid active power filters are used. Each single-phase hybrid active power filter has the same topology and the same control strategy as described above. The parameters are the same as the parameters in Table 1 and Table 2.

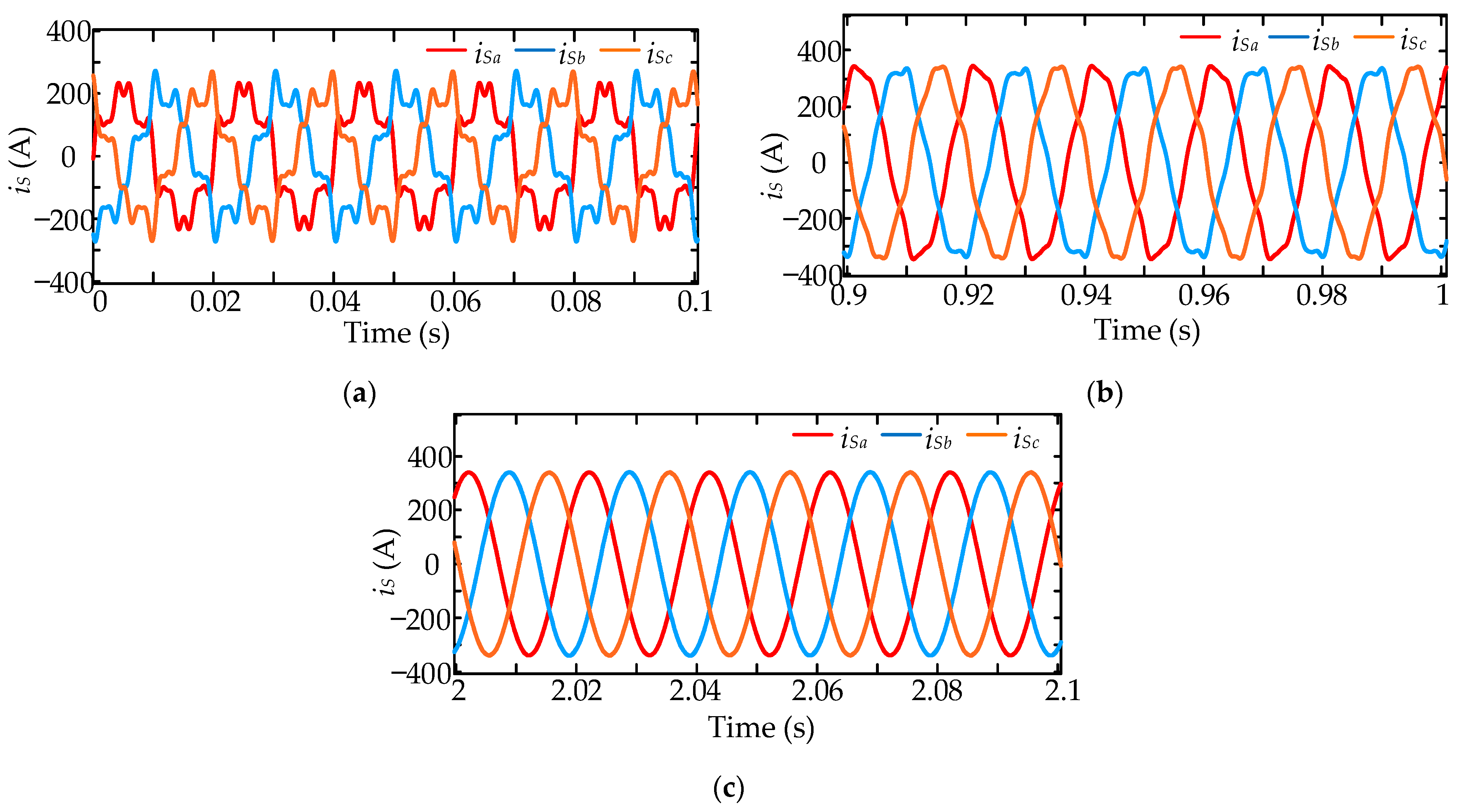
Figure 15 shows the waveforms of the supply current i_S under different compensation strategies in the three-phase simulation. The waveform of i_S without any compensation is shown in Figure 15a. The waveform of i_S with passive compensation is shown in Figure 15b. The waveform of i_S with hybrid compensation is shown in Figure 15c.

In Figure 15a, taking phase A as an example, without any compensation, the THD of the supply current i_Sa is 26.29%. The distortion of 5th, 7th, and 11th harmonics of i_Sa is 19.56%, 14.64%, and 9.71%, respectively. In Figure 15b, with passive compensation, the THD of i_Sa is reduced to 5.81%. Further, the distortion of 5th, 7th, and 11th harmonics are 4.55%, 3.37%, and 1.29%, respectively. In Figure 15c, with hybrid compensation, the THD of i_Sa is reduced to 0.29%.

6. Experiments

In order to verify the feasibility of the proposed HAPF, a small prototype of multi-coupled coils is designed and manufactured as shown in Figure 1b. Then, an experimental platform of the hybrid active power filter with multi-coupled coils is built according to the topology in Figure 4.

The structure schematic diagram of the HAPF experimental platform is shown in Figure 16. The platform is composed of the system power supply, harmonic source, and the proposed HAPF. The RMS value of the system voltage is transformed from 220 V to 36 V through a step-down transformer. The harmonic source is an adjustable harmonic current source. The HAPF with multi-coupled coils is composed of an active power filter and passive filter. The active power filter consists of the main circuit, detection circuit, and control circuit.

The experimental platform of HAPF with multi-coupled coils is shown in Figure 17. The main experimental parameters other than the inductance parameters of the multi-coupled coils are shown in

Table 3. Main experimental parameters.

Categories	Variables	Value
Supply-system parameters	voltage	36 V
	frequency	50 Hz
	LS	0.12 mH
Load harmonic parameters	amplitude of 3rd harmonic	14.1 A
Passive filter parameters	C3	352.9 μF
	C4	1269.7 μF
	C5	399.1 μF

.

The inductance parameters of the multi-coupled coils in the platform are shown in

Table 4. Inductance matrix of multi-coupled coils in experimental platform.

Inductance/μH	Lg	L1	L2	L3	L4	L5
Lg	980.0	155.0	37.1	258.8	13.2	45.9
L1	155.0	80.1	10.8	86.4	3.4	11.4
L2	37.1	10.8	106.8	90.2	9.0	57.5
L3	258.8	86.4	90.2	746.7	17.5	79.6
L4	13.2	3.4	9.0	17.5	872.8	62.7
L5	45.9	11.4	57.5	79.6	62.7	687.7

.

The impedance–frequency characteristic of the passive filter in the experiment is measured by voltammetry as shown in Figure 18. From Figure 18, it can be seen that the measured tuned frequencies of the passive filter are 145 Hz, 247 Hz, and 347 Hz, which slightly deviate from the frequencies of the 3rd, 5th, and 7th harmonics.

In the experiment, the load harmonic current source injects the 3rd harmonic current into the power grid, whose amplitude is 14.1 A.

Figure 19 shows the experimental waveform of the supply current i_S under different compensation strategies. The experimental waveform of i_S without compensation is shown in Figure 19a. The experimental waveform of i_S with passive compensation is shown in Figure 19b. The experimental waveform of i_S with hybrid compensation is shown in Figure 19c.

From Figure 19a, it can be seen that i_S contains the obvious 3rd harmonic. The amplitude of the fundamental component of the supply current i_S is 23.65 A and the THD is 60.95%. The distortion of the 3rd harmonic of supply current i_S is 60.68%.

From Figure 19b, it can be seen that amplitude of the fundamental component of i_S is 43.9 A, which is larger than that before compensation because of the increase of capacitive fundamental current. The THD of i_S is reduced to 15.93%. The distortion of the 3rd harmonic is reduced to 13.22%. At the same time, the distortion of the 5th harmonic is 5.92%, and the distortion of the 7th harmonic is 6.16%.

In passive compensation, the 5th and 7th harmonic currents appear in the supply current i_S, which is caused by the very small impedance of the system transformer in the experiment. For the 5th and 7th harmonics, the impedance of the passive filter branch is very small, so the 5th and 7th harmonics are introduced from the power grid.

From Figure 19c, it can be seen that the amplitude of the fundamental component of the supply current i_S is 43.26 A and the THD is reduced to 3.08%. The 3rd, 5th, 7th harmonics of i_S are greatly eliminated. Thus, it is reasonable to conclude that the proposed hybrid compensation method is feasible.

7. Conclusions

This paper proposes a novel hybrid active power filter with multi-coupled coils. The passive filter of the proposed HAPF adopts the structure of multi-coupled coils, which can reduce the required space of the inductors. The active power filter of the proposed HAPF adopts a coupled inductor instead of a transformer to connect with the passive filter. The active power filter can inject the compensation current into the passive filter branch through spatial magnetic coupling. At the same time, through spatial magnetic coupling, the active power filter can absorb active power from the passive filter branch to maintain the capacitor voltage.

To verify the effectiveness of the proposed scheme, a simulation model of a 10 kV hybrid active power filter with multi-coupled coils is built in MATLAB/Simulink. Furthermore, an experimental platform of hybrid active power filter with multi-coupled coils is built. Simulations and experiments in this paper verify the feasibility of the proposed HAPF.

(1)

The passive filter with multi-coupled coils can save the required space of the inductors on the premise of eliminating characteristic harmonics.

(2)

The active power filter of the proposed HAPF can improve the filtering effect of the passive filter. The current injection through spatial magnetic coupling is effective and feasible.

(3)

Since the connection method of spatial magnetic coupling, whether the active power filter is open-circuited or short-circuited, the filtering effect of the passive filter can still be guaranteed, which enhances the reliability of the filter.

In the simulation and experiment, it can be found that the inductance matrix of the multi-coupled coils directly affects the performance of the filter. Therefore, the parameter optimization of the multi-coupled coils is worthy of further research.