Smooth-Transition Simple Digital PWM Modulator for Four-Switch Buck-Boost Converters
Abstract
:1. Introduction
2. Operation of the 4SBB Converter
2.1. Bypass and Saturation Modes
2.2. Buck-Boost Mode
2.3. Buck+Boost Mode
3. Smooth Transition DPWM
3.1. Ideal Smooth Transition DPWM
3.2. Simplified Smooth Transition DPWM
3.3. Simplified Smooth Transition DPWM with Distributed Conversion Ratio Steps
3.4. Complete Smooth Transition DPWM with Hysteresis and Dead-Times
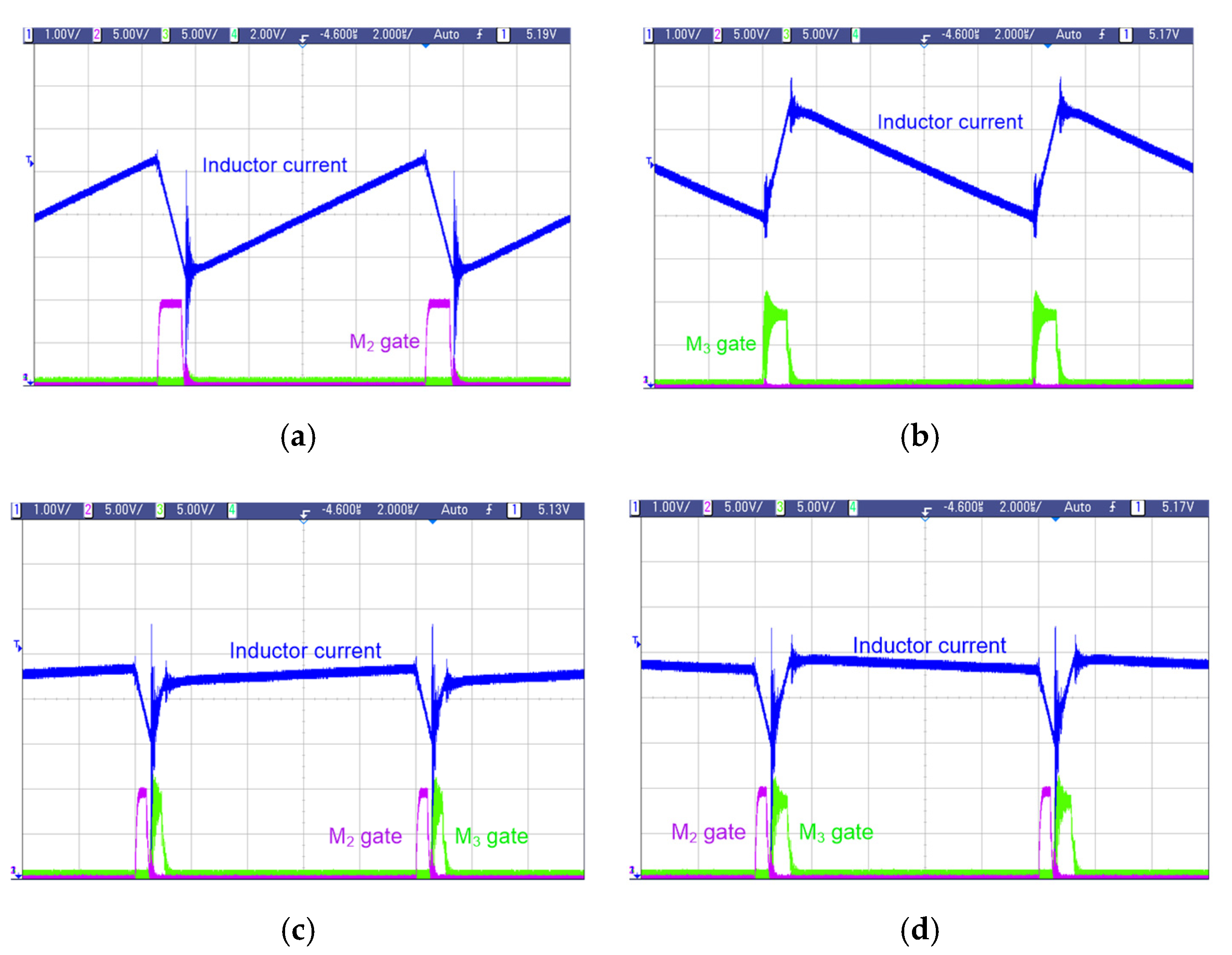
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| PWM | Pulse Width Modulation |
| 4SBB | 4-Switch Buck-Boost |
| DC | Direct Current |
| ADC | Analog to Digital Converter |
| DSC | Digital Signal Controller |
| DPWM | Digital Pulse Width Modulation |
| FPGA | Field Programmable Gate Array |
| IC | Integrated Circuit |
| MOSFET | Metal-Oxide-Semiconductor Field-Effect Transistor |
| ASIC | Application Specific Integrated Circuit |
References
- Ghanem, M.C.; Al-Haddad, K.; Roy, G. A New Single Phase Buck-Boost Converter with Unity Power Factor. In Proceedings of the Conference Record of the 1993 IEEE Industry Applications Conference Twenty-Eighth IAS Annual Meeting, Toronto, ON, Canada, 2–8 October 1993; pp. 785–792. [Google Scholar]
- D’Antonio, M.; Shi, C.; Wu, B.; Khaligh, A. Design and Optimization of a Solar Power Conversion System for Space Applications. IEEE Trans. Ind. Appl. 2019, 55, 2310–2319. [Google Scholar] [CrossRef]
- Ramos-Paja, C.A.; Bastidas-Rodríguez, J.D.; González, D.; Acevedo, S.; Peláez-Restrepo, J. Design and Control of a Buck–Boost Charger-Discharger for DC-Bus Regulation in Microgrids. Energies 2017, 10, 1847. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.-W.; Chen, K.-H.; Chen, Y.-M. Modeling and Controller Design for a Four-Switch Buck-Boost Converter in Distributed Maximum Power Point Tracking PV System Applications. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 1663–1668. [Google Scholar]
- Thi Kim Nga, T.; Park, S.-M.; Park, Y.-J.; Park, S.-H.; Kim, S.; Van Cong Thuong, T.; Lee, M.; Hwang, K.; Yang, Y.; Lee, K.-Y. A Wide Input Range Buck-Boost DC–DC Converter Using Hysteresis Triple-Mode Control Technique with Peak Efficiency of 94.8% for RF Energy Harvesting Applications. Energies 2018, 11, 1618. [Google Scholar] [CrossRef] [Green Version]
- Ma, J.; Zhu, M.; Zhang, J.; Cai, X. Improved Asynchronous Voltage Regulation Strategy of Non-Inverting Buck-Boost Converter for Renewable Energy Integration. In Proceedings of the 2015 IEEE 2nd International Future Energy Electronics Conference (IFEEC), Taipei, Taiwan, 1–4 November 2015; pp. 1–5. [Google Scholar]
- Tsai, Y.-Y.; Tsai, Y.-S.; Tsai, C.-W.; Tsai, C.-H. Digital Noninverting-Buck–Boost Converter With Enhanced Duty-Cycle-Overlap Control. IEEE Trans. Circuits Syst. II 2017, 64, 41–45. [Google Scholar] [CrossRef]
- Restrepo, C.; Konjedic, T.; Calvente, J.; Giral, R. Hysteretic Transition Method for Avoiding the Dead-Zone Effect and Subharmonics in a Noninverting Buck–Boost Converter. IEEE Trans. Power Electron. 2015, 30, 3418–3430. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Liu, Y.; Xue, Y. Four-Switch Buck–Boost Converter Based on Model Predictive Control With Smooth Mode Transition Capability. IEEE Trans. Ind. Electron. 2021, 68, 9058–9069. [Google Scholar] [CrossRef]
- Callegaro, L.; Ciobotaru, M.; Fletcher, J.E. An Intelligent Pass-Through Algorithm for Non-Inverting Buck-Boost Solar Power Optimizers. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE ’19 ECCE Europe), Genova, Italy, 3–5 September 2019; pp. P.1–P.10. [Google Scholar]
- Waffler, S.; Kolar, J.W. A Novel Low-Loss Modulation Strategy for High-Power Bidirectional Buck–Boost Converters. IEEE Trans. Power Electron. 2009, 24, 1589–1599. [Google Scholar] [CrossRef]
- Moon, J.; Lee, J.; Kim, S.; Ryu, G.; Hong, J.-P.; Lee, J.; Jin, H.; Roh, J. 60-V Non-Inverting Four-Mode Buck–Boost Converter With Bootstrap Sharing for Non-Switching Power Transistors. IEEE Access 2020, 8, 208221–208231. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, G.; See, K.W. Systematic Derivation of Dead-Zone Elimination Strategies for the Noninverting Synchronous Buck–Boost Converter. IEEE Trans. Power Electron. 2018, 33, 3497–3508. [Google Scholar] [CrossRef]
- Tsai, C.-H.; Tsai, Y.-S.; Liu, H.-C. A Stable Mode-Transition Technique for a Digitally Controlled Non-Inverting Buck–Boost DC–DC Converter. IEEE Trans. Ind. Electron. 2015, 62, 475–483. [Google Scholar] [CrossRef]
- Akhilesh, K.; Lakshminarasamma, N. Dead-Zone Free Control Scheme for H-Bridge Buck–Boost Converter. IEEE Trans. Ind. Appl. 2020, 56, 6619–6629. [Google Scholar] [CrossRef]
- Ma, J.; Zhu, M.; Li, X.; Cai, X. Bumpless Transfer of Non-Inverting Buck Boost Converter among Multiple Working Modes. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 1909–1914. [Google Scholar]
- Xilinx, Inc. Virtex-4 Family Overview. Available online: https://www.xilinx.com/support/documentation/data_sheets/ds112.pdf (accessed on 20 December 2021).


















| d[n] Ranges | dbuck[n] | dboost[n] | Conversion Ratio (M) | Trajectory |
|---|---|---|---|---|
| B-C1 | ||||
| C1-C | ||||
| C-D |
| d[n] Ranges | dbuck[n] | dboost[n] | Conversion Ratio (M) | Trajectory |
|---|---|---|---|---|
| B-C | ||||
| C-C1 | ||||
| C1-D |
| d[n] | dbuck[n] | dboost[n] | Trajectory |
|---|---|---|---|
| B–C | |||
| C–D |
| Implementation | Error | Normalized |
|---|---|---|
| dbuck,max = 0.95, dboost,min = 0.05. One step in the Boost transition | 1.04 × 10−5 | 4.16 |
| dbuck,max = 0.95, dboost,min = 0.05. Two steps distributed | 2.50 × 10−6 | 1 |
| dbuck,max = 0.95, dboost,min = 0.05. Buck-Boost mode. | 8.09 × 10−4 | 323.6 |
| dbuck,max = 0.90, dboost,min = 0.10. One step in the Boost transition | 2.13 × 10−4 | 4.34 |
| dbuck,max = 0.90, dboost,min = 0.10. Two steps distributed | 4.90 × 10−5 | 1 |
| dbuck,max = 0.90, dboost,min =0.10. Buck-Boost mode | 3.17 × 10−3 | 64.69 |
| Mode | Output |
| Buck | dbuck[n] = d[n] dboost[n] = 0 |
| Buck+Boost (Trajectory B-C) | dbuck[n] = dbuck,B2 + d[n] − dbuck,max dboost[n] = dboost,min + dtboost |
| Buck+Boost (Trajectory C–D) | dbuck[n] = dbuck,max dboost[n] = dboost,min + d[n] − dbuck,max + dbuck,B2 + dtboost |
| Boost | dbuck[n] = 1 dboost[n] = d[n] − 1 |
| Input voltage: | v1 = 24 V |
| Output voltage: | v2 = 12–36 V |
| Maximum power: | Pmax = 500 W |
| Switching frequency: | fsw = 100 kHz |
| MOSFETs: | IRFB4310Z |
| Inductance value: | L = 8 µH |
| Output capacitance: | C2 = 470 µF |
| Maximum duty cycle: | dbuck,max = 0.90 |
| Minimum duty cycle: | dboost,min = 0.10 |
| Dead times: | dtboost = 0.01 |
| Hysteresis: | h = 0.02 |
| Modulator | Finite State Machine | D-Type Flip-Flop | Adder/Subtractor | Multiplier | Comparator |
|---|---|---|---|---|---|
| Ideal | 1 | 73 | 5 | 2 | 5 |
| Simplified | 1 | 73 | 9 | 0 | 5 |
| Mode | Efficiency | Output Voltage Regulation | Computational Cost | Complexity | Scalability |
|---|---|---|---|---|---|
| Pass-through [10] | High | Low | Low | Low | High |
| One-mode modulation [13] | Low | High | Medium | Low | High |
| Duty-locking [7] | Medium | Medium | Medium | Medium | Medium |
| Hysteretic control [8] | Medium | Medium | Medium | Medium | Medium |
| Model-predictive control [9] | Medium | Medium | High | High | Low |
| This work | Medium | Medium | Low | Medium | High |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernandez, M.; Rodriguez, A.; Rodríguez, M.; Vazquez, A.; Fernandez, P.; Arias, M. Smooth-Transition Simple Digital PWM Modulator for Four-Switch Buck-Boost Converters. Electronics 2022, 11, 100. https://doi.org/10.3390/electronics11010100
Fernandez M, Rodriguez A, Rodríguez M, Vazquez A, Fernandez P, Arias M. Smooth-Transition Simple Digital PWM Modulator for Four-Switch Buck-Boost Converters. Electronics. 2022; 11(1):100. https://doi.org/10.3390/electronics11010100
Chicago/Turabian StyleFernandez, Miguel, Alberto Rodriguez, Miguel Rodríguez, Aitor Vazquez, Pablo Fernandez, and Manuel Arias. 2022. "Smooth-Transition Simple Digital PWM Modulator for Four-Switch Buck-Boost Converters" Electronics 11, no. 1: 100. https://doi.org/10.3390/electronics11010100
APA StyleFernandez, M., Rodriguez, A., Rodríguez, M., Vazquez, A., Fernandez, P., & Arias, M. (2022). Smooth-Transition Simple Digital PWM Modulator for Four-Switch Buck-Boost Converters. Electronics, 11(1), 100. https://doi.org/10.3390/electronics11010100








