FPGA in the Loop Implementation for Observer Sliding Mode Control of DFIG-Generators for Wind Turbines

Abstract

This paper presents a new contribution of the nonlinear control technique of electrical energy in a wind energy system. The nonlinear sliding mode technique used to control the powers of the DFIG-Generator is connected to the power grid by two converters (grid side and machine side). The proposed model is validated using tracking and robustness tests with a real wind speed. The control was developed under Matlab/Simulink, and the FPGA in the Loop technique was used to design the DFIG model. By employing a co-simulation, the purpose is to test the controller for the FPGA simulated model or system in its entirety. The results obtained by the cο-simulation show the efficiency of the proposed model in terms of speed and robustness with a rate THD = 0.95, and the proposed model of the sliding mode controller shows a significant improvement in the quality of energy produced by the wind system.

1. Introduction

In the last three decades, renewable energy sources have garnered considerable interest. Due to technological developments, cost reductions, and rising demand, they have become a realistic option, particularly in developing nations. However, reconfiguring the power system network will necessitate a significant transition away from conventional to renewable energy-based energy production due to its limited nature, environmental effect, and sustainability, as well as the global annual increase in energy consumption [1].

The wind is the most environmentally friendly, dependable, cost-effective, and adaptable renewable energy source for power producers to integrate into electrical grids [2]. Due to its compact size and low cost, high efficiency, long-term operation, low acoustic noise, wide operating range, and flexibility in four-quadrant active and reactive power regulation, DFIG is widely employed in current variable-speed WECS for wind energy production [3].

The control system is designed to ensure that the DFIG’s terminal voltage and frequency remain constant regardless of wind speed changes or auxiliary load. However, creating a control system for grid-integrated WECS is a significant task due to the unpredictable nature of wind speed [4]. In addition, it evaluates the wind energy system’s overall efficiency and adds to the structural stability of the power converters [5]. As a result, considerable research has been conducted to improve the performance of control loops.

While classic controllers based on linear proportional integral (PI) perform admirably in a wide variety of control applications, they have severe limitations, including machine parameter variations [6,7]. Throughout the decades, numerous unique control strategies have been proposed to replace the standard control strategy in order to improve accuracy and precision performance. Backstepping control [8,9], intelligent control [10,11], model predictive control [12,13], and sliding mode control [14,15] are all examples of these controllers.

The conventional sliding mode method produces an undesired chattering effect that might be detrimental to the system. Thus, it is appropriate to investigate sliding mode algorithms that inherit all of the SMC’s features and attenuate chattering phenomena in a regulated manner [16,17,18].

The purpose of this article is to describe the application of an upgraded sliding mode adaptive nonlinear control to a WECS-DFIG that is controlled by power converters (grid and generator sides). Additionally, the primary purpose is to prevent chattering and improve the performance of wind systems operating under changeable wind reference conditions. Our contribution to this work is to guarantee and improve the operation of a wind energy system using a nonlinear model and a nonlinear control technique and increase the system’s performance using an optimized model of the sliding mode.

In this work, an implementation on the FPGA target of our control model has been developed. The main objective is to develop and validate the model controller validated in simulation (Matlab and Simulink). The FPGA in the Loop (HILS) simulation technique is a real-time simulation technique with the use of I/O from the board that allows us to test and verify the operation of the system under different loads and conditions.

After the Section 1, Section 2 is dedicated to modeling of the system (WECS), Section 3 discusses the basic principle and the design procedure of the proposed sliding mode technique control. In Section 4, the co-simulation results of the proposed control are presented, analyzed, and then compared with other controls results. The last section of this paper is devoted to a brief conclusion.

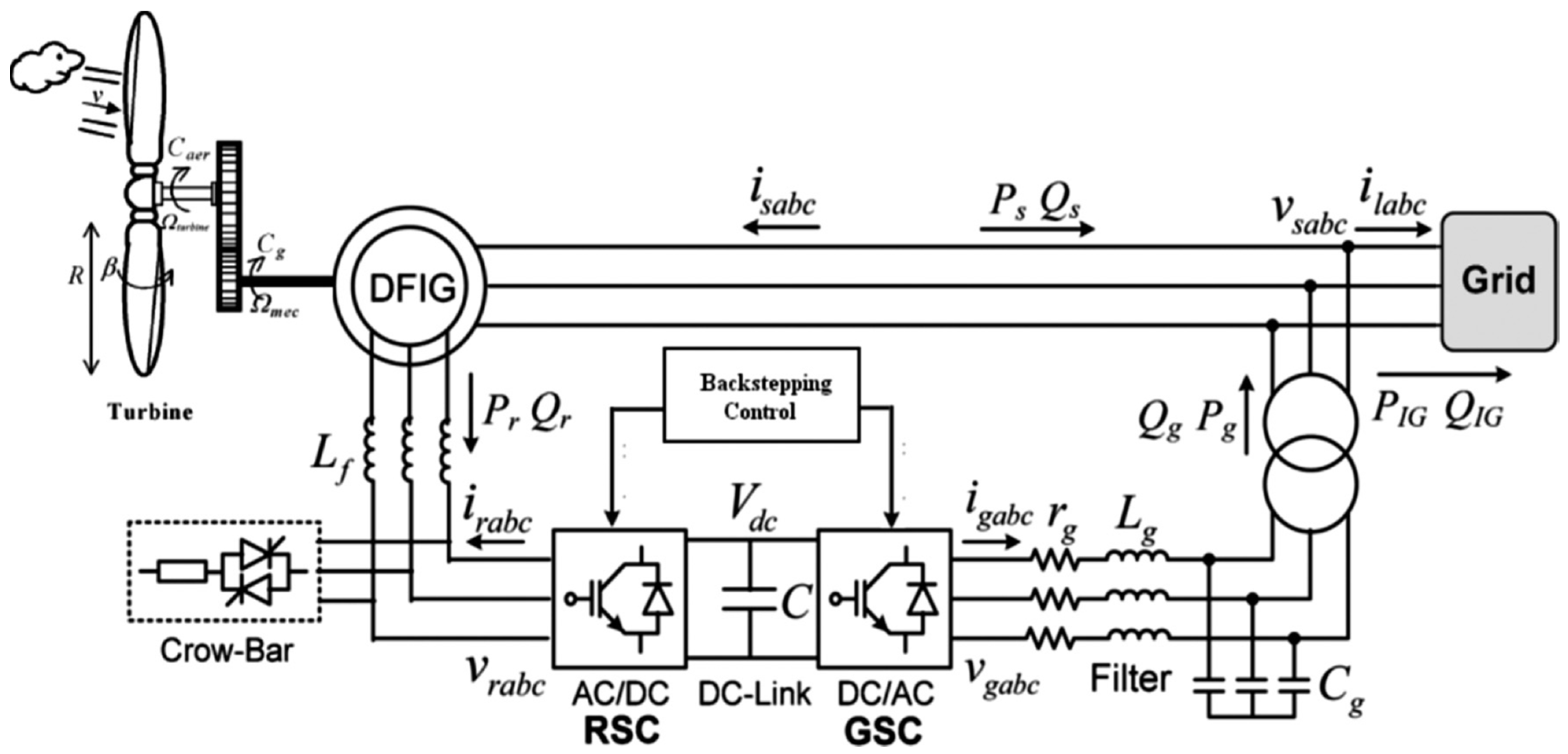
2. Presentation of the Wind Turbine Conversion Chain

The wind turbine conversion chain is composed of a wind turbine consisting of three blades, fixed on a drive shaft, which is connected to a gearbox, a DFIG generator, inverter mode (RSC), and the other mode (GSC) presented in Figure 1 [19].

• Wind Turbine Model

The authors of [21] have carefully described the process of a wind turbine, and the following equations briefly describe its model:

$$\{\begin{array}{c}{\mathrm{P}}_{\mathrm{aero}}=\frac{1}{2}·{\mathrm{C}}_{\mathrm{p}-\max }\left(\mathsf{\lambda },\mathsf{\beta }\right)·\mathsf{\rho }·\mathsf{\pi }·{\mathrm{R}}^2·{\mathrm{v}}^3\\ \mathsf{\lambda }=\frac{\mathrm{R}·\Omega \mathrm{t}}{\mathrm{v}}\\ {\mathrm{C}}_{\mathrm{p}-\mathrm{Max}}=\frac{16}{27}=0.5925\\ {\mathrm{C}}_{\mathrm{p}}\left(\mathsf{\lambda },\mathsf{\beta }\right)={\mathrm{C}}_1\left(\frac{{\mathrm{C}}_2}{\mathrm{A}}-{\mathrm{C}}_3·\mathsf{\beta }-{\mathrm{C}}_4\right){\mathrm{e}}^{\frac{-{\mathrm{C}}_5}{\mathrm{A}}}+{\mathrm{C}}_6\end{array}$$

(1)

The parameters “C₁…C₆” are constant depending on the geometry of the wind turbine.

• Gearbox Model

$$\{\begin{array}{c}{\Omega }_{\mathrm{t}}=\frac{{\Omega }_{\mathrm{mec}}}{\mathrm{G}}\\ {\mathrm{C}}_{\mathrm{g}}=\frac{{\mathrm{C}}_{\mathrm{aero}}}{\mathrm{G}}\end{array}$$

(2)

• The Mechanichal Shaft Models

The proposed mechanical model is characterized by the following equations [22,23,24,25]:

$$\begin{array}{c}{\mathrm{J}}_{\mathrm{tot}}=\frac{{\mathrm{J}}_{\mathrm{t}}}{{\mathrm{G}}^2}+{\mathrm{J}}_{\mathrm{g}}\\ {\mathrm{C}}_{\mathrm{mec}}={\mathrm{J}}_{\mathrm{tot}}·\frac{{\mathrm{d}\Omega }_{\mathrm{mec}}}{\mathrm{dt}}={\mathrm{C}}_{\mathrm{g}}-{\mathrm{C}}_{\mathrm{em}}-{\mathrm{C}}_{\mathrm{f}}\end{array}$$

(3)

With:

$${\mathrm{C}}_{\mathrm{f}}=\mathrm{f}·{\Omega }_{\mathrm{mec}}$$

(4)

• DFIG Mode after Park Transformation

Applying the Park transformation on the DFIG-Generator, we get the following equations:

$$\{\begin{array}{c}{\mathrm{v}}_{\mathrm{sd}}={\mathrm{R}}_{\mathrm{s}}·{\mathrm{I}}_{\mathrm{sd}}+\frac{\mathrm{d}{\Phi }_{\mathrm{sd}}}{\mathrm{dt}}-{\mathsf{\omega }}_{\mathrm{s}}·{\Phi }_{\mathrm{sq}}\\ {\mathrm{v}}_{\mathrm{sq}}={\mathrm{R}}_{\mathrm{s}}·{\mathrm{I}}_{\mathrm{sq}}+\frac{\mathrm{d}{\Phi }_{\mathrm{sq}}}{\mathrm{dt}}+{\mathsf{\omega }}_{\mathrm{s}}·{\Phi }_{\mathrm{sd}}\\ {\mathrm{v}}_{\mathrm{rd}}={\mathrm{R}}_{\mathrm{r}}·{\mathrm{I}}_{\mathrm{rd}}+\frac{\mathrm{d}{\Phi }_{\mathrm{rd}}}{\mathrm{dt}}-{\mathsf{\omega }}_{\mathrm{r}}·{\Phi }_{\mathrm{rq}}\\ {\mathrm{v}}_{\mathrm{rq}}={\mathrm{R}}_{\mathrm{r}}·{\mathrm{I}}_{\mathrm{rq}}+\frac{\mathrm{d}{\Phi }_{\mathrm{rq}}}{\mathrm{dt}}-{\mathsf{\omega }}_{\mathrm{r}}·{\Phi }_{\mathrm{rd}}\\ {\Phi }_{\mathrm{sd}}={\mathrm{L}}_{\mathrm{s}}·{\mathrm{I}}_{\mathrm{sd}}+\mathrm{M}·{\mathrm{I}}_{\mathrm{rd}}\\ {\Phi }_{\mathrm{sq}}={\mathrm{L}}_{\mathrm{s}}·{\mathrm{I}}_{\mathrm{sq}}+\mathrm{M}·{\mathrm{I}}_{\mathrm{rq}}\\ {\Phi }_{\mathrm{rd}}={\mathrm{L}}_{\mathrm{r}}·{\mathrm{I}}_{\mathrm{rd}}+\mathrm{M}·{\mathrm{I}}_{\mathrm{sd}}\\ {\Phi }_{\mathrm{rq}}={\mathrm{L}}_{\mathrm{r}}·{\mathrm{I}}_{\mathrm{rq}}+\mathrm{M}·{\mathrm{I}}_{\mathrm{sq}}\\ {\mathrm{P}}_{\mathrm{s}}={\mathrm{v}}_{\mathrm{sd}}·{\mathrm{I}}_{\mathrm{sd}}+{\mathrm{v}}_{\mathrm{sq}}·{\mathrm{I}}_{\mathrm{sq}}\\ {\mathrm{Q}}_{\mathrm{s}}={\mathrm{v}}_{\mathrm{sq}}·{\mathrm{I}}_{\mathrm{sd}}+{\mathrm{v}}_{\mathrm{sd}}·{\mathrm{I}}_{\mathrm{sq}}\\ {\mathrm{P}}_{\mathrm{r}}={\mathrm{v}}_{\mathrm{rd}}·{\mathrm{I}}_{\mathrm{rd}}+{\mathrm{v}}_{\mathrm{rq}}·{\mathrm{I}}_{\mathrm{rq}}\\ {\mathrm{Q}}_{\mathrm{r}}={\mathrm{v}}_{\mathrm{rq}}·{\mathrm{I}}_{\mathrm{rd}}+{\mathrm{v}}_{\mathrm{rd}}·{\mathrm{I}}_{\mathrm{rq}}\end{array}$$

(5)

• Converters Model

The DC-Bus in Figure 1 illustrates the structure [22,26,27].

The following equations characterize the continuous bus:

$$\{\begin{array}{c}{\mathrm{W}}_{\mathrm{dc}}={\displaystyle \int }{\mathrm{P}}_{\mathrm{c}}·\mathrm{d}\mathrm{t}=\frac{1}{2}·\mathrm{C}·{\mathrm{V}}_{\mathrm{dc}}^2\\ \frac{\mathrm{d}{\mathrm{V}}_{\mathrm{dc}}^2}{\mathrm{dt}}=\frac{2}{\mathrm{C}}\left({\mathrm{P}}_{\mathrm{f}}-{\mathrm{P}}_{\mathrm{r}}\right)\end{array}$$

(6)

• Filter (RL) Model

The filter model in the park reference is:

$$\{\begin{array}{c}{\mathrm{v}}_{\mathrm{df}}=-{\mathrm{R}}_{\mathrm{f}}·{\mathrm{I}}_{\mathrm{df}}-{\mathrm{L}}_{\mathrm{f}}·\frac{{\mathrm{dI}}_{\mathrm{df}}}{\mathrm{dt}}+{\mathsf{\omega }}_{\mathrm{s}}·{\mathrm{L}}_{\mathrm{f}}·{\mathrm{I}}_{\mathrm{qf}}\\ {\mathrm{v}}_{\mathrm{qf}}=-{\mathrm{R}}_{\mathrm{f}}·{\mathrm{I}}_{\mathrm{qf}}-{\mathrm{L}}_{\mathrm{f}}·\frac{{\mathrm{dI}}_{\mathrm{qf}}}{\mathrm{dt}}-{\mathsf{\omega }}_{\mathrm{s}}·{\mathrm{L}}_{\mathrm{f}}·{\mathrm{I}}_{\mathrm{df}}+{\mathrm{v}}_{\mathrm{s}}\end{array}$$

(7)

3. Sliding Mode Control

The objective of the SMC control technique is to drive the path of the system state to reach the sliding surface for a period of time.

The evolution of a system subjected to a control rule is no longer determined by the system or external perturbations but by the sliding surface’s attributes. As a result, the system will be robust to uncertainty (system specific) and disruptions (system wide), as the control entirely rejects them.

Sliding mode control’s purpose is to synthesize a surface S(x,t) such that all system trajectories exhibit the appropriate tracking, control, and stability behavior. Additionally, the purpose is to determine a control rule (switching) U(x,t) capable of attracting and maintaining all state trajectories on the sliding surface.

Three complimentary processes comprise the design of the sliding mode control algorithm.

❖

The choice of the sliding surface

Because the sliding surface is a scalar function, the error of the controlled variable slides along it and tends to the phase plane’s origin. As a result, the surface S(x) denotes the system’s desired dynamic behavior [28,29,30].

The sliding surface proposed is:

$$\mathrm{S}\left(\mathrm{x}\right)={\left(\frac{\mathrm{d}}{\mathrm{dt}}+\mathsf{\delta }\right)}^{\mathrm{r}-1}\times \mathrm{e}\left(\mathrm{x}\right)$$

(8)

This control’s purpose is to keep the surface S(x) trending toward zero. The latter is a linear differential equation with a unique solution of e(x) = 0 when the parameter δ is chosen appropriately.

With the following:

$\mathsf{\delta }$: Positive gain that interprets the bandwidth of the desired control;

e(x): the deviation on the variable to be controlled e(x) = xd − x;

r: relative degree, the smallest positive integer representing the number of times it is necessary to derive to make the control appear.

❖

The establishment of the existence condition

The existence and convergence conditions specify the conditions under which the system’s dynamics converge to the sliding surface and remain stationary in the presence of disturbances. One way of determining the stability of the sliding mode control is based on LYAPUNOV’s second theorem.

❖

The determination of the control law

The control rule must be determined once the sliding surface and convergence criterion are specified. Its goal is to confine the system’s state trajectories to reach and then remain on the sliding surface notwithstanding the existence of uncertainty. In other words, the control law must be attractive to the sliding surface on a local level [31,32,33,34].

3.1. Control of the Converter on the DFIG RSC Side

For r = 1, the active and reactive power slip area is given by:

$$\{\begin{array}{c}\mathrm{S}\left({\mathrm{P}}_{\mathrm{s}}\right)={\mathrm{e}}_1={\mathrm{P}}_{\mathrm{sref}}-{\mathrm{P}}_{\mathrm{s}}\\ \mathrm{S}\left({\mathrm{Q}}_{\mathrm{s}}\right)={\mathrm{e}}_2={\mathrm{Q}}_{\mathrm{sref}}-{\mathrm{Q}}_{\mathrm{s}}\end{array}$$

(9)

The following equation expresses the derivative of this surface:

$$\{\begin{array}{c}\mathrm{S}({\dot{\mathrm{P}}}_{\mathrm{s}})={\dot{\mathrm{e}}}_1={\dot{\mathrm{P}}}_{\mathrm{sref}}-{\dot{\mathrm{P}}}_{\mathrm{s}}\\ \mathrm{S}({\dot{\mathrm{Q}}}_{\mathrm{s}})={\dot{\mathrm{e}}}_2={\dot{\mathrm{Q}}}_{\mathrm{sref}}-{\dot{\mathrm{Q}}}_{\mathrm{s}}\end{array}$$

(10)

With:

$${\dot{\mathrm{P}}}_{\mathrm{s}}=-\frac{{\mathrm{v}}_{\mathrm{s}}·\mathrm{M}}{{\mathrm{L}}_{\mathrm{s}}}{\dot{\mathrm{I}}}_{\mathrm{rq}}$$

(11)

$${\dot{\mathrm{Q}}}_{\mathrm{s}}=\frac{{\mathrm{v}}_{\mathrm{s}}^2}{{\mathsf{\omega }}_{\mathrm{s}}·{\mathrm{L}}_{\mathrm{s}}}-\frac{{\mathrm{v}}_{\mathrm{s}}·\mathrm{M}}{{\mathrm{L}}_{\mathrm{s}}}{\dot{\mathrm{I}}}_{\mathrm{rd}}$$

(12)

$${\dot{\mathrm{I}}}_{\mathrm{rd}}=\frac{{\mathrm{V}}_{\mathrm{rd}}}{{\mathrm{L}}_{\mathrm{r}}·\mathsf{\sigma }}-\frac{{\mathrm{R}}_{\mathrm{r}}}{{\mathrm{L}}_{\mathrm{r}}·\mathsf{\sigma }}·{\mathrm{I}}_{\mathrm{rd}}+{\mathsf{\omega }}_{\mathrm{r}}·{\mathrm{I}}_{\mathrm{rq}}$$

(13)

$${\dot{\mathrm{I}}}_{\mathrm{rq}}=\frac{{\mathrm{V}}_{\mathrm{rq}}}{{\mathrm{L}}_{\mathrm{r}}·\mathsf{\sigma }}-\frac{{\mathrm{R}}_{\mathrm{r}}}{{\mathrm{L}}_{\mathrm{r}}·\mathsf{\sigma }}·{\mathrm{I}}_{\mathrm{rq}}-{\mathsf{\omega }}_{\mathrm{r}}·{\mathrm{I}}_{\mathrm{rd}}-{\mathsf{\omega }}_{\mathrm{r}}·\frac{\mathrm{M}·{\mathrm{V}}_{\mathrm{s}}}{{\mathrm{L}}_{\mathrm{r}}·{\mathrm{L}}_{\mathrm{s}}·\mathsf{\sigma }·{\mathsf{\omega }}_{\mathrm{s}}}$$

(14)

The derivative of the sliding surface is given by:

$$\{\begin{array}{c}{\dot{\mathrm{e}}}_1={\dot{\mathrm{P}}}_{\mathrm{sref}}+\frac{{\mathrm{V}}_{\mathrm{s}}·\mathrm{M}}{{\mathrm{L}}_{\mathrm{s}}}(\frac{{\mathrm{V}}_{\mathrm{rq}}}{{\mathrm{L}}_{\mathrm{r}}·\mathsf{\sigma }}-\frac{{\mathrm{R}}_{\mathrm{r}}}{{\mathrm{L}}_{\mathrm{r}}·\mathsf{\sigma }}{\mathrm{I}}_{\mathrm{rq}}-{\mathsf{\omega }}_{\mathrm{r}}{\mathrm{I}}_{\mathrm{rd}}-{\mathsf{\omega }}_{\mathrm{r}}{\mathrm{V}}_{\mathrm{s}}\frac{\mathrm{M}}{{\mathrm{L}}_{\mathrm{r}}·{\mathrm{L}}_{\mathrm{s}}·{\mathsf{\omega }}_{\mathrm{s}}·\mathsf{\sigma }})\\ {\dot{\mathrm{e}}}_2={\dot{\mathrm{Q}}}_{\mathrm{sref}}+\frac{{\mathrm{V}}_{\mathrm{s}}·\mathrm{M}}{{\mathrm{L}}_{\mathrm{s}}}(\frac{{\mathrm{V}}_{\mathrm{rd}}}{{\mathrm{L}}_{\mathrm{r}}·\mathsf{\sigma }}-\frac{{\mathrm{R}}_{\mathrm{r}}}{{\mathrm{L}}_{\mathrm{r}}·\mathsf{\sigma }}{\mathrm{I}}_{\mathrm{rd}}+{\mathsf{\omega }}_{\mathrm{r}}{\mathrm{I}}_{\mathrm{rq}})\end{array}$$

(15)

$$\{\begin{array}{c}{\mathrm{e}}_{1,2}=0\\ {\dot{\mathrm{e}}}_{1,2}=0\\ {\mathrm{V}}_{\mathrm{rdn}}={\mathrm{V}}_{\mathrm{rqn}}=0\end{array}$$

(16)

By replacing Equation (16) in Equation (15), the expression for the equivalent command ${\mathrm{V}}_{\mathrm{eq}}$ is as follows [14]:

$$\{\begin{array}{c}{\mathrm{V}}_{\mathrm{rdeq}}=-\frac{{\mathrm{L}}_{\mathrm{r}}·{\mathrm{L}}_{\mathrm{s}}·\mathsf{\sigma }}{\mathrm{M}·{\mathrm{V}}_{\mathrm{s}}}{\dot{\mathrm{Q}}}_{\mathrm{sref}}+{\mathrm{R}}_{\mathrm{r}}·{\mathrm{I}}_{\mathrm{rd}}-{\mathsf{\omega }}_{\mathrm{r}}·{\mathrm{L}}_{\mathrm{r}}·\mathsf{\sigma }·{\mathrm{I}}_{\mathrm{rq}}\\ {\mathrm{V}}_{\mathrm{rqeq}}=-\frac{{\mathrm{L}}_{\mathrm{r}}·{\mathrm{L}}_{\mathrm{s}}·\mathsf{\sigma }}{\mathrm{M}·{\mathrm{V}}_{\mathrm{s}}}{\dot{\mathrm{P}}}_{\mathrm{sref}}+{\mathrm{R}}_{\mathrm{r}}·{\mathrm{I}}_{\mathrm{rq}}+{\mathsf{\omega }}_{\mathrm{r}}·{\mathrm{L}}_{\mathrm{r}}·\mathsf{\sigma }·{\mathrm{I}}_{\mathrm{rd}}+{\mathsf{\omega }}_{\mathrm{r}}{\mathrm{V}}_{\mathrm{s}}\frac{\mathrm{M}}{{\mathrm{L}}_{\mathrm{s}}·{\mathsf{\omega }}_{\mathrm{s}}}\end{array}$$

(17)

The stabilizing control is [19]:

$$\{\begin{array}{c}{\mathrm{V}}_{\mathrm{rdn}}={\mathrm{K}}_{\mathrm{d}}·\mathrm{Sat}\left({\mathrm{e}}_1\right)\\ {\mathrm{V}}_{\mathrm{rqn}}={\mathrm{K}}_{\mathrm{q}}·\mathrm{Sat}\left({\mathrm{e}}_2\right)\end{array}$$

(18)

Hence, the expression for the total controls V_rd and V_rq is as follows:

$$\{\begin{array}{c}{\mathrm{V}}_{\mathrm{rd}}=-\frac{{\mathrm{L}}_{\mathrm{r}}·{\mathrm{L}}_{\mathrm{s}}·\mathsf{\sigma }}{\mathrm{M}·{\mathrm{V}}_{\mathrm{s}}}·{\dot{\mathrm{Q}}}_{\mathrm{sref}}+{\mathrm{R}}_{\mathrm{r}}·{\mathrm{I}}_{\mathrm{rd}}-{\mathsf{\omega }}_{\mathrm{r}}·{\mathrm{L}}_{\mathrm{r}}·\mathsf{\sigma }·{\mathrm{I}}_{\mathrm{rq}}+{\mathrm{K}}_{\mathrm{d}}\mathrm{Sat}\left({\mathrm{e}}_2\right)\\ \begin{array}{c}{\mathrm{V}}_{\mathrm{rq}}=-\frac{{\mathrm{L}}_{\mathrm{r}}·{\mathrm{L}}_{\mathrm{s}}·\mathsf{\sigma }}{\mathrm{M}·{\mathrm{V}}_{\mathrm{s}}}·{\dot{\mathrm{P}}}_{\mathrm{sref}}+{\mathrm{R}}_{\mathrm{r}}·{\mathrm{I}}_{\mathrm{rq}}+{\mathsf{\omega }}_{\mathrm{r}}·{\mathrm{L}}_{\mathrm{r}}·\mathsf{\sigma }·{\mathrm{I}}_{\mathrm{rd}}+{\mathsf{\omega }}_{\mathrm{r}}·\mathrm{M}·\frac{{\mathrm{V}}_{\mathrm{s}}}{{\mathrm{L}}_{\mathrm{s}}·{\mathsf{\omega }}_{\mathrm{s}}}+{\mathrm{K}}_{\mathrm{q}}\mathrm{Sat}\left({\mathrm{e}}_1\right)\end{array}\end{array}$$

(19)

3.2. Control of the Converter on the GSC Grid Sid

We consider the sliding mode surface proposed by SLOTINE. For r = 1, we obtain the following equation [33,34,35]:

$$\{\begin{array}{c}\mathrm{S}\left({\mathrm{P}}_{\mathrm{f}}\right)={\mathrm{e}}_3={\mathrm{P}}_{\mathrm{fref}}-{\mathrm{P}}_{\mathrm{f}}\\ \mathrm{S}\left({\mathrm{Q}}_{\mathrm{f}}\right)={\mathrm{e}}_4={\mathrm{Q}}_{\mathrm{fref}}-{\mathrm{Q}}_{\mathrm{f}}\end{array}$$

(20)

The following equation gives the derivative of the sliding surface [36]:

$$\{\begin{array}{c}{\dot{\mathrm{e}}}_3={\dot{\mathrm{P}}}_{\mathrm{sref}}+\frac{{\mathrm{V}}_{\mathrm{s}}·{\mathrm{R}}_{\mathrm{f}}}{{\mathrm{L}}_{\mathrm{f}}}{\mathrm{I}}_{\mathrm{qf}}+\frac{{\mathrm{V}}_{\mathrm{s}}\left({\mathrm{V}}_{\mathrm{qfeq}}+{\mathrm{V}}_{\mathrm{qfn}}\right)}{{\mathrm{L}}_{\mathrm{f}}}+{\mathsf{\omega }}_{\mathrm{s}}·{\mathrm{V}}_{\mathrm{s}}·{\mathrm{I}}_{\mathrm{df}}-\frac{{\mathrm{V}}_{\mathrm{s}}^2}{{\mathrm{L}}_{\mathrm{f}}}\\ {\dot{\mathrm{e}}}_4={\dot{\mathrm{Q}}}_{\mathrm{sref}}-\frac{{\mathrm{V}}_{\mathrm{s}}·{\mathrm{R}}_{\mathrm{f}}}{{\mathrm{L}}_{\mathrm{f}}}{\mathrm{I}}_{\mathrm{df}}-\frac{{\mathrm{V}}_{\mathrm{s}}\left({\mathrm{V}}_{\mathrm{dfeq}}+{\mathrm{V}}_{\mathrm{dfn}}\right)}{{\mathrm{L}}_{\mathrm{f}}}+{\mathsf{\omega }}_{\mathrm{s}}·{\mathrm{V}}_{\mathrm{s}}·{\mathrm{I}}_{\mathrm{qf}}\end{array}$$

(21)

With:

$$\{\begin{array}{c}{\mathrm{V}}_{\mathrm{dfeq}}=\frac{{\mathrm{L}}_{\mathrm{f}}}{{\mathrm{V}}_{\mathrm{s}}}{\dot{\mathrm{Q}}}_{\mathrm{sref}}-{\mathrm{R}}_{\mathrm{f}}·{\mathrm{I}}_{\mathrm{df}}+{\mathrm{L}}_{\mathrm{f}}·{\mathsf{\omega }}_{\mathrm{s}}·{\mathrm{I}}_{\mathrm{qf}}\\ {\mathrm{V}}_{\mathrm{qfeq}}=\frac{{\mathrm{L}}_{\mathrm{f}}}{{\mathrm{V}}_{\mathrm{s}}}{\dot{\mathrm{P}}}_{\mathrm{sref}}-{\mathrm{R}}_{\mathrm{f}}·{\mathrm{I}}_{\mathrm{qf}}-{\mathrm{L}}_{\mathrm{f}}·{\mathsf{\omega }}_{\mathrm{s}}·{\mathrm{I}}_{\mathrm{df}}+{\mathrm{V}}_{\mathrm{s}}\end{array}$$

(22)

The following equation expresses the stabilizing control:

$$\{\begin{array}{c}{\mathrm{V}}_{\mathrm{dfn}}={\mathrm{K}}_{\mathrm{dfn}}·\mathrm{Sat}\left({\mathrm{e}}_4\right)\\ {\mathrm{V}}_{\mathrm{qfn}}={\mathrm{K}}_{\mathrm{qfn}}·\mathrm{Sat}\left({\mathrm{e}}_3\right)\end{array}$$

(23)

With:

$$\{\begin{array}{c}{\mathrm{V}}_{\mathrm{fd}}=-\frac{{\mathrm{L}}_{\mathrm{f}}}{{\mathrm{V}}_{\mathrm{s}}}·{\dot{\mathrm{Q}}}_{\mathrm{fref}}-{\mathrm{R}}_{\mathrm{f}}·{\mathrm{I}}_{\mathrm{df}}+{\mathsf{\omega }}_{\mathrm{s}}·{\mathrm{L}}_{\mathrm{f}}·{\mathrm{I}}_{\mathrm{qf}}+{\mathrm{K}}_{\mathrm{dfn}}\mathrm{Sat}\left({\mathrm{e}}_4\right)\\ \begin{array}{c}{\mathrm{V}}_{\mathrm{fq}}=-\frac{{\mathrm{L}}_{\mathrm{f}}}{{\mathrm{V}}_{\mathrm{s}}}·{\dot{\mathrm{P}}}_{\mathrm{fref}}-{\mathrm{R}}_{\mathrm{f}}·{\mathrm{I}}_{\mathrm{qf}}-{\mathsf{\omega }}_{\mathrm{s}}·{\mathrm{L}}_{\mathrm{f}}·{\mathrm{I}}_{\mathrm{df}}+{\mathrm{V}}_{\mathrm{s}}+{\mathrm{K}}_{\mathrm{qfn}}\mathrm{Sat}\left({\mathrm{e}}_3\right)\end{array}\end{array}$$

(24)

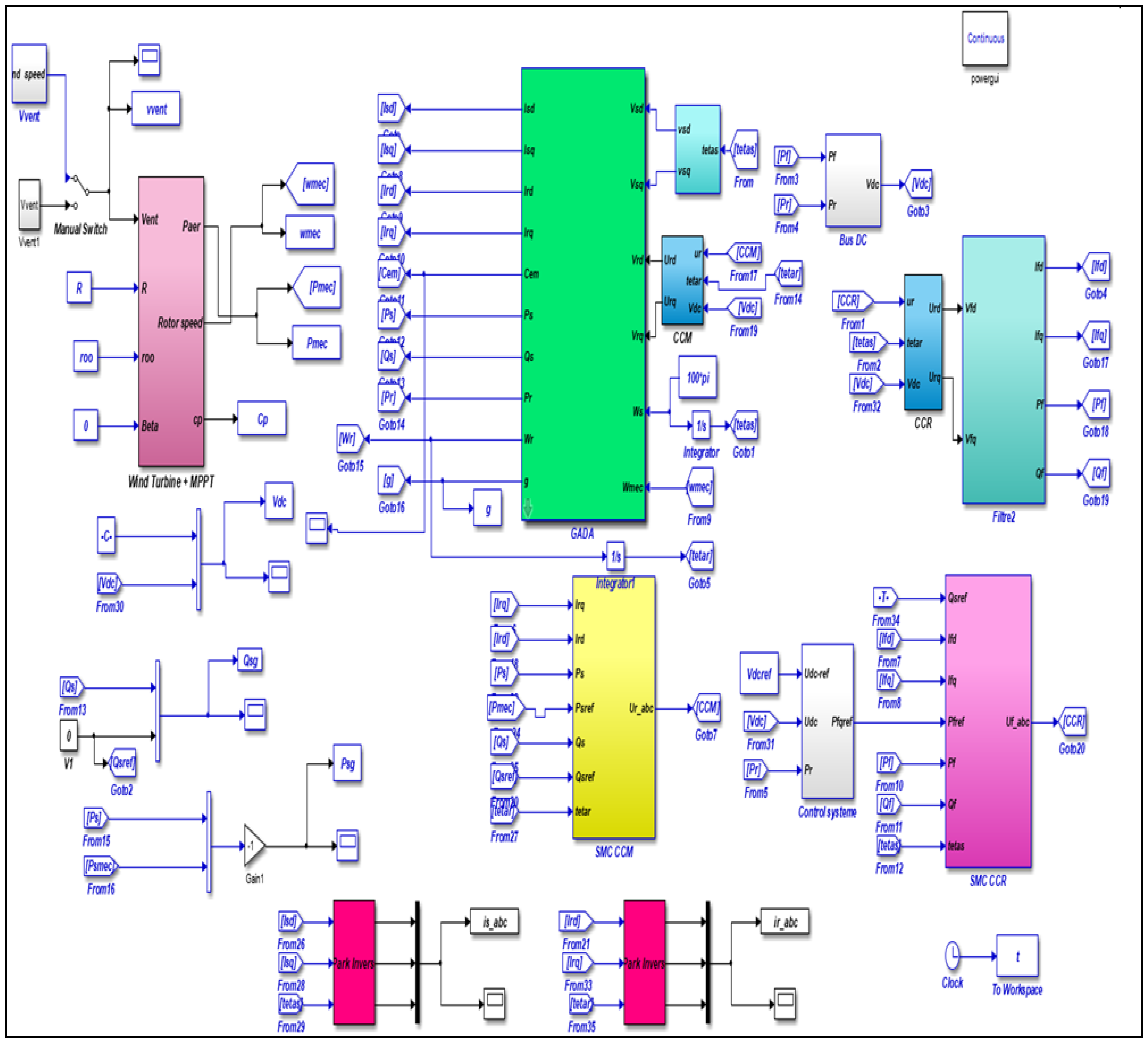
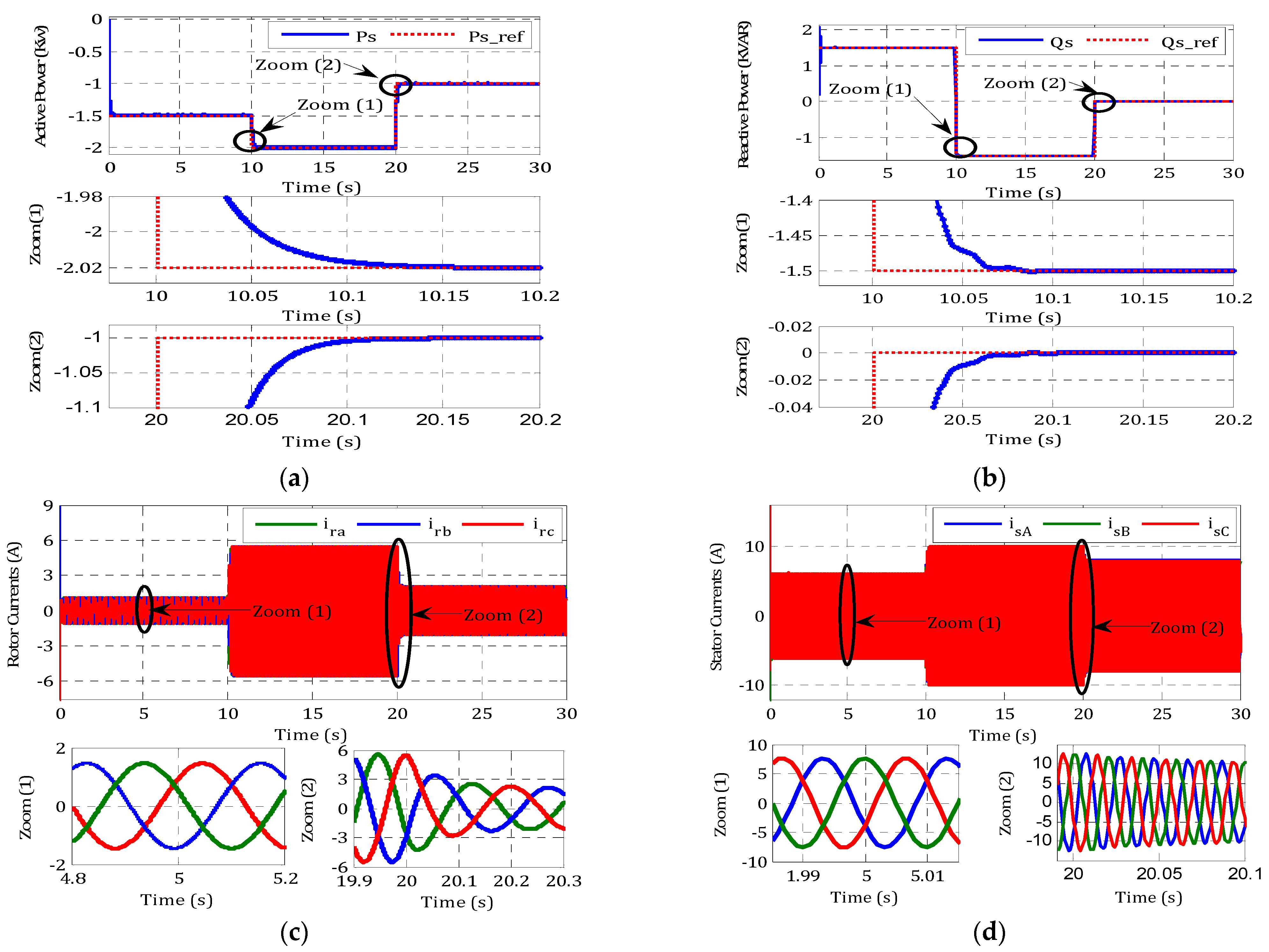
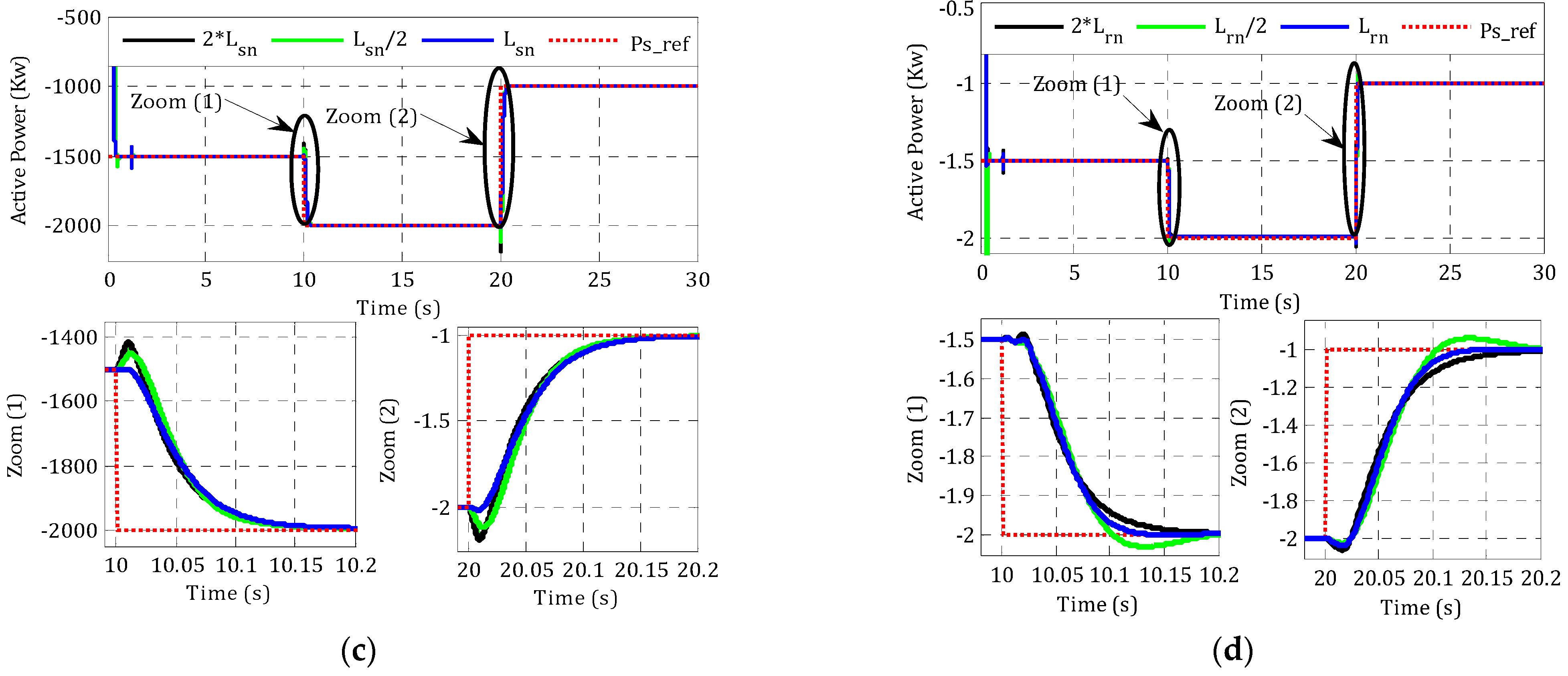
4. Results and Simulation

The tracking and robustness tests were carried out on Matlab and Simulink in order to validate the proposed model. To evaluate the performance of sliding mode control applied to a grid-connected wind power system, FPGA in the Loop was carried out.

In order to verify the results obtained by the simulations, FPGA in the Loop was proposed (Figure 2), which is realized with a co-simulation by the FPGA Nexys 4 DDR target. The machine’s model realized in Matlab/Simulink was converted into a digital model in order to facilitate the generation of the VHDL code using the “System Generator” tool. The sampling period used is of the order Ts = 5 μs, and the frequency linked to the FPGA is 50 MHz (

Table A1. The DFIG and wind turbine parameters.

DFIG Generator			Wind Turbine
Parameters	Symbol	Values	Parameters	Symbol	Values
Power Generator	Ps	1.5 KW	Radius of the turbine blade	R	20 m
Stator Resistance	Rs	4.85 Ω	Specific density of air	ρ	1.22 kg/m3
Rotor Resistance	Rr	3.805 Ω	Tip-speed ratio	λopt	8
Stator Inductance	Ls	274 mH	Optimal power coefficient	Cp	0.45
Rotor Inductance	Lr	258 mH

).

4.1. Real Wind Profile

The wind profile used for these tests is wind data from the Dakhla Morocco site (Figure 3).

We remark that the generator well follows the references of the powers without overshoot and with an almost null error.

Figure 4 present the THD for current and voltage.

The THD is clearly (6.29%) at the level of the rotor current, for only (0.16%) at the level of the stator current.

4.2. Step Wind Profile

Step references are applied to the active and reactive power of the system (Figure 5).

The results in Figure 6 show the following:

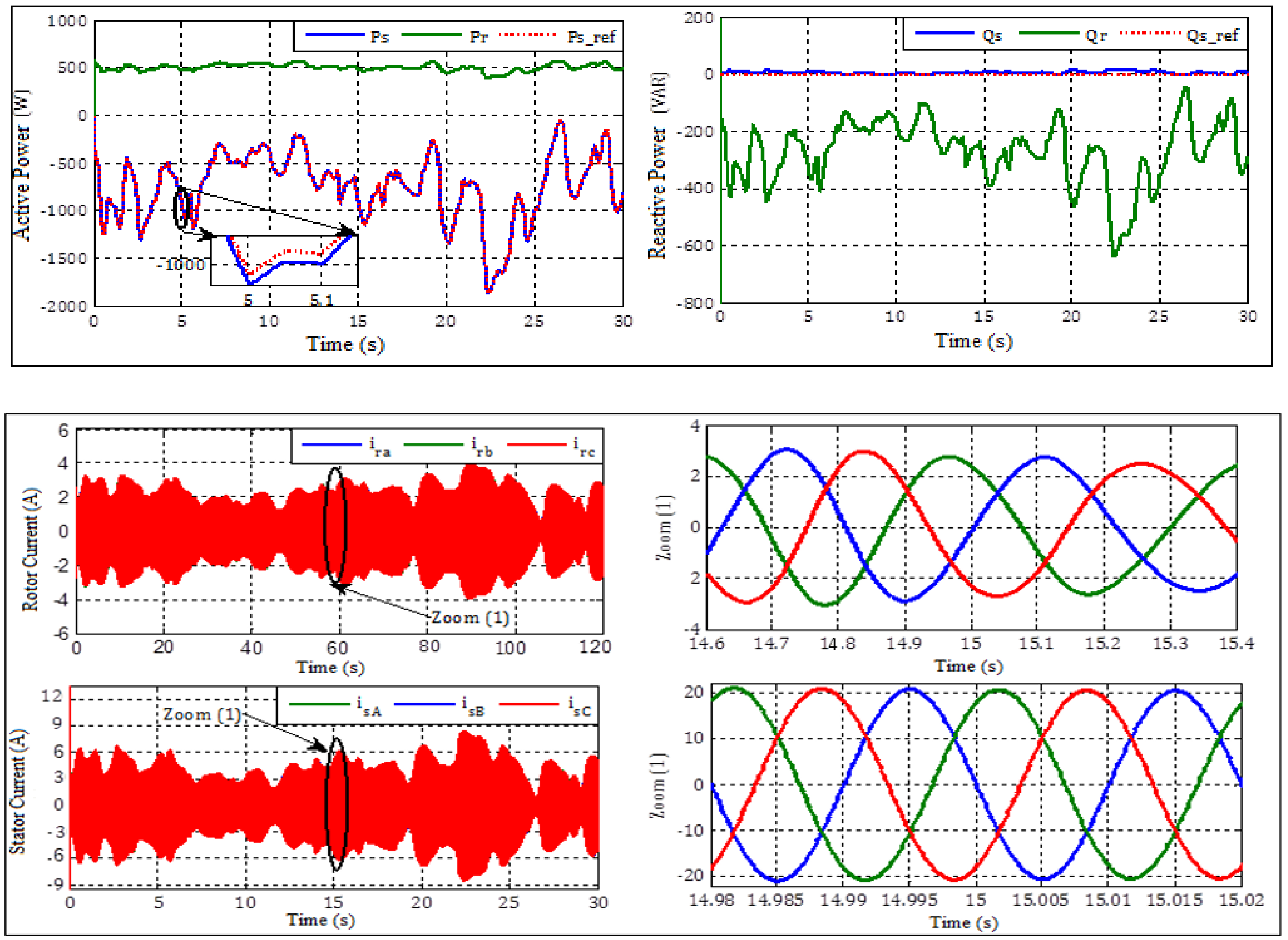
• Better monitoring of active and reactive power.
• Better power factor due to improved reactive power.
• Very good performance monitoring with the references with an error of 0.067%.
• Better responses of the currents Is and Ir despite the variation imposed by the torque.
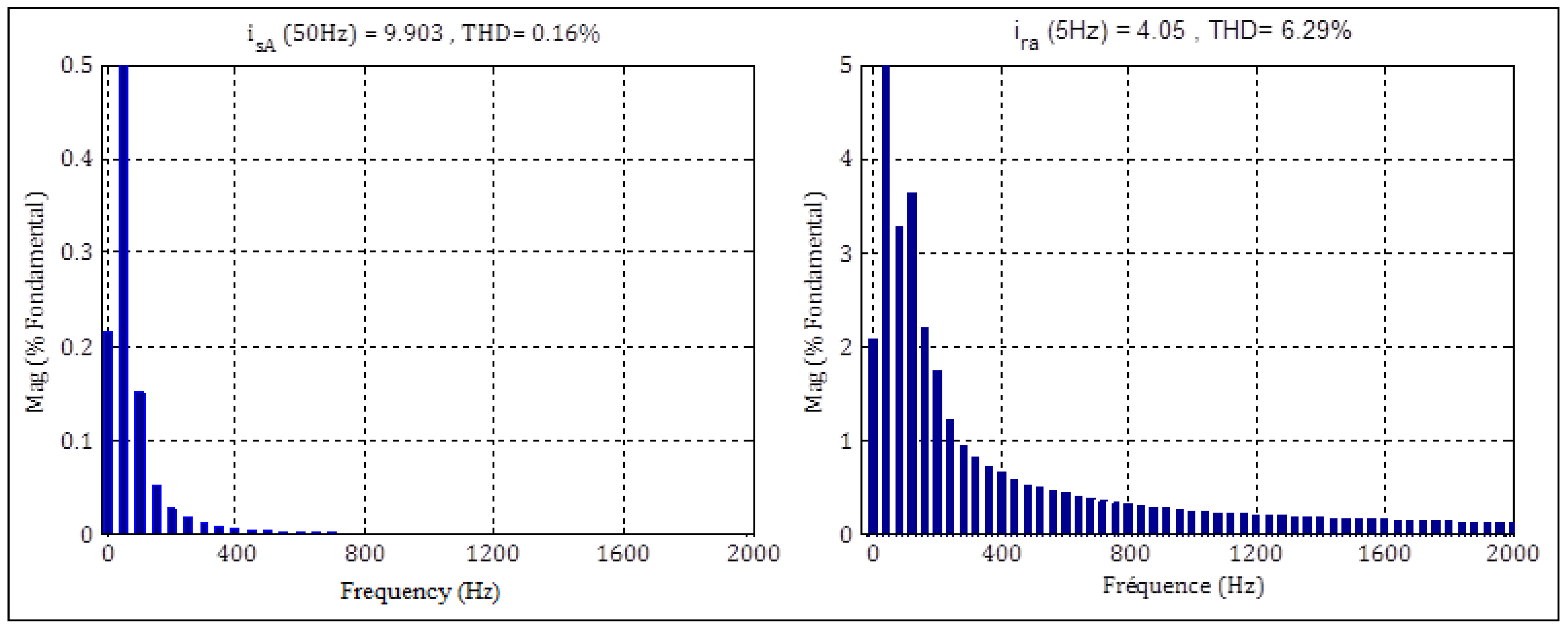
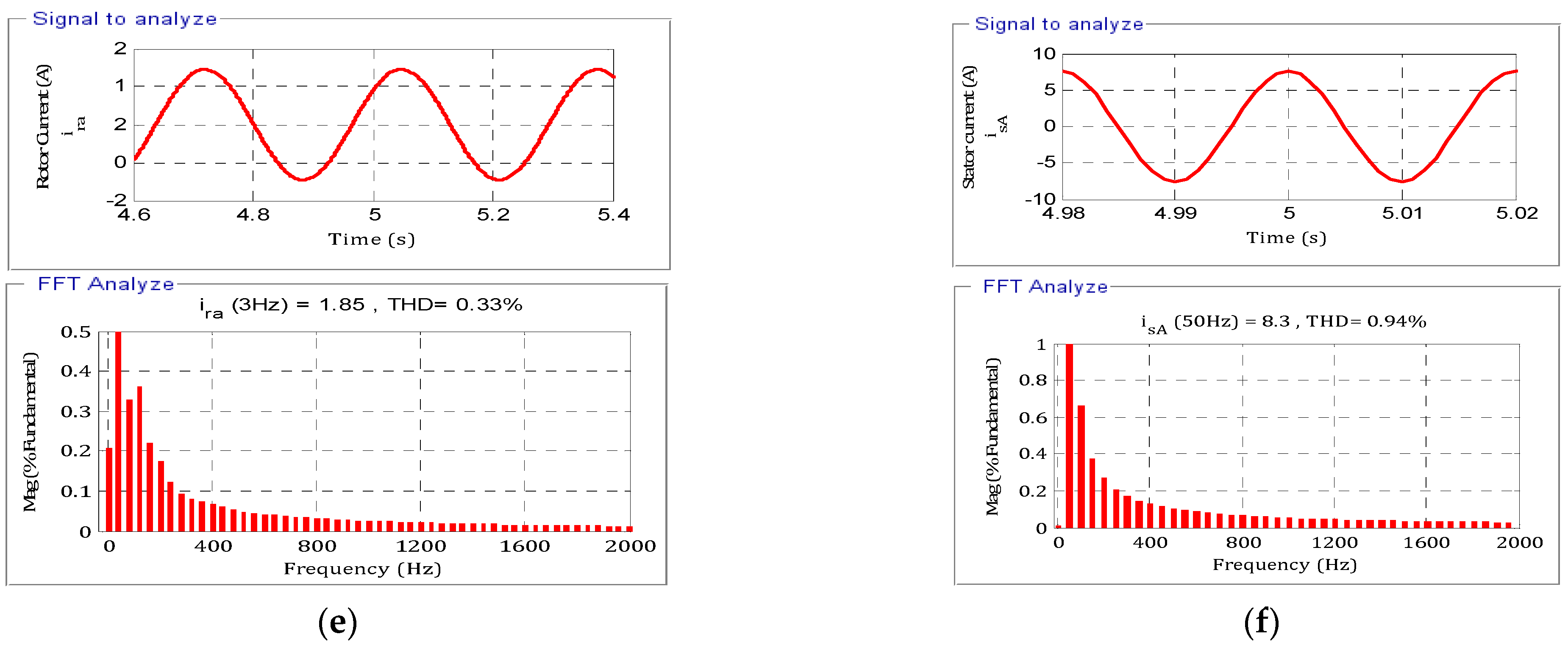
• The form of the current is sinusoidal with a frequency of 50 Hz for the stator current and 3 Hz for the rotor current.
• The THD is 0.33% for the current Ir and is 0.94% for the current Is.

To demonstrate the advantages and the superiority of the proposed control it is interesting to compare it with other techniques in the literature. It is noted here that these techniques were not performed under the same conditions because it is really rare to find many works done under similar conditions. From

Table 1. Comparison with technical control.

Publication Paper	Technical Methods	Response Time(s)	Error (%)	THD (%)
[27]	Fuzzy SMC	0.32	-	-
[28]	PI	0.030	1.25	-
	RST	0.028	0.06	-
[26]	SMC based backstepping	0.05	-	2.98
[13]	DTC	0.12	-	18.8
	FSC	0.16	-	8.26
	MPDC	0.15	-	8.17
Proposed technique	Proposed sliding mode control	0.015	0.15	1.25

, it can be seen that the proposed control based offers a low total harmonic distortion (THD = 1.25%) compared with the other techniques. Additionally, it presents acceptable results in terms of rapidity and precision compared to other methods, which are characterized by Error = 0.15% and Tr = 0.015 s.

5. Conclusions

This work proposes an enhanced sliding mode control strategy to a variable wind speed-based DFIG-Generator. The performance of the control was verified through a co-simulation between the Matlab/Simulink environment and HIL-based FPGA. The simulation results and the comparative study confirmed that the proposed control is more suitable for a wind power conversion system based on the DFIG variable speed.