Bubble-Proof Algorithm for Wave Union TDCs
Abstract
:1. Introduction
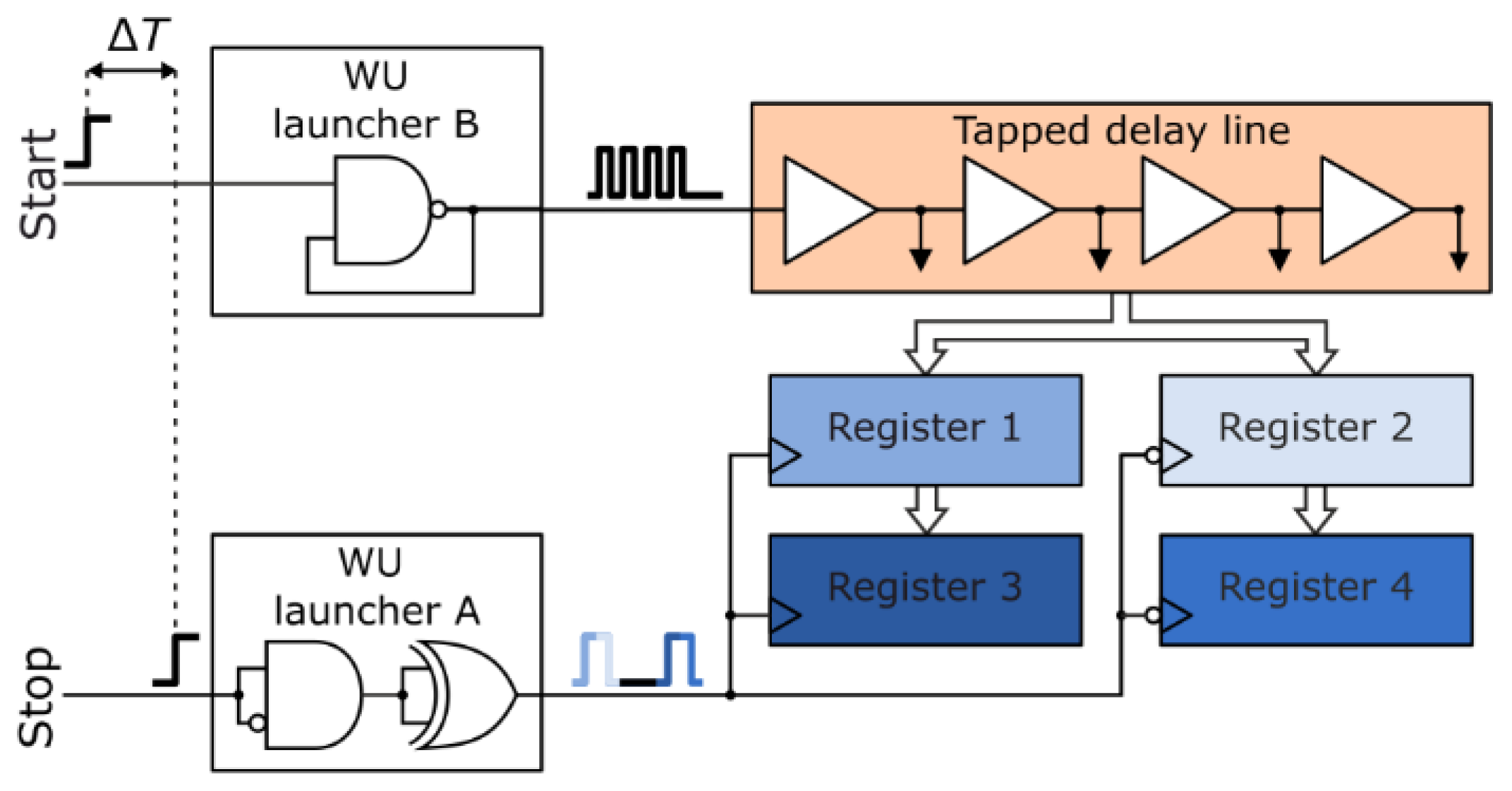
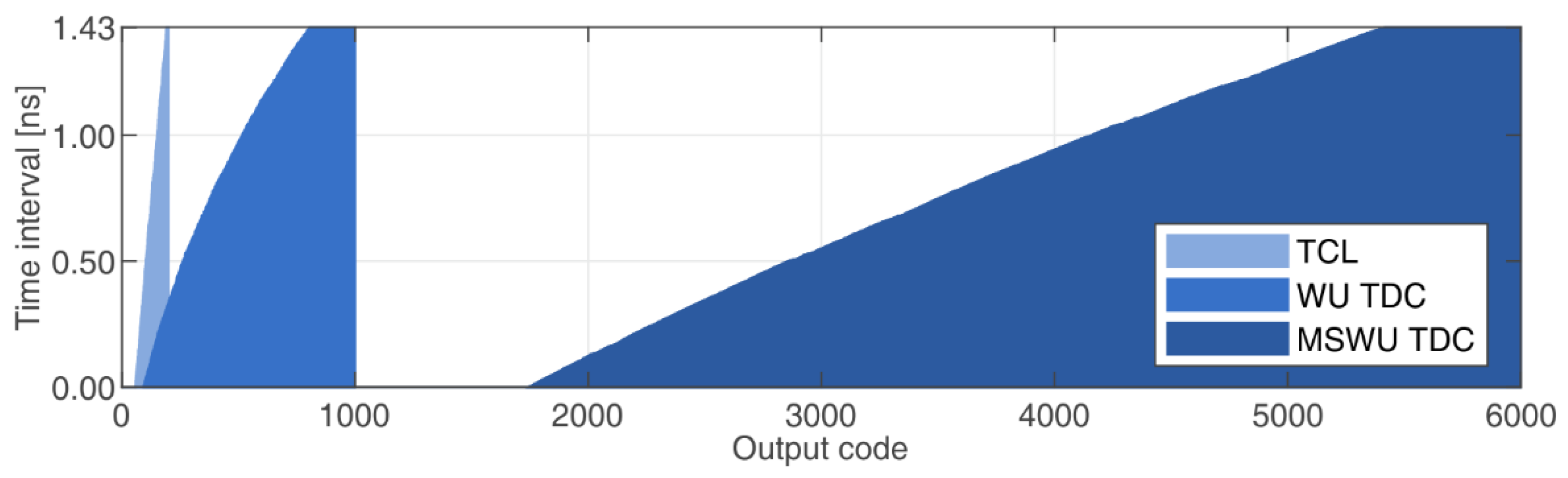
2. Multisampling Wave Union TDC
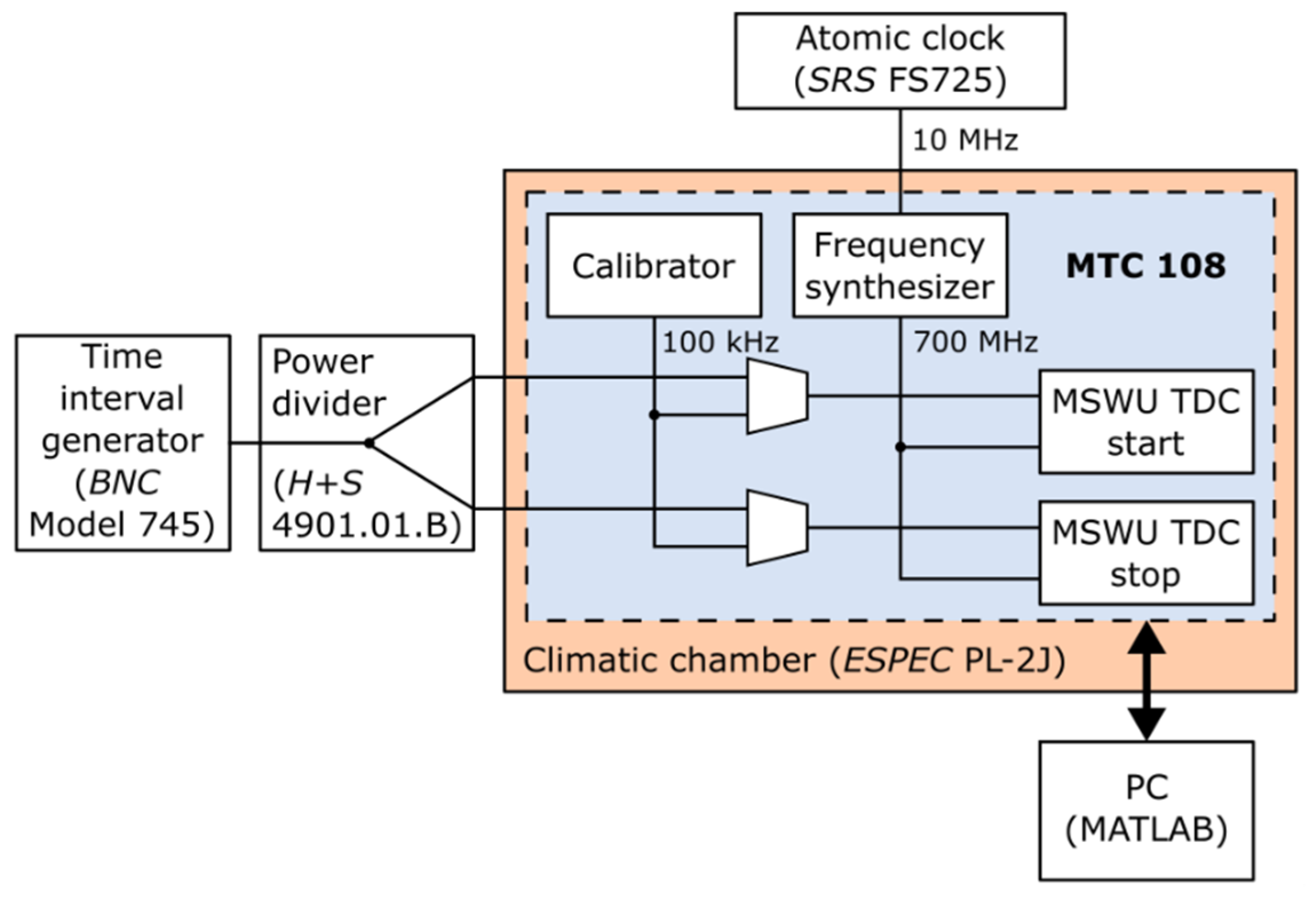
3. Test Setup
4. Encoding Algorithms
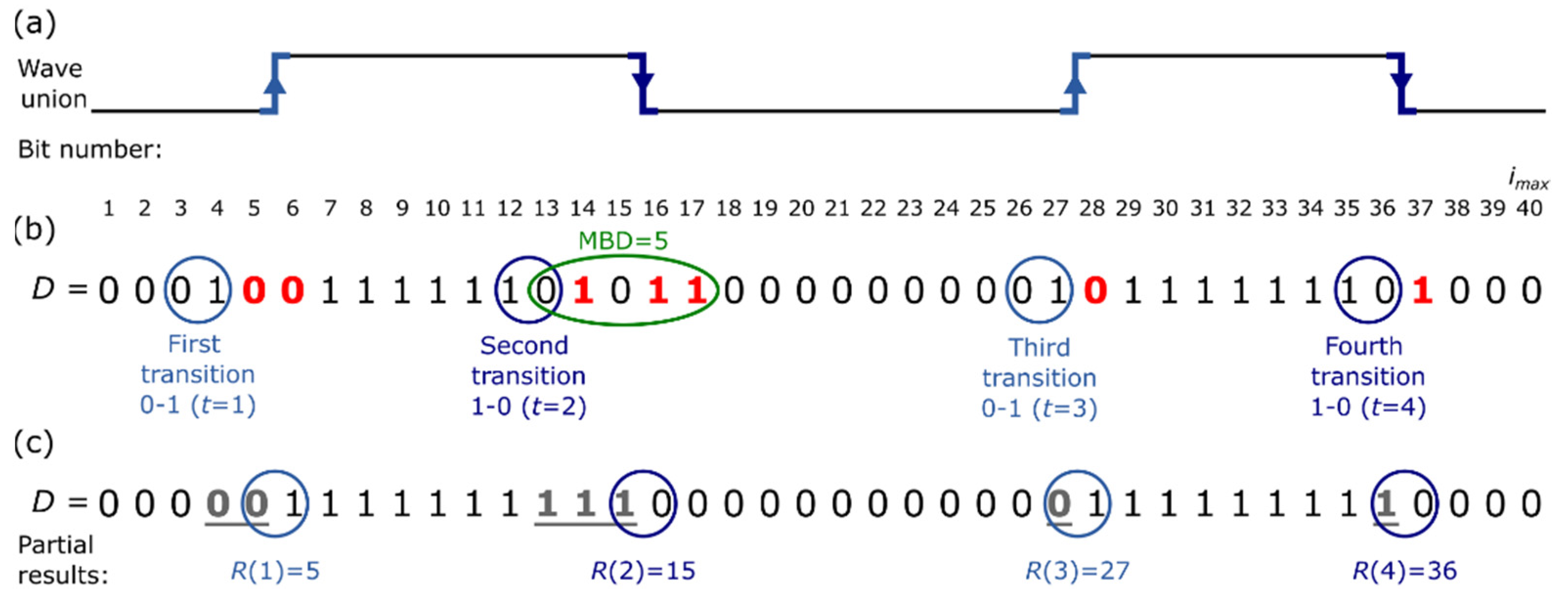
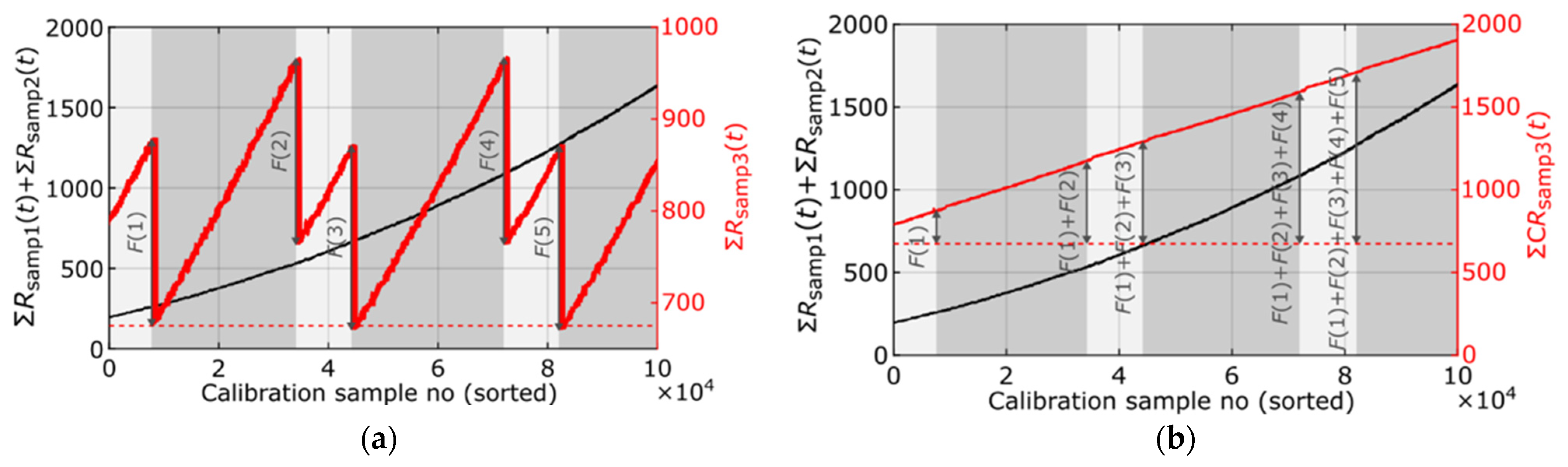
4.1. Pre-Encoder: Counter-Based
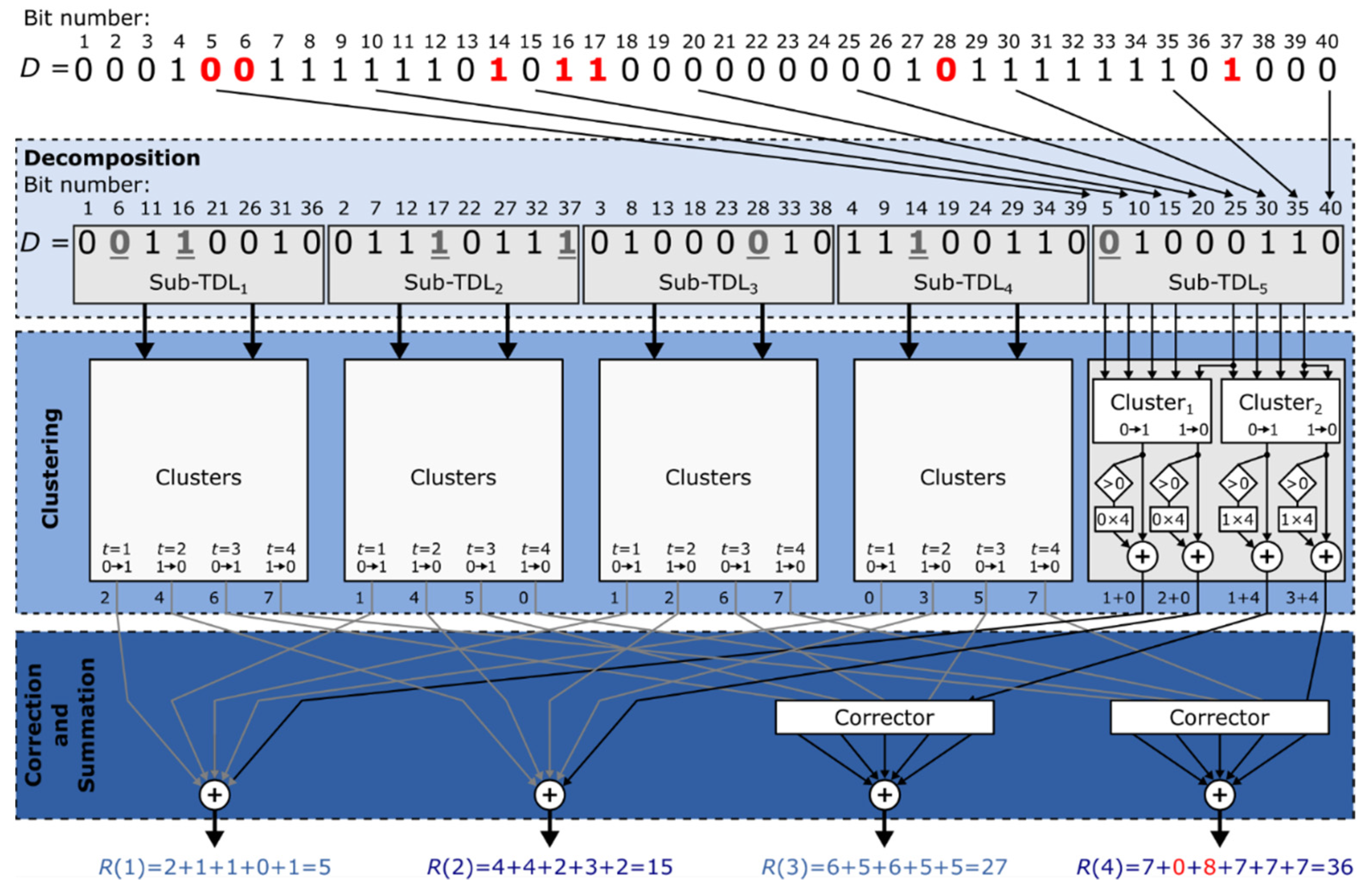
4.2. Pre-Encoder: Decomposition and Clustering-Based
4.3. Post-Encoder
5. Measurement Results
6. Discussions
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wu, J.; Shi, Z. The 10-ps wave union TDC: Improving FPGA TDC resolution beyond its cell delay. In Proceedings of the IEEE Nuclear Science Symposium Conference Record, Dresden, Germany, 19–25 October 2008; pp. 3440–3446. [Google Scholar]
- Neiser, A.; Adamczewski-Musch, J.; Hoek, M.; Koenig, W.; Korcyl, G.; Linev, S.; Maier, L.; Michael, J.; Palka, M.; Penschuck, M.; et al. TRB3: A 264 channel high precision TDC platform and its applications. J. Instrum. 2013, 8, C12043. [Google Scholar] [CrossRef]
- Zhang, W.; Sun, H.; Edwards, C.; Gong, D.; Huang, X.; Liu, C.; Liu, T.; Liu, T.; Olsen, J.; Sun, Q.; et al. A Low-Power Time-to-Digital Converter for the CMS Endcap Timing Layer (ETL) Upgrade. IEEE Trans. Nucl. Sci. 2021, 68, 1984–1992. [Google Scholar] [CrossRef]
- Szplet, R.; Sondej, D.; Grzęda, G. High-Precision Time Digitizer Based on Multiedge Coding in Independent Coding Lines. IEEE Trans. Instrum. Meas. 2016, 65, 1884–1894. [Google Scholar] [CrossRef]
- Xie, W.; Chen, H.; Zang, Z.; Li, D.D.-U. Multi-channel high-linearity time-to-digital converters in 20 nm and 28 nm FPGAs for LiDAR applications. In Proceedings of the 6th International Conference on Event-Based Control Communication and Signal Processing (EBCCSP), Krakow, Poland, 23–25 September 2020. [Google Scholar]
- Kwiatkowski, P.; Sondej, D.; Szplet, R. A brief review of wave union TDCs. In Proceedings of the 7th International Conference on Event-Based Control Communication and Signal Processing (EBCCSP), Krakow, Poland, 22–25 June 2021. [Google Scholar]
- Liu, C.; Wang, Y. A 128-Channel, 710 M Samples/Second, and Less than 10 ps RMS Resolution Time-to-Digital Converter Implemented in a Kintex-7 FPGA. IEEE Trans. Nucl. Sci. 2015, 62, 773–783. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, X.; Song, Z.; Kuang, J.; Cao, Q. A 3.0-ps rms precision 277-MSamples/s throughput time-to-digital converter using multi-edge encoding scheme in a Kintex-7 FPGA. IEEE Trans. Nucl. Sci. 2019, 66, 2275–2281. [Google Scholar] [CrossRef]
- Wu, J. Several Key Issues on Implementing Delay Line Based TDCs Using FPGAs. IEEE Trans. Nucl. Sci. 2010, 57, 1543–1548. [Google Scholar] [CrossRef]
- Säll, E.; Vesterbacka, M. A multiplexer based decoder for flash analog-to-digital converters. In Proceedings of the IEEE Region 10 Conference TENCON 2004, Chiang Mai, Thailand, 24 November 2004; pp. 250–253. [Google Scholar]
- Bayer, E.; Traxler, M. A high-resolution (<10 ps RMS) 48-channel time-to-digital converter (TDC) implemented in a field programmable gate array (FPGA) . IEEE Trans. Nucl. Sci. 2011, 58, 1547–1552. [Google Scholar] [CrossRef]
- Hu, X.; Zhao, L.; Liu, S.; Wang, J.; An, Q. A stepped-up tree encoder for the 10-ps wave union TDC. IEEE Trans. Nucl. Sci. 2013, 60, 3544–3549. [Google Scholar] [CrossRef]
- Wang, Y.; Kuang, J.; Liu, C.; Cao, Q. A 3.9-ps RMS Precision Time-to-Digital Converter Using Ones-counter Encoding Scheme in a Kintex-7 FPGA. IEEE Trans. Nucl. Sci. 2017, 64, 2713–2718. [Google Scholar] [CrossRef]
- Knittel, G. A Novel Encoder for TDCs. Appl. Reconfigurable Comput. (Lect. Notes Comput. Sci.) 2019, 11444, 48–57. [Google Scholar]
- Xie, W.; Chen, H.; Li, D.D.-U. Efficient time-to-digital converters in 20 nm FPGAs with wave union methods. IEEE Trans. Ind. Electron. 2021, 69, 1021–1031. [Google Scholar] [CrossRef]
- Garzetti, F.; Corna, N.; Lusardi, N.; Geraci, A. Time-to-Digital Converter IP-Core for FPGA at State of the Art. IEEE Access 2021, 9, 85515–85528. [Google Scholar] [CrossRef]
- Jiao, Y.; Zhang, Q.; Chen, W.; Zhou, L.; Chen, C. A resource-saving dual channel time-to-digital converter with shared tapped delay line in FPGAs. J. Instrum. 2021, 16, P01012. [Google Scholar] [CrossRef]
- Song, Z.; Wang, Y.; Kuang, J. A 256-channel, high throughput and precision time-to-digital converter with a decomposition encoding scheme in a Kintex-7 FPGA. J. Instrum. 2018, 13, P05012. [Google Scholar] [CrossRef]
- Chen, H.; Li, D.D.-U. Multichannel, Low Nonlinearity Time-to-Digital Converters Based on 20 and 28 nm FPGAs. IEEE Trans. Ind. Electron. 2019, 66, 3265–3274. [Google Scholar] [CrossRef] [Green Version]
- Sondej, D.; Szymanowski, R.; Szplet, R. Methods of precise determining the transfer characteristic of picosecond time-to-digital converters. Metrol. Meas. Syst. 2021, 28, 539–549. [Google Scholar]
- Kwiatkowski, P.; Szplet, R. Multisampling wave union time-to-digital converter. In Proceedings of the 6th International Conference on Event-Based Control Communication and Signal Processing (EBCCSP), Krakow, Poland, 23–25 September 2020. [Google Scholar]
- Szplet, R.; Kwiatkowski, P.; Różyc, K.; Jachna, Z.; Sondej, T. Picosecond-precision multichannel autonomous time and frequency counter. Rev. Sci. Instrum. 2017, 88, 125101. [Google Scholar] [CrossRef] [PubMed]
- Kalisz, R. Review of methods for time interval measurements with picosecond resolution. Metrologia 2004, 41, 17–32. [Google Scholar] [CrossRef] [Green Version]
- Rivoir, J. Statistical linearity calibration of time-to-digital converters using a free-running ring oscillator. In Proceedings of the 15th Asian Test Symposium, Fukuoka, Japan, 20–23 November 2006; pp. 1–6. [Google Scholar]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwiatkowski, P.; Sondej, D.; Szplet, R. Bubble-Proof Algorithm for Wave Union TDCs. Electronics 2022, 11, 30. https://doi.org/10.3390/electronics11010030
Kwiatkowski P, Sondej D, Szplet R. Bubble-Proof Algorithm for Wave Union TDCs. Electronics. 2022; 11(1):30. https://doi.org/10.3390/electronics11010030
Chicago/Turabian StyleKwiatkowski, Paweł, Dominik Sondej, and Ryszard Szplet. 2022. "Bubble-Proof Algorithm for Wave Union TDCs" Electronics 11, no. 1: 30. https://doi.org/10.3390/electronics11010030
APA StyleKwiatkowski, P., Sondej, D., & Szplet, R. (2022). Bubble-Proof Algorithm for Wave Union TDCs. Electronics, 11(1), 30. https://doi.org/10.3390/electronics11010030





